2. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001;
3. 西藏大学 工学院, 西藏 拉萨 850000;
4. 哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨 150001;
5. 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学), 工业和信息化部, 黑龙江 哈尔滨 150001;
6. 中国船舶工业系统工程研究院 水声对抗技术重点实验室, 北京 100036
2. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China;
3. College of Engineering, Tibet University, Lhasa, 850000, China;
4. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China;
5. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
6. National Key Laboratory of Science and Technology on Underwater Acoustic Antagonizing, China State Shipbuilding Corporation Systems Engineering Research Institute, Beijing 100036, China
随着海洋权益逐渐得到重视和水声工程技术的不断发展,海洋目标探测系统与信号处理技术逐渐成为水声技术研究的重点。水下目标探测技术的研究,对于海洋国土防卫具有重要的战略意义,海洋救援、海洋环境检测和海洋水下通信网络等对此也存在着广泛的应用需求[1-3]。
单个矢量水听器通常由1个声压传感器和2个(或3个)振速传感器组成,既能够测量声压信号,还可以共点同时输出质点振速信号,捕获比传统声压水听器更多的声场信息,获得更高的处理增益[4]。单个矢量水听器即具有偶极子指向性,仅依靠单个矢量水听器就可以在360°空间内估计目标方位[5]。
传统的矢量信号处理为平均声强器和复声强器。平均声强器算法简单,但是不能区分多目标。复声强器是一种频域处理方法,相对复杂,但是更加有效,能够区分多目标,尤其对于线谱目标具有良好的检测能力。此外,通过计算各个频点上不同坐标轴上信号分量大小,经过统计累积可以估计出目标方位。在矢量水听器发展的过程中研究人员相继提出了各种不同的单矢量水听器目标检测算法,但“复声强器”以其算法简单有效的特点,是在实际工程中应用最为广泛的方法[3-7]。
单个矢量水听器的空间指向性“太胖”,由此获得的空间增益有限。为了提高单个矢量水听器对线谱目标的探测能力,获得高分辨的方位估计结果,需要探索检测能力更强的处理技术。本文基于高斯白噪声环境背景[9-10],提出了单矢量水听器声压振速组合通道自适应增强和自适应抵消技术,将其分别应用于线谱检测和方位估计,使单矢量水听器的目标检测处理增益得到了提高,获得了高分辨的目标方位估计,具有一定的研究价值和工程应用前景。
1 信号测量模型与组合指向性 1.1 单矢量水听器的测量模型考虑在远场条件下,线谱声源平面波入射到单个矢量水听器(vector hydrophone, VH)上的测量模型[4],如图 1所示。

|
Download:
|
| 图 1 单矢量水听器测量模型 Fig. 1 A model of vector hydrophone measurement | |
二维矢量水听器共点测量并输出的声场声压和振速信息的表达式为[4]:
| $ \left\{ {\begin{array}{*{20}{l}} {p(t) = s(t)}\\ {{v_x}(t) = \frac{1}{{\rho c}}s(t){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {{v_y}(t) = \frac{1}{{\rho c}}s(t){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \end{array}} \right. $ | (1) |
式中θ为信号的水平入射角度。上式说明声压通道是无指向性的,振速通道具有偶极子指向性,且与入射信号频率无关。进一步通过不同通道间的组合,可以获得单矢量水听器的单边指向性。
1.2 组合指向性根据文献[4]所述,对声压通道和振速通道进行组合变换,能够获得单边指向性。首先组合2个正交的振速分量vx和vy,获得相互正交的偶极子指向性的组合振速vc和vs为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_c} = {\mathit{\boldsymbol{v}}_x}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi + {\mathit{\boldsymbol{v}}_y}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi = s(t){\rm{cos}}(\theta - \varphi )}\\ {{\mathit{\boldsymbol{v}}_s} = - {\mathit{\boldsymbol{v}}_x}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi + {\mathit{\boldsymbol{v}}_y}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi = s(t){\rm{sin}}(\theta - \varphi )} \end{array}} \right. $ | (2) |
式中:x(t)为目标源辐射声信号的波形;φ为引导方位, 是vc的主极大方向,也是vs的指向性零点。通过引导方向可以形成覆盖全空间的多波束,然后进行检测确定目标是否存在。
本文提出并应用的声压与振速组合形式为:
| $ {[p(t) + {\mathit{\boldsymbol{v}}_c}(t)]{\mathit{\boldsymbol{v}}_c}( - t) = {s^2}(t){B_c}(\theta )} $ | (3) |
和
| $ {[p(t) + {\mathit{\boldsymbol{v}}_c}(t)]{\mathit{\boldsymbol{v}}_s}( - t) = {s^2}(t){B_s}(\theta )} $ | (4) |
其中Bc(θ)和Bs(θ)定义为幅度归一化后的指向性函数:
| $ {{B_c}(\theta ) = {\rm{co}}{{\rm{s}}^2}\left( {\frac{{\theta - \varphi }}{2}} \right){\rm{cos}}(\theta - \varphi )} $ | (5) |
| $ {{B_s}(\theta ) = {\rm{co}}{{\rm{s}}^2}\left( {\frac{{\theta - \varphi }}{2}} \right){\rm{sin}}(\theta - \varphi )} $ | (6) |
式(5)和式(6)表示的都是单边指向性的方向图。Bc的方向性图的最大值对应的是Bs的零点。当一信号位于导向方位上时,此时由两路组合信号对消输出获得的残差能量最大。
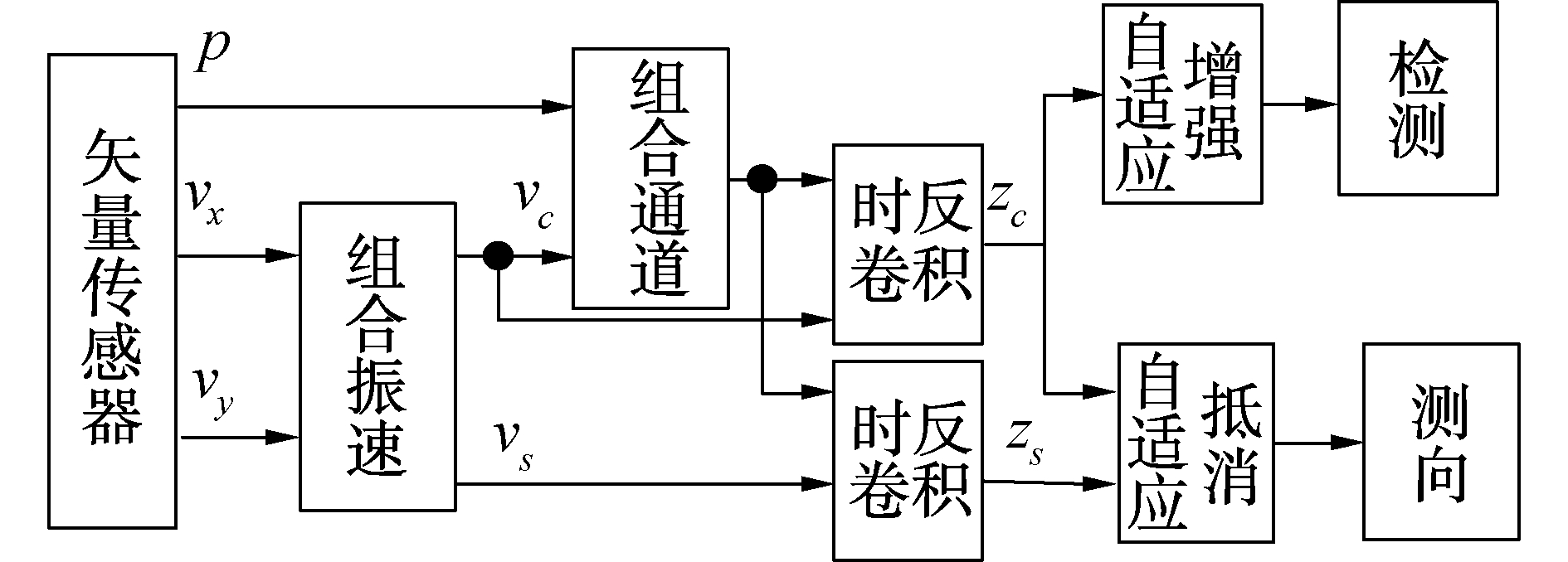
2 线谱检测与方位估计技术本文提出的单矢量组合通道间自适应增强与抵消用于线谱检测和目标方位估计方法的技术流程框图如图 2所示。
|
Download:
|
| 图 2 技术流程 Fig. 2 Flowchart of the proposed techniques | |
在海洋波导中目标信号的声压与振速是相关的,而各项同性环境干扰的声压和振速是不相关的或相关很弱[4]。据此提出了线谱信号时反卷积(time reversal convolution, TRC)的处理技术[5]。时反卷积计算上包括信号的时间反转和卷积运算。在高斯白噪声背景下,单矢量水听器在水下声场中的声压通道测量输出为:
| $ p(t) = s(t) + {n_p}(t) $ | (7) |
组合振速通道输出为:
| $ {{\mathit{\boldsymbol{v}}_c}(t) = s(t){\rm{cos}}(\theta - \varphi ) + {n_{vc}}(t)} $ | (8) |
| $ {{\mathit{\boldsymbol{v}}_s}(t) = s(t){\rm{sin}}(\theta - \varphi ) + {n_{vs}}(t)} $ | (9) |
式中假设矢量水听器不同通道之间的噪声互不相关,即np(t)、nvc(t)和nvs(t)是互不相关的白噪声。对于目标信号,声压通道和组合振速通道的时反卷积计算,就是互相关运算[11]:
| $ \begin{array}{*{20}{c}} {[p(t) + {\mathit{\boldsymbol{v}}_c}(t)]*{\mathit{\boldsymbol{v}}_c}( - t) = 2{R_s}(t) \cdot }\\ {{B_c}(\theta ,\varphi ) + \frac{1}{2}{R_n}(t) + {n_{{z_c}}}(t)} \end{array} $ | (10) |
式(10)中包括源信号的自相关函数与方向图的乘积、高斯白噪声的自相关函数以及运算过程中产生的交叉项噪声。对一个正弦信号s(t)时反卷积后得到:
| $ \begin{array}{*{20}{c}} {s(t)*s( - t) = \int\limits_{ - \infty }^\infty s (\tau )s(\tau - t){\rm{d}}\tau = }\\ {\frac{{{A^2}}}{2}{\rm{cos}}(\omega \tau ) = {R_{ss}}(\tau )} \end{array} $ | (11) |
式(11)说明线谱信号时反卷积输出是其自相关函数,且输出频率与原信号频率一样。由于噪声不相关的性质,不同通道噪声时反卷积输出的相关函数小,可以在一定程度上抵抗噪声。但仅靠时反卷积处理抵抗干扰的能力有限,必须再进一步进行后置处理。
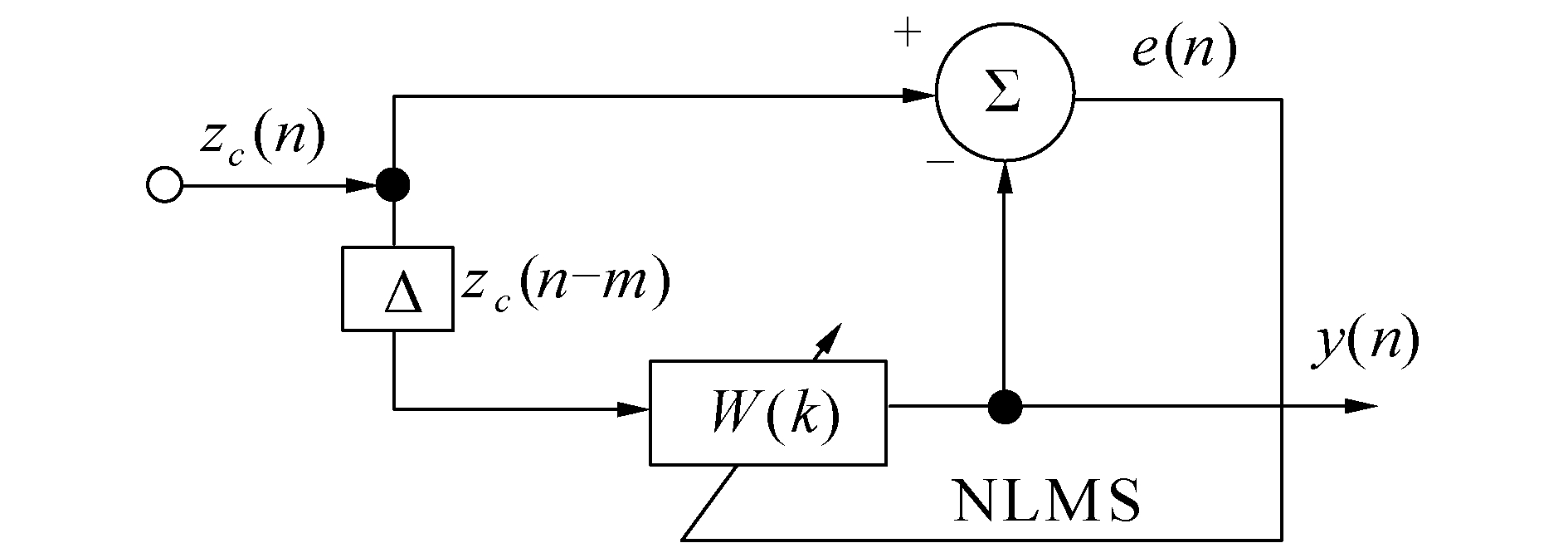
2.2 时反卷积输出后置自适应增强对于线谱信号,最有效的就是FFT线谱检测,本文提出对矢量水听器组合通道线谱信号进行自适应增强,在频域检测进行线谱检测,能够取得良好效果。图 3给出了自适应增强器的处理框图。
|
Download:
|
| 图 3 自适应线谱增强算法 Fig. 3 Block diagram of the adaptive line enhancement algorithm | |
自适应滤波器在最小均方(least mean square, LMS)准则下,根据输入调节权值,并作用于其中一路信号。之后两路信号相抵输出残差,对输入进行反馈,继续调整权值,逐步达到收敛平稳的状态。这里的zc(n)是zc(t)的离散采样信号:
| $ {\mathit{\boldsymbol{z}}_c}(t) = [p(t) + {\mathit{\boldsymbol{v}}_c}(t)]*{\mathit{\boldsymbol{v}}_c}( - t) $ | (12) |
根据前述单矢量组合通道指向性与输入信号和时间无关,且根据卷积的性质容易证得式(12)组合获得的指向性对应于式(5)。式中vc(-t)是为了获得时反增益。式(11)已经证得自相关对于单频信号的频率没有影响,不影响后续检测,而自相关之后不相关噪声会集中到输出函数的中心点上,将中心点或者中心附近几个点置零,可以对不相关噪声进行抑制。
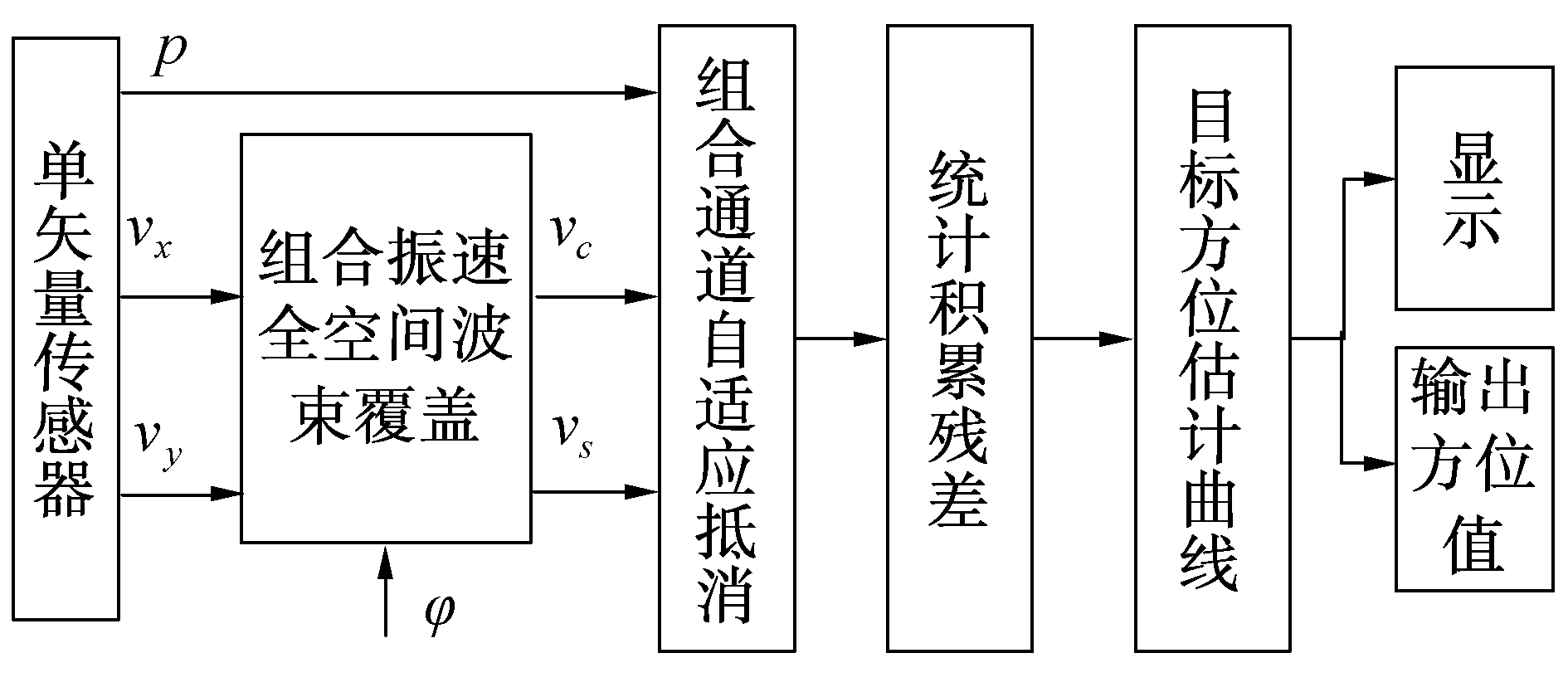
2.3 自适应对消与目标方位估计通过目标检测器确定目标存在后,需要进一步确定目标的方位。单矢量组合通道间自适应对消目标方位估计具体方法和原理,如图 4所示。
|
Download:
|
| 图 4 方位估计流程 Fig. 4 Flowchart of the azimuth estimation | |
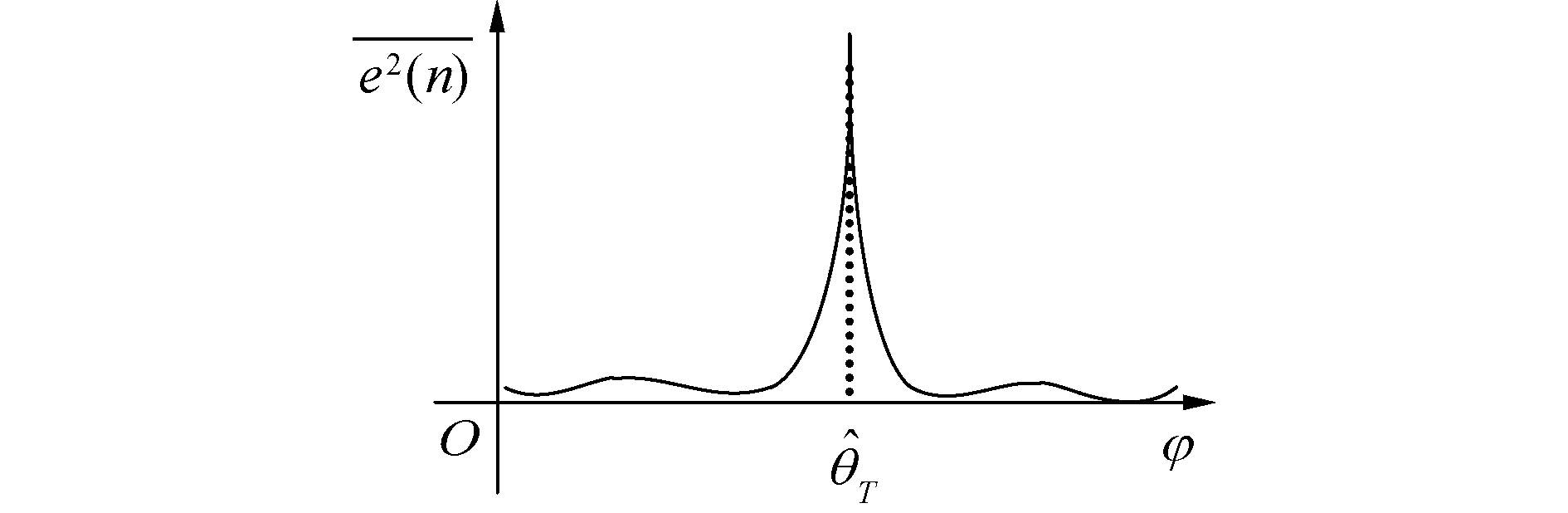
如图 5所示,方位结果估计是根据全空间不同方向上,单矢量组合通道间信号对消之后的残差信号能量统计结果,获得方位估计曲线,最大值对应的角度即为目标方位估计结果:
|
Download:
|
| 图 5 自适应抵消器输出残差能量曲线 Fig. 5 Curve of residual energy output by adaptive cancellation | |
| $ {\hat \theta _T} = \{ \varphi :{\rm{max}}[\sum\limits_{k = 1}^N {{\varepsilon ^2}} (\varphi ,k)]\} $ | (13) |
据此可以对目标方位进行估计。
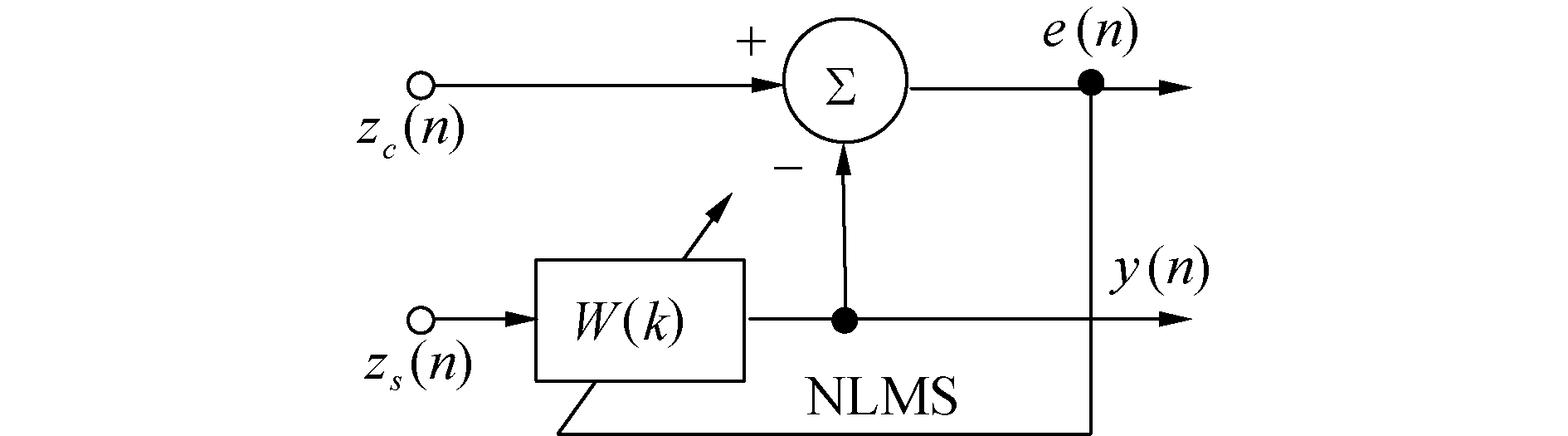
在方位估计的算法中使用到的自适应对消技术框图如图 6所示,输入的zs(n)为zs(t)的离散采样信号:
|
Download:
|
| 图 6 自适应抵消算法 Fig. 6 Block diagram of the adaptive cancelling algorithm | |
| $ {\mathit{\boldsymbol{z}}_s}(t) = [p(t) + {\mathit{\boldsymbol{v}}_c}(t)]*{\mathit{\boldsymbol{v}}_s}( - t) $ | (14) |
获得式(6)的方向图,根据2个方向图之间最大值和零值之间残差的关系,进而估计目标方位。
3 仿真与性能分析 3.1 检测性能分析为了说明所提算法在性能上的提升,对所提算法的检测性能进行蒙特卡洛仿真,获得检测器的ROC曲线和检测概率随信噪比的变化曲线,并与纯声压检测和复声强器的检测性能进行对比。
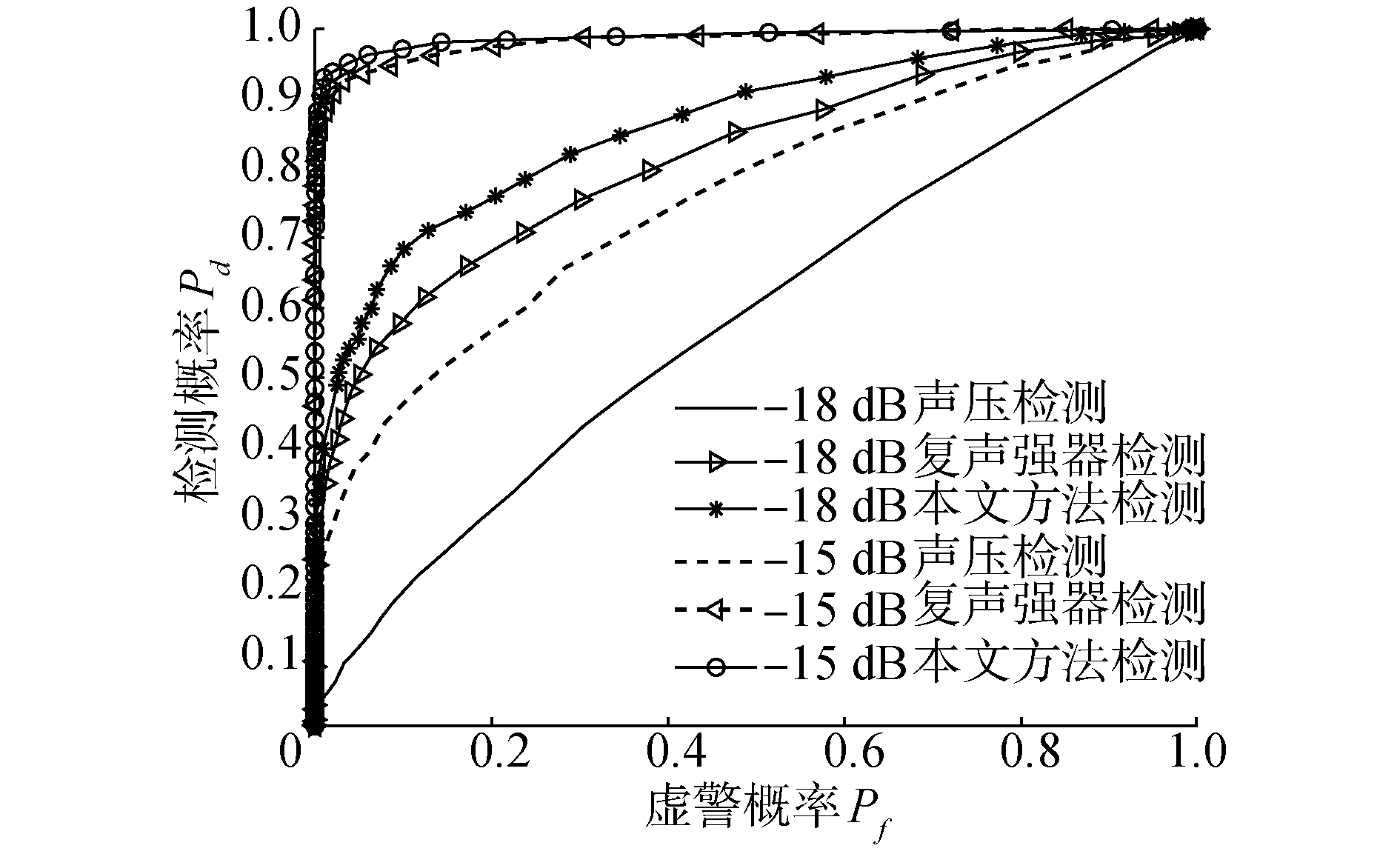
仿真实例1:信号为时长1 s的750 Hz单频信号,采样率为6 000 Hz,信噪比(此处为带宽内信噪比,仿真中带宽为200 Hz)设置为-18 dB和-15 dB,分别使用本文所提方法、声压检测方法和复声强器对目标信号进行检测,蒙特卡洛仿真试验次数为1 000次,统计获得的ROC曲线如图 7所示。当信噪比为-18 dB、虚警概率为0.1时,3种方法的检测概率分别为0.21、0.58和0.65。说明本文所提算法的检测性能要优于传统的纯声压信号线谱检测和复声强器的检测,即在相同虚警概率的情况下,目标的检测概率更高。
|
Download:
|
| 图 7 ROC曲线 Fig. 7 ROC Curves | |
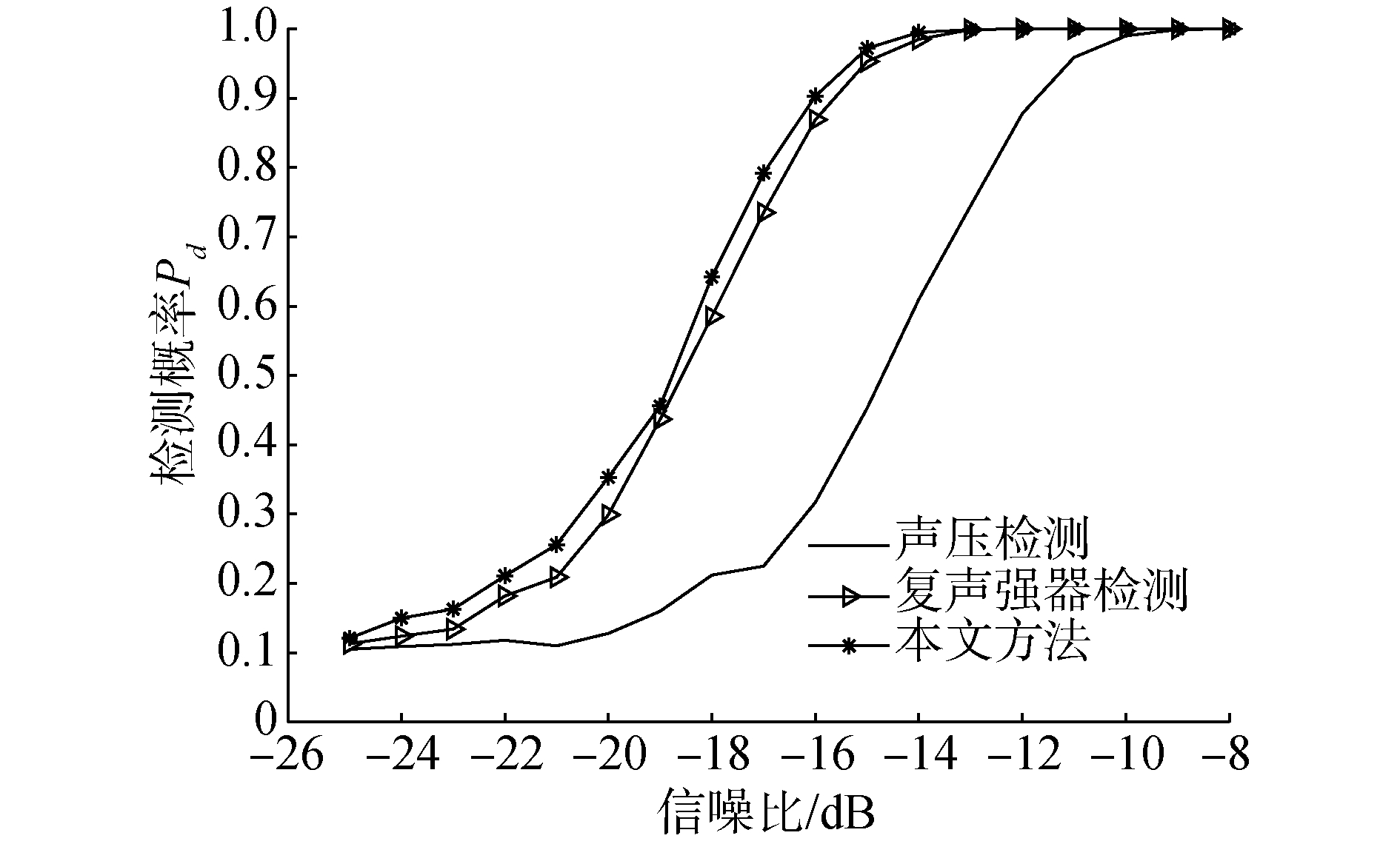
仿真实例2:仿真参数保持不变,在带宽内信噪比为-25~-8 dB,虚警概率为0.1的条件下,进行2种不同方法检测概率随信噪比变化的仿真,蒙特卡洛仿真次数为1 000次,结果如图 8所示。对比3种方法检测概率随信噪比的变化关系:所提方法和复声强检测性能明显优于仅依靠声压信息的线谱检测。在同一信噪比条件下,恒虚警检测时所提方法大于复声强器的检测概率。
|
Download:
|
| 图 8 检测概率和信噪比的关系 Fig. 8 Detection probability versus SNR | |
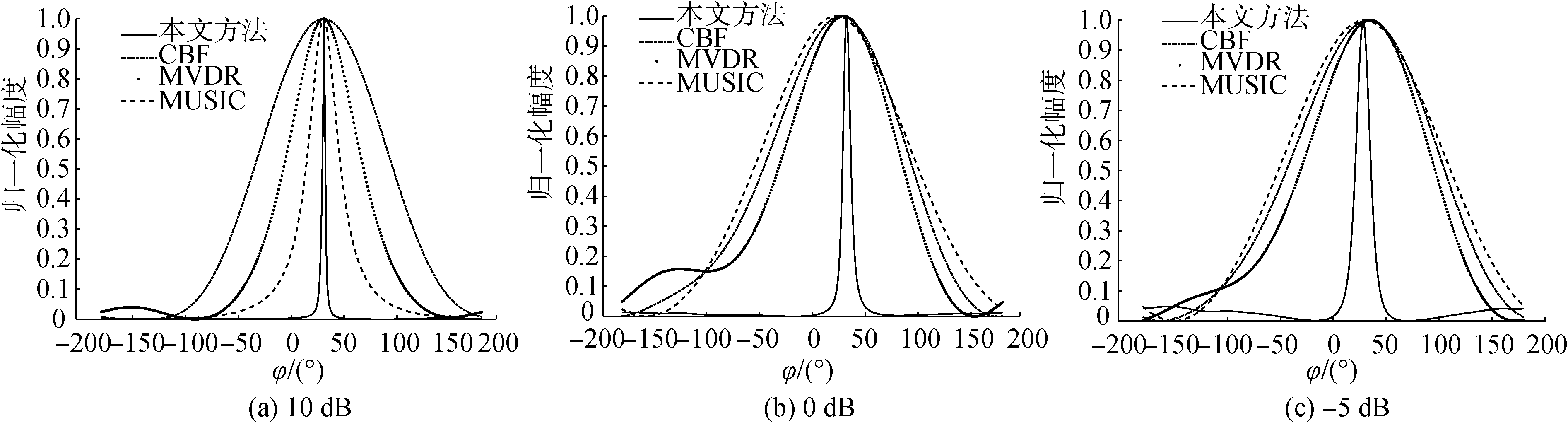
仿真实例3:仿真参数保持不变,带宽内信噪比分别为10、0和-5 dB,目标真实方位为30°,波束空间覆盖步距为1°,分别使用所提方法、常规CBF、MVDR、MUSIC算法进行方位估计[11],对比结果如图 9所示。
|
Download:
|
| 图 9 方位估计仿真结果对比 Fig. 9 Comparison of azimuth estimation simulation results | |
对比上述4种方法目标方位结果,能够得到以下结论:1)信噪比较高时,4种方法均能有效地估计目标方位;2)所提方法的半功率(幅值一半)空间宽度最小,目标空间分辨率最高,MUSIC次之,MVDR再次之,CBF的分辨率最低;3)随着信噪比的降低,4种方法的空间分辨能力和目标方位估计准确度都有所降低,MUSIC受信噪比影响最大,所提方法目标估计准确度的稳健性更高。
仿真实例4:目标仿真参数与仿真实例1中的参数相同,在带宽内信噪比为-15~5 dB范围,进行目标方位估计均方根误差(RMSE)随信噪比变化的仿真,蒙特卡洛仿真次数为1 000次,结果如图 10所示。4种估计方法获得的RMSE均随信噪比的增大而减小;相同信噪比条件下,本文所提方法目标估计的RMSE最小,且更快收敛到容许偏差范围内。上述结果验证了所提方法的有效性,在性能上比其他方法更优。

|
Download:
|
| 图 10 测向均方根误差 Fig. 10 RMSE of azimuth estimation | |
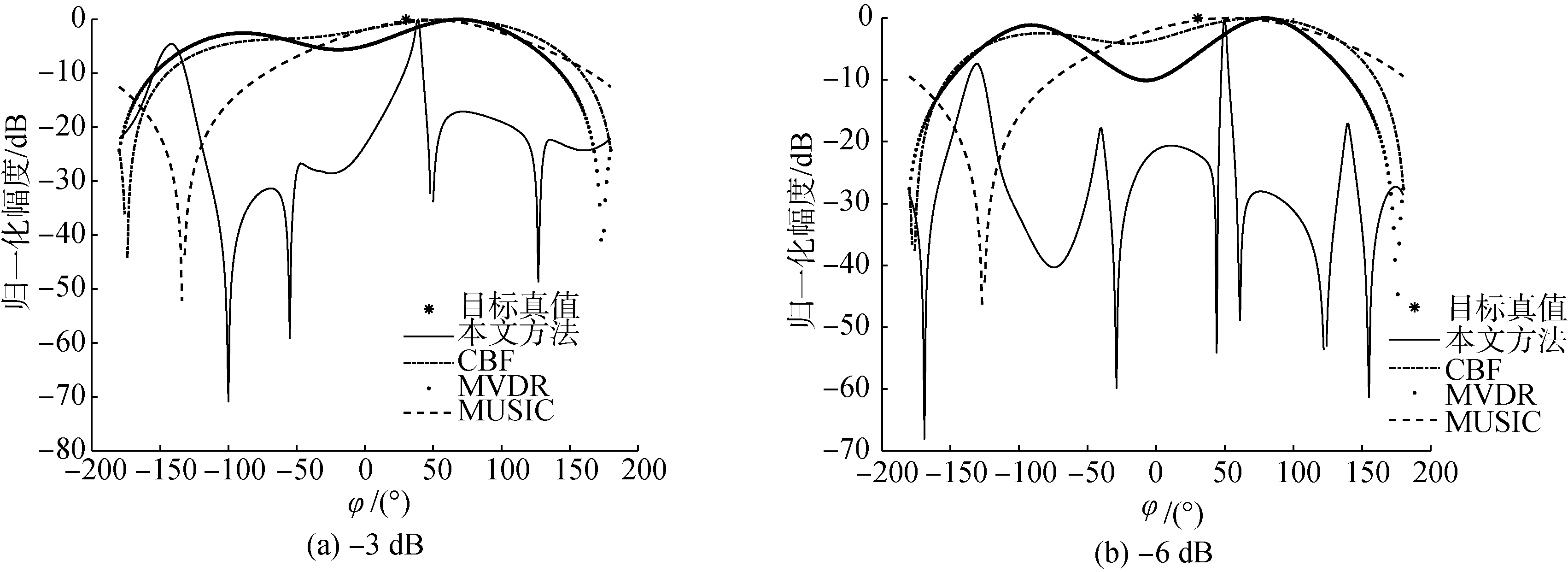
仿真实例5:仿真参数与仿真实例1中的信号参数相同,在带宽内信噪比为5 dB时,目标位于30°方位,X通道幅度误差为-3 dB和-6 dB时方位估计结果如图 11所示。当通道间幅度特性不一致时,几种方法的方位估计精度均下降,且幅度误差越大精度下降越严重。从直观上看,所提方法的性能下降程度要小于其他几种方法。除方位估计产生误差之外,方位估计结果谱图畸变也不明显。
|
Download:
|
| 图 11 幅度变化对方位估计的影响 Fig. 11 The influence of amplitude varying on the azimuth estimation | |
为了验证所提算法的有效性,使用2016年5月丹江口水库的外场试验数据对所提方法进行验证,评估不同算法在实际工程环境中的性能表现。
4.1 线谱目标检测试验信号频率750 Hz,时长1 s的CW信号,其原始试验数据的信噪比为6.5 dB,其中在650 Hz到850 Hz带宽内的信噪比为18.5 dB,接收信号的时域波形和时频特性如图 12所示。在接收信号的信噪比条件下,3种方法都能有效地进行目标检测,为了验证本文所提方法在低信噪比条件下的良好性能,通过改变信号与水库实际环境背景噪声比值的大小,调整带宽内信噪比分别为-10、-13和-15 dB,对比结果示于图 13中。

|
Download:
|
| 图 12 接收信号 Fig. 12 The received signal | |

|
Download:
|
| 图 13 检测结果对比 Fig. 13 Comparison of detection results | |
在3组不同信噪比条件下,声压检测效果均最差,复声强检测效果较其有明显提高,所提方法性能最优,产生的毛刺干扰最少,对噪声抑制能力最强。随着信噪比的降低3种方法的检测性能均有所下降,低信噪比时,声压检测几乎失效,但是复声强器和所提方法仍然能够有效进行目标检测。
4.2 线谱目标方位估计在处理过程中,将信噪比调整到5、0和-5 dB,试验数据处理结果如图 14所示。相比于CBF、MVDR和MUSIC,所提方法的目标方位估计准确度最高,方位谱最窄,有更高的目标分辨能力。此外随着信噪比的降低,4种方法的方位估计性能均有所下降尤其是由于能量泄漏在150°附近出现镜像伪峰。但是所提方法性能下降程度远小于CBF、MVDR和MUISIC,说明了所提方法在试验数据处理中的有效性和优越性。

|
Download:
|
| 图 14 方位估计试验结果对比 Fig. 14 Comparison of azimuth estimation experimental results | |
1) 提出的基于单矢量水听器通道自适应增强的目标线谱检测,通过组合通道的时反卷积噪声抑制和自适应线谱增强,能够有效提高低信噪比条件下水下目标的检测概率。
2) 提出的基于自适应抵消残差能量的方位估计方法,与CBF、MVDR和MUSIC相比,能够获得高分辨的目标方位估计结果,在低信噪比条件下,能够保持更高的目标方位估计的准确度。矢量传感器出现幅相误差时,方位估计精度下降。
本文为单矢量水声目标探测系统提供了一种技术途径,具有实际的工程应用价值。
| [1] |
时胜国, 李赢, 杨德森, 等. 中心对称声矢量圆阵的相干双声源方位估计方法[J]. 哈尔滨工程大学学报, 2019, 40(7): 1187-1193. SHI Shengguo, LI Ying, YANG Desen, et al. Direction-of-arrival estimation of two coherent signals based on centrosymmetric circular acoustic vector-sensor arrays[J]. Journal of Harbin Engineering University, 2019, 40(7): 1187-1193. (  0) 0)
|
| [2] |
刘淞佐, 周锋, 孙宗鑫, 等. 单矢量水听器OFDM水声通信技术实验[J]. 哈尔滨工程大学学报, 2012, 33(8): 941-947. LIU Songzuo, ZHOU Feng, SUN Zongxin, et al. Experimental study of OFDM underwater acoustic communication using a vector hydrophone[J]. Journal of Harbin Engineering University, 2012, 33(8): 941-947. DOI:10.3969/j.issn.1006-7043.201111055 (  0) 0)
|
| [3] |
梁国龙, 张柯, 范展. 单矢量水听器方位频率联合估计算法[J]. 哈尔滨工程大学学报, 2013, 34(1): 46-50. LIANG Guolong, ZHANG Ke, FAN Zhan. Algorithm research of joint azimuth-frequency estimation via a single vector hydrophone[J]. Journal of Harbin Engineering University, 2013, 34(1): 46-50. (  0) 0)
|
| [4] |
惠俊英, 惠娟. 矢量信号处理基础[M]. 北京: 国防工业出版社, 2009: 6-15. HUI Junying, HUI Juan. Vector signal processing fundamental theory[M]. Beijing: National Defense Industry Press, 2009: 6-15. (  0) 0)
|
| [5] |
ZHAO Anbang, MA Lin, MA Xuefei, et al. An improved azimuth angle estimation method with a single acoustic vector sensor based on an active sonar detection system[J]. Sensors, 2017, 17(2): 412. (  0) 0)
|
| [6] |
李楠松, 朴胜春, 宋海岩, 等. 浅海中单矢量水听器高分辨方位估计方法[J]. 哈尔滨工程大学学报, 2014, 35(2): 208-215. LI Nansong, PIAO Shengchun, SONG Haiyan, et al. Research on High-resolution DOA based on single vector hydrophone in shallow water[J]. Journal of Harbin Engineering University, 2014, 35(2): 208-215. (  0) 0)
|
| [7] |
柳艾飞, 杨德森, 时胜国, 等. 各向同性噪声场中单矢量传感器虚源消除MUSIC测向方法[J]. 声学学报, 2019, 44(4): 698-706. LIU Aifei, YANG Desen, SHI Shengguo, et al. MUSIC Direction of arrival estimation method with virtual source elimination for single vector sensor under isotropic ambient noise background[J]. Acta acustica, 2019, 44(4): 698-706. (  0) 0)
|
| [8] |
刘伯胜, 雷家煜. 水声学原理[M]. 2版. 哈尔滨: 哈尔滨工程大学出版社, 2010: 31-32. LIU Bosheng, LEI Jiayu. Underwater acoustics theory[M]. 2nd ed. Harbin: Harbin Engineering University Press, 2010: 31-32. (  0) 0)
|
| [9] |
ZHAO Zhishan, ZHAO Anbang, HUI Juan, et al. A frequency domain adaptive matched filter for active sonar detection[J]. Sensors, 2017, 17(7): 1565. DOI:10.3390/s17071565 (  0) 0)
|
| [10] |
马伯乐, 朱世强, 孙贵青. 一种声矢量阵最小方差无畸变方位估计算法[J]. 兵工学报, 2019, 40(1): 153-158. MA Bole, ZHU Shiqiang, SUN Guiqing. A minimum variance distortionless response azimuth estimation algorithm of acoustic vector array[J]. Acta armamentarii, 2019, 40(1): 153-158. DOI:10.3969/j.issn.1000-1093.2019.01.018 (  0) 0)
|
| [11] |
ZHAO Anbang, MA Lin, HUI Juan, et al. Open-lake experimental investigation of azimuth angle estimation using a single acoustic vector sensor[J]. Journal of sensors, 2018, 2018: 4324902. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


