水下声学定位通常采用距离交会方式[1],水下距离的精确测量受时间测量和声速测量等相关误差影响[2]。借助于高精度的信号检测技术和时延估计方法,在作用距离覆盖范围内测时能够达到优于0.1 ms的精度[3]。声速受深度、温度、盐度等环境因素的综合影响,且存在空变性和时变性[4]。此外,声波在海水中传播产生声线弯曲现象[5]。在高精度水下声学定位中,利用声速剖面(sound velocity profile,SVP)代替固定声速值,并采用分层计算和逐层追加的声线跟踪方法对声线弯曲进行改正[6]。但在深海定位中,SVP的层数较多时,声线跟踪的运算时间显著增加,从而降低了定位效率[7-12]。因此,在保证定位精度的前提下,为了提高水下声学定位计算效率,减少声线跟踪的运算时间,有必要研究实用高效的SVP精简方法。
人工法能够实现SVP的精简,但人工法在精简SVP的过程中易遗漏SVP的特征点,同时效率低下[13]。文献[7]利用Douglas-Peucker算法[14]对原始SVP进行精简,基本解决了声线跟踪精度与计算量之间的矛盾。文献[8]和[9]分别提出了等效声速剖面模型和基于面积差的SVP简化方法,提高了多波束测深效率。文献[10]选用一定宽度的窗口对SVP进行滑动平均,将窗口中声速的平均值作为窗口中心深度的声速值,以此精简SVP,提升了多波束回声测深系统的效率。文献[11]引入等效声速剖面思想,将SVP划为几段,根据等效声速对每段等间隔分层,以提高定位的效率。文献[12]对选定窗口内的声速值进行曲线拟合,计算曲线最大曲率,并以此作为精简SVP的依据,提升了定位效率。以上研究一定程度上精简了原始SVP,提升了多波束测深与水下声学定位的计算效率,但还存在遗漏原始SVP的特征点及在不同深度的定位精度较低等问题。
针对上述问题,本文引入优化聚类算法,提出了一种基于K-Means++[15]的SVP精简方法。该方法采用K-Means++算法实现了对原始SVP的自动精简,有效地解决了定位精度与定位计算效率之间的矛盾。
1 基于K-Means++的SVP精简方法K-Means算法[16]是聚类算法中的主要算法之一,1967年MacQueen首次提出K-Means算法,该算法的基本原理为:预先确定类别数和初始簇中心将样本集聚为几类,并通过迭代优化获得最终的聚类结果。K-Means算法原理简单,收敛速度快,对大型样本集能高效聚类。但K-Means算法受初始化簇中心的影响较大,当随机初始化簇中心选取不当时,聚类过程非常耗时且聚类结果误差较大。针对这一问题,文献[15]提出了K-Means++算法。K-Means++算法与K-Means算法的原理基本一致,它是对K-Means算法随机初始化簇中心的优化。相较于K-Means算法,K-Means++算法虽然在初始化簇中心时,增加了计算量,但在整个聚类过程中,其显著地提升了计算效率和改善了聚类结果误差。
通过层内常梯度声线跟踪原理[6]得知,每一层有一个常梯度,如果相邻层的常梯度相同,将这2层合并为一层后不会降低层内常梯度声线跟踪的计算精度。根据此原理,本文提出一种基于K-Means++的SVP精简方法,算法流程见图 1。
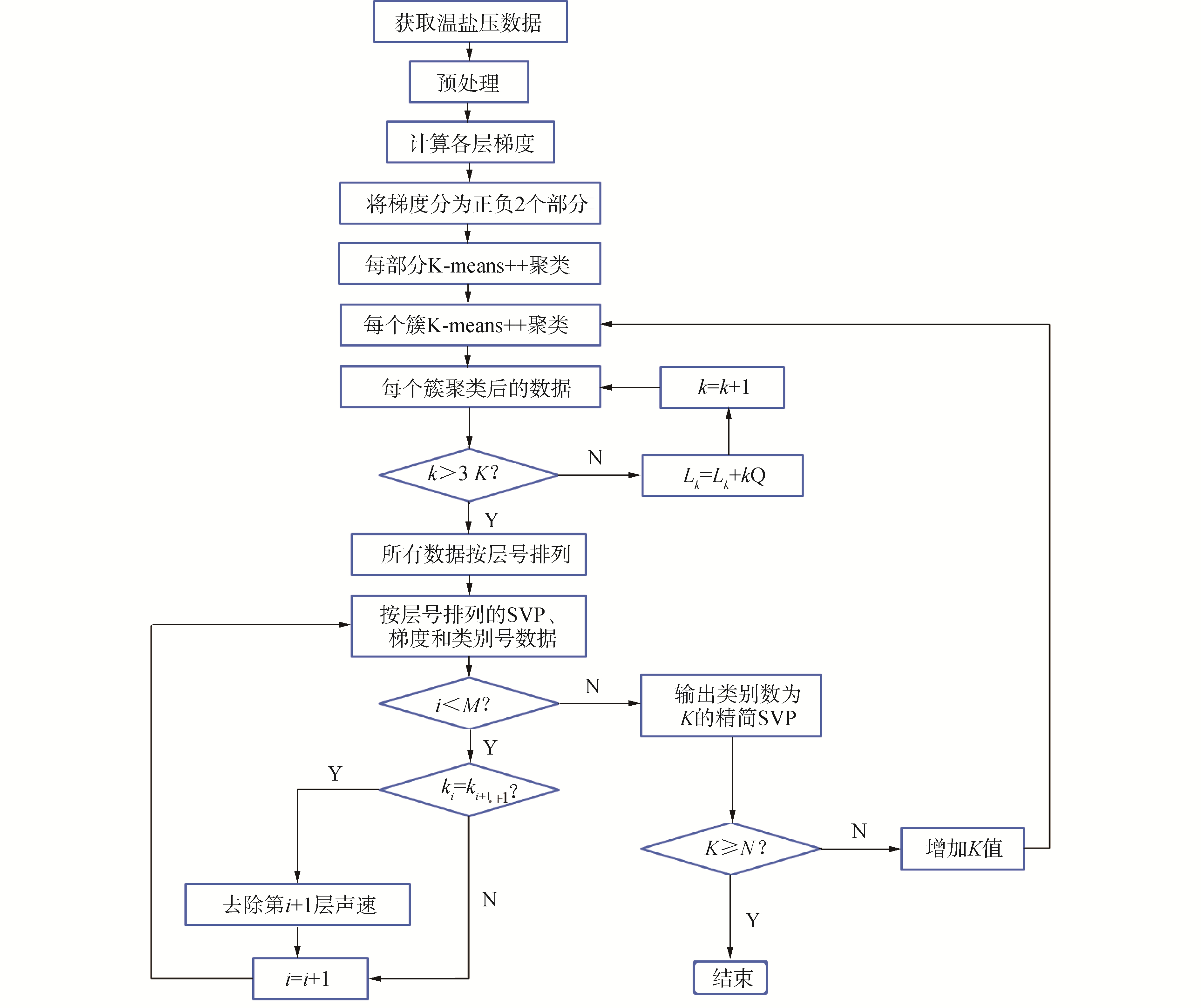
|
Download:
|
| 图 1 算法流程 Fig. 1 Algorithm flow chart | |
为验证基于K-Means++SVP精简方法的有效性,在中国Argo资料中心发布数据中,选取具有代表性[17]的SVP(中国Argo实时资料中心发布温盐压数据,采用W.D.wilson精确声速经验公式[18]计算得到SVP)用于浮标定位,将精简后SVP的定位结果与原始SVP的定位结果进行对比分析。浮标定位中的定位模型为圆曲线模型[19],声线跟踪方法为层内常梯度声线跟踪方法,解算结果为定位绝对偏差,即应答器解算坐标值与坐标真值的差值。
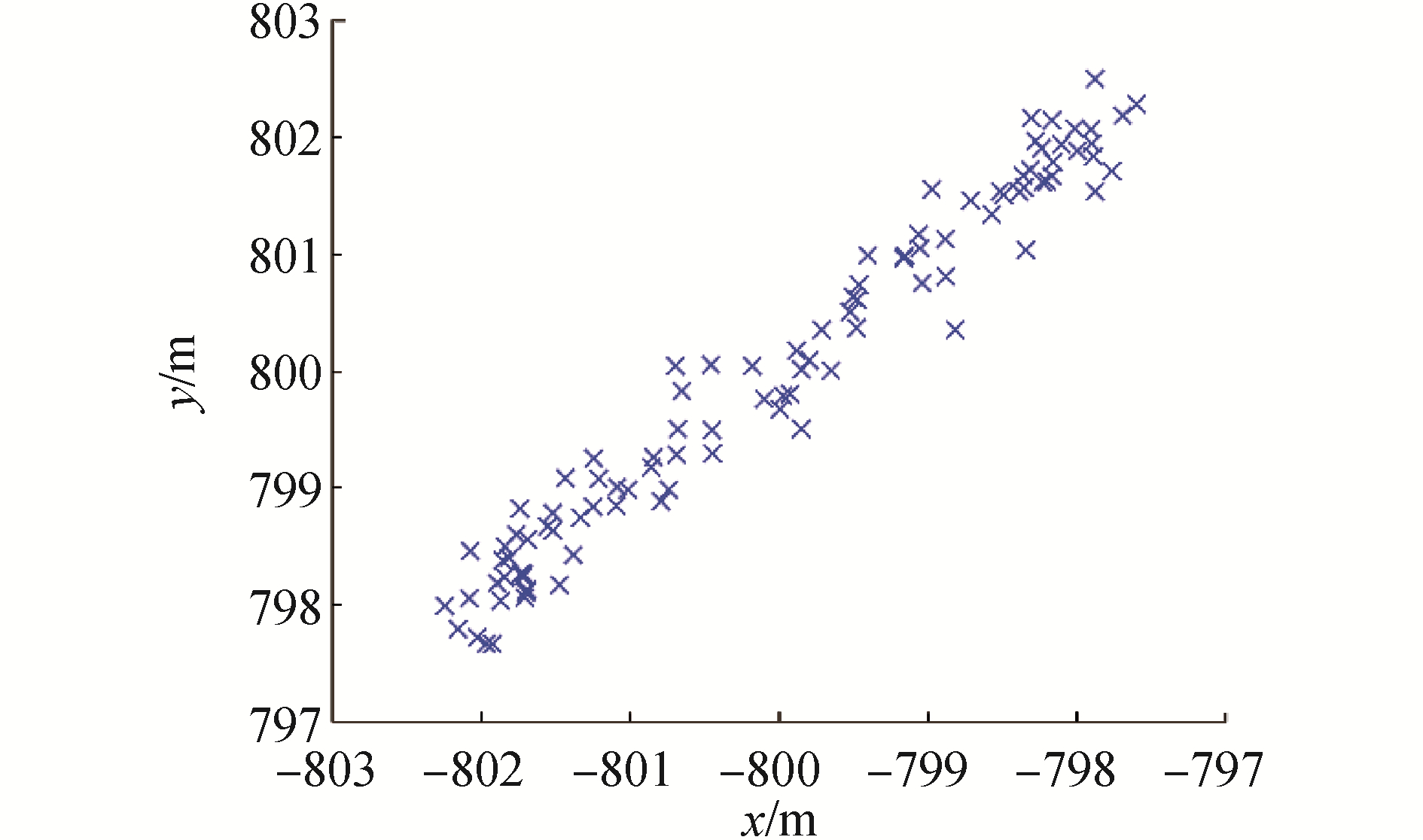
2.1 浮标定位仿真实验设计海表面4个浮标的模拟三维坐标分别为B1(-800,-800,0)、B2(-800,800,0)、B3(800,800,0)、B4(800,-800,0),海底4个应答器的模拟三维坐标分别为T1(0,0,-1 000)、T2(0,50,-1 000)、T3(50,0,-1 000)、T4(50,50,-1 000),单位均为m,模拟历元为100个历元,原始SVP的深度范围为0~1 000 m,采样间隔为1 m。海面余弦波动振幅为2 m,应答器时延偏差为8 cm,测量时间引起的测距中误差为10 cm。浮标和应答器的相对位置示意图如图 2所示,浮标B2坐标放大图如图 3。实验中计算平台的处理器型号为Intel(R) Core(TM) i5-6500,内存大小为8 G。

|
Download:
|
| 图 2 浮标和应答器模拟坐标示意 Fig. 2 Schematic diagram of buoy and transponder simulation coordinates | |
|
Download:
|
| 图 3 浮标B2 100个历元坐标示意 Fig. 3 Schematic diagram of buoy B2 100 epoch coordinates | |
为检验精简后SVP是否保留了原始SVP的特征点,选取类别数2~10精简SVP,并将精简后的SVP与原始SVP对比分析,如图 4和表 1所示。图 4对类别数2、4、5和10的精简结果进行展示,其余不再赘述。表 1中的类别数1表示原始SVP。

|
Download:
|
| 图 4 不同类别数精简SVP与原始SVP对比 Fig. 4 Comparison of different categories of streamlined SVP and original SVP | |
| 表 1 不同类别数的SVP精简结果 Table 1 SVP streamlined results for different categories |
特征率指精简后SVP所包含原始SVP的特征信息,其计算公式为:
| $ {\sigma _i} = \frac{{{P_i}}}{P} \times 100\% $ | (1) |
式中:i表示类别数;Pi表示类别数为i精简后SVP层数;P表示原始SVP层数。
由图 4和表 1可知,类别数较小时,特征率较低,精简后的SVP与原始SVP差异较大。随着类别数增加,特征率不断提高,精简后的SVP逐渐与原始SVP重合。当类别数增加到5时,特征率为11.9%,精简后的SVP与原始SVP基本完全重合。表明本实验中特征率大于等于11.9%时,精简后的SVP基本保留了原始SVP所有特征,确保了原始SVP的空间结构。
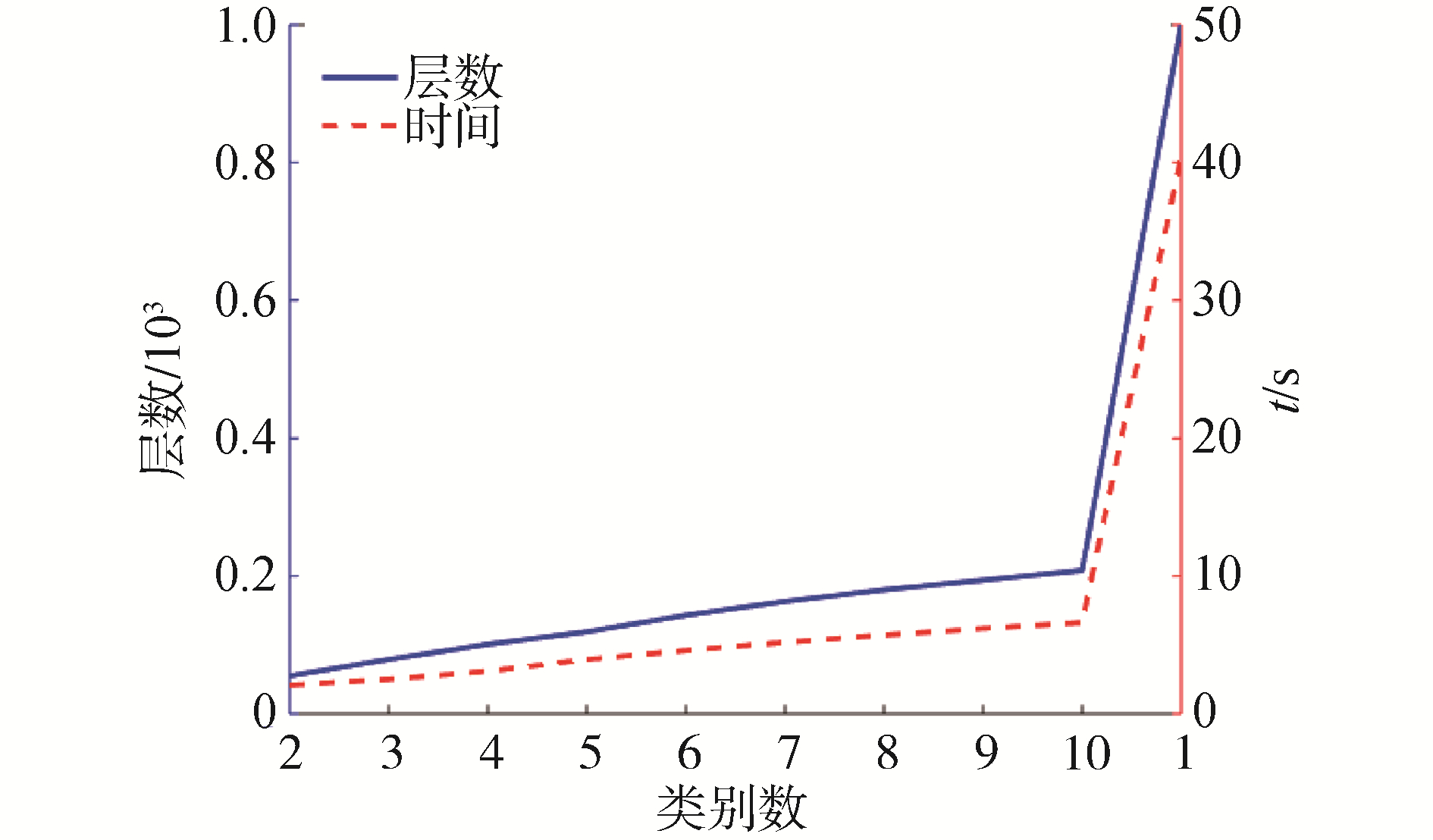
2.3 不同类别数定位结果分析为比较精简后SVP与原始SVP的定位结果,从定位效率和定位精度2个方面进行分析,如图 5、表 2和图 6所示。类别数为1表示原始SVP的定位结果。
|
Download:
|
| 图 5 不同类别数精简SVP的层数和定位时间 Fig. 5 Layers and positioning time of streamlined SVP for different categories | |
| 表 2 不同类别数的应答器定位误差 Table 2 Transponder positioning error of different categories |
|
Download:
|
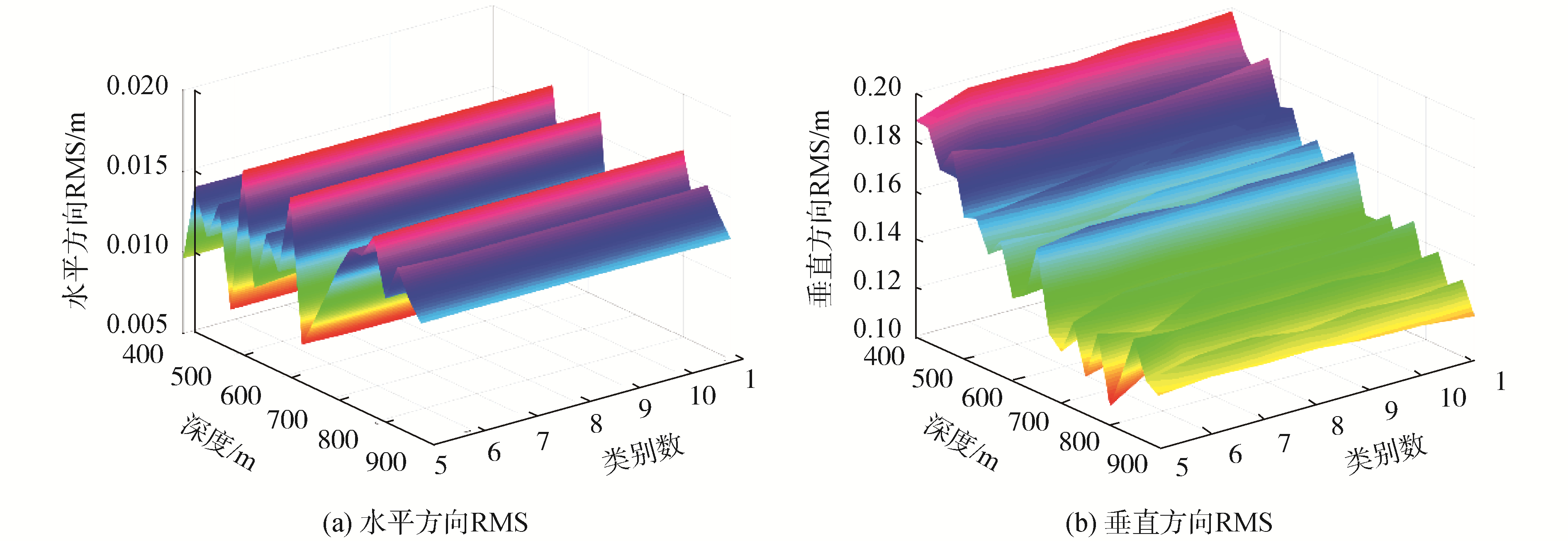
| 图 6 不同深度定位结果RMS Fig. 6 RMS of positioning results for different depths | |
定位效率方面:由图 5可知,类别数从2到10,精简后SVP的层数从55层到208层,远小于原始SVP的1 000层,精简后SVP的定位时间从2.1 s到6.6 s,也远小于原始SVP的40.4 s,定位时间缩短了83.6%~94.9%,定位效率较原始SVP大幅度提升。
定位精度方面:由表 2可知,类别数从2到4,精简后SVP的水平最大误差从0.058 7 m降低到0.038 5 m,垂直最大误差从0.757 2 m降低到0.160 4 m,垂直最小误差从0.744 3 m降低到0.147 5 m,水平平均误差从0.020 2 m降低到0.010 1 m,垂直平均误差从0.748 3 m降低到0.151 5 m。类别数从4到5,精简后SVP的垂直最大误差从0.160 4 m减小到0.122 1 m,垂直最小误差从0.147 5 m减小到0.108 2 m,垂直平均误差从0.151 5 m减小到0.113 2 m。类别数从5到10,精简后SVP的各个误差基本保持不变,并与原始SVP的定位误差基本一致。
上述实验表明,随着类别数增加,定位误差逐渐减小,当类别数大于等于5时,精简后SVP的定位精度与原始SVP区别不大,差别为毫米级,而定位计算效率显著高于原始SVP。
2.4 不同深度定位精度分析采用精简后的SVP进行水下定位时,虽然保证了原始SVP采样深度处的定位精度,但可能会使该水域其他深度处的定位精度产生较大误差[9]。
为验证采用本文方法精简的SVP在其他深度处的定位精度,对精简后SVP的不同深度定位结果进行分析,并与原始SVP进行比较,如图 6所示。由上述实验可知,当类别数大于等于5时,精简后SVP的定位精度与原始SVP基本相同,所以本实验的类别数为5~10。本实验中浮标布设间距为1 600 m,考虑声线入射角, 设置深度区间为400~900 m。本文原始SVP测量处的深度为1 000 m。
由图 6(a)可知,深度为400 m,精简后SVP定位结果的水平方向RMS(root mean square)为0.009 6~0.009 7 m,原始SVP为0.009 7 m;深度为600 m,精简后SVP定位结果的水平方向RMS为0.011 4~0.011 5 m,原始SVP为0.011 4 m;深度为900 m,精简后SVP定位结果的水平方向RMS为0.012 4~0.012 5 m,原始SVP为0.012 4 m。由图 6(b)可知,深度为400 m,精简后SVP定位结果的垂直方向RMS为0.188 7~0.197 1 m,原始SVP为0.198 7 m;深度为600 m,精简后SVP定位结果的垂直方向RMS为0.133 9~0.148 5 m,原始SVP为0.149 9 m;深度为900 m,精简后SVP定位结果的垂直方向RMS为0.120 8~0.123 2 m,原始SVP为0.118 9 m。再由图 6可知,同一深度不同类别数所对应的颜色基本相同,表明同一深度精简后SVP的RMS与原始SVP基本相同(水平方向RMS基本一致,垂直方向RMS差别为0~0.018 2 m)。通过实验数据分析可知,本文方法在不同深度进行水下定位时,精简后SVP各个深度处的定位精度与原始SVP相应深度处的定位精度基本一致。
3 结论1) 本文提出的一种基于K-Means++的SVP精简方法采用不同类别数对原始SVP进行精简,当类别数大于等于5时(5表示本算例的类别数阈值),精简后SVP基本保留了原始SVP的所有特征。
2) 精简后SVP的定位精度与原始SVP基本相同,而定位效率明显高于原始SVP;在不同深度进行水下定位,精简后SVP的定位精度与原始SVP基本一致。
3) 由于不同SVP受区域、时间、采样等因素影响,因此其他算例中的类别数阈值可能会与本算例略有不同,但本文所提方法和所得规律性结论均具有普适性。
4) 本文方法实现了原始SVP的自动精简,精简后的SVP在确保原始SVP空间结构和水下定位精度的前提下,缩短了声线跟踪的运算时间,进而显著提高了水下定位计算效率,具有良好的工程应用价值。
| [1] |
ZHANG Jucheng, HAN Yunfeng, ZHENG Cuie, et al. Underwater target localization using long baseline positioning system[J]. Applied acoustics, 2016, 111: 129-134. DOI:10.1016/j.apacoust.2016.04.009 (  0) 0)
|
| [2] |
RAMEZANI H, LEUS G. Accurate ranging in a stratified underwater medium with multiple isogradient sound speed profile layers[J]. IFAC proceedings volumes, 2012, 45(5): 146-151. DOI:10.3182/20120410-3-PT-4028.00025 (  0) 0)
|
| [3] |
张居成.深水长基线定位导航技术研究[D].哈尔滨: 哈尔滨工程大学, 2014. ZHANG Jucheng. Research of deepwater LBL positoning and navigation technology[D]. Harbin: Harbin Engineering University, 2014. (  0) 0)
|
| [4] |
HUANG Chenfen, GERSTOFT P, HODGKISS W S. Effect of ocean sound speed uncertainty on matched-field geoacoustic inversion[J]. The journal of the acoustical society of America, 2008, 123(6): EL162-EL168. DOI:10.1121/1.2908406 (  0) 0)
|
| [5] |
齐娜, 田坦. 多波束条带测深中的声线跟踪技术[J]. 哈尔滨工程大学学报, 2003, 24(3): 245-248. QI Na, TIAN Tan. Ray tracing in multi-beam swath bathymetry[J]. Journal of Harbin Engineering University, 2003, 24(3): 245-248. DOI:10.3969/j.issn.1006-7043.2003.03.003 (  0) 0)
|
| [6] |
刘伯胜, 雷家煜. 水声学原理[M]. 2版. 哈尔滨: 哈尔滨工程大学出版社, 2010. LIU Bosheng, LEI Jiayu. The principle of hydroacoustics[M]. 2nd ed. Harbin: Harbin Engineering University Press, 2010. (  0) 0)
|
| [7] |
张志伟, 暴景阳, 金山. 一种多波束测深声线跟踪自适应分层方法[J]. 海洋测绘, 2018, 38(1): 23-26, 42. ZHANG Zhiwei, BAO Jingyang, JIN Shan. A self-adapting division method for ray-tracing of multibeam echosounding[J]. Hydrographic surveying and charting, 2018, 38(1): 23-26, 42. DOI:10.3969/j.issn.1671-3044.2018.01.006 (  0) 0)
|
| [8] |
GENG Xueyi, ZIELINSKI A. Precise multibeam acoustic bathymetry[J]. Marine geodesy, 1999, 22(3): 157-167. DOI:10.1080/014904199273434 (  0) 0)
|
| [9] |
郑根, 张红梅, 冯磊, 等. 基于面积差的声速剖面自适应简化方法[J]. 测绘学报, 2018, 47(10): 1415-1423. ZHENG Gen, ZHANG Hongmei, FENG Lei, et al. An adaptive simplification method of SVP based on area difference[J]. Acta geodaetica et cartographica sinica, 2018, 47(10): 1415-1423. DOI:10.11947/j.AGCS.2018.20170232 (  0) 0)
|
| [10] |
BEAUDOIN J, SMYTH S, FURLONG A, et al. Streamlining sound speed profile pre-processing: case studies and field trials[C]//Proceedings of 2011 U.S. Hydrographic Conference. Tampa, FL, USA, 2011: 811.
(  0) 0)
|
| [11] |
张居成, 郑翠娥, 孙大军. 用于声线跟踪定位的自适应分层方法[J]. 哈尔滨工程大学学报, 2013, 34(12): 1497-1501. ZHANG Jucheng, ZHENG Cuie, SUN Dajun. A self-adapting division method for ray-tracing positioning[J]. Journal of Harbin Engineering University, 2013, 34(12): 1497-1501. (  0) 0)
|
| [12] |
李圣雪, 王振杰, 聂志喜, 等. 一种适用于深海长基线定位的自适应分层声线跟踪法[J]. 海洋通报, 2015, 34(5): 491-498. LI Shengxue, WANG Zhenjie, NIE Zhixi, et al. A self-adapting division ray-tracing method in the long baseline acoustic positioning[J]. Marine science bulletin, 2015, 34(5): 491-498. (  0) 0)
|
| [13] |
ZHAO Dineng, WU Ziyin, ZHOU Jieqiong, et al. A new method of automatic SVP optimization based on MOV algorithm[J]. Marine geodesy, 2015, 38(3): 225-240. DOI:10.1080/01490419.2015.1006798 (  0) 0)
|
| [14] |
DOUGLAS D H, PEUCKER T K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J]. Cartographica, 1973, 10(2): 112-122. (  0) 0)
|
| [15] |
ARTHUR D, VASSILVITSKⅡ S. k-means++: The advantages of careful seeding[C]//Proceedings of the eighteenth annual ACM-SIAM symposium on Discrete algorithms. New Orleans, USA, 2007: 1027-1035.
(  0) 0)
|
| [16] |
MACQUEEN J B. Some methods for classification and analysis of multivariate observations[C]//Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability. Berkeley, 1967: 281-297.
(  0) 0)
|
| [17] |
MUNK W H. Sound channel in an exponentially stratified ocean, with application to SOFAR[J]. The journal of the acoustical society of America, 1974, 55(2): 220-226. (  0) 0)
|
| [18] |
WILSON W D. Speed of sound in sea water as a function of temperature, pressure, and salinity[J]. The journal of the acoustical society of America, 1960, 32(6): 641-644. DOI:10.1121/1.1908167 (  0) 0)
|
| [19] |
王燕, 梁国龙. 一种适用于长基线水声定位系统的声线修正方法[J]. 哈尔滨工程大学学报, 2002, 23(5): 32-34. WANG Yan, LIANG Guolong. Correction of sound velocity in long baseline acoustic positioning system[J]. Journal of Harbin Engineering University, 2002, 23(5): 32-34. DOI:10.3969/j.issn.1006-7043.2002.05.008 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


