2. 高技术船舶与深海开发装备协同创新中心, 上海 200240
2. Collaborative Innovation Center for Advanced Ship and Deep-Exploration, Shanghai 200240, China
内波在全球各大海域均频繁出现[1],是发生在海洋内部稳定密度跃层中的一种波动,人们很难通过肉眼观察到,而内孤立波作为一种特殊的内波,具有尺度大、能量集中等特点[2-3],其引起流场和密度场的迅速变化会对海洋工程结构物的局部结构强度以及水下潜体造成严重威胁[4],因此进行其流场的特征分析具有重要的意义。国内外学者在描述孤立子以及分层流体间的内孤立波理论方面均做出了贡献,依次提出KdV (Korteweg-de Vries)[5]、eKdV (extended KdV)[6]和MCC (Miyata-Choi-Camassa)[7]等理论模型。随后Camassa等[8]又对MCC理论进行了适用性研究,结果表明,在弱色散条件下,MCC理论与实验及数值模拟结果均吻合良好。Kodaira等[9]则运用分层流体开展实验研究,利用浪高仪测量波形和波速等数据,并与KdV和MCC模型作出比较,总结出不同振幅内孤立波的适用性,给出KdV和MCC模型自由表面条件下的解。国内孤立波理论模型研究方面,Chen等[10]通过实验研究发现KdV理论对于绝大多数小尺度内孤立波是适用的。黄文昊等[11]以水和盐水作为分层流体进行物理实验研究了3种理论模型的适用性条件,为非线性和色散情况作了一个定量的表述。王旭等[12]依据上述3种内孤立波理论模型的适用性条件,采用数值模拟方法,研究了内孤立波对直立圆柱的载荷特性。盛立等[13]对文献[5]附录中给出的方程模型中的系数进行了修正,推导得到了基于该方程模型的内孤立波定态解解析表达式,研究了上述三类理论模型的传播演化特性。目前针对内孤立波的解析及实验研究较为完备,但是实验室中采用的分层流体多存在扩散效应,不能跟孤立子解析模型采用的假设完全对应,缺少对理论孤立子模型伴生流场的实验研究。
在实验中运用PIV技术捕捉流场数据具有一定的优势[14],国内外也有众多学者把此方法运用到内孤立波的流场分析中。Moore等[15]利用2种密度的盐水作为分层流体,利用PIV技术测量速度场和密度场,研究了内波爬坡过程中的破碎类型。孟静等[16]同样运用PIV技术记录了由2种密度盐水作为分层流体所生成内孤立波的速度场。殷文明等[17]同年利用PIV技术读取了内孤立波波剖面序列,该实验所产生内孤立波亦用不同密度盐水作为分层流体。而在分析内孤立波破碎的混合过程方面,黄鹏起等[18]应用PIV技术记录数据,并计算了涡度、湍动能和湍耗散率。需要知道的是,在这些文献中,均利用的是“互溶”型2种液体,即水和盐水或2种不同密度的盐水作为分层流体来生成内孤立波,并结合PIV技术测量流场数据,来进行相关特性的分析,且针对内孤立波诱发的流场特征存在实验捕捉和分析不足。
为规避流体间的扩散作用,以研究理论孤立子内孤立波流场的特征形式,本文基于不相溶的硅油和水在实验室制造一种强分层流体系统,采用重力塌陷法生成孤立子形式的内孤立波进行演化实验。首先将实验波形与理论解进行了对比,其次运用PIV技术读取流场数据,分析了内孤立波在传播过程中速度场和涡量场的特征形式。
1 实验设置实验在大连理工大学船舶工程学院小型内波水槽中进行。水槽主尺度为5 m×0.43 m×0.55 m(长×宽×高),为规避扩散作用,采用不相溶且密度不同的2种液体构造强分层流体系统。上层流体为密度ρ1=(0.941±0.001)×103kg/m3,运动学粘度为v1=1×10-5 m2/s的二甲基硅油,下层流体为密度ρ2=(1.003±0.001)×103kg/m3,运动学粘度为v2=1×10-6 m2/s2的水。采用重力塌陷法生成内孤立波。在水槽另一侧装有楔形消波装置,用来消除反射波对数据测量的影响,水槽整体布置如图 1(a)、(b)所示,其中h1为上层流体深度,h2为下层流体深度,xL为塌陷区域宽度,di为塌陷区域高度。

|
Download:
|
| 图 1 实验总布置 Fig. 1 General layout of experiment | |
为获得波形及流场特征,对每个工况分别使用染色剂和PIV重复2次实验,染色剂与PIV实验均采用加拿大Pointgrey公司制造生产的GS3-U3-60QS6C-C型号的CCD相机,放置于距抽板3.5 m位置处。染色剂实验中,相机的帧速率为25 Hz,分辨率为2 736×2 192像素,染试剂使水进行染色,从而对饱和度直方图使用阈值分割和形态学闭运算获得内孤立波波形。
PIV实验选用能够发出纯绿色片状光源(光源夹角60°)的激光器,激光器布置在水槽上方,垂直向下照射,如图 1所示。分别在两层流体中混入密度为1.03×103 kg/m3,表面积为24 μm、体积为31 μm的聚苯乙烯来作为示踪粒子,即使粒子的比重相对于硅油偏大,但会在硅油粘度的作用下长时间保持悬浮状态,并可以清晰刻画流场特征,此时相机的帧速率为42 Hz,分辨率为1 368×1 096像素。PIV实验在暗室中进行,通过在相机镜头前安装偏振镜并采用黑色背景色,最大程度的降低了反射光与折射光对实验测量的影响,在得到高质量的流场时间序列图片后,使用互相关法对图像进行分析处理[19]。对于本实验搭建的水槽可完成造波及内孤立波波形和流场特征的提取,最终染色剂和PIV效果如图 2所示。

|
Download:
|
| 图 2 实验效果 Fig. 2 Experimental rendering | |
目前,针对内孤立波的孤立子描述有KdV、eKdV、MCC等理论模型。其中,KdV是最早描述孤立子的一类理论模型,它的前提条件是非线性和色散性是平衡的,但对于大振幅内孤立波来说,两者很有可能不平衡,所以KdV理论存在一个极限振幅,不适用于大振幅内孤立波[6-8]。eKdV理论通过在KdV理论中加入一个立方非线性项使方程不再满足非线性和色散性的平衡,但仍然存在一个极限振幅的情况。而目前最为准确的孤立子模型为MCC理论,在弱色散条件下不对非线性进行限制,属于完全非线性两层流体孤立子理论模型。
现存在的大多内孤立波理论是基于刚盖假定下得出的,但真实海洋和实验室环境均存在自由表面,Kodaira等[9]提出在自由表面条件下的强非线性MCC理论解(MCC-FS),相较于其他波面方程对内孤立波的表达更为准确。该方程假设自由表面波面位于z=h1+ζ1处,交界面位于z=ζ2处,即自由表面波面方程为ζ1,两层流体的交界面波面方程为ζ2,则MCC-FS可以表示为二阶微分方程组:
| $ \begin{array}{c} \alpha_{j 1} \eta_{1}^{\prime \prime}+\alpha_{j 2} \eta_{2}^{\prime \prime}+\alpha_{j 3} \eta_{1}^{\prime 2}+\alpha_{j 4} \eta_{3}^{\prime 2}+\alpha_{j s} \eta_{1}^{\prime} \eta_{2}^{\prime}=\alpha_{j 6} \\ j=1, 2 \end{array} $ | (1) |
式中:η1=h1+ζ1-ζ2;
| $ \begin{aligned} &\eta_{2}=h_{2}+\zeta_{2};\\ &\alpha_{11}=\frac{1}{3} \frac{c^{2} h_{1}^{2}}{\eta_{1}}, \alpha_{12}=\frac{1}{2} \frac{c^{2} h_{1}^{2}}{\eta_{1}}, \\ &\alpha_{13}=-\frac{1}{6} \frac{c^{2} h_{1}^{2}}{\eta_{1}}, \alpha_{14}=\frac{1}{2} \frac{c^{2} h_{1}^{2}}{\eta_{1}^{2}}, \alpha_{15}=0, \\ &\alpha_{16}=-g\left[\left(\eta_{1}-h_{1}\right)+\left(\eta_{2}-h_{2}\right)\right]+\\ &\frac{1}{2} c^{2}\left[1-\left(\frac{h_{1}}{\eta_{1}}\right)^{2}\right]\\ &\alpha_{21}=\frac{1}{2} \frac{\rho c^{2} h_{1}^{2}}{\eta_{1}}, \alpha_{22}=\frac{\rho c^{2} h_{1}^{2}}{\eta_{1}}+\frac{1}{3} \frac{c^{2} h_{2}^{2}}{\eta_{2}}, \\ &\alpha_{23}=-\frac{1}{2} \frac{\rho c^{2} h_{1}^{2}}{\eta_{1}^{2}}, \alpha_{24}=-\frac{1}{6} \frac{c^{2} h_{2}^{2}}{\eta_{2}^{2}}, \alpha_{25}=-\frac{\rho c^{2} h_{1}^{2}}{\eta_{1}^{2}}, \\ &\alpha_{26}=-g\left[\rho\left(\eta_{1}-h_{1}\right)+\left(\eta_{2}-h_{2}\right)\right]+\\ &\frac{1}{2} c^{2}\left[1-\left(\frac{h_{2}}{\eta_{2}}\right)^{2}\right]。\end{aligned} $ |
为评价本实验造波有效性,将生成的内孤立波波形与理论解进行对比。针对h1:h2=1:5,选取无量纲波幅ζ/h1=0.875以及ζ/h1=1.323的工况,提取内孤立波波面数据,并将波形与KdV、eKdV、MCC等理论解波形进行对比,如图 3(a)、(b)所示,其中c为波速,横坐标为无量纲相位,纵坐标为无量纲振幅。

|
Download:
|
| 图 3 实验波形与理论波形对比 Fig. 3 The comparison between experimental waveform and theoretical solutions | |
根据图 3可以看出,本实验能生成与孤立子模型吻合良好的内孤立波,且与MCC-FS方程控制的波面最为贴近,满足Kodaira等[9]对内孤立波的描述方式,可进一步研究其伴生流场特征。
2.2 速度场演变特性分析为研究不同波幅内孤立波流场的特征,通过控制造波塌陷区高度生成不同波幅的内波,设置上层流体深度h1=5 cm,下层流体深度h2=25 cm,塌陷区域宽度xL=35 cm,无因次化塌陷区域高度di/h1=0.6,1.2,1.8,2.4(分别为工况1~工况4)的4组工况进行实验(本实验生成均为自左向右传播的下凹型内孤立波)。以初始时刻两层流体的交界线为x轴,CCD相机视野中心竖直方向为z轴,分别取内孤立波传播方向、垂直向上为x轴和z轴的正方向,建立XOZ二维直角坐标系对速度场、涡量场进行分析。
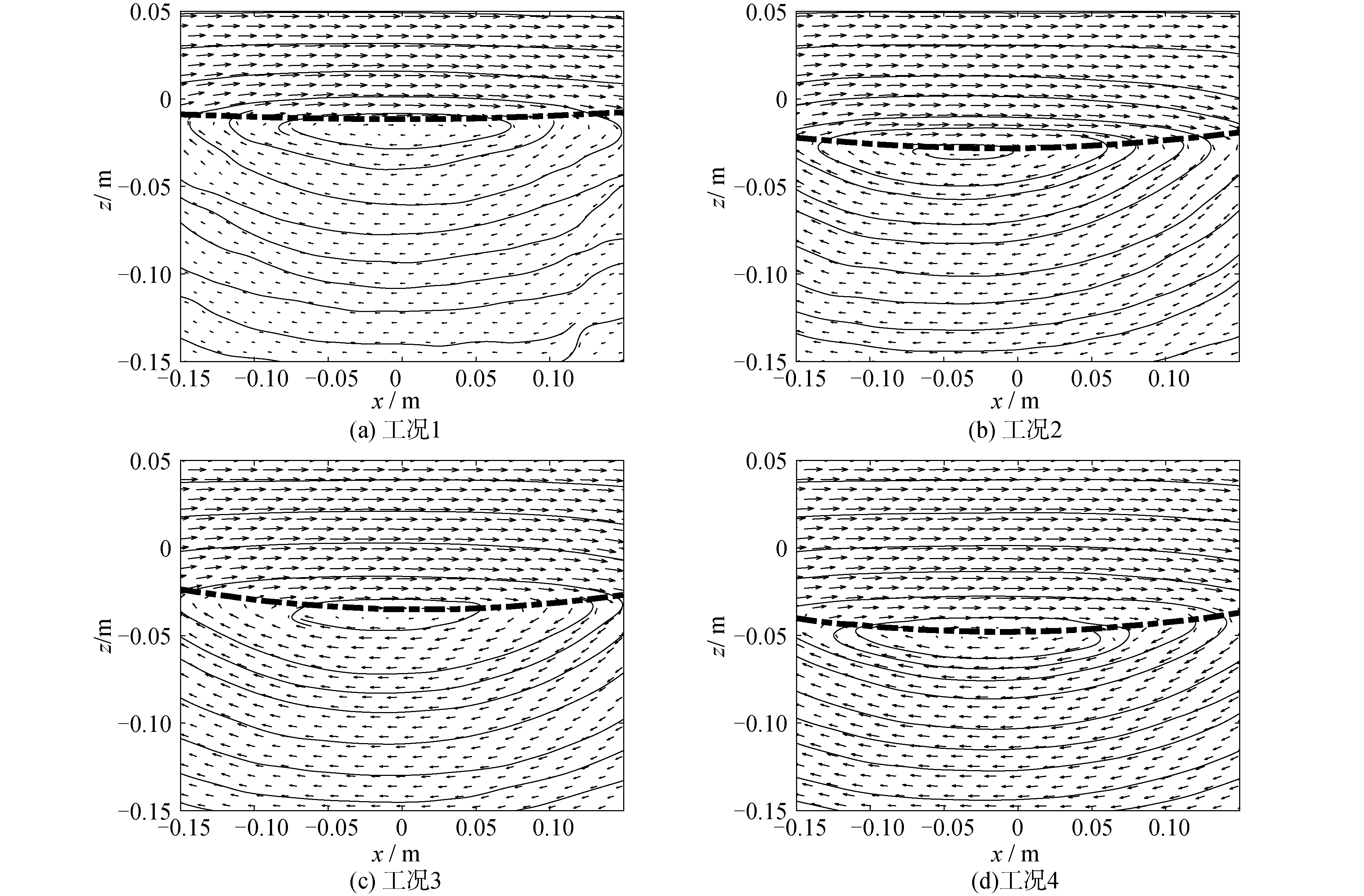
图 4给出了工况1~工况4波谷传播到视野中心时刻的速度场分布情况,图中带有箭头的短线为速度矢量,较细实线为流线,较粗虚线为内孤立波波面线。从图中可以看出,以波谷位置处的垂向线为轴,其左右两侧呈现高度对称性。以波面线为界,波面线上方的流体质点运动速度与内孤立波传播方向相同,下方流体质点的运动速度则与内孤立波传播方向相反,且在波面线附近流体质点的运动速度最小。在内孤立波传播方向的前半部分,上下层流体均呈现向下运动的趋势,后半部分则相反,整个速度场表现为一个围绕波面线顺时针的漩涡形状。
|
Download:
|
| 图 4 内孤立波速度场分布 Fig. 4 Internal solitary wave velocity field distribution | |
从图 4结合表 1可以看出,上下层流体质点的运动速度均随着内孤立波振幅的增大而增大,且在传播过程中存在明显的剪切流,可为实际海洋中内孤立波在传播过程中对海洋工程结构物和海洋内部物质的输送规律提供一定参考价值[20-21]。上述除流体质点的速度幅值外4个工况表现出相似性,下面就仅以工况2为例研究内孤立波传播过程中流场变化以及流场分布情况。
| 表 1 速度幅值 Table 1 Velocity amplitude |
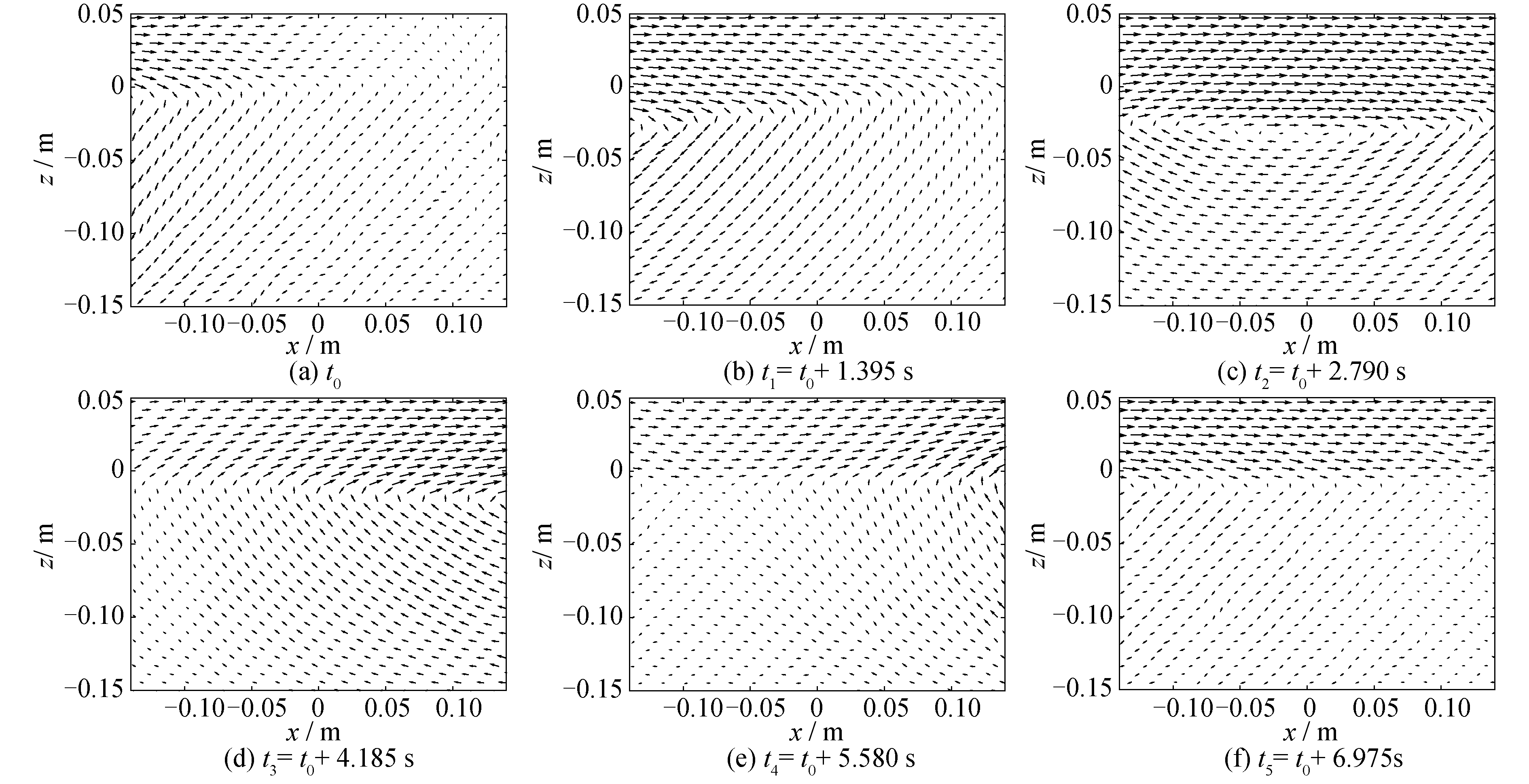
图 5给出工况2内孤立波刚传播到CCD相机视野范围内至完全离开视野范围的时间序列图像。现以坐标为(0,-0.05)处的流体质点为例分析内孤立波向前传播过程中对此质点的运动规律:t0~t1时刻,受内孤立波前部流场的影响,质点呈现向左下方的运动趋势,随着内孤立波的向前传播;t1~t2时刻,流体质点处于内孤立波波谷附近,此时质点的运动速度接近于零;t2~t3时刻,受到内孤立波后部流场的影响,质点先向左上方运动;t4时刻,内孤立波大部分离开视野范围,此时此处的质点速度又趋近于零。通过观察整个速度场随时间变化的过程,内孤立波在传播过程中速度场可以保持顺时针涡旋的形状稳定向前传播。同时发现,t5时刻当内孤立波完全离开视野范围时,下层流体质点的速度已经几乎为零,但上层流体仍保持水平流动,且该水平速度与内孤立波经过时的水平速度相比衰减很小。
|
Download:
|
| 图 5 内孤立波速度场时间序列 Fig. 5 Time series of internal solitary wave velocity field | |
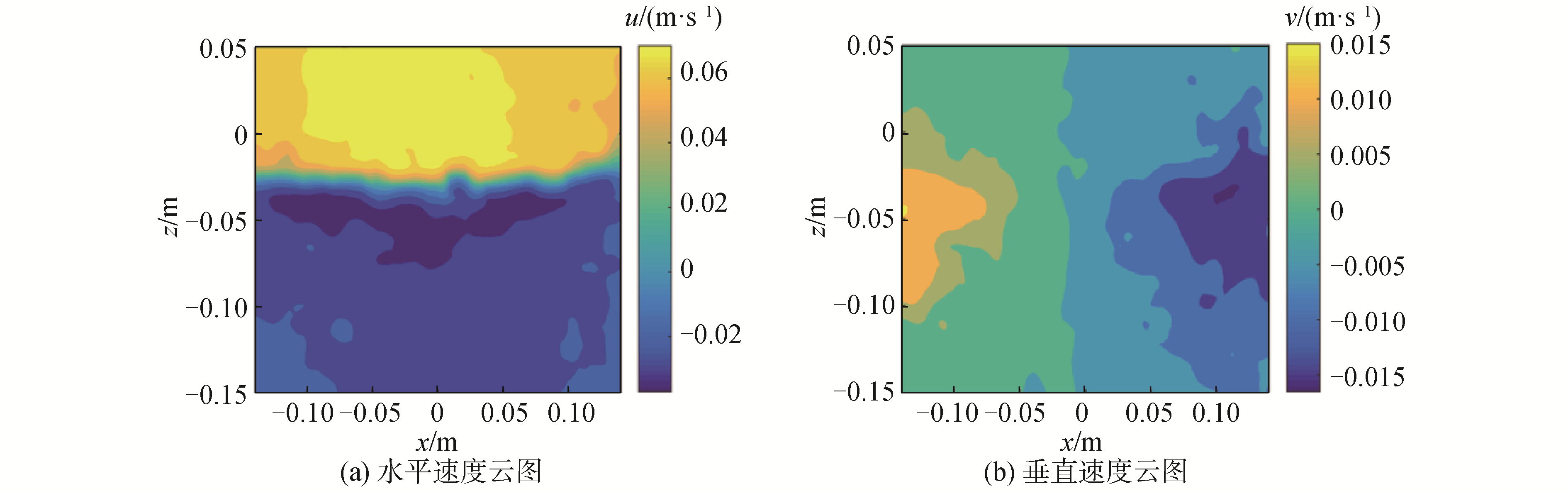
图 6给出工况2中水平方向(图 6(a))和垂直方向(图 6(b))的速度分布云图,可以观察发现,内孤立波的水平速度分量大小总体上要大于垂向速度分量大小。且在水平速度分量云图中可以看出,上层流体速度大小要明显大于下层流体速度大小,由此可知,在内孤立波传播过程中上层流体以水平流动为主要流动形式;而垂向速度分量,以内孤立波最大位移处的垂向线为轴,两层呈近似对称分布。
|
Download:
|
| 图 6 速度分布云图 Fig. 6 Cloud maps of velocity distributions | |
图 7以工况2为例,选取4个监测点给出水平速度分量在不同上下层流体深度处随时间变化的时历曲线。其中,z1为静止时刻上层流体的中心位置,z2为1/2振幅位置,z3为波谷下方2 cm位置,z4为波谷下方6 cm位置,黑色点划线则为波谷传播至视野中心时刻(t=8.214 s)。从图中可以看出,4个位置的水平速度大小和持续时间关于波谷呈现了同样高度对称性。不同的是,内孤立波波面以上(z1和z2位置),z2位置处水平速度绝对值大于零的持续时间短于z1位置,即z2比z1位置速度变化更加剧烈,但波面以下(z3和z4位置),水平速度绝对值大于零的持续时间则近乎相同。

|
Download:
|
| 图 7 4种不同深度水平流速时历曲线 Fig. 7 Time series of four difference depth horizontal velocity | |
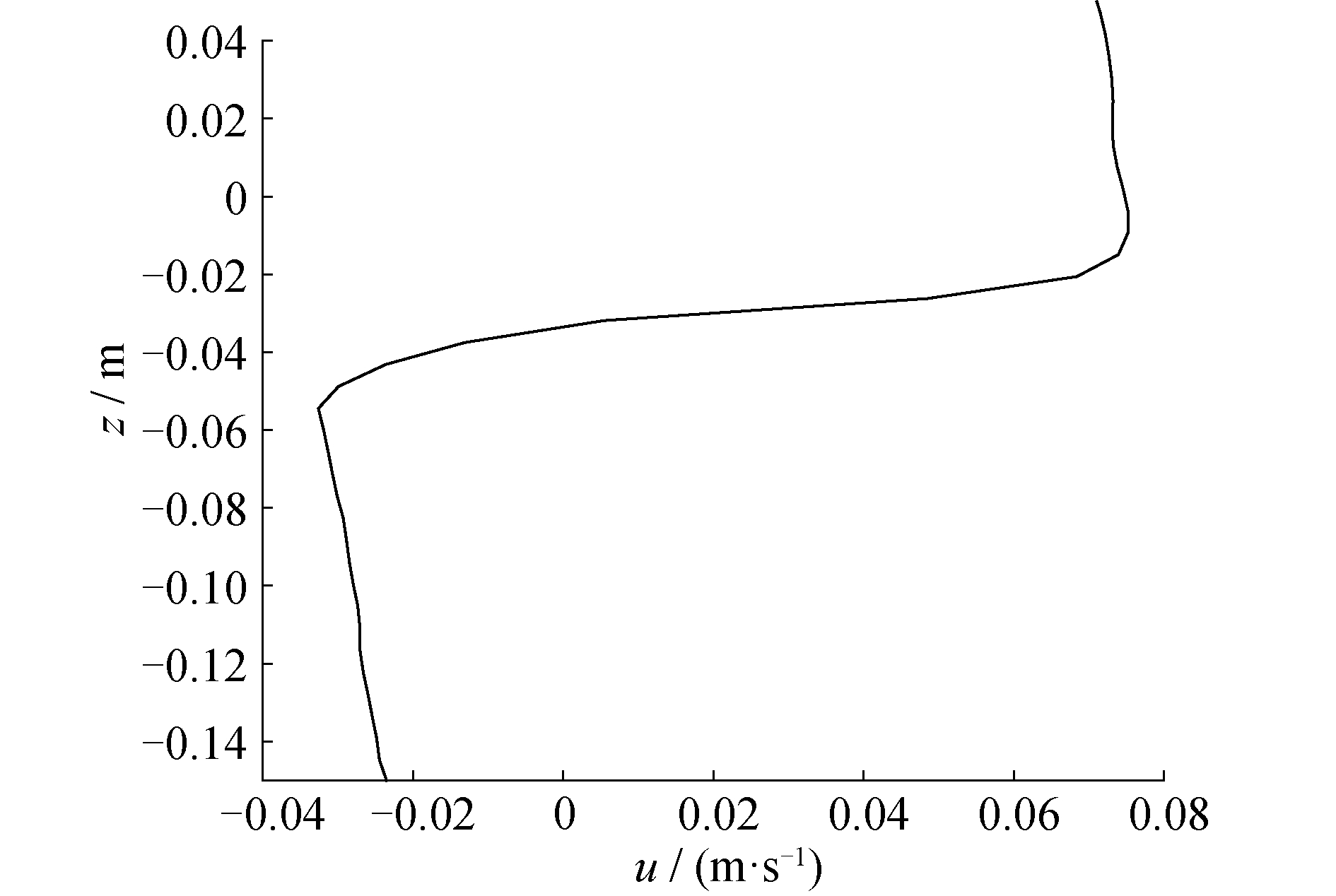
图 8为工况2的波谷位置垂直方向上水平流速沿水深方向的分布曲线,由图中所得,从自由表面处,随着水深的增加,其水平流速基本保持不变,当水深增加到某一位置时,流速开始迅速减小并在波谷处附近减小到零。在波面以下,水平流速方向相反,随着水深增加,水平流速的绝对值先迅速增大至某个值后缓慢减小,由此可见,波面附近速度的变化最为剧烈,这与图 7所描述的现象趋于一致。
|
Download:
|
| 图 8 波谷位置水平流速沿垂直方向分布曲线 Fig. 8 Trough position horizontal velocity distribution curve along the vertical direction | |
图 9给出工况1~工况4涡量场空间分布情况(与图 7相对应),取涡量逆时针为正,可以看出,对于本实验所生成的内孤立波,波面涡旋呈顺时针方向,且在内孤立波波面附近处的涡强度最大,随着内孤立波振幅的增大,涡量场变得更加剧烈的同时也保持着高度的相似性。

|
Download:
|
| 图 9 涡量场分布 Fig. 9 Vorticity field distribution | |
图 10以工况2为例给出涡量谷值(最大负涡量)在x=0处随时间变化曲线,结果表明,最大负涡量在内孤立波传播过程中呈现先增大后又减小的趋势,7~9 s内孤立波波谷经过此处,为负涡量最大时段,12~17 s,由于尾波的存在,最大负涡量值再次出现一个较小幅度的先增大后减小的趋势,随着内孤立波完全离开视野范围,涡量值在零附近小幅度波动。虽然涡量谷值随时间变化存在小幅度的振荡,流场表现出一定的紊乱。但其时历曲线的总体趋势与内孤立波波形具有相似的形态,说明内孤立波波面附近流场变化的剧烈程度。

|
Download:
|
| 图 10 涡量谷值时历曲线 Fig. 10 Time series of minimum vorticity | |
图 11给出4个工况下波谷垂向位置涡量值在竖直方向的分布情况。从图中可以看出,4个工况涡量值从自由表面处向下到波谷上方某一位置在零附近以较小的幅度波动,随着流体深度的增加则呈现先增大后减小的趋势,到波谷位置处涡量达到最大值,随后又在零附近波动,但下层流体涡量值在零附近的波动幅度稍大于上层流体。对于4个工况来说,涡量在竖直方向变化的整体趋势大致相同,随着波幅的增大,涡量最大值以及最大值所处位置逐渐增加,但涡量值从增加到减小的变化过程所对应的流体深度并未显著增加,仍然保持在一定范围内。

|
Download:
|
| 图 11 波谷位置涡量垂向分布 Fig. 11 The vertical distribution of vorticity at the trough position | |
1) 实验波形与多组理论解进行比较,与现存最为准确的MCC理论解吻合最佳,能够生成稳定传播的内孤立波,并可准确测量其流场数据,实验结果可为理论孤立波的伴生流场提供依据并且可为实际海洋内孤立波流场特征提供一定参考。
2) 内孤立波在传播过程中速度场有较好的稳定性与对称性,波面线以上流体质点速度与内孤立波传播方向相同,波面线以下流体速度与内孤立波传播方向相反。上层流体的水平速度分量占据整个速度的主要部分,且在波面附近流体质点的速度变化最为剧烈。
3) 围绕内孤立波波面涡呈顺时针方向,随内波波幅增大涡量场表现形式相似,且涡量峰值随时间变化趋势与内孤立波波形基本趋于一致,涡量最大值出现在波谷附近,波谷垂向位置涡量从增大到减小的过程所对应流体深度的变化并未随波幅的增大而显著增加。
| [1] |
JACKSON C. Internal wave detection using the moderate resolution Imaging spectroradiometer (MODIS)[J]. Journal of geophysical research:oceans, 2007, 112(C11): C11012. DOI:10.1029/2007JC004220 (  0) 0)
|
| [2] |
DUDA T F, LYNCH J F, IRISH J D, et al. Internal tide and nonlinear internal wave behavior at the continental slope in the northern South China Sea[J]. IEEE journal of oceanic engineering, 2004, 29(4): 1105-1130. DOI:10.1109/JOE.2004.836998 (  0) 0)
|
| [3] |
KLYMAK J M, PINKEL R, LIU C, et al. Prototypical solitons in the South China Sea[J]. Geophysical research letters, 2006, 33(L1160711). (  0) 0)
|
| [4] |
CHAKRABARTI S. Handbook of offshore engineering (2-volume set)[M]. Amsterdam: Elsevier Ltd, 2005.
(  0) 0)
|
| [5] |
DE VRIES G. XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves[J]. The London, Edinburgh, and Dublin philosophical magazine and journal of science, 1895, 39(240): 422-443. DOI:10.1080/14786449508620739 (  0) 0)
|
| [6] |
FUNAKOSHI M, OIKAWA M. Long internal waves of large amplitude in a two-layer fluid[J]. Journal of the physical society of japan, 1986, 55(1): 128-144. DOI:10.1143/JPSJ.55.128 (  0) 0)
|
| [7] |
CHOI W, CAMASSA R. Fully nonlinear internal waves in a two-fluid system[J]. Journal of fluid mechanics, 1999, 396: 1-36. DOI:10.1017/S0022112099005820 (  0) 0)
|
| [8] |
CAMASSA R, CHOI W, MICHALLET H, et al. On the realm of validity of strongly nonlinear asymptotic approximations for internal waves[J]. Journal of fluid mechanics, 2006, 549: 1-23. DOI:10.1017/S0022112005007226 (  0) 0)
|
| [9] |
KODAIRA T, WASEDA T, MIYATA M, et al. Internal solitary waves in a two-fluid system with a free surface[J]. Journal of fluid mechanics, 2016, 804: 201-223. DOI:10.1017/jfm.2016.510 (  0) 0)
|
| [10] |
CHEN Chenyuan, HSU J R C, CHENG M H, et al. An investigation on internal solitary waves in a two-layer fluid:propagation and reflection from steep slopes[J]. Ocean engineering, 2007, 34(1): 171-184. DOI:10.1016/j.oceaneng.2005.11.020 (  0) 0)
|
| [11] |
黄文昊, 尤云祥, 王旭, 等. 有限深两层流体中内孤立波造波实验及其理论模型[J]. 物理学报, 2013, 62(8): 084705. HUANG Wenhao, YOU Yunxiang, WANG Xu, et al. Wave-making experiments and theoretical models for internal solitary waves in a two-layer fluid of finite depth[J]. Acta physica sinica, 2013, 62(8): 084705. (  0) 0)
|
| [12] |
王旭, 林忠义, 尤云祥. 内孤立波与直立圆柱体相互作用特性数值模拟[J]. 哈尔滨工程大学学报, 2015, 36(1): 6-11. WANG Xu, LIN Zhongyi, YOU Yunxiang. Numerical simulation for the interaction characteristics of internal solitary waves with a vertical circular cylinder[J]. Journal of Harbin Engineering University, 2015, 36(1): 6-11. (  0) 0)
|
| [13] |
盛立, 王怡然, 尤云祥, 等. 有限深两层流体中内孤立波传播演化理论模型研究[J]. 水动力学研究与进展(A辑), 2016, 31(6): 659-672. SHENG Li, WANG Yiran, YOU Yunxiang, et al. Investigation on propagation and evolution models for internal solitary waves in a two layer fluid system of finite depth[J]. Chinese journal of hydrodynamics, 2016, 31(6): 659-672. (  0) 0)
|
| [14] |
许联锋, 陈刚, 李建中, 等. 粒子图像测速技术研究进展[J]. 力学进展, 2003(04): 533-540. XU Lianfeng, CHEN Gang, LI Jianzhong, et al. Reserch progress of particle image velocimetry[J]. Advances in mechanics, 2003(04): 533-540. DOI:10.3321/j.issn:1000-0992.2003.04.010 (  0) 0)
|
| [15] |
MOORE C D, KOSEFF J R, HULT E L. Characteristics of bolus formation and propagation from breaking internal waves on shelf slopes[J]. Journal of fluid mechanics, 2016, 791: 260-283. DOI:10.1017/jfm.2016.58 (  0) 0)
|
| [16] |
孟静, 王树亚, 陈旭, 等. 内孤立波对小直径直立桩柱作用力的实验研究[J]. 海洋与湖沼, 2018, 49(3): 535-540. MENG Jing, WANG Shuya, CHEN Xu, et al. An experimental study on the force of internal solitary wave on a cylinder of small diameter[J]. Oceanologia et limnologia sinica, 2018, 49(3): 535-540. (  0) 0)
|
| [17] |
殷文明, 郭海燕, 廖发林, 等. 内孤立波对不同水深竖直圆柱体水平作用力分析[J]. 中国海洋大学学报, 2018, 48(9): 125-131. YIN Wenming, GUO Haiyan, LIAO Falin, et al. Analysis of horizontal forces on vertical cylinders under internal solitary waves in different depths[J]. Periodical of Ocean University of China, 2018, 48(9): 125-131. (  0) 0)
|
| [18] |
黄鹏起, 陈旭, 孟静, 等. 内孤立波破碎所致混合的实验研究[J]. 海洋与湖沼, 2016, 47(3): 533-539. HUANG Pengqi, CHEN Xu, MENG Jing, et al. An experimental study on mixing induced by internal solitary wave breaking[J]. Oceanologia et limnologia sinica, 2016, 47(3): 533-539. (  0) 0)
|
| [19] |
段俐, 康琦, 申功炘. PIV技术的粒子图像处理方法[J]. 北京航空航天大学学报, 2000, 26(1): 79-82. DUAN Li, KANG Qi, SHEN Gongxin. Image processing method of PIV technique[J]. Journal of Beijing University of Aeronautics and Astronautics, 2000, 26(1): 79-82. DOI:10.3969/j.issn.1001-5965.2000.01.022 (  0) 0)
|
| [20] |
CHEN Min, CHEN Ke, YOU Yunxiang. Experimental investigation of internal solitary wave forces on a semi-submersible[J]. Ocean engineering, 2017, 141: 205-214. DOI:10.1016/j.oceaneng.2017.06.027 (  0) 0)
|
| [21] |
BOEGMAN L, STASTNA M. Sediment resuspension and transport by internal solitary waves[J]. Annual review of fluid mechanics, 2019, 51: 129-154. DOI:10.1146/annurev-fluid-122316-045049 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


