2. 海洋信息获取与安全工业和信息化部重点实验室(哈尔滨工程大学), 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
水声探测有主动探测和被动探测2种方式。主动探测是指声呐发射声波,通过对回波信号的处理实现对目标的探测。被动探测是指声呐不发射声波,通过处理被探测目标的辐射噪声实现对目标的探测。长期以来,被动探测以其探测距离远、隐蔽性好的优点得到了广泛应用。然而,随着隐身技术的发展,潜艇辐射噪声正在以平均每年1 dB的速度逐年降低,这给被动探测带来了十分严峻的挑战[1]。鉴于被动探测的局限性,主动探测受到了足够的重视,并得到了充分的发展。在一些对隐蔽性没有要求的场景下,例如海港监测,主动探测往往能胜任更加复杂的探测任务[2-3]。然而,在主动探测中,混响的干扰是无法回避的。在某些情况下,目标回波会常常被淹没在混响之中。而且,混响与发射信号有着强相干性,很难通过常规的方法抑制和消除。
对于如何降低混响给主动探测带来的不良影响进而实现更好的探测性能,科研人员做了长期大量的研究。Kay等[4]提出了一种使用自回归预白化的方法来抑制混响。该方法的核心思想是使用少量混响数据来构建一个自回归滤波器,通过滤波来抑制混响。此后,高阶统计算法[5]、归一化最小均方算法[6]和变步长算法[7]相继被提出用于改进预白化方法。这类方法的基本假设是混响恒定不变。在大多情况下,这种假设条件并不能严格满足。因此,在混响较为复杂的环境下,其混响抑制能力十分有限。如果发射信号是线性调频(LFM)信号,那么混响可以通过时频域的处理进行抑制。Wigner-Ville分布(WVD)是一种优秀的时频转换方法。水鹏朗等[8]利用交叉平滑伪WVD对相邻的2个接收信号进行处理,并利用两个结果的特征检测目标。夏云龙等[9]在WVD之前增加了时间反转镜的处理实现了对多重散射的抑制。尽管在数值仿真中WVD能良好表示信号的能量分布,但在实际应用中交叉项的影响仍然限制了该类方法的性能。于歌等[10]利用分数傅里叶变换(FrFT)对LFM信号进行了能量聚焦,达到了抑制混响提高探测性能的效果,但这种方法的缺点是FrFT变换的阶次很难选择。
本文提出了一种基于随机算法的抗混响探测方法,着眼于对各帧信号之间关联特性的分析。不同于传统的探测方法对一帧数据的处理,本文方法是将累积的多帧数据进行联合处理。采用了低秩结构提取的计算抑制了混响,并在计算过程中对数据矩阵进行了非负约束,最终以迭代的形式实现了在强混响的环境下对移动目标的探测。本文方法能在低信混比的条件下探测到目标。
1 抗混响目标探测方法 1.1 低秩结构提取低秩矩阵近似在数据分析和科学计算中扮演着一个重要的角色,截断奇异值分解(truncated singular value decomposition)、秩呈现QR分解(rank-revealing QR decomposition)都可以作是低秩矩阵近似的一种形式。随机算法为低秩矩阵近似提供了一个强有力的工具。在很多情况下,随机算法比矩阵正交分解的算法,在精确程度、计算速度和鲁棒性上有着明显的优势。
考虑一个矩阵X∈RM×N,其潜在的低秩结构的秩为r。对其进行线性测量,即
| $ \left\{\begin{array}{l} \boldsymbol{Y}=\mathit{\pmb{\Omega X}} \\ \boldsymbol{\tilde{Y}}=\mathit{\pmb{\tilde{\Omega}}} \boldsymbol{X}^{\mathrm{T}} \end{array}\right. $ |
式中:Ω∈Rr×M和
| $ \boldsymbol{L}=\tilde{\boldsymbol{Y}}^{\mathrm{T}}\left(\mathit{\pmb{\Omega}} \tilde{\boldsymbol{Y}}^{\mathrm{T}}\right)^{\dagger} \boldsymbol{Y} $ | (1) |
来提取[12]。式中(·)†表示矩阵的广义逆。为了提高低秩结构提取的精度,可以采用双向投影的方式进行改进[13]。先进行行投影,即:
| $ {\mathit{\boldsymbol{Y}}_1} = {\mathit{\pmb{\varOmega} \pmb{X}}} $ | (2) |
然后以Y1为感知矩阵进行列投影,即:
| $ {\mathit{\boldsymbol{Y}}_2} = {\mathit{\boldsymbol{Y}}_1}{\mathit{\boldsymbol{X}}^{\rm{T}}} = \mathit{\boldsymbol{ \boldsymbol{\varOmega} X}}{\mathit{\boldsymbol{X}}^{\rm{T}}} $ | (3) |
最后用Y2为感知矩阵替换Ω对X重新进行行投影,即:
| $ {\mathit{\boldsymbol{Y}}_3} = {\mathit{\boldsymbol{Y}}_2}\mathit{\boldsymbol{X}} = \mathit{\mathit{\pmb{\varOmega} \boldsymbol{X}}}{\mathit{\boldsymbol{X}}^{\rm{T}}}\mathit{\boldsymbol{X}} $ | (4) |
结合式(1)~(4),则改进后的低秩结构提取公式为:
| $ \boldsymbol{L}=\boldsymbol{Y}_{2}^{\mathrm{T}}\left(\boldsymbol{Y}_{2} \boldsymbol{Y}_{2}^{\mathrm{T}}\right)^{\dagger} \boldsymbol{Y}_{3} $ | (5) |
本文方法的应用背景为在浅海对近距离的移动目标进行探测。首先做2点假设:1)声线沿直线传播;2)在时间上,前后帧混响具有较强的相关性。实际环境中,这2点假设十分容易满足。浅海可以认为是一个等声速梯度的环境,因而声线不会发生弯曲。而且由于距离较近,声信号非几何衰减可以忽略,几何衰减可以用自动增益控制进行补偿。混响主要有海面散射、海水体积散射、海底界面散射三种来源。在浅海中,由于海底散射产生的混响占接收到混响中的主要部分。海底结构一般十分稳定,因此声呐接收到的各帧混响虽然不会完全相同,但会具有很强的相关性。
考虑一个主动声呐重复发射一个脉冲信号N次,将第n个和第n+1个脉冲信号之间的接收信号进行波束形成,得到B[n]∈RNr×Nθ。其中,Nr是矩阵在距离方向上的维度,Nθ矩阵在角度方向上的维度。定义xn∈RNrNθ×1为B[n]的向量化,即:
| $ \boldsymbol{x}_{n}=\left[\boldsymbol{b}_{1}[n] ; \boldsymbol{b}_{2}[n] ; \cdots ; \boldsymbol{b}_{j}[n] ; \cdots ; \boldsymbol{b}_{N_{\theta}}[n]\right] $ |
式中,bj[n]为B[n]的第j列。则多帧接收的数据可以用一个NrNθ×N的矩阵来表示,即
| $ \boldsymbol{X}=\left[\boldsymbol{x}_{1}, \boldsymbol{x}_{2}, \cdots, \boldsymbol{x}_{n}, \cdots, \boldsymbol{x}_{N}\right] $ |
前文中提到,混响具有强相关性,则多帧数据矩阵X的各列具有强相关性,因此X必定具有潜在的低秩结构。之所以称X具有低秩结构而不是直接称X为低秩矩阵,是因为X各列中存在非相关的分量。这些非相关的分量对X的影响是少量的、局部的,因此X可以被分解为一个低秩矩阵和一个稀疏矩阵加和的形式,即:
| $ \boldsymbol{X}=\boldsymbol{L}+\boldsymbol{S} $ | (6) |
式中:L∈RNrNθ×N表示低秩部分,其包含了混响的相关部分,S∈RNrNθ×N表示稀疏部分,其包含了运动目标、混响的非相关部分和噪声。一般情况下,运动目标的能量要大于混响的非相关部分和噪声,S∈RNrNθ×N可以进一步拆分为S′∈RNrNθ×N和Z∈RNrNθ×N两部分。S′包含了运动目标,Z包含了混响的非相关部分和噪声,可以用一个阈值ξ来区分二者,即:
| $ \begin{aligned} \boldsymbol{S^{\prime}} &=\operatorname{Th}_{\xi}[\boldsymbol{S}] \\ \boldsymbol{Z} &=\boldsymbol{S}-\boldsymbol{S^{\prime}} \end{aligned} $ |
式中:Thξ[·]为阈值函数,若Si, j、S′i, j分别为S、S′第i行、第j列的元素,则
| $ S_{i, j}^{\prime}=\operatorname{Th}_{\xi}\left[S_{i, j}\right]=\left\{\begin{array}{ll} S_{i, j}, & S_{i, j}>\xi \\ 0, &其他 \end{array}\right. $ |
于是式(6)可以写成:
| $ \mathit{\boldsymbol{X}}{\rm{ = }}\mathit{\boldsymbol{L}}{\rm{ + }}\mathit{\boldsymbol{S}}{\rm{' + }}\mathit{\boldsymbol{Z}} $ |
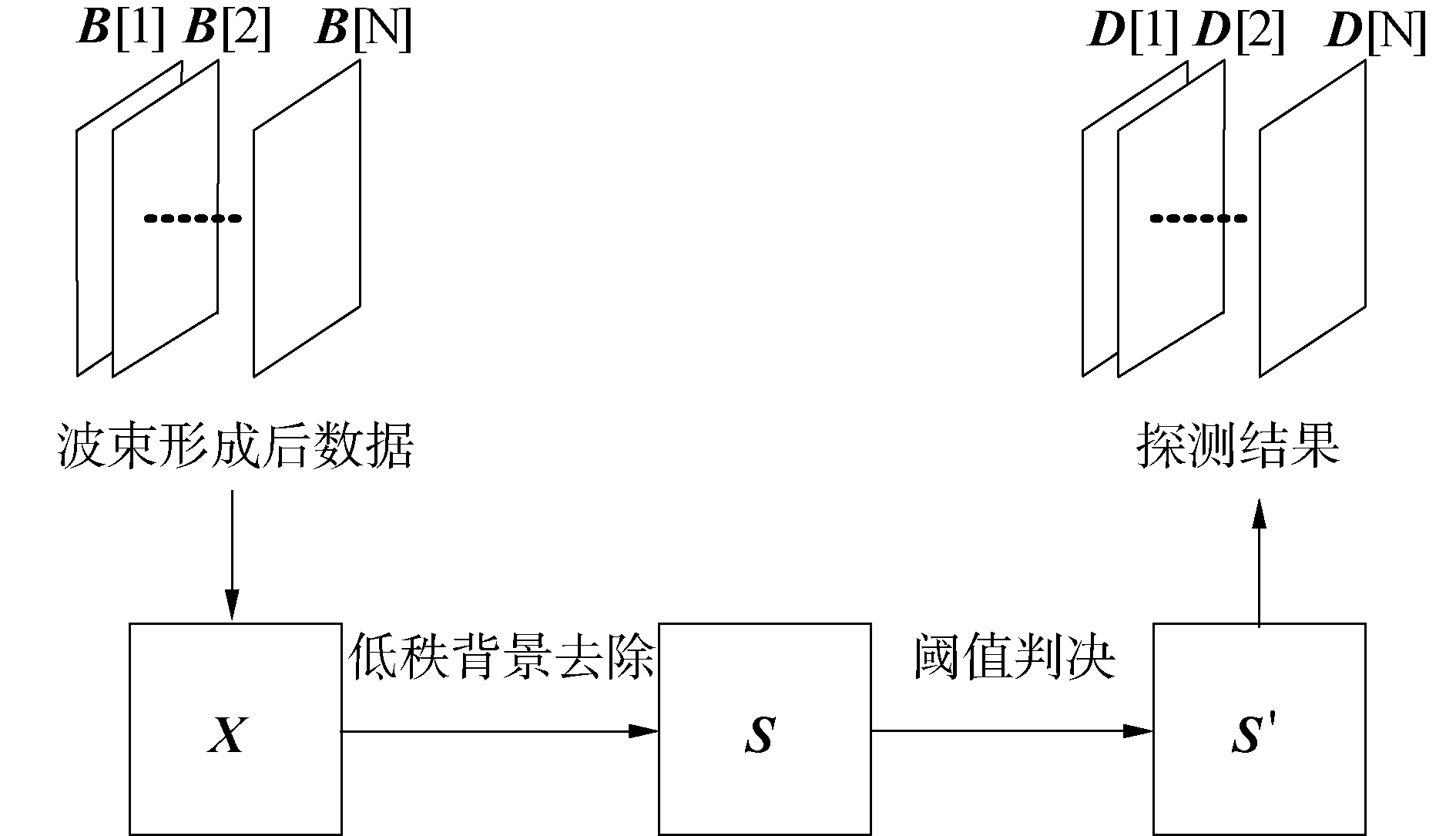
将得到的S′进行逆向量化可以得到每一帧数据的探测结果D[n]∈RNr×Nθ。整个数据处理流程如图 1所示。
|
Download:
|
| 图 1 数据处理流程 Fig. 1 Processing flow of the beamforming data | |
上述过程的关键在于如何求得L并从X。虽然1.1节中介绍了如何提取矩阵的低秩结构,但是对于低秩结构非常明显的矩阵,很难将低秩部分和稀疏部分进行分离。为了解决这一问题,本文加入了对矩阵的非负约束,并使用迭代方法。因为处理的数据为波束形成后的数据,所以分解后的矩阵都应该是非负矩阵。加入非负约束是迭代的前提,通过迭代可以使低秩结构提取逐步精确。目标探测方法步骤总结如下:
1) 设置输入参数。数据序列{B[n]},最大迭代次数K,门限ξ,相对误差上限ε;
2) 初始化。令S=0,生成感知矩阵Ω,向量化{B[n]}→X, X=XT;
3) 迭代。
for k =1: K // K次迭代
Y1=Ω
L=Y2T(Y2Y2T)†Y3 //低秩结构提取
S=X-L //计算数据矩阵稀疏部分
S=Th0[S]//非负约束
If ‖X-S-L‖F/‖X‖F < ε, break; end
//判断是否终止迭代,‖·‖ F为Frobenius范数
end
4) 阈值检测。S′=Thξ[S];
5) 逆向量化并输出探测结果。S′=S′T, S′→{D[n]}。
值得注意的是,数据矩阵X中的低秩结构来源于混响,而各帧混响具有强相关性,则X的低秩部分秩应该为1,即r=1。另外,声呐数据的数据量一般不会很大,因此NrNθ
为了讨论在不同情况下本文目标探测方法的性能,接下来将进行一系列的数值仿真。在对检测算法进行数值仿真之前首先需要建立一个混响模型。定义R[n]∈RNr×Nθ为波束空间中的第n帧混响序列,则各帧混响可以由下式得到
| $ \mathit{\boldsymbol{R}}[n] = {\rm{ }}\beta \mathit{\boldsymbol{R}}\left[ 0 \right] + (1 - {\rm{ }}\beta )\mathit{\boldsymbol{A}}[n] $ | (7) |
式中:β是一个用来控制混响相关和非相关部分比例的参数;R[0]表示初始能量分布,它由实际水域中散射体的分布和性质决定;A[0]表示第n帧混响的非相关部分。若Ai, j[n]表示A[n]的第i行、第j列的元素,则:
| $ {A_{i, j}}[n] = {\rm{ }}\alpha {A_{i, j}}[n{\rm{ }} - 1] + (1 - {\rm{ }}\alpha )v $ | (8) |
式中:0 < α < 1是一个随机变量,控制着混响非相关部分变化的剧烈程度。
使用上述混响模型生成20帧混响。参数设置为Nr=200, Nθ=60, α=0.8, β=0.8,Ai, j[0]=0;R[0]是一个服从二维瑞利分布的随机矩阵,其尺度参数设置为1,v是一个服从高斯分布的随机变量,其期望为0,方差为1。在生成的混响数据中添加一个移动目标,目标强度为0.5,用矩阵T[n]∈RNr×Nθ来表示第n帧混响中添加的目标。若Ti, j[n]表示矩阵T[n]的第i行、第j列的元素,则
| $ T_{i, j}[n]=\left\{\begin{array}{l} 0.5 \;\;目标出现位置\\ 0\;\;其他位置 \end{array}\right. $ |
使用此数据进行一次抗混响目标探测实验,实验结果如图 2所示。图 2(a)原始数据的某一帧由于强混响的存在,目标被掩埋在混响之中,几乎不能被分辨出来。图 2(b)是经过低秩提取后各帧中非相关部分,其中包括运动目标和混响中时变的部分。从图中可以看出,原本在图 2(a)中隐藏的目标显现出来了,但是结果中还残留了一部分干扰。图 2(c)是经过阈值判决得到的目标探测结果。由于残留的干扰较弱,经过阈值判决后,残留干扰被完全消除了。将各帧目标探测的结果进行叠加,于是得到了目标的运动轨迹,如图 2(d)所示。数值仿真结果表明,本文所提出的抗混响探测方法在理论上是可行的。

|
Download:
|
| 图 2 抗混响目标探测仿真结果 Fig. 2 Simulation results of target detection with reverberation suppression | |
为了定性分析本文方法在不同混响环境下的效果,下文将进行进一步讨论。定义各帧的探测误差为:
| $ {\rm{E}}[n] = {\left\| {\mathit{\boldsymbol{T}}[n] - \mathit{\boldsymbol{D}}[n]} \right\|_{\rm{F}}} $ |
本文用探测误差来衡量探测能力。探测误差越小,说明探测方法的能力越强。
调整混响模型参数α和β,其他参数保持和之前数值仿真一致,得到数值仿真结果如图 3所示。图 3(a)为保持β=0.8不变,α分别取值为0.2、0.4、0.6、0.8和1时的探测误差。图 3(b)为保持α=0.8不变,β分别取值为0.2、0.4、0.6、0.8和1时的探测误差。从图 3中可以看出,在α和β相同的情况下各帧的探测误差有所波动但基本维持在同一水平上;而保持α和β其中之一不变,逐步增大另一个参数时,探测误差逐渐变小。由式(7)和(8)可知,α和β共同决定着各帧混响之间的相关性,α和β越大,各帧混响之间的相关性就越强。因此可以得出结论,混响的相关性越强,本文探测方法的性能就越好。

|
Download:
|
| 图 3 抗混响目标探测探测误差 Fig. 3 Detection error of target detection with reverberation suppression | |
为了验证算法的实际探测能力,在黑龙江省哈尔滨市松花江进行了外场实验。操作一个遥控无人潜水器(ROV)作为此次实验待探测的目标,使用前视声呐对其进行探测。此次实验收集到25帧数据,每帧数据波束形成后得到一个230×60的矩阵,其中在距离方向上有230个采样点,在角度方向上有60个采样点。数据处理过程中对距离和能量都进行了归一化。实验数据处理结果如图 4所示。

|
Download:
|
| 图 4 抗混响目标探测实验结果 Fig. 4 Experiment results of target detection with reverberation suppression | |
图 4(a)原始数据的某一帧,由于强混响干扰的存在,目标的具体位置很难被分辨出。图 4(b)是经过低秩提取后各帧中非相关部分,其中包括运动目标和混响中时变的部分。从中可以看出,大部分混响已经被移除,运动目标开始显露出来,但是由于残留的混响干扰范围较大,目标在图中并非十分明显。图 4(c)是经过阈值判决得到的目标探测结果。残留混响虽然影响面积很大,但是能量并不是很强,通过阈值判决后,图 4(c)中目标依然被清晰地探测出来。图 4(d)是将各帧目标探测的结果进行叠加得到的目标的运动轨迹。该结果与数值仿真结果类似,都十分清晰。实验结果表明,本文方法在真实环境中也是有效的。
3 结论1) 随机算法作为一种高效的算法,能够对矩阵的低秩部分进行的提取。
2) 本文对多帧接收数据组成的矩阵进行了低秩结构提取,并在处理过程中加入了非负约束条件,最终以迭代的方式成功实现了混响和目标的分离。本文提出的方法在理论上是可行的。
3) 本文所提出的方法在不同条件下,性能有所差异。数值仿真表明,各帧混响的相关性越强,目标探测效果就越好。
4) 本文所提出的方法在实际中也具有良好的探测性能,具有良好的推广前景。
| [1] |
杨益新, 韩一娜, 赵瑞琴, 等. 海洋声学目标探测技术研究现状和发展趋势[J]. 水下无人系统学报, 2018, 26(5): 369-387. YANG Yixin, HAN Yi'na, ZHAO Ruiqin, et al. Ocean acoustic target detection technologies:a review[J]. Journal of unmanned undersea systems, 2018, 26(5): 369-387. (  0) 0)
|
| [2] |
张杨梅.水下小目标主动探测关键技术研究[D].西安: 西北工业大学, 2017. ZHANG Yangmei. Research on the key technologies of active detection of underwater small target[D]. Xi'an: Northwestern Polytechnical University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10699-1018792669.htm (  0) 0)
|
| [3] |
李晖宙, 刘正红, 毛盾. 基于蛙人探测声纳序列图像的水下小目标跟踪算法[J]. 舰船电子工程, 2018, 38(2): 26-30, 34. LI Huizhou, LIU Zhenghong, MAO Dun. Underwater small target tracking algorithm based on diver detection sonar image sequences[J]. Ship electronic engineering, 2018, 38(2): 26-30, 34. DOI:10.3969/j.issn.1672-9730.2018.02.007 (  0) 0)
|
| [4] |
KAY S, SALISBURY J. Improved active sonar detection using autoregressive prewhiteners[J]. The journal of the acoustical society of America, 1990, 87(4): 1603-1611. DOI:10.1121/1.399408 (  0) 0)
|
| [5] |
TRUCCO A, DI SERIO S, MURINO V. Buried object detection by auto-regressive pre-whitening[C]//Proceedings of MTS/IEEE Riding the Crest into the 21st Century. Seattle, WA, USA, 1999: 126-132.
(  0) 0)
|
| [6] |
BESBES H, JEBARA S B. The pre-whitened NLMS: a promising algorithm for acoustic echo cancellation[C]//Proceedings of the 9th International Conference on Electronics, Circuits and Systems. Dubrovnik, Croatia, 2002: 875-878.
(  0) 0)
|
| [7] |
BESBES H, JEBARA S B. A variable step size pre-whitened sign algorithm with quantized normalizing factor. Application to acoustic echo cancellation[C]//Proceedings of the 2004 12th European Signal Processing Conference. Vienna, Austria, 2004: 709-712.
(  0) 0)
|
| [8] |
SHUI Penglang, LIU Hongwei, BAO Zheng. Range-spread target detection based on cross time-frequency distribution features of two adjacent received signals[J]. IEEE transactions on signal processing, 2009, 57(10): 3733-3745. DOI:10.1109/TSP.2009.2029715 (  0) 0)
|
| [9] |
XIA Yunlong, PIAO Shengchun, FU Yongqing. Combination of WVD with TRM on detection of LFM signal in inhomogeneous medium[C]//Proceedings of the 2009 4th IEEE Conference on Industrial Electronics and Applications. Xi'an, China, 2009: 3864-3867.
(  0) 0)
|
| [10] |
YU Ge, PIAO Shengchun, HAN Xiao. Fractional Fourier transform-based detection and delay time estimation of moving target in strong reverberation environment[J]. IET radar, sonar & navigation, 2017, 11(9): 1367-1372. (  0) 0)
|
| [11] |
WOOLFE F, LIBERTY E, ROKHLIN V, et al. A fast randomized algorithm for the approximation of matrices[J]. Applied and computational harmonic analysis, 2008, 25(3): 335-366. DOI:10.1016/j.acha.2007.12.002 (  0) 0)
|
| [12] |
FAZEL M, CANDES E, RECHT B, et al. Compressed sensing and robust recovery of low rank matrices[C]//Proceedings of the 2008 42nd Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 2008: 1043-1047.
(  0) 0)
|
| [13] |
ZHOU Tianyi, TAO Dacheng. GoDec: Randomized low-rank & sparse matrix decomposition in noisy case[C]//Proceedings of the 28th International Conference on Machine Learning. Bellevue, WA, USA, 2011.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


