曲线梁桥因其外形美观、适应性强的特点,而被广泛应用于各类山区公路和城市道路的桥梁工程。由于其平面不规则,地震作用下的受力更为复杂[1]。当采用隔震体系时,为了满足其位移需求,边墩处通常采用四氟滑板橡胶支座,但已有研究表明,地震作用下,由于边墩四氟滑板橡胶支座可发生相对滑移,上部结构的地震作用将主要由中墩来承担,从而会导致边墩、中墩受力不均衡。针对此问题,目前通常采用隔震支座加阻尼器的组合方法对结构的地震响应进行控制。粘滞阻尼器的力-位移滞回曲线非常饱满,耗能限位能力强,能在不增加地震惯性力的情况下,有效地控制桥梁结构的位移响应[2-3]。此外,粘滞阻尼器还具有构造简单、便于施工、受激励频率和温度影响小的特点,因此很受工程技术人员的青睐,成为减小桥梁结构关键部位地震响应的主要手段之一[4-7]。
为了使粘滞阻尼器达到预期的效果,有必要对其参数进行优化分析。对此,国内外诸多学者开展了相关研究。文献[8]通过建立与粘滞阻尼器参数相关的拉格朗日方程,利用顺序搜索法求解阻尼器参数的最优解。文献[9]为优化粘滞阻尼器对双塔斜拉桥的减震效果,应用最小二乘回归分析法建立关键截面参数与阻尼参数之间的数学模型,以控制截面内力和变形最小为原则,通过求解拟合方程的极值得到最优设计参数。文献[10]针对现有阻尼器参数优化方法的缺陷,基于斜拉桥的随机地震响应,通过最小化粘滞阻尼器的阻尼力得到阻尼器参数的最优解。以上关于粘滞阻尼器参数优化的研究对象均是斜拉和悬索等大跨度柔性桥梁,针对连续梁桥的相关研究还不够系统,特别是对曲线连续梁桥则更为少见[11-12]。显然,对隔震曲线连续梁桥采用粘滞阻尼器进行减震控制优化研究有待进一步加强。
为此,本文以某三跨隔震曲线连续梁桥为研究对象,采用非线性动力时程法,分析了粘滞阻尼器阻尼系数和速度指数对其地震响应的影响。在此基础上,基于零阶优化算法,以各墩墩底剪力之和为目标函数,进行了粘滞阻尼器参数优化分析,旨在为隔震曲线连续梁桥的减震设计与研究提供参考。
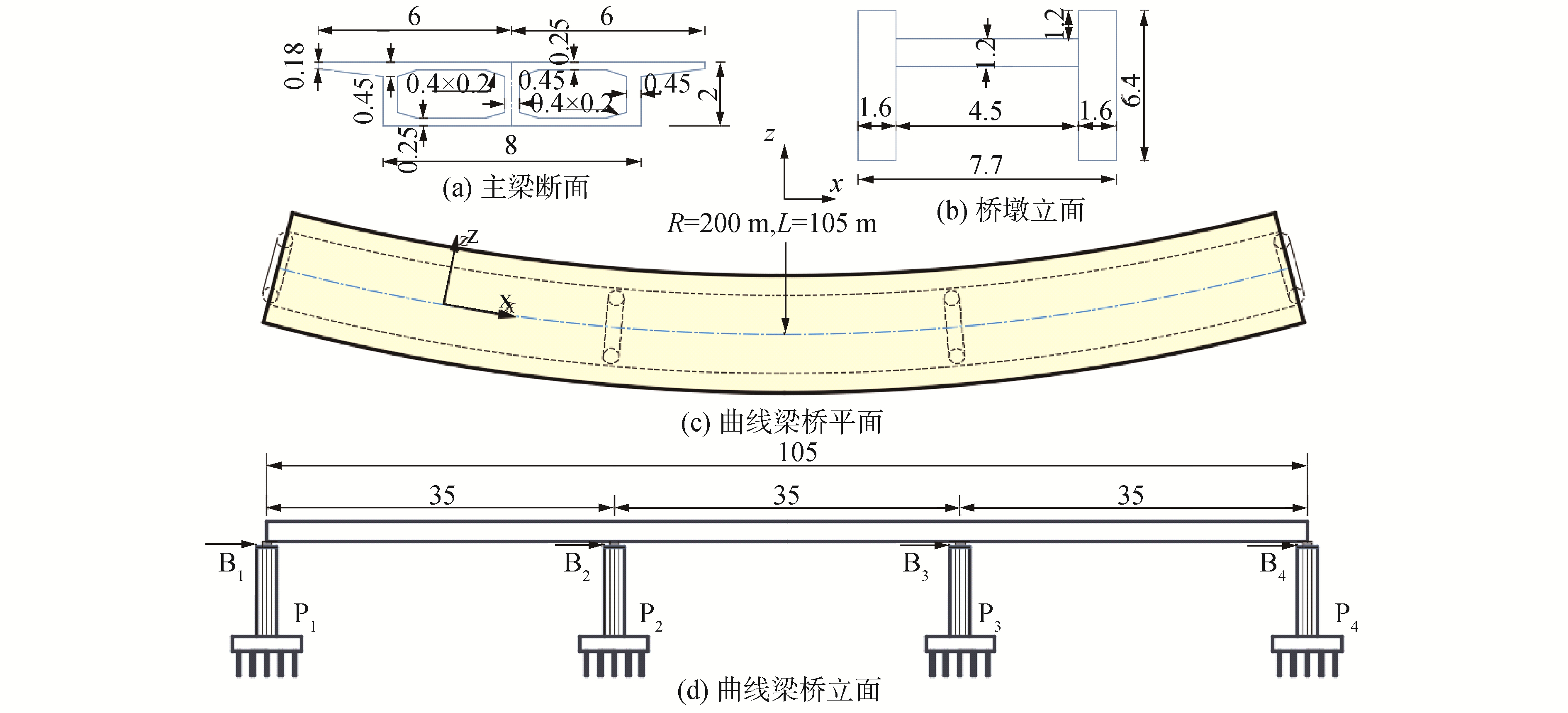
1 隔震曲线连续梁桥分析模型该隔震曲线连续梁桥跨度为3×35 m,位于曲率半径为200 m的平曲面上。主梁采用现浇预应力混凝土箱梁,其截面为单箱双室,桥墩采用圆形双柱墩,其具体尺寸分别见图 1(a)、(b)。中墩、边墩处支座类型分别为铅芯橡胶支座、四氟滑板橡胶支座。该隔震曲线连续梁桥构造图如图 1所示,其中,桥墩编号为P1~P4,支座编号为B1~B4。由设计资料可知,该桥址区的抗震设防烈度为9度,场地类别为二类。
|
Download:
|
| 图 1 隔震曲线连续梁桥构造(单位: m) Fig. 1 The structure of the isolated continuous curved girder bridge (unit: m) | |
基于ANSYS建立该桥的空间有限元模型,如图 2所示。主梁、横梁和桥墩采用弹性梁单元模拟,中墩铅芯橡胶支座、边墩四氟滑板橡胶支座水平切向和径向均采用COMBIN40单元模拟,竖向采用COMBIN14单元模拟。铅芯橡胶支座和四氟滑板橡胶支座的力学模型分别如图 2(a)和(b)所示,其优化前的力学模型参数如表 1所示。主梁和支座之间采用刚性单元连接,桥墩底部固接,未考虑桩土相互作用。

|
Download:
|
| 图 2 隔震曲线连续梁桥有限元模型 Fig. 2 Finite element model of the isolated continuous curved girder bridge | |
| 表 1 隔震支座简化力学模型参数 Table 1 Simplified mechanical parameters of isolation bearings |
根据场地剪切波速,从PEER地震动数据库中选取了3条地震波,其信息如表 2所示。根据《公路桥梁抗震设计细则》[13],将地震动主、次分量的加速度峰值分别调整为0.4、0.34 g。本文仅研究了水平双向地震动输入的情况,未考虑竖向地震动的影响。
| 表 2 地震加速度记录 Table 2 Acceleration records of the earthquake |
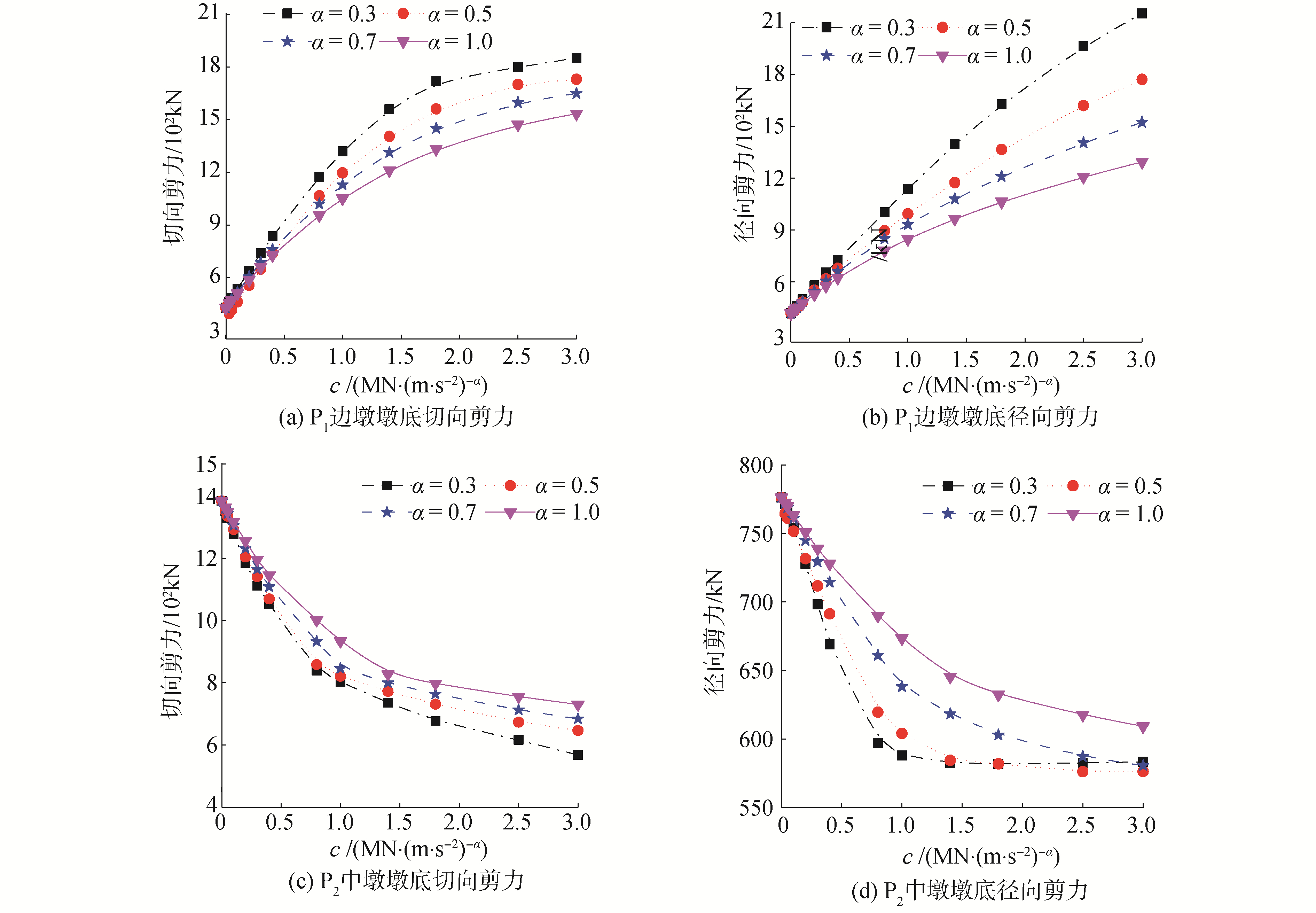
地震作用下,当该桥边墩四氟滑板橡胶支座发生相对滑移时,该支座提供的恢复力不再增加,上部结构的地震作用将主要通过铅芯橡胶支座传递给中墩来承担,从而导致边、中墩受力不均衡。因此,在两边墩处沿径向和切向各设置一个粘滞阻尼器。以期增大结构阻尼,减小支座位移,同时有效调节结构内力在各墩之间的分配。下面以内侧四氟滑板橡胶支座(B1)和内侧桥墩(P1、P2)为研究对象,分析粘滞阻尼器参数对其地震响应的影响。其中,阻尼系数c取值范围为0~3 MN·(m/s)-α,速度指数α分别取0.3、0.5、0.7、1.0。Northern Calif-03地震动作用下的计算结果如图 3、图 4所示。

|
Download:
|
| 图 3 c和α对B1支座位移的影响 Fig. 3 The effect of c and α on the displacement of the B1 bearing | |
|
Download:
|
| 图 4 c和α对桥墩墩底剪力的影响 Fig. 4 The effect of c and α on the shear force at the bottom of piers | |
由图 3可知,当α一定时,支座切向和径向位移随着c的增大而减小,且逐渐趋于平缓,c取值在0~1 MN·(m/s)-α内,对支座切向和径向位移的影响较为显著;当c一定时,支座切向和径向位移随着α的减小而减小。当c和α分别取3 MN·(m/s)-α和0.3时,支座切向和径向位移减幅均高达88.89%。由此说明,当c和α取值合理时,粘滞阻尼器可以对隔震曲线连续梁桥的位移响应进行较好的控制。由图 4可知,当α一定时,边墩墩底切向和径向剪力随着c的增大而增大,而中墩的变化规律相反;当c一定时,α越小,对中、边墩墩底切向和径向剪力的影响越大。
由此可知,存在一个最优的c和α,可以使得边、中墩受力更为均衡,同时有效减小支座位移。以上粘滞阻尼器的参数敏感性分析提供了一个参数取值范围,为了进一步得到最优参数的具体值,以下进行优化分析。
3 粘滞阻尼器参数优化 3.1 零阶优化算法零阶优化算法是在一定次数的抽样基础上,拟合设计变量、状态变量和目标函数的响应函数,从而寻求最优解,故又可称其为子问题方法。函数曲线的形式可采用线性拟合、平方拟合或平方交叉项拟合。对于含设计变量和状态变量的约束问题,可采用罚函数将其转化为无约束的最小值问题[14]。
该方法是建立在目标函数及状态变量近似的基础上,若采用平方交叉项拟合,则目标函数的拟合公式为:
| $ \hat{f}=a_{0}+\sum\limits_{i}^{n} a_{i} x_{i}+\sum\limits_{i}^{n} \sum\limits_{j}^{n} b_{i j} x_{i} x_{j} $ | (1) |
式中:xi、xj为设计变量;a0、ai、bij为拟合系数,拟合系数随迭代过程而变,由加权最小二乘法确定。
利用罚函数将上述有约束问题的目标函数转化为无约束问题的目标函数[15],其拟合公式为:
| $ \begin{aligned} \min F\left(X, p_{k}\right)=& \hat{f}+f_{0} p_{k}\left[\sum\limits_{i=1}^{n} X\left(x_{i}\right)+\sum\limits_{i=1}^{m_{1}} G\left(g_{i}\right)+\right.\\ &\left.\sum\limits_{i=1}^{m_{2}} H\left(h_{i}\right)+\sum\limits_{i=1}^{m_{3}} W\left(w_{i}\right)\right] \end{aligned} $ | (2) |
式中:xi为设计变量;gi、hi、wi为状态变量;X、G、H、W为对应的罚函数;f0为目标函数参考值;pk为响应面参数;无约束目标F(X, pk)为响应面函数,随设计变量X及响应面参数pk而变化。
3.2 优化模型的建立基于零阶优化算法,对粘滞阻尼器参数进行优化分析。优化过程中,阻尼系数c和阻尼指数α为设计变量,其取值范围为:
| $ \left\{\begin{array}{l} c_{1}^{l}-\rho_{1} \leqslant c_{1} \leqslant c_{1}^{u}+\rho_{1} \\ c_{2}^{l}-\rho_{1} \leqslant c_{2} \leqslant c_{2}^{u}+\rho_{1} \\ \alpha_{1}^{l}-\rho_{1} \leqslant \alpha_{1} \leqslant \alpha_{1}^{u}+\rho_{1} \\ \alpha_{2}^{l}-\rho_{1} \leqslant \alpha_{2} \leqslant \alpha_{2}^{u}+\rho_{1} \end{array}\right. $ | (3) |
式中:上标u、l代表上下限,其中,c1l=c2l=0.6 MN·(m/s)-α、cu1=cu2=1.8 MN·(m/s)-α、α1l=α2l=0.3、αu1=αu2=1.0,ρ1=2×10-2。设计变量初始值设定为c1=0.8 MN·(m/s)-α、α1=0.5和c2=0.6 MN·(m/s)-α、α2=0.5。这些值的选用参考了以上参数敏感性分析的结果。
将支座位移作为含有约束条件的状态变量,以各墩底切向剪力绝对值之和为目标函数fob:
| $ f_{\mathrm{ob}}=\min \left(\sum\limits_{i=1}^{4}\left|F_{i}\right|\right), \left\{\begin{array}{l} \left|U_{i-\mathrm{T}}\right| \leqslant 0.2+\rho_{2} \\ \left|U_{i-\mathrm{R}}\right| \leqslant 0.15+\rho_{2} \end{array}\right. $ | (4) |
式中:Fi为单墩墩底切向剪力;Ui-T为支座切向位移;Ui-R为支座径向位移;ρ2为容差,其值为1×10-3。
3.3 优化结果分析由于Northern Calif-03地震作用下的结构地震响应最大,基于上述优化模型,开展粘滞阻尼器参数优化分析。优化后的切向粘滞阻尼器参数c和α分别为0.775 MN·(m/s)-α、0.411;径向粘滞阻尼器参数c和α分别为0.386 MN·(m/s)-α、0.633。
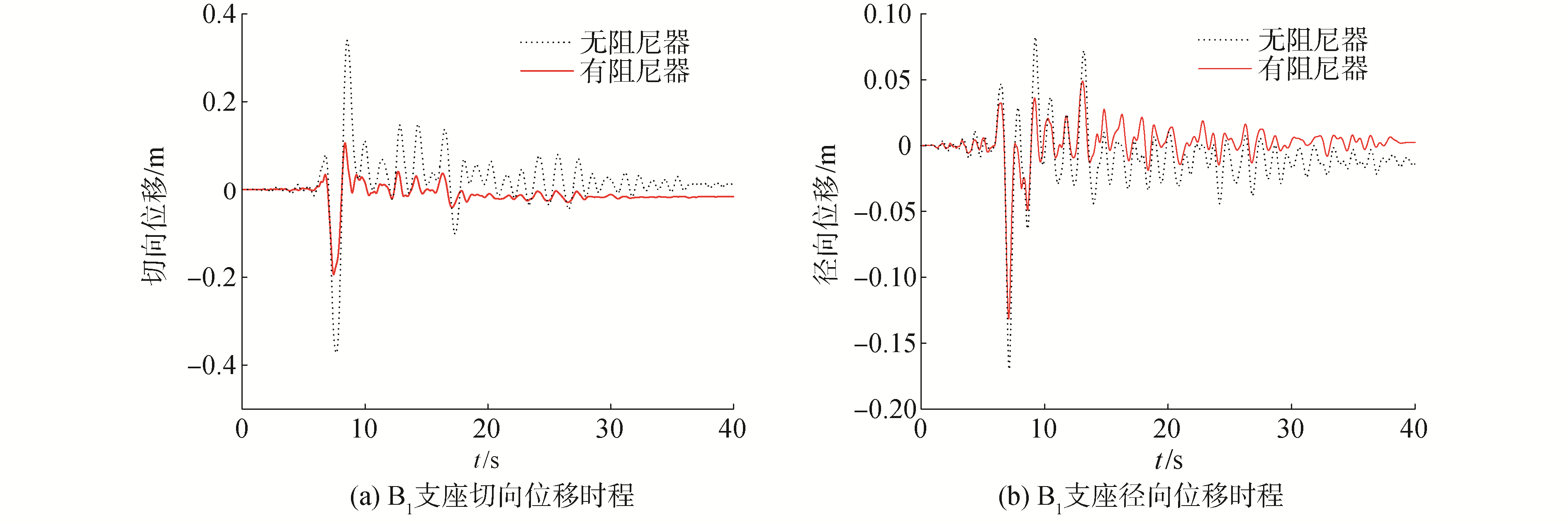
为了分析隔震曲线连续梁桥粘滞阻尼器优化后的减震效果,基于上述优化后的参数,采用非线性动力时程法,进行了有、无粘滞阻尼器时支座位移和墩底剪力的对比分析,其结果分别如表 3、4所示,相应的支座位移和墩底剪力时程曲线如图 5、6所示。
| 表 3 支座位移及其减震率 Table 3 The displacement of bearings and its damping rate |
| 表 4 墩底剪力及其减震率 Table 4 The shear force at the bottom of piers and its damping rate |
|
Download:
|
| 图 5 支座位移时程 Fig. 5 The displacement time history of the bearing | |

|
Download:
|
| 图 6 墩底剪力时程 Fig. 6 The shear time history at the bottom of piers | |
由表 3和图 5可知,阻尼器优化后,支座切向和径向位移减震率分别在47%和22.2%以上,切向位移和径向位移分别在0.2 m和0.15 m以内。两中墩支座和两边墩支座的位移减震率分别保持一致,而中墩支座与边墩支座间的位移减震率相差较大。中墩支座的切向位移减震率高于边墩支座,而边墩支座的径向位移减震率高于中墩支座。
由表 4和图 6可知,阻尼器优化后,边墩墩底切向剪力明显增大,最大增加了139.1%,最小也达到了106.8%,中墩墩底切向剪力减震率在38.3%以上。边墩墩底径向剪力增大的幅度相对较小,但也在77.5%以上,而中墩墩底径向剪力的减震率最大仅9.1%。值得注意的是,设置阻尼器后,虽然各墩墩底剪力之和仅变化了1.6%,但中墩与边墩的墩底剪力差值大幅度减小,其中,切向剪力差值由956 kN减小为220 kN,径向剪力差值由441 kN减小为130 kN,边、中墩受力更为均衡。总体而言,在边墩处设置粘滞阻尼器,对边墩墩底剪力的影响大于中墩,对墩底切向剪力的影响大于径向。
4 结论1) 合理的粘滞阻尼器参数可以使隔震曲线连续梁桥边、中墩在地震作用下的受力更为均衡,同时有效控制桥梁位移。
2) 采用优化后的粘滞阻尼器参数,支座位移减幅明显,切向和径向位移的减幅分别在47%和22.2%以上。中墩支座的切向位移减幅高于边墩支座,而边墩支座的径向位移减幅高于中墩支座。
3) 设置粘滞阻尼器前后的各墩墩底剪力之和基本无变化,但墩底剪力差值大幅度减小,边、中墩受力更为均衡。
| [1] |
王丽, 周锡元, 闫维明. 曲线梁桥地震响应的简化分析方法[J]. 工程力学, 2006, 23(6): 77-84. WANG Li, ZHOU Xiyuan, YAN Weiming. Simplified analysis method for seismic response of curved bridges[J]. Engineering mechanics, 2006, 23(6): 77-84. (  0) 0)
|
| [2] |
徐艳, 童川, 李建中. 设置纵桥向粘滞阻尼器的斜拉桥的简化动力模型[J]. 华南理工大学学报(自然科学版), 2019, 47(4): 90-98. XU Yan, TONG Chuan, LI Jianzhong. Seismic mitigation analysis of viscous dampers for curved continuous girder bridge[J]. Journal of South China University of Technology (natural science edition), 2019, 47(4): 90-98. (  0) 0)
|
| [3] |
马长飞, 胡可, 汪正兴, 等. 芜湖长江公路二桥斜置粘滞阻尼器动力性能监测[J]. 世界桥梁, 2019, 47(5): 65-68. MA Changfei, HU Ke, WANG Zhengxing, et al. Dynamic behavior monitoring for inclined viscous dampers of Second Wuhu Changjiang River highway brige[J]. World bridges, 2019, 47(5): 65-68. (  0) 0)
|
| [4] |
SINGH M P, MORESCHI L M. Optimal placement of dampers for passive response control[J]. Earthquake engineering & structural dynamics, 2002, 31(4): 955-976. (  0) 0)
|
| [5] |
IMPOLLONIA N, PALMERI A. Seismic performance of buildings retrofitted with nonlinear viscous dampers and adjacent reaction towers[J]. Earthquake engineering & structural dynamics, 2018, 47(5): 1329-1351. (  0) 0)
|
| [6] |
BOUGTEB Y, RAY T. Choice between series and parallel connections of hysteretic system and viscous damper for seismic protection of structures[J]. Earthquake engineering & structural dynamics, 2018, 47(1): 237-244. (  0) 0)
|
| [7] |
POLLINI N, LAVAN O, AMIR O. Minimum-cost optimization of nonlinear fluid viscous dampers and their supporting members for seismic retrofitting[J]. Earthquake engineering & structural dynamics, 2017, 46(12): 1941-1961. (  0) 0)
|
| [8] |
AYDIN E, BODUROGLU M H, GUNEY D. Optimal damper distribution for seismic rehabilitation of planar building structures[J]. Engineering structures, 2007, 29(2): 176-185. (  0) 0)
|
| [9] |
巫生平, 张超, 房贞政. 斜拉桥粘滞阻尼器设计方案及参数回归分析[J]. 桥梁建设, 2014, 44(5): 21-26. WU Shengping, ZHANG Chao, FANG Zhenzheng. Design schemes and parameter regression analysis of viscous dampers for cable-stayed bridge[J]. Bridge construction, 2014, 44(5): 21-26. (  0) 0)
|
| [10] |
王波, 马长飞, 刘鹏飞, 等. 基于随机地震响应的斜拉桥粘滞阻尼器参数优化[J]. 桥梁建设, 2016, 46(3): 17-22. WANG Bo, MA Changfei, LIU Pengfei, et al. Parameter optimization of viscous damper for cable-stayed bridge based on stochastic seismic response[J]. Bridge construction, 2016, 46(3): 17-22. (  0) 0)
|
| [11] |
LIU Yi, QI Xingjun, WANG Yijian, et al. Seismic mitigation analysis of viscous dampers for curved continuous girder bridge[J]. Applied mechanics and materials, 2011, 90-93: 1230-1233. (  0) 0)
|
| [12] |
李正英, 蒋林均, 李正良. 曲线连续梁桥不同减隔震方案对比分析[J]. 振动与冲击, 2016, 35(10): 157-161, 173. LI Zhengying, JIANG Linjun, LI Zhengliang. Comparative analysis of seismic control schemes for continuous curved girder bridges[J]. Journal of vibration and shock, 2016, 35(10): 157-161, 173. (  0) 0)
|
| [13] |
中华人民共和国交通运输部. JTG/T B02-01-2008, 公路桥梁抗震设计细则[S].北京: 人民交通出版社, 2008. Ministry of Transport of the People's Republic of China. JTG/T B02-01-2008, Guidelines for seismic design of highway bridges[S]. Beijing: China Communications Press, 2008. (  0) 0)
|
| [14] |
王浩, 王付全, 李爱群, 等. 大跨度缆索支撑桥梁分阶段有限元模型修正[J]. 工程力学, 2009, 26(10): 111-116. WANG Hao, WANG Fuquan, LI Aiqun, et al. Multi-phase FE model updating on long-span cable-supported bridges[J]. Engineering mechanics, 2009, 26(10): 111-116. (  0) 0)
|
| [15] |
郭彤, 李爱群, 费庆国, 等. 零阶与一阶优化算法在悬索桥模型修正中的应用对比分析[J]. 振动与冲击, 2007, 26(4): 35-38. GUO Tong, LI Aiqun, FEI Qingguo, et al. Application comparison between zero-order and first-order optimization methods in model updating of suspension bridges[J]. Journal of vibration and shock, 2007, 26(4): 35-38. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


