2. 苏州大学 苏州纳米科技协同创新中心, 江苏 苏州 215123;
3. 哈尔滨工程大学 机电工程学院, 黑龙江 哈尔滨 150001;
4. 苏州大学 附属第一医院, 江苏 苏州 215000
2. Collaborative Innovation Center of Suzhou Nano Science and Technology, Soochow University, Suzhou 215123, China;
3. School of Mechanical and Electric Engineering, Harbin Engineering University, Harbin 150001, China;
4. The First Affiliated Hospital of Soochow University, Suzhou 215000, China
随着计算机辅助手术技术的成熟发展,借助计算机来帮助医生进行术前规划、术中导航,已经逐渐成为一种普通的方式。一般计算机手术导航主要有2类:第一种方法试将术前CT图像与术中病人暴露的脊骨的三维空间进行3D-3D配准。此方法虽然可以术中较精确的实行导航,但由于需要暴露患者脊柱来放标志点,给患者造成了巨大的伤害,不满足当前对微创手术的定义。另一种方法主要通过患者术前CT三维图像与术中X光图像进行3D-2D图像的实时配准。虽然精度相对3D-3D配准略低,但可以减小病人的解剖创口,降低术中病人的痛苦。除此以外,X光机成像设备相对较为紧凑,操作比较方便,相比于CT成像设备,它具有更小的辐射,减少了对医生和病人的伤害[1]。
从配准的实质出发,目前研究中所涉及到的2D-3D配准方法大致有以下3种[2-4],即基于灰度、梯度和特征的配准方法。基于特征的配准方法一般需要进行边缘检测,将边缘检测到的轮廓图像作为配准的框架或基准。但是其需要对影像进行分割,这在某种程度上也展示了配准的准确性往往取决于分割的准确性。与此同时此方法对图像的要求较高,对边缘检测、图像分割等算法也具有较大的依赖性,所以实施起来有一定的难度,而且配准精度不高。基于梯度的方法一般需要从术前CT图像图像提取3D梯度矢量场(表面法线),需要通过X射线源发出穿过当前3D位置的光线来定义的位置处提取X射线图像的2D梯度矢量。这种方法非常的复杂,可实施性比较低,而且配准失败的概率比较大。在目前的研究中发现基于图像灰度的配准方法相对于上述的两种方法较为稳定,但是由于使用了大量的灰度信息,导致在配准效率上要略低。
针对上述的情况,本文提出一种基于区域贡献的归一化互信息与多分辨率策略相结合的2D-3D配准方法,首先对参考图像进行轮廓提取,然后对所提取的图像轮廓进行区域分类,再通过每块区域的贡献计算归一化互信息的值,以减少在使用互信息测度方法时由于灰度级数差距较大导致的误配准,多分辨率策略在2D-3D配准中的应用有效减少了由于插值与测度方法计算量过大导致的效率较低的问题。
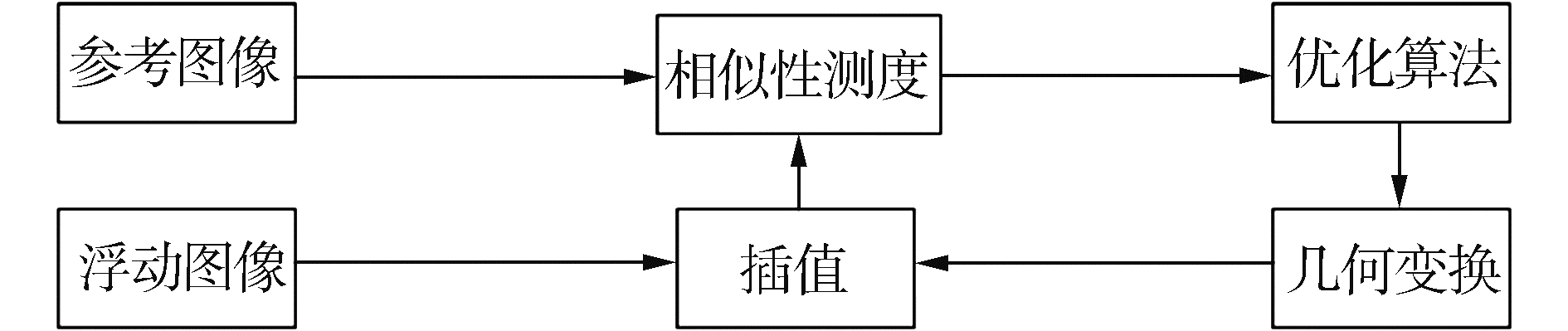
1 基于区域贡献的归一化互信息与多分辨率的配准算法 1.1 基于灰度信息的2D-3D配准框架如图 1所示,一般基于灰度信息的2D-3D配准流程大多数要经过几何变换,优化算法,图像插值,和相似性测度这4个部分。正常在做医学图像研究分析的时候,大多将患者的几个图像放在一起进行对比分析结果。医学图像配准主要通过保持一幅图像固定不变,对另外一幅图像进行空间变换,使其上标志点与第1幅图像上的标记点对应重合。这样可以人体上的解剖点能够在2幅图像上对应空间位置一致,能够帮助医生在术中实时找到病灶点位置。
|
Download:
|
| 图 1 基于灰度信息的图像配准系统框架 Fig. 1 Image registration system framework based on gray information | |
在2D-3D配准过程中,首先保持参考图像不变,然后开始对生成浮动图像设置一个大致合理的初始几何变换参数。在几何变换的过程中,难免出现变换后的图像的像素点坐标不是整数的问题。要解决此问题,此时需要引入插值法,通过插值法来找出原来图像控制点上的像素值;随后设定一个合适的相似性测度值,对参考图像和浮动图像的相似性进行评判,是否到达预先设定的最优值;如果未达到,则重复上述步骤,直至能够找到一个合适的几何变换参数来满足之前设定的精度要求[5-7]。
1.2 基于CT与X光图的2D-3D配准方法配准过程中的浮动图像主要将从虚拟射线源发射出来的X射线穿过CT切片,和每个CT的切片的交点在使用插值法后得到每个交点的CT值。将CT累加值通过映射成灰度图像就能得到DRR图像。参考图像一般选择脊柱模型的X光图。为了能使浮动图像在空间中能更加自由的变换,故此配准框架采用了欧拉几何变换,能够使浮动图像更加方便的实现平移、旋转。为了能够最快找到几何变换参数,本文还引用了梯度下降法,沿梯度下降方向寻求极小值[8]。除上述外,配准框架还包含了基于区域贡献的归一化互信息法、光线投射法以及多分辨金子塔配准法。这些方法都能有效提高配准速度。
1.2.1 光线投射插值法手术过程中获取的X光图像为二维图像,术前CT图像为三维图像。因此需要将3D体素投射到二维空间中,采用数字影像重建技术[9-12]方法来进行插值。通过光线投射法可以模拟该方法模拟X光射线穿过CT体数据的整个过程,同时可以计算出计算在不同介质中X光经衰减、吸收后,最终在投影平面上的像素值。具体的数字影像重建原理如图 2所示。

|
Download:
|
| 图 2 数字影像重建原理 Fig. 2 Principle of digital image reconstruction | |
一般情况下,当X射线穿过某均匀介质时,其的衰减大致表示为:
| $ I = {I_0}{{\rm{e}}^{ - \mu d}} $ | (1) |
式中:I0为初始时刻输入射线的强度;μ为不同介质中的衰减系数;d为X射线穿过的距离。人体脊柱受血肉的包围,因此各部分的衰减系数一般不同。在拍摄X光图的过程中,式(1)一般可改写为:
| $ I = {I_0}{{\rm{e}}^{ - \sum\limits_{i = 1}^n {{\mu _i}{d_i}} }} $ | (2) |
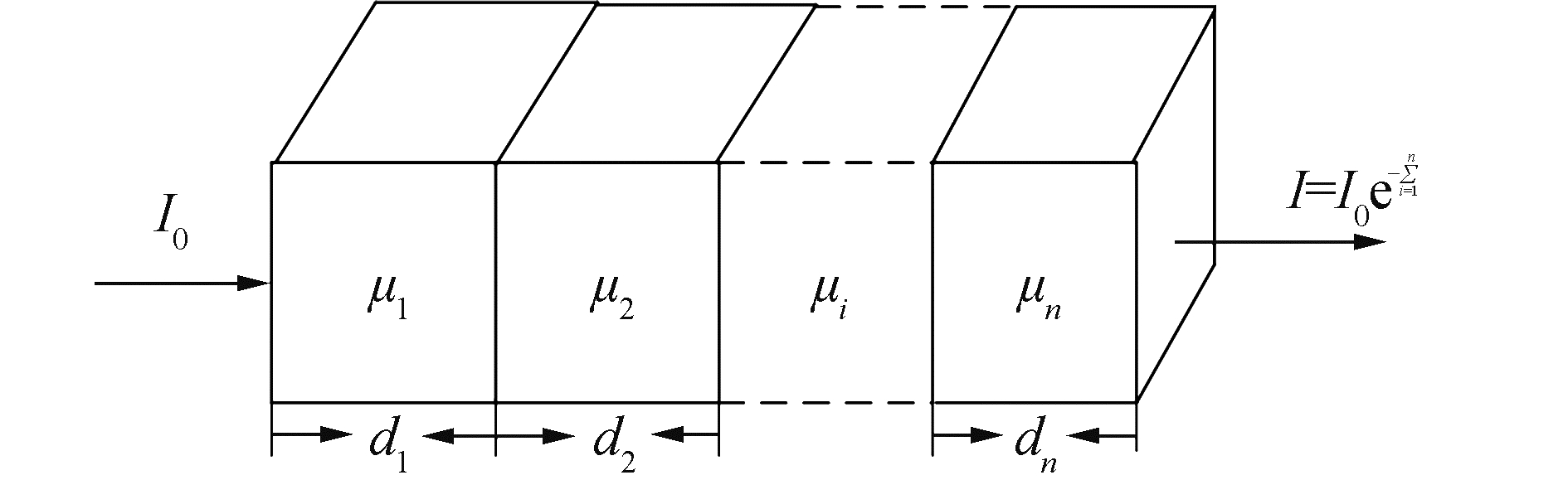
式中:μi和di表示人体不同组织i的大致线性衰减系数和穿过人体血肉组织i的距离。X射线的衰减模型如图 3所示。
|
Download:
|
| 图 3 X射线衰减模型 Fig. 3 X-ray attenuation model | |
一般通过CT值可以计算出线性衰减系数,推广之后得到一般计算公式可以表示为:
| $ \mu = \frac{{H\cdot {\mu _{{\rm{water}}}}}}{{1{\rm{ }}000}} + {\mu _{{\rm{water}}}} $ | (3) |
X光射线穿过体数据的衰减可以通过查表获得,式(3)改写为:
| $ \mu = \left( {\frac{H}{{1{\rm{ }}000}} + 1} \right)\cdot {\mu _{{\rm{water}}}}\cdot F $ | (4) |
式中:F为转换因子。
1.2.2 基于区域贡献的归一化互信息测度互信息在在早期的信息论中,经常用它来作为一种信息的度量,以表达两件事情之间的关联性[13]。目前通常将2幅医学图像之间的相似程度通过互信息来衡量。在对互信息进行定义的过程中,必须要对熵的定义有一个清晰的了解。在医学图像配准环节中,经常一个系统的不确定性和它的复杂性可以通过熵来描述[14]。假设通过以下定义来定义图像A的熵:
| $ H\left( A \right) = - \sum\limits_a p \left( a \right){\rm{log}}{\kern 1pt} p\left( a \right) $ | (5) |
此时针对图像A和B的相关性进行统计,一般与之相对就需要用联合熵表示,大致定义如下所示:
| $ H\left( {A,B} \right) = - \sum\limits_{a,b} p \left( {a,b} \right){\rm{log}}{\kern 1pt} p\left( {a,b} \right) $ | (6) |
图像A和B的互信息可以由上的定义得到:
| $ \begin{array}{l} I\left( {A,B} \right) = H\left( B \right) - H\left( {B|A} \right) = H\left( A \right) + H\left( B \right) - \\ H\left( {A,B} \right) = \sum\limits_{a,b} p \left( {a,b} \right){\rm{log}}{\kern 1pt} \frac{{p\left( {a,b} \right)}}{{p\left( a \right)\cdot p\left( b \right)}} \end{array} $ | (7) |
互信息测度方法的缺点是一般情况下在图像重叠区域较少时,由于图像采样点的减少,参与互信息统计的像素点数也随之减少,因此在图像灰度值差距较小的情况下,容易造成误配准。根据联合熵与个体熵之间的关系,得到归一化互信息:
| $ W\left( {A,B} \right) = \frac{{H\left( A \right) + H\left( B \right)}}{{H\left( {A,B} \right)}} $ | (8) |
本文提出了一种基于区域贡献的归一化互信息测度方法,在进行区域分割后,对图像中包含各种不同信息的区域进行贡献评价,以减少背景等无关区域对图像配准的影响。如图所示,将配准所用的图像分割为一系列的区域,对参考图像进行轮廓提取后,根据各部分区域对互信息测度的贡献度,将能够表现出脊柱特征的轮廓所在区域设为一类区域,将脊柱轮廓内部包含的区域设为二类区域,将背景等与配准无关的区域设为三类区域,由此可以实现对配准图像区域贡献的划分。主要划分区域如图 4所示。

|
Download:
|
| 图 4 参考图像的轮廓提取与区域划分 Fig. 4 Outline extraction and regional division of reference images | |
对三类区域之间的归一化互信息分别进行求解,根据其贡献度进行加权,可以得到:
| $ \begin{array}{l} W\left( {A,B} \right) = \alpha \cdot \frac{{H({A_1}) + H({B_1})}}{{H({A_1},{B_1})}} + {\rm{ }}\\ \beta \cdot \frac{{H({A_2}) + H({B_2})}}{{H({A_2},{B_2})}} + \theta \cdot \frac{{H({A_3}) + H({B_3})}}{{H({A_3},{B_3})}} \end{array} $ | (9) |
式中:α+β+θ=1,α>β>θ。由此,将基于区域贡献的互信息测度方法用于对参考图像以及经过光线投射插值后的浮动图像进行相似性测度对比,从而进一步判断2D-3D配准的结果是否满足预先设定值的要求。
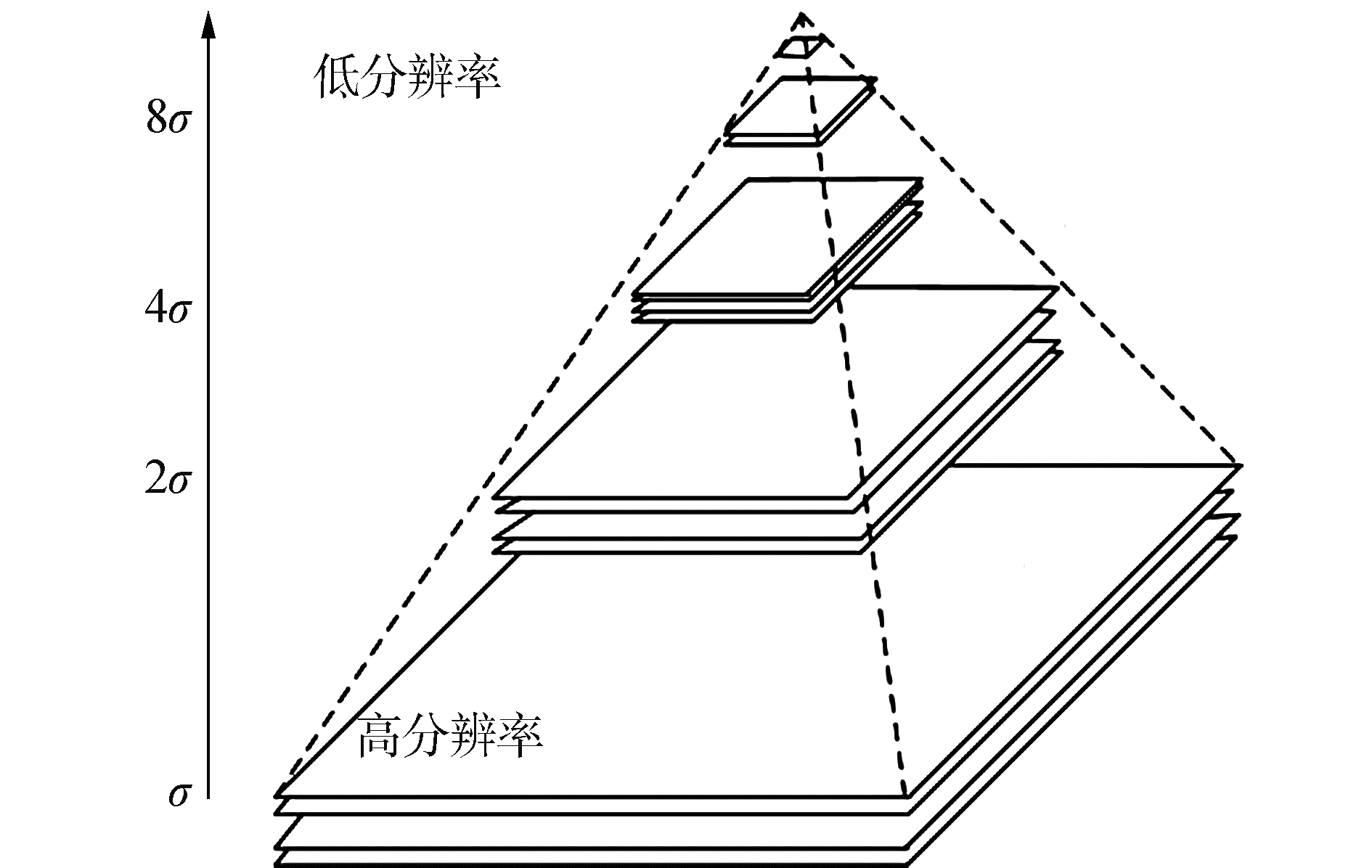
1.2.3 多分辨率策略由于在图像配准框架中采用了光线投射与互信息测度算法,这2种算法具有较高的复杂度,因此可能会导致配准的效率较低。在保证配准精度的前提下,为了提高配准效率,本文在配准环节中引入了多分辨率策略。可以用类似金字塔的形式来阐释这一算法,通过将一开始具有高分辨率的图像细分到n层具有不同分辨率的子图像,按从下往上的顺序依次排列。采取从底部到顶端的方式进行配准,将最初的高分辨率图像放在底部,将第n级低分辨率的图像放在最顶部[15-16]。
引入多分辨率配准方法需要首先将参考图像和浮动图像进行对应n层的划分。配准过程遵循由上而下,从最顶端最低分辨率的图像开始,将其配准的结果作为配准初始解。由于一开始配准计算量相对较小,时间较短,这样就可以依次将上一层的配准结果作为下一层配准的初始解,从而缩短大量的配准时间。整个实验过程从粗配准到精配准,配准效率得到很大的提高。
|
Download:
|
| 图 5 多分辨率策略下的金字塔 Fig. 5 Multi-resolution pyramid | |
整个操作导航的实验平台大概通过C形臂X光机,电脑工作站,带标记的脊柱模型,NDI光学跟踪器等组成。具体如图 6所示。

|
Download:
|
| 图 6 实验平台硬件图 Fig. 6 Experimental platform hardware diagram | |
本次2D-3D配准实验基于ITK与MFC开发包联合编程的基础之上完成。一开始需要进行脊柱正位图像的初始参数选取,一般包括旋转和平移,选取的初始配准参数:rx=270°,ry=3°,rz=180°,tx=30 mm, ty=60 mm, tz=-120 mm。
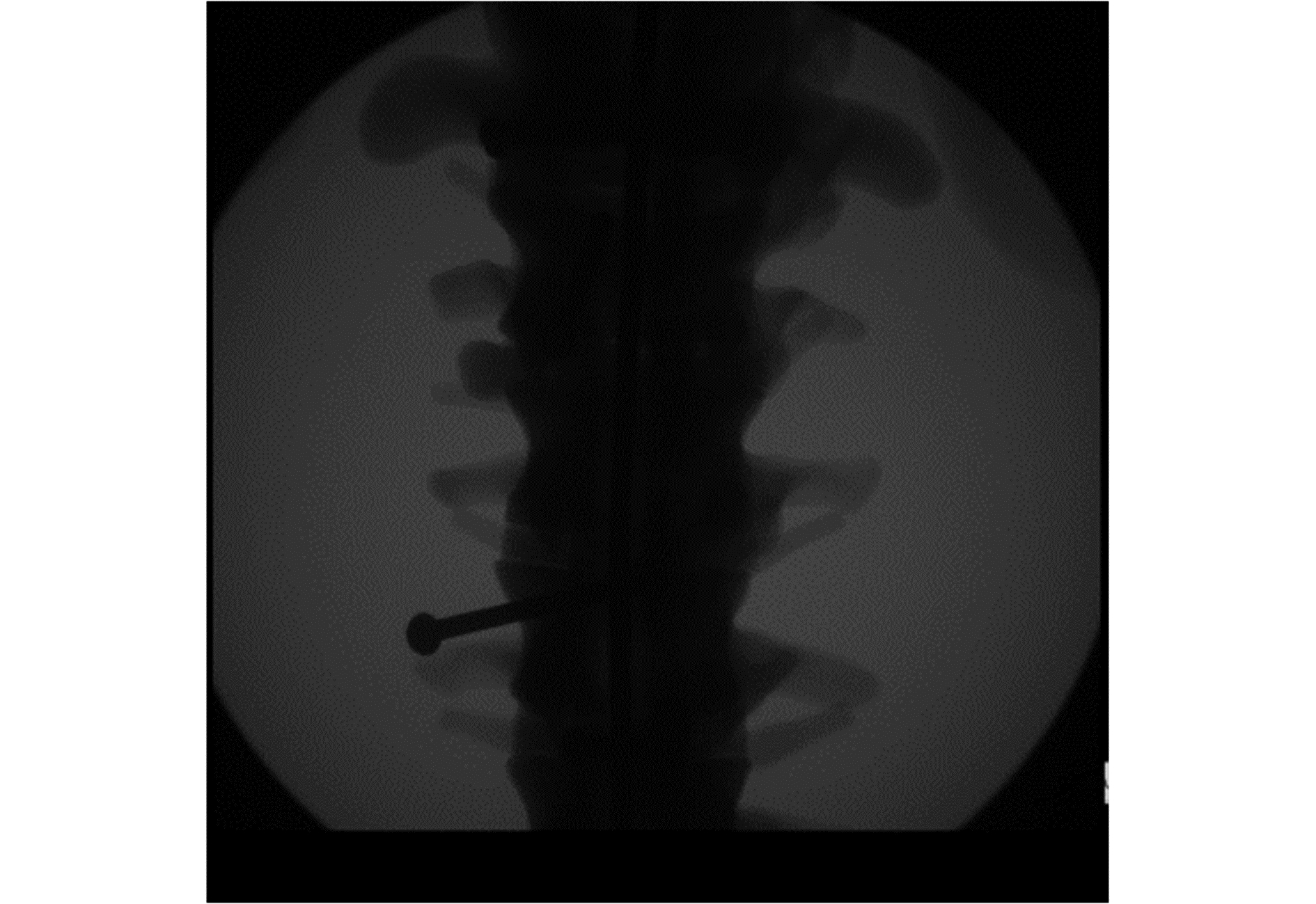
为了控制合理的配准时间和配准精度,在配准过程中,将最大的配准步长设为0.1,最小的配准步长设为0.001,通过50次迭代。在CT切片当中选取80张分辨率为768×768的DICOM格式的切片作为浮动图像。将如图 7所示的X光图像作为本次实验的参考图像,选取干扰性较小的脊柱中间区域进行配准实验。
|
Download:
|
| 图 7 脊柱正位参考图像 Fig. 7 Front reference image of the spine | |
分别采用互信息测度法与基于区域贡献的归一化互信息测度法得到的最终配准参数如表 1所示,图 8为用配准后参数生成的DRR图像。
| 表 1 脊柱正位图像配准后参数 Table 1 Front image registration parameters of the spine |

|
Download:
|
| 图 8 脊柱正位配准后的DRR图像 Fig. 8 DRR image of the front registration of the spine | |
从图 8中可以看出,采用基于区域贡献的归一化互信息测度方法进行配准,具有较高的配准精度。为了对其进行定量分析,对其相似性测度值与配准时间进行了对比,通过相似性测度来展现配准的精度。如表 2所示,对2种测度方法得到的最终脊柱正位DRR图像与脊柱正位参考图像的互信息与相关系数进行了计算,并给出了使用多分辨率策略前后的配准时间。
2.3 脊柱侧位图像2D-3D配准与此同时为了验证基于区域贡献归一化互信息测度的多分辨率2D-3D配准方法的可行性以及优越性,尝试进行多角度配准。选择同段脊柱侧位图像进行配准,选取的同段脊柱侧位初始配准参数:选取的初始配准参数:rx=270°,ry=3°,rz=-90°,tx=-200 mm, ty=-140 mm, tz=-120 mm。
| 表 2 改进前后算法脊柱正位图像相似性测度值与配准时间对比 Table 2 Comparison of image similarity measure and registration time on the front of the spine before and after the improved algorithm |
配准中保持迭代次数,最大、最小步长不变。浮动图像依然选用80张分辨率为768×768的DICOM格式CT切片。采取实验的步骤,脊柱侧位参考图像为如图 9所示的X光图像。

|
Download:
|
| 图 9 脊柱侧位参考图像 Fig. 9 Spine lateral reference image | |
重复实验步骤,分别采用用互信息测度法与基于区域贡献的归一化互信息测度法进行配准实验,得到的最终配准参数如表 3所示,其中图 10为用配准后参数生成的脊柱侧位DRR图像。
| 表 3 脊柱侧位图像配准后参数 Table 3 Parameters after registration of the lateral image of the spine |
|
Download:
|
| 图 10 脊柱侧位配准后生成的DRR图像 Fig. 10 DRR image generated after lateral registration of the spine | |
从图 10中依然可以看出,采用基于区域贡献的归一化互信息测度方法在脊柱侧位图像进行配准,依然适用。对2种测度方法得到的最终脊柱侧位DRR图像与脊柱侧位参考图像的互信息与相关系数进行计算,并给出了使用多分辨率策略前后的配准时间,具体实验数据如表 4所示。
| 表 4 改进前后算法脊柱侧位图像配准相似性测度值与配准时间对比 Table 4 Comparison of image registration similarity measure value and registration time before and after the improved algorithm |
从表 2和表 4中可以看出,用基于区域贡献的归一化互信息测度的2D-3D配准方法得到的配准参数,不管是在脊柱正位还是脊柱侧位生成的DRR图像与参考图像的相似性测度值都要高于仅用互信息测度的配准方法,其相关系数提高了约58%,其整体配准精度提高了40%左右,证明该相似性测度方法具有较高的配准精度。同时可以适用于多个角度的脊柱图像的2D-3D配准,具有一定的可操作性以及较广的适用性。另外,从配准时间可以看出,将多分辨率配准策略应用在2D-3D配准中,可以将配准时间缩短为原来的53%,较为有效地提高了实际配准的效率。
2.4 改变步长后的脊柱正位图像2D-3D图像配准在实验过程中将最大步长和最小步长分别改为0.05和0.000 1,其余参数保持不变,研究此时步长的改变对配准精度以及时间是否有直接的影响。采用实验1中的脊柱正位初始参数,表 5所示为改变配准步长后,分别用互信息测度法与基于区域贡献的归一化互信息测度法得到的最终配准参数。图 11为用改变步长后的配准后参数生成的脊柱正位DRR图像。
| 表 5 改变步长后脊柱正位图像配准后参数 Table 5 Parameters after registration of the lateral image of the spine |

|
Download:
|
| 图 11 改变步长后的脊柱正位配准后生成的DRR图像 Fig. 11 DRR image generated after registration of the frontal image of the spine after changing the step size | |
从图 11中可以看出,改变配准步长后采用基于区域贡献的归一化互信息测度方法在脊柱侧位图像进行配准,配准精度较高。通过相似性测度值与配准时间进行了对比,其所要的配准时间相对于之前的步长更久,精度略有提升,有一定的提升效果。具体实验数据如表 6所示。
| 表 6 步长改变后改进前后算法脊柱正位图像相似性测度值与配准时间对比 Table 6 Comparison of the image similarity measure and registration time of the frontal image of the algorithm before and after the step change |
从表 6可以看出,当配准步长变为0.05,最小步长设为0.000 1之后,脊柱正位图像的相似性测度值在改进算法前后都有了一定程度的提高,即配准的精度相对有了一定的提高。脊柱正位图像的相似性测度值相对于改变步长之前提升了大概8%,其使用多分辨率算法花费的配准时间相较于改变步长之前的分别增加了6%和12%。从实验数据可以看出,在步长变小的时候,配准精度相对提高8%,但配准时间增加12%。由此得出虽然精度有所提高,但在手术过程中时间的延迟将会对医生的手术造成一定的影响,也会直接导致患者的手术风险进一步的提高。所以在满足精度要求的同时,尽量缩短手术时间,可以极大的提升手术的成功的概率。
3 结论1) 通过实验可以看出,在不同的步长情况下,同段脊柱的同位置配准时间和精度有所不同,当步长变小时,配准精度相对提高,但取而代之的是配准时间相对变长。需要寻求一个合适的步长,能够在配准时间和精度之间找到一个平衡。
2) 采用基于区域贡献的归一化互信息与多分辨率算法后,所需要的配准时间仍然较长,需要进一步缩短配准时间,使医生能够提高手术成功率。
3) 所采取的实验对象为脊柱模型,与实际动物或人体实验仍然存在一定的差距,在人体或动物脊柱外围存在一定的肌肉组织和皮肤,在实际过程中可能会导致可操作性降低。
4) 在手术过程中,把脊柱图像配准看成类似“刚体”的配准,其实质上脊柱在手术过程中仍然存在一定的变形,解决变形问题,有利于进一步提高配准精度,降低手术风险。
| [1] |
宋国立, 韩建达, 赵忆文. 骨科手术机器人及其导航技术[J]. 科学通报, 2013, 58(S2): 8-19. SONG Guoli, HAN Jianda, ZHAO Yiwen. Review of orthopedic surgery robot and navigation technology[J]. Chinese science bulletin, 2013, 58(S2): 8-19. (  0) 0)
|
| [2] |
GUAN Shaoya, WANG Tianmiao, MENG Cai, et al. A review of point feature based medical image registration[J]. Chinese journal of mechanical engineering, 2018, 31: 76. DOI:10.1186/s10033-018-0275-9 (  0) 0)
|
| [3] |
DANG H, OTAKE Y, SCHAFER S, et al. Robust methods for automatic image-to-world registration in cone-beam CT interventional guidance[J]. Medical physics, 2012, 39(10): 6484-6498. DOI:10.1118/1.4754589 (  0) 0)
|
| [4] |
SELMI S Y, PROMAYON E, TROCCAZ J. Hybrid 2D-3D ultrasound registration for navigated prostate biopsy[J]. International journal of computer assisted radiology and surgery, 2018, 13(7): 987-995. DOI:10.1007/s11548-018-1736-4 (  0) 0)
|
| [5] |
王雷, 高欣, 崔学理, 等. 基于灰度距离融合的2D/3D刚性配准[J]. 光学精密工程, 2014, 22(10): 2815-2824. WANG Lei, GAO Xin, CUI Xueli, et al. 2D/3D rigid registration by integrating intensity distance[J]. Optics and precision engineering, 2014, 22(10): 2815-2824. (  0) 0)
|
| [6] |
WU Jian, KIM M, PETER J, et al. Evaluation of similarity measures for use in the intensity-based rigid 2D-3D registration for patient positioning in radiotherapy[J]. Medical physics, 2009, 36(12): 5391-5403. DOI:10.1118/1.3250843 (  0) 0)
|
| [7] |
MARKELJ P, TOMAŽEVIČ D, LIKAR B, et al. A review of 3D/2D registration methods for image-guided interventions[J]. Medical image analysis, 2012, 16(3): 642-661. DOI:10.1016/j.media.2010.03.005 (  0) 0)
|
| [8] |
AUDRITO G, DAMIANI F, VIROLI M. Optimal single-path information propagation in gradient-based algorithms[J]. Science of computer programming, 2018, 166: 146-166. DOI:10.1016/j.scico.2018.06.002 (  0) 0)
|
| [9] |
张薇, 黄毓瑜, 栾胜, 等. 基于灰度的二维/三维图像配准方法及其在骨科导航手术中的实现[J]. 中国医学影像技术, 2007, 23(7): 1080-1084. ZHANG Wei, HUANG Yuyu, LUAN Sheng, et al. Implementation of intensity-based 2D/3D image registration in orthopaedic navigation system[J]. Chinese journal of medical imaging technology, 2007, 23(7): 1080-1084. DOI:10.3321/j.issn:1003-3289.2007.07.038 (  0) 0)
|
| [10] |
张翼, 王满宁, 宋志坚. 脊柱手术导航中分步式2D/3D图像配准方法[J]. 计算机辅助设计与图形学学报, 2007, 19(9): 1154-1158, 1165. ZHANG Yi, WANG Manning, SONG Zhijian. Multi-Step 2D/3D image registration in image-guided spine surgery[J]. Journal of computer-aided design & computer graphics, 2007, 19(9): 1154-1158, 1165. (  0) 0)
|
| [11] |
刘坤, 吕晓琪, 谷宇, 等. 快速数字影像重建的2维/3维医学图像配准[J]. 中国图象图形学报, 2016, 21(1): 69-77. LIU Kun, LV Xiaoqi, GU Yu, et al. The 2D/3D medical image registration algorithm based on rapid digital image reconstruction[J]. Journal of image and graphics, 2016, 21(1): 69-77. (  0) 0)
|
| [12] |
刘达, 谢永召, 倪自强, 等. 基于局部方差采样的2D/3D医学图像配准技术[J]. 高技术通讯, 2013, 23(8): 827-832. LIU Da, XIE Yongzhao, NI Ziqiang, et al. 2D/3D medical image registration based on local variance sampling[J]. Chinese high technology letters, 2013, 23(8): 827-832. DOI:10.3772/j.issn.1002-0470.2013.08.008 (  0) 0)
|
| [13] |
MAES F, COLLIGNON A, VANDERMEULEN D, et al. Multimodality image registration by maximization of mutual information[J]. IEEE transactions on medical imaging, 1997, 16(2): 187-198. (  0) 0)
|
| [14] |
KNOPS Z F, MAINTZ J B A, VIERGEVER M A, et al. Normalized mutual information based registration using k-means clustering and shading correction[J]. Medical image analysis, 2006, 10(3): 432-439. DOI:10.1016/j.media.2005.03.009 (  0) 0)
|
| [15] |
LI Guohe, GAO Jiaying, KAFKA O L, et al. Implementation and application of the multiresolution continuum theory[J]. Computational mechanics, 2019, 63(4): 631-647. DOI:10.1007/s00466-018-1613-6 (  0) 0)
|
| [16] |
KURTZ C, STUMPF A, MALET J P, et al. Hierarchical extraction of landslides from multiresolution remotely sensed optical images[J]. Isprs journal of photogrammetry and remote sensing, 2014, 87: 122-136. DOI:10.1016/j.isprsjprs.2013.11.003 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


