激光追踪测量系统具有测量范围大、测量效率高、精度高、操作简单等优点,广泛应用于飞行器制造、汽车制造、船舶制造等领域[1-4]。激光追踪测量系统利用高分辨率的激光干涉测量方法实现高精度跟踪测量,主要应用于机床校准、工件检测。电机的高精度追踪控制技术是激光追踪测量系统的关键技术,电机控制的性能直接影响激光追踪测量系统对空间随动目标的跟踪速度和跟踪精度,要求电机具有快速的转矩响应,处于最内环的电流控制器性能就成为影响控制系统整体性能的关键。
对电流控制器的设计,最常见是PI控制方法,其结构简单、调整方便。但是传统的PI控制属于线性控制,仅适用于负载变化小且没有较多干扰的场合,其控制性能易受内外多种因素影响,不利于应用到强耦合、多输入输出的非线性时变的永磁同步电机控制系统中[5]。预测控制是一种从工业过程控制中发展起来的计算机控制算法,与传统控制方法相比最大的区别在于能够考虑到控制量对未来的影响,通过在线滚动优化不断反馈校正,在一定程度上克服了由模型误差和不确定性干扰所带来的影响,具有更快的动态响应速度和更高的稳态精度,增强了系统的鲁棒性。Malesani等[6]提出了无差拍电流预测控制算法,实现了对电机基于模型的运动控制,该方法对电机模型参数的失配比较敏感。Morel等[7-8]提出根据逆变器输出的不同电压矢量来预测下一控制周期的电流,该方法仅通过一个评价函数唯一确定电压矢量的输出,电流频响较快,同时存在电流纹波。王伟华等[9-10]提出了增量预测算法,避免了传统PI控制所带来的超调和震荡,同时仍然保留PI闭环控制改善传统预测控制对电机参数的依赖性,但牺牲了响应速度。张永昌等[11]提出基于快速矢量选择的永磁同步电机模型预测控制,只需一次预测即可选出最优电压矢量,降低了算法的复杂度和计算量,但权重系数的确定仍缺乏有效的理论支持。Siami等[12]对传统预测电流控制进行扩展研究,提高了系统对参数不确定性的鲁棒性,在预测的不同阶段考虑预测误差的影响,增加了预测精度。
在激光追踪测量系统中,为了提高驱动电机内环电流控制器的动静态响应特性,本文基于扩张状态观测器研究了电流预测控制算法,并利用Matlab/Simulink进行仿真分析,驱动电机可获得快速的转矩响应,有利于有效改善激光追踪测量系统对空间随动目标的追踪速度和追踪精度。
1 激光追踪测量系统的电机控制算法 1.1 永磁同步电机的数学模型建立本文所研究的Harmonic谐波减速电机为永磁同步电机(permanent magnet synchronous motor, PMSM),由永磁体励磁产生同步旋转磁场来实现能量的转换[13]。为简化分析,在不影响控制性能的前提下忽略铁心的饱和效应、忽略涡流和磁滞损耗、忽略温度、频率对电机参数的影响;假设转子上无阻尼绕组且永磁体无阻尼作用、气隙磁场呈正弦分布、三相绕组均匀对称且绕组中感应电感为正弦波[14]。
如图 1所示,永磁同步电机在旋转过程中,ABC三相静止坐标系下的PMSM数学模型较复杂,不利于动态分析和控制设计。令α轴与A相轴线重合,α轴逆时针垂直方向即为β轴,将其从ABC三相静止坐标系转化至αβ两相静止坐标系下,以消除三相坐标系中的旋转分量。但是,αβ两相静止坐标系下PMSM仍存在交流成分的电分量,其两轴电感仍是相关于位置角θ的函数,不利于采用与直流电机类似的控制策略,增加了控制与分析难度。因此,将αβ两相静止坐标系绕PMSM中心旋转,使得α轴与磁轴重合,坐标系便可随电机同步旋转,即αβ两相静止坐标系转化为两相同步旋转dq坐标系[15]。

|
Download:
|
| 图 1 PMSM的解析模型示意 Fig. 1 Analytical model diagram of PMSM | |
PMSM模型的电压方程为:
| $ \left( {\begin{array}{*{20}{l}} {{u_d}}\\ {{u_q}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} R&{ - \omega {L_q}}\\ {\omega {L_d}}&R \end{array}} \right)\left( {\begin{array}{*{20}{l}} {{i_d}}\\ {{i_q}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{L_d}}&0\\ 0&{{L_q}} \end{array}} \right)\frac{{\rm{d}}}{{{\rm{d}}t}}\left( {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}} \end{array}} \right) + {\psi _{f0}}\left( {\begin{array}{*{20}{l}} 0\\ \omega \end{array}} \right) $ | (1) |
式中:ud、uq、id、iq分别为dq坐标系下PMSM定子绕组的电压、电流;R为dq坐标系下PMSM定子绕组的电阻;ω为PMSM的电磁角速度;Ld、Lq为dq坐标系下PMSM定子绕组的等效电感;ψf0为PMSM的永磁体在定子绕组上产生磁链的幅值。
dq坐标系下,d轴与q轴的电感相同,有Ld=Lq=L,则PMSM模型的电磁转矩方程式为:
| $ {T_e} = \frac{3}{2}{P_n}{\psi _{f0}}{i_q} $ | (2) |
式中:Te为dq坐标系下PMSM的电磁转矩;Pn为PMSM的极对数。
因此,dq坐标系下PMSM模型的机械运动方程式为:
| $ J\frac{{{\rm{d}}{\omega _r}}}{{{\rm{d}}t}} = {T_e} - {T_L} - B{\omega _r} $ | (3) |
式中:J为dq坐标系下PMSM的转动惯量;TL为dq坐标系下PMSM的负载转矩(输出转矩);B为PMSM的粘滞摩擦系数;ωr为PMSM的转子角速度,与电磁角速度ω关系为ω=Pnωr。
将式(2)代入式(3),可得:
| $ \frac{{{\rm{d}}{\omega _r}}}{{{\rm{d}}t}} = \frac{{3{P_n}{\psi _{f0}}}}{{2J}}{i_q} - \frac{{{T_L}}}{J} - \frac{B}{J}{\omega _r} $ | (4) |
结合式(1),可求得dq坐标系下的PMSM模型的状态方程式为:
| $ \left[ {\begin{array}{*{20}{c}} {\frac{{{\rm{d}}{i_d}}}{{{\rm{d}}t}}}\\ {\frac{{{\rm{d}}{i_q}}}{{{\rm{d}}t}}}\\ {\frac{{{\rm{d}}{\omega _r}}}{{{\rm{d}}t}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{R}{L}}&{{P_n}{\omega _r}}&0\\ { - {P_n}{\omega _r}}&{ - \frac{R}{L}}&{ - \frac{{{P_n}{\psi _\beta }}}{L}}\\ 0&{\frac{{3{P_n}{\psi _\beta }}}{{2J}}}&{ - \frac{B}{J}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{i_d}}\\ {{i_q}}\\ {{\omega _r}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\frac{{{u_d}}}{L}}\\ {\frac{{{u_q}}}{L}}\\ { - \frac{{{T_L}}}{J}} \end{array}} \right] $ | (5) |
激光追踪测量系统的电机内环选用电流控制电流预测控制(current predictive control, CPC)算法,在一定程度上克服由模型误差和不确定性干扰所带来的影响。并采用id=0矢量控制方式,避免了直轴电流,使电机所有电流均用于产生电磁转矩,电流控制效率高,具有良好的控制性能和调速性能[17]。
PMSM的d、q轴电流可作为状态变量,根据式(5)可构造PMSM的状态空间函数,矩阵形式为:
| $ \mathit{\boldsymbol{\dot i}} = A\mathit{\boldsymbol{i}} + B\mathit{\boldsymbol{u}} + D $ | (6) |
由于PMSM控制系统的采样周期Ts很小,在一个控制周期内可认为u是恒定不变的;此外,PMSM的旋转电动势D的变化相对于电流环变化较为缓慢,也可以认为在一个周期内旋转电动势D恒定不变[18-21]。
令t0=kTs, t=(k+1)Ts,采用一阶欧拉前向离散化方法对式(6)所述的状态方程进行离散化,可得PMSM离散化的电流预测控制模型:
| $ \mathit{\boldsymbol{i}}\left( {k + 1} \right) = \mathit{\boldsymbol{F}}\left( k \right) \cdot \mathit{\boldsymbol{i}}\left( k \right) + \mathit{\boldsymbol{Gu}}\left( k \right) + \mathit{\boldsymbol{H}}\left( k \right) $ | (7) |
其中:
将PMSM当前周期的参考电流给定值i*(k)=(idref*(k), iqref*(k))T作为下一周期的电流预测值i(k+1)=(id(k+1), iq(k+1))T,结合当前PMSM的运行状态i(k),可计算得到PMSM电流跟随指令所需作用的电压矢量u(k)方程式为:
| $ \mathit{\boldsymbol{u}}\left( k \right) = {\mathit{\boldsymbol{G}}^{ - 1}}\left[ {{\mathit{\boldsymbol{i}}^ * }\left( k \right) - \mathit{\boldsymbol{F}}\left( k \right) \cdot \mathit{\boldsymbol{i}}\left( k \right) - \mathit{\boldsymbol{H}}\left( k \right)} \right] $ | (8) |
在实际的PMSM系统中,电流对给定值i*(k)的跟随效果欠佳,将会影响控制器的控制效果;随着工况的变化,易失配的PMSM参数将会带来电机模型的计算误差,导致控制电机的电流抖动。因此,状态观测器可通过观测PMSM系统d、q轴的实际电流来实现对预测电流的修正;同时构造扩张状态变量对PMSM系统内外扰动进行同步评估,实现对PMSM系统输出电压的实时修正。
将PMSM的d、q轴电流电压作为状态观测器的输入输出,令:
| $ {\mathit{\boldsymbol{X}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{i}}_d}}\\ {{\mathit{\boldsymbol{i}}_q}} \end{array}} \right],\mathit{\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{u}}_d}}\\ {{\mathit{\boldsymbol{u}}_q}} \end{array}} \right] $ | (9) |
X1、U分别作为状态观测器的状态变量和输入量,因此可得到PMSM的电流状态方程式为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot X}}}_1} = f\left( {{\mathit{\boldsymbol{X}}_1}} \right) + {B_0}\mathit{\boldsymbol{U}} + \mathit{\boldsymbol{W}}}\\ {\mathit{\boldsymbol{Y}} = {\mathit{\boldsymbol{X}}_1}} \end{array}} \right. $ | (10) |
式中:f(X1)=
将f(X1)看作是PMSM控制系统的内部扰动,其中包含电感L和电机非线性因素的影响,与PMSM其他未知干扰W共同扩张成状态观测器一个新的状态变量X2,即:
| $ {\mathit{\boldsymbol{X}}_2} = f\left( {{\mathit{\boldsymbol{X}}_1}} \right) + \mathit{\boldsymbol{W}} $ | (11) |
基于扩张状态观测器,观测值Z1(对PMSM交直轴电流X1的估计)对电流预测控制器输入量进行修正;观测值Z2(对PMSM控制系统所有内外扰动X2的估计)对电流预测控制器输出量进行实时补偿。经扩张状态观测器修正补偿后PMSM电流精确跟随指令所需作用的电压矢量u*(k)方程式为:
| $ \begin{array}{*{20}{c}} {\left[ {\begin{array}{*{20}{l}} {\bar u_{{\rm{der}}}^ * \left( k \right)}\\ {\bar u_{{\rm{qref}}}^ * \left( k \right)} \end{array}} \right] = {\mathit{\boldsymbol{G}}^{ - 1}}\left\{ {\left[ {\begin{array}{*{20}{c}} {(1 - \gamma ){Z_{1d}}(k)}\\ {\gamma i_{{\rm{qref}}}^ * (k) + (1 - \gamma ){\mathit{\boldsymbol{Z}}_{1q}}(k)} \end{array}} \right]} \right.}\\ {\left. { - \mathit{\boldsymbol{F}}(k)\left[ {\begin{array}{*{20}{c}} {{i_d}(k)}\\ {{i_q}(k)} \end{array}} \right] - \mathit{\boldsymbol{H}}(k)} \right\} - \rho \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Z}}_{2d}}(k)}\\ {{Z_{2q}}(k)} \end{array}} \right]} \end{array} $ | (12) |
式中:γ为PMSM的电流修正权重因子;ρ为PMSM扰动量的补偿系数;Z1d、Z1q分别为Z1在d、q轴的电流观测量;Z2d、Z2q分别为Z2在d、q轴的扰动观测量。
根据上述PMSM电流环控制的数学模型,基于扩张状态观测器的电流预测控制(extended state observer-current predictive control, ESO-CPC)算法改进了激光追踪控制系统的电机电流控制器设计,其算法结构图如图 2所示。扩张状态观测器的观测量Z1可有效修正电流环的电流输入,观测量Z2可实时补偿电流环的电压输出。

|
Download:
|
| 图 2 基于扩张状态观测器的电流预测算法结构图 Fig. 2 Structure diagram of current prediction algorithm based on extended state observer | |
根据基于扩张状态观测器的电流预测控制算法的激光追踪测量系统电机模型,在Matlab/Simulink中构建仿真模型,如图 3所示。直流电压源、万用电桥和永磁同步电机共同组成系统的主电路,其中负载转矩由Step控件提供加载,电机的定子三相电流、转子转速、转子转角和电磁转矩可由Scope空间实时观测。在基于ESO-CPC的激光追踪测量系统电机的仿真模型中,设定d轴的参考电流为零,电机反馈速度与设定速度的差值经速度调节器作q轴的参考电流[22-23]。

|
Download:
|
| 图 3 基于ESO-CPC的激光追踪测量系统电机Simulink仿真模型 Fig. 3 Motor Simulink simulation model of laser tracking measurement system based on ESO-CPC | |
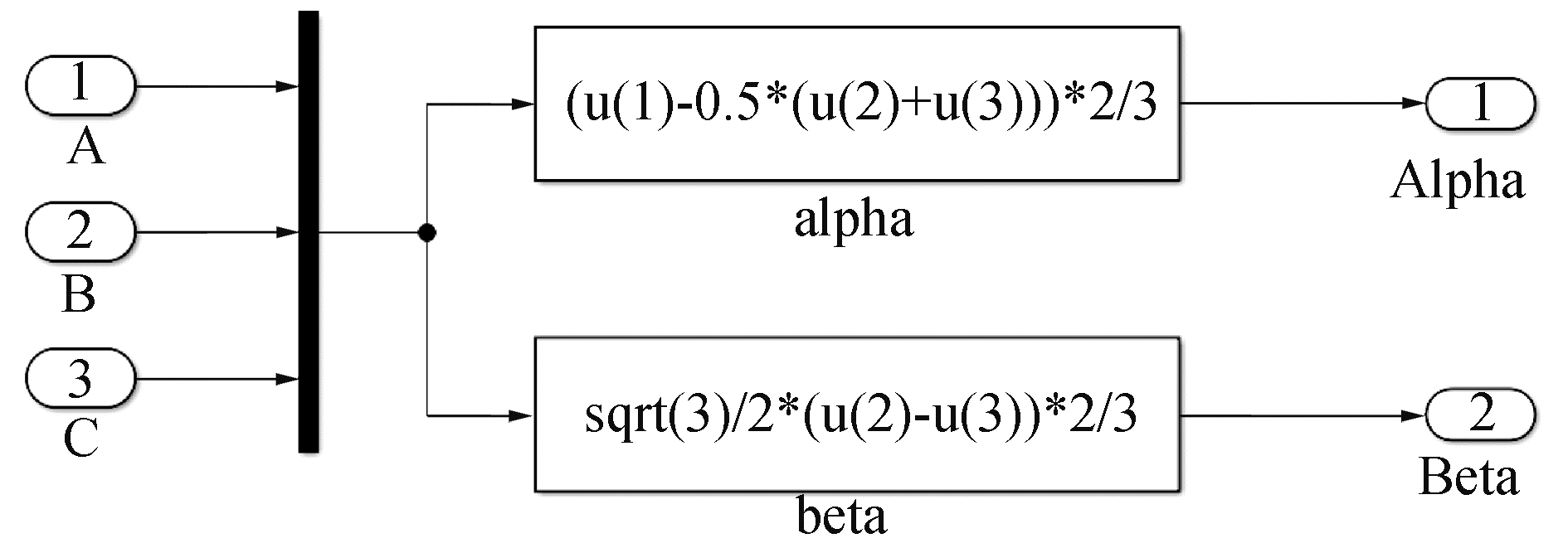
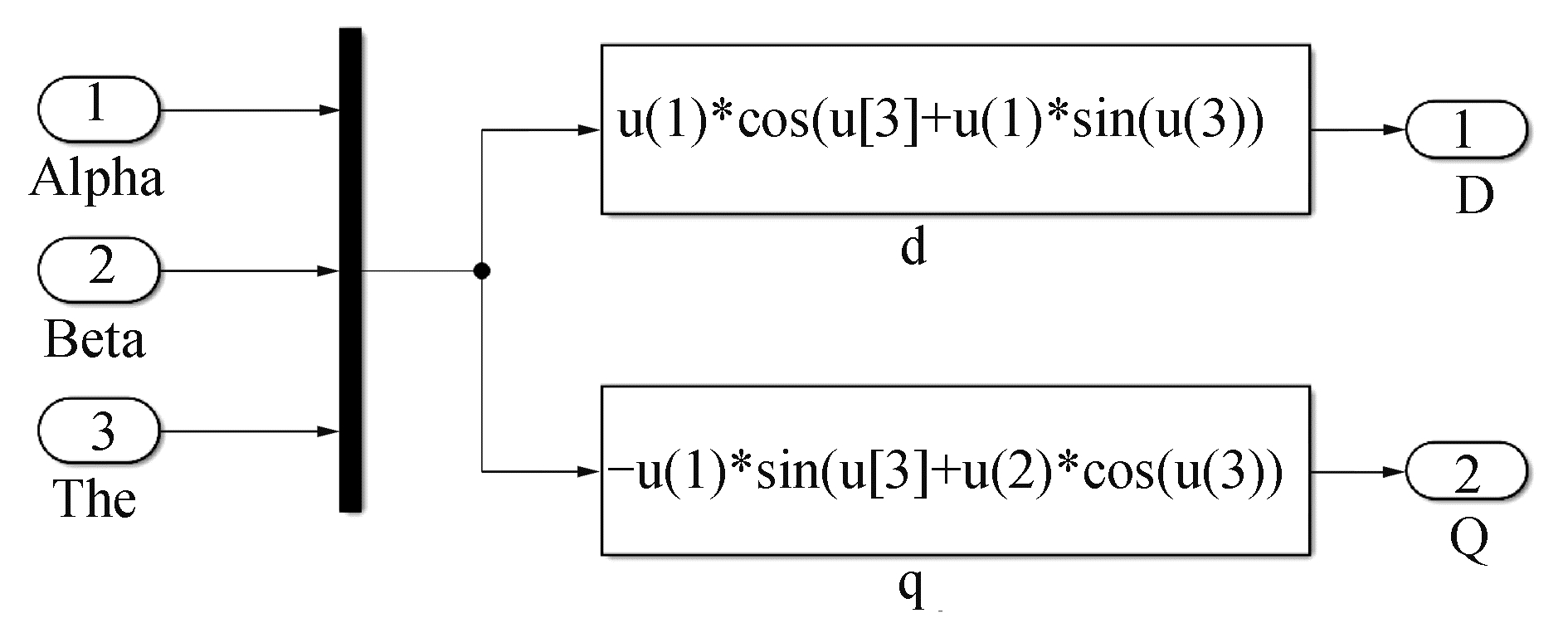
为简化控制电机模型,可将电机三相绕组电流产生的磁动势按平面矢量的叠加原理进行合成和分解, 使得实际电动机的三相绕组可由两相正交绕组等效。图 4~6分别为基于ESO-CPC的激光追踪测量系统电机Simulink仿真模型中Clark变换、Park变换和Anti_Park变换3个坐标系变换模块,实现ABC-αβ-dq坐标系间的正变换和逆变换。
|
Download:
|
| 图 4 Clark变换模块仿真模型 Fig. 4 Clark transform module simulation model | |
|
Download:
|
| 图 5 Park变换模块仿真模型 Fig. 5 Park transform module simulation model | |

|
Download:
|
| 图 6 Anti_Park变换模块仿真模型 Fig. 6 Anti_Park transform module simulation model | |
电流预测控制CPC control模块由Simulink环境提供的Matlab function模块实现,代替传统的PI控制,避免了模型误差和不确定性干扰的影响,Simulink仿真模型如图 7所示。

|
Download:
|
| 图 7 电流预测控制的Simulink仿真模型 Fig. 7 SIMULINK simulation model of current predictive control | |
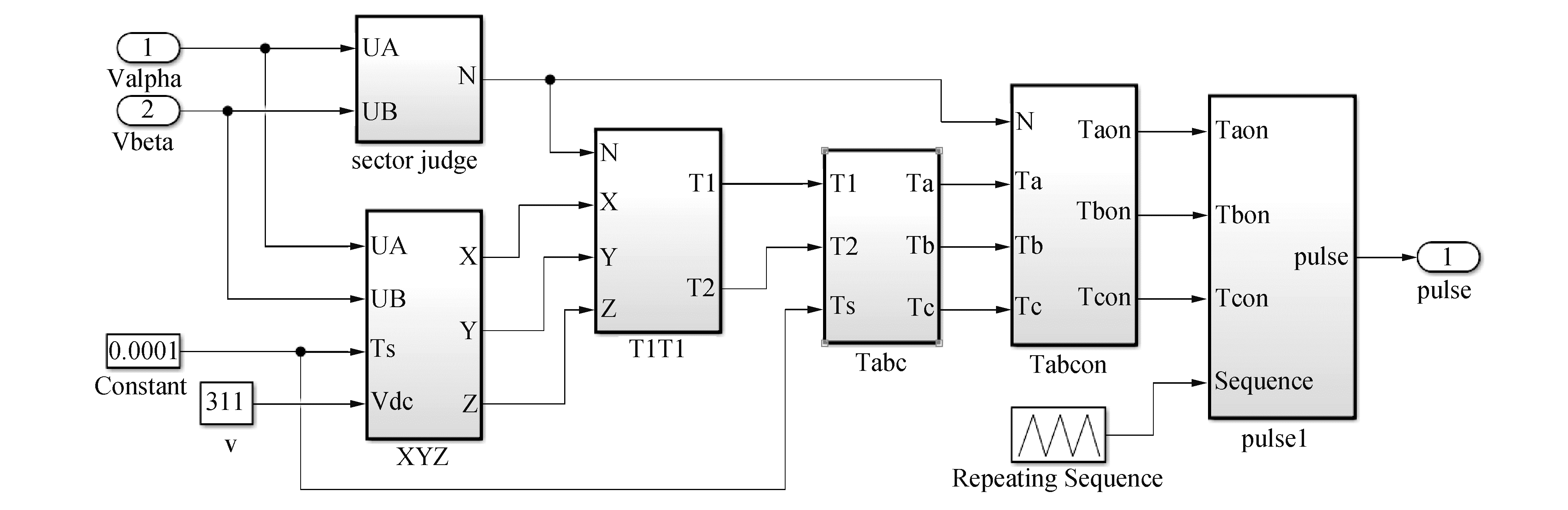
SVPWM模块是以三相对称正弦波电压供电时三相对称电动机定子理想磁链圆为参考标准,以三相逆变器不同开关模式作适当的切换,从而形成PWM波,使控制电机获得幅值恒定的圆形磁场。SVPWM模块的Simulink仿真模型如图 8所示。
|
Download:
|
| 图 8 SVPWM的Simulink仿真模型 Fig. 8 Simulink simulation model of SVPWM | |
扩张状态观测ESO模块通过电流观测量和扰动观测量的反馈,对PMSM系统内外扰动进行评估,以修正PMSM系统内环的电压输出。内外扰动估计Z2在d轴的扰动观测量Simulink仿真如图 9所示,同理可得到交直电流估计Z1在d、q轴的电流观测量以及内外扰动估计Z2在q轴的扰动观测量。

|
Download:
|
| 图 9 扩张状态观测模块的Simulink仿真模型 Fig. 9 SIMULINK simulation model of extended state observation module | |
为了检验基于ESO-CPC的激光追踪测量系统电机Simulink模型的正确性,对本文所建立的激光追踪测量系统电流控制模型进行了Simulink仿真实验。仿真实验选用Harmonic的FHA-C mini系列谐波减速电机,其主要参数如表 1所示。
| 表 1 电机主要参数 Table 1 Main parameters of motor |
给定转速n0=1 000 rad/s,在t=0时,启动控制电机;在t=0.1时,给电机加一个力矩为10 N·m的负载,观测控制电机三相定子绕组电流仿真波形、电磁转矩仿真波形和电机转速仿真波形变化。为了便于突出本文所建立的激光追踪测量系统基于ESO-CPC模型的有效性和优越性,与图 10所示的激光追踪测量系统电流PI控制算法模型进行比较分析。

|
Download:
|
| 图 10 激光追踪测量系统电流PI控制Simulink仿真模型 Fig. 10 Simulink simulation model of current PI control for laser tracking measurement system | |
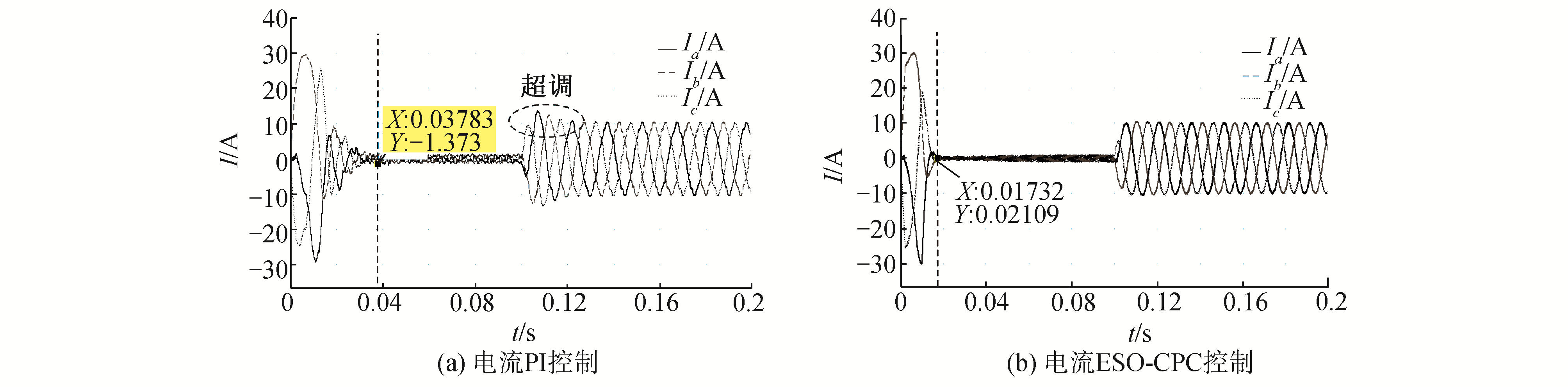
激光追踪测量系统电机三相定子绕组电流的Simulink仿真波形图,如图 11所示。其中,图 11(a)为电机电流采用PI算法控制时三相定子绕组电流的波形变化;图 11(b)为电机电流采用ESO-CPC预测算法控制时三相定子绕组电流的波形变化。从图 11中可以看出,控制电机上电后,电机的三相定子绕组电流略有震荡后达到稳态;相比于PI控制算法,采用ESO-CPC预测控制算法使电机达到稳态的时间更短,提高了20.56 ms。在t=0.1时刻给电机加一个力矩为10 N·m的负载后,采用ESO-CPC预测控制算法控制电机,电机并未超调震荡便可迅速到达稳态,稳定后最大峰峰值比PI算法控制减小了0.76 A,且三相正弦波曲线更为平滑、无杂波。
|
Download:
|
| 图 11 电机三相定子绕组电流的Simulink仿真波形图 Fig. 11 Simulink simulation waveform of motor three-phase stator winding current | |
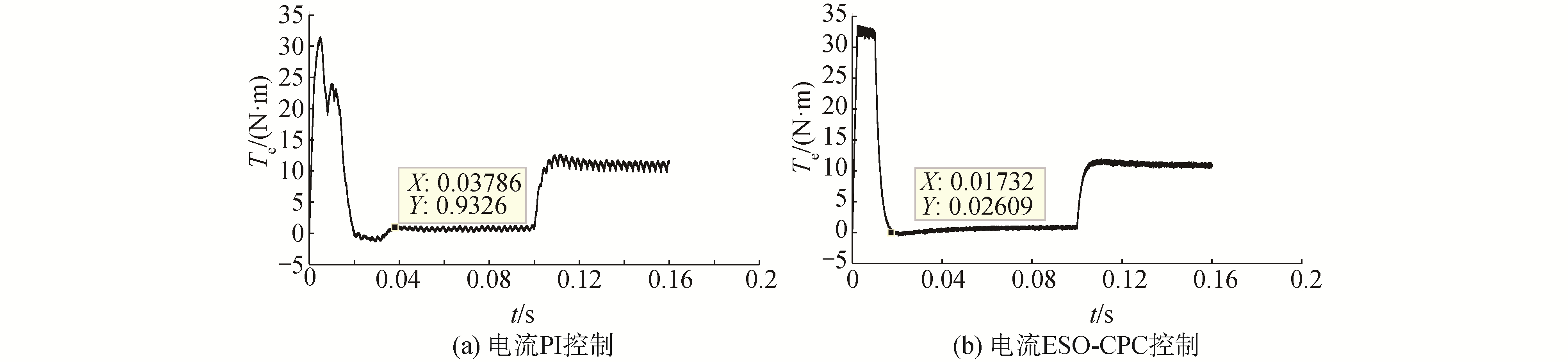
激光追踪测量系统电机电磁转矩的Simulink仿真波形图,如图 12所示。其中,图 12(a)为电机电流采用PI算法控制时电磁转矩的波形变化;图 12(b)为电机电流采用ESO-CPC预测算法控制时电磁转矩的波形变化。从图 12中可以看出,控制电机上电后,迅速达到最大转矩并快速回到稳定值;其变化趋势与电机三相定子绕组电流的变化趋势相同,采用ESO-CPC预测控制算法比采用PI控制算法使电机达到稳态的时间更短。在增加负载后,采用ESO-CPC预测控制算法的电机迅速到达稳态,且变化平稳。
|
Download:
|
| 图 12 电机电磁转矩的Simulink仿真波形图 Fig. 12 Simulink simulation waveform of motor electromagnetic torque | |
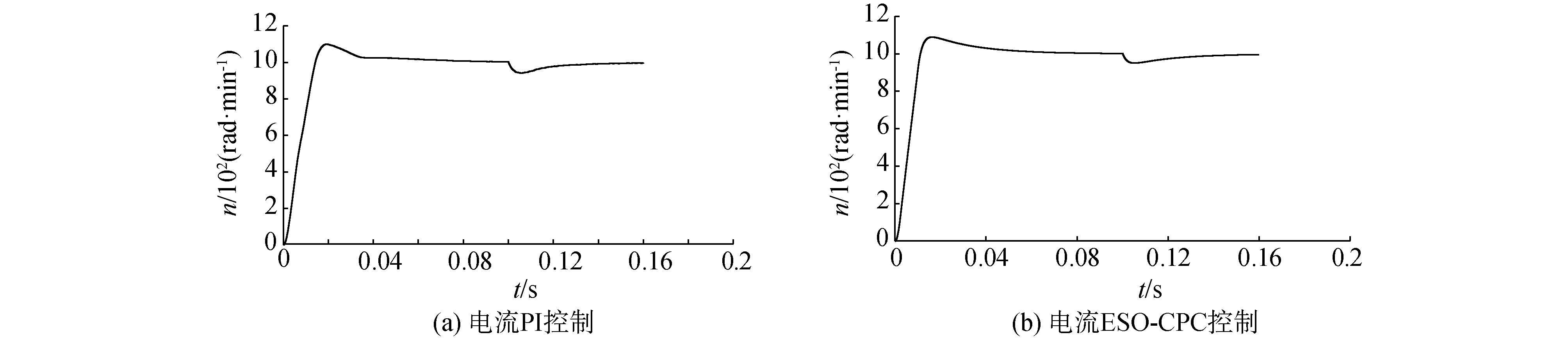
激光追踪测量系统电机转速的Simulink仿真波形图,如图 13所示。其中,图 13(a)为电机电流采用PI算法控制时转速的波形变化;图 13(b)为电机电流采用ESO-CPC预测算法控制时转速的波形变化。从图 13中可以看出,控制电机上电后,电机转速迅速增大,在微小震荡后快速回到给定值。相比于PI控制算法,采用ESO-CPC预测控制算法使电机转速上升时间小,超调量小,更快到达给定的稳定转速值。
|
Download:
|
| 图 13 电机转速的Simulink仿真波形图 Fig. 13 Simulink simulation waveform of motor speed | |
基于扩张状态观测器的电流预测算法作用于激光追踪测量系统电机的内环电流控制设计,缩短了激光追踪测量系统电机转矩达到稳定值的时间,并且减小了电机转速的超调量,电机运行更加平稳。因此,激光追踪测量系统的电流预测控制具有较好的动态响应特性和速度控制特性,系统稳定、操作方便,是理想的控制模型。
4 结论1) 本文结合永磁同步电机的数学模型和激光追踪测量系统的电流预测控制方法,建立了基于扩张状态观测器电流预测控制算法的激光追踪测量系统电机模型,并运用Simulink实现了激光追踪测量系统电机控制的建模与仿真。
2) 通过仿真实验可以看出,基于扩张状态观测器的电流预测控制,克服了由模型误差和不确定性干扰的影响,并对内外扰动进行评估,有效解决了失配问题导致的电机模型计算误差和电流抖动,使激光追踪测量系统控制电机具有较好的动态响应特性和速度控制特性,并且系统运行稳定。
3) 本文提出的建模和仿真方法为精密伺服控制系统的设计和调试提供了一种研究方案。
| [1] |
陈洪芳, 孙衍强, 王亚韦, 等. 高精度激光追踪测量方法及实验研究[J]. 中国激光, 2018, 45(1): 0104003. CHEN Hongfang, SUN Yanqiang, WANG Yawei, et al. High-precision laser tracking measurement method and experimental study[J]. Chinese journal of lasers, 2018, 45(1): 0104003. (  0) 0)
|
| [2] |
张博, 彭军. 激光跟踪测量系统[J]. 计测技术, 2006, 26(4): 5-6, 41. ZHANG Bo, PENG Jun. Laser tracker system for measurement[J]. Metrology & measurement technology, 2006, 26(4): 5-6, 41. DOI:10.3969/j.issn.1674-5795.2006.04.002 (  0) 0)
|
| [3] |
宋辉旭, 石照耀. 激光追踪仪的基本原理及应用[J]. 工具技术, 2015, 49(4): 58-91. SONG Huixu, SHI Zhaoyao. Application and basic principle of laser tracer[J]. Tool engineering, 2015, 49(4): 58-91. (  0) 0)
|
| [4] |
LAU K, HOCKEN R, HAYNES L. Robot performance measurements using automatic laser tracking techniques[J]. Robotics and computer-integrated manufacturing, 1985, 2(3/4): 227-236. (  0) 0)
|
| [5] |
ZMOOD D N, HOLMES D G, BODE G H. Frequency-domain analysis of three-phase linear current regulators[J]. IEEE transactions on industry applications, 2001, 37(2): 601-610. DOI:10.1109/28.913727 (  0) 0)
|
| [6] |
MALESANI L, MATTAVELLI P, BUSO S. Robust dead-beat current control for PWM rectifiers and active filters[J]. IEEE transactions on industry applications, 1999, 35(3): 613-620. DOI:10.1109/28.767012 (  0) 0)
|
| [7] |
LIN-SHI X, MOREL F, LLOR A M, et al. Implementation of hybrid control for motor drives[J]. IEEE transactions on industrial electronics, 2007, 54(4): 1946-1952. DOI:10.1109/TIE.2007.898303 (  0) 0)
|
| [8] |
MOREL F, LIN-SHI X, RETIF J M, et al. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive[J]. IEEE transactions on industrial electronics, 2009, 56(7): 2715-2728. DOI:10.1109/TIE.2009.2018429 (  0) 0)
|
| [9] |
王伟华, 肖曦. 提高PMSM电流环动态性能的增量预测算法[J]. 清华大学学报(自然科学版), 2013, 57(3): 1019-1024. WANG Weihua, XIAO Xi. Incremental predictive algorithm for the current loop in a PMSM to improve dynamic performance[J]. Journal of Tsinghua University (science and technology), 2013, 57(3): 1019-1024. (  0) 0)
|
| [10] |
ZHU Hao, XIAO Xi, LI Yongdong. PI type dynamic decoupling control scheme for PMSM high speed operation[C]//Proceedings of the 25th Annual IEEE Applied Power Electronics Conference and Exposition (APEC). Palm Springs, CA, USA: IEEE, 2010: 1736-1739.
(  0) 0)
|
| [11] |
张永昌, 杨海涛, 魏香龙. 基于快速矢量选择的永磁同步电机模型预测控制[J]. 电工技术学报, 2016, 31(6): 66-73. ZHANG Yongchang, YANG Haitao, WEI Xianglong. Model predictive control of permanent magnet synchronous motors based on fast vector selection[J]. Transactions of china electrotechnical society, 2016, 31(6): 66-73. DOI:10.3969/j.issn.1000-6753.2016.06.008 (  0) 0)
|
| [12] |
SIAMI M, KHABURI D A, ABBASZADEH A, et al. Robustness improvement of predictive current control using prediction error correction for permanent-magnet synchronous machines[J]. IEEE transactions on industrial electronics, 2016, 63(6): 3458-3466. DOI:10.1109/TIE.2016.2521734 (  0) 0)
|
| [13] |
寇宝泉, 程树康. 交流伺服电机及其控制[M]. 北京: 机械工业出版社, 2008. KOU Baoquan, CHENG Shukang. AC servo motor and its control[M]. Beijing: China Machine Press, 2008. (  0) 0)
|
| [14] |
骆再飞, 蒋静坪, 许振伟. 交流伺服系统及其先进控制策略综述[J]. 机床与液压, 2002(6): 7-10. LUO Zaifei, JIANG Jingping, XU Zhenwei. Overviews of AC servo system and its advanced control strategies[J]. Machine tool & hydraulics, 2002(6): 7-10. DOI:10.3969/j.issn.1001-3881.2002.06.002 (  0) 0)
|
| [15] |
牛里.交流永磁同步伺服系统电流环带宽拓展技术研究[D].哈尔滨: 哈尔滨工业大学, 2010. NIU Li. The research of current-loop band with expanding technology for AC-PMSM servo system[D]. Harbin: Harbin Institute of Technology, 2010. (  0) 0)
|
| [16] |
林伟杰.永磁同步电机伺服系统控制策略的研究[D].浙江: 浙江大学, 2005. LIN Weijie. Research on control strategy of permanent magnet synchronous motor servo system[D]. Zhejiang: Zhejiang University, 2005. (  0) 0)
|
| [17] |
高丽媛.永磁同步电机的模型预测控制研究[D].浙江: 浙江大学, 2013. GAO Liyuan. Research of model predictive control in permanent magnet synchronous motor drives[D]. Zhejiang: Zhejiang University, 2013. (  0) 0)
|
| [18] |
王正, 常浩. 永磁同步电机矢量控制系统研究[J]. 沈阳工业大学学报, 2007, 29(3): 307-311. WANG Zheng, CHANG Hao. Research on vector control system of permanent magnet synchronous motor[J]. Journal of Shenyang University of Technology, 2007, 29(3): 307-311. DOI:10.3969/j.issn.1000-1646.2007.03.016 (  0) 0)
|
| [19] |
王伟华, 肖曦. 永磁同步电机高动态响应电流控制方法研究[J]. 中国电机工程学报, 2013, 33(21): 117-123. WANG Weihua, XIAO Xi. A current control method for permanent magnet synchronous motors with high dynamic performance[J]. Proceedings of the CSEE, 2013, 33(21): 117-123. (  0) 0)
|
| [20] |
王伟华, 肖曦, 刘欢, 等. 电流增量预测控制策略参数稳定域拓展[J]. 电工技术学报, 2014, 29(3): 50-56. WANG Weihua, XIAO Xi, LIU Huan, et al. Expanding parameter stability region for incremental predictive control strategy of current[J]. Transactions of China electrotechnical society, 2014, 29(3): 50-56. DOI:10.3969/j.issn.1000-6753.2014.03.007 (  0) 0)
|
| [21] |
吴冰. 基于MATLAB/Simulink & Sim Power Systems的永磁同步电机(PMSM)矢量控制系统建模与仿真[J]. 电子机械工程, 2008, 24(3): 57-59, 64. WU Bing. Modeling and simulation of PMSM vector control system based on MATLAB/Simulink & Sim Power Systems[J]. Electro-mechanical engineering, 2008, 24(3): 57-59, 64. DOI:10.3969/j.issn.1008-5300.2008.03.016 (  0) 0)
|
| [22] |
高延荣, 舒志兵, 耿宏涛. 基于Matlab/Simulink的永磁同步电机(PMSM)矢量控制仿真[J]. 机床与液压, 2008, 36(7): 296-299. GAO Yanrong, SHU Zhibing, GENG Hongtao. Simulation of PMSM with vector control based on Matlab[J]. Machine tool & hydraulics, 2008, 36(7): 296-299. DOI:10.3969/j.issn.1001-3881.2008.07.097 (  0) 0)
|
| [23] |
安群涛, 李波, 王有琨. 采用SVPWM的永磁同步电动机系统建模与仿真[J]. 微电机, 2006, 39(9): 38-41. AN Quntao, LI Bo, WANG Youkun. Modeling and simulation of PMSM system using SVPWM[J]. Micromotors, 2006, 39(9): 38-41. DOI:10.3969/j.issn.1001-6848.2006.09.011 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


