RV减速器是工业关节机器人的核心关键零部件,因其承载能力大、抗冲击等优点通常被用于机器人躯干等关节的减速。但是其结构相比其他类型的行星减速器复杂,因而对于零件的加工精度要求非常苛刻,另一方面对其零部件精度检测的难度也相对较大。RV减速器包括两级行星减速,第1级是渐开线直齿轮行星传动,第2级是摆线针轮行星传动。与普通的摆线行星减速器相比,通过调节RV减速器第1级的传动比就可以使得整体的传动比变化范围非常广泛。因为RV减速器的输出轴由行星架代替,减少了输出机构的尺寸,所以相比摆线行星减速器,它的轴向尺寸更加紧凑。并且输出轴采用双支撑结构,其整体刚性也比普通的摆线减速器提高很多。国内外学者对RV减速器等摆线针轮传动进行了大量研究,其中YANG等[1]针对摆线传动中的加工误差、设计参数以及传动性能之间的关系进行了研究,推导了传动侧隙和扭矩波动的计算公式。何卫东等[2-3]建立了RV减速器的力学模型,并根据各齿啮合时的间隙分布,提出了摆线轮优化的数学模型。李充宁等[4]量化了摆线齿廓误差和减速器传动精度之间的关系,通过综合啮合误差来评价减速器的传动性能。Hertz[5]接触理论是建立摆线针齿接触模型的一种常用方法,并在此基础上可以进一步研究减速器参数对啮合刚度的影响。对于齿轮传动误差的研究方法除了通过理论分析各个因素的影响外,运用统计学的方法能够更直观地得到齿轮系统传动误差的分布情况[6]。SHIN等[7]通过速度瞬心和齐次坐标变换的方法分别研究了4种类型的摆线减速器。MENG等[8]建立了2 K-H摆线针轮行星传动误差的数学模型。单面啮合测量的方法能够得到齿轮切向综合误差、齿距偏差和偏心等类型的偏差,为研究RV减速器传动误差的测试方法提供了参考[9]。RV减速器的传动精度一直是国内外研究的一个热点,其中摆线针轮传动是最大的影响因素[10-13]。摆线针轮啮合时的接触力和轴承的摩擦力矩对减速器的刚性和回差有重要的影响[14-15],通过合理地对摆线齿廓修形以形成适当的啮合间隙,可以有效地减小摆线针轮之间的啮合接触力[16-17],进一步减少接触齿面摩擦热流量的产生[18]。但是很少有文献针对RV减速器摆线针轮传动中多齿啮合过程进行单独分析,从而研究摆线针齿啮合时接触力的变化过程对RV减速器传动精度的影响[19-22]。本文对摆线针轮多齿啮合过程进行了理论分析,建立了RV减速器动力学仿真模型。通过仿真计算得到了摆线针齿啮合时各齿接触点处的法向接触力、齿面间的摩擦力和摆线齿廓上接触应力的变化过程,并对RV减速器样机进行了传动性能测试。
RV减速器共包括输入齿轮轴、输出轴(行星架)和针轮3个自由度,任意固定其中的一个构件可以组成不同传动比的机构,也可以不固定任何构件来组成差动机构。因为行星直齿轮和曲柄轴用花键连接,所以在本文中将其看着一个构件。在机器人关节中通常将RV减速器用作减速机构,一般情况下固定针轮,由电机带动输入齿轮轴旋转,经过第一级行星减速后将运动传递给曲柄轴,再由曲柄轴带动摆线轮和针轮啮合,最终由输出轴(行星架)将运动输出。因为摆线针轮传动级的传动比大,而且是传动链的末端,所以摆线针轮的运动规律对整个减速器的传动精度起着关键作用。因此,本文主要针对摆线针轮的多齿啮合过程进行分析。
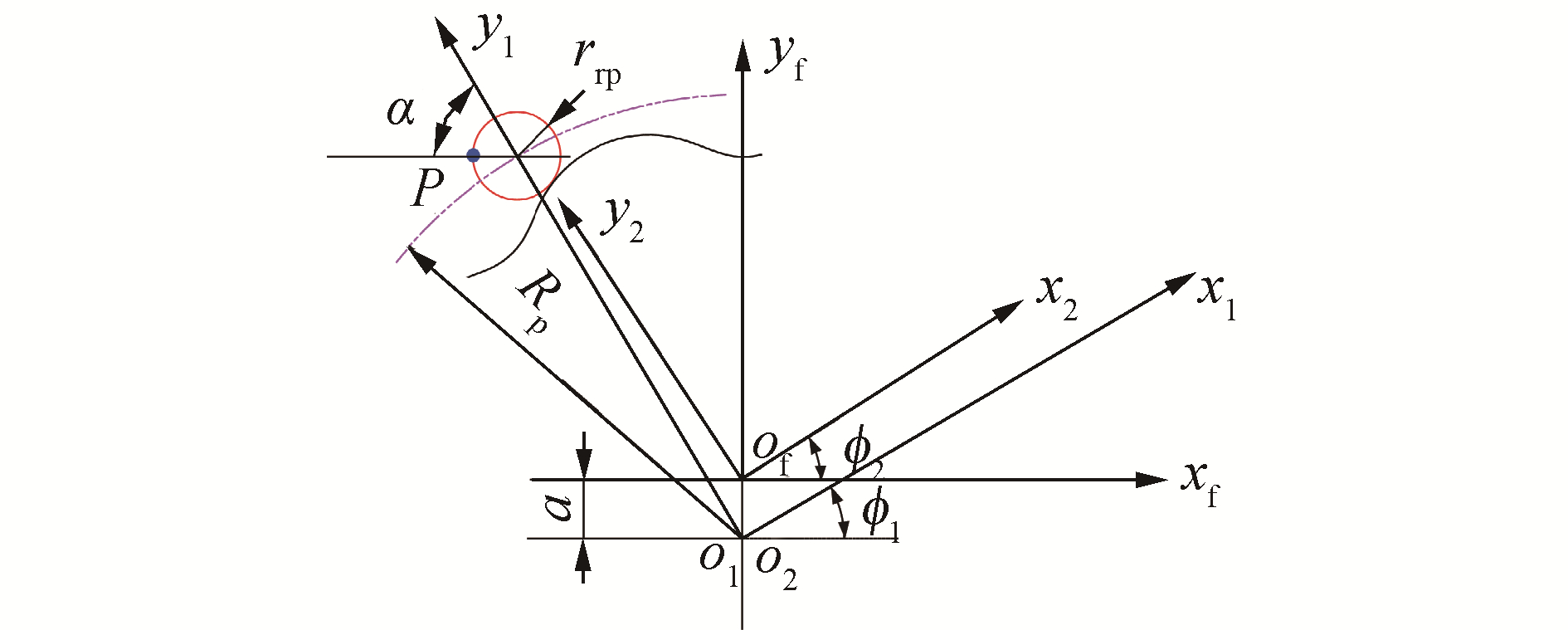
1 摆线针轮传动数学模型 1.1 摆线针轮啮合方程摆线针轮啮合时空间坐标系中的啮合点轨迹是针齿圆弧的一部分,所以根据齿轮的啮合原理建立如图 1所示坐标系。图中Sf(xf-of-yf)是参考坐标系,S1(x1-o1-y1)是针轮坐标系,S2(x2-o2-y2)是摆线轮坐标系。摆线轮坐标系的原点与参考坐标系的原点重合,针轮和摆线轮坐标原点的偏心距为a, Rp是针齿分布圆半径,rrp是针齿壳半径,由几何关系可以得到针齿上某点P在针轮坐标系中的位置坐标为:
| $ {r_1}\left( \alpha \right) = \left[ {\begin{array}{*{20}{c}} {{x_1}\left( \alpha \right)}\\ {{y_1}\left( \alpha \right)}\\1 \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {r_{rp}}\sin \alpha }\\ {{R_p} + {r_{rp}}\cos \alpha }\\ 1 \end{array}} \right] $ | (1) |
|
Download:
|
| 图 1 摆线针轮传动坐标系 Fig. 1 Cycloid-pin drive coordinate system | |
根据摆线针轮传动设计的传动比可以将两者的相对运动关系表示为:
| $ {\phi _2} = \frac{{{Z_p}}}{{{Z_p} + m}}{\phi _1} $ | (2) |
式中:ϕ1是针轮的绕参考坐标系旋转的角度;ϕ2是摆线轮绕参考坐标系旋转的角度;Zp是针轮的齿数;m是摆线轮和针轮的齿数差。
iH定义为摆线针轮传动比:
| $ {i^H} = \frac{{{Z_p}}}{{{Z_p} + m}} $ | (3) |
通过坐标变换可以将针轮齿廓上的P点运动轨迹转换到摆线轮坐标系下,从而得到与之共轭的摆线齿廓方程为:
| $ {r_2}\left( {\alpha ,{\phi _1}} \right) = {\mathit{\boldsymbol{M}}_{21}}\left( {{\phi _1}} \right) \cdot {r_1}\left( \alpha \right) $ | (4) |
其中坐标变换矩阵M21(ϕ1)为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{M}}_{21}}\left( {{\phi _1}} \right) = {\mathit{\boldsymbol{M}}_{2f}}{\mathit{\boldsymbol{M}}_{f1}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\cos \left( {{\phi _1} - {\phi _2}} \right)}&{ - \sin \left( {{\phi _1} - {\phi _2}} \right)}&{ - a\sin {\phi _2}}\\ {\sin \left( {{\phi _1} - {\phi _2}} \right)}&{\cos \left( {{\phi _1} - {\phi _2}} \right)}&{ - a\cos {\phi _2}}\\ 0&0&1 \end{array}} \right]} \end{array} $ | (5) |
因此,已知摆线传动的设计参数a、rrp、Rp、Zp、m,则可得到摆线轮在参考坐标系Sf(xf-of-yf)中的实际齿廓方程为:
| $ \left\{ \begin{array}{l} x = {R_p} \cdot \cos \left[ {\left( {1 - {i^H}} \right){\phi _1}} \right] - a \cdot \cos \left( {{i^H}{\phi _1}} \right) + \\ \;\;\;\;\frac{{{r_{rp}}}}{{\sqrt {1 + {K^2} - 2K\cos {\phi _1}} }} \cdot \\ \;\;\;\;\left[ { - \cos \left[ {\left( {1 - {i^H}} \right){\phi _1}} \right] + K \cdot \cos \left( {{i^H}{\phi _1}} \right)} \right]\\ y = {R_p} \cdot \sin \left[ {\left( {1 - {i^H}} \right){\phi _1}} \right] + a \cdot \sin \left( {{i^H}{\phi _1}} \right) - \\ \;\;\;\frac{{{r_{rp}}}}{{\sqrt {1 + {K^2} - 2K\cos {\phi _1}} }} \cdot \left[ {\sin \left[ {\left( {1 - {i^H}} \right){\phi _1}} \right] + } \right.\\ \;\;\;\;\left. {K \cdot \sin \left( {{i^H}{\phi _1}} \right)} \right] \end{array} \right. $ | (6) |
式中:K称为短幅系数,是针齿节圆和分布圆半径之比:
| $ K = \frac{{a{Z_p}}}{{{R_p}}} $ | (7) |
在建立摆线针轮啮合方程的基础就可以对摆线针轮多齿啮合的动态过程进行分析,摆线针齿啮合时的几何关系如图 2所示。

|
Download:
|
| 图 2 摆线针齿啮合几何模型 Fig. 2 Meshing geometry model of cycloid-pin | |
图 2中rp和rc分别是针轮和摆线轮啮合时的节圆半径,针轮和摆线轮节圆圆心分别是O1和O2,点P是两节圆的节点;a是摆线轮和针轮的偏心距;第i个针齿的圆心是Opi;ΔO1POpi称为啮合三角形,其中ϕi是摆线针轮啮合时的接触角,ψi是法向角,θi是曲柄轴的旋转角,li是啮合点的法向力臂长度。当摆线针轮啮合时由于输出轴受到负载扭矩作用,摆线轮将向受力方向旋转一个微小的角度Δβ, 同时参与啮合的摆线针齿将产生接触变形δi,从而产生相应的赫兹接触应力来抵抗负载作用。Δβ与δi用关系式表示为:
| $ {\delta _i} = \Delta \beta {l_i} $ | (8) |
因为摆线针齿啮合点处的法向力fi与接触变形δi成正比关系,因此摆线针齿啮合点处法向力臂长度最大时其啮合点处的法向接触力也最大,法向力臂长度li可以求得:
| $ {l_i} = a{Z_c}\sin {\phi _i} $ | (9) |
某一摆线针齿啮合时的法向接触力为:
| $ {f_i} = \frac{{1.1M}}{{K{Z_c}{R_p}}} \cdot \frac{{\sin {\theta _i}}}{{\sqrt {1 + {K^2} - 2K\cos {\theta _i}} }} $ | (10) |
式中:M是负载扭矩;Zc是摆线轮齿数。
根据法向接触力可以进一步求得啮合点处的赫兹接触应力,其计算式为:
| $ {P_{hi}} = \frac{{3{f_i}}}{{2{\rm{ \mathsf{ π} }}\rho _w^2}} $ | (11) |
式中:ρw是摆线针齿的当量曲率半径:
| $ {\rho _w} = {\rho _0} + {r_{rp}} $ | (12) |
式中:ρ0是摆线齿廓的曲率半径:
| $ {\rho _0} = \frac{{{{\left( {1 + {K^2} - 2K \cdot \cos \theta } \right)}^{\frac{3}{2}}} \cdot {R_p}}}{{K\left( {1 + {Z_p}} \right) \cdot \cos \theta - 1 - {Z_p} \cdot {K^2}}} $ | (13) |
将式(10)、(12)代入式(11)中计算得到接触齿面赫兹接触应力。
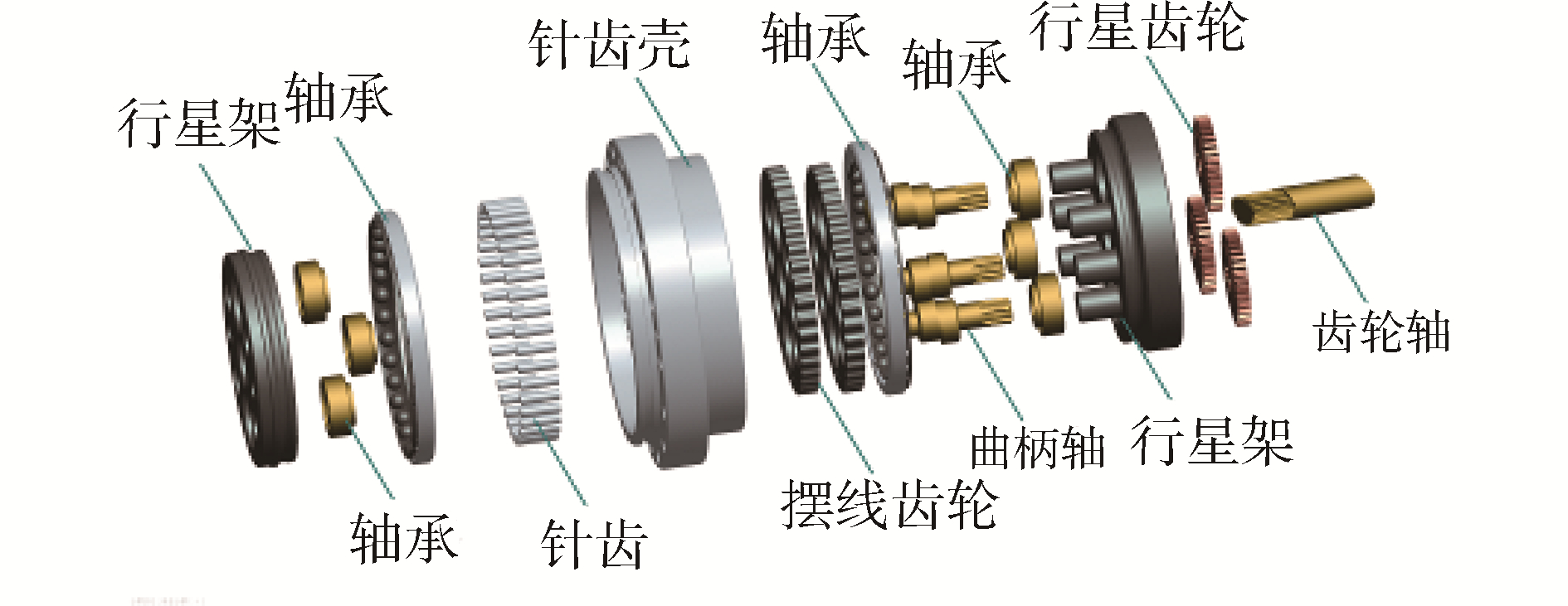
2 RV减速器动力学仿真 2.1 有限元仿真模型建立本文根据RV减速器样机参数,使用有限元仿真软件ANSYS建立了RV减速器动力学仿真几何模型,如图 3所示。RV减速器的模型参数如表 1所示,RV减速器有限元仿真时的动力学参数设置如表 2所示。采用冲击函数迭代计算啮合点接触力,接触单元的刚度和阻尼分别为105N/mm和50 N·s/mm。
|
Download:
|
| 图 3 RV减速器有限元仿真几何模型 Fig. 3 Finite element simulation geometry model of RV reducer | |
| 表 1 RV减速器样机参数 Table 1 Parameters of RV reducer prototype |
| 表 2 RV减速器有限元模型动力学参数 Table 2 Dynamic parameters of finite element model of RV reducer |
基于该有限元仿真模型,本文研究了RV减速器在不同负载扭矩作用下摆线针齿啮合时齿面接触状态的变化过程,得到了各啮合齿面接触点处的法向接触力、摩擦力和接触应力分布结果,从而为合理设计摆线齿廓和改善摆线针齿啮合状况提供参考。
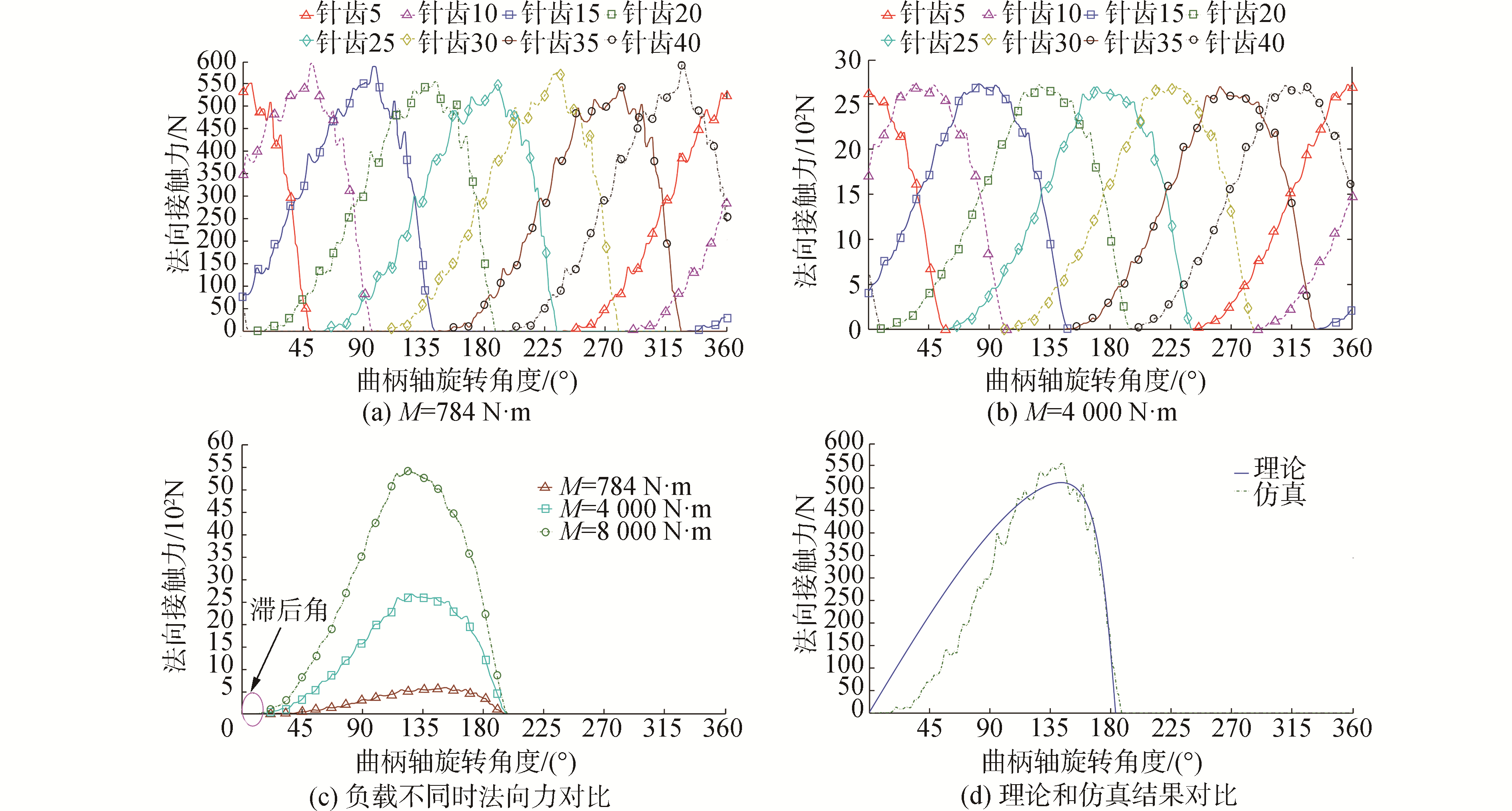
2.2 摆线针齿啮合时法向接触力通过有限元仿真计算得到曲柄轴旋转一周摆线针齿啮合过程中的法向接触力曲线如图 4所示。图 4(a)是RV减速器在额定负载784 N·m时摆线轮齿分别与第5、10、15、20、25、30、35、40个针齿啮合时的法向接触力。本文仿真模型中针轮一共有40个针齿,为了便于看清曲线的变化规律,图中只显示了部分摆线针齿啮合时的接触力。从图 4(a)中曲线分布可以看出,摆线轮齿廓与针轮上各个针齿相继进入啮合和退出啮合,理论上未经修形的摆线齿廓在任意时刻都会有一半的轮齿参与啮合传动,从图中的仿真结果可以得到验证。通过图 4(a)也可以看出每个摆线轮齿只有半个齿廓与针齿啮合传动,而且摆线齿廓凸的部分和凹的部分参与啮合的时间长度不同,摆线凸的齿廓参与啮合传动的时间相比凹的齿廓要长。图 4(a)中各个摆线针齿啮合时的法向接触力曲线不是很光滑,原因是轴承刚度和阻尼变化所引起的接触力波动。图 4(b)是负载扭矩为4 000 N·m时各个摆线针齿啮合时的法向接触力,与额定负载扭矩时的法向接触力相比曲线上的小波峰减少,曲线相对光滑。此时各摆线针齿啮合时的最大法向接触力接近2 500 N·m,增加的幅度几乎与负载扭矩的变化成线性关系。从负载扭矩分别为784、4 000和8 000 N·m时,第20个摆线针齿啮合的变化曲线也可以看出(如图 4(c)所示),随着负载扭矩的增加,摆线针齿啮合时的法向接触力也线性增加。另外从图 4(c)中也可以看出,3条曲线的起始位置相对零点滞后了一个角度。如果输出轴在没有负载扭矩的情况下,第20个针齿与摆线齿廓会在零点处开始啮合,但是由于负载扭矩的作用,摆线轮会因弹性变形旋转一个微小角度,也就是图 4(c)中曲线的滞后角。
|
Download:
|
| 图 4 摆线针齿啮合时法向接触力 Fig. 4 Contact force of cycloid-pin | |
图 4(d)是摆线针齿啮合时法向接触力理论公式(10)计算得到的法向接触力与有限元仿真结果对比,此时负载扭矩为RV减速器额定扭矩784 N·m。从图 4(d)可以看出,法向接触力理论曲线与有限元仿真曲线趋势基本相同,从而可以验证理论计算公式的正确性。但是理论公式中没有考虑摆线针齿啮合时弹性变形所引起的滞后角影响,所以图 4(d)中法向接触力理论曲线正好当曲柄轴旋转180°范围内有数值。另外,理论值在摆线齿廓凸的部分与仿真曲线也存在差别,而在摆线齿廓凹的部分理论曲线与仿真曲线相似度较好。
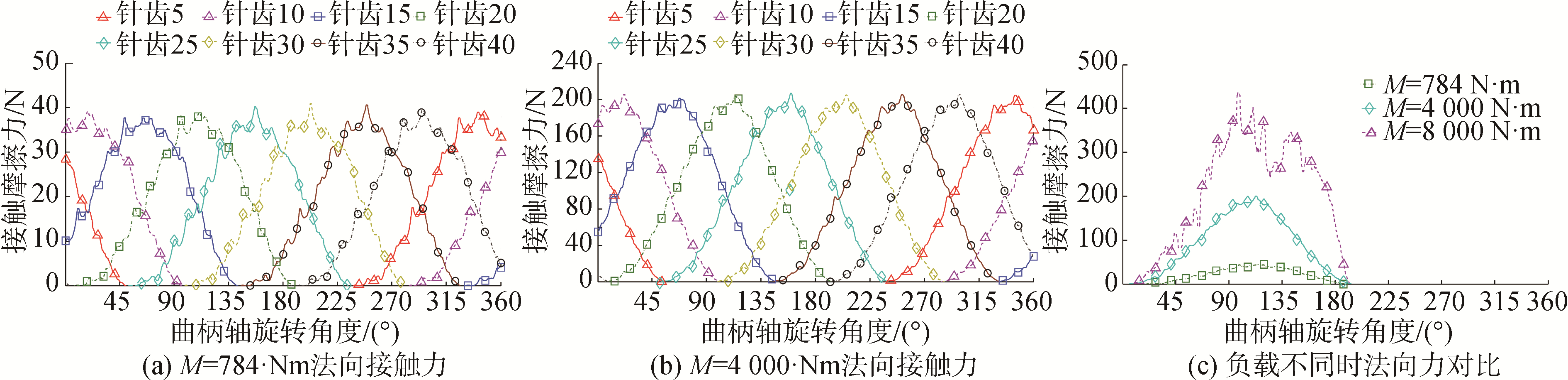
2.3 摆线针齿啮合时齿面摩擦力图 5是摆线针齿啮合时的齿面摩擦力变化曲线,其中图 5(a)是当额定负载扭矩时的各摆线针齿接触摩擦力,曲线的分布规律与法向接触力相似,但与法向接触力曲线不同的是摩擦力曲线在整个啮合齿廓部分基本对称,说明最大摩擦力所在齿廓位置发生了变化。图 5(b)是负载扭矩为4 000 N·m时各摆线针齿啮合时的摩擦力曲线,其曲线的变化趋势与额定负载扭矩时的一致,而且其摩擦力最大值基本与输出轴负载扭矩的变化成比例关系,这点从图 5(c)也可以看出。图 5(c)是负载扭矩分别为784、4 000和8 000 N·m时第20个针齿摩擦力曲线,图中最大摩擦力的变化基本与负载扭矩成线性比例,但是由于负载扭矩增大,也将引起齿面接触摩擦力的波动。
|
Download:
|
| 图 5 摆线针齿啮合时齿面摩擦力 Fig. 5 Friction force of cycloid-pin | |
本文通过有限元方法计算得到了某一时刻单个摆线齿面上接触应力的分布,从而更全面地研究摆线针齿啮合时齿面接触状态的变化规律。图 6是单个摆线齿廓曲面几何模型,用齿廓和齿宽方向来描述齿面接触应力的分布规律。图 7是当额定负载扭矩时,曲柄轴分别旋转270°和330°计算得到的摆线齿廓接触应力分布。
|
Download:
|
| 图 6 单个摆线齿廓曲面 Fig. 6 Single cycloid tooth profile surface | |

|
Download:
|
| 图 7 摆线齿廓接触应力分布 Fig. 7 Distribution of contact stress in cycloid tooth profile surface | |
由图 7可以看出,随着曲柄轴旋转,摆线齿面上的接触应力沿着齿廓方向移动。接触应力沿齿宽方向基本相同,但是由于应力集中影响,端面两侧处的接触应力较大。从图 7中也可以看出,摆线针齿在某一位置啮合时齿面接触应力的影响区域约占单个摆线齿廓的1/6区域,并且所占区域的大小随着负载扭矩的变化而改变。
3 RV减速器传动性能测试本文在高精度的RV减速器综合性能测试平台上对RV减速器的传动性能进行了测试, 测试试验台如图 8所示。试验台主要配置包括高精度动态伺服电机及控制系统、加载装置、高精度编码器和扭矩传感器等。RV减速器输入端和输出端的角度编码器检测精度分别是2.06″和1.13″,满足RV减速器传动精度检测的要求。

|
Download:
|
| 图 8 RV减速器样机传动性能测试装置 Fig. 8 Transmission performance test device of RV reducer prototype | |
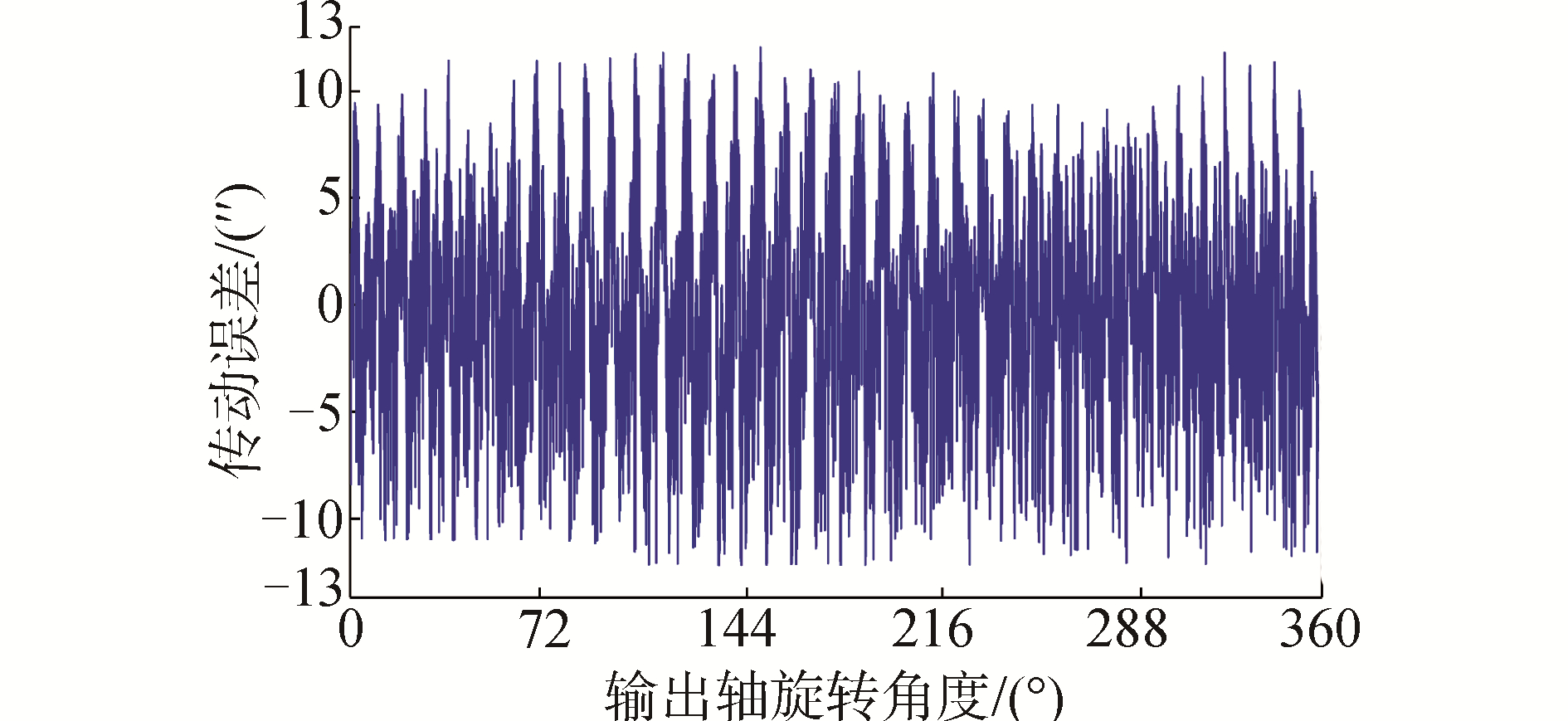
本文在RV减速器综合测试平台上对RV减速器样机进行了多项性能测试,其中传动误差是RV减速器最重要的一项性能指标,其数值大小对RV减速器的传动精度起到关键作用。本文所测试的RV减速器样机传动误差如图 9所示,此时RV减速器输出轴转速为额定转速15 rad/min。从测试结果可以看出被测RV减速器样机的传动误差小于30″, 属于高传动精度等级的减速器。为了具体分析传动误差的来源,本文通过傅里叶变换对传动误差曲线进行了频谱分析,其结果如图 10所示。图中幅值最大的频率为10 Hz,另外几个小峰值也接近其倍频。通过计算得到输出轴的旋转频率为0.25 Hz,而幅值最大的频率正好是其40倍频,本文被测样机的针齿数Zp为40,当输出轴旋转一周时,摆线轮与针轮啮合过40个针齿。由于行星齿轮传动级中没有对应的齿轮啮合频率,可以确定10 Hz频率是摆线针轮啮合引起。又因为摆线针轮啮合是RV减速器传动链的末端,其传动误差幅值不会经过传动链得到衰减,所以会对RV减速器传动精度产生较大影响。从图 10中也可以看出,10 Hz的频率所占峰值最大,而其他小的峰值频率都是经过其传动比衰减后的幅值。
|
Download:
|
| 图 9 RV减速器样机传动误差 Fig. 9 Transmission error of RV reducer prototype | |

|
Download:
|
| 图 10 RV减速器样机传动误差频谱 Fig. 10 Transmission error frequencies of RV reducer prototype | |
通过以上的理论分析可知曲柄轴旋转一圈摆线轮转过一个针齿角度,因此摆线针轮每啮合一个齿的周期将在传动误差曲线中得到反映,所以按照曲柄轴的旋转圈数将RV减速器传动误差等份成相应的分段曲线如图 11所示。从图中可以清楚地看出摆线针轮每个齿啮合传动的误差形状基本一致,由此可以说明摆线针轮每个齿啮合的周期在RV减速器传动误差中得到了充分反映。在此基础上可以进一步计算得到各个摆线针齿啮合周期时传动误差的标准差分量如图 12所示,从图中可以看出摆线轮与针轮在后半部分啮合位置所对应传动误差的标准差较大,从而可以间接判断摆线针轮在此部分位置啮合时各个摆线针齿之间的匹配性较差,因此可以针对性的提高此部分的齿廓精度。

|
Download:
|
| 图 11 RV减速器样机分段传动误差 Fig. 11 Sectional transmission error of RV reducer prototype | |

|
Download:
|
| 图 12 RV减速器分段传动误差的标准差分量 Fig. 12 Standard deviation component of the sectional transmission error | |
1) 经过与仿真结果对比,理论公式中没有考虑摆线针轮弹性变形所引起的滞后角影响,而且摆线齿廓凸的部分与仿真结果存在一些差别。当负载扭矩变化时,摆线针齿啮合时的法向接触力和摩擦力基本与输出轴负载扭矩成线性比例关系。
2) 摆线齿面上的接触应力在齿宽方向上基本相同,但在两端面附近的齿廓由于受到应力集中的影响会增大。在齿廓方向上,啮合点附近的齿面区域都会产生接触应力,而且区域的大小受到负载扭矩的影响。
3) 被测RV减速器样机属于高精度等级的精密减速器,通过对其传动误差的频谱分析验证了摆线针轮传动是引起RV减速器传动误差的主要原因。通过摆线针轮不同位置啮合时传动误差的标准差分量可以间接地判断各摆线针齿啮合位置的匹配性,从而可以针对误差较大位置进行齿廓修配,进一步提高RV减速器整体精度。
| [1] |
YANG D C H, BLANCHE J G. Design and application guidelines for cycloid drives with machining tolerances[J]. Mechanism and machine theory, 1990, 25(5): 487-501. DOI:10.1016/0094-114X(90)90064-Q (  0) 0)
|
| [2] |
何卫东, 李力行, 徐永贤, 等. 高精度RV传动的受力分析及传动效率[J]. 机械工程学报, 1996, 32(4): 104-110. HE Weidong, LI Lixing, XU Yongxian, et al. Analysis on the forces and efficiency of RV transmission for high precision[J]. Chinese journal of mechanical engineering, 1996, 32(4): 104-110. DOI:10.3321/j.issn:0577-6686.1996.04.018 (  0) 0)
|
| [3] |
何卫东, 李力行, 李欣. 机器人用高精度RV减速器中摆线轮的优化新齿形[J]. 机械工程学报, 2000, 36(3): 51-55. HE Weidong, LI Lixing, LI Xin. New optimized tooth-profile of cycloidal gear of high precision RV reducer used in robot[J]. Chinese journal of mechanical engineering, 2000, 36(3): 51-55. DOI:10.3321/j.issn:0577-6686.2000.03.012 (  0) 0)
|
| [4] |
李充宁, 刘继岩, 孙涛. 2K-V型行星传动中摆线针轮啮合的传动精度研究[J]. 机械工程学报, 2001, 37(4): 62-65. LI Chongning, LIU Jiyan, SUN Tao. Study on transmission precision of cycloidal pin gear in 2K-V planetary drives[J]. Chinese journal of mechanical engineering, 2001, 37(4): 62-65. (  0) 0)
|
| [5] |
张大卫, 王刚, 黄田, 等. RV减速机动力学建模与结构参数分析[J]. 机械工程学报, 2001, 37(1): 69-74. ZHANG Dawei, WANG Gang, HUANG Tian, et al. Dynamic formulation of RV reducer and analysis of structural parameters[J]. Chinese journal of mechanical engineering, 2001, 37(1): 69-74. DOI:10.3321/j.issn:0577-6686.2001.01.016 (  0) 0)
|
| [6] |
陈文华, 朱海峰, 樊晓燕. 齿轮系统传动误差的蒙特卡洛模拟分析[J]. 仪器仪表学报, 2004, 25(4): 435-437, 444. CHEN Wenhua, ZHU Haifeng, FAN Xiaoyan. Monte-Carlo simulation analysis of transmission error for gear drive systems[J]. Chinese journal of scientific instrument, 2004, 25(4): 435-437, 444. DOI:10.3321/j.issn:0254-3087.2004.04.005 (  0) 0)
|
| [7] |
SHIN J H, KWON S M. On the lobe profile design in a cycloid reducer using instant velocity center[J]. Mechanism and machine theory, 2006, 41(5): 596-616. DOI:10.1016/j.mechmachtheory.2005.08.001 (  0) 0)
|
| [8] |
MENG Yunhong, WU Changlin, LING Liping. Mathematical modeling of the transmission performance of 2K-H Pin cycloid planetary mechanism[J]. Mechanism and machine theory, 2007, 42(7): 776-790. DOI:10.1016/j.mechmachtheory.2006.07.003 (  0) 0)
|
| [9] |
石照耀, 鹿晓宁, 陈昌鹤, 等. 面齿轮单面啮合测量仪的研制[J]. 仪器仪表学报, 2013, 34(12): 2715-2721. SHI Zhaoyao, LU Xiaoning, CHEN Changhe, et al. Development of single-flank rolling tester for face gears[J]. Chinese journal of scientific instrument, 2013, 34(12): 2715-2721. (  0) 0)
|
| [10] |
SHAN Lijun, LIN Yuting, HE Weidong. Analysis of nonlinear dynamic accuracy on RV transmission system[J]. Advanced materials research, 2012, 510: 529-535. DOI:10.4028/www.scientific.net/AMR.510.529 (  0) 0)
|
| [11] |
杨玉虎, 张洁, 许立新. RV传动机构精度分析[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(7): 623-628. YANG Yuhu, ZHANG Jie, XU Lixin. Precision analysis of RV transmission mechanism[J]. Journal of Tianjin University (science and technology), 2013, 46(7): 623-628. (  0) 0)
|
| [12] |
XU Lixin, YANG Yuhu. Dynamic modeling and contact analysis of a cycloid-pin gear mechanism with a turning arm cylindrical roller bearing[J]. Mechanism and machine theory, 2016, 104: 327-349. DOI:10.1016/j.mechmachtheory.2016.06.018 (  0) 0)
|
| [13] |
HAN Linshan, GUO Fei. Global sensitivity analysis of transmission accuracy for RV-type cycloid-pin drive[J]. Journal of mechanical science and technology, 2016, 30(3): 1225-1231. DOI:10.1007/s12206-016-0226-2 (  0) 0)
|
| [14] |
于东, 张进华, 王东峰, 等. RV减速器主轴承摩擦力矩理论计算及特性分析[J]. 浙江大学学报(工学版), 2017, 51(10): 1928-1936, 1947. YU Dong, ZHANG Jinhua, WANG Dongfeng, et al. Theoretical calculation and analysis on friction torque in RV reducer main bearing[J]. Journal of Zhejiang University (engineering science), 2017, 51(10): 1928-1936, 1947. DOI:10.3785/j.issn.1008-973X.2017.10.006 (  0) 0)
|
| [15] |
石照耀, 徐航, 林家春, 等. 精密减速器回差测量与评价体系研究[J]. 仪器仪表学报, 2018, 39(6): 56-63. SHI Zhaoyao, XU Hang, LIN Jiachun, et al. Research on measurement and evaluation system of precision reducer lost motion[J]. Chinese journal of scientific instrument, 2018, 39(6): 56-63. (  0) 0)
|
| [16] |
LI Xuan, LI Chaoyang, WANG Yawen. Analysis of a cycloid speed reducer considering tooth profile modification and clearance-fit output mechanism[J]. Journal of mechanical design, 2017, 139(3): 033303. DOI:10.1115/1.4035541 (  0) 0)
|
| [17] |
王若宇, 高凤强, 刘暾东. RV减速器摆线轮齿廓修形建模与补偿研究[J]. 仪器仪表学报, 2018, 39(3): 81-88. WANG Ruoyu, GAO Fengqiang, LIU Tundong. Study on modification and compensation of tooth profile of RV reducer cycloidal gear[J]. Chinese journal of scientific instrument, 2018, 39(3): 81-88. (  0) 0)
|
| [18] |
李威, 胡岳龙. RV减速器摆线齿轮热分析[J]. 哈尔滨工程大学学报, 2017, 38(10): 1560-1567. LI Wei, HU Yuelong. Thermal analysis of cycloidal gear for the RV reducer[J]. Journal of Harbin Engineering University, 2017, 38(10): 1560-1567. (  0) 0)
|
| [19] |
梁帅锋, 邓效忠, 李天兴, 等. 机器人RV减速器摆线针轮传动轮齿接触分析[J]. 机械传动, 2017, 41(11): 17-22. LIANG Shuaifeng, DENG Xiaozhong, LI Tianxing, et al. Tooth contact analysis of cycloidal pinwheel drive in RV reducer of robot[J]. Journal of mechanical transmission, 2017, 41(11): 17-22. (  0) 0)
|
| [20] |
许立新, 杨玉虎. 一种摆线针轮传动多齿啮合接触特性分析方法[J]. 中国机械工程, 2016, 27(10): 1382-1387. XU Lixin, YANG Yuhu. A general method for multi-tooth contact analysis of cycloid-pin gear transmission[J]. China mechanical engineering, 2016, 27(10): 1382-1387. DOI:10.3969/j.issn.1004-132X.2016.10.017 (  0) 0)
|
| [21] |
XU Lixin, CHEN Bingkui, LI Chaoyang. Dynamic modelling and contact analysis of bearing-cycloid-pinwheel transmission mechanisms used in joint rotate vector reducers[J]. Mechanism and machine theory, 2019, 137: 432-458. DOI:10.1016/j.mechmachtheory.2019.03.035 (  0) 0)
|
| [22] |
WANG Hui, SHI Zhaoyao, YU Bo, et al. Transmission performance analysis of RV reducers influenced by profile modification and load[J]. Applied sciences, 2019, 9(19): 4099. DOI:10.3390/app9194099 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


