2. 浙江大学宁波理工学院 机能学院, 浙江 宁波 315100
2. College of Mechanical and Energy Engineering, Ningbo Institute of Technology, Zhejiang University, Ningbo 315100, China
Savoniu型水轮机(S型水轮机)最早由芬兰工程师Savonius发明[1],除早先用于风力发电外,近些年在潮流能发电领域也得到广泛应用。潮流能作为一种可再生能源,具有储量大、能源密度高且环境影响小等特点[2]。S型水轮机作为一种阻力型垂直轴水轮机具有转速低,启动力矩大以及结构简单制造成本低等优点。虽然阻力型垂直轴水轮机最大功率系数低于升力型垂直轴水轮机[3],但阻力型水轮机是通过阻挡前方来流,使迎流的2个叶片形成的阻力差旋转做功,所以相比升力型水轮机,S型水轮机具有更好的减流效果。近些年随着海洋养殖业的不断发展,深海养殖渔场、海洋牧场等概念不断被提出,网箱已朝着深远海,大型化的趋势不断发展[4]。深远海一般存在风大浪急,流速较快的现象,容易造成养殖设施和物种的破坏,在养殖渔场外围应用S型水轮机不仅可以捕能供养殖渔场使用,还可以减流实现对网箱的保护作用,对远海养殖业发展具有重要的作用。
为了提高S型水轮机的捕能系数,近20年,国内外学者在水轮机的辅助结构、基本参数以及水轮机组合形式等方面开展了大量的实验及数值理论分析研究。边佩翔等[5]通过数值计算研究重叠率对S型水轮机水动力特性的影响,发现最佳重叠率在0.15左右。Talukdar等[6]针对S型水轮机基本参数进行数值和试验研究,并指出当双叶片半圆形水轮机的重叠率、叶尖速比及高径比分别为0.89、0.15以及0.7时,其功率系数最大。田文龙等[7]发现椭圆叶片Savonius风力机在扁度为0.72的时发电性能最佳。Kamoji等[8]对螺旋形状的S型叶片进行试验,结果表明螺旋形水轮机具有更好的自启动性。Golecha等[9]通过在S型水轮机前端适当位置放置挡流板,以减少在叶片在回转过程中产生的负力矩,同时发现水轮机功率系数随级数增加而减小。张亮等[10]参考风力机的扩散器的原理设计了一种适用于垂直轴叶片的导流罩。Yao等[11]提出一种整流式Savonius叶轮整流罩,此整流罩不区分流向,在特定参数下最大功率系数可达48%。孙晓晶等[12]发现相比于单个水轮机,带有聚能遮蔽板结构的双S型水轮机性能大幅度提高。Ahmed等[13]研究多个S型水轮机的叶片形状,组合形式等参数对转速及功率的影响。Kumar等[14]发现改变S型水轮机叶片的形状也可大幅度提高捕能效率。
以上研究中发现,为了提高发电效率,学者们通过对不同结构参数下S型水轮机的水动力特性及其捕能效果进行了大量的研究,但鲜有学者提及针对S型水研究轮机的减流特性对其后方流场进行分析。仅黄六一等[15]通过试验的方法研究过方形箱网结构的减流效果。本文应用Star-CCM仿真软件,对S型水轮机后方流场进行数值理论研究,并进一步解释S形水轮机减流机理,找出速度场变化规律,制定减流效果判定标准从而研究叶尖速比对S型水轮机减流特性的影响。
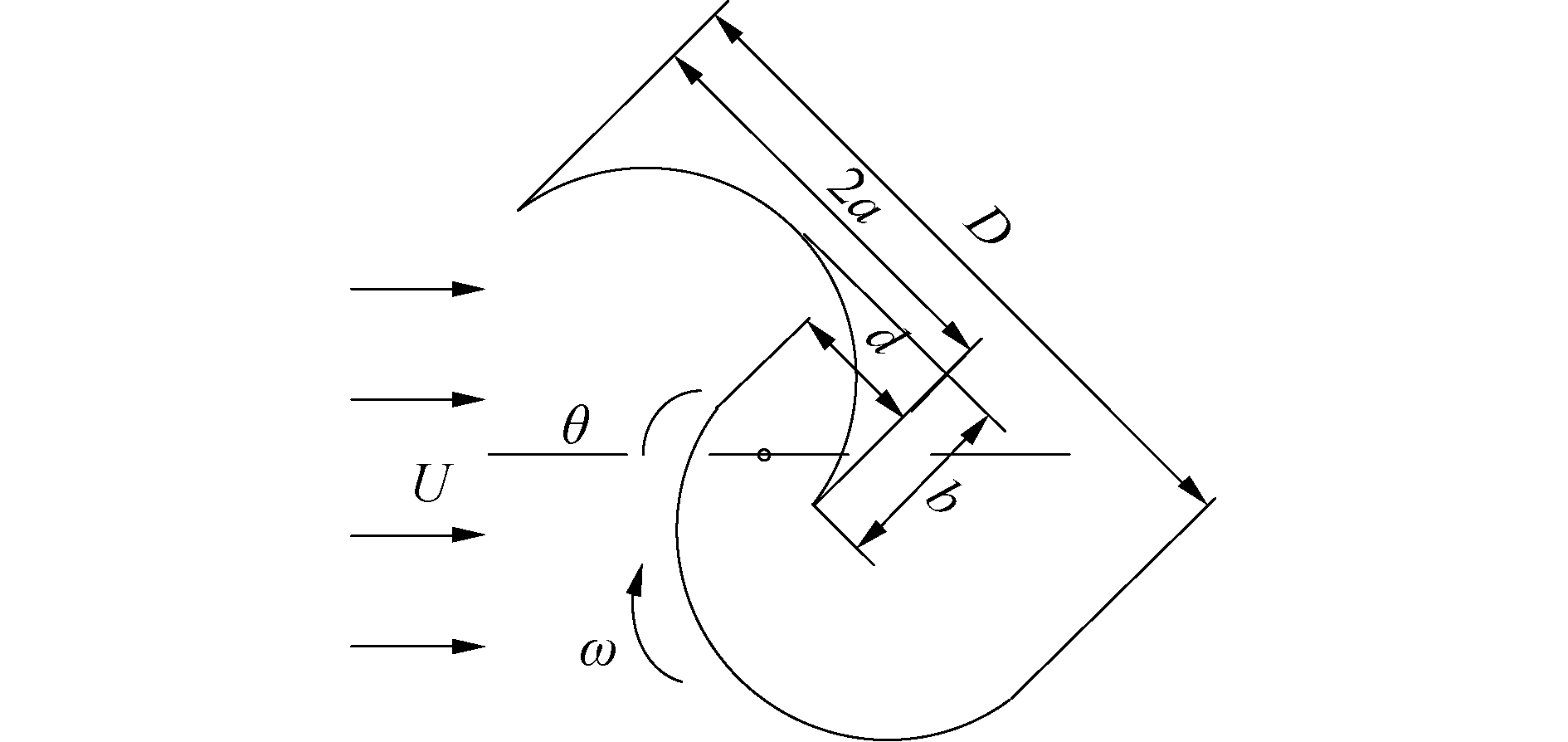
1 S型水轮机基本参数和仿真方法 1.1 基本参数叶尖速比、重叠率以及叶片数量和形状是影响S型水轮机水动力特性的主要参数,本文考虑能量守恒定律,将参考Talukdar[6]实验最优捕能结构参数(双叶片,重叠率0.15,曲率1,叶尖速比0.9)分析S型水轮机的减流性能。图 1为半圆形双叶片S型水轮机工作示意图。重叠率e、曲率ε以及叶尖速比TSR定义为:
|
Download:
|
| 图 1 S型水轮机工作示意 Fig. 1 Working dirgram of the Savonius trubine 注:U.来流速度;θ.当前水轮机旋转角度;ω.叶轮旋转速度;D.叶轮直径;d. 2个叶片之间的间隙。 | |
| $ {e = d/D} $ | (1) |
| $ {\varepsilon = b/a} $ | (2) |
| $ {{\rm{TSR}} = \frac{{\omega D}}{{2U}}} $ | (3) |
S型水轮机的减流性能则通过速度的衰减系数Ca和相对衰减长度La进行判断:
| $ {L_a} = L/D $ | (4) |
| $ {C_a} = \frac{{U - u}}{U} $ | (5) |
式中:ρ为流体密度;L为有效衰减长度;u为流场某一点的速度,其余参数如图 1所示。
1.2 S型水轮机数值仿真模型建立S型水轮机旋转时,在叶片周围及后方形成大量的涡流,促使流场运动变得十分复杂。本文采用CFD仿真软件Star-CCM对水轮机周围及后方流场进行数值模拟,此CFD软件具备较成熟的算法,丰富的物理模型,完善的多面体网格生成以及稳定的滑移网格技术,可在S型水轮机水动力学分析中,对流场中的湍流精确模拟,具有较高的仿真精度。由于仿真几何模型均采用直叶片,叶片展长方面的影响可以忽略,所以本文将采用二维CFD数值仿真计算,可大幅度地减少计算量,而又不影响计算精度。
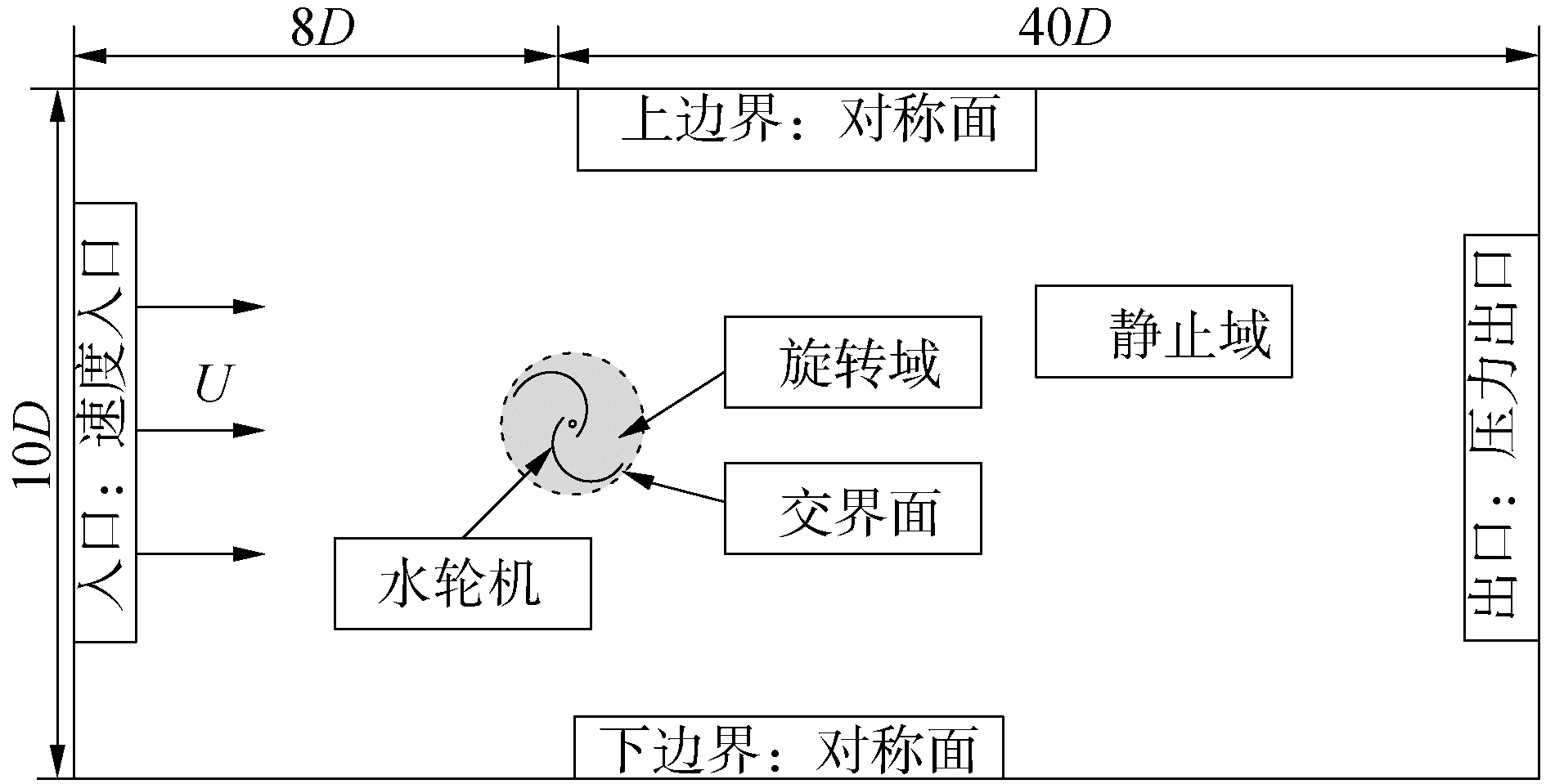
为了减少计算量,本文将采用滑移网格技术模拟水轮机转动,如图 2所示将整个仿真区域分为静止域和旋转域。为了防止仿真区域过小与仿真结构体相互影响,并且S型水轮机后方减流区域较长,则需将仿真区域设置足够大。如图 2所示仿真区域长48D,宽10D,且水轮机距前方速度入口边界8D。在边界条件设置方面,左侧入口边界设置为速度入口,给定速度幅值及湍流参数;右侧出口边界设置为压力出口;上下边界设置为对称平面;叶轮设置为无滑移壁面。
|
Download:
|
| 图 2 计算域及边界条件 Fig. 2 Computing domains and boundary conditions | |
计算域的网格划分如图 3(a)所示,同时采用2种非结构化网格对整个区域进行划分,旋转域内使用六面体网格,静止域内使用切割体网格。如图 3(b)所示,为了提高交接面处插值的精度,减小数值传递误差,对交界面附近网格加密,并且在交界面两侧各生成一层棱柱层网格,尺寸一致;同样,由于叶片附近流场变化剧烈,为了提高计算精度和更好的研究S型水轮机后方流场变化规律,叶片周围及后方区域网格进行加密。如图 3(c)所示,在叶片表面生成5层棱柱层,第1层厚度为2 mm,增长率1.2,叶片表面Y+值分布在30~100。经过网格无关性验证,将壁面首层网格长度分别设为2、1.5和1 mm,对应的网格总数分别为40万、50万以及65万个,发现计算结果差别不到2%,为了减少运算量,整个计算域网格数量大约为40万个。

|
Download:
|
| 图 3 网格划分 Fig. 3 Mesh generation | |
仿真基于RANS标准k-ε两方程湍流模型,并采用混合壁面处理函数实现两层模型。控制方程压力插值在空间离散上采用Standard方式,二阶迎风格式;时间离散上采用一阶隐式格式,时间步长0.005 s。数值解法使用压力—速度耦合:SIMPLE算法,每个时间步内部迭代50次,残差收敛标准为10-5。为了验证仿真模型的准确性将仿真结果与Parag K. Talukdar[6]的实验结果进行对比,如图 4所示。从图中可以发现,本文模拟结果与实验结果基本吻合,因此利用本文数值模拟方法预测S型水轮机后方流场变化规律是可行的。

|
Download:
|
| 图 4 仿真模型验证 Fig. 4 Validation of the simulation model | |
为了分析S型水轮机减流机理,本文将从S型水轮机的启动前后2个状态入手观察其减流效果。叶片静止时,θ角设定为90°,因为此时叶片迎流面最大,可对流场造成最大影响;叶片旋转时,叶尖速比设定为捕能最佳速比0.9[6]。从图 5状态速度云图对比发现,启动后S型水轮机的减流效果明显优于启动前,而且减速效果显著。从后方速度场分析来看,启动前,速度场大小分布不均匀且变化大,而启动后速度场分布较为均匀;再从流线角度分析,虽然启动前后S型水轮机对前方来流都存在一定的阻挡作用,但由于启动前来流受到流场的干扰,又回到后方流程且速度增大,而启动后的来流在水轮机的阻挡下可以很好的从两侧绕开,只有一小部分进入后方流场。

|
Download:
|
| 图 5 S型水轮机速度场及流线 Fig. 5 Velocity field and streamline of Savonius turbine | |
通过S型水轮机启动后旋转至90°和180°时的速度矢量场,可进一步解释水轮机减流机理。如图 6所示,矢量场中存在许多水质点运动碰撞区(方形区域内),尤其方形1区域内,水轮机前方水质点在凸叶片旋转的推动下,朝着与叶片垂直的方向运动,并与前方来流水质点发生激烈碰撞,这种直接碰撞是造成S型水轮机具有减流效果的主要原因之一。此外,从图中可以发现叶轮尾流中有涡流形成(圆形区域内),涡流(如图 6(b)圆形2)的形成一方面是由于如图 6(a)方形区域2中水质点的碰撞;另一方面是由于叶轮旋转结构造成(如图 6(b)圆形3)。从涡流带动水质点的运动可以看出,涡旋总是阻止前方来流水质点进入水轮机后方流场(如圆形涡流周围所示),并且运动方向与水轮机后方旋转带动的水质点运动方向相反,减小水轮机旋转对后方流场的影响的同时促使涡流逐渐减小至消失(如2图圆形1内对比所示)。所以发现尾流中形成的涡流是保障水轮机具有良好减流效果的另一主要因素。综上可知,S型水轮机减流机理在于除了迎流凹叶面可以阻挡来流水质点外,在水轮机旋转域内,受凸叶片运动影响的水质点,总是与来流或后方涡流的水质点发生碰撞,产生减流效果的同时还可以形成新的可以阻止两侧边界水质点进入水轮机后方流场的涡流,从而使得S型水轮机在旋转状态时具有较好的减流效果。

|
Download:
|
| 图 6 S型水轮机旋转状态速度矢量 Fig. 6 Velocity vector field of rotating Savonius turbine | |
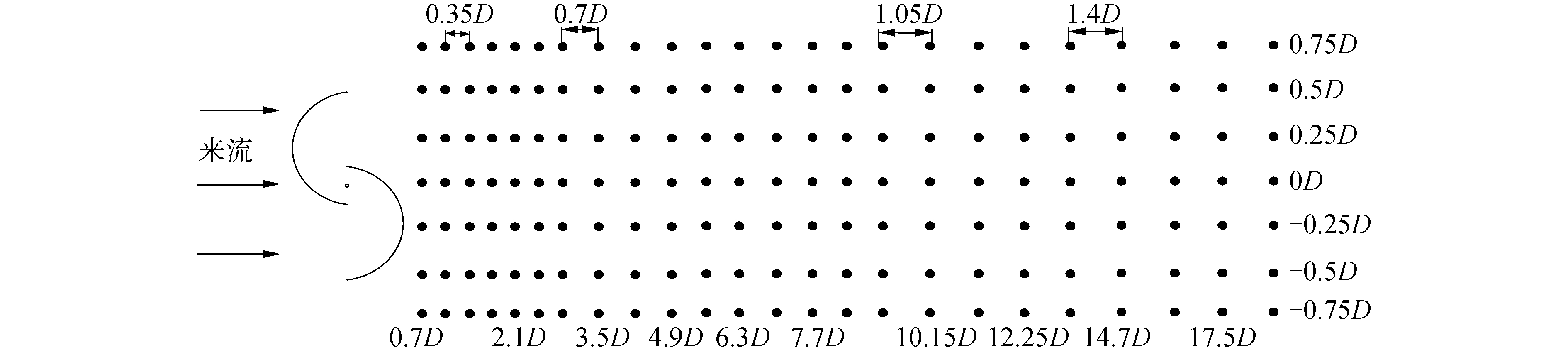
为了了解S型水轮机后方流场速度变化规律判断减流区域分布情况,将在水轮机后方布置175个测速点对流场各位置的速度变化进行实时监测。具体布置如图 7所示,水轮机的旋转中心位于0D处,在纵向上均匀布置7个测速点间隔0.25D,在水平方向上布置25个测速点,水轮机尾流区域内测速点较为密集,但随着距离的加大分布密度逐渐减小。
|
Download:
|
| 图 7 速度探针分布示意 Fig. 7 The distribution of velocity probes | |
图 8显示了不同横向位置各个监测点速度时历曲线,可分析不同位置的速度随时间的变化规律。所有检测点在一定时间后速度均呈现周期性变化;在纵向上远离0D的曲线波动较为激烈,而横向上离0D越远周期波动越小,当距离达到15D时,速度历史曲线近似为直线。产生这些现象的主要原因在于尾流场中上下两侧有涡旋产生使得速度场变化剧烈,随着流体向后传播涡旋逐渐消散流场趋于稳定。

|
Download:
|
| 图 8 不同横向位置上各速度监测点时历曲线 Fig. 8 The distribution of velocity probes | |
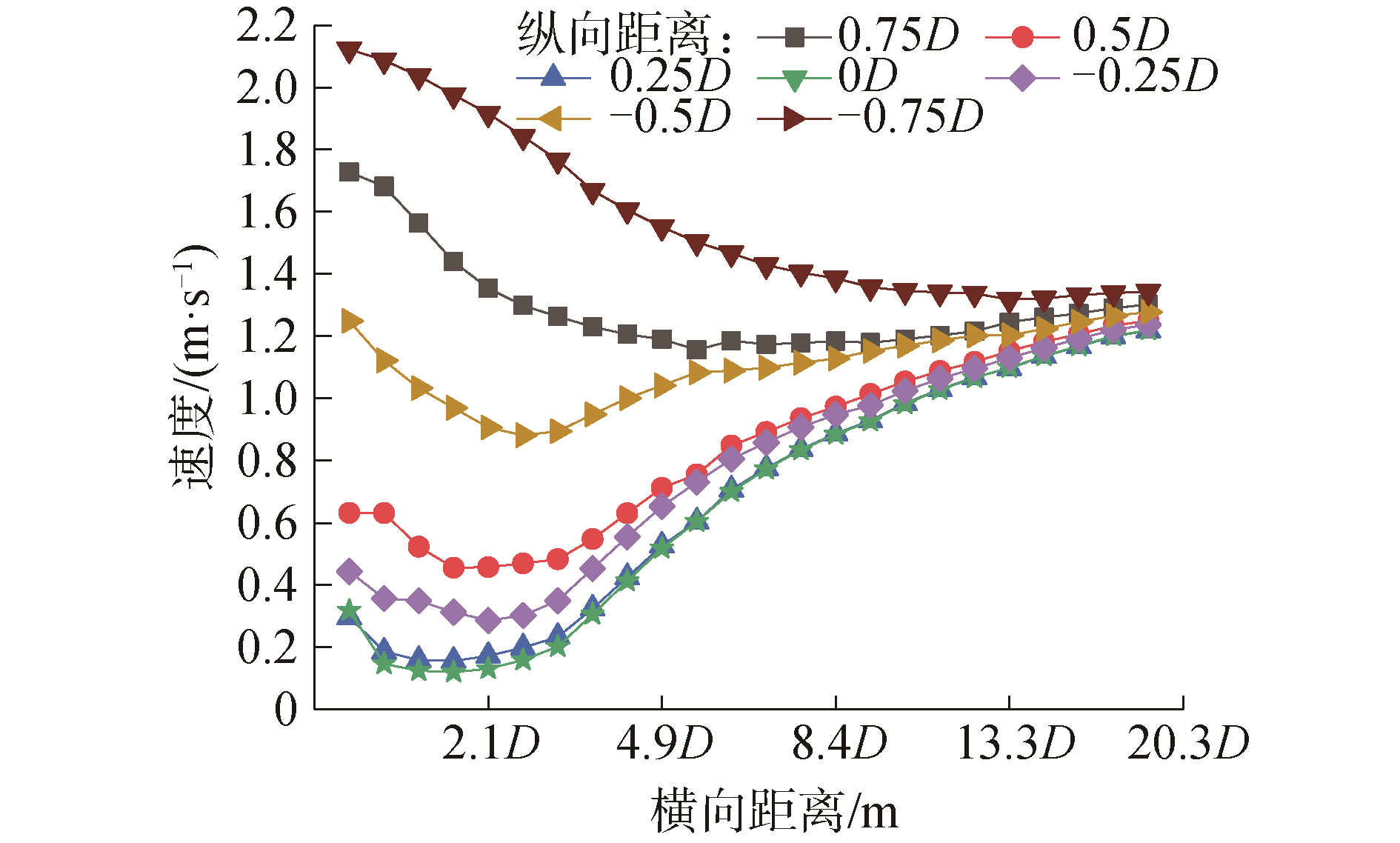
介于各点速度在一定时间后呈周期性变化,本文将通过其平均值研究S型水轮机后方流场速度衰减分布情况。各点在一个周期内的平均速度如图 9所示,从图中可以发现,横向上的各点速度值均随着距离加大呈现先减小后增大的趋势,尤其0D、0.25D、-0.25D这3条曲线呈“S”型;纵向上可观测到各曲线之间无交叉,所有曲线从小到大的排列依次为:0D,0.25D,-0.25D,0.5D,-0.5D,0.75D,-0.75D,全场最小速度0.12 m/s在纵向距离0D,横向距离1.75D处得到,所以从各曲线情况来看,S型水轮机后方流域速度场分布较为规律。主要原因在于,横向上由于涡流的形成和消散以及外部流场的影响使各点速度先减小后增大,而纵向上由于越靠近0D处,涡旋影响的水质点碰撞越激烈,所以减流效果越明显;另一方面由于S型水轮凸面回转时推动表面水质点快速进入后下方流场影响此区域减流效果。
|
Download:
|
| 图 9 TSR=0.9时各监测点平均速度 Fig. 9 Average velocity of probes, TSR=0.9 | |
除了研究S型水轮机后方速度场变化规律外,还需确定S型水轮机后方减流有效覆盖区域范围。如图 9所示,所有测速点中除了0.75D以及-0.75D前端的几点外,其余位置均小于来流速度1.5 m/s,但有些点的速度过于接近来流速度,减速效果不明显,所以本文将规定有效减流区域内的速度衰减系数应高于0.2(速度低于1.2 m/s)。横向上,由于纵向0D所在曲线的值最小,有效减流长度延伸的最远,其余曲线随着离0D越远有效减流长度逐渐缩短;在纵向上,由于-0.75D中所有点的速度衰减系数均小于0.2,所以不在有效减流区域内,而对称的0.75D在横向延伸到4.2D后进入到有效减流区域,所以纵向有效区域在4.2D前为-0.5D至0.5D,4.2D后为-0.5D至-0.75D,在随着横向距离增加到11.2D后再逐渐减小至没有。图 10为S型水轮机后方流场周期变化后,某一时刻带有等值线的速度云图,从速度等值线上可以更直接的观察到S型水轮机有效减流区域呈一个“剑”形,同时此形状也符合上文描述速度场变化规律。
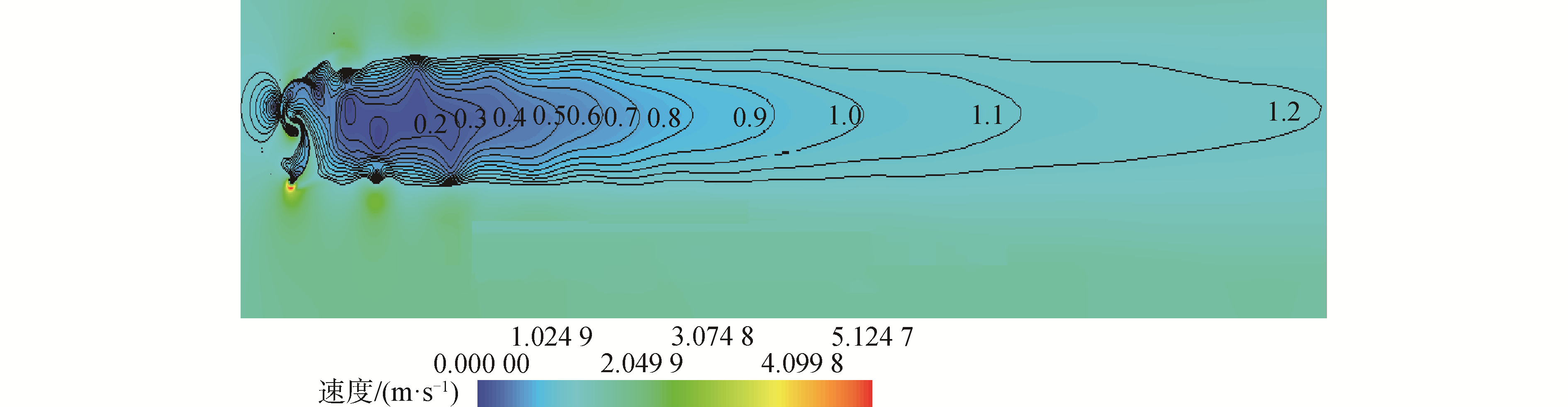
|
Download:
|
| 图 10 S型水轮机带有等值线的速度 Fig. 10 Velocity field with isoline of Savonius turbine | |
考虑在不影响S型水轮机的捕能效率的情况下,参考Talukdar[6]实验结果,将本文研究的叶尖速比设置在0.5~1.2。首先如图 9所示在叶尖速比0.9的情况下,横向距离1.75D左右中各点速度最小,则使用横向1.75D所有点一个周期内速度平均值可以最好的评价水轮机的减流强度。但观察图 11中2个极限叶尖速比工作情况下的各监测点速度变化情况,显然并不是在横向1.75D的平均值最小,说明不同叶尖速比下,各横向中平均速度最小值位置发生改变。另一方面从图 9和图 11中可以看出,在3种叶尖速比的情况下纵向位置0D处中的各点速度值最小,则此处的有效衰减长度最大。综上所述,考虑不同叶尖速比S型水轮机后方速度场变化规律的情况下,本文规定使用所有横向位置中平均速度衰减系数最大值Ca以及纵向0D位置的相对衰减长度La对S型水轮机的减流强度和范围进行评价。

|
Download:
|
| 图 11 极限叶尖速比情况下各监测点平均速度 Fig. 11 Average velocity of probes at the limit TSR | |
根据S型水轮机的减流特性评价标准计算出不同叶尖速比下的Ca以及La如图 12所示。从图 12(a)中可以发现水轮机的Ca随叶尖速比的变化先增加后减小,在叶尖速比达到1.1时得到最大值0.73;La随叶尖速比的变化如图 12(b)所示,呈现先减小后增大再减小的趋势,在叶尖速比0.8处达到最大值15.6;由于在流速不变的情况下,叶尖速比越大,叶片凸面向前转动时带动的水质点运动加快并与前方来流水质点发生更激烈的碰撞,有助于提高减流效果;但叶尖速比增加到一定程度后,凹面对水质点的阻挡不断减弱,而且由凸面回转带动进入后方流场的水质点速度也不断加快,反而影响了S型水轮机的减流效果,这也是在高叶尖速比的情况下Ca和La减小的主要原因。
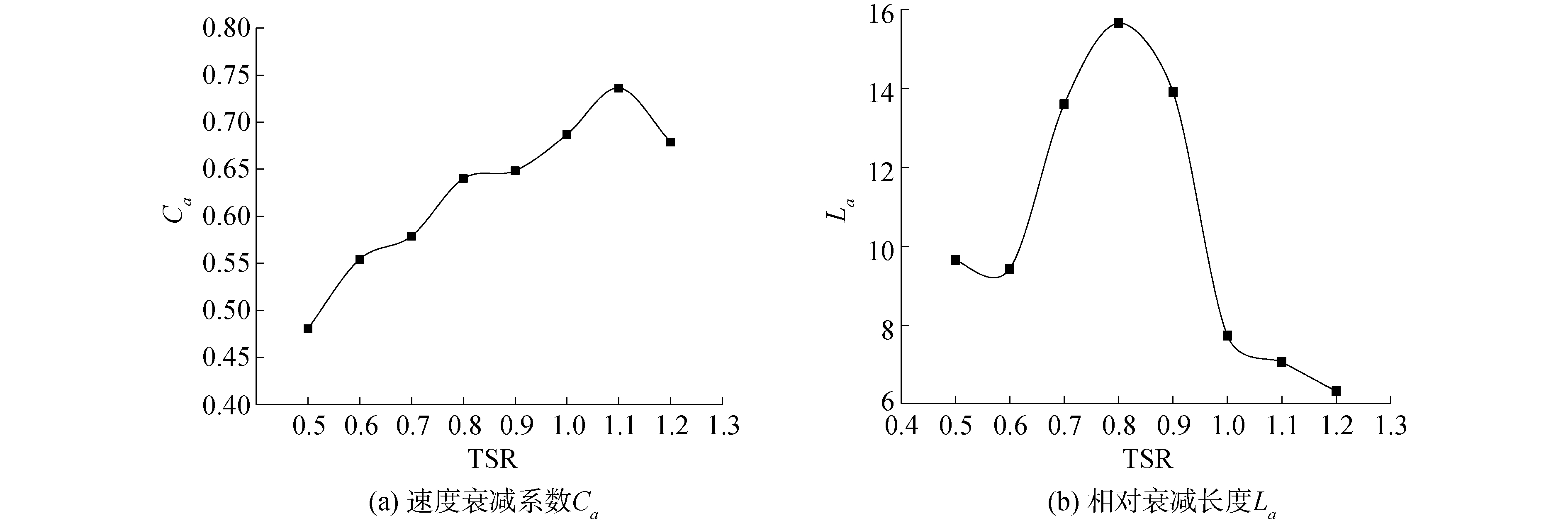
|
Download:
|
| 图 12 不同叶尖速比S型水轮机的Ca和La Fig. 12 Ca and La of SHT at different TSR | |
1) 由于叶片对来流水质点的阻挡、碰撞以及尾流场中涡流的作用,使得转动的S型水轮机在后方迎流面呈“剑”形区域内,具有很好的减流效果。
2) S型水轮机后方减流有效区域内速度场分布较为规律。纵向上越靠近0D处减流效果越好,并且凹面后方区域减流效果优于凸面;横向上随着与水轮机距离加大,减流效果先增加后减小再逐渐衰减至没有。
3) 叶尖速比对S型水轮机的减流效果有较大的影响,并通过比较各叶尖速比的Ac和LA发现减流最佳叶尖速比工作范围在0.8~1.0,其中最大速度衰减系数0.73以及最大有效相对衰减长度15.6分别在叶尖速比1.1和0.8处发现。
| [1] |
JAOHINDY P, MCTAVISH S, GARDE F, et al. An analysis of the transient forces acting on Savonius rotors with different aspect ratios[J]. Renewable energy, 2013, 55: 286-295. DOI:10.1016/j.renene.2012.12.045 (  0) 0)
|
| [2] |
刘富铀, 赵世明, 张智慧, 等. 我国海洋能研究与开发现状分析[J]. 海洋技术, 2007, 26(3): 118-120. LIU Fuyou, ZHAO Shiming, ZHANG Zhihui, et al. Analysis on research and development of oceanic energy in China[J]. Ocean technology, 2007, 26(3): 118-120. DOI:10.3969/j.issn.1003-2029.2007.03.033 (  0) 0)
|
| [3] |
KUMAR A, SAINI R P. Performance parameters of Savonius type hydrokinetic turbine-a review[J]. Renewable and sustainable energy reviews, 2016, 64: 289-310. DOI:10.1016/j.rser.2016.06.005 (  0) 0)
|
| [4] |
朱玉东, 鞠晓晖, 陈雨生. 我国深海网箱养殖现状、问题与对策[J]. 中国渔业经济, 2017, 35(2): 72-78. ZHU Yudong, JU XiaoHui, CHEN Yusheng. Offshore cage aquaculture of China:current situation, problems and countermeasures[J]. Chinese fisheries economics, 2017, 35(2): 72-78. DOI:10.3969/j.issn.1009-590X.2017.02.011 (  0) 0)
|
| [5] |
边佩翔, 杨志宏, 王勇, 等. Savonius式水轮机水动力学性能[J]. 浙江大学学报(工学版), 2018, 52(2): 268-272. BIAN peixiang, YANG Zhihong, WANG Yong, et al. Hydrodynamic performance of Savonius water turbine[J]. Journal of Zhejiang University (engineering science), 2018, 52(2): 268-272. (  0) 0)
|
| [6] |
TALUKDAR P K, SARDAR A, KULKARNI V, et al. Parametric analysis of model Savonius hydrokinetic turbines through experimental and computational investigations[J]. Energy conversion and management, 2018, 158: 36-49. DOI:10.1016/j.enconman.2017.12.011 (  0) 0)
|
| [7] |
田文龙, 宋保维, 毛昭勇. 椭圆叶片Savonius风力机叶轮气动性能数值计算[J]. 中国电机工程学报, 2014, 34(32): 5796-5802. TIAN Wenlong, SONG Baowei, MAO Zhaoyong. Numerical investigation of a Savonius wind turbine with elliptical blades[J]. Proceedings of the CSEE, 2014, 34(32): 5796-5802. (  0) 0)
|
| [8] |
KAMOJI M A, KEDARE S B, PRABHU S V. Performance tests on helical Savonius rotors[J]. Renewable energy, 2009, 34(3): 521-529. (  0) 0)
|
| [9] |
GOLECHA K, ELDHO T I, PRABHU S V. Influence of the deflector plate on the performance of modified Savonius water turbine[J]. Applied energy, 2011, 88(9): 3207-3217. DOI:10.1016/j.apenergy.2011.03.025 (  0) 0)
|
| [10] |
张亮, 孙科, 罗庆杰. 潮流水轮机导流罩的水动力设计[J]. 哈尔滨工程大学学报, 2007, 28(7): 734-737. ZHANG Liang, SUN Ke, LUO Qingjie. Hydrodynamic design of diversion cover for a tidal-stream hydro turbine[J]. Journal of Harbin Engineering University, 2007, 28(7): 734-737. DOI:10.3969/j.issn.1006-7043.2007.07.003 (  0) 0)
|
| [11] |
YAO Y X, TANG Z P, WANG X W. Design based on a parametric analysis of a drag driven VAWT with a tower cowling[J]. Journal of wind engineering and industrial aerodynamics, 2013, 116: 32-39. DOI:10.1016/j.jweia.2012.11.001 (  0) 0)
|
| [12] |
孙晓晶, 罗大海, 黄典贵, 等. 带聚能垂直轴水轮机组间耦合特性的试验研究[J]. 工程热物理学报, 2012, 33(12): 2088-2091. SUN Xiaojing, LUO Dahai, HUANG Diangui, et al. Experimental study of a new vertical axis water current device[J]. Journal of engineering thermophysics, 2012, 33(12): 2088-2091. (  0) 0)
|
| [13] |
AHMED M R, FAIZAL M, LEE Y H. Optimization of blade curvature and inter-rotor spacing of Savonius rotors for maximum wave energy extraction[J]. Ocean engineering, 2013, 65: 32-38. DOI:10.1016/j.oceaneng.2013.02.005 (  0) 0)
|
| [14] |
KUMAR A, SAINI R P. Performance analysis of a single stage modified Savonius hydrokinetic turbine having twisted blades[J]. Renewable energy, 2017, 113: 461-478. DOI:10.1016/j.renene.2017.06.020 (  0) 0)
|
| [15] |
黄六一, 梁振林, 宋伟华, 等. 方形箱网结构减流效果试验[J]. 中国水产科学, 2007, 14(5): 860-863. HUANG Liuyi, LIANG Zhenlin, SONG Weihua, et al. Experimental study on effect of reducing current velocity by square net cage structure[J]. Journal of fishery sciences of China, 2007, 14(5): 860-863. DOI:10.3321/j.issn:1005-8737.2007.05.023 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


