2. 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学)工业和信息化部, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology; Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
阵列信号处理是现代信号处理领域的重要分支,被广泛的应用在雷达、声呐中,高分辨波束形成技术作为提高声呐目标探测性能的重要手段,几十年来一直是国内外学者的研究热点。但是由于声呐阵列规模的逐渐增大和本艇的机动等特殊性的应用环境,使得理想的阵列流型和长时间信号平稳性难以保证,导致了许多高分辨阵列信号处理方法的实际应用效果并不理想。近年来具有高稳健性和实时性(小快拍、短样本)特征的高分辨阵列处理方法已成为了阵列信号处理中新的研究热点。
由于经典的常规波束形成算法受到空域傅里叶变换极限分辨能力的限制,如何突破瑞利限曾一度成为广大学者的重要研究方向。自Capon波束形成技术被提出以来,产生了一批高分辨空间谱估计方法,比如谐波分析法[1]、最大熵法[2]、最小方差无畸变响应法(minimum variance distortionless response, MVDR)[3]、基于ARMA (autoregressive moving average model)的线性预测法,MUSIC (multiple signal classification)[4]算法,ESPRIT (estimating signal parameter via rotational invariance techniques)[5]算法等。由于MVDR和MUSIC以及ESPRIT这类经典的高分辨处理方法无法分辨相干源,之后又出现了一系列的解相干处理方法。空间平滑技术其基本思想是利用均匀线阵的平移不变性,将阵列划分为多个重叠子阵,通过对所有子阵协方差矩阵的平均来解相干。但在水声信号处理领域,由于经典类高分辨处理算法对阵列流形精度要求高、低信噪比性能下降严重等问题,实用性一直受到质疑。学者们又针对具有良好干扰抑制效果的MVDR算法开展了稳健性算法研究,典型的方法有线性约束最小方差算法[6]、对角加载方法[7],基于特征空间波束形成等方法[8]。但是根据经典的阵列信号处理理论,稳健性、高分辨与处理增益往往不可兼得,高分辨方法稳健性差,而为了提高稳健性对权值进行对角加载这类方法往往又会导致实际处理增益下降,现有方法大多是在这三者之间寻找平衡点,所以每种方法都会有应用局限性。
到了20世纪,人们开始利用其他学科的成果来解决阵处理中的高分辨问题,凸优化理论也被应用到阵列信号处理中,Eldar等[9]运用凸优化理论,将波束形成问题转化为二阶锥优化问题,突破了传统波束形成方法中存在的未能求取全局最优解的局限。随后,压缩感知理论被推广于阵列信号处理领域[10],相比于前几种高分辨算法,该方法的优点是可应用于小快拍数据,无需预先估计声源个数,可应用于阵元数少于声源数的情形等,但受噪声功率估计误差影响较大,且计算量大,使工程应用受限。
Yang[11-12]将反卷积算法与波束形成相结合,提出一种高增益稳健反卷积波束形成技术,并应用到声压阵和圆阵的处理中,对反卷积波束形成的稳健性、分辨率和增益方面进行了验证,改善效果显著。但文献中所提出的基于Richardson-Lucy(RL)的反卷积波束形成方法只适用于PSF具有移不变特性的阵列中。针对上述问题,文献[13]针对矢量阵PSF的移变性,将非负最小二乘(nonnegative least-squares, NNLS)和DAMAS (deconvolution approach for the mapping of acoustic sources)算法应用到矢量阵中,并提出了一种改进的R-L算法[13-14],该方法在低信噪比的情况下与NNLS和DAMAS相比,具有更窄的主瓣宽度,更低的旁瓣和更高的稳健性。多目标情况下的常规波束形成空间谱输出可以看成每一个角度的指向性图和该角度的源强度乘积之和,在数学上可以用一个叠加积分来表示。如果阵列的PSF具有移不变性,此时叠加积分可以被表示为卷积过程。因此,对常规波束输出空间谱和自然指向性函数反卷积可以得到目标函数。
在实际阵列信号处理中,由于应用场景和需求的不同,阵列的形式多种多样,除了等间距直线阵、圆阵、矢量阵等典型阵列形式外,不等间距阵、十字阵、面阵等阵列形式也是常采用的阵列形式。本文主要分析了水声常用阵列结构PSF的特点,将多种典型阵列按照卷积模型类型进行了分类综述,将其划分为波束图移变阵列和波束图移不变阵列。然后分别总结了移不变和移变模型阵列的反卷积波束形成典型求解方法,以期为反卷积技术在水声阵列信号处理中的应用提供一定的指导。
1 移不变点扩散函数的反卷积波束形成问题 1.1 移不变的点扩散函数定义在空间域处理中,有一大类阵列的自然指向性函数直接或者通过简单的变换就能够具有PSF移不变的特点。在这里移不变的定义就是指向某个角度的波束输出是和角度无关的,其可以看做自然指向性函数的移位,即R(θ|ϑ)=R(θ-ϑ)。或者在某一个变换域具有波束输出具有移不变性,不同位置的波束输出可以视指向性函数的移位。这种移不变性可能是在一维,也可能是在二维或高维空间。
1.2 典型移不变模型阵列 1.2.1 圆阵对于某些阵列,PSF是移不变条件是可以直接满足的,例如,一个等间距圆阵,如果仅考虑二维平面的情况下其自然指向性函数为:
| $ R(\theta ) = \sum\limits_{n = 1}^N {{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi }}{{{\lambda ^r}}}\left( {{\rm{cos}}\left( {\frac{{2\pi (n - 1)}}{N} - \theta } \right)} \right)}}} /N $ | (1) |
式中:N为阵元数;r为圆阵半径;λ为波长。则其在角度ϑ的指向性函数可表示为:
| $ R(\theta |\vartheta ) = \sum\limits_{n = 1}^N {{{\rm{e}}^{ - {\rm{j}}\frac{{2\pi }}{\lambda }r\left[ {\left( {{\rm{cos}}\left( {\frac{{2\pi (n - 1)}}{N} - \theta } \right)} \right) - \left( {{\rm{cos}}\left( {\frac{{2\pi (n - 1)}}{N} - \vartheta } \right)} \right)} \right]}}} /N $ | (2) |
当阵元数N满足N>4πr/λ+2时,指向性函数可以近似为:
| $ R(\theta |\vartheta ) \approx |{{\rm{J}}_0}|\left( {\frac{{4\pi r}}{\lambda }{\rm{sin}}\frac{{\theta - \vartheta }}{2}} \right) $ | (3) |
其中,J0(x)为零阶贝塞尔函数:
| $ {{\rm{J}}_0}(x) = \sum\limits_{k = 0}^\infty {{{( - 1)}^k}} \left[ {{{\left( {\frac{x}{2}} \right)}^{2k}}/{{(k!)}^2}} \right] $ | (4) |
此时,圆阵ϑ方向的指向性函数R(θ|ϑ)是θ-ϑ的函数,即R(θ|ϑ)=R(θ-ϑ),近似具有关于方位ϑ的移不变性质。
常规波束形成功率谱P(θ)可以看成每一个角度的指向性函数R(θ|ϑ)和该角度的信源强度S(ϑ)乘积之和,在数学上可以用叠加积分表示:
| $ P(\theta ) = \int R (\theta |\vartheta )S(\vartheta ){\rm{d}}\vartheta $ | (5) |
由于圆阵的指向性函数具有移不变特性,波束输出叠加积分的过程可以等效为卷积过程:
| $ P(\theta ) = \int R (\theta \backslash \vartheta )S(\vartheta ){\rm{d}}\vartheta = R(\theta ) * S(\theta ) $ | (6) |
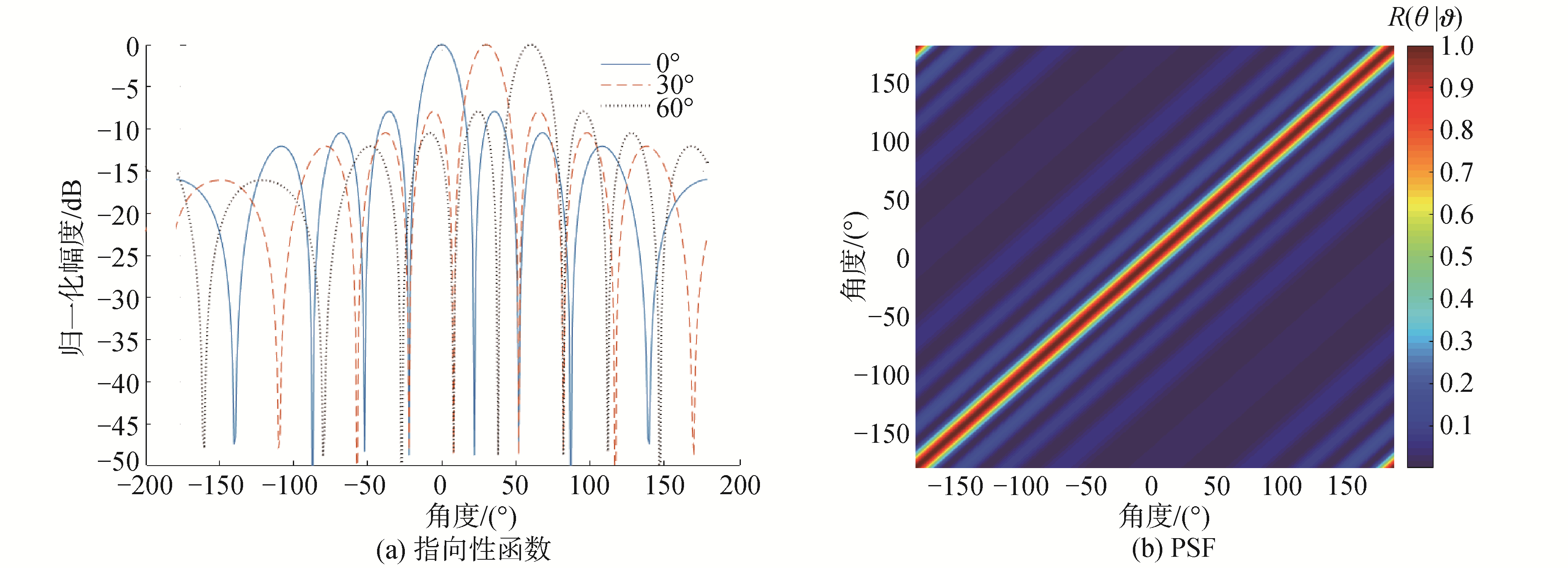
窄带信号频率3 kHz,圆阵的阵元数20,半径0.5 m,改变信号的方向,源1的方位为0°,源2为30°,源3为60°。指向不同角度的圆阵指向性函数如图 1所示,可以看出圆阵的指向性函数是自然指向性函数的圆周移位,因此是移不变的。
|
Download:
|
| 图 1 指向不同角度的圆阵的指向性函数 Fig. 1 The PSF of a circular array steering to different angles | |
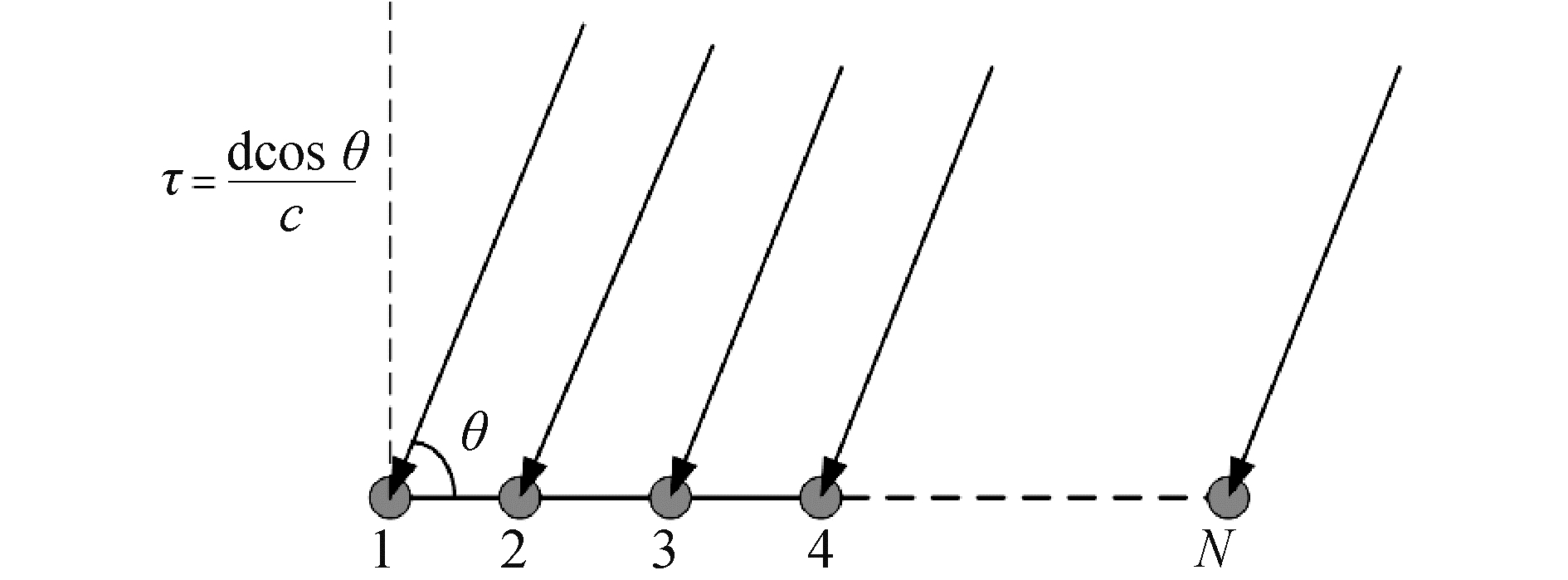
另外还有一类阵列的指向性函数是需要进行一定的映射变换才能够满足移不变性质的,例如均匀等间距声压线阵、非均匀线阵。以均匀声压线阵为例,均匀线阵几何模型图如图 2所示。其自然指向性函数为:
|
Download:
|
| 图 2 均匀线阵模型 Fig. 2 Array geometry for uniform line array | |
| $ R(\theta ) = {\left| {\frac{{{\rm{sin}}\left( {\frac{{N\pi d}}{\lambda }{\rm{cos}}\theta } \right)}}{{N{\rm{sin}}\left( {\frac{{\pi d}}{\lambda }{\rm{cos}}\theta } \right)}}} \right|^2} $ | (7) |
其在角度ϑ方向的指向性函数为:
| $ R(\theta |\vartheta ) = {\left| {\frac{{{\rm{sin}}\left( {\frac{{N\pi d}}{\lambda }({\rm{cos}}\theta - {\rm{cos}}\vartheta )} \right)}}{{N{\rm{sin}}\left( {\frac{{\pi d}}{\lambda }({\rm{cos}}\theta - {\rm{cos}}\vartheta )} \right)}}} \right|^2} $ | (8) |
这里取平方是为了和CBF的功率谱对应,显然R(θ|ϑ)≠R(θ-ϑ)。因此,叠加过程不能直接用卷积过程代替。但是经过简单的变换,单位线阵的自然指向性函数具有关于cos θ移不变的性质,即有R(cosθ|cos ϑ)=R(cos θ-cos ϑ)。
因此均匀线阵波束输出可以等效为卷积过程:
| $ \begin{array}{*{20}{l}} {P({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) = \int R ({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta |{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta )S({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta ) {\rm{dcos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) * S({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )} \end{array} $ | (9) |
窄带信号,信号频率500 Hz,直线阵的阵元数20,阵元间距半波间距,信号来波方位的余弦值分别为0、0.25和0.5。指向不同角度的声压线阵的指向性函数如图 3所示,可以看出指向不同角度的指向性函数和角度无关,具有移不变性,可以看做自然指向性函数的移位。

|
Download:
|
| 图 3 指向不同角度的声压线阵的指向性函数 Fig. 3 The PSF of ULA steering to different angles | |
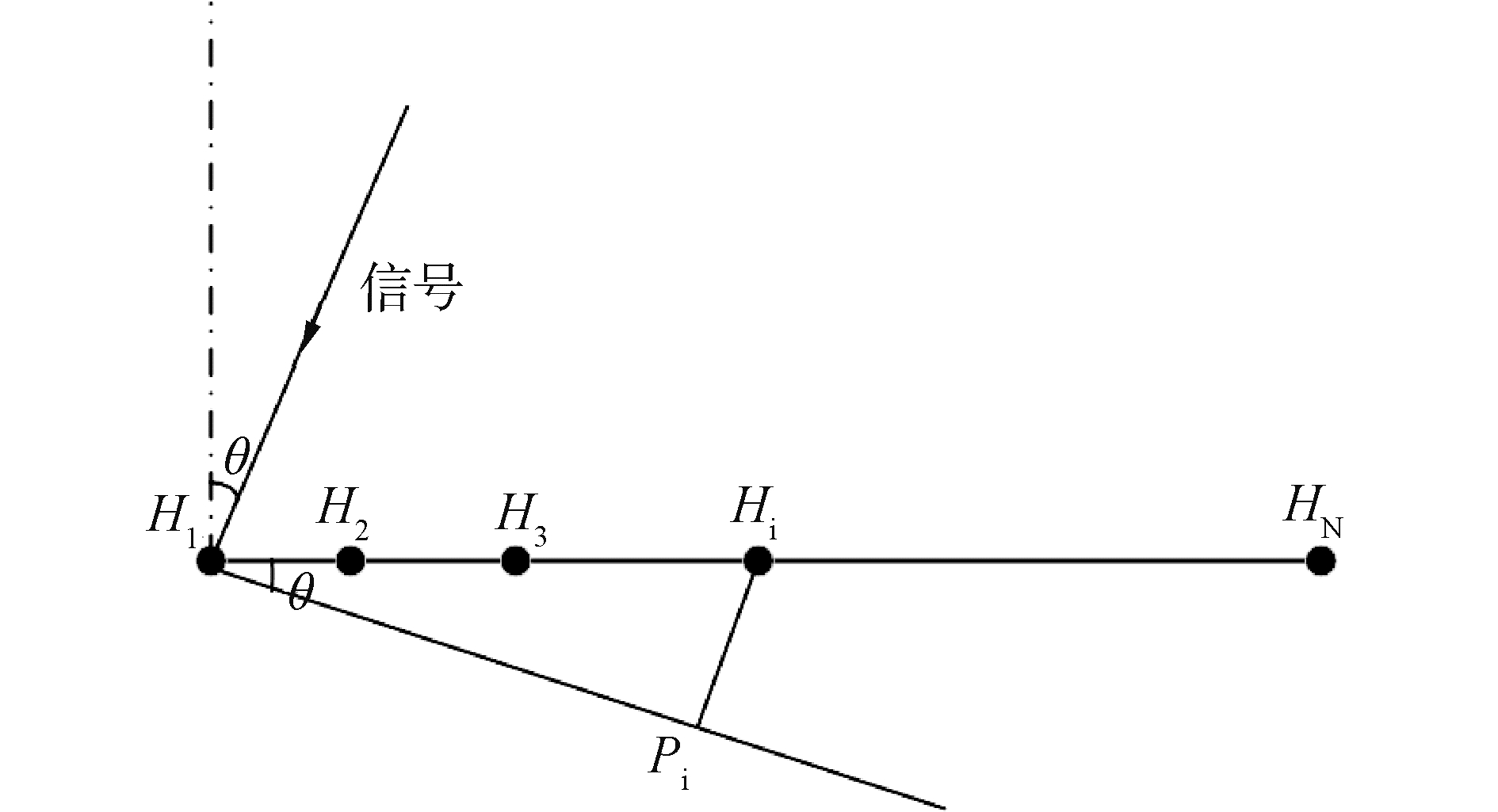
假设N个声压传感器非均匀的分布在同一条直线上,信号从阵列的远场入射,如图 4所示。
|
Download:
|
| 图 4 非均匀线阵模型 Fig. 4 Array geometry for non-uniformly linear array | |
|
Download:
|
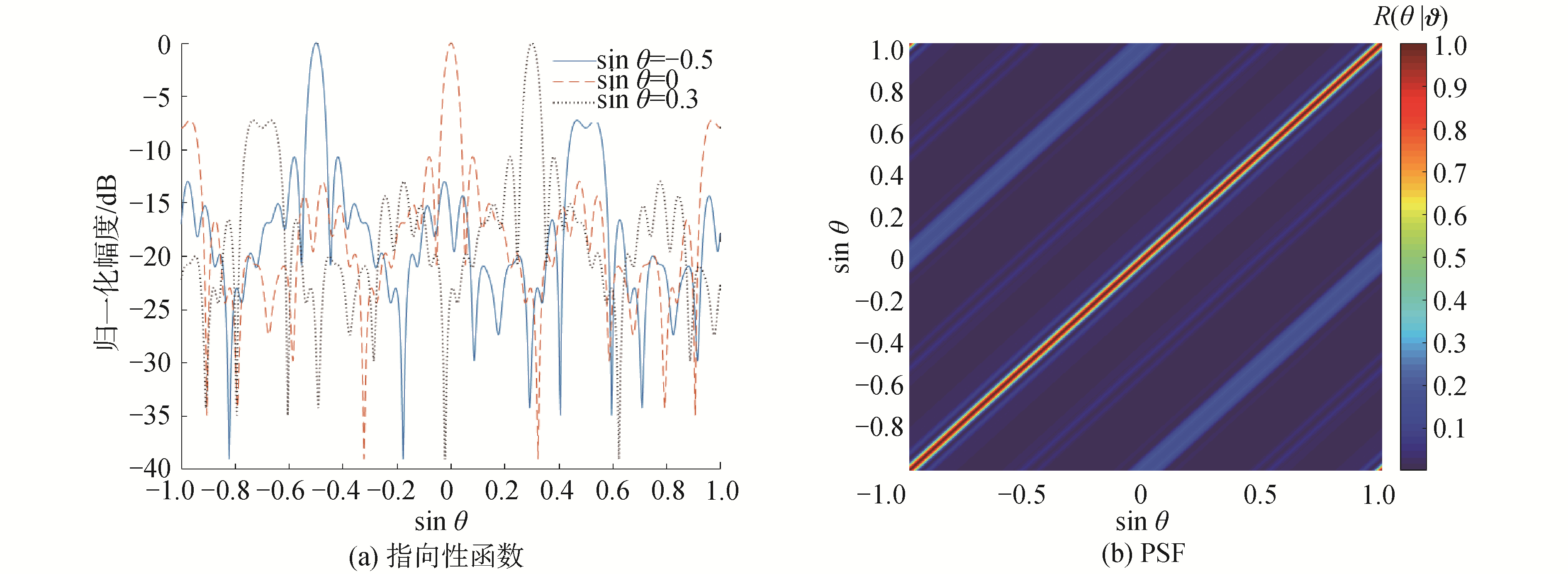
| 图 5 指向不同角度的非均匀声压线阵的指向性函数 Fig. 5 The PSF of NLA steering to different angles | |
假设入射信号是单频信号,第1个阵元H1接收到的信号是Acos(2πft),把1号阵元当做参考阵元,那么第i个传感器接收到的信号为:
| $ {s_i}(t) = A{\rm{cos}}(2\pi ft + {\varphi _i}),i = 1,2, \cdots ,N $ | (10) |
其中φi为声程差HiPi导致的相位差:
| $ {\phi _i} = 2\pi f\frac{{{H_i}{P_i}}}{c} = 2\pi f\frac{{{H_1}{H_i}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }}{c} $ | (11) |
将阵元接收到的信号相加,整个阵列的输出为:
| $ \begin{array}{*{20}{c}} {s(t) = \sum\limits_{n = 1}^N A {\rm{cos}}(2\pi ft + {\phi _i}) = }\\ {A{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\pi f(\sum\limits_{n = 1}^N {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\phi _i}} ) - A{\rm{sin}}{\kern 1pt} {\kern 1pt} 2\pi f(\sum\limits_{n = 1}^N {{\rm{sin}}{\kern 1pt} {\kern 1pt} {\phi _i}} )} \end{array} $ | (12) |
将s(t)取平方并归一化得到的指向性函数为:
| $ R(\theta ) = \frac{1}{{{N^2}}}[{(\sum\limits_{n = 1}^N {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\phi _i}} )^2} + {(\sum\limits_{n = 1}^N {{\rm{sin}}{\kern 1pt} {\kern 1pt} {\phi _i}} )^2}] $ | (13) |
相似地,其在角度ϑ方向的指向性函数为:
| $ \begin{array}{*{20}{c}} {R(\theta |\vartheta ) = \frac{1}{{{N^2}}}[(\sum\limits_{n = 1}^N {{\rm{cos}}{\kern 1pt} ({\phi _i} - {\phi _{ij}}){)^2}} + }\\ {(\sum\limits_{n = 1}^N {{\rm{sin}}{\kern 1pt} {\kern 1pt} ({\phi _i} - {\phi _{i\vartheta }}){)^2}} ] = }\\ {\frac{1}{{{N^2}}}[(\sum\limits_{n = 1}^N {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\pi f\frac{{{H_1}{H_i}}}{c}({\rm{sin}}\theta - {\rm{sin}}\vartheta ){)^2}} + }\\ {(\sum\limits_{n = 1}^N {{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 2\pi f\frac{{{H_1}{H_i}}}{c}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta ){)^2}} ]} \end{array} $ | (14) |
显然,非均匀线阵的指向性函数是sinθ-sin ϑ的函数,因此非均匀线阵的PSF是关于角度的正弦值的移不变函数,R(θ|ϑ)=R(sinθ-sin ϑ)。非均匀线阵常规波束形成功率可以写做如下卷积过程:
| $ \begin{array}{*{20}{l}} {P({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) = \int R ({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta |{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta )S({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta ) {\rm{dsin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) * S({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )} \end{array} $ | (15) |
为了说明非均匀线阵移不变性,以20元非均匀阵为例,各阵元的位置分别选取半波间距阵列的[1, 2, 3, 4, 5, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 27, 30, 31, 35]号阵元构成非等间距阵列。信号是500 Hz单频信号,其中λ对应信号频率的波长。
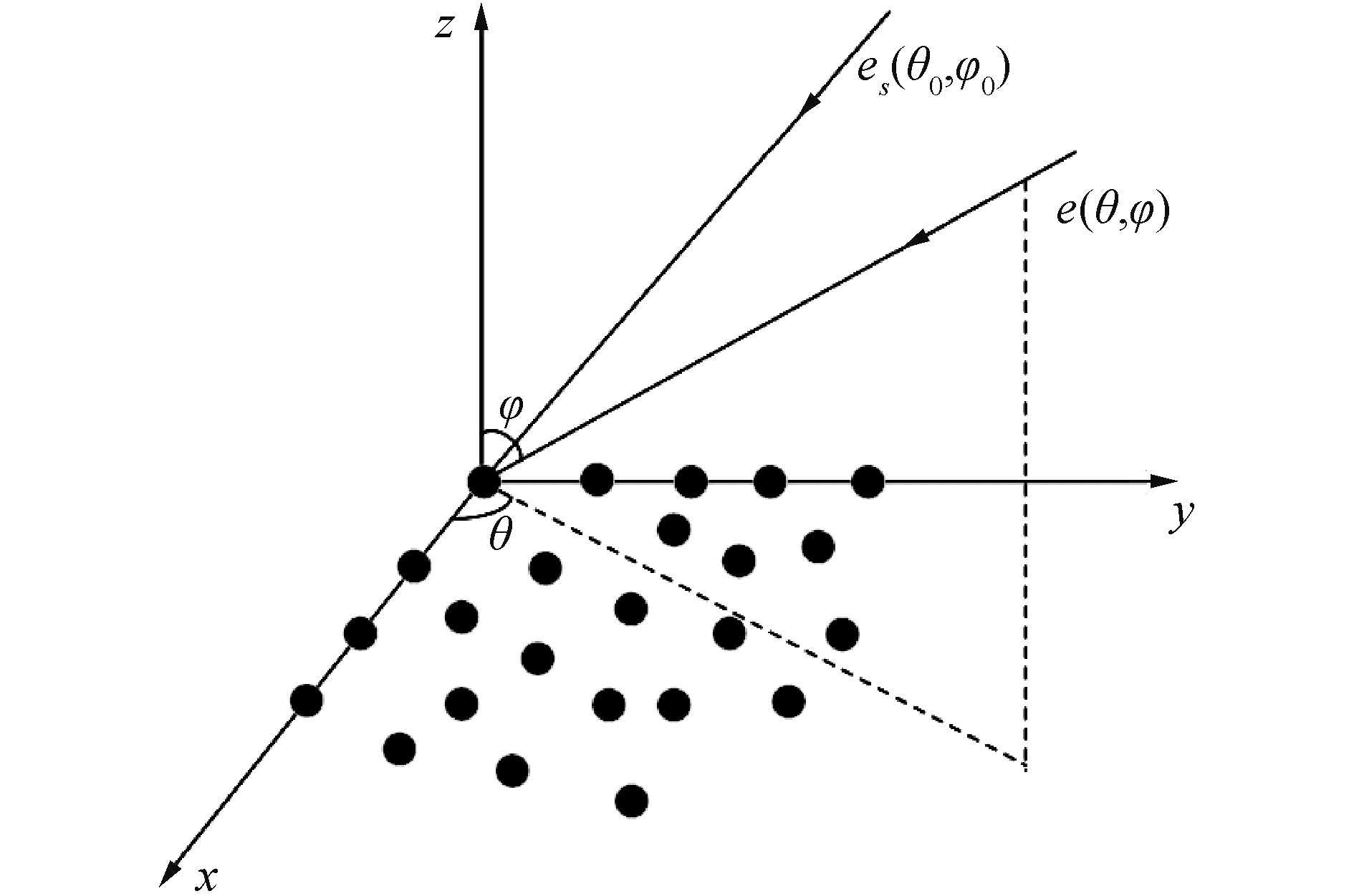
1.2.3 远场平面阵一个任意分布的N元平面阵,如图 6所示放置于xoy平面,假设信号从(θ0, φ0)方位以远场平面波入射,N个阵元位置坐标分别为[xn, yn],n=1, 2, …, N。则第n个阵元与参考阵元之间的声程差为:
|
Download:
|
| 图 6 任意面阵模型 Fig. 6 Array geometry for planar array | |
| $ {\beta _n} = k({x_n}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta + {y_n}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) $ | (16) |
其中,k为波数,k=ω/c=2π/λ,λ为信号的波长,定义ux=sin φcosθ,uy=sin φsinθ,那么基阵的阵列流形向量为a(k)=(e(-jk(uxx1+uyy1)), …, e(-jk(uxxN+uyyN)))T,常规波束形成器的加权向量为wc=a(θ0, ϕ0)/M。因此常规波束形成的指向性函数为:
| $ \begin{array}{*{20}{c}} {{R_p}({u_x},{u_{x0}},{u_y},{u_{y0}}) = |{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{a}}(\theta ,\varphi ){|^2} = }\\ {{{\left| {\frac{1}{N}\sum\limits_{n = 1}^N {{\rm{exp}}} \{ {\rm{j}}k[{x_n}({u_x} - {u_{x0}}) + {y_n}({u_y} - {u_{y0}})]\} } \right|}^2} = }\\ {{R_p}({u_x} - {u_{x0}},{u_y} - {u_{y0}})} \end{array} $ | (17) |
故面阵的波束可以看做是一个关于ux=sinφ·cosθ和uy=sin φsinθ的二维移不变函数,且ux和uy都在[-1, 1]范围内,因此可以将矩形面阵归为PSF移不变阵的二维反卷积求解问题。以矩形阵为例说明平面阵的二维反卷积问题,矩形阵仿真条件:X轴阵元数8,Y轴阵元数8,信号形式为频率500 Hz单频信号,阵元间距为1.5 m。
图 7是矩形面阵在不同角度所对应的单目标指向性函数。由图可见,2个指向性函数形状相同,只是进行了平移,因此面阵的指向性函数可以看成是移不变的。

|
Download:
|
| 图 7 矩形阵指向不同角度的三维指向性函数 Fig. 7 PSF of rectangle array steering to different source angles | |
对于移不变的点扩散函数,常用的卷积方法有CLEAN[15]、DAMAS[16]、NNLS[17]、R-L[18-19]算法等。在其基础上又衍生出适用于相干信号的CLEAN-C算法,基于傅里叶变换的快速DAMAS2[20]和DAMAS3[20]算法,基于稀疏信号重构的SC-DAMAS[21]算法,基于小波变换计算网格的快速DAMAS算法[22],基于傅里叶变换的FFT-NNLS算法等。Klaus在文献[17]中比较了DAMAS,NNLS, 基于傅里叶变化的DAMAS2, FFT-NNLS和R-L算法,结果表明DAMAS和NNLS不要求PSF是移不变的,而DAMAS2, FFT-NNLS和RL算法适用于PSF移不变的反卷积问题中,且RL算法和DAMAS, NNLS相比具有更低的计算量。文献[23]将CLEAN算法,DAMAS, NNLS和R-L算法应用到三维空气声源定位中,结果表明几种方法都能显著提高声源分辨能力,但在处理相干源时R-L的效果最好。文献[24]分析比较了DAMAS, NNLS和ISCA 3种反卷积算法,结果表明DAMAS的定位误差精度最差,ISCA有最高的定位精度和最高的稳健性。在这里简要介绍几种常用的反卷积算法。
1.3.1 DAMAS将系统的输入输出描述成线性方程组的形式:
| $ \mathit{\boldsymbol{P}} = \mathit{\boldsymbol{RS}} + \mathit{\boldsymbol{N}} $ | (18) |
式中:P代表常规波束形成的输出;R代表基阵的指向性函数PSF;S代表源的分布函数;N代表噪声。DAMAS是在忽略噪声的条件下用高斯赛德尔方法求解线性方程组。对于线性移不变的PSF,矩阵R是Toeplitz矩阵且是一个半正定对称阵。
高斯赛德尔方法通过引入正约束来解决式(18),迭代过程:
| $ {r_n^{(i)} = \sum\limits_{{n^\prime } = 1}^{n - 1} {{\mathit{\boldsymbol{R}}_{n{n^\prime }}}} S_{{n^\prime }}^{(i + 1)} + \sum\limits_{{n^\prime } = n}^N {{\mathit{\boldsymbol{R}}_{n{n^\prime }}}} S_{{n^\prime }}^{(i)} - {P_{nn}}} $ | (19) |
| $ {S_n^{(i + 1)} = {\rm{max}}(S_n^{(i)} - \frac{{r_n^i}}{{{\mathit{\boldsymbol{R}}_{nn}}}},0)} $ | (20) |
式中:n=1, 2, …, N, i=1, 2, …, K, 其中N是扫描的点数,K是迭代的次数;rn(i)是每次迭代的残差;rn(1)的初始值是Pn。高斯赛德尔收敛的条件是PSF矩阵是对角占优阵,即矩阵中主对角线元素的绝对值大于其所在行的其他元素绝对值之和。
1.3.2 NNLS算法最小二乘问题,其基本原理可以推广到阵列反卷积处理,具体方法是在常规波束输出,矢量阵点扩散函数字典,声源目标函数之间建立差函数方程组,通过最小化差函数的原则来实现对目标函数S的求解,获取声源的分布,矩阵为:
| $ \phi = {\left\| {\mathit{\boldsymbol{RS}} - \mathit{\boldsymbol{P}}} \right\|_2} $ | (21) |
式中:P是矢量阵常规波束形成输出空间谱;R是所有角度矢量阵的指向性函数形成的指向性函数字典矩阵;S是反映声源方位和强度信息的目标函数。对于上述方程组求解可以采用梯度投影法,该方法的核心是负梯度方向指向标量场下降最快的方向,通过在ϕ关于S的负梯度方向上按特定步长反复迭代搜索来求得S的结果。计算的具体步骤可以参考文献[13]。
NNLS算法并不局限于移不变反卷积模型求解,只需要获得阵列所有方位的指向性函数矩阵即可。需要注意的是,对于移不变模型采用NNLS算法时可采用FFT变换域计算的方式实现快速计算,但这并不适用于移变模型阵列。该方法并不局限于矢量阵。对结构固定不变的阵列该方法都适用。
1.3.3 R-L算法R-L算法是一种基于贝叶斯理论的迭代方法,该方法被广泛用于图像复原中。R-L算法中要求PSF是移不变的,在阵列信号处理中,就是指基阵的波束图是和角度无关的(指向某一个角度的波束图都可以看做自然指向性函数的移位),R-L算法的迭代方程为:
| $ \begin{array}{*{20}{l}} {{{\hat P}^i}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) = \int R ({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta )S({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta ){\rm{dsin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) * {S^i}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )} \end{array} $ | (22) |
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {S^{i + 1}}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta ) = {S^i}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta )\int R ({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta ) \cdot }\\ {\frac{{P({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )}}{{{{\hat P}^i}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )}}{\rm{dsin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta = {S^i}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta )\left[ {R({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )*\frac{{P({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )}}{{{{\hat P}^i}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )}}} \right]} \end{array} $ | (23) |
| $ \begin{array}{*{20}{c}} {S({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) = \mathop {{\rm{argmin}}}\limits_h L(P({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ),\hat P({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )) = }\\ {\mathop {{\rm{argmin}}}\limits_h L(P({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ),\int_{ - \infty }^{ + \infty } R ({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta ){S^i}({\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )) \cdot }\\ { {\rm{dsin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta \le \varepsilon } \end{array} $ | (24) |
式中:
R-L算法是一个迭代的过程,当常规波束形成得到的功率谱和每次迭代得到的功率谱估计值之差越小,则认为迭代得到的目标函数最接近真实的声源分布,取的极小值后可以停止迭代。迭代的次数也可以通过最小均方误差来决定,当常规波束输出P(sin θ)和每次迭代解卷积求得的信号再和基阵自然指向性卷积结果
以均匀分布声压线阵为例,分析阵列的PSF是移不变的反卷积问题求解。由式(9)可知,ULA的波束输出为:
| $ P({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) = R({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) * S({\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta ) $ | (25) |
基于阵列的参数可以得到阵列的自然指向性函数,对接收到的数据做常规波束形成可以得到波束输出的方位谱,对常规波束输出空间谱P(θ)和自然指向性函数R(θ)反卷积可以得到目标函数S(θ),其理想情况下是δ函数,必然是对目标方位的高分辨估计结果。关于PSF是移不变的反卷积问题求解引用文献[14]中所采用的R-L方法。
为了说明反卷积波束形成算法在PSF是移不变的阵列的应用效果,以圆阵为例进行仿真分析。
仿真条件同图 1,为理想无噪声条件下,双目标的仿真结果图。图 8说明常规波束输出的空间谱是阵列的PSF和信号的目标强度函数的卷积。与CBF相比,反卷积波束形成方法有更窄的主瓣和更低的旁瓣。

|
Download:
|
| 图 8 双目标圆阵仿真结果 Fig. 8 Simulation results of two target for circular array | |
在空间域处理中,有一大类阵列的自然指向性函数具有PSF移变的特点,移变的定义就是指向某个角度的波束输出是和角度有关的,即R(θ|ϑ)≠R(θ-ϑ),不可以看做自然指向性函数的简单移位。但与一般的时域系统相比,空间域上的移变问题有一个典型特点:在水声中一般是将具有固定拓扑结构指的阵列去采集声信号,对于任意形状的阵列,当阵列拓扑结构固定后,PSF无论是移不变还是移变都是可以预先测定得到的,如果采用测量获得的PSF函数由于其包含了对阵型误差等因素等影响的校正会有更好的反卷积求解效果。
2.1.1 矢量阵以均匀矢量线阵为例来说明这一问题,角度定义同图 1。与声压阵相似,直线声矢量阵的波束输出可以写为[16]:
| $ {P_v}(\theta ) = \int_0^{2\pi } {{R_v}} (\theta |\vartheta )S(\vartheta ){\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta {\rm{d}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta $ | (26) |
式中:Rv(θ|ϑ)矢量阵指向ϑ的指向性函数;S(ϑ)是以方位为变量的目标信源强度分布函数;θ和ϑ分别代表扫描角度和目标信号方位。
矢量阵在90°方向指向性函数为:
| $ {R_v}(\theta ) = \frac{{(1 + {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta )}}{2}\left| {\frac{{{\rm{sin}}\left( {\frac{{N\pi d}}{\lambda }{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \right)}}{{N{\rm{sin}}\left( {\frac{{\pi d}}{\lambda }{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \right)}}} \right| = u(\theta ){R_p}(\theta ) $ | (27) |
式中:Rp(θ)为声压阵的自然指向性函数,可以看出,矢量阵的自然指向性函数Rv(θ)为声压阵自然指向性函数Rp(θ)与一个角度指向因子u(θ)=(1+cosθ)/2的乘积。
指向ϑ方向的矢量阵指向性函数为:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {R_v}(\left. \theta \right|\vartheta ) = \\ \frac{{(1 + {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\theta - \vartheta } \right))}}{2}\left| {\frac{{{\rm{sin}}\left( {\frac{{N\pi d}}{\lambda }\left( {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta } \right)} \right)}}{{N{\rm{sin}}\left( {\frac{{\pi d}}{\lambda }\left( {{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta - {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \vartheta } \right)} \right)}}} \right| \end{array} $ | (28) |
比较Rv(θ)和Rv(θ|ϑ),不难发现Rv(θ|ϑ)≠Rv(θ-ϑ),也不可通过简单的正弦,余弦变换将其变为移不变函数。因为,u(θ)=(1+cosθ)/2是关于θ移不变的函数,而Rp(θ)是关于cosθ的移不变函数,二者相乘后无法通过简单的变量代换将其等效为某个统一变量的移不变模型。
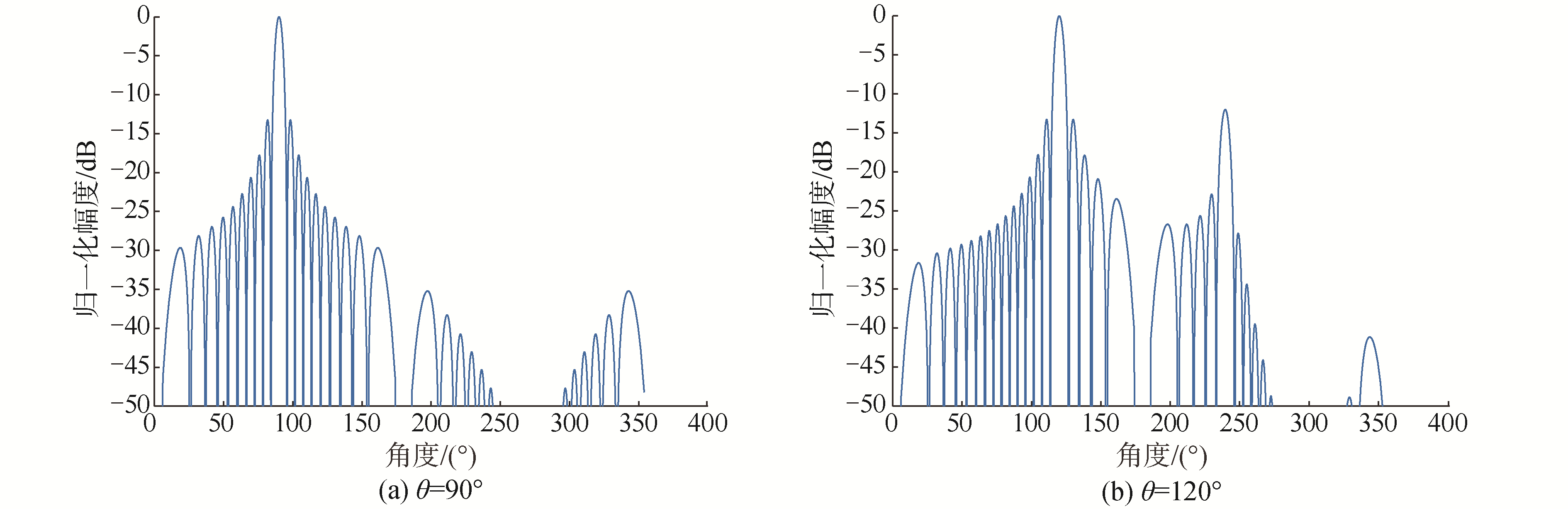
矢量阵仿真:20元均匀分布矢量阵,阵元间距3.75 m,为信号频率半波间距,信号频率200 Hz,采样频率20 kHz。改变信号的方向,指向不同角度的矢量阵的指向性函数如图 9所示,可以看出不同角度的矢量阵的指向性函数是移变的,不是自然指向性函数的移位。而且尽管矢量有一定的抗左右模糊作用,但是其效果与目标方位有关,在端射方向附近效果仍然较差,会在对称方向形成伪峰。
|
Download:
|
| 图 9 指向不同角度的矢量阵指向性函数 Fig. 9 PSF of VSLA steering to different source angles | |
共形阵是传感器附着在非平面载体表面上的阵列,简称共形阵。由于其具有良好的空气动力学特性,可以充分利用导流罩的纵向空间,增加基阵有效孔径,共形阵正被当做一种新型布阵方式应用在新型声呐系统中。
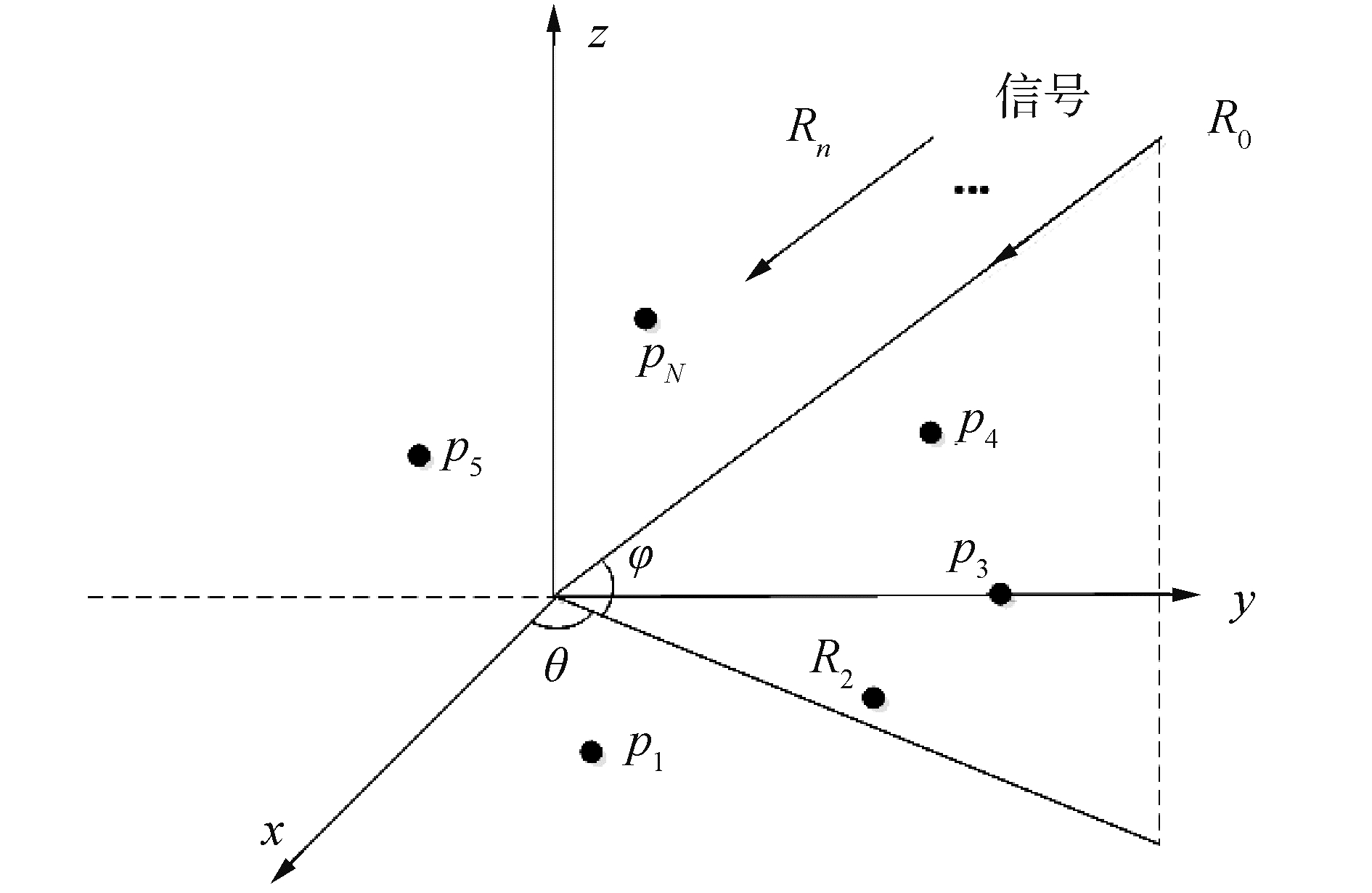
假设各阵元的位置pn是随机分布,如图 10所示,第nth个传感器的位置坐标为pn=[xn, yn, zn]。K个平面波从阵列的远场入射,简单起见,假设K=1。θ和ϕ分别是方位角和俯仰角,定义信号传播方向的单位向量可以表示为:u=-[cos θcos ϕ, sin θcos ϕ, sin ϕ]T,把原点当做参考点时,第nth个传感器相对于参考点的时延差为:
|
Download:
|
| 图 10 任意分布阵列模型 Fig. 10 Arbitrary conformal array geometry | |
| $ \begin{array}{*{20}{c}} {{\tau _n} = \frac{{{\mathit{\boldsymbol{v}}^{\rm{T}}}(\theta ){p_m}}}{c} = }\\ { - \frac{1}{c}({x_n}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi + {y_n}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi + {z_n}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \phi )} \end{array} $ | (29) |
式中c为声速。
若入射信号为Acos(2πft),那么第nth个传感器接收到的信号为:
| $ {s_n}(t) = A{\rm{cos}}[2\pi f(t + {\tau _n})] $ | (30) |
将接收到的信号求和,并将幅度归一化并且取平方,得到阵列的指向性函数为:
| $ R(\theta ,\varphi ) = {\left| {\frac{1}{N}E({{[\sum\limits_{n = 1}^N {{\rm{cos}}} (2\pi f(t + {\tau _n}))]}^2})} \right|^2} $ | (31) |
相似的,其在角度ϑ方向的指向性函数为:
| $ \begin{array}{*{20}{c}} {R(\theta ,\varphi ) = }\\ {{{\left| {\frac{1}{N}E([\sum\limits_{n = 1}^N {{\rm{cos}}} {{(2\pi f(t + ({\tau _n}(\theta ) - {\tau _n}(\vartheta ))))}^2})} \right|}^2}} \end{array} $ | (32) |
显然,共形阵的指向性函数不具有规律可言,是移变函数。为了对该问题简要说明,这里采用半椭圆阵列来说明共形阵反卷积波束形成问题。对于共形阵声呐(非成像声呐),探测目标为阵所在平面内的远距离目标,即只考虑目标方位方向上的一维求解问题,此时是一维移变反卷积问题。
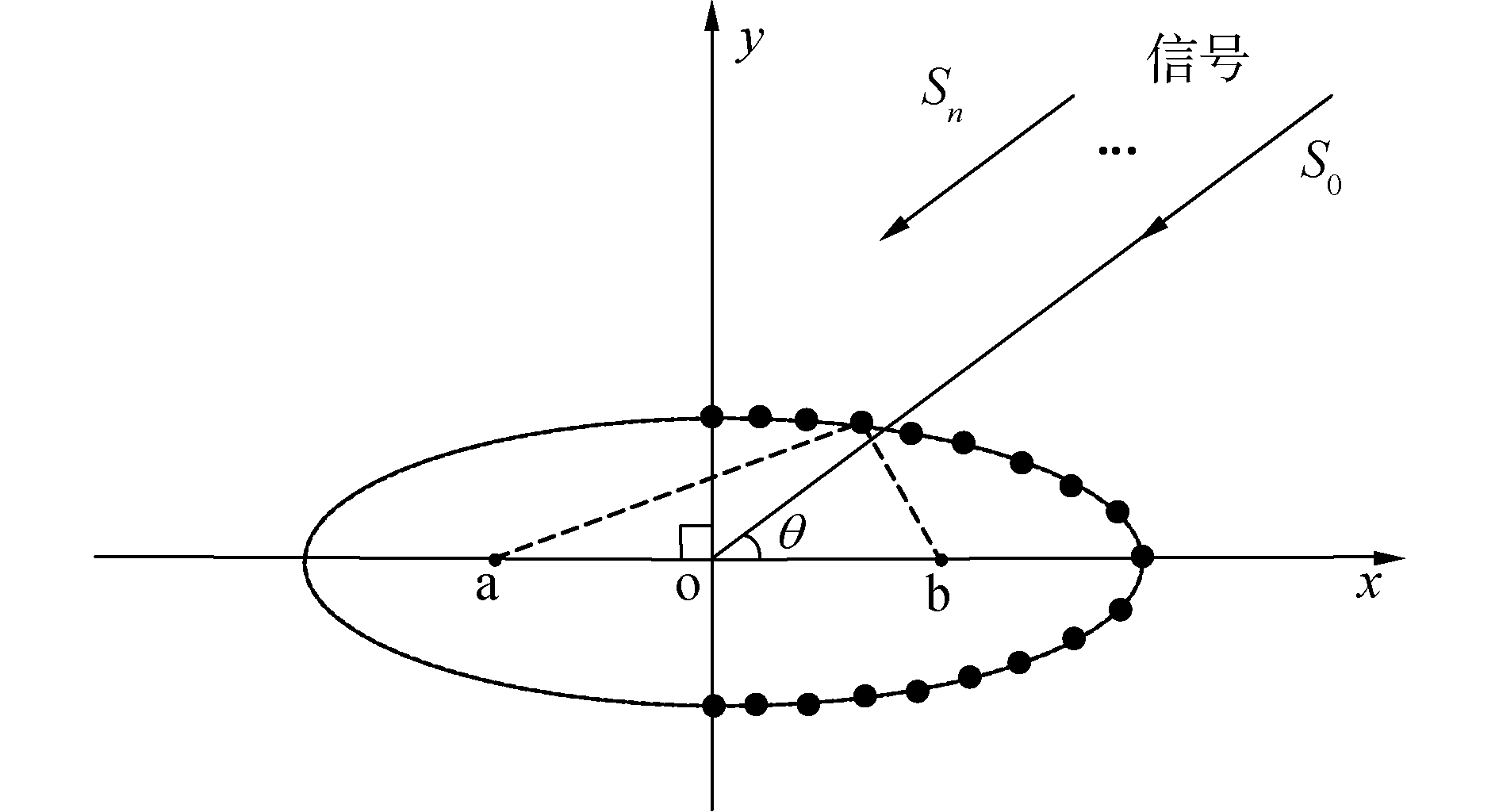
将41个传感器如图 11所示,放置在椭圆轨迹上,椭圆方程是4y2+x2=100;每个传感器在x轴的位置是xn, 其中xn=[0:0.5:10]∪[9.5:-0.5:0]。
|
Download:
|
| 图 11 椭圆形共形阵模型 Fig. 11 Oval conformal array geometry | |
信号频率为1 kHz,改变信号的方向,指向不同角度的共形阵的指向性函数如图 12所示,可以看出不同角度的共形阵的指向性函数是移变的,不是自然指向性函数的移位。

|
Download:
|
| 图 12 指向不同角度的共形阵指向性函数 Fig. 12 PSF of conformal array steering to different source angles | |
文献[14]针对矢量阵分析比较了3种反卷积波束形成方法,DAMAS,NNLS和改进的R-L算法。改进的R-L算法在低信噪比的情况下与NNLS和DAMAS相比,具有更窄的主瓣宽度,更低的旁瓣和更高的稳健性。因此针对空间域反卷积问题点扩散函数移变情况的特点——移变但可预知的特点,应用文献[14]中提出的改进R-L反卷积算法。
对于矢量阵等一类PSF具有移变特性阵列来说,虽然PSF不具有移不变性,却具有可预测性,即对任意目标角度,阵列的指向性函数值是可预测的,因此可以用预测得到的R(θ|ϑ)来代替反卷积求解过程中的移位过程R(θ-ϑ)。由于在线性移变系统中PSF的总能量不是恒定的,即M(θ)=∫R(θ|ϑ)dϑ是关于扫描角度的函数,不是定值。因此不可以直接用文献[11]中的R-L算法。对移变阵列的反卷积波束形成问题,用作者在文献[14]中提出的扩展R-L算法,具体的推导过程可以参见该文献。求解过程为:
| $ {S^{i + 1}}(\vartheta ) = {S^i}(\vartheta )\int {\frac{{\bar R(\theta |\vartheta )}}{{\int {\bar R} (\theta |\vartheta ){S^i}(\vartheta ){\rm{d}}\vartheta }}} \bar P(\theta |\vartheta ){\rm{d}}\theta $ | (33) |
式中:R (θ|ϑ)=R(θ|ϑ)/M(θ)是PSF移变阵列的归一化指向性函数,是可通过公式计算、仿真或者实际测量获得的,并可提前预存的指向性函数;P(θ|ϑ)=P(θ|ϑ)/M(θ)是归一化的波束形成方位谱,P(θ|ϑ)是通过常规波束形成器得到的方位谱。相似的,迭代的次数也可以通过二者的二阶距即均方误差判别。
上述方法在空间域处理中并不限于之前提到的几种阵列,凡是指向性函数移变但可预测的情况都适用,而对于具有固定拓扑结构的实际阵列PSF都是可以预先测定得到的,因此适用的阵列形式非常广泛。该方法亦可推广到非空间域阵列信号处理领域的其他单位冲击响应移变但可预测的系统中。
为了证明反卷积波束形成方法在PSF是移变阵列波束形成中的使用性能,以椭圆形共形阵为例进行仿真分析,椭圆形共形阵的参数见2.1.2节。图 13展现了预存的不同角度指向性函数(PSF)。

|
Download:
|
| 图 13 预存的不同角度共形阵指向性函数 Fig. 13 The predefined beam pattern | |
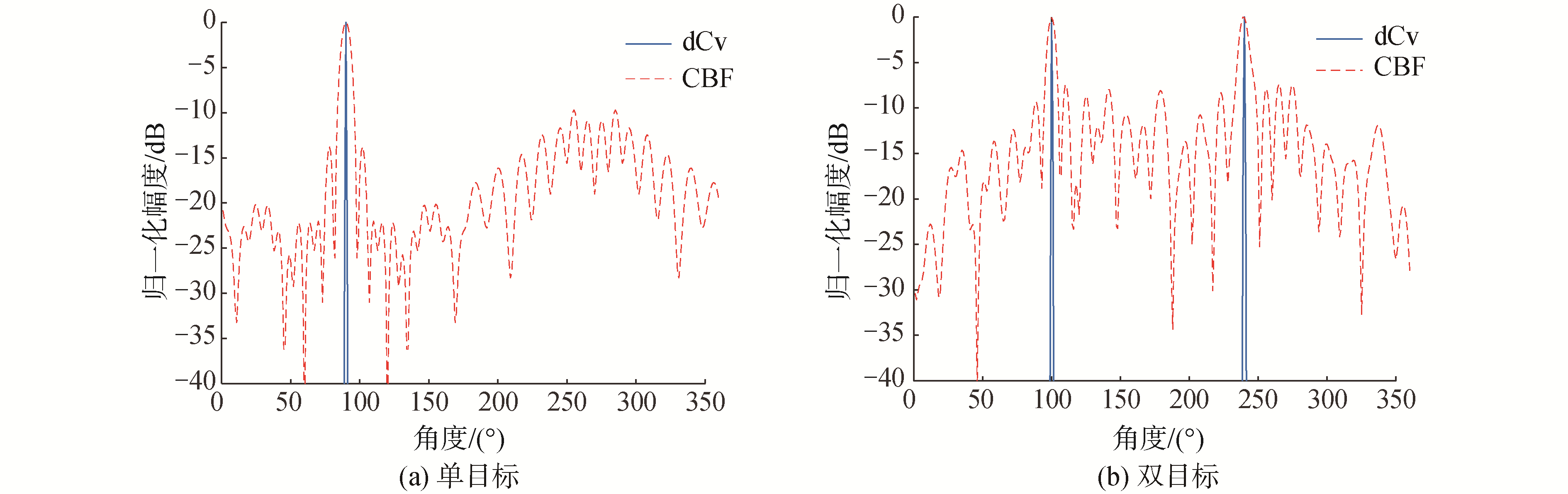
图 14是对单目标及双目标的共形阵做CBF与dCv的仿真对比结果,阵列结构同图 12,图 14(a)是单目标,信号方位90°,图 14(b)是等强度的双目标,信号方位是100°和240°。
|
Download:
|
| 图 14 共形阵CBF和dCv的波束输出对比 Fig. 14 Comparison of dCv and CBF in conformal array | |
通过上图可以看出,新方法可以很好地将反卷积波束形成算法应用到具有任意结构的共形阵这种PSF具有移变性的阵列中。与CBF相比,dCv方法有更高的角度分辨能力和低的旁瓣,同时能准确估计出多目标信号的功率值。
通过上述具有椭圆形状的共形阵的仿真结果也证明了文中所提出的PSF移变模型的反卷积波束形成方法是具有可行性的。
3 结论1) 文章介绍了水下阵列信号处理中的反卷积问题。对多种水下常用阵列形式的波束形成卷积模型进行了分析推导,将其按照卷积模型类型进行了分类综述,划分为波束图移变阵列和波束图移不变阵列。
2) 圆阵、均匀声压线列阵、非均匀声压线列阵均是一维移不变阵列,平面阵是二维移不变阵列,矢量阵和共形阵是移变阵列。
本文总结了移不变和移变模型阵列的反卷积波束形成典型求解方法,是对各类典型水下阵列卷积模型的基础总结归纳。
| [1] |
KAY S M, MARPLE S L. Spectrum analysis-A modern perspective[J]. Proceedings of the IEEE, 1981, 69(11): 1380-1419. DOI:10.1109/PROC.1981.12184 (  0) 0)
|
| [2] |
BURG J P. Maximum entropy spectral analysis[J]. Journal of China institute of communications, 1975, 17(4): 1519-1533. (  0) 0)
|
| [3] |
CAPON J. High-resolution frequency-wavenumber spectrum analysis[J]. Proceedings of the IEEE, 1969, 57(8): 1408-1418. DOI:10.1109/PROC.1969.7278 (  0) 0)
|
| [4] |
SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE transactions on antennas and propagation, 1986, 34(3): 276-280. (  0) 0)
|
| [5] |
KUNG S Y, ARUN K S, RAO D V B. State-space and singular-value decomposition-based approximation methods for the harmonic retrieval problem[J]. Journal of the optical society of America, 1983, 73(12): 1799-1811. DOI:10.1364/JOSA.73.001799 (  0) 0)
|
| [6] |
CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE transactions on aerospace and electronic systems, 1988, 24(4): 397-401. DOI:10.1109/7.7181 (  0) 0)
|
| [7] |
COX H, ZESKIND R, OWEN M. Robust adaptive beamforming[J]. IEEE transactions on acoustics, speech, and signal processing, 1987, 35(10): 1365-1376. DOI:10.1109/TASSP.1987.1165054 (  0) 0)
|
| [8] |
FELDMAN D D, GRIFFITHS L J. A projection approach for robust adaptive beamforming[J]. IEEE transactions on signal processing, 1994, 42(4): 867-876. (  0) 0)
|
| [9] |
ELDAR Y, LUO Zhiquan, MA Ken, et al. Convex optimization in signal processing[J]. IEEE signal processing magazine, 2010, 27(3): 19-145. (  0) 0)
|
| [10] |
XENAKI A, GERSTOFT P, MOSEGAARD K. Compressive beamforming[J]. The journal of the acoustical society of America, 2014, 136(1): 260-271. (  0) 0)
|
| [11] |
YANG T C. Deconvolved conventional beamforming for a horizontal line array[J]. IEEE journal of oceanic engineering, 2018, 43(1): 160-172. DOI:10.1109/JOE.2017.2680818 (  0) 0)
|
| [12] |
YANG T C. Performance analysis of superdirectivity of circular arrays and implications for sonar systems[J]. IEEE journal of oceanic engineering, 2019, 44(1): 156-166. DOI:10.1109/JOE.2018.2801144 (  0) 0)
|
| [13] |
SUN Dajun, MA Chao, YANG T C, et al. Improving the performance of a vector sensor line array by deconvolution[J]. IEEE journal of oceanic engineering. DOI:10.1109/JOE.2019.2912586 (  0) 0)
|
| [14] |
孙大军, 马超, 梅继丹, 等. 基于非负最小二乘的矢量阵反卷积波束形成方法[J]. 哈尔滨工程大学学报, 2019, 40(7): 1217-1223. SUN Dajun, MA Chao, MEI Jidan, et al. Deconvolved conventional beamforming of a vector-sensor array based on non-negative least squares[J]. Journal of Harbin Engineering University, 2019, 40(7): 1217-1223. (  0) 0)
|
| [15] |
DOUGHERTY R, STOKER R. Sidelobe suppression for phased array aeroacoustic measurements[C]//Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference. Toulouse, France, 1998.
(  0) 0)
|
| [16] |
BROOKS T F, HUMPHREYS W M. A deconvolution approach for the mapping of acoustic sources (DAMAS) determined from phased microphone arrays[J]. Journal of sound and vibration, 2006, 294(4/5): 856-879. (  0) 0)
|
| [17] |
EHRENFRIED K, KOOP L. Comparison of iterative deconvolution algorithms for the mapping of acoustic sources[J]. AIAA journal, 2007, 45(7): 1584-1595. DOI:10.2514/1.26320 (  0) 0)
|
| [18] |
RICHARDSON W H. Bayesian-based iterative method of image restoration[J]. Journal of the optical society of America, 1972, 62(1): 55-59. DOI:10.1364/JOSA.62.000055 (  0) 0)
|
| [19] |
LUCY L B. An iterative technique for the rectification of observed distributions[J]. Astronomical journal, 1974, 79(6): 745-754. (  0) 0)
|
| [20] |
DOUGHERTY R P. Extensions of DAMAS and benefits and limitations of deconvolution in beamforming[C]//Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference. Monterey, California, 2005.
(  0) 0)
|
| [21] |
YARDIBI T, LI J, STOICA P, et al. Sparsity constrained deconvolution approaches for acoustic source mapping[J]. Journal of the acoustical society of America, 2008, 123(5): 2631-2642. (  0) 0)
|
| [22] |
MA Wei, LIU Xun. Improving the efficiency of DAMAS for sound source localization via wavelet compression computational grid[J]. Journal of sound and vibration, 2017, 395: 341-353. DOI:10.1016/j.jsv.2017.02.005 (  0) 0)
|
| [23] |
CHU Zhigang, YANG Yang, HE Yansong. Deconvolution for three-dimensional acoustic source identification based on spherical harmonics beamforming[J]. Journal of sound and vibration, 2015, 344: 484-502. DOI:10.1016/j.jsv.2015.01.047 (  0) 0)
|
| [24] |
COMESANA D F, FERNANDEZ-GRANDE E, TIANA-ROIG E, et al. A novel deconvolution beamforming algorithm for virtual phased arrays[C]//Proceedings of Internoise 2013. Austria, 2013.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


