材料动态断裂实验的基本思路是测量载荷、加载点位移等物理量来计算动态应力强度因子(dynamic stress intensity factor,DSIF)。较早的研究工作主要是测量试样在加载过程中的载荷、位移,代入相应的经验公式计算动态应力强度因子[1-4];随着光学测量技术的发展,裂纹扩展过程也可以被观察到[5-7],甚至可以得到试样表面任一时刻的应变分布[8-9];应变片法在动态断裂测试中也得到广泛应用[10-11],常用来标定其他方法;近年来,部分学者将实验与数值模拟相结合,发展了实验-数值法[12-14]。这种方法通过实验测得载荷、起裂时间等参数,采用有限元软件计算动态应力强度因子,进而确定材料动态断裂韧性。相对于静态断裂力学,动态断裂力学需要考虑材料的应变率效应与惯性效应。由于数学上的困难,人们对动态断裂的研究尚不深入,动态断裂力学的理论框架并不完备[15]。对于动态载荷作用下裂纹起裂的问题,主流观点认为裂纹尖端应力应变场的形式与静态问题相似,具有分离变量形式的解[16]。该解只有在接近裂纹尖端的区域才能成立,故称渐近解。渐近解是联系宏观量与微观量的桥梁,前面提到的各种动态应力强度因子测定与求解方法均以静态渐近解为基础。裂纹尖端塑性区的存在严重地限制了渐近解的应用。此外,对于不同构型的试样,其载荷工况与边界条件各不相同,边界对裂尖应力应变场的影响也不能一概而论。
本文基于分离式Hopkinson拉杆(split-Hopkinson tension bar)实验装置,提出一种改进的紧凑拉伸剪切(compact tension shear specimen loaded, MCTS)试样,用于II型动态断裂测试[17]。本文采用有限元软件ABAQUS对改进的紧凑拉伸剪切试样在I型与II型载荷工况下进行了数值模拟,通过分析试样裂尖应变场与渐近解的差异来讨论静态渐近解在动态问题中的适用性。
1 裂尖应力应变场渐近解裂尖应力应变场的渐近解的表达式为:
| $ \left\{ \begin{array}{l} {\sigma _{ij}} = \frac{1}{{\sqrt {2{\rm \pi} r} }}\begin{array}{*{20}{l}} {[{K_{\rm I}}(t)f_{ij}^{\rm I}(\theta ) + {K_{{\rm I}{\rm I}}}(t)f_{ij}^{{\rm I}{\rm I}}(\theta )]} \end{array}\\ {\varepsilon _{ij}} = \frac{1}{{\sqrt {2{\rm \pi} r} }}\begin{array}{*{20}{l}} {[{K_{\rm I}}(t)g_{ij}^{\rm I}(\theta ) + {K_{{\rm I}{\rm I}}}(t)g_{ij}^{{\rm I}{\rm I}}(\theta )]} \end{array} \end{array} \right. $ | (1) |
平面应力状态下,式(1)中fij(θ)、gij(θ)的表达式分别为:
| $ \left\{ \begin{array}{l} f_{11}^{\rm I} = \cos \frac{\theta }{2}\left( {1 - \sin \frac{\theta }{2}\sin \frac{{3\theta }}{2}} \right)\\ f_{11}^{{\rm I}{\rm I}} = - \sin \frac{\theta }{2}\left( {2 + \cos \frac{\theta }{2}\cos \frac{{3\theta }}{2}} \right)\\ f_{22}^{\rm I} = \cos \frac{\theta }{2}\left( {1 + \sin \frac{\theta }{2}\sin \frac{{3\theta }}{2}} \right)\\ f_{22}^{{\rm I}{\rm I}} = \sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{{3\theta }}{2} \end{array} \right. $ | (2) |
| $ \left\{ \begin{array}{l} g_{11}^{\rm I} = \frac{1}{E}\cos \frac{\theta }{2}\left( {1 - \nu - (1 + \nu )\sin \frac{\theta }{2}\sin \frac{{3\theta }}{2}} \right)\\ g_{11}^{{\rm I}{\rm I}} = - \frac{1}{E}\sin \frac{\theta }{2}\left( {2 + (1 + \nu )\cos \frac{\theta }{2}\cos \frac{{3\theta }}{2}} \right)\\ g_{22}^{\rm I} = \frac{1}{E}\cos \frac{\theta }{2}\left( {1 - \nu + (1 + \nu )\sin \frac{\theta }{2}\sin \frac{{3\theta }}{2}} \right)\\ g_{22}^{{\rm I}{\rm I}} = \frac{1}{E}\sin \frac{\theta }{2}\left[ {2\nu + (1 + \nu )\cos \frac{\theta }{2}\cos \frac{{3\theta }}{2}} \right] \end{array} \right. $ | (3) |
渐近解满足静态问题的平衡方程σij, j=0,而对于动态问题惯性效应必须要考虑,平衡方程化为σij, j=ρui, tt,二者形式明显不同,那么静态问题的渐近解应用于动态问题的依据何在?
Sun[18]指出,裂纹尖端区域应力具有奇异性,应力对坐标的导数也是奇异的,而位移是有限的,因此平衡方程左边远远大于右边,基于上述假设,在裂尖附近将静态问题的渐近解应用于动态问题是合理的;而在距离裂尖较远处渐近解不适用。文献[18]虽然给出定性的解释,但并未提及裂尖“附近”的具体范围。
2 改进的紧凑拉伸剪切试样数值模拟改进的紧凑拉伸剪切试样的几何构型与尺寸如图 1所示,通过特殊设计的夹具能够实现Ⅰ型与Ⅱ型加载,试样与分离式Hopkinson拉杆装置的装配图见图 2。Ⅱ型加载时需要在试样侧面施加垂直于侧面的位移约束。

|
Download:
|
| 图 1 改进的紧凑拉伸剪切试样几何尺寸 Fig. 1 Geometry of MCTS specimen | |

|
Download:
|
| 图 2 改进的紧凑拉伸剪切试样装配图 Fig. 2 Assembly of MCTS specimen | |
改进的紧凑拉伸剪切试样与分离式Hopkinson拉杆装置的材料参数如表 1所示,其中采用双线性随动强化模型来表征试样的塑性,分离式Hopkinson拉杆装置的其他部分采用线弹性模型。
| 表 1 有限元模型材料属性 Table 1 Material properties of finite element models |
将冲击拉伸试验测得的波形进行滤波处理,作为入射杆端部施加的载荷[19],如图 3所示;试样裂尖网格划分如图 4所示,在裂尖采用三棱柱奇异单元,半径1 mm,围绕裂尖32等分;其他部分采用六面体单元,宽度0.25 mm。

|
Download:
|
| 图 3 SHTB入射波 Fig. 3 Incident wave of SHTB | |

|
Download:
|
| 图 4 改进的紧凑拉伸剪切试样裂纹尖端网格划分 Fig. 4 Mesh at crack tip of MCTS specimen | |
动态应力强度因子的定义为:
| $ \left\{ \begin{array}{l} {K_{\rm I}} = \mathop {\lim }\limits_{r \to 0} \sqrt {2{\rm \pi} r} {\left. {{\sigma _{22}}} \right|_{\theta = 0}}\\ {K_{{\rm I}{\rm I}}} = \mathop {\lim }\limits_{r \to 0} \sqrt {2{\rm \pi} r} {\left. {{\sigma _{12}}} \right|_{\theta = 0}} \end{array} \right. $ | (4) |
式(4)中坐标均为裂尖局部坐标。对于Ⅱ型载荷工况,局部坐标与全局坐标相同,对于Ⅰ型载荷工况,局部坐标相对于全局坐标顺时针旋转90°。
改进的紧凑拉伸剪切试样裂尖塑性区如图 5所示。图中标示出来的节点周围单元塑性应变均为零,且距离裂尖最近。定义为塑性影响区的边界,记作rp。由图可见,相同的入射波作用下,Ⅰ型裂尖塑性区rp的最大值是Ⅱ型的2倍。

|
Download:
|
| 图 5 裂纹尖端塑性区 Fig. 5 Plastic zone at crack tip | |
根据定义式(4),计算出裂纹延长线上各节点每一时刻的“应力强度”并线性拟合,其截距为这一时刻的动态应力强度因子数值解[20]。数据处理过程如下:从塑性影响区边界开始,选取相邻的7个节点进行线性拟合,依次重复此步骤,当截距变化量小于1%时记录截距值,再重复3次,取截距的平均值作为动态应力强度因子值。计算出动态应力强度因子数值解如图 6所示。
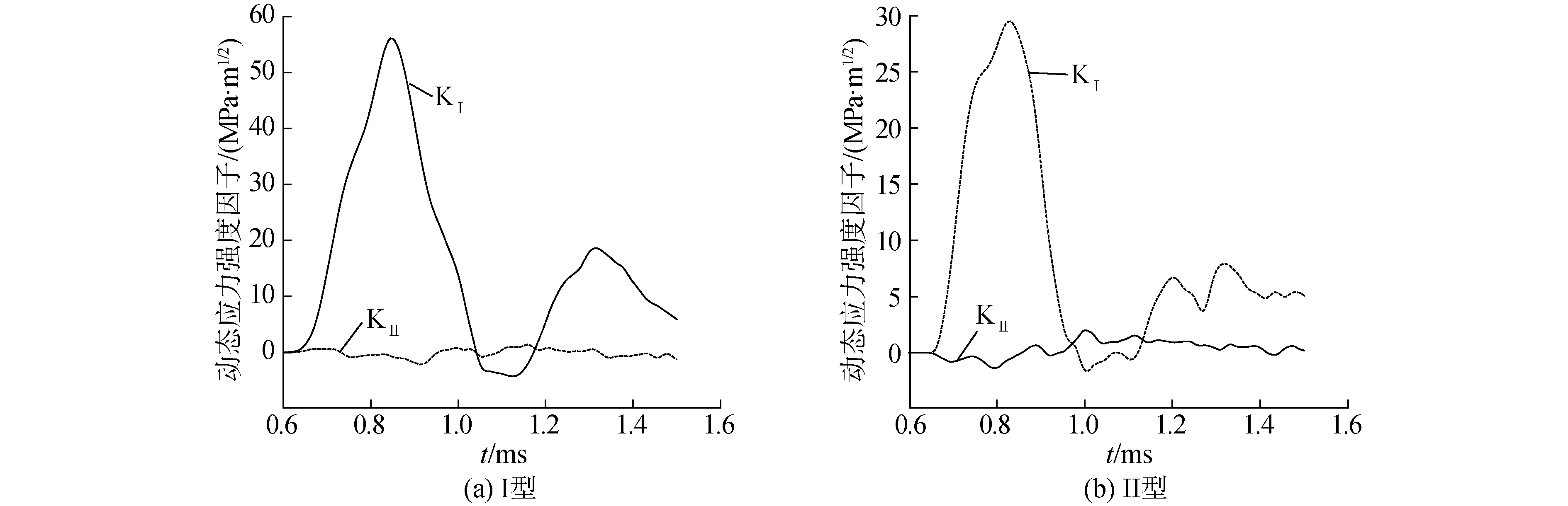
|
Download:
|
| 图 6 动态应力强度因子数值解 Fig. 6 Numerical solution of DSIF | |
根据定义已经求得动态应力强度因子的数值解,将其代入静态渐近解的表达式,任一节点应变都可求出。将式(2)写成矩阵形式:
| $ \left[ \begin{array}{l} \varepsilon _{11}^{(1)}\\ \varepsilon _{22}^{(2)} \end{array} \right] = \left[ \begin{array}{l} \frac{{g_{11}^{\rm I}({\theta _1})}}{{\sqrt {2{\rm \pi} {r_1}} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{g_{11}^{{\rm I}{\rm I}}({\theta _1})}}{{\sqrt {2{\rm \pi} {r_1}} }}\\ \frac{{g_{22}^{\rm I}({\theta _2})}}{{\sqrt {2{\rm \pi} {r_2}} }}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{g_{22}^{{\rm I}{\rm I}}({\theta _2})}}{{\sqrt {2{\rm \pi} {r_2}} }} \end{array} \right]\left[ \begin{array}{l} {K_{\rm I}}\\ {K_{{\rm I}{\rm I}}} \end{array} \right] $ | (5) |
Rittel[21]提出一种双应变片求解动态应力强度因子的实验方法,其中r1、θ1、r2、θ2分别为应变片1、2在裂尖局部坐标系内的坐标,反解式(5)即可求出动态应力强度因子。本文将通过式(5)计算的值称为渐近解,通过有限元分析得到的解称为数值解,二者之间的关系如图 7所示。可以看出,若节点应变渐近解与数值解不相同,则动态应力强度因子渐近解与数值解也会存在误差。本节在不同方向上选取节点,分析其应变渐近解与数值解之间的差异。

|
Download:
|
| 图 7 应变分析流程 Fig. 7 Flow graph of strain analysis | |
实验结果表明,裂纹往往在动态应力强度因子达到极大值之前开始扩展[12],在这个时间段内讨论应变渐近解与数值解的误差是有意义的。本文讨论的范围从动态应力强度因子达到0.1倍最大值开始,达到最大值为止。限于篇幅,文中只列出±90°、±67.5°、±45°、±22.5°和0°方向上节点应变渐近解与数值解在讨论范围内绝对误差的最大值、平均值以及绝对误差最大值与应变分量最大值之比(记为相对误差,在括号内标注)。Ⅰ型与Ⅱ型2种载荷工况分别如表 2、表 3所示。
| 表 2 节点应变误差(Ⅰ型载荷工况) Table 2 Error of nodal strain (mode Ⅰ loading) |
| 表 3 节点应变误差(Ⅱ型载荷工况) Table 3 Error of nodal strain (mode Ⅱ loading) |
ε11、ε22在θ=0°及θ=±22.5°方向上相对误差平均值小于20%。ε11误差最小的节点位于θ=0°,r=2.52 mm处,编号为1 023;除该节点外,ε22误差最小的节点位于θ=-22.5°,r=3.02 mm处,编号为1 051。其应变曲线分别如图 8(a)、(b)所示。将节点1 023的应变分量ε11,节点1 051的应变分量ε22代入式(5)反解出动态应力强度因子,并与数值解对比。如图 8(c)所示。可见KⅠ渐近解与数值解误差很小,而KⅡ误差很大。由于KⅡ数值解约等于零,且系数矩阵存在零元素,故KⅡ渐近解明显偏离数值解。

|
Download:
|
| 图 8 Ⅰ型载荷工况节点应变及动态应力强度因子渐近解与数值解对比 Fig. 8 Nodal strain and comparison of asymptotic solution and numerical solution of DSIF for mode Ⅰ loading | |
对于Ⅱ型载荷工况,应变误差相对Ⅰ型载荷工况更小。ε11在θ=-45°、θ=-67.5°方向上相对误差小于10%;ε22在θ=45°方向上相对误差小于10%。ε11相对误差最小的节点位于θ=-67.5°,r=3.52 mm处,编号为1109;ε22误差最小的节点位于θ=45°,r=2.77 mm处,编号为962。其应变曲线分别如图 9(a)、(b)所示。将节点1109的应变分量ε11,节点962的应变分量ε22代入式(5),解出动态应力强度因子如图 9(c)所示。可见动态应力强度因子渐近解与数值解几乎完全重合。
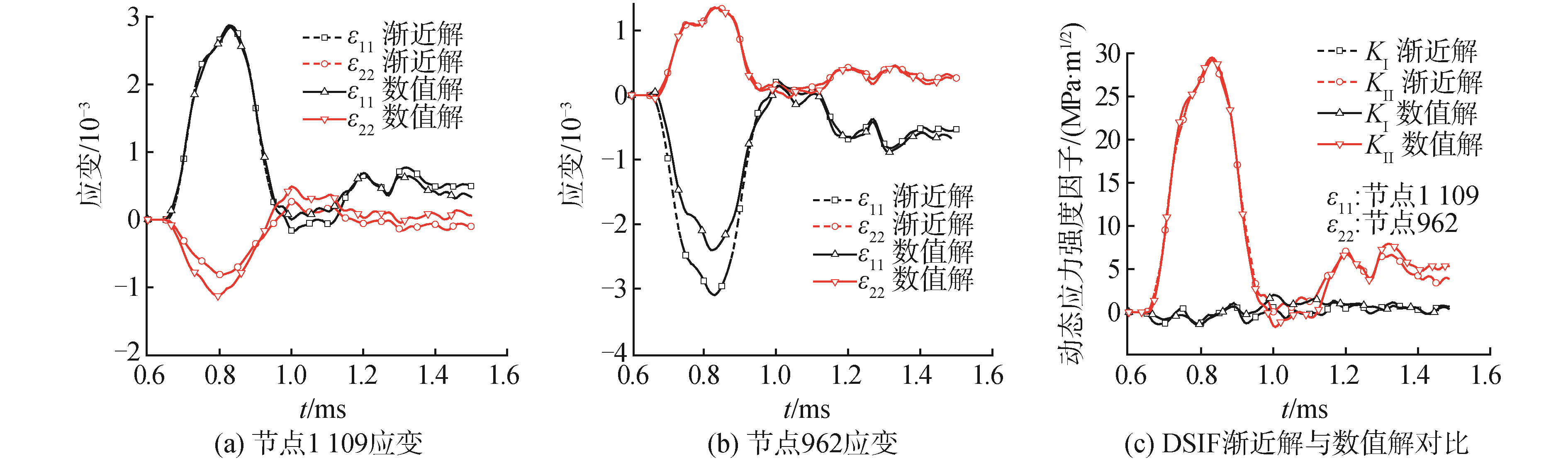
|
Download:
|
| 图 9 Ⅱ型载荷工况节点应变及DSIF渐近解与数值解对比 Fig. 9 Nodal strain and comparison of asymptotic solution and numerical solution of DSIF for mode Ⅱ loading | |
考察各方向上各节点应变绝对误差最大值与应变分量最大值之比,取其平均值如表 4。可见多数方向上节点应变分量渐近解与数值解相差较大,一些方向上相差极大,其原因是这些方向上相应的节点应变分量渐近解或数值解约等于零。
| 表 4 各方向节点应变相对误差平均值 Table 4 Average error of nodal strain in different orientations |
对于Ⅰ型载荷工况,由于塑性影响区尺度较大,所选节点距离裂尖较远,受边界影响更大,因此各方向上节点应变误差相对Ⅱ型载荷工况较大。对于Ⅱ型载荷工况,裂尖塑性影响区尺度较小,应变误差相对较小。
图 10显示了2种载荷工况下节点应变渐近解与数值解相对误差小于15%的区域,称为应变理想区。应变理想区位于rp~2rp。对于Ⅰ型载荷工况,ε11与ε22的理想区重合,位于θ=0°附近;而对于Ⅱ型载荷工况,ε11与ε22的理想区分别位于θ=-45°与θ=45°附近。可见静态渐近解适用的区域非常有限。

|
Download:
|
| 图 10 应变理想区 Fig. 10 Suitable zone of strain solution | |
在应变理想区内选取4组节点计算动态应力强度因子并分析渐近解与数值解的误差,2种载荷工况分别如表 5所示。可见在节点应变相对误差不大的条件下,动态应力强度因子相对误差与节点应变相对误差量级相同;限于篇幅文中不再列出动态应力强度因子曲线。
| 表 5 动态应力强度因子渐近解与数值解的误差 Table 5 Error of DSIFs between asymptotic and numerical solutions |
1) 裂尖应变场的解析解在特定方向上与数值解较为接近(Δε≤10%),而在其他方向上有较大差异。对于I型载荷工况,误差较小的方向是0°附近;对于II型载荷工况则是±45°附近。
2) DSIF解析解与数值解的相对误差取决于节点应变的相对误差,2者在相同数量级。
3) 静态渐近解在动态断裂问题中的适用范围非常有限,且与试样载荷工况有关。应针对具体问题分别讨论。
| [1] |
ANDERSON T L. Fracture mechanics-fundamentals and applications[M]. Boca Raton: CRC Press, 1991: 3-21.
(  0) 0)
|
| [2] |
李玉龙, 刘元镛. 用弹簧质量模型求解三点弯曲试样的动态应力强度因子[J]. 固体力学学报, 1994, 15(1): 75-79. LI Yulong, LIU Yuanyong. Determination of dynamic stress intensity of specimen of three points bending by spring-mass model[J]. Acta mechanica solida sinica, 1994, 15(1): 75-79. (  0) 0)
|
| [3] |
JIANG Fengchun, ROHATGI A, VECCHIO K S, et al. Analysis of the dynamic responses for a pre-cracked three-point bend specimen[J]. International journal of fracture, 2004, 127(1): 147-165. DOI:10.1023/B:FRAC.0000035058.03627.30 (  0) 0)
|
| [4] |
李清, 于强, 徐文龙, 等. 应变片法确定Ⅰ型裂纹动态应力强度因子试验研究[J]. 岩土力学, 2018, 39(4): 1211-1218. LI Qing, YU Qiang, XU Wenlong, et al. Experimental research on determination of dynamic stress intensity factor of type-I crack using strain gage method[J]. Rock and soil mechanics, 2018, 39(4): 1211-1218. (  0) 0)
|
| [5] |
卢芳云. 霍普金森杆实验技术[M]. 北京: 科学出版社, 2013: 1-10. LU Fangyun. Hopkinson bar techniques[M]. Beijing: Science Press, 2013: 1-10. (  0) 0)
|
| [6] |
JIANG Fengchun, VECCHIO K S. Experimental investigation of dynamic effects in a two-bar/three-point bend fracture test[J]. Review of scientific instruments, 2007, 78(6): 063903. DOI:10.1063/1.2746630 (  0) 0)
|
| [7] |
崔新忠, 范亚夫, 陈捷. 685均质钢静动态断裂韧性实验研究[J]. 实验力学, 2012, 27(3): 326-334. CUI Xinzhong, FAN Yafu, CHEN Jie. Experimental research of quasi-static and dynamic fracture toughness of 685 homogeneous steel[J]. Journal of experimental mechanics, 2012, 27(3): 326-334. (  0) 0)
|
| [8] |
邹广平, 汪艳伟, 唱忠良, 等. 基于数字散斑相关法的紧凑拉伸试样断裂韧性实验研究[J]. 实验力学, 2015, 30(3): 275-281. ZOU Guangping, WANG Yanwei, CHANG Zhongliang, et al. Experimental study of compact tension specimen fracture toughness based on digital speckle correlation method[J]. Journal of experimental mechanics, 2015, 30(3): 275-281. (  0) 0)
|
| [9] |
XING Haozhe, ZHANG Qianbing, RUAN Dong, et al. Full-field measurement and fracture characterisations of rocks under dynamic loads using high-speed three-dimensional digital image correlation[J]. International journal of impact engineering, 2018, 113: 61-72. DOI:10.1016/j.ijimpeng.2017.11.011 (  0) 0)
|
| [10] |
DALLY J W, SANFORD R J. Strain-gage methods for measuring the opening-mode stress-intensity factor, KI[J]. Experimental mechanics, 1987, 27(4): 381-388. (  0) 0)
|
| [11] |
樊鸿, 张盛, 王启智. 用应变片法确定混凝土动态起裂时间的研究[J]. 振动与冲击, 2010, 29(1): 153-156. FAN Hong, ZHANG Sheng, WANG Qizhi. Determining dynamic fracture initiation time for concrete with strain gauge method[J]. Journal of vibration and shock, 2010, 29(1): 153-156. DOI:10.3969/j.issn.1000-3835.2010.01.033 (  0) 0)
|
| [12] |
XU Zejian, LI Yulong. A novel method in determination of dynamic fracture toughness under mixed mode I/II impact loading[J]. International journal of solids and structures, 2012, 49(2): 366-376. DOI:10.1016/j.ijsolstr.2011.10.011 (  0) 0)
|
| [13] |
ZHU Shifan, CAO Yang, GUO Chunhuan, et al. An experimental-numerical hybrid method to determine dynamic elastic-plastic fracture toughness[J]. Key engineering materials, 2013, 577-578: 517-520. DOI:10.4028/www.scientific.net/KEM.577-578.517 (  0) 0)
|
| [14] |
JIANG Fengchun, VECCHIO K S. Hopkinson bar loaded fracture experimental technique:a critical review of dynamic fracture toughness tests[J]. Applied mechanics reviews, 2009, 62(6): 060802. DOI:10.1115/1.3124647 (  0) 0)
|
| [15] |
范天佑. 断裂动力学原理与应用[M]. 北京: 北京理工大学出版社, 2006: 1-19. FAN Tianyou. The principles and applications of fracture kinetics[M]. Beijing: Beijing Institute of Technology Press, 2006: 1-19. (  0) 0)
|
| [16] |
RAVI-CHANDAR K. Dynamic fracture[M]. Austin, USA: Elsevier Science, 2004: 27-47.
(  0) 0)
|
| [17] |
邹广平, 谌赫, 唱忠良. 一种基于SHTB的II型动态断裂实验技术[J]. 力学学报, 2017, 49(1): 117-125. ZOU Guangping, CHEN He, CHANG Zhongliang. A modified mode II dynamic fracture test technique based on SHTB[J]. Chinese journal of theoretical and applied mechanics, 2017, 49(1): 117-125. (  0) 0)
|
| [18] |
SUN C T, JIN Z H. Fracture mechanics[M]. Waltham: Academic Press, 2012: 35-61.
(  0) 0)
|
| [19] |
沈昕慧.应力波加载下材料动态断裂韧性相关实验技术研究[D].哈尔滨: 哈尔滨工程大学, 2016. SHEN Xinhui. Investigation on dynamic fracture toughness experimental technique under stress wave load[D]. Harbin: Harbin Engineering University, 2016. https://kns.cnki.net/KCMS/detail/detail.aspx?dbcode=CDFD&dbname=CDFDLAST2017&filename=1017242446.nh&v=Mjc1MDFYMUx1eFlTN0RoMVQzcVRyV00xRnJDVVI3cWZiK1pvRnlyZ1ZyL0lWRjI2R2JHOEhOWElxWkViUElSOGU= (  0) 0)
|
| [20] |
解德, 钱勤, 李长安. 断裂力学中的数值计算方法及工程应用[M]. 北京: 科学出版社, 2009: 1-35. XIE De, QIAN Qin, LI Chang'an. Numerical methods and engineering application in fracture mechanics[M]. Beijing: Science Press, 2009: 1-35. (  0) 0)
|
| [21] |
RITTEL D. A hybrid experimental-numerical investigation of dynamic shear fracture[J]. Engineering fracture mechanics, 2005, 72(1): 73-89. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


