材料在生产和使用过程中会产生一系列细小裂纹而带缝工作，这些裂缝极有可能导致材料的破坏，甚至结构的失效^[1]。因此在材料中预制裂纹，研究裂纹扩展规律是解决含缺陷材料破坏问题的一种较为常见的手段。有限元等基于传统连续介质力学的数值方法在结构变形分析中取得了巨大的成功，但是它在不连续处没有定义，存在奇异性，在解决材料的破坏问题上举步维艰。新近兴起的近场动力学理论^[2]采用位移的空间积分形式完全重构了传统连续介质力学理论，这种积分型方程在不连续处仍有定义，且形式不变，实现了对连续介质和非连续介质力学行为的统一描述，能模拟材料中裂纹自发地萌生和扩展，是一种特别适合模拟材料破坏的力学理论和方法。Silling^[2]提出了键基近场动力学理论，它将物质点间的相互作用视为它们中心受力的键，这种中心力模型只有一个参数，即键刚度(或微观模量)，称为传统键基近场动力学模型(或单参数键基近场动力学模型，bond-based peridynamics，BPD)。

均匀各向同性线弹性材料的力学属性须由2个独立的弹性参数才能完全表述，采用单参数键基PD模型描述其力学行为时，2个独立弹性参数将被缩减为1个参数，必然导致某一个弹性参数将以恒定的形式固化到中心力模型中。例如泊松比参数被固化成常数，在平面应力状态下，泊松比只能是1/3，平面应变状态和三维应力状态下，泊松比只能是1/4^[3]。毫无疑问，这种泊松比恒定的要求大大限制了传统键基近场动力学理论的适用范围。为此，Silling^[4]又提出了态基近场动力学理论，它是通过考虑两物质点邻域内所有键的集合作用来增强材料的本构描述。与键基近场动力学模型中2物质点间的作用仅由它俩自身决定不同，态基近场动力学模型中2物质点间的作用须考虑2物质点邻域内所有物质点^[5]，是一种典型的多体相互作用。因此，态基近场动力学方法的计算复杂性以及对资源的耗费都较键基近场动力学有了更高的要求。于是，为了保留传统键基近场动力学模型的简单性以及数值实施的稳定性，部分学者仍立足于键基近场动力学模型的两体间相互作用，通过引入切向键^[6-8]、引入键的转角^[9]、力量补偿方案^[10]或以梁换键^[11-12]等方式扩展键基近场动力学理论，突破了泊松比的限制。其中，通过引入切向键或键的转角等方式增加2物质点间的切向作用较为便捷，对传统键基近场动力学模型改动很小。Prakash等^[9]通过引入法向弹簧，提出一种二维双参数键基近场动力学模型。Zhou等^[6-7]基于超弹性理论提出一种三维两参数共轭键基近场动力学模型。Zhu^[8]等通过增加键的转角，提出双参数键基近场动力学模型。当泊松比取上述恒定值时(如在平面应力状态下，泊松比取1/3)，两参数都能退化为单参数。但一些模型^{[6-7, 9]}退化后的参数与传统单参数键基近场动力学的参数并不相同。

本文在BPD模型的基础上，通过键内直接添加切向刚度系数，提出一种单键双参数键基近场动力学模型(TBPD)，推导模型的双参数与材料弹性参数之间的转换关系，建立TBPD模型单键断裂条件。然后探讨不同泊松比下BPD模型和TBPD模型的适用性，最后，采用TBPD模型，研究裂纹间距和随机分布的细小裂纹对平行双裂纹薄板破坏的影响。

1 单键双参数键基近场动力学方法 1.1 理论模型

传统键基近场动力学模型认为宏观连续体在其所在空间域Ω内由大量物质点组成，物质点以初始构型的位置X作为标记，携有体积V_X和质量密度ρ。任一物质点X仅在其有限的“域”内通过键与其他物质点X′存在相互作用力f。域是以该物质点为中心，以δ为半径的范围，记域内所有其他物质点为H_δ={X′∈Ω: X′－X ≤δ}，据牛顿第二定律，物质点X在t时刻的运动方程为：

$ \rho \mathit{\boldsymbol{\ddot u}} = \int_{{H_\delta }} {\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{u}},{\mathit{\boldsymbol{X}}^\prime } - \mathit{\boldsymbol{X}},t)} {\rm{d}}{\mathit{\boldsymbol{V}}_{{X^\prime }}} + \mathit{\boldsymbol{b}}(\mathit{\boldsymbol{X}},t) $

(1)

式中：$\mathit{\boldsymbol{\ddot u}} = \frac{{{\partial ^2}\mathit{\boldsymbol{u}}(\mathit{\boldsymbol{X}}, t)}}{{\partial {t^2}}}$为加速度；b为体力密度；f表示本构力函数，包含了物质点的所有本构信息，表示t时刻单位体积的物质点X′施加于物质点X的体力密度；u和u′分别表示t时刻两物质点的位移。通常，采用ξ=X′－X表示初始时刻两物质点的相对位置，η=u′－u表示在t时刻它们的相对位移，则t时刻两物质点的相对位置为ξ+η。

传统键基近场动力学模型将物质点间的相互作用视为它们中心受力的键，键仅有一个刚度系数，表示法向作用，故这里称之为单键单参数键基近场动力学模型。

在传统键基近场动力学模型的基础上，通过键内直接添加切向刚度系数，使其具有法向和切向双刚度，并称之为单键双参数键基近场动力学模型，如图 1所示。

在该双参数键基近场动力学模型中，键的法向刚度沿着平行于键的初始方向(${\mathit{\boldsymbol{\widehat e}}_n}{\rm{||}}\mathit{\boldsymbol{\xi }}$)，键的切向刚度沿着垂直于键初始方向(${{{\mathit{\boldsymbol{\widehat e}}}_t} \bot \mathit{\boldsymbol{\xi }}}$)。${\mathit{\boldsymbol{\widehat e}}_n}$和${\mathit{\boldsymbol{\widehat e}}_t}$分别表示沿键初始方向和垂直于该方向的单位矢量：

$ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat e}}}_n} = {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {{\mathit{\boldsymbol{\hat e}}}_1} + {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {{\mathit{\boldsymbol{\hat e}}}_2}}\\ {{{\mathit{\boldsymbol{\hat e}}}_t} = - {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {{\mathit{\boldsymbol{\hat e}}}_1} + {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta {{\mathit{\boldsymbol{\hat e}}}_2}} \end{array}} \right. $

(2)

式中：${\mathit{\boldsymbol{\widehat e}}_1}$和${\mathit{\boldsymbol{\widehat e}}_2}$为初始构型所在坐标系的单位矢量；θ为键的初始方向角。

此时，X和X′间键的微观弹性应变密度(单位体积的应变能密度)为:

$ \omega = \frac{1}{2}{c_n}{\left( {\frac{{{\eta _n}}}{\xi }} \right)^2}\xi + \frac{1}{2}{c_t}{\left( {\frac{{{\eta _t}}}{\xi }} \right)^2}\xi $

(3)

式中：c_n和c_t分别为法向和切向刚度系数；η_n和η_t分别是η沿着${\mathit{\boldsymbol{\widehat e}}_n}$和${\mathit{\boldsymbol{\widehat e}}_t}$的分量；η_n/ξ和η_t/ξ分别表示键在${\mathit{\boldsymbol{\widehat e}}_n}$和${\mathit{\boldsymbol{\widehat e}}_t}$方向的伸长率。

将每个键的应变能都等分给键两端的物质点，则物质点X的宏观弹性应变能密度为：

$ {W^{{\rm{PD}}}}(\mathit{\boldsymbol{X}}) = \frac{1}{2}\int_{{H_\delta }} \omega {\rm{d}}{V_{{X^\prime }}} $

(4)

对点力f是键的微观弹性应变能密度ω对该键相对位移矢量η的导数：

$ \mathit{\boldsymbol{f}} = \frac{{\partial \omega (\mathit{\boldsymbol{\eta }},\mathit{\boldsymbol{\xi }})}}{{\partial \mathit{\boldsymbol{\eta }}}} = \frac{{{c_n}{\eta _n}{{\mathit{\boldsymbol{\hat e}}}_n} + {c_t}{\eta _t}{{\mathit{\boldsymbol{\hat e}}}_t}}}{\xi } $

(5)

以示区别，传统BPD模型的对点力^[14]为：

$ {\mathit{\boldsymbol{f}}_{{\rm{BPD}}}} = cs \mathit{\boldsymbol{\hat e}}_n^\prime $

(6)

式中：s=(|ξ+η| － |ξ|)/ |ξ|为t时刻键的伸长率；$\mathit{\boldsymbol{\widehat e}}_n'$_n=(ξ+η)/ ξ+η为该时刻键所在方向的单位矢量。在小变形下，有：

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat e}}_n^\prime \approx {{\mathit{\boldsymbol{\hat e}}}_n}}\\ {|\xi + \mathit{\boldsymbol{\eta }}| \approx |\xi | + \mathit{\boldsymbol{\eta }} \cdot {{\mathit{\boldsymbol{\hat e}}}_n} = |\xi | + {\eta _n}} \end{array}} \right. $

(7)

则式(6)可改写为：

$ {\mathit{\boldsymbol{f}}_{{\rm{BPD}}}} \approx \frac{{c{\eta _n}{{\mathit{\boldsymbol{\hat e}}}_n}}}{\xi } $

(8)

TBPD模型与BPD模型一样，两物质点间的作用仅由两物质点自身状态决定，与其他物质点无关。因此，可取出δ邻域内任意两物质点进行单独分析，初始时刻，它们的相对位置为ξ=|ξ|${\mathit{\boldsymbol{\widehat e}}_n}$=l₀${\mathit{\boldsymbol{\widehat e}}_n}$。

假定弹性体在小变形情况下发生均匀应变ε_ij，根据Cauchy-Born准则，初始构型中物质点X的邻近区域在${\mathit{\boldsymbol{\widehat e}}_n}$方向上的微键${\mathit{\boldsymbol{\widehat e}}_n}$ds₀，映射到当前构型为F${\mathit{\boldsymbol{\widehat e}}_n}$ds₀, F是物质点X变形梯度张量，其分量表示为：

$ {F_{ij}} = \frac{{\partial {x_i}}}{{\partial {X_j}}} = \frac{{\partial {u_i}}}{{\partial {X_j}}} + {\delta _{ij}} $

(9)

式中δ_ij为Kronecker符号。于是，Green应变张量E可表示为：

$ {E_{ij}} = \frac{1}{2}({F_{ki}}{F_{kj}} - {\delta _{ij}}) = \frac{1}{2}\left( {\frac{{\partial {u_i}}}{{\partial {X_j}}} + \frac{{\partial {u_j}}}{{\partial {X_i}}} + \frac{{\partial {u_k}}}{{\partial {X_i}}}\frac{{\partial {u_k}}}{{\partial {X_j}}}} \right) $

(10)

小变形时有|∂u_i/∂X_j| << 1，略去位移梯度的乘积项，Green应变E变为Cauchy应变ε，则式(9)变为：

$ {F_{ij}} = {\delta _{ij}} + {\varepsilon _{ij}} + {\omega _{ij}} $

(11)

式中：${\omega _{ij}} = \frac{1}{2}\left({\frac{{\partial {u_i}}}{{\partial {X_j}}} - \frac{{\partial {u_j}}}{{\partial {X_i}}}} \right)$为刚体转动张量，当弹性体具有足够的位移约束时，刚体位移(包括刚体转动)可忽略不计，即ω_ij=0。式(11)可进一步简化为F_ij=δ_ij+ε_ij。由于整个物体具有均匀的应变场，因此所有物质点的都具有相同的变形梯度F。初始构型中物质点X和X′间键${\mathit{\boldsymbol{\widehat e}}_n}$l₀，映射到当前构型为F${\mathit{\boldsymbol{\widehat e}}_n}$l₀=${\mathit{\boldsymbol{\widehat e}}_n}$l₀+ε${\mathit{\boldsymbol{\widehat e}}_n}$l₀，则两物质点间相对位移矢量η=ε${\mathit{\boldsymbol{\widehat e}}_n}$l₀，将位移矢量按法向和切向进行分解，得：

$ \left\{ {\begin{array}{*{20}{l}} {{\eta _n} = \mathit{\boldsymbol{\eta }} \cdot {{\mathit{\boldsymbol{\hat e}}}_n} = {l_0}{\varepsilon _{ij}}{{\hat e}_{nj}}{{\hat e}_{ni}}}\\ {{\eta _t} = \mathit{\boldsymbol{\eta }} \cdot {{\mathit{\boldsymbol{\hat e}}}_t} = {l_0}{\varepsilon _{ij}}{{\hat e}_{nj}}{{\hat e}_{ti}}} \end{array}} \right. $

(12)

将方程(3)代入方程(4)，得物质点X的宏观弹性应变能密度：

$ {W^{{\rm{PD}}}}(\mathit{\boldsymbol{X}}) = \frac{1}{2}\int_{{H_\delta }} {\frac{1}{{2\xi }}} ({c_n}\eta _n^2 + {c_t}\eta _t^2){\rm{d}}{V_{{X^\prime }}} $

(13)

将方程(12)代入方程(13)化简得：

$ \begin{array}{*{20}{l}} {{W^{{\rm{PD}}}}(\mathit{\boldsymbol{X}}) = \left( {\frac{1}{{16}}\pi h{\delta ^3}{c_n} + \frac{1}{{48}}\pi h{\delta ^3}{c_t}} \right)(\varepsilon _{11}^2 + \varepsilon _{22}^2) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{1}{{12}}\pi h{\delta ^3}{c_n} + \frac{1}{{12}}\pi h{\delta ^3}{c_t}} \right)\varepsilon _{12}^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{1}{{24}}\pi h{\delta ^3}{c_n} - \frac{1}{{24}}\pi h{\delta ^3}{c_t}} \right){\varepsilon _{11}}{\varepsilon _{22}}} \end{array} $

(14)

式中h为材料厚度。在经典连续介质力学中，平面应力状态的应变能密度为：

$ \begin{array}{*{20}{l}} {{W^{{\rm{CCM}}}}(\mathit{\boldsymbol{X}}) = \frac{E}{{2(1 - {\nu ^2})}}(\varepsilon _{11}^2 + \varepsilon _{22}^2) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{E}{{1 + \nu }}\varepsilon _{12}^2 + \frac{{E\nu }}{{1 - {\nu ^2}}}{\varepsilon _{11}}{\varepsilon _{22}}} \end{array} $

(15)

对于任一物质点X，在相同的应力状态下，近场动力学的弹性应变能密度W(X)和连续介质力学的应变能密度W^CCM(X)必须相等。即平面应力状态下不论ε_ij取何值，都应有W^PD(X)=W^CCM(X)，于是，方程(14)和方程(15)中(ε₁₁²+ε₂₂²)、ε₁₂²和ε₁₁ε₂₂的系数需对应相等，由此可列出3个独立方程，求解该方程组可得TBPD模型的参数c_n和c_t与弹性模量E和泊松比ν的关系为：

$ {c_n} = \frac{{6E}}{{\pi h{\delta ^3}(1 - \nu )}},{c_t} = \frac{{6E(1 - 3\nu )}}{{\pi h{\delta ^3}(1 - {\nu ^2})}} $

(16)

式(16)中的法向刚度参数c_n与传统键基近场动力学的微模量^[14]完全相同。若方程(14)和方程(15)中采用平面应变状态下或者三维状态下的应变能密度，则可得到对应应力状态下TBPD模型的微模量与材料弹性参数间的转换关系，如表 1所示。

不难验证，当切向刚度系数c_t=0时，TBPD模型退化后参数c_n与BPD模型参数完全相同，且有方程(5)右边表达式将退化成方程(8)右边表达式，则此时，TBPD模型将近似为BPD模型。微模量参数c_n和c_t作为键基PD的刚度系数，必须满足c_n≥0且c_t≥0。因此TBPD模型的泊松比适用范围为：平面应变和三维情形时－1 < ν≤1/4，平面应力时-1 < ν≤1/3。

值得指出的是，表 1转换关系与Zhu等^[8]相同，但两者引入切向刚度的方法和推导过程并不同。TBPD模型通过键内直接增加切向刚度系数，在小变形条件下，以均匀应变工况，得到模型的双参数与材料弹性参数的转换公式。Zhu等^[8]未就双参数键基PD模型开展破坏分析，本文接下来将讨论TBPD模型的断裂准则及其破坏应用。

1.2 单键断裂条件

这里采用能量准则作为判断单键断裂的依据，即键中包含的微观应变能密度ω(η, ξ)超过某个极限值ω_c(η, ξ)(简记为ω_c)时，认为该键断裂，将不再传递力的作用。

考虑含裂纹CD的无限大板，板厚h，裂纹长度为2a。当裂纹CD穿过某一物质点的邻域时，所有被裂纹穿过的键都将断裂，存储在这些键中的应变能也被耗散。如图 2所示，键AB将发生断裂，存储在该键中的应变能ω_cV_AV_B将被耗散，其中V_A和V_B分别为物质点A和物质点B携带的体积，当V_A和V_B趋于无限小时，所有因裂纹CD而耗散的键的总应变能用积分表示为：

$ U = \int_{{\varOmega _A}} {\int_{{\varOmega _B}} {{\omega _c}} } {\rm{d}}{V_B}{\rm{d}}{V_A},{r_{{\rm{AB}}}} \le \delta {\rm{ 且 }}AB \cap CD \ne \emptyset $

(17)

式中：Ω_A和Ω_B分别表示位于裂纹CD两侧的物质点A和物质点B的取值范围，它们须满足一定的断键条件，即线段AB的距离r_AB≤δ，且线段AB和线段CD有交点。

对于所有距裂纹CD垂直距离为z的物质点，其球形邻域与裂纹CD有非零交集的物质点的取值范围为图 2所示的平行裂纹CD平面，以A点为中心，半径为$a + \sqrt {{\delta ^2} - {z^2}} $的圆域S_A。当然，圆域S_A内不是所有物质点都能被CD完全分隔成2部分，如图 2中的物质点A₁。但通过增补分隔邻域体积的几何方法，可以证明，物质点A₁与物质点A₂(过D点铅直线且与物质点A₁等距)被裂纹CD分隔的邻域体积之和等于圆域中心物质点A被CD分隔的邻域体积，即：

$ {\varOmega _{{B_1}}} + {\varOmega _{{B_2}}} = {\varOmega _B} $

(18)

则对于所有距裂纹CD垂直距离为z的物质点，因裂纹CD而耗散的键的总应变能为：

$ \begin{array}{*{20}{c}} {{U_z} = {\rm{d}}z\int_{{S_A}} {\int_{{\varOmega _B}} {{\omega _c}} } {\rm{d}}{V_B}{\rm{d}}{S_A} = }\\ {{\rm{d}}z\int_{S_A^\prime } {\rm{d}} S_A^\prime \cdot \int_{{\varOmega _{Bz}}} {{\omega _c}} {\rm{d}}{V_B} = 2ah{\rm{d}}z\int_{{\varOmega _{Bz}}} {{\omega _c}} {\rm{d}}{V_B}} \end{array} $

(19)

式中：dz为物质点A携带体积在z轴的长度，S′ _A为裂纹CD在直线AA₂所在水平面上的投影区。

记G_c为产生每单位裂纹表面所需的能量，则：

$ \begin{array}{*{20}{c}} {{G_c} = \frac{1}{{2ah}}\int_0^\delta {{U_z}} = \int_0^\delta {\int_{{\Omega _{Bz}}} {{\omega _c}} } {\rm{d}}{V_B}{\rm{d}}z = }\\ {2h\int_0^\delta {\int_z^\delta {\int_0^{{\rm{arccos}}\left( {\frac{z}{\xi }} \right)} {{\omega _c}} } } \xi {\rm{d}}\xi {\rm{d}}\theta {\rm{d}}z} \end{array} $

(20)

与传统BPD模型相类似，将ω_c假定为ξ的线性函数，即:

$ {\omega _c}(\mathit{\boldsymbol{\eta }},\mathit{\boldsymbol{\xi }}) = {\omega _{c0}}\xi $

(21)

将式(21)代入式(20)，得:

$ {G_c} = 2h\int_0^\delta {\int_z^\delta {\int_0^{{\rm{arccos}}\left( {\frac{z}{\xi }} \right)} {{\omega _{c0}}} } } \xi \xi {\rm{d}}\xi {\rm{d}}\theta {\rm{d}}z = \frac{1}{2}h{\omega _{c0}}{\delta ^4} $

(22)

故

$ {\omega _{c0}} = \frac{{2{G_c}}}{{h{\delta ^4}}} $

(23)

由式(3)、式(21)和式(23)知，TBPD模型的单键断裂条件为：

$ \frac{\omega }{\xi } = \frac{1}{2}{c_n}{\left( {\frac{{{\eta _n}}}{\xi }} \right)^2} + \frac{1}{2}{c_t}{\left( {\frac{{{\eta _t}}}{\xi }} \right)^2} > {\omega _{c0}} $

(24)

在采用TBPD方法计算过程中，一旦键满足式(24)，则该键断裂且永久失效。不难验证，当切向刚度系数c_t=0时，TBPD模型的单键断裂条件可退化后为BPD模型的单键断裂条件，即：

$ s > {s_c} = \sqrt {\frac{{4{G_c}}}{{ch{\delta ^4}}}} $

(25)

式中c和s_c分别为BPD模型中键的微观模量以及键的临界伸长率。

在TBPD模型中，键断裂与否采用状态函数μ(ξ, t)来记录。物质点的损伤通过物质点邻域内键的断裂程度，用函数φ(X, t)来计算，μ(ξ, t)和φ(X, t)具体的表达式可参考文献[15]。

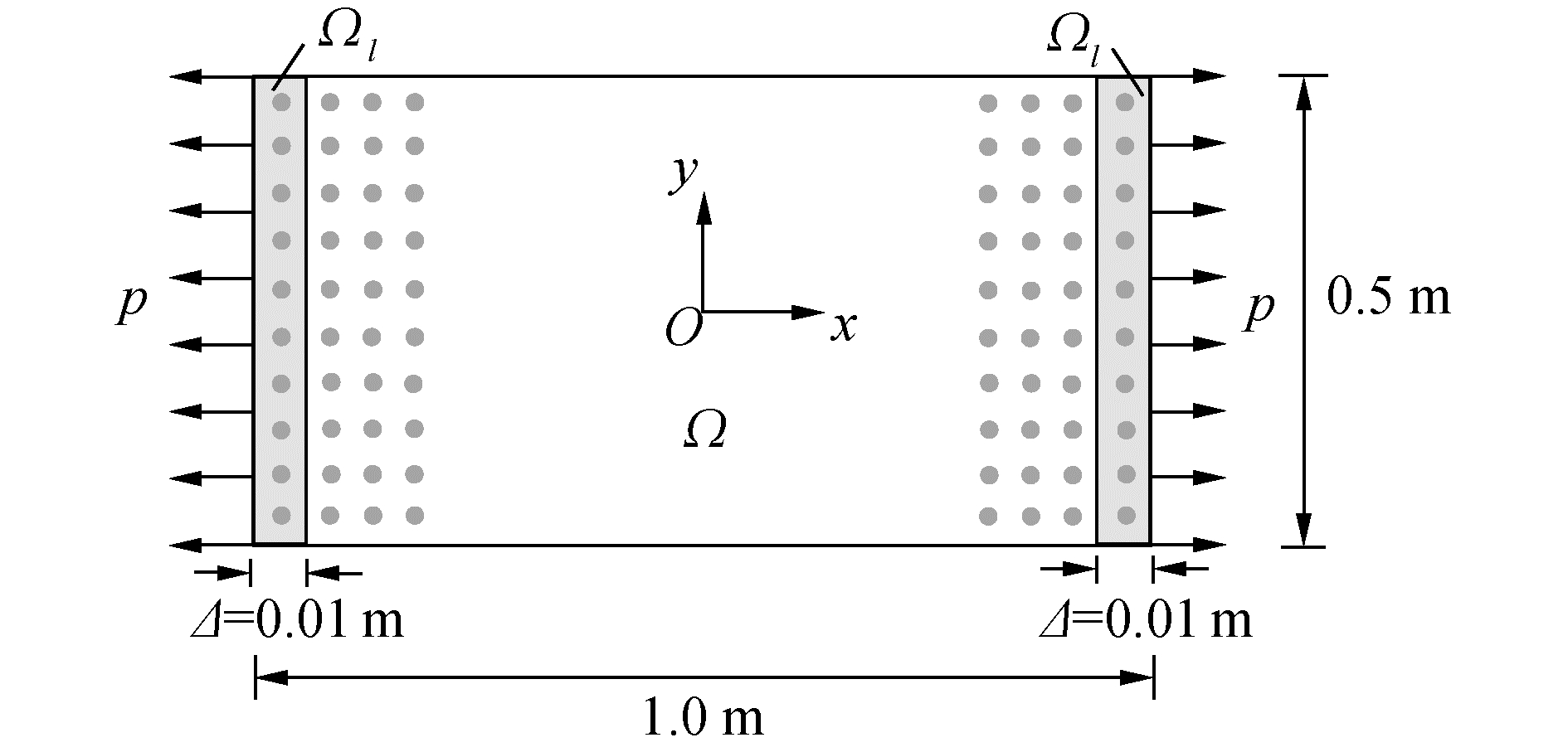
2 模型验证

算例1  尺寸为1 m×0.5 m的长方形薄板，板厚0.01 m，其弹性模量200 GPa，密度7 850 kg/m³，沿两短边作用p=200 MPa的均匀法向拉力，采用BPD和TBPD模型分别计算，物质点间距Δ=0.01 m，邻域半径δ=3.015Δ，拉伸荷载通过转变成体力荷载p/Δ，施加在两短边最外一层的真实物质点上^[14]，如图 3所示。

1) 当泊松比ν=1/3时，如图 4所示，采用BPD模型或TBPD模型计算的位移结果都与解析解很好地吻合。采用TBPD方法计算的位移u_x的最大相对误差为3.25%，分布在薄板4个角点附近，这是由近场动力学的边界效应导致的。

2) 当泊松比ν∈[0, 1/3]时，采用反算泊松比方法^[8-9]和计算物质点的位移u_x的相对误差来验证BPD和TBPD模型的合理性，结果列于表 2和表 3。

由表 2可知，BPD模型无论材料泊松比怎么取值，反算泊松比总是0.332 8，当ν≠1/3时相对误差大，这证实了它仅适合用来描述前面所说的特定泊松比材料。而采用TBPD模型时，反算泊松比值与真实泊松比非常接近，相对误差为0.16%~0.70%。故它较适合用来描述泊松比在一定范围内的材料力学行为。此外，采用TBPD模型计算，在ν∈[0, 1/3]时，位移u_x的误差全部小于5.0%，且随着泊松比的减小，误差逐渐减小；而采用BPD模型计算，在ν∈[0, 0.20]时，位移u_x的误差全部大于5.0%，且泊松比越小，相对误差越大。

算例2  边长为1.0 m的正方形薄板，板厚0.01 m，弹性模量200 GPa，泊松比ν=0.10，密度7 850 kg/m³，沿薄板四周施加_x=0.25y，_y=0.25x的剪切位移边界条件。采用TBPD模型计算，物质点间距Δ=0.01 m，邻域半径δ=3Δ，剪切位移边界条件是施加在薄板外围宽度为δ的3层虚拟物质点上^[14]，如图 5所示。

如图 6所示，采用TBPD模型计算的位移结果与解析解高度吻合，位移u_x和u_y的最大相对误差都为0.202%。

算例3   边长为50 mm的正方形薄板，中心有一长度2a=10 mm的水平裂纹，弹性模量192 GPa，密度8 000 kg/m³，泊松比ν=1/3，临界断裂能83 kJ/m²，在薄板上、下边界作用大小20 m/s的均匀法向速度荷载。分别采用BPD和TBPD模型进行计算，物质点间距Δ=0.25 mm，邻域半径δ=3.015Δ，计算时步取1.3367E-8 s，上、下两边的速度边界条件是施加在薄板上下边以外宽度为δ的3层虚拟物质点上^[14]。

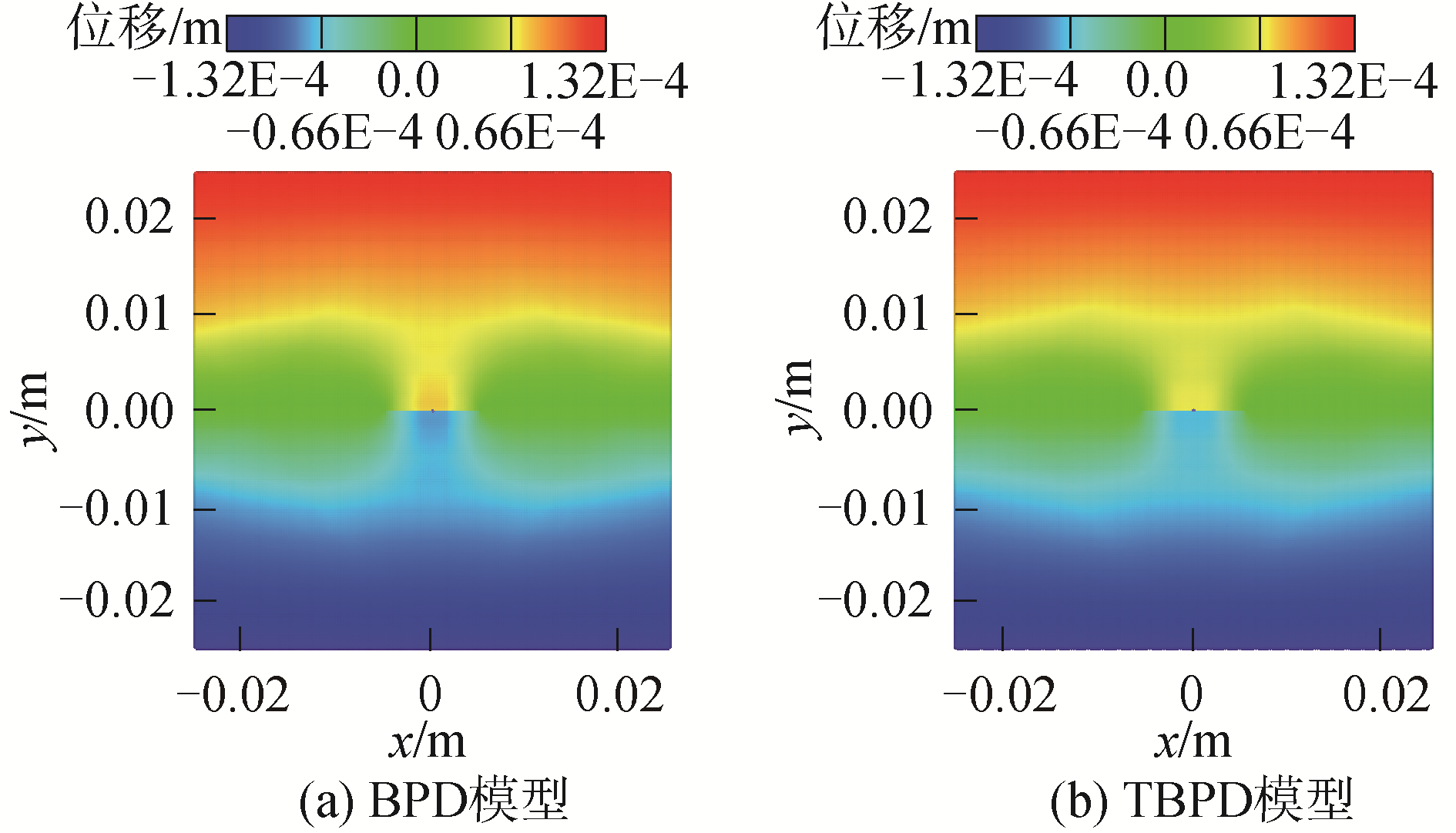
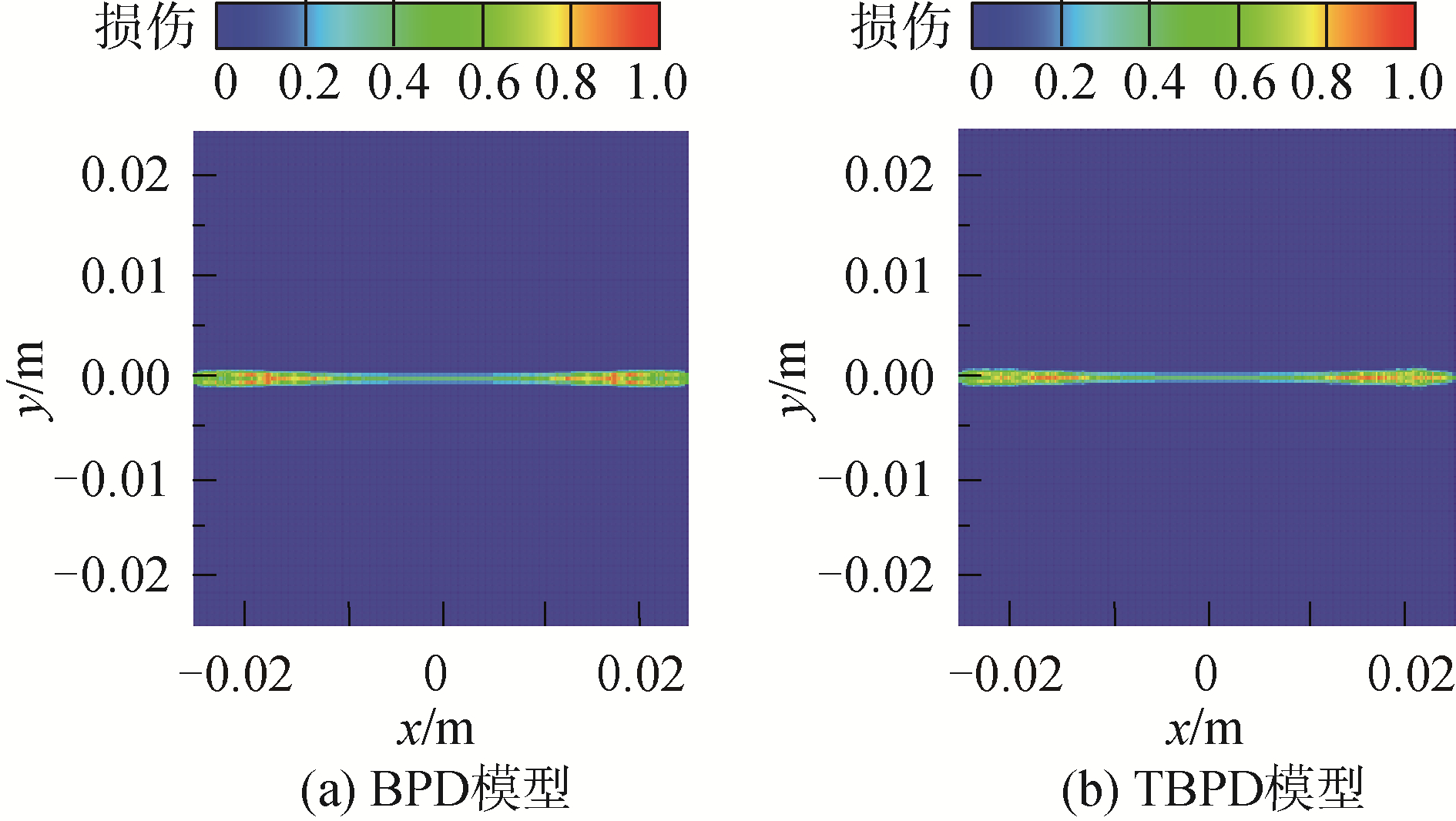
采用BPD和TBPD模型计算时，薄板都是在裂纹左右两端同时启裂，然后各自向左右两侧沿水平方向扩展，最终贯通薄板。薄板在启裂和贯通时刻稍有差异，但薄板破坏耗时基本相同，相关数据列于表 4中。如图 7所示，取t=6.68 μs时刻的位移进行对比，两模型计算的位移u_y差异甚微。如图 8所示，取t=24.09 μs时刻的薄板破坏形态进行对比，两模型计算的结果几乎相同。

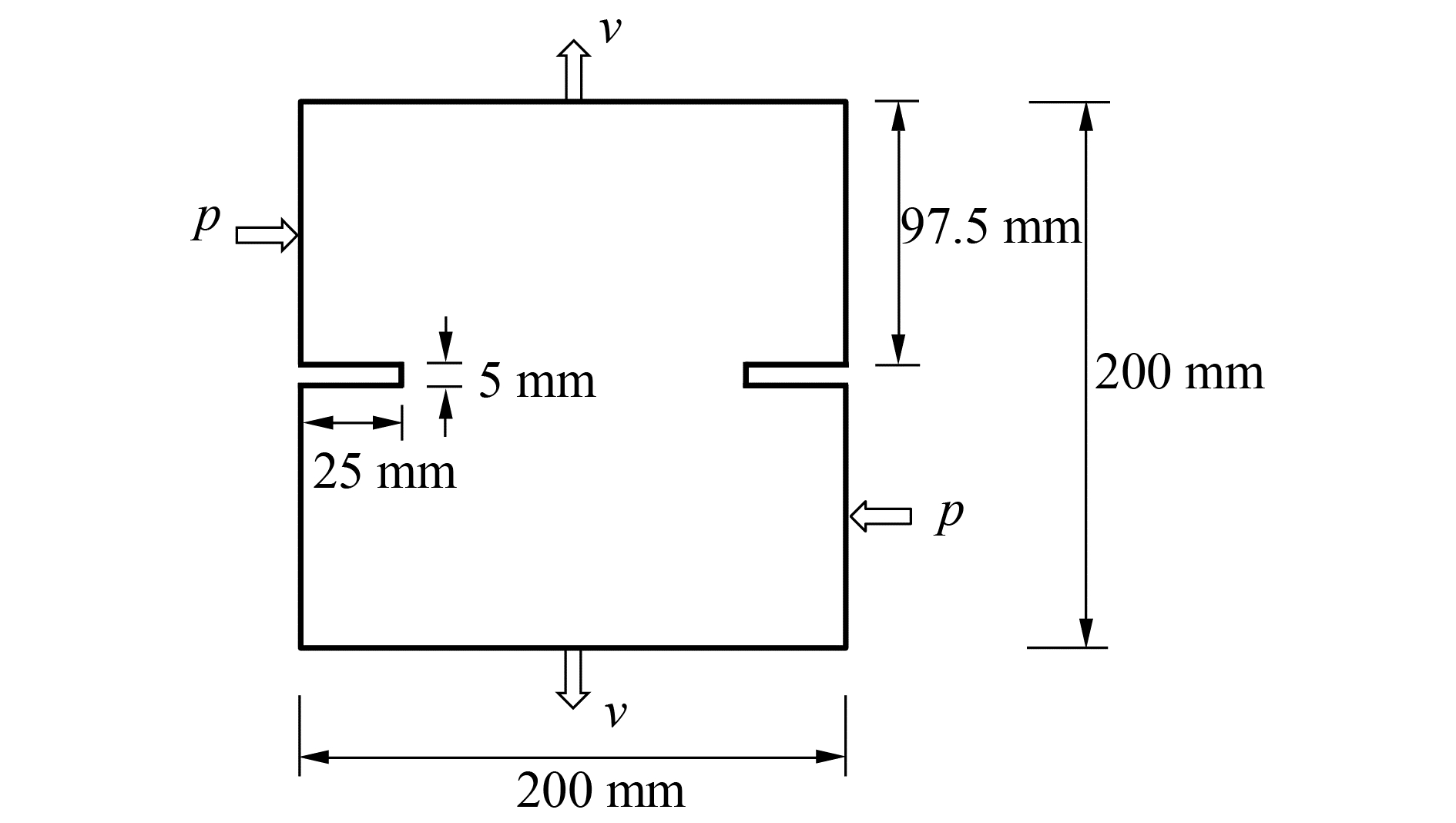
算例4  边长200 mm的正方形薄板，其弹性模量为30 GPa，密度2 265 kg/m³，Ⅰ型能量释放率G_Ιc=110 J/m2，Ⅱ型能量释放率G_IIc=10G_Ic，泊松比0.2。在试件中部的左右两侧各有一条长25 mm，宽5 mm的预制裂纹^[16]，如图 9所示。首先在薄板左侧上半部分和右侧下部分都水平施加合力为5 kN的均布力p，然后在薄板上下边界施加v=10 mm/s的速度荷载。采用TBPD模型计算，物质点间距Δ=4 mm，邻域半径δ=3.015Δ，计算步长1.0×10^-7 s，左右两侧的均布力p通过转变成体力荷载p/Δ后，施加在薄板该部位的最外一层，宽度为Δ的真实物质点上，速度荷载v作用在薄板以外宽度为δ的3层虚拟物质点上。

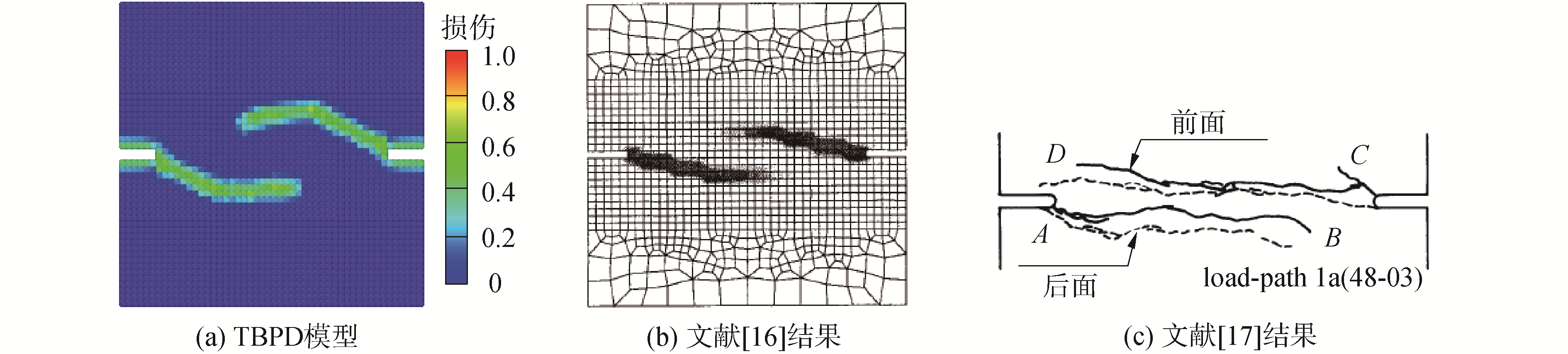
图 10(a)给出了采用TBPD模型计算得到的薄板的最终破坏形态，它与OŽBOLT等采用基于微平面模型的有限元代码模拟的结果^[16]和试验结果^[17]基本相同，如图 10(b)、(c)所示。

上述算例分别从薄板连续变形的定量计算和薄板破坏形态模拟2个方面都验证了TBPD模型的合理性和有效性。

3 平行双裂纹薄板的受拉破坏

如图 11所示，一边长为50 mm的正方形薄板，中部预制有长2a=10 mm的2条水平裂纹，记为主裂纹①和主裂纹②，两裂纹纵向间距为d。薄板的弹性模量为203 GPa，泊松比0.3，密度为7 850 kg/m³，在薄板上、下边界作用大小20 m/s的均匀法向速度荷载。所用参数与赵金海等^[18]相同，采用TBPD模型进行计算，物质点间距Δ=0.5 mm，邻域半径δ=3.015Δ，计算步长取1.336 7×10^-8 s。按以下2种情形分别计算和讨论：

1) 平行双裂纹间距d取3 mm、5mm和7 mm时，对薄板破坏形态的影响；2)平行双裂纹间距d=3 mm时，考虑3种随机分布的细小裂纹对薄板破坏形态的影响。

3.1 裂纹间距的影响

d取3 mm、5mm和7 mm时，裂纹扩展路径如图 12(b)、(c)、(d)所示。薄板破坏过程都是在裂纹左右两端同时启裂，水平延伸一定距离后，裂纹①斜向上方、裂纹②斜向下方继续扩展，两裂纹纵向间距越来越大，直至贯通薄板。裂纹间距对薄板破坏模式影响不大，但对于裂纹水平延伸距离、扩展角度、裂纹贯通后纵向间距、起裂和贯通时间都有一定影响，如表 5所示。随着裂纹间距的增大，裂纹起裂时刻提前，水平延伸长度逐渐减小，但裂纹偏移角度、贯通间距和贯通时刻却随之增大。

值得注意的是，图 12(b)破坏模式与赵金海等基于传统BPD模型所得结果^[18]有很大差异，文献[18]给出的破坏模式如图 13所示，其双裂纹水平延伸一定距离后，都斜向薄板水平中心交汇成一条裂纹，然后水平延伸，直至贯通薄板。鉴于传统BPD模型只能模拟ν=1/3的材料的力学行为^[3]，所以将它用于模拟其他泊松比材料时，裂纹扩展路径将可能出现失真或失效的情形。

3.2 3种随机细小裂纹的影响

在平行双裂纹薄板内，裂纹间距d=3 mm时考虑3种随机细小裂纹的分布，细小裂纹长度取0~2 mm，细小裂纹布置方式和破坏形态见图 14。

如图 14(a)~(d)所示，当细小裂纹主要分布在某一主裂纹附近时，该主裂纹将沿着垂直于加载方向扩展直至贯通，而另一主裂纹几乎没有扩展。如图 14(e)、(f)所示，当细小裂纹分布在主裂纹的某一端附近，则主裂纹沿着分布有细小裂纹的这一端在荷载作用下扩展贯通，而该主裂纹的另一端只发生较小变化。对比图 12(b)可以看出，随机细小裂纹的分布在一定程度上会抑制某一主裂纹在单侧或两侧的扩展，导致薄板的破坏形态发生显著的改变。

4 结论

1) 在不计刚体转动和小变形条件下，以均匀应变工况，一次得到了模型的双参数与材料弹性参数的转换公式。且切向刚度系数的引入，使双参数键的性能较单参数键更加完备，解决问题的能力更强。BPD模型只能模拟特定泊松比材料的力学行为，否则材料的反算泊松比、位移结果存在较大误差，破坏模式也可能失真；TBPD模型突破了特定泊松比的限制，能够模拟泊松比在一定范围内的材料力学行为，退化后的模型参数与传统BPD的参数完全相同。

2) 以能量准则作为判断单键断裂的依据，详细给出了TBPD模型单键断裂条件，在特定泊松比情形下，它可退化为BPD模型的单键断裂条件。

3) 在一定条件下，平行双裂纹的纵向间距对薄板的破坏过程产生一定的影响，随着双裂纹纵向间距的增大，裂纹起裂时刻提前，水平延伸长度逐渐减小，但裂纹偏移角度、贯通间距和贯通时刻却随之增大。随机细小裂纹的分布在一定程度上会抑制某一主裂纹在单侧或两侧的扩展，导致薄板的破坏形态发生显著的改变。