小型无人机在军事和民用领域中日益受到重视,应用越来越广泛[1],但由于其自身尺寸的限制,只能在空中停留较短时间,限制了小型无人机的应用,如何提升小型无人机续航性能是当下的研究热点之一。动态滑翔技术是一种新兴的适用于小型无人机的增程控制技术,通过控制飞行策略即能有效利用风场能量减少小型无人机飞行能量消耗,是现在国际上的研究的前沿技术之一。
漂泊信天翁是动物界中动态滑翔应用的典型示例,Sachs G等[2-3]通过计算得出信天翁能够以81 W飞行功率,在13.2 d内不间断飞往西南太平洋,消耗相当于5.6~11.9 L汽油的能量,远超其自身能量储备。Rayleigh[4]分析了信天翁利用海面梯度风场从梯度风场中获取能量的方式,并提出了Rayleigh循环,奠定了动态滑翔的研究基础。
近年来,随着计算机数值仿真能力的不断提升,许多研究者试图通过计算机数值仿真及优化手段对动态滑翔进行研究。Zhao[5]利用NPSOL软件模拟了利用动态滑翔技术后飞机的最小燃油消耗,Gao等[6]利用能量最优原则进行了应用动态滑翔技术航路规划,寻找到了飞机能量消耗最小的飞行路径。Lawrance等[7-8]则分别设计开发了让自主飞行的小型无人机依照风场自主选择动态滑翔路径的方式。Deittert等[9]利用微分平滑方法对远程无动力动态滑翔飞行路径进行了研究。国内近年对于动态滑翔的研究也取得了一定的成果,朱炳杰等[10]利用高斯伪谱法对动态滑翔最优航迹中的能量变化进行了计算。刘多能等[11]利用Runge-Kutta积分方法针对迁移形态与环绕形态的不同类型的动态滑翔飞行轨迹进行了优化分析。单上求等[12]研究了动态滑翔飞行过程中的能量转化机理。
目前,关于动态滑翔的研究集中于飞行轨迹的优化,对于飞行器采用理想化模型,较少关注飞行器本身。本文改进了Runge-Kutta积分轨迹优化方法,减少了优化系统的设计变量与约束的个数,并对该方法进行了验证;从能量的角度分析了动态滑翔过程中的风场能量吸收和机械能损耗规律;采用改进后的动态滑翔优化方法,研究了飞行器重量、最大升力系数、展弦比及风场强度变化指数等对飞行器动态滑翔的影响规律。
1 动态滑翔飞行建模 1.1 风场建模侧向梯度风场广泛存在水面及地面上方数十米的大气中,处于小型无人机的主要应用范围内,是应用动态滑翔的前提。梯度风场常用的幂数模型表示为:
| $ {V_W} = {V_R}{\left( {\frac{h}{{{H_R}}}} \right)^p} $ | (1) |
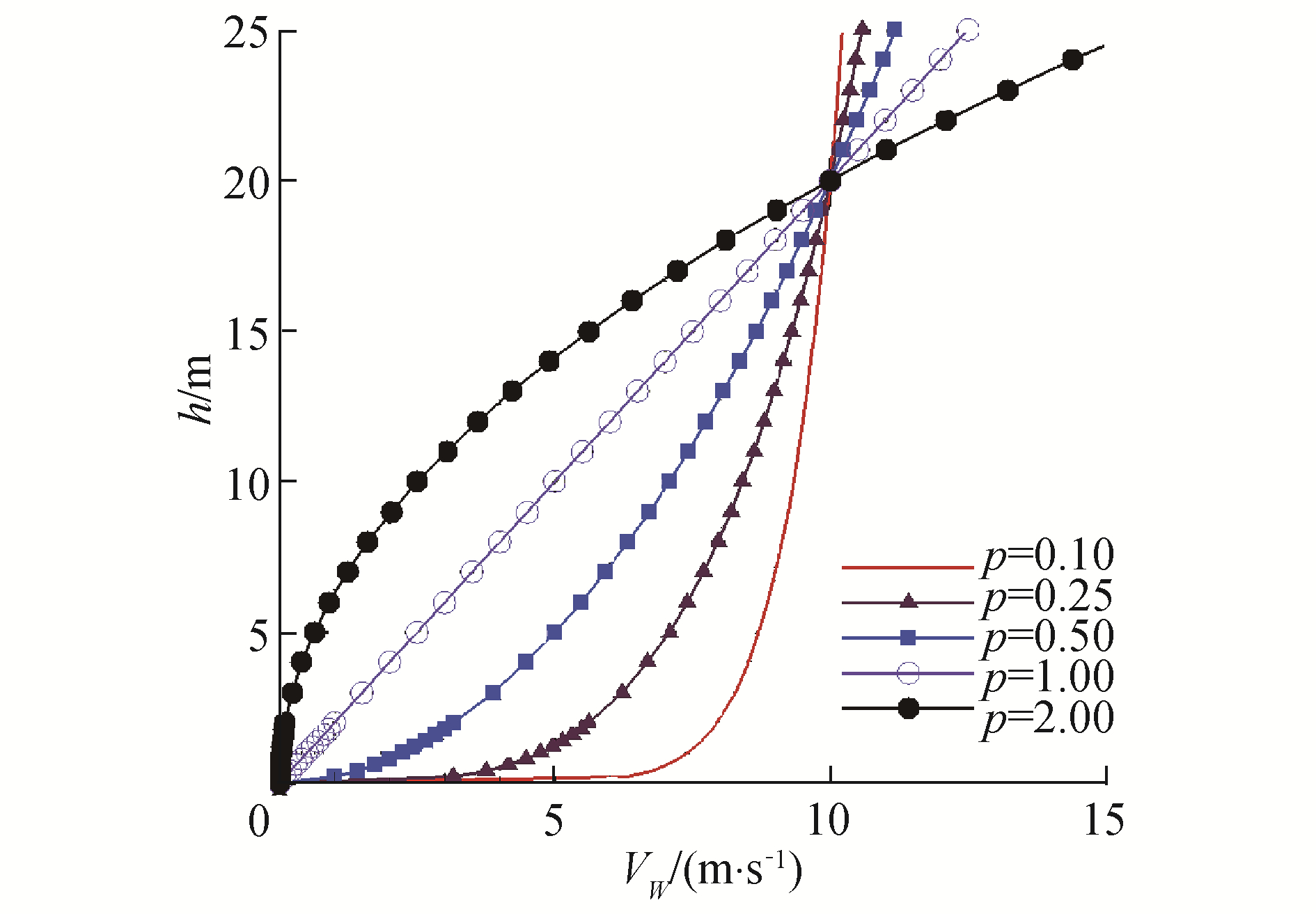
式中:VW指风场中随不同高度h变化对应的侧向风速;HR与VR则指风场代表高度与对应的代表风速。指数p被称为风场强度变化指数,表征梯度风场的变化强度。不同p值在HR=20 m, VR=10 m/s对风场的影响如图 1所示:
|
Download:
|
| 图 1 不同p值下的梯度风场模型 Fig. 1 Wind field model with different p | |
根据相关文献[9],并综合考虑本文小型无人机应用范围,最终选取p=0.25,HR=20 m。在飞行仿真过程中,假设风场风速方向沿地轴系+X轴方向,地轴系坐标原点在仿真初始飞行器重心对应海平面零高度水平投影处。
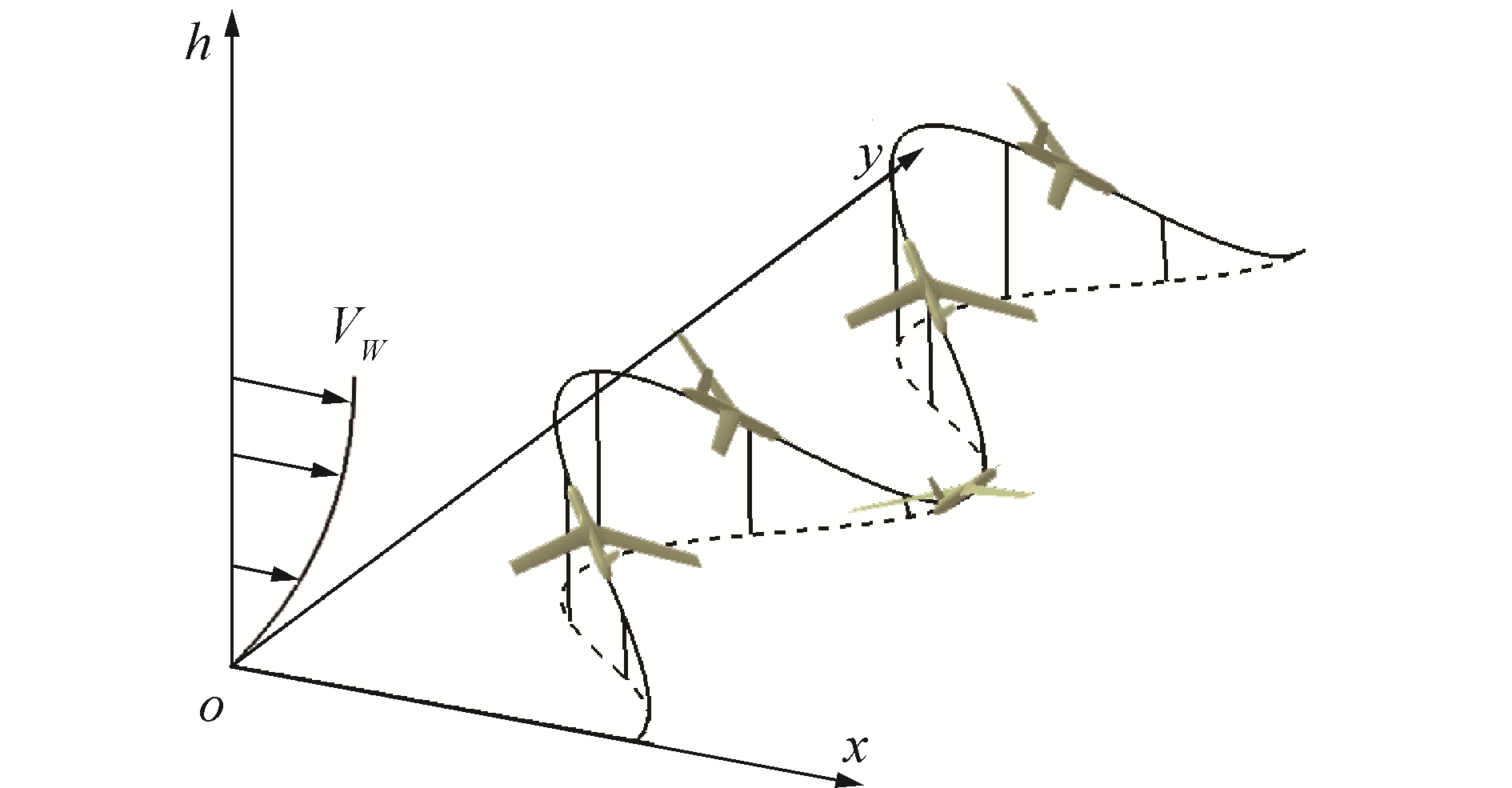
1.2 动态滑翔原理介绍动态滑翔飞行策略如图 2所示。
|
Download:
|
| 图 2 动态滑翔示意 Fig. 2 Path of dynamic soaring | |
参考信天翁的飞行模式对小型无动力无人机进行分析,在侧向梯度风场中,无动力飞行器的侧向速度受风场影响的表达式为:
| $ m\dot V = - D - mg{\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma - m{\dot V_W}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi $ | (2) |
飞机机械能表示为:
| $ E = mgh + \frac{1}{2}m{V^2} $ | (3) |
式中:V为飞行器相对地面速度;ψ为飞行器航迹偏角;γ为航迹倾角;D为飞行器阻力;m和h分别为飞行器质量与飞行高度。小型无人机单位质量能量相对时间的变化率表示为:
| $ \dot e = {\left( {\frac{E}{{mg}}} \right)^\prime } = \dot h + \frac{1}{g}V\dot V $ | (4) |
同时,引入辅助公式
| $ {\dot h = V{\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma } $ | (5) |
| $ {{{\dot V}_W} = \frac{{{\rm{d}}{V_W}}}{{{\rm{d}}h}}\dot h} $ | (6) |
将式(2)、(5)和(6)代入式(4)进行整理可以得到
| $ \dot e = - \frac{{{\rm{d}}{V_W}}}{{{\rm{d}}h}}\frac{1}{g}{V^2}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi - \frac{{DV}}{{mg}} $ | (7) |
具体推导可参考文献[13]。式(7)反映了飞行器飞行过程中的能量变化率,其中第2项是飞行过程中由于气动阻力等影响带来的能量损耗,第1项则是梯度风场对能量的影响。合理调整航迹倾角γ与航迹偏角ψ使得sin γsin ψ < 0,从而使得第1项为正,即飞行器从风场中获取能量。因此,通过合理的飞行控制及航迹规划,能够使得飞行器在不损失机械能的条件下完成飞行,进而提升航程或航时。
1.3 飞行动力学建模飞行动力学模型采用三自由度模型,其主要的轴系及角的定义如图 3所示。

|
Download:
|
| 图 3 动力学模型角度及坐标定义 Fig. 3 Forces acting on UAV and angles | |
该模型中飞行器动力学及运动学模型表达为:
| $ \left\{ {\begin{array}{*{20}{l}} {m\dot V = - D - mg{\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma - m{{\dot V}_W}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }\\ {mV{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma \dot \psi = L{\rm{sin}}{\kern 1pt} {\kern 1pt} \mu - m{{\dot V}_W}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi }\\ {mV\dot \gamma = L{\rm{cos}}{\kern 1pt} {\kern 1pt} \mu + m{{\dot V}_W}{\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi - mg{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma }\\ {\dot h = V{\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma }\\ {\dot x = V{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi + {V_W}}\\ {\dot y = V{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi } \end{array}} \right. $ | (8) |
式中:μ为滚转角;L、D分别为升力与阻力;(x, y, h)为飞行器在地轴系下的坐标。升力与阻力计算采用简化模型如下:
| $ \left\{ {\begin{array}{*{20}{l}} {L = \rho {S_w}{C_L}{V^2}/2}\\ {D = \rho {S_w}{C_D}{V^2}/2}\\ {{C_D} = {C_{D0}} + {K_D}C_L^2} \end{array}} \right. $ | (9) |
式中:CL和CD分别是升力与阻力系数;CD0为零升阻力系数; KD为诱导阻力因子。
动态滑翔数值仿真研究中常用的模型之一为信天翁等效模型[5],该模型主要参数如表 1所示。
| 表 1 飞行器模型基准参数 Table 1 Aircraft model reference parameters |
无动力动态滑翔飞行动力学模型表示为:
| $ \mathit{\boldsymbol{\dot x}}(t) = f(\mathit{\boldsymbol{x}}(t),\mathit{\boldsymbol{u}}(t)) $ | (10) |
式中:x=[V, ψ, γ, h, x, y]为系统的状态向量;u=[μ, CL]为输入控制向量。
动态滑翔航迹优化问题的目的就是找到合适的输入控制向量u,使得目标函数J在满足约束条件的前提下取得最优。在求解航迹优化问题时,将飞行航迹近似为M个离散点拟合而成的曲线,每个离散点都拥有各自对应的状态向量x与控制向量u,因此轨迹状态及控制未知量共有(6+2)×M个。飞行总时长tf和风场特征风速VR也是飞行轨迹优化中的重要参数。因此轨迹的总的设计变量向量可表示为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{X}}_0} = ({x_{1,1}}, \cdots ,{x_{6,1}}, \cdots ,{x_{1,M}}, \cdots ,{x_{6,M}},}\\ {{u_{1,1}},{u_{2,1}}, \cdots ,{u_{1,M}},{u_{2,M}},{t_f},{V_R}) = }\\ {(\mathit{\boldsymbol{x}}_1^{\rm{T}},\mathit{\boldsymbol{x}}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{x}}_M^{\rm{T}},\mathit{\boldsymbol{u}}_1^{\rm{T}},\mathit{\boldsymbol{u}}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{u}}_M^{\rm{T}},{t_f},{V_R})} \end{array} $ | (11) |
离散后的系统可采用Runge-Kutta积分方法[11]进行递推求解,其基本表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta t = {t_f}/(M - 1)}\\ {{{\hat u}_j} = ({u_j} + {u_{j + 1}})/2}\\ {k_{i,j}^1 = {f_i}({x_j},{{\hat u}_j})}\\ {k_{i,j}^2 = {f_i}({x_j} + k_{i,j}^1\Delta t/2,{{\hat u}_j})}\\ {k_{i,j}^3 = {f_i}({x_j} + k_{i,j}^2\Delta t/2,{{\hat u}_j})}\\ {k_{i,j}^4 = {f_i}({x_j} + k_{i,j}^3\Delta t,{{\hat u}_j})} \end{array}} \right. $ | (12) |
由式(12)可知,总设计变量共有8M+2个。当M=100时,共有802个设计变量,数量较多,同时还需满足6(M-1)个等式约束:
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{i + 6(j - 1)}} = {x_{i,j + 1}} - {x_{i,j}} - }\\ {(k_{i,j}^1 + 2k_{i,j}^2 + 2k_{i,j}^3 + k_{i,j}^4)\Delta t/6} \end{array} $ | (13) |
该系统设计变量与约束较多,求解复杂,需要对该求解方法进行简化。由于该系统必须满足飞行动力学模型的递推关系,飞行轨迹可以由初始点的状态向量和各点的控制向量完全决定,因此,将前后点间的等式约束直接转化为对后点的递推求解:
| $ {x_{i,m + 1}} = {x_{i,m}} + (k_{i,m}^1 + 2k_{i,m}^2 + 2k_{i,m}^3 + k_{i,m}^4)\Delta t/6 $ | (14) |
同时,设计变量减少到2M+8个,设计变量向量为:
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}} = ({x_{1,1}}, \cdots ,{x_{6,1}},{u_{1,1}},{u_{2,1}}, \cdots ,{u_{1,M}},{u_{2,M}},{t_f},{V_R}) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\mathit{\boldsymbol{x}}_1^{\rm{T}},\mathit{\boldsymbol{u}}_1^{\rm{T}},\mathit{\boldsymbol{u}}_2^{\rm{T}}, \cdots ,\mathit{\boldsymbol{u}}_M^{\rm{T}},{t_f},{V_R})} \end{array} $ | (15) |
这样便有效减少了设计变量6M-6个及约束M-1个,提高了轨迹优化的效率。
飞行器在完成一个理想的动态滑翔循环后应能返回初始飞行状态,以保证该循环的可重复性。根据这一条件,得到约束如下:
| $ \left\{ {\begin{array}{*{20}{l}} {V({t_f}) = V({t_0})}\\ {\lambda ({t_f}) = \lambda ({t_0})}\\ {h({t_f}) = h({t_0})} \end{array}} \right. $ | (16) |
同时为保证航向不致改变太多,对航迹倾角进行约束:
| $ |\psi ({t_f}) - \psi ({t_0})| \le \Delta {\psi _{{\rm{max}}}} $ | (17) |
本文如无特殊说明,Δψmax取值为57.3°。为保证飞行器飞行安全,在飞行过程中还应避免飞行器及其机翼不能触地或没入水中,转化为高度约束有:
| $ h - \frac{1}{2}b|{\rm{sin}}(\mu )| \ge {h_{{\rm{min}}}} $ | (18) |
Sachs[5]的研究中则只采用了h≥0.5 m的最小高度约束,进行方法验证时采用和Sachs相同的高度约束条件,后续研究中则采用式(18)作为高度约束条件。
为保证动态滑翔周期性的实现,飞行器损失的机械能需要通过梯度风场得到补充,外界必需的风场强度越弱说明飞行器动态滑翔能力越强,因此,能够完成完整的动态滑翔周期的最小梯度风场代表风速就成为了一个评价动态滑翔能力的重要指标,同时也适合作为优化目标:
| $ {\rm{min}}{\kern 1pt} {\kern 1pt} J(X) = {V_R} $ | (19) |
该优化问题使用伪谱法和非线性规划求解器SNOPT优化求解,应用软件为Matlab R2013a。
2.2 动态滑翔轨迹优化仿真验证本文参考Sachs的研究[5]对上述优化模型进行验证。表 2给出了优化初始参数设置。
| 表 2 初始参数设置 Table 2 Initial parameter setting |
表 3给出了该飞行轨迹的部分参数,并和Sachs的研究进行了对比。图 4为航迹对比图。图 5则给出了整个飞行过程中从外界风场中获取的能量及飞行能量损耗的变化趋势,图 6给出了飞行速度、升力控制量及滚转角控制量的优化结果。
| 表 3 动态滑翔优化结果 Table 3 Optimization results of dynamic soaring |
|
Download:
|
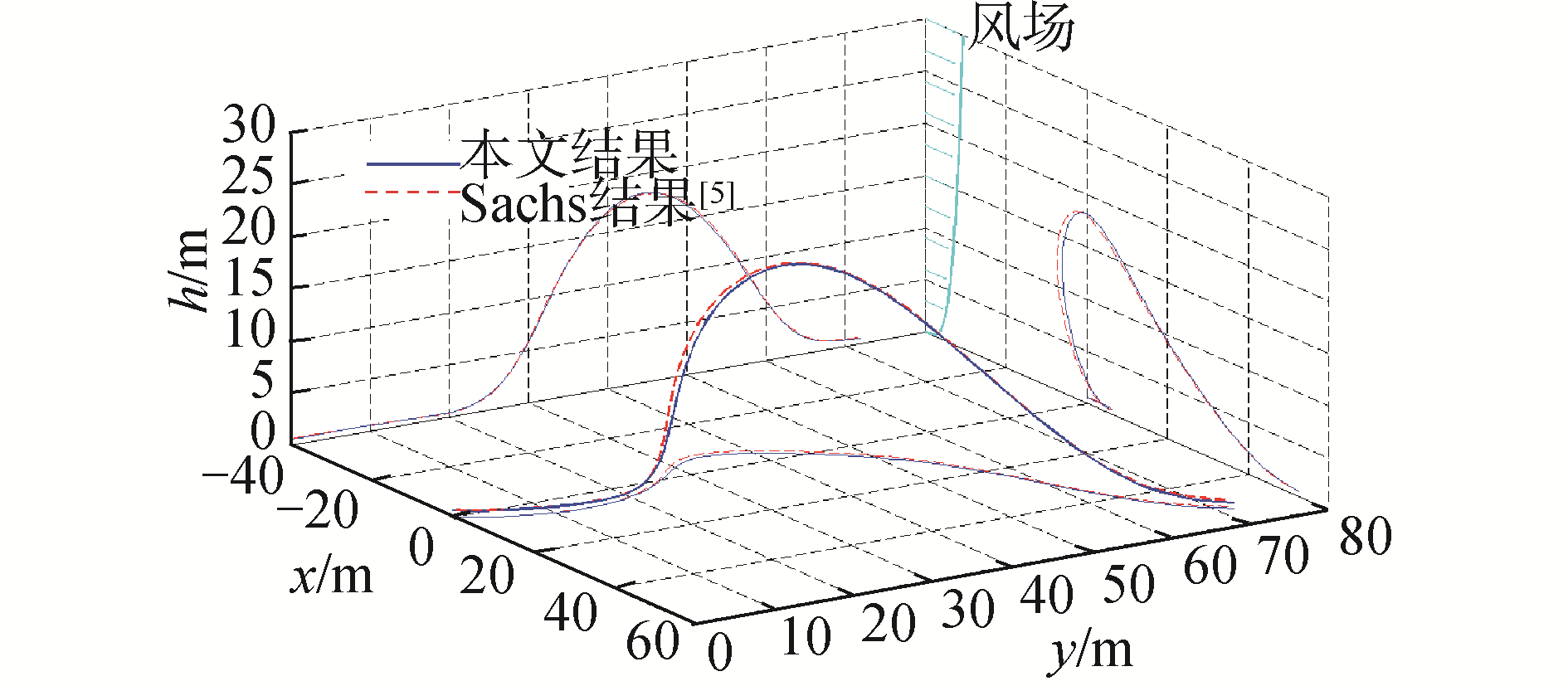
| 图 4 动态滑翔最小代表速度对应航迹 Fig. 4 Optimal dynamic soaring cycle requiring minimum wind strength | |

|
Download:
|
| 图 5 本文飞行器能量变化曲线 Fig. 5 Energy change of optimal dynamic soaring cycle | |

|
Download:
|
| 图 6 动态滑翔对应控制及状态变量 Fig. 6 Variables of optimal dynamic soaring cycle | |
图 4和图 6中实线与点划线的对比,两者基本吻合,说明优化仿真的结果趋势和Sachs文献中的结果吻合的较好,说明改进型Runge-Kutta积分优化模型能够有效完成动态滑翔轨迹优化,可以用于进一步的动态滑翔参数分析研究。
图 5中实线和点划线分别为为飞行器从风场中获取和飞行中消耗的的能量变化量,对应式(7)中的第1项与第2项随时间的积分量,2者的表达式:
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta {E_{{\rm{ gain }}}} = - mg\int_0^t {\frac{{{\rm{d}}{V_W}}}{{{\rm{d}}h}}} \frac{1}{g}{V^2}{\rm{sin}}{\kern 1pt} {\kern 1pt} \gamma {\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \psi {\rm{d}}t}\\ {\Delta {E_{{\rm{ lose }}}} = mg\int_0^t {\frac{{DV}}{{mg}}} {\rm{d}}t = \int_0^t D V{\rm{d}}t} \end{array}} \right. $ | (20) |
图 5中2条线之间的差量(阴影部分)即是飞行器机械能的变化量,最终2条线在终点处相交表明最终飞行器的总机械能保持和初始值相同。对比图 4和图 6,在最初受高度约束顺风飞行的阶段(t < 1 s)飞行器从风场中获取能量有限,接近于零;t>1 s后,飞行器开始逆风爬升,并在t=4 s左右进入高空转弯,随后进入顺风下降阶段至飞行周期结束,飞行器应用动态滑翔原理,在逆风爬升和顺风下降阶段均从风场内获取了足够的能量以抵消无动力飞行器在飞行过程中消耗的能量,这说明动态滑翔技术能够从风场中获取能量,有效提升飞行器滞空能力。
3 飞行器总体参数对动态滑翔能力的影响为了探究具有更适合动态滑翔飞行的飞行器形式,针对飞行器重量、最大升力系数、展弦比及风场强度变化指数等因素对飞行器动态滑翔性能的影响开展研究。为保证研究顺利进行,采用假设由于控制变量的方法通过调整翼型等变量,使本文中某一总体参数变化时其余参与讨论的总体参数及表 1中出现的量仍保持相同,以方便后续讨论。飞行器模型基准参数采用表 1中的数据,初值和表 2相同。
3.1 飞行器重量飞行器重量决定了飞行器执行任务的能力,研究重量与动态滑翔能力之间的关系对动态滑翔在实际中的应用有着重要的意义。
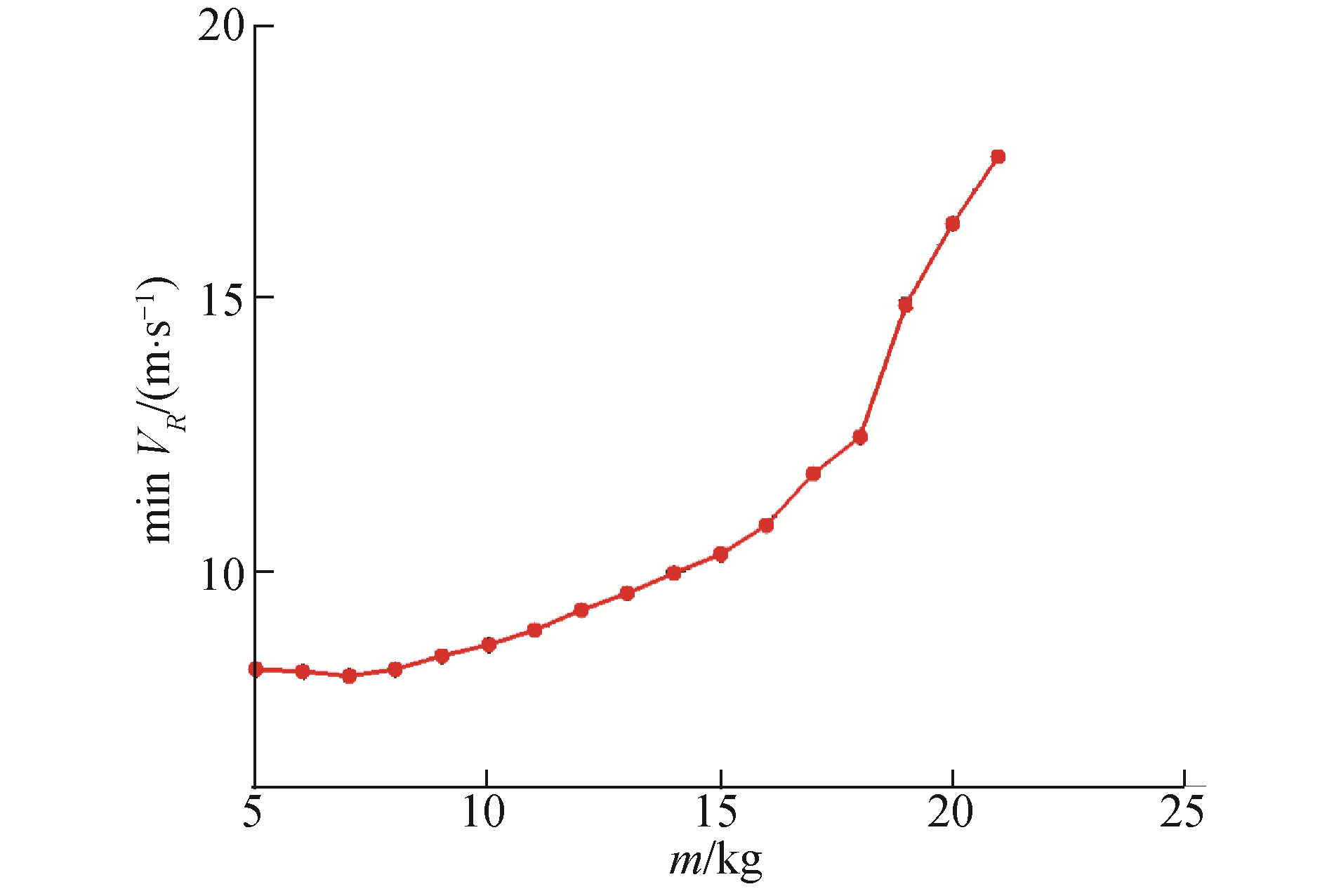
图 7为模型其他参数完全相同的条件下,不同重量飞行器所需的最小风场代表速度VR越小说明飞行器动态滑翔能力相对越强。从图中可以看出,在重量处于较小值的条件下,动态滑翔能力基本不受影响;随着重量的增大,动态滑翔所需的风场代表速度逐渐增大,且增大速度大于线性增长。在模型CLmax=1.5的约束下,常规巡航能够支持的最大重量为17.8 kg,而在图中当重量超过这一最大重量时,所需的风场强度急剧增长。在飞行器升力不足以维持巡航飞行的条件下,飞行器须要需要通过动态滑翔机动维持飞行高度,对外界能量获取有更大需求,造成了所需的风场代表速度急剧增大的现象。
|
Download:
|
| 图 7 飞行器重量对动态滑翔能力的影响 Fig. 7 Influence of UAV mass on dynamic soaring results | |
更进一步探讨翼载对行器动态滑翔性能的影响。翼载是单位机翼面积上的飞行器重量,在动态滑翔飞行动力学模型中主要体现为飞行器质量与机翼面积2个常量的比值,因此本文从飞行器重量变化与机翼面积变化2方面对比分析翼载对动态滑翔能力的影响。
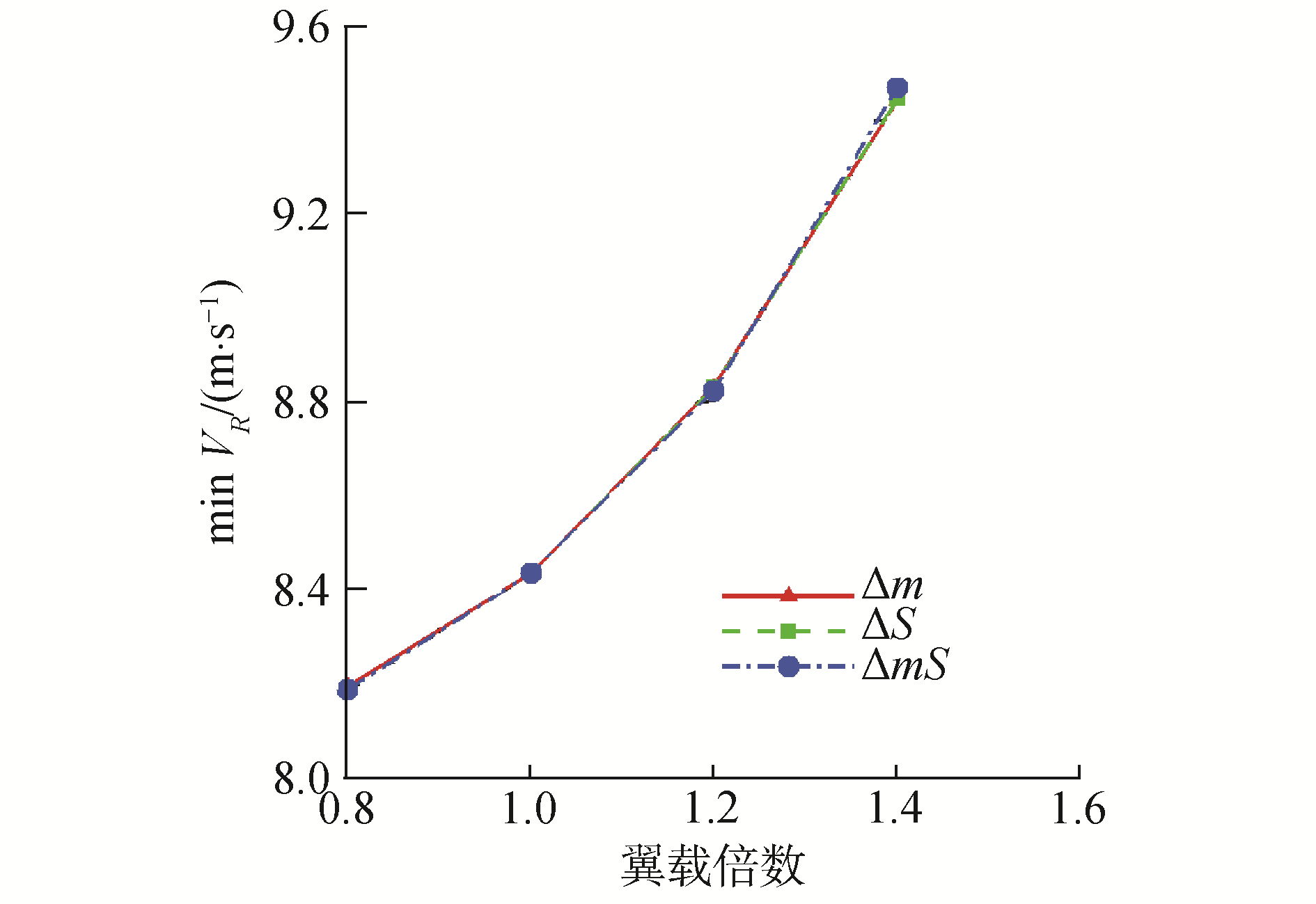
表 4中反映了通过改变飞行器重量(m0.8,m1.2,m1.4构型)、飞行器机翼面积(假设气动参数不改变,S0.8,S1.2,S1.4构型)及同时改变重量和机翼面积(mS0.8,mS1.2,mS1.4构型)等方式改变翼载进而对动态滑翔能力产生的影响,并在图 8中对3种不同方式(分别对应Δm、ΔS、ΔmS,横坐标为翼载的倍数N)进行了对比。
| 表 4 翼载对动态滑翔能力的影响 Table 4 Influence of wing load on dynamic soaring ability |
|
Download:
|
| 图 8 翼载对动态滑翔能力的影响 Fig. 8 Influence of wing load on dynamic soaring results | |
通过对比可以发现,大翼载需要更大的最小代表风速,即较小的翼载动态滑翔能力较强;相同翼载条件下飞行器具有相同的动态滑翔能力。翼载较小的飞行器机动性能较好,而机动性能较强的飞行器在逆风爬升、顺风俯冲及侧风机动中更有优势,因此小翼载飞行器动态滑翔能力更强。对于重量较大的飞行器,可以通过增大机翼面积的方式减小翼载,从而使得其动态滑翔能力获得一定提升。
3.2 最大升力系数最大升力系数CLmax关系到飞行器能够提供的最大升力,是和飞行性能密切相关的总体参数。在动态滑翔飞行动力学模型中,最大升力系数是关键控制变量CL的主要约束,对动态滑翔过程影响较大。通过调整控制变量中最大升力系数的限制,分析其对动态滑翔能力的影响。
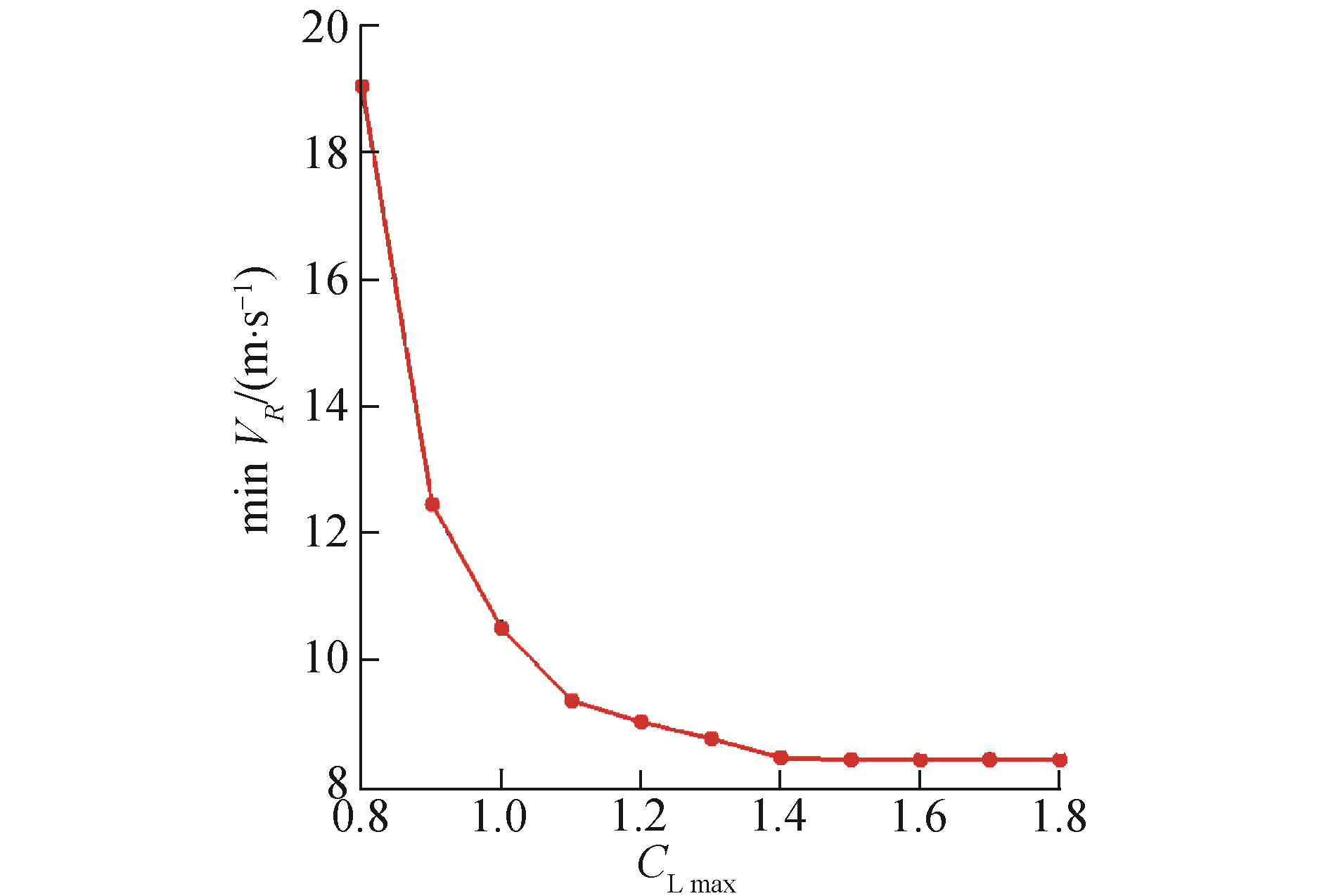
图 9表现了最大升力系数对动态滑翔所需最小代表风速的影响。可以看到,当最大升力系数约束大于1.4时,最小代表风速未发生明显变化,随着最大升力系数逐渐下降,飞行器能够提供的最大升力也随之下降,所需风场代表速度急剧增长,该现象与飞行器重量超过最大升力时表现一致,是由于飞行器须要通过动态滑翔维持飞行,对动态滑翔能力提出了更大要求。可见,足够大的最大升力系数是维持飞行器动态滑翔能力的必要条件。
|
Download:
|
| 图 9 最大升力系数对动态滑翔能力的影响 Fig. 9 Influence of CLmax on dynamic soaring results | |
展弦比在动态滑翔飞行动力学模型中的主要影响可以归结为2个:
1) 影响阻力系数中诱导阻力因子KD的大小:
| $ {K_D} = \frac{1}{{\pi {\rm{AR}}}} $ | (21) |
诱导阻力因子与展弦比大小呈反比。为保证控制变量,假设展弦比的变化对其他气动变量无明显影响。
2) 为保证飞行器与地面高度的约束不变,飞行器翼展固定的条件下,机翼面积随展弦比变化。按照公式,有:
| $ {S_w} = \frac{{{b^2}}}{{{\rm{AR}}}} $ | (22) |
通过对飞行动力学模型中相关量的调整,对展弦比对动态滑翔能力的影响进行研究。
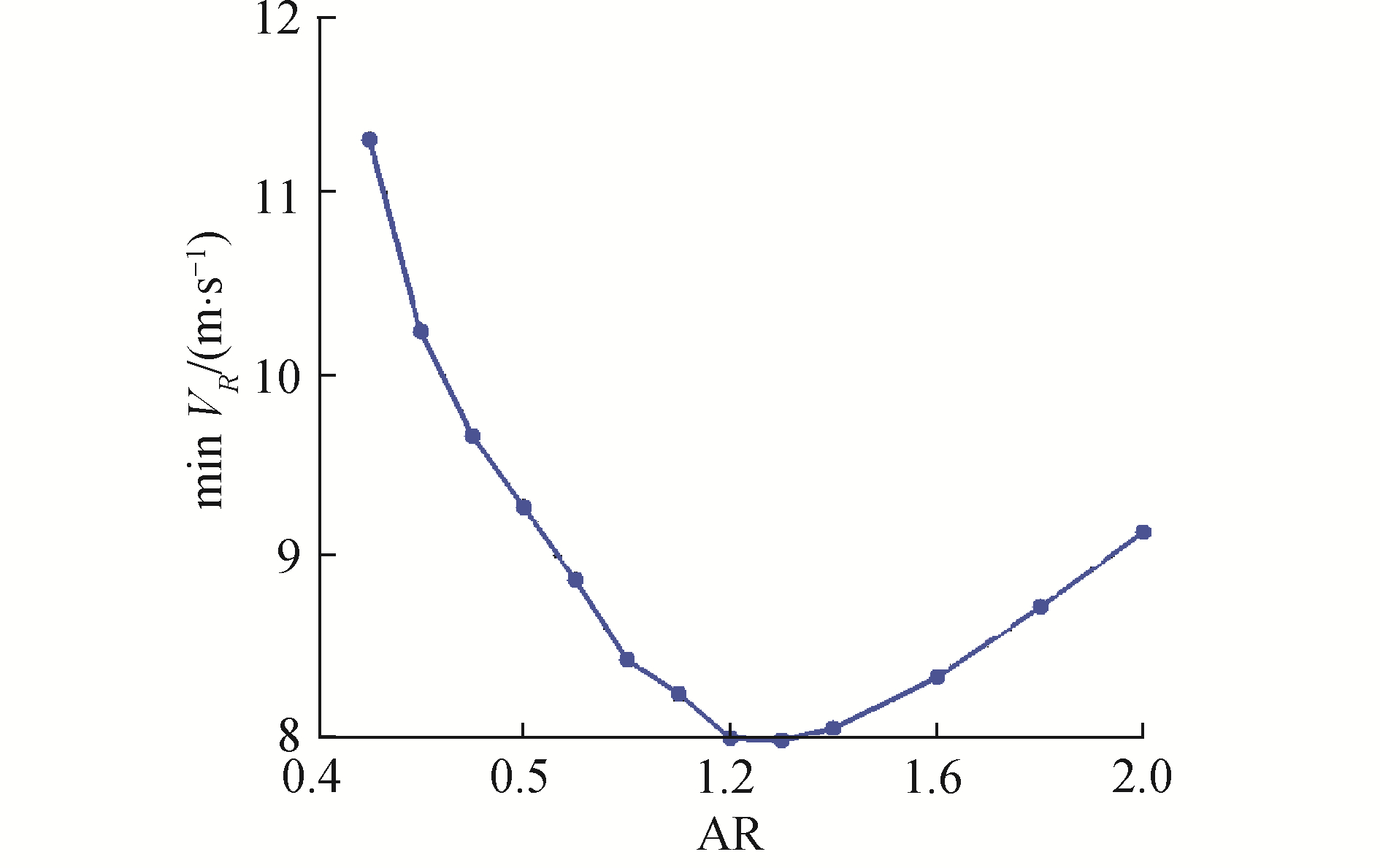
图 10中横坐标为相对于原始模型展弦比变化的倍数,纵坐标为动态滑翔最小代表风场速度。随着展弦比的增大,诱导阻力因子和机翼面积均会减小,阻力特性得到优化的同时全机翼载出现上升,因此会出现动态滑翔最小代表风场速度先下降在升高的趋势,即动态滑翔能力先提高后降低。所以展弦比变化中能够找到最适点,如图 10中1.2倍AR值处,在此展弦比下飞行器动态滑翔能力最强。
|
Download:
|
| 图 10 展弦比对动态滑翔能力的影响 Fig. 10 Influence of aspect ratio on dynamic soaring results | |
除去飞行器自身总体参数,风场的形态对动态滑翔能力也有影响,风场强度变化指数p表征了不同地域环境条件下地表梯度风场的差异,主要由地面环境决定,其对动态滑翔能力的影响也应被纳入研究之中。研究中的无人机总体参数和表 1一致。
从图 11中可以看到,较大的风场强度变化指数p会使需求的最小风场代表速度降低,这主要是由于p的增大使得3~20 m的dVW/dh增大,有利于飞行器从风场中获取能量,进而得到更强的动态滑翔能力。

|
Download:
|
| 图 11 风场强度变化指数对动态滑翔能力的影响 Fig. 11 Influence of wind power law exponent on dynamic soaring results | |
1) 基于信天翁三自由度动力学模型,改进了Runge-Kutta积分方法构建了动态滑翔航迹优化方法模型,并结合轨迹的递推求解特点对该方法进行了进一步简化,有效减少了所需考虑的变量及约束个数。对该方法进行了验证,证明动态滑翔方法能够有效减少飞行器机械能损失,同时该优化模型能够为进一步研究飞行器的动态滑翔能力提供数据和方法的支持。
2) 利用改进型Runge-Kutta积分优化模型对飞行器部分总体参数对动态滑翔能力的影响进行了探究。通过对比不同总体参数下所需的最小风场代表速度来评估其对动态滑翔能力的影响。拥有较小重量、小翼载、足够大的最大升力系数、合适的展弦比的飞行器具有更好的机动能力,而机动性能较强的飞行器在逆风爬升、顺风俯冲及侧风机动中更有优势。这样的飞行器具有更好的动态滑翔能力。同时,风场强度变化指数更大的风场能够提供更大的侧风梯度,对动态滑翔相对更加有利。
由于整个飞行过程中的能量变化较为复杂,而瞬时的能量变化公式不能反映整体情况,因此利用能量变化公式对总体参数与动态滑翔能力之间关系进行定性定量分析暂时较为困难,但可以作为今后的研究方向之一进行探索。
| [1] |
高永, 李冰, 李本威, 等. 电动小型无人机起飞总重估算方法研究[J]. 西北工业大学学报, 2017, 35(S1): 93-97. GAO Yong, LI Bing, LI Benwei, et al. A study of estimating take-off weight for electric-powered mini-UAV[J]. Journal of Northwestern Polytechnical University, 2017, 35(S1): 93-97. (  0) 0)
|
| [2] |
SACHS G, TRAUGOTT J, NESTEROVA A P, et al. Flying at no mechanical energy cost:disclosing the secret of wandering albatrosses[J]. PLoS one, 2012, 7(9): e41449. DOI:10.1371/journal.pone.0041449 (  0) 0)
|
| [3] |
SACHS G, BUSSOTTI P. Application of optimal control theory to dynamic soaring of Seabirds[M]//GIANNESSI F, MAUGERI A. Variational Analysis and Applications. Boston, MA: Springer, 2005: 975-994.
(  0) 0)
|
| [4] |
RAYLEIGH. The soaring of birds[J]. Nature, 1883, 27(701): 534-535. DOI:10.1038/027534a0 (  0) 0)
|
| [5] |
ZHAO Y J. Optimal patterns of glider dynamic soaring[J]. Optimal control applications and methods, 2004, 25(2): 67-89. DOI:10.1002/oca.739 (  0) 0)
|
| [6] |
GAO Chen, LIU H H T. Dynamic soaring surveillance in a gradient wind field[C]//Proceedings of AIAA Guidance, Navigation, and Control (GNC) Conference. Boston, MA, 2013.
(  0) 0)
|
| [7] |
LAWRANCE N R J, SUKKARIEH S. Autonomous exploration of a wind field with a gliding aircraft[J]. Journal of guidance, control, and dynamics, 2011, 34(3): 719-733. DOI:10.2514/1.52236 (  0) 0)
|
| [8] |
LANGELAAN J W, ALLEY N, NEIDHOEFER J. Wind field estimation for small unmanned aerial vehicles[J]. Journal of guidance, control, and dynamics, 2011, 34(4): 1016-1030. DOI:10.2514/1.52532 (  0) 0)
|
| [9] |
DEITTERT M, RICHARDS A, TOOMER C A, et al. Engineless unmanned aerial vehicle propulsion by dynamic soaring[J]. Journal of guidance, control, and dynamics, 2009, 32(5): 1446-1457. DOI:10.2514/1.43270 (  0) 0)
|
| [10] |
朱炳杰, 侯中喜. 无人机风梯度滑翔过程中能量变化[J]. 国防科技大学学报, 2015, 37(1): 78-83. ZHU Bingjie, HOU Zhongxi. Energy transformation in dynamic soaring of unmanned aerial vehicles[J]. Journal of National University of Defense Technology, 2015, 37(1): 78-83. (  0) 0)
|
| [11] |
LIU Duoneng, HOU Zhongxi, GUO Zheng, et al. Optimal patterns of dynamic soaring with a small unmanned aerial vehicle[J]. Proceedings of the institution of mechanical engineers, part G:journal of aerospace engineering, 2017, 231(9): 1593-1608. DOI:10.1177/0954410016656875 (  0) 0)
|
| [12] |
单上求, 侯中喜, 朱炳杰, 等. 动态滑翔动力学建模与风梯度能量获取[J]. 国防科技大学学报, 2015, 37(4): 45-49. SHAN Shangqiu, HOU Zhongxi, ZHU Bingjie, et al. Dynamics modeling of dynamic soaring and energy gaining from the wind gradient[J]. Journal of National University of Defense Technology, 2015, 37(4): 45-49. (  0) 0)
|
| [13] |
GAO Xianzhong, HOU Zhongxi, GUO Zheng, et al. Energy extraction from wind shear:reviews of dynamic soaring[J]. Proceedings of the institution of mechanical engineers, part G:journal of aerospace engineering, 2015, 229(12): 2336-2348. DOI:10.1177/0954410015572267 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


