2. 海军工程大学 电气工程学院, 湖北 武汉 430033;
3. 中国人民解放军 92941部队44分队, 辽宁 葫芦岛 125000
2. College of Electrical Engineering, Naval University of Engineering, Wuhan 430033, China;
3. Unit of 92941 of PLA, Huludao 125000, China
船舶静电场来源于船舶的腐蚀防腐电流,主要包括静态电场信号(static electric field,SE)和静态电位信号(underwater electric potential,UEP),船舶静电场具有明显的分布特征[1-2],包含着船舶的位置信息,且受环境的影响相对较小,可以用来对船舶进行跟踪定位,作为声学跟踪的一个有效补充。但是对UEP信号的测量需要参考电极,参考电极要求离测量电极有一定的距离,这为实际中的电位传感器布设增加了难度。SE信号的测量需要三轴电场传感器,对制作工艺要求较高,特别是三轴传感器的正交性及与姿态传感器的对准。利用电位差(difference of UEP,DUEP)DUEP对舰船进行跟踪,即采用多组电位传感器组,每一组传感器以其中一个电位传感器的UEP信号为基准,该组中其余电位传感器的UEP信号与其做差,将差值作为观测信号。DUEP信号直接将传感器组中的一个电极作为基准电极,相比UEP观测信号,省去了参考电极的负担;相比SE观测信号,DUEP信号对传感器要求相对简单,电场信号的定义为E=dU/dl,可见DUEP信号与SE信号是很接近的,但是利用DUEP作为观测信号,电位传感器阵列可以有更自由的组合方式。
另外,针对实际电场跟踪问题,有2个问题需要考虑:1)对于船舶电场跟踪的应用场合,水下武器系统而言,大部分系统平时是处于睡眠状态,当值更引信检测到目标时,才会引发各系统动作。电场跟踪系统也是一样,平时处于睡眠状态,当确认目标出现以后,跟踪系统开始工作,对目标进行跟踪。因此,船舶电场跟踪的第一步工作是对船舶目标的检测,文献[3]提出了一种基于功率谱的船舶静电场实时检测算法,本质上是通过设定的浮动阈值进行分段功率谱进行滑动检测,本文将引入此方法将其与跟踪检测算法相融合。2)所有船舶电场可利用的观测信号都面临一个先验信息缺失的问题,为此本文引入滤波器组的方法,以卡尔曼滤波为代表的滤波估值算法可以根据传感器量测信息对目标的相关参数进行实时的估计,在目标跟踪领域获得越来越广泛的研究和应用[4-11]。并以渐进扩展卡尔曼滤波(progressive extended kalman filter,PEKF)为基本滤波单元,以解决基于DUEP信号的船舶跟踪中先验信息缺失的问题。
1 船舶跟踪问题 1.1 状态空间模型船舶状态空间模型的形式为[12]:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k} = \mathit{\boldsymbol{a}}({\mathit{\boldsymbol{x}}_{k - 1}}) + {\mathit{\boldsymbol{w}}_{k - 1}}}\\ {{\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{h}}({\mathit{\boldsymbol{x}}_k}) + {\mathit{\boldsymbol{v}}_k}} \end{array}} \right. $ | (1) |
式中:xk∈Rn为k时刻的n维状态向量;yk∈Rm为k时刻m维观测向量;状态转移函数a:Rn→Rn;观测函数h:Rn→Rm;wk-1∈Rn为状态噪声向量,vk∈Rm为观测噪声向量,且wk-1~N(0, Qk-1),vk~N(0, Rk),Qk-1为过程噪声协方差矩阵,Rk为观测噪声协方差矩阵,{wk-1}和{vk}不相关。
1.1.1 观测方程在船舶静电场的各种建模方法中,点电流法建模精度高,更加贴近船舶实际[13]。
依据点电流法,船舶可以等效为N个点电流等间距构成的均匀线阵模型(简称点电流阵列)来描述。阵列中每个点电流的电流密度为Ipi,间隔为ld。海水中某场点Pf处的电位信号U可等效为N个点电流产生的电位叠加。
| $ U = \frac{1}{{4\pi \sigma }}\sum\limits_{i = 1}^N {{I_{{\rm{p}}i}}} K({I_{{\rm{p}}i}},{P_{\rm{f}}}) $ | (2) |
式中:K(Ipi, Pf)为点电流Ipi和场点Pf之间的距离函数,在空气—海水—海床3层均匀介质(如图 1所示)条件下为:

|
Download:
|
| 图 1 空气—海水—海床3层均匀介质坐标系 Fig. 1 Air-seawater-seabed three-layer uniform media coordinate system | |
| $ \begin{array}{l} K({I_{{\rm{p}}i}},P) = \frac{1}{{\sqrt {{r^2} + {{(z - {z_i})}^2}} }} + \frac{1}{{\sqrt {{r^2} + {{(z + {z_i} - 2h)}^2}} }} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{m = 1}^\infty {{k^m}} \left[ {\frac{1}{{\sqrt {{r^2} + {{(z + {z_i} - 2h + 2mH)}^2}} }} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{\sqrt {{r^2} + {{(z + {z_i} - 2h - 2mH)}^2}} }} + \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{\sqrt {{r^2} + {{(z - {z_i} + 2mH)}^2}} }} + \frac{1}{{\sqrt {{r^2} + {{(z - {z_i} - 2mH)}^2}} }}} \right] \end{array} $ | (3) |
式中:H为海水深度;h为传感器深度;k=(σ-σ1)/(σ+σ1)为海底反射系数;σ为海水电导率;σ1为海床电导率;m为反射层数,实际计算中其上限值可取10~20,r2=(x-xi)2+(y-yi)2。
对一个电位传感器组,以其中一个电位传感器为基准,其电位为U0,其余电位传感器的信号为Uj。则在第j(j=1, 2, …, J)个电位传感器量测到的目标信号可建模如下:
| $ {y^{(j)}} = {U_j} - {U_0} + v_k^{(j)} - v_k^{(0)} $ | (4) |
式中
| $ {\mathit{\boldsymbol{y}}_k} = \mathit{\boldsymbol{h}}({\mathit{\boldsymbol{x}}_k}) + {\mathit{\boldsymbol{v}}_k} = \left[ {\begin{array}{*{20}{c}} {{h^{(1)}}({\mathit{\boldsymbol{x}}_k})}\\ {{h^{(2)}}({\mathit{\boldsymbol{x}}_k})}\\ \vdots \\ {{h^{(J)}}({\mathit{\boldsymbol{x}}_k})} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {v_k^{(1)}}\\ {v_k^{(2)}}\\ \vdots \\ {v_k^{(J)}} \end{array}} \right] $ | (5) |
船舶目标的状态量xk包含目标位置、速度、点电流阵列:
| $ {\mathit{\boldsymbol{x}}_k} = {[{\mathit{\boldsymbol{r}}_k},{\mathit{\boldsymbol{V}}_k},{\mathit{\boldsymbol{I}}_p}]^{\rm{T}}} $ | (6) |
式中:rk=[x, y, z]T;Vk=[Vx, Vy]T(忽略z方向上运动);Ip=[Ip1, Ip2, …, IpN]T。
船舶目标具有低动态特性,其运动状态
| $ \mathit{\boldsymbol{x}}_k^{(r,V)} = {\mathit{\boldsymbol{\varPhi }}_m}\mathit{\boldsymbol{x}}_{k - 1}^{(r,V)} + {\mathit{\boldsymbol{\varGamma }}_m}\mathit{\boldsymbol{w}}_{k - 1}^{(r,V)} $ | (7) |
式中:Φm为运动状态转移矩阵;Γm为噪声增益矩阵。
| $ {\mathit{\boldsymbol{\varPhi }}_m} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{I}}_{3 \times 3}}}&\begin{array}{l} {T_s}{\mathit{\boldsymbol{I}}_{2 \times 2}}\\ {{\bf{0}}_{1 \times 2}} \end{array}\\ {{{\bf{0}}_{2 \times 3}}}&{{\mathit{\boldsymbol{I}}_{2 \times 2}}} \end{array}} \right];{\mathit{\boldsymbol{\varGamma }}_m} = \left[ {\begin{array}{*{20}{c}} {\frac{{T_s^2}}{2}{\mathit{\boldsymbol{I}}_{2 \times 2}}}\\ {{{\bf{0}}_{1 \times 2}}}\\ {{T_s}{\mathit{\boldsymbol{I}}_{2 \times 2}}} \end{array}} \right] $ |
DWNA模型假设加速度为高斯白噪声,即:
| $ \mathit{\boldsymbol{ \boldsymbol{\varSigma} }} = {\rm{E}}[{\mathit{\boldsymbol{w}}_k}\mathit{\boldsymbol{w}}_k^{\rm{T}}] = {\rm{diag}} (\sigma _x^2,\sigma _\gamma ^2) $ | (8) |
式中σx、σy分别为x、y方向上的加速度噪声强度。
点电流阵列强度量值为常量,加一个比较小的噪声即可。则全状态方程为:
| $ {\mathit{\boldsymbol{x}}_k} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{x}}_{k - 1}} + {\mathit{\boldsymbol{w}}_{k - 1}} $ | (9) |
式中:
船舶电场跟踪中,滤波估值方法对方位信息最为敏感,也是决定跟踪效果的关键因素。滤波器组的基本原理是在不知目标真实方位的情况下,假定目标从多个不同方位而来,同时起始多个滤波器,即设定多个滤波器组的初值:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat x}}_0^{(j)} = {{[{{(\mathit{\boldsymbol{\hat r}}_0^{(j)})}^{\rm{T}}},{{(\mathit{\boldsymbol{v}}_0^{(j)})}^{\rm{T}}},\mathit{\boldsymbol{I}}_p^{(j)}]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{\hat r}}_0^{(j)} = {{[{{\mathit{\boldsymbol{\hat r}}}_{xy,0}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _j},{{\mathit{\boldsymbol{\hat r}}}_{xy,0}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _j},z]}^{\rm{T}}}}\\ {\mathit{\boldsymbol{v}}_0^{(i)} = {{[ v{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _j},v{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\psi _j}]}^{\rm{T}}}} \end{array}} \right. $ | (10) |
式中ψj为假定的目标方位角。
假定多个初值后,利用最大似然选择法,选择出最接近真实目标轨迹的跟踪轨迹。
由上述分析可知:
| $ \left\{ {\begin{array}{*{20}{l}} {{x_0} \in \{ x_0^{(j)}\} _{j = 1}^N}\\ {x_0^{(j)}\backsim N(\hat x_0^{(j)},P_0^{(j)})}\\ {P(x_0^{(j)}) = \mu _0^{(j)} = \frac{1}{N}} \end{array}} \right. $ | (11) |
式中:x0为真实目标初值;
根据贝叶斯定理,在给定当前观测值序列y1:k条件下,候选初值
| $ \begin{array}{l} \mu _k^{(j)} = p(x_0^{(j)}|{y_{1:k}}) = \frac{{p({y_k}|x_0^{(j)},{y_{1:k - 1}})\mu _{k - 1}^{(j)}}}{{\sum\limits_{i = 1}^N p ({y_k}|x_0^{(i)},{y_{1:k - 1}})\mu _{k - 1}^{(i)}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{L_k^{(j)}\mu _{k - 1}^{(j)}}}{{\sum\limits_{i = 1}^N {L_k^{(i)}} \mu _{k - 1}^{(i)}}} = \frac{{\prod\limits_{i = 1}^k {L_i^{(j)}} }}{{\sum\limits_{i = 1}^N {\prod\limits_{m = 1}^k {L_m^{(i)}} } }},j = 1,2, \cdots ,N \end{array} $ | (12) |
式中:p(yk|
由于k时刻的归一化操作不会改变分子项
| $ \begin{array}{*{20}{c}} {{\rm{ln}}L_k^{(j)} = {\rm{ln}}N(\mathit{\boldsymbol{z}}_k^{(j)};0,\mathit{\boldsymbol{S}}_k^{(j)}) = }\\ { - \frac{1}{2}(m{\rm{ln}}2\pi + {\rm{ln}}|S_k^{(j)}| + {{(\mathit{\boldsymbol{z}}_k^{(j)})}^{\rm{T}}}{{(S_k^{(j)})}^{ - 1}}\mathit{\boldsymbol{z}}_k^{(j)})} \end{array} $ | (13) |
进而可得对数似然函数
| $ \tilde \mu _k^{(j)} = {\rm{ln}}\prod\limits_{i = 1}^k {L_i^{(j)}} = \sum\limits_{i = 1}^k {{\rm{ln}}} L_i^{(j)} $ | (14) |
利用各模型中的最大似然值进行归一化,即:
| $ \tilde \mu _k^{(j)} \Leftarrow \tilde \mu _k^{(j)} - \mathop {{\rm{max}}}\limits_j (\tilde \mu _k^{(j)}) $ | (15) |
PEKF相比于传统卡尔曼滤波有更好的收敛性和稳定性[14-15],其基本步骤为:
1) 时间更新。
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_{k|k - 1}} = \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{P}}_{k - 1|k - 1}}{\mathit{\boldsymbol{F}}^{\rm{T}}} + {\mathit{\boldsymbol{Q}}_{k - 1}}}\\ {{{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}} = \mathit{\boldsymbol{F}}{{\mathit{\boldsymbol{\hat x}}}_{k - 1|k - 1}}} \end{array}} \right. $ |
式中:
2) 观测更新。
① 初始化
② For i=1, 2, …, Npu
| $ {{\mathit{\boldsymbol{S}}_{i - 1}} = {\mathit{\boldsymbol{H}}_{i - 1}}{\mathit{\boldsymbol{P}}_{i - 1}}\mathit{\boldsymbol{H}}_{i - 1}^{\rm{T}} + {\mathit{\boldsymbol{R}}_k}/\delta \lambda } $ |
| $ {{\mathit{\boldsymbol{K}}_i} = {\mathit{\boldsymbol{P}}_{i - 1}}\mathit{\boldsymbol{H}}_{i - 1}^{\rm{T}}\mathit{\boldsymbol{S}}_{i - 1}^{ - 1}} $ |
| $ {{{\mathit{\boldsymbol{\hat x}}}_i} = {{\mathit{\boldsymbol{\hat x}}}_{i - 1}} + {\mathit{\boldsymbol{K}}_i}({\mathit{\boldsymbol{y}}_k} - \mathit{\boldsymbol{h}}({{\hat x}_{i - 1}}))} $ |
| $ {{\mathit{\boldsymbol{P}}_i} = (\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{K}}_i}{\mathit{\boldsymbol{H}}_{i - 1}}){\mathit{\boldsymbol{P}}_{i - 1}}} $ |
③
当n=1,PEKF退化为EKF。
综上所述,可给出FBS-PEKF跟踪算法步骤如下:
1) 确定假设目标距离数K及每个距离上起始的滤波器数量NF,确定滤波器的初始条件
2) 从k=1时刻开始,对每个初值模型进行PUEKF滤波,得到各个滤波器的输出, 即{
3) 利用式(14)更新k-1时刻权值,得到当前时刻各初值模型的似然值
4) 输出k时刻最大似然选择的滤波器结果
| $ \{ {i_{{\rm{max}}}},{j_{{\rm{max}}}}\} = \mathop {{\rm{max}}}\limits_{i,j} (\tilde \mu _k^{(i,j)}) $ | (16) |
5) 对似然值进行归一化。
6) 回到步骤2)或终止滤波。
3 基于功率谱的静电场检测技术舰船静电场能量主要集中在DC~0.1 Hz的低频段。海洋环境电场主要是由于海浪运动切割地磁场产生的感应电场,其能量主要集中在0.1 Hz以下,在短时间(15~30 min)内,海浪的变化可视为平稳随机过程。即海洋环境电场的能量在短时间内不会发生明显变化,而当舰船出现时,目标周围电场将引起低频频段内的能量发生改变,这为以低频频段内的能量和作为特征检测舰船电场提供了可能。静电场检测算法的基本步骤为:
1) 计算特征值。假设检测开始时刻为t,对检测时刻t以及之前的N-1个数据{x(n), x(n-1), …, x(n-N+1)}进行功率谱估计,取特征量为谱估计后所得序列中与特征频段对应的M点频谱值的平均:
| $ P = \frac{1}{M}\sum\limits_{i = 1}^M {{P_k}} $ | (17) |
2) 确定阈值。取检测时刻t之前某段时间特征量的平均值为阈值,计算检测时刻t之前w个特征量的平均值PAve=(Pn-1+Pn-2+…+Pn-w)/w,取检测阈值为T0=βPAve,其中β为阈值因子,β的取值可根据要求的虚警概率和检测概率确定。
3) 判决条件。当t时刻的特征量Pt>T0时认为满足判别条件,即目标出现一次,若不满足条件则回到步骤1),对t+1时刻继续进行滑动检测。
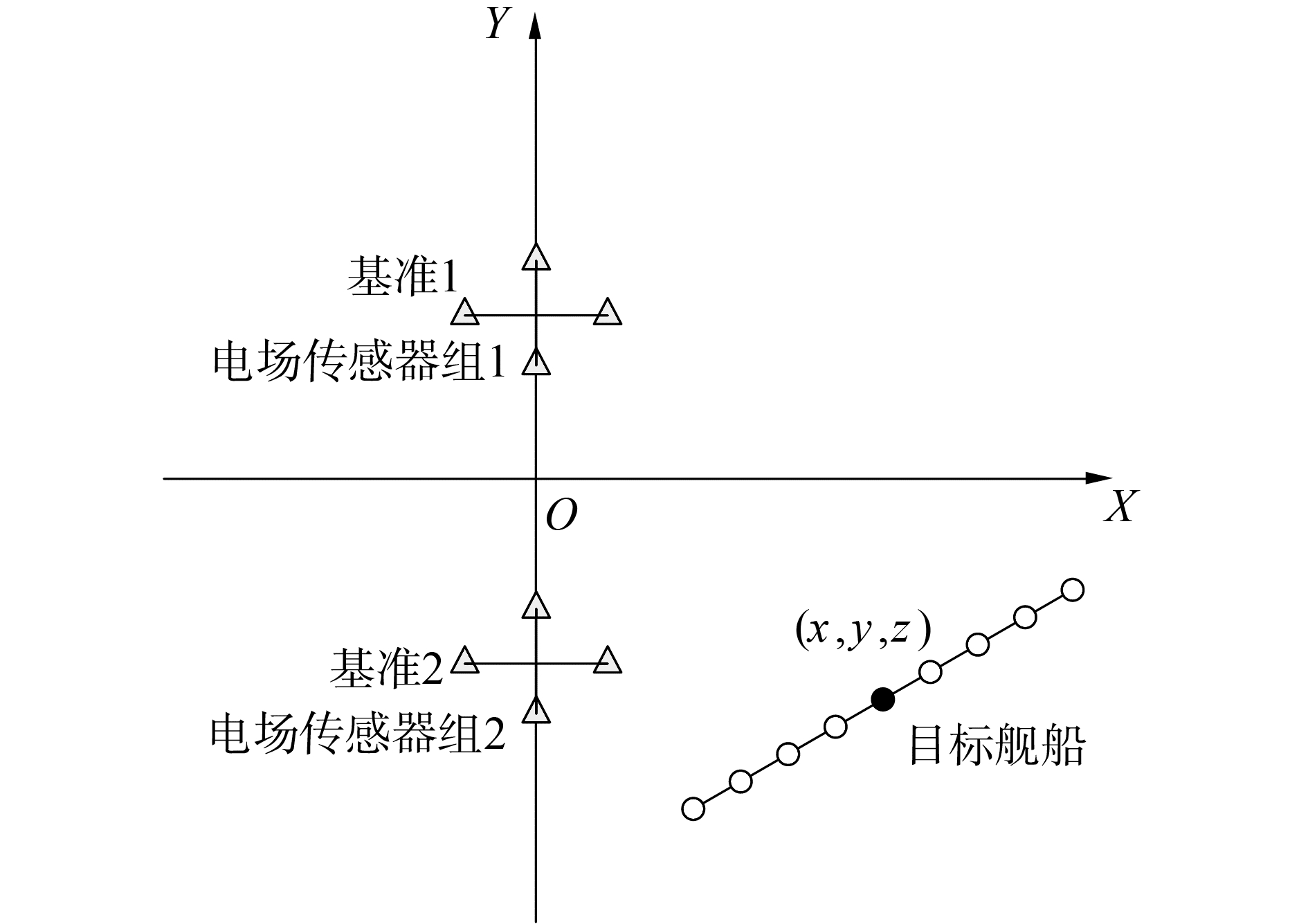
4 仿真结果及分析设计如图 2所示的仿真实验,采用9个点电源模拟舰船,每个电场传感器组包含4个电位传感器。模拟舰船的点电源阵列为Ip=[4.07, -0.68, …, -1.39]T(由某型船舶Beasy数据利用点电源建模法反演得到),ld=15 m;以传感器阵列为基础建立右手坐标系,传感器所在线为Y轴,传感器中心点为坐标原点,X轴过原点垂直于Y轴,Z轴向上;电位传感器组的位置为o1=[0 48 0;0 50 0;0.8 49 0;-0.8 49 0],o2=[0-48 0;0-50 0;0.8-49 0;-0.8 -49 0];舰船起始位置r0=[1 040,-30,-4.57]T,初始速度为V0=[-10, -2]T;过程加速度噪声强度σx=σy=0.001,α=0.001;观测噪声协方差矩阵Rk=σ2I2×2,σ=1×10-9;传感器深度Hsensor=50 m;海水深度Hsea=51 m;海水电导率σ1=4 S/m;海水电导率σ1=0.04 S/m。
|
Download:
|
| 图 2 基于电位差的舰船跟踪示意 Fig. 2 A schematic diagram of ship tracking based on potential difference | |
滤波算法中假设目标点电源数量为3,点电源初值为[-10, 30, -20],ld=33 m。对功率谱滑动检测器进行配置:信号采样率100 Hz,滑动窗长度为500,检测门限窗数为4,滑动间隔为1 s,连续3 s检测到目标则认为目标存在。对滤波器组进行配置:信号采样率1 Hz;检测到目标后假定目标水面初始距离为900 m;在该距离上起始NF=4个PEKF滤波器,各个滤波器的假设方位分别为π/4、3π/4、5π/4、7π/4。
选择位置分量在k时刻的均方根误差(root mean square errors at k moment of r position component,
| $ {\rm{ RMSE}} _k^r = \sqrt {\frac{1}{{MC}}\sum\limits_{i = 1}^{MC} {{\rm{ tr }}} [({r_k} - {{\hat r}_k}){{({r_k} - {{\hat r}_k})}^{\rm{T}}}} $ | (18) |
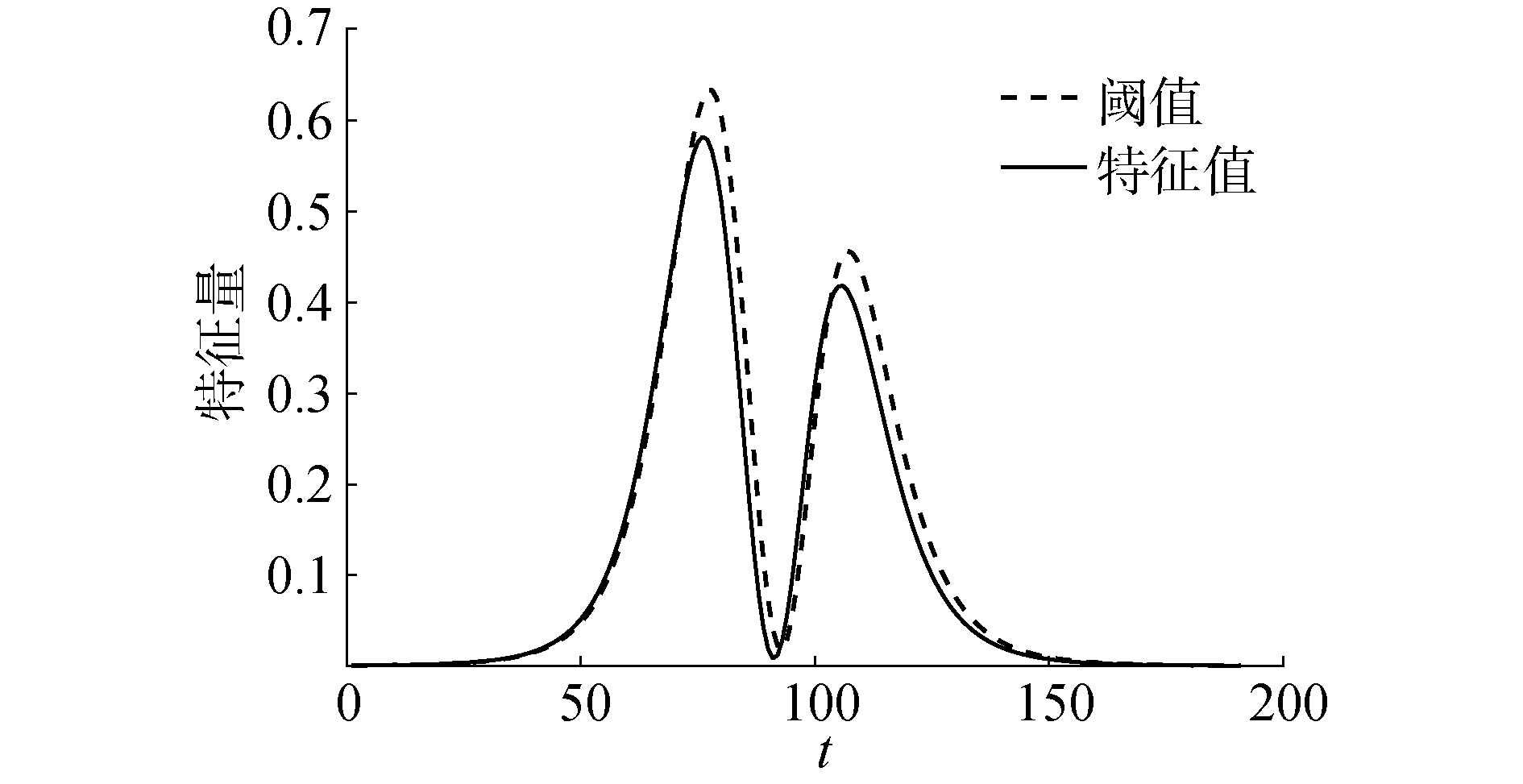
如图 3~图 6所示滤波器组的跟踪结果。其中图 3是阈值——特征值曲线;图 4是滤波器组中4个滤波器的
|
Download:
|
| 图 3 阈值-特征值曲线 Fig. 3 The curve of threshold-eigenvalue | |

|
Download:
|
|
图 4 滤波器组的 |
|

|
Download:
|
|
图 5 滤波器组的 |
|
|
Download:
|
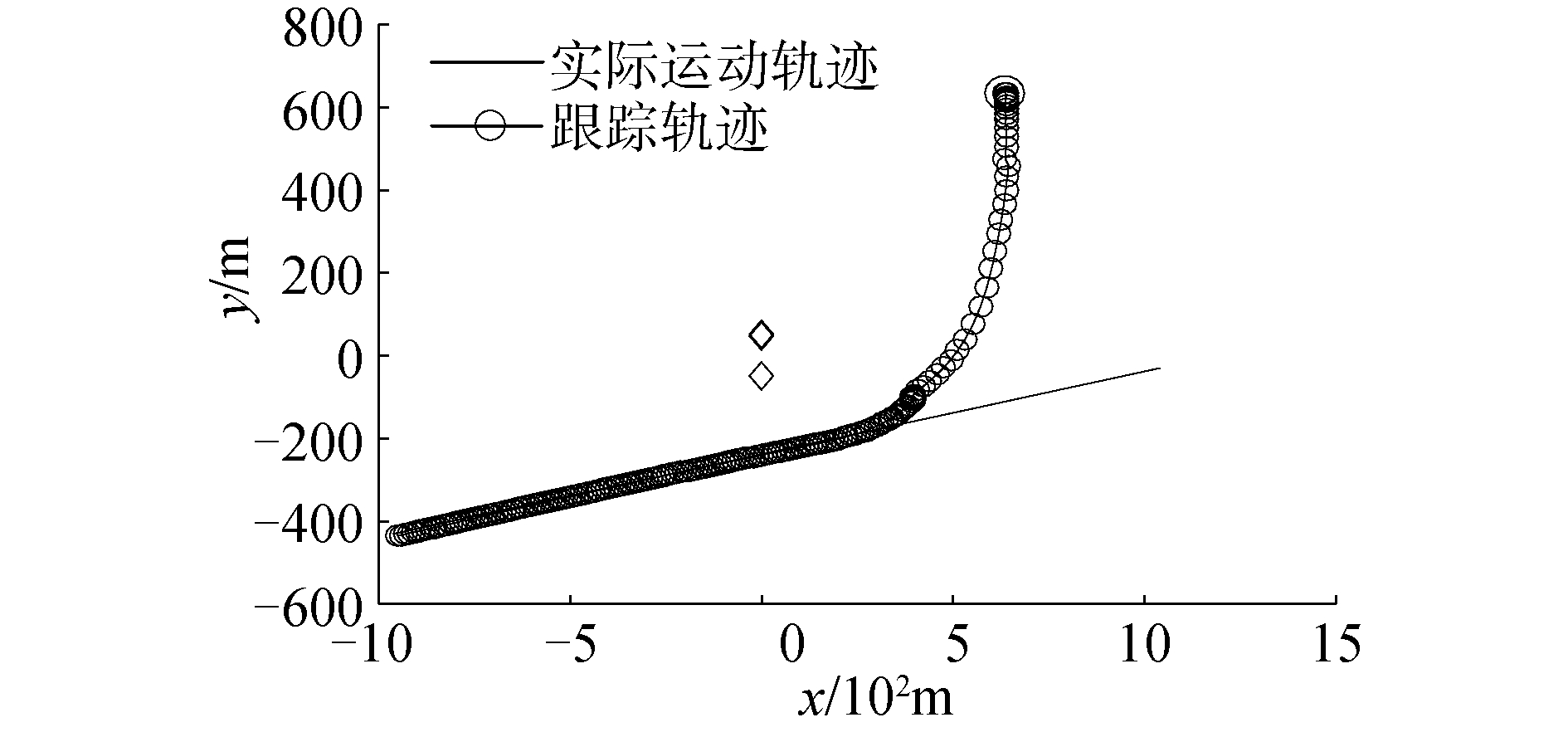
| 图 6 最优跟踪轨迹 Fig. 6 Optimal tracking trajectory | |
从跟踪结果中可以得到以下几点结论:
1) 基于DUEP对船舶目标进行跟踪是可行的,且具有较高的精度;
2) 滑动检测算法有效,能够及时的检测到目标,并起始滤波(图 3);
3) 最大似然选择法能够选择正确的跟踪轨迹,对数似然函数值最大的曲线对应的为轨迹1(图 5、图 6);
4) 从跟踪结果来看,只有轨迹1是收敛的,表明基于DUEP的船舶电场跟踪也是对方位信息最为敏感(图 4、图 6);
5) 由于船舶在纵向和横向的尺度不同,因此对其在纵向和横向的跟踪精度要求是不同的,从图 6中可以看出,在船舶横向上,跟踪精度是很高的,
1) 利用船舶DUEP信号可有效实现船舶的信号检测和跟踪,相比于UEP和SE,DUEP量级更大抗干扰性更强,对方位信息最为敏感,且对传感器的布设要求低。
2) 基于最大似然选择法的滤波器组方法可有效解决静态电位差跟踪中初始位置、速度等先验信息缺失问题。基于静态电位差的船舶电场跟踪方法是可行的,且利用工程实现,对利用船舶电场信号对船舶进行跟踪具有重要的意义。
| [1] |
谭浩, 陈聪, 蒋治国. 船舶水下电场的预测方法[J]. 国防科技大学学报, 2016, 38(6): 168-172. TAN Hao, CHEN Cong, JIANG Zhiguo. Electric field prediction method for ships at sea[J]. Journal of National University of Defense Technology, 2016, 38(6): 168-172. (  0) 0)
|
| [2] |
陈聪, 蒋治国, 姚陆锋, 等. 浅海中潜艇腐蚀相关静态电磁信号特征[J]. 海军工程大学学报, 2014, 26(3): 1-6. CHEN Cong, JIANG Zhiguo, YAO Lufeng, et al. Characteristic analysis of corrosion-related static electromagnetic field produced by a submarine in shallow sea[J]. Journal of Naval University of Engineering, 2014, 26(3): 1-6. (  0) 0)
|
| [3] |
李松, 石敏, 栾经德, 等. 舰船轴频电场信号特征提取与检测方法[J]. 兵工学报, 2015, 36(S2): 220-224. LI Song, SHI Min, LUAN Jingde, et al. The feature extraction and detection for shaft-rate electric field of a ship[J]. Acta armamentarii, 2015, 36(S2): 220-224. (  0) 0)
|
| [4] |
秦永元, 张洪钺, 汪叔华. 卡尔曼滤波与组合导航原理[M]. 3版. 西安: 西北工业大学出版社, 2015. QIN Yongyuan, ZHANG Hongyue, WANG Shuhua. Kalman filtering and combined navigation principle[M]. 3rd ed. Xian: Northwestern Polytechnical University Press, 2015. (  0) 0)
|
| [5] |
KALMAN R E. A new approach to linear filtering and prediction problems[J]. Journal of basic engineering, 1960, 82(1): 35-45. DOI:10.1115/1.3662552 (  0) 0)
|
| [6] |
JULIER S, UHLMANN J, DURRANT-WHYTE H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE transactions on automatic control, 2000, 45(3): 477-482. DOI:10.1109/9.847726 (  0) 0)
|
| [7] |
魏喜庆, 宋申民. 基于容积卡尔曼滤波的卫星姿态估计[J]. 宇航学报, 2013, 34(2): 193-200. WEI Xiqing, SONG Shenmin. Cubature Kalman filter-based satellite attitude estimation[J]. Journal of astronautics, 2013, 34(2): 193-200. DOI:10.3873/j.issn.1000-1328.2013.02.007 (  0) 0)
|
| [8] |
MAHALANABIS A K, FAROOQ M. A second-order method for state estimation of non-linear dynamical systems[J]. International journal of control, 1971, 14(4): 631-639. DOI:10.1080/00207177108932073 (  0) 0)
|
| [9] |
陆珊珊, 王伟, 王国玉. 采用粒子滤波的雷达波束方位指向估计[J]. 国防科技大学学报, 2016(1): 74-77. LU Shanshan, WANG Wei, WANG Guoyu. Estimate of radar beam's azimuth using particle filter[J]. Journal of National University of Defense Technology, 2016(1): 74-77. (  0) 0)
|
| [10] |
HO Y, LEE R. A Bayesian approach to problems in stochastic estimation and control[J]. IEEE transactions on automatic control, 1964, 9(4): 333-339. DOI:10.1109/TAC.1964.1105763 (  0) 0)
|
| [11] |
GUSTAFSSON F, HENDEBY G. Some relations between extended and unscented Kalman filters[J]. IEEE transactions on signal processing, 2012, 60(2): 545-555. DOI:10.1109/TSP.2011.2172431 (  0) 0)
|
| [12] |
刘妹琴, 兰剑. 目标跟踪前沿理论与应用[M]. 北京: 科学出版社, 2015. LIU Meiqin, LAN Jian. Advanced theory and application of target tracking[M]. Beijing: Science Press, 2015. (  0) 0)
|
| [13] |
姜润翔, 胡英娣, 龚沈光. 基于点电源的船舶静态电场深度换算方法研究[J]. 电波科学学报, 2014, 29(4): 685-693. JIANG Runxiang, HU Yingdi, GONG Shenguang. Depth conversion of the vessel static electric field based on point charge source[J]. Chinese journal of radio science, 2014, 29(4): 685-693. (  0) 0)
|
| [14] |
BIRSAN M. Recursive Bayesian method for magnetic dipole tracking with a tensor gradiometer[J]. IEEE transactions on magnetics, 2011, 47(2): 409-415. DOI:10.1109/TMAG.2010.2091964 (  0) 0)
|
| [15] |
DE MELO F E, MASKELL S, FASIOLO M, et al. Stochastic particle flow for nonlinear high-dimensional filtering problems[J]. arXiv: 1511.01448v3, 2017.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


