三体船作为一种高性能船舶,其具有稳性与耐波性优良、高速航行下阻力小以及甲板面积充分扩展等性能优点。甲板面积宽大的军用三体船具有更大的甲板容积以布置火力装备和直升机,且破舱稳性良好即生存能力较强。对于三体船一类高速船而言,在保证舰船结构安全的前提下对船舶结构质量轻化可有效提高三体船各项性能指标。由于三体船结构复杂,相对于三体船水动力性能的研究而言,三体船结构优化设计发展较慢,相关研究较少:杨德喜[1]计算了三体船连接桥结构应力分布,为提高连接桥结构强度提出了3种设计方法,即增加横舱壁数量、增加支柱结构数量以及增加湿甲板的厚度,并基于通过校核计算验证其有效性;邓乐[2]和杨赵华[3]依据多种多体船资料,对三体车客渡轮进行结构初步设计,并根据其结构特点对船体结构进行有限元计算校核,同时对不同结构形式的连接桥性能进行分析比较,结果表明:密加筋形式结构为目标类型船舶连接桥最优结构形式;张丽等[4]以规范为主要依据进行边界约束条件的设计,通过利用Isight软件集中数据对船舶结构做优化分析,该工作为研究人员将Isight软件广泛应用于船舶的结构优化设计奠定了基础;张会新等[5]重点应用参数优化和形状优化技术对船底板架进行结构优化,优化后的结构重量较未优化重量减少15.82%;Ehlers[6]应用粒子群算法对高强度钢船舶结构进行优化分析,将该方法应用于LNG船碰撞问题时,可以有效地对船体高强度钢材使用率进行优化分析;甄春博等[7]以高性能三体船为例,采用三维势流理论和整船有限元分析的谱分析直接计算方法,分析表明,疲劳寿命可靠度随着疲劳寿命的增加而增大,疲劳问题严重区域较小;任慧龙等[8]提出三维时域非线性水弹性理论和非线性设计波法计算三体船纵向波浪载荷,结果分析表明,巡航工况下计算值与规范值接近,极限工况下计算值远大于规范值,并建议在校核三体船结构强度时,增加极限工况。
相对于传统半经验设计方法而言,基于工程力学原理与计算机辅助设计技术的连续结构拓扑优化设计方法[9-12]以及离散结构拓扑优化设计方法[13-14],可更好地实现船舶结构轻量化设计,在保证舰船结构安全的前提下实现三体船结构质量轻化[15],目前该方类方法已经广泛应用于汽车,土木工程,航天航空等行业[16-17]。
但目前关于三体船主要结构拓扑优化的研究较少。针对当前研究现状,本文以英国劳氏船级社《Rules for The Classification of Trimarans》[18]为依据进行载荷设计,以国外一具体三体船主要非水密舱壁结构初步设计为结构优化原型,应用有限元法对目标结构进行强度分析,同时在保证结构强度符合设计规范的前提下,以应力传递及分布最优为目标,对舱壁结构进行拓扑优化,并对优化后的舱壁结构进行强度分析,对比各工况及不同减重情况下的应力,同时将本文的优化结果与实船舱壁进行对比分析,对三体船横舱壁拓扑优化结果进行评估,为船舶主要结构拓扑优化设计提供技术参考。
1 拓扑优化 1.1 构建优化模型拓扑优化的基本思想是在给定设计区域内寻求材料的最优分布。选择适当的优化目标,建立合理的模型,是进行结构拓扑优化的基础。本文根据变密度方法建立优化模型,其具有敏度推导简单,计算效率高的特点,将优化区域划分为有限个单元,以单元的相对密度为设计变量,每个单元的相对密度表示为:
| $ {\rho _i} = \left\{ \begin{array}{l} 1,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i \in {\mathit{\Omega} ^{\rm mat}}\\ 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i \in \mathit{\Omega} /{\mathit{\Omega} ^{\rm mat}} \end{array} \right. $ | (1) |
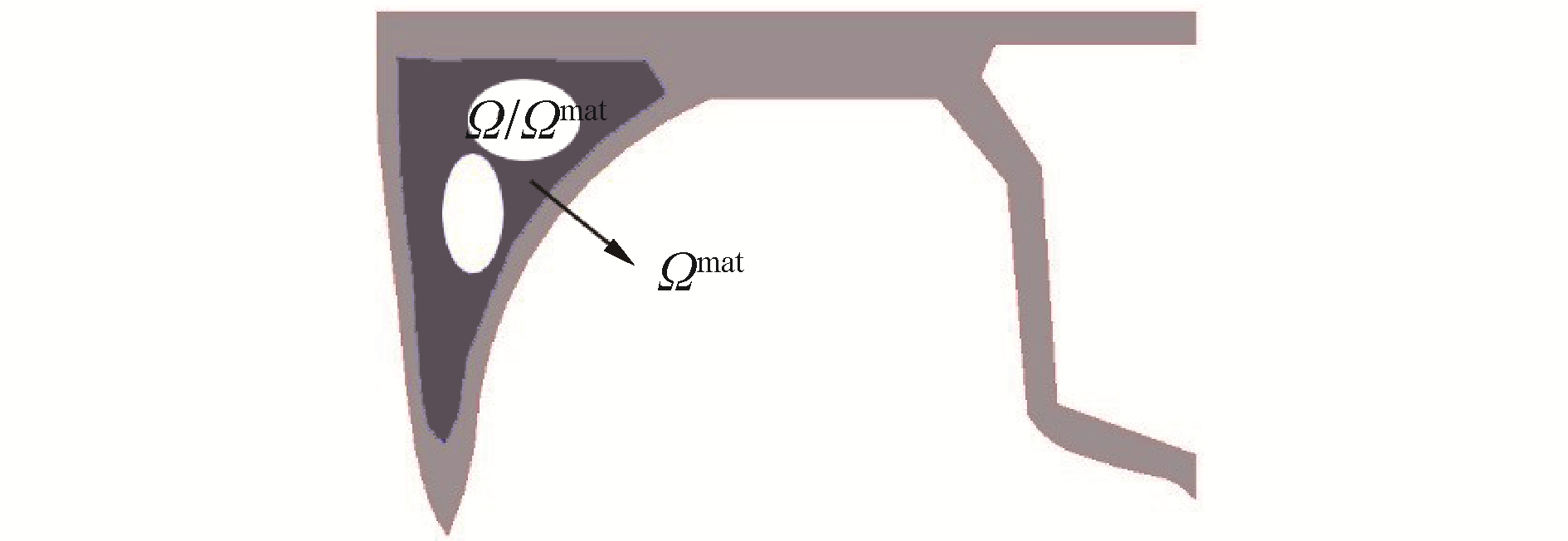
式中:ρi为单元相对密度;i为有限个单元的标号;Ωmat表示保留材料的区域;Ω表示整个设计区域;ρi=1表示该区域存在材料,反之则表示该区域不存在材料。图 1为本文优化的模型,根据单元的相对密度,可得到:
|
Download:
|
| 图 1 三体船横舱壁结构模型 Fig. 1 Transverse bulkhead structure model of trimaran | |
| $ \int_\mathit{\Omega} {{\rho _i}{\rm d}\mathit{\Omega} \le {V_0},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \le {\rho _i} \le 1,i \in \mathit{\Omega} } $ | (2) |
式中V0表示设计域总体积。受体积约束,以结构的柔顺度最小化为优化目标的模型表达式为:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\rm Find} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\rho _i},i = 1,2, \cdots ,m} \end{array}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm min}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{C}} = {\mathit{\boldsymbol{F}}^{\rm T}}\mathit{\boldsymbol{u}}} \end{array}\\ \begin{array}{*{20}{l}} {\rm s.t.} \end{array}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} V/{V_0} - f \le 0\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {{\kern 1pt} \mathit{\boldsymbol{Ku}} = \mathit{\boldsymbol{F}}} \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 < {\rho _{\rm min}} < {\rho _i} \le 1{\kern 1pt} \end{array} \right. $ | (3) |
式中:m为单元总数;目标函数C表示结构总柔顺度;F是整体的载荷向量,u是位移矢量;V表示优化后的总体积,f为体积比;K为整体刚度矩阵;为了防止刚度矩阵出现奇异,引入单元相对密度下限ρmin=0.001。
1.2 求解算法与敏度分析模型建立完成后,进行拓扑优化求解时,一般要求解约束函数与目标函数的敏度值。为避免求解离散值设计问题[19](0-1问题),Zhou等[20]提出惩罚的固体各向同性微结构(SIMP)模型,其单元弹性模量与单元的相对密度之间存在如下关系:
| $ {E_i} = \rho _i^pE_i^0,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,m $ | (4) |
式中:Ei为第i个单元的弹性模量;
| $ p \ge {p^ * } = {\rm max}\left\{ {\frac{2}{{1 - {\gamma _0}}},\frac{4}{{1 + {\gamma _0}}}} \right\},2D模型 $ | (5) |
| $ p \ge {p^ * } = {\rm max}\left\{ {15\frac{{1 - {\gamma _0}}}{{7 - 5{\gamma _0}}},\frac{3}{2}\frac{{1 - {\gamma _0}}}{{1 - 2{\gamma _0}}}} \right\},3D模型 $ | (6) |
式中γ0为给定材料的泊松比,其取值不同时,对应不同的惩罚因子下限p*。对目标函数最小柔顺度进行敏度分析,总柔顺度表达式为:
| $ \mathit{\boldsymbol{C}} = {\mathit{\boldsymbol{F}}^{\rm T}}\mathit{\boldsymbol{u}} = {\mathit{\boldsymbol{F}}^{\rm T}}\mathit{\boldsymbol{u}} - {{\mathit{\boldsymbol{\hat u}}}^{\rm T}}(\mathit{\boldsymbol{Ku}} - \mathit{\boldsymbol{F}}) $ | (7) |
式中
| $ \frac{{\partial \mathit{\boldsymbol{C}}}}{{\partial {\rho _i}}} = ({\mathit{\boldsymbol{F}}^{\rm T}} - - {{\mathit{\boldsymbol{\hat u}}}^{\rm T}}\mathit{\boldsymbol{K}})\frac{{\partial \mathit{\boldsymbol{u}}}}{{\partial {\rho _i}}} - {{\mathit{\boldsymbol{\hat u}}}^{\rm T}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{u}} $ | (8) |
又K具有对称性,通过建立伴随方程K
| $ \frac{{\partial \mathit{\boldsymbol{C}}}}{{\partial {\rho _i}}} = - {{\mathit{\boldsymbol{\hat u}}}^{\rm T}}\frac{{\partial \mathit{\boldsymbol{K}}}}{{\partial {\rho _i}}}\mathit{\boldsymbol{u}} $ | (9) |
再根据式(3)中的插值关系,目标函数的最终敏度计算表达式可简化为:
| $ \frac{{\partial \mathit{\boldsymbol{C}}}}{{\partial {\rho _i}}} = - p\rho _i^{p - 1}\mathit{\boldsymbol{u}}_i^{\rm T}\mathit{\boldsymbol{k}}_i^0{\mathit{\boldsymbol{u}}_i} $ | (10) |
式中:ui为第i个单元对应的位移向量;
以一般三体船舱壁结构为优化结构,舱壁材料屈服强度σs=235 MPa,许用应力σe=235×0.85=199.75 MPa,杨氏模量E=2.1×105 MPa,泊松比υ=0.3,钢材密度ρ=7 850 kg/m3,由于结构的对称性,故取半个舱壁,对其进行应力分析与结构拓扑优化。《Rules for The Classification of Trimarans》有关三体船强度校核的规定指出:三体船的连接桥为强度校核重点之一。结合《Rules for The Classification of Trimarans》与本文选取舱壁结构,选定的载荷为:水平弯矩、横向分离弯矩中拱状态、横向分离弯矩中垂状态、纵向扭矩,如图 2所示。结合本文优化的对象,本节需要校核迎浪、横浪和斜浪不同状况下共7个工况,具体方式见表 1。

|
Download:
|
| 图 2 载荷示意 Fig. 2 Schematic diagram of loading | |
| 表 1 三体船舱壁结构校核工况 Table 1 Check condition trimaran bulkhead structure check condition |
本文在做舱壁结构有限元分析时未考虑静水弯矩及横向扭矩。利用有限元软件计算得到各工况下的舱壁结构应力分布结果如图 3所示,舱壁结构优化前各工况最大应力值见表 2。

|
Download:
|
| 图 3 各工况下舱壁应力分布云图 Fig. 3 Bulkhead stress distribution cloud map under various working conditions | |
| 表 2 舱壁结构优化前各工况最大应力值 Table 2 Maximum stress value of each condition before optimization of bulkhead structure |
由表 2可知,舱壁结构在工况5工况下应力最大值达到189.1 MPa,其所在的危险截面位置为连接桥区域,是校核工况中应力最大值,此时舱壁结构应力最大值小于材料的许用应力值。因此,7个工况均满足强度要求。
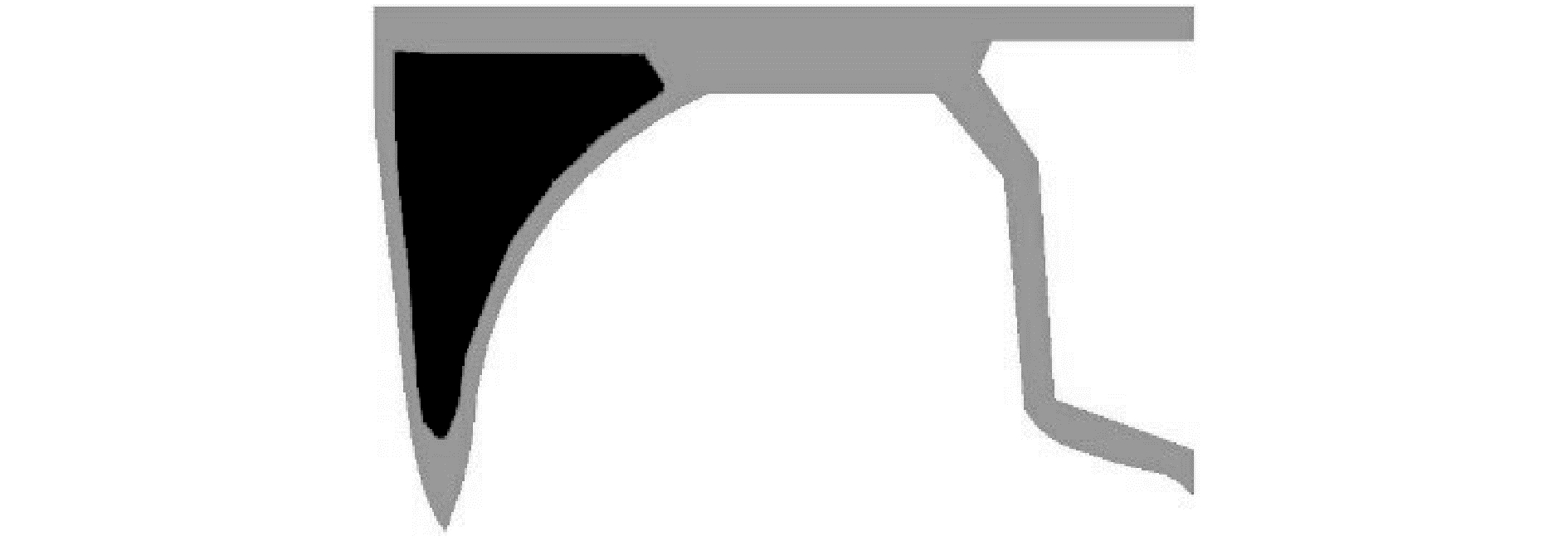
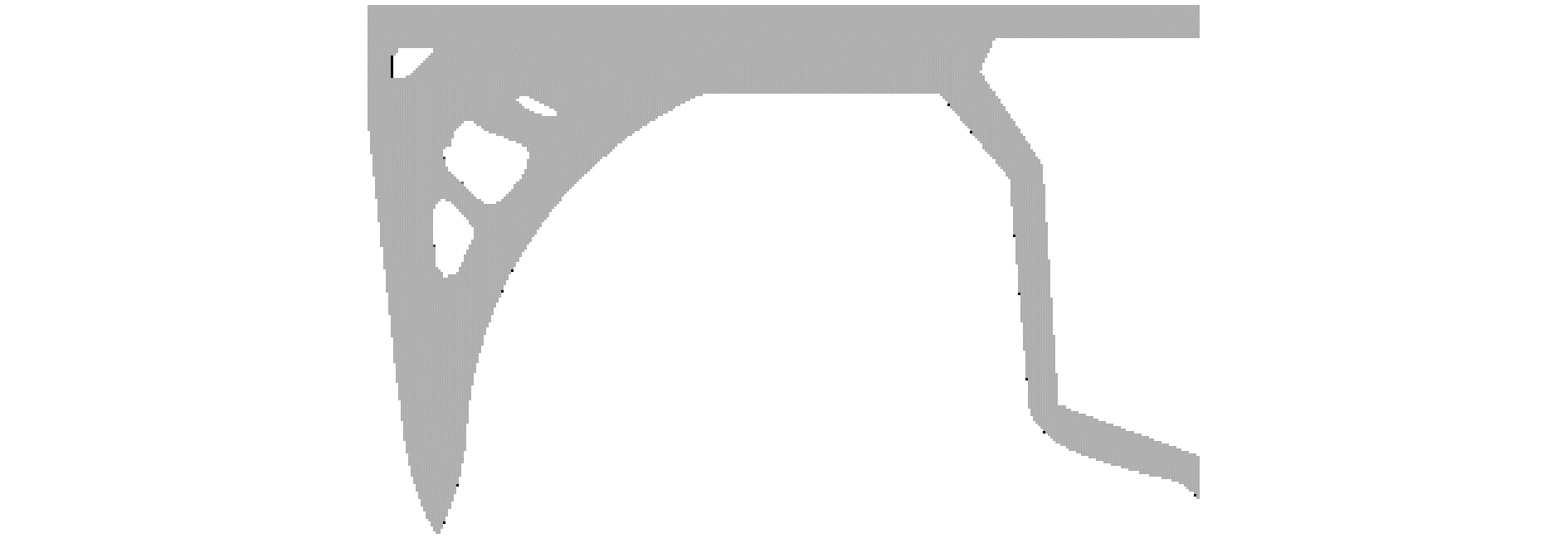
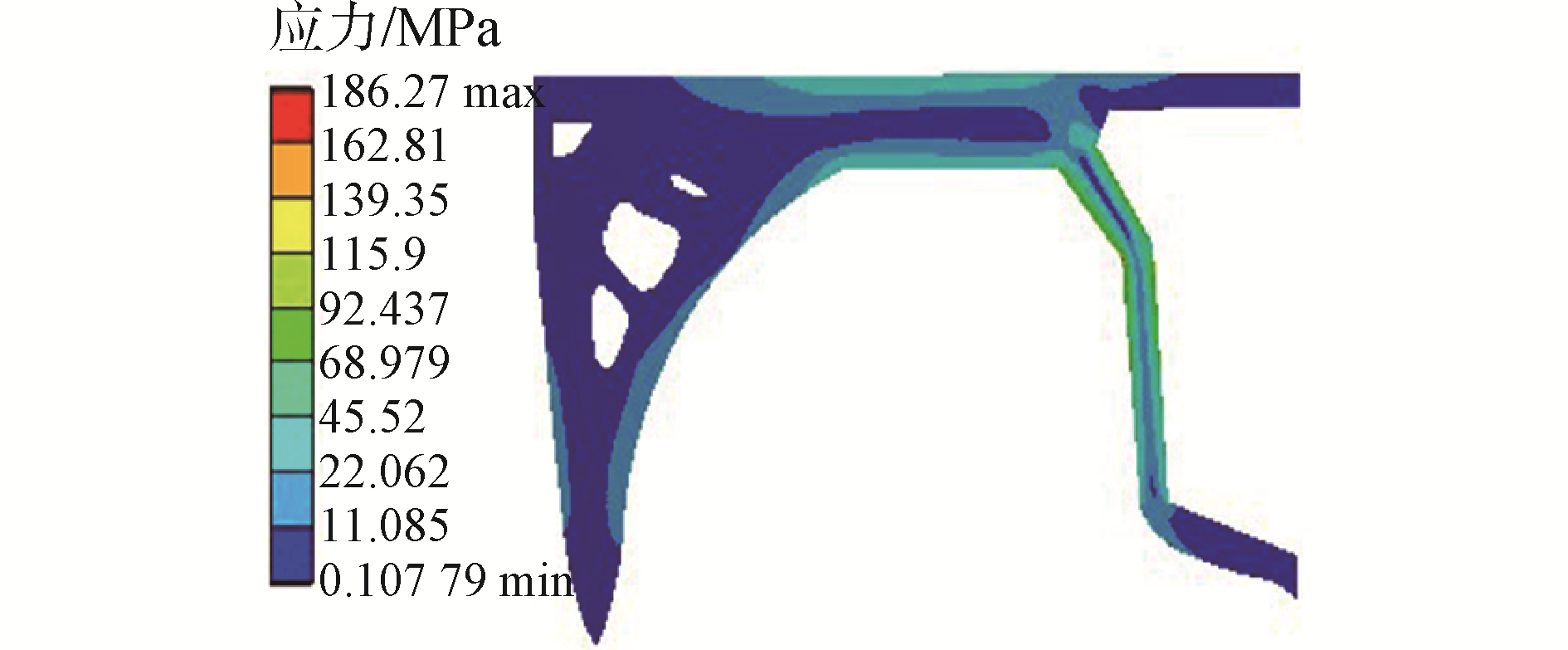
2.2 舱壁结构的拓扑优化分析由2.1节可知,CASE5对应的三体船舱壁结构最大应力值最大,为189.1 MPa。本节将对CASE5下的三体船舱壁结构进行拓扑优化,在保证舱壁结构安全的前提下尽可能减小舱壁体积。图 4黑色区域为优化区域,灰色区域为保形区域。令三体船舱壁体积减少20%为约束条件,图 5为CASE5下光顺后的三体船半舱壁结构。将CASE5下经过光顺的三体船舱壁结构导入有限元软件中进行静态结构分析,得到优化后三体船舱壁结构应力分布,结果如图 6所示。
|
Download:
|
| 图 4 优化区域 Fig. 4 Optimization area | |
|
Download:
|
| 图 5 优化后的舱壁结构 Fig. 5 Optimized bulkhead structure | |
|
Download:
|
| 图 6 优化后三体船舱壁结构应力分布 Fig. 6 Optimized stress distribution of trimaran bulkhead structure | |
对比图 6与图 3在CASE5下的计算结果可知:在斜浪中,计算载荷和约束条件相同前提下,拓扑优化前、后三体船舱壁结构的应力最大值结果相近:优化后舱壁结构最大应力值为186.27 MPa,与优化前舱壁结构应力最大值相差2.83 MPa,且由应力分布图可知,最大应力均位于连接桥与主船体连接处附近,可以认为三体船舱壁结构在拓扑优化前后的最大应力值及应力分布基本一致。
改变三体船舱壁体积的保形量。将体积约束条件分别修改为体积减少比例30%、40%、50%、60%,图 7为CASE5不同体积约束条件下的三体船舱壁拓扑优化结果。将CASE5不同体积约束条件下经过光顺的三体船舱壁结构导入有限元软件进行静态结构分析,得到优化后三体船舱壁结构最大应力结果(见表 3)。由表 3结果可知:CASE5不同体积约束条件下优化后三体船舱壁的应力分布及应力最大值不同,体积减少比例与舱壁结构应力最大值不存在正相关关联,例如,当三体船舱壁减少体积比例为原体积40%时,此时的舱壁应力最大值要高于体积减少比例30%和50%时的舱壁应力;当三体船舱壁减少体积比例为原体积30%时,此时的舱壁应力最大值要低于体积减少比例20%和40%时的舱壁应力;当三体船舱壁优化区域体积减少比例为40%时,舱壁的应力最大值与优化前CASE5下应力最大值最为接近。拓扑优化属于概念设计阶段,优化结果一般要后期调整,再进行生产,当三体船舱壁优化区域体积减少比例为50%时,舱壁出现少量额外微孔,但还能找出出其主要构型;而当比例达到60%时,舱壁结构材料布局出现大量微孔结构,实际生产较为困难,故该优化结果不可取。

|
Download:
|
| 图 7 不同体积约束条件下的三体船舱壁拓扑优化结果 Fig. 7 Topology optimization results of trimaran bulkhead under different volume constraints | |
| 表 3 CASE5时优化舱壁结构应力统计 Table 3 Optimization of bulkhead structural stress statistics at CASE5 |
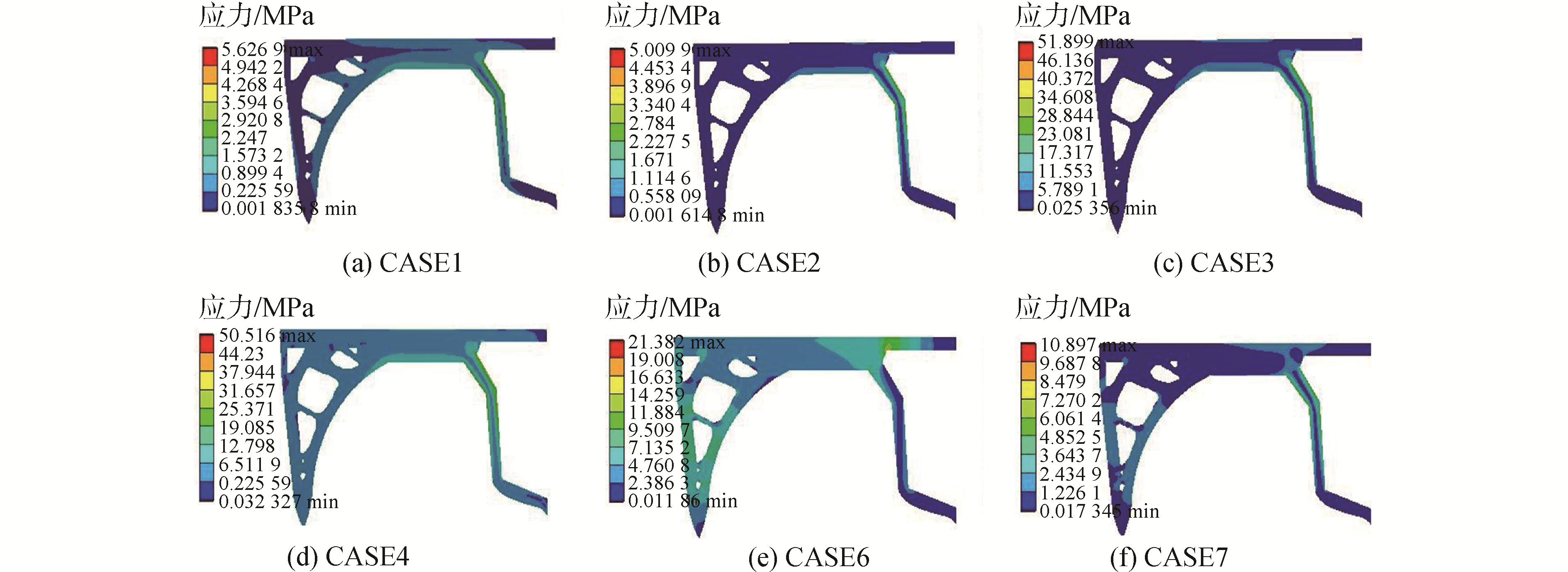
由表 3可知,当CASE 5体积减少比例达到50%时优化后舱壁的最大应力小于材料许用应力,下面以该优化结果为模型在其他校核工况下进行有限元分析,计算结果如图 8所示。
|
Download:
|
| 图 8 优化后强度校核云图 Fig. 8 Optimized intensity check cloud chart | |
由图 8可以看出,CASE 5下体积减少比例达到50%时优化后的舱壁结构,在其他校核工况下的最大等效应力均小于材料的许用应力,满足强度要求。
2.4 实船对比验证图 9为Austal公司的“独立”号三体船分段建造现场,从图中可以看到舱段中水密横舱壁的结构和加强筋布置。根据图 9所示的舱壁结构建立有限元模型,按照CASE 5校核工况进行加载和约束设置,并对其进行静力分析,分析结果见图 10。

|
Download:
|
| 图 9 “独立”号舱段建造现场 Fig. 9 Independent section construction site | |

|
Download:
|
| 图 10 CASE 5下舱壁应力分布 Fig. 10 Stress distribution of bulkhead under CASE5 | |
由计算结果可知,该舱壁结构在CASE5下的最大应力为191.8 MPa,小于材料的许用应力。改变三体船舱壁设计域内的体积减少比例,使其分别为:20%、30%、40%,对其进行结构拓扑优化,图 11为实船舱壁在不同体积比约束下优化后的应力云图,其结果见表 4。

|
Download:
|
| 图 11 Stress distribution of bulkhead under CASE5 Fig. 11 Stress cloud map after optimization under different volume constraints | |
| 表 4 CASE5时优化舱壁结构应力统计 Table 4 Optimization of bulkhead structural stress statistics at CASE5 |
由表 4可知:当舱壁优化区域体积减少30%时,舱壁的应力最大值与优化前CASE5下应力的最大值最接近,同时再次说明体积减少比例与舱壁结构应力最大值不存在正相关关联;当舱壁优化区域体积减少40%时,其最大应力与材料的许用应力基本相等,最大应力为199.69 MPa。
当舱壁优化区域体积减少20%、30%时,优化后舱壁中保留下来的连接材料的分布,与图 9中实船横舱壁的加强筋布置相似,因此按照该比例下优化后的结构形式,以截面为10 mm×70 mm的梁单元代替加强筋,建立水密舱壁模型并在CASE5下进行有限元分析。此外,为证明特定工况下拓扑优化结果的合理性,又进行了两组计算,分别为:将优化前的舱壁厚度增加1 mm,按照实船结构形式布置加强筋。同等条件下,计算结果如图 12所示。

|
Download:
|
| 图 12 等效应力计算结果 Fig. 12 Equivalent stress calculation results | |
由图 12可知,在CASE5下3组计算的最大应力结果与图 10原舱壁计算结果相比均有所减小。与原舱壁相比,按照优化结果进行加筋的舱壁最大应力降低了33.21 MPa,增厚舱壁的最大应力降低了28.06 MPa,按实船构型加筋的舱壁最大应力降低了4.74 MPa。结果表明:CASE5工况下,按拓扑优化结果进行加强筋布置对水密舱壁强度性能的改善更加有效。
实际船舶舱壁的加强筋布置要考虑的因素较多,而本文研究重点是舱壁结构的拓扑优化,对于结构分析方面考虑的不是很全面。因此,上述结果仅证明:特定工况下通过拓扑优化方法可以找到结构的最佳传力构型,拓扑优化方法可以为结构加筋方式提供指导。
3 结论1) 通过特定工况不同体积约束条件下优化后三体船舱壁的有限元结果可知,舱壁结构应力最大值与优化区域的体积减少比例之间不存在正相关关系,通过提高体积保形率降低舱壁应力的方法并不合理。
2) 通过变密度拓扑优化方法,对三体船非水密舱壁进行拓扑优化,得到了设计域内材料的最佳布局,能够在保证结构强度的前提下,减少舱壁优化区域内50%的结构重量,实现非水密舱壁的轻量化设计。
3) 通过与实船舱壁结构的对比,优化区域体积减少30%时,舱壁优化区域内的连接材料与实船舱壁中的加强筋布置相相似,充分验证了本文所用结构拓扑优化方法的合理性。
4) 通过3组水密舱壁的对比,在CASE5下按优化结果来布置加强筋后,舱壁结构强度更好,结果表明:合理的材料布置能够有效改善结构的强度,拓扑优化技术可在特定工况下为舱壁结构的加筋布置提供指导。
| [1] |
杨德喜.高速三体船结构设计与强度评估[D].哈尔滨: 哈尔滨工程大学, 2010. YANG Dexi. Structure design and strength assessment of high speed trimarans[D]. Harbin: Harbin Engineering University, 2010. http://d.wanfangdata.com.cn/thesis/Y1808111 (  0) 0)
|
| [2] |
邓乐.高速三体船结构力学特性研究[D].武汉: 武汉理工大学, 2008. DENG Le. Study on mechanics characteristics of high-speed trimaran[D]. Wuhan: Wuhan University of Technology, 2008. http://d.wanfangdata.com.cn/thesis/Y1365442 (  0) 0)
|
| [3] |
杨赵华.高速三体船结构轻型化设计研究[D].武汉: 武汉理工大学, 2008. YANG Zhaohua. Design and research on light structure of high-speed trimaran ship[D]. Wuhan: Wuhan University of Technology, 2008. http://d.wanfangdata.com.cn/thesis/Y1365624 (  0) 0)
|
| [4] |
张丽, 王德禹. 基于Isight的3100TEU集装箱船中剖面优化设计[J]. 船海工程, 2007, 36(5): 16-18. ZHANG Li, WANG Deyu. Optimization design of mid-section of 3100 TEU container ship based on Isight[J]. Ship & ocean engineering, 2007, 36(5): 16-18. DOI:10.3963/j.issn.1671-7953.2007.05.006 (  0) 0)
|
| [5] |
张会新, 杨德庆. 典型船舶板架拓扑与形状优化设计[J]. 中国舰船研究, 2015, 10(6): 27-33, 59. ZHANG Huixin, YANG Deqing. Typical shape and topology optimization design of the ship grillage structure[J]. Chinese journal of ship research, 2015, 10(6): 27-33, 59. DOI:10.3969/j.issn.1673-3185.2015.06.005 (  0) 0)
|
| [6] |
EHLERS S. A particle swarm algorithm-based optimization for high-strength steel structures[J]. Journal of ship production and design, 2012, 28(1): 1-9. (  0) 0)
|
| [7] |
甄春博, 王天霖, 于鹏垚. 船体结构疲劳可靠性分析的直接计算方法[J]. 哈尔滨工程大学学报, 2018, 39(4): 664-667. ZHEN Chunbo, WANG Tianlin, YU Pengyao. Direct calculation approach for fatigue reliability analysis of ship structures[J]. Journal of Harbin Engineering University, 2018, 39(4): 664-667. (  0) 0)
|
| [8] |
任慧龙, 陈亮亮, 李辉, 等. 三体船波浪设计载荷的三维时域水弹性理论研究[J]. 哈尔滨工程大学学报, 2016, 37(1): 19-23. REN Huilong, CHEN Liangliang, LI Hui, et al. Study of the design wave loads of a trimaran based on 3D time-domain hydroelastic theory[J]. Journal of Harbin Engineering University, 2016, 37(1): 19-23. (  0) 0)
|
| [9] |
BENDSOE M P, KIKUCHI N. Generating optimal topologies in structural design using a homogenization method[J]. Computer methods in applied mechanics and engineering, 1998, 71(2): 197-224. DOI:10.1016/0045-7825(88)90086-2 (  0) 0)
|
| [10] |
BENDSØE M P. Optimal shape design as a material distribution problem[J]. Structural optimization, 1989, 1(4): 193-202. DOI:10.1007/BF01650949 (  0) 0)
|
| [11] |
XIE Y M, STEVEN G P. A simple evolutionary procedure for structural optimization[J]. Computers & structures, 1993, 49(5): 885-896. DOI:10.1016/0045-7949(93)90035-C (  0) 0)
|
| [12] |
ALLAIRE G, JOUVE F. TOADER A M. A level-set method for shape optimization[J]. Comptes rendus mathematique, 2002, 334(12): 1125-1130. DOI:10.1016/S1631-073X(02)02412-3 (  0) 0)
|
| [13] |
CHENG G D, GUO X. ε-relaxed approach in structural topology optimization[J]. Structural optimization, 1997, 13(4): 258-266. (  0) 0)
|
| [14] |
SU Ruiyi, GUI Liangjin, FAN Zijie. Topology and sizing optimization of truss structures using adaptive genetic algorithm with node matrix encoding[C]//Proceedings of the 5th International Conference on Natural Computation. Tianjin, China, 2009. https://ieeexplore.ieee.org/document/5362845
(  0) 0)
|
| [15] |
邱伟强, 杨德庆, 高处, 等. 基于拓扑优化的油船货舱结构设计研究[J]. 船舶, 2016, 27(5): 1-11. QIU Weiqiang, YANG Deqing, GAO Chu, et al. Structural design in cargo tank region for oil tankers based on topology optimization[J]. Ship & boat, 2016, 27(5): 1-11. DOI:10.3969/j.issn.1001-5388.2016.05.001 (  0) 0)
|
| [16] |
MUNK D J, VERSTRAETE D, VIO G A. Effect of fluid-thermal-structural interactions on the topology optimization of a hypersonic transport aircraft wing[J]. Journal of fluids and structures, 2017, 75: 45-76. DOI:10.1016/j.jfluidstructs.2017.08.007 (  0) 0)
|
| [17] |
OKTAY E, AKAY H U, MERTTOPCUOGLU O. Parallelized structural topology optimization and CFD coupling for design of aircraft wing structures[J]. Computers & fluids, 2011, 49(1): 141-145. (  0) 0)
|
| [18] |
Lloyd's Register (LR). Incorporating Notice No. 1, The rules for the classification of trimaran[S]. 2006.
(  0) 0)
|
| [19] |
OLSEN G R, VANDERPLAATS G N. Method for nonlinear optimization with discrete design variables[J]. AIAA journal, 1989, 27(11): 1584-1589. DOI:10.2514/3.10305 (  0) 0)
|
| [20] |
ZHOU M, ROZVANY G I N. The COC algorithm, Part II:topological, geometrical and generalized shape optimization[J]. Computer methods in applied mechanics and engineering, 1991, 89(1/2/3): 309-336. DOI:10.1016/0045-7825(91)90046-9 (  0) 0)
|
| [21] |
BENDSOE M P, SIGMUND O. Topology optimization:theory, methods and applications[M]. New York: Springer, 2003.
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


