折叠式夹层板作为一种新式结构,具有良好的抗冲击性能[1],进行理论预报公式研究有利于快速评估舰船结构在爆炸载荷作用下的损伤变形。从设计应用角度出发,简化的理论预报公式可以更好的指导相关结构的设计评估。
对于折叠式夹层板的力学性能,国内外学者均进行了一系列研究。由于夹层板属于复合结构,因此在研究夹层板力学性能时,研究人员往往将芯层等效成实心板,对夹层板进行整体研究[2-3]。梁军等[4]利用等效方法对方形蜂窝夹层板在冲击载荷作用下的塑性残余变形进行了理论研究,并与有限元结果进行对比,证明了该方法的可行性。尹群等[5]研究了新式芯层层舱壁结构的抗冲击性能,分析了冲击波单独作用以及冲击波和碎片联合作用下新式芯层层舱壁的结构响应,发现新式结构的吸能效率显著提高,在冲击波作用下具有更优的防护性能。Li[6]和Zhu[7]应用LS-DYNA分别研究了爆炸载荷作用下铝质球形泡沫夹层板以及矩形蜂窝夹层板的动态响应,发现球面形夹层板比柱面形夹层板具备更好抵抗爆炸载荷的性能,同时与试验结果进行对比,证明了有限元分析技术的有效性与可行性。Langdon[8]对比分析了聚苯乙烯及铝质蜂窝夹层板在空爆载荷作用下的试验及数值仿真结果,发现两者吻合度较好,在保证结果准确性的前提下,有限元仿真分析可以有效节约研究成本,提高计算效率。俞鞠梅[9]利用ABAQUS有限元软件研究了空爆载荷作用下折叠式夹层板的防护性能,发现夹层板主要通过芯层结构的塑性变形来吸收或耗散冲击波能量,与加筋板进行对比,折叠式夹层板在冲击载荷下的响应衰减更快,可以有效改善结构的冲击环境。学者们还针对圆管型夹层板抗爆性能进行了研究,结果表明芯层单元数量较少时,面板会成为主要吸能构件,芯层的数量和厚度是夹层板吸能效率的主要影响因素[10-11]。在此基础上,还研究了不同速率纵向冲击载荷作用下芯层的变形模式,研究发现在低速冲击时,芯层对称收缩,在高速冲击时,芯层沿一侧斜倾[12]。
本文以折叠式夹层板为研究对象,基于动能定理、能量守恒以及塑性力学的相关理论,建立夹层板塑性变形的简化解析计算公式,并与相关仿真计算进行对比分析,验证计算公式得有效性,同时对简化公式进行完善,为夹层板结构的工程设计和抗冲击性能评估提供参考。
1 冲击载荷响应分析根据爆炸冲击载荷的作用特点,可以把折叠式夹层板的冲击响应过程简化为3个阶段[13]:第1阶段夹层板由于冲击获得初始动能(图 1(a));第2阶段夹层板的芯层在面板作用下出现压缩变形(图 1(b));第3阶段夹层板面板与芯层达到共同速度后,夹层板发生整体塑性变形(图 1(c))。

|
Download:
|
| 图 1 折叠式夹层板动态响应过程 Fig. 1 Dynamic response process of folded sandwich panel | |
夹层板在受到冲击波作用时,其变形迅速超越弹性阶段而进入塑性阶段,所以在分析时忽略其弹性的影响,将夹层板视为理想刚塑性材料。爆炸冲击波作用在夹层板上,当压力波正入射一个刚性固定的夹层板面板时,单位面积上的反射冲量为[14]:
| $ I = 2{I_ + } = 2{A_i}\frac{{\sqrt[3]{{m_e^2}}}}{r} $ | (1) |
式中:Ai为系数,一般取200~250[15];me为炸药TNT当量,kg;r为爆距,m;I+为入射冲量。
在爆炸冲击波作用下,夹层板只有迎爆面获得初始速度,忽略边界的影响,此时初始动能为:
| $ {E_i} = \frac{1}{2}S{\rho _f}{t_f}v_i^2 = \frac{{{I^2}S}}{{2{\rho _f}{t_f}}} $ | (2) |
式中:S为夹层板的面积,m2;ρf为夹层板材料密度,kg/m3;tf为夹层板面板厚度,m;vi为初始速度,m/s。
1.2 夹层板芯层压缩夹层板迎爆面获得初始速度后,芯层开始压缩至与迎爆面面板达到共同的速度,此时动能为:
| $ {E_k} = \frac{1}{2}S(2{\rho _f}{t_f} + {\rho _c}{h_c})v_k^2 = \frac{{{I^2}S}}{{2(2{\rho _f}{t_f} + {\rho _c}{h_c})}} $ | (3) |
式中:vk为夹层板面板和芯层的共同速度,m/s;ρc为芯层的等效密度,kg/m3;ρc=ρρf,其中ρ为芯层的相对密度系数;hc为芯层高度,m。
夹层板在压缩过程中必然伴随着能量的转化,爆炸冲击波的部分能量被夹层板芯层吸收为夹层板的塑性应变能,该部分能量为:
| $ {E_a} = {E_i} - {E_k} $ | (4) |
矩形夹层板芯层压缩变形用双三角函数表示为:
| $ w(x,y) = {w_{mn}}{\rm{sin}}\left( {\frac{\pi }{2} + \frac{{m\pi x}}{L}} \right){\rm{sin}}\left( {\frac{\pi }{2} + \frac{{n\pi y}}{B}} \right) $ | (5) |
在芯层上取微面积dxdy,则该面积上的吸能ΔEa=σ(x, y)dxdyw(x, y),因此横向方向吸能与变形间的关系为:
| $ \begin{array}{*{20}{l}} {{E_a} = {\sigma _c}\int_{ - L/2}^{L/2} {\int_{ - B/2}^{B/2} {{w_{mn}}} } {\rm{sin}}\left( {\frac{\pi }{2} + \frac{{m\pi x}}{L}} \right) \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{sin}}\left( {\frac{\pi }{2} + \frac{{n\pi y}}{B}} \right){\rm{d}}x{\rm{d}}y = {w_{mn}}\frac{{4LB}}{{{\pi ^2}}}{\sigma _c}} \end{array} $ | (6) |
式中:σc为芯层等效屈服强度,Pa,取为σc=
联立式(4)~(6)可得:
| $ {w_{mn}} = \frac{{{\pi ^2}}}{{4LB{\sigma _c}}}({E_i} - {E_k}) $ | (7) |
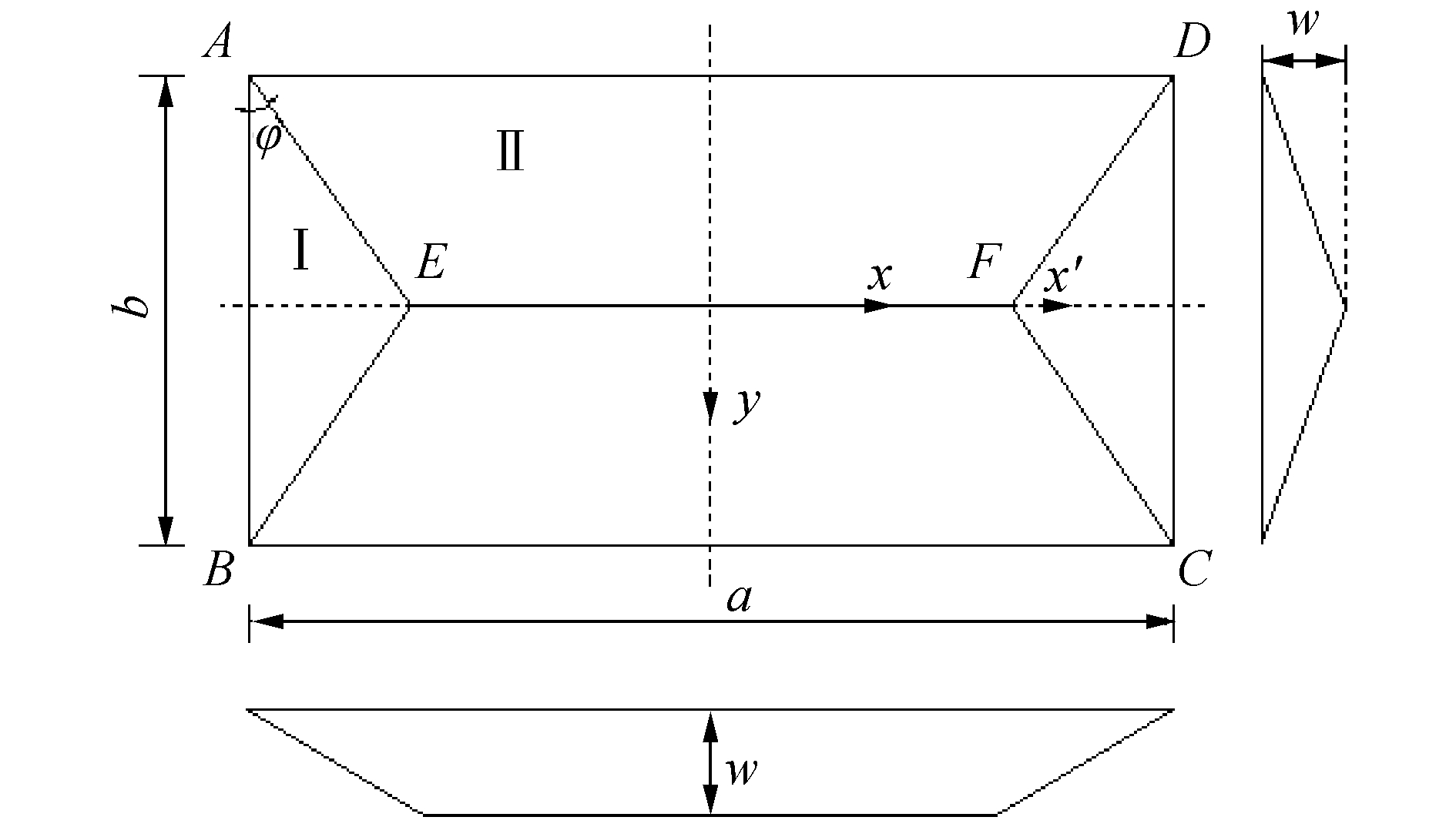
在芯层压缩完成之后,夹层板继续变形产生塑性弯曲和拉伸,其动能将主要转化为弯曲应变能和拉伸应变能。假设夹层板四周刚固,其整体塑性变形模式如图 2所示。
|
Download:
|
| 图 2 固支夹层板的塑性变形模式 Fig. 2 Plastic deformation mode of the clamed sandwich panel | |
在冲击载荷作用下,夹层板形成刚性区域Ⅰ和刚性区域Ⅱ,产生塑性铰线,位移场则表示:
| $ {w_{i{\rm{I}}}} = \frac{{b{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi - 2{x^\prime }}}{{b{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}w,{w_{i{\rm{II}}}} = \frac{{b - 2y}}{b}w $ | (8) |
其中φ可确定为:
| $ {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi = \sqrt {3 + {\xi ^2}} - \xi ,\xi = b/a $ | (9) |
由于夹层板的弯矩和膜力的影响,单位长度铰线的内能耗散率为:
| $ {E_D} = (M + N{w_i}){\theta _i} $ | (10) |
夹层板在变形过程中结构的总虚功为:
| $ {E_p} = \sum\limits_{i = 1}^n {\int_{{l_i}} {(M + N{w_i})} } {\theta _i}{\rm{d}}{l_i} $ | (11) |
式中:M为夹层板的弯矩,N·m;N为夹层板的膜力,N;wi为铰线处的横向位移,m;θi为第i根铰线的转角,rad;li为第i根铰线的长度,m;n为铰线根数。
夹层板结构一般属于对称结构,因此变形过程铰线处的耗散总能量可表示为:
| $ \begin{array}{*{20}{l}} {{E_p} = 2\int_{{l_{AB}}} {(M + N{w_i})} {\theta _{AB}}{\rm{d}}{l_{AB}} + 2\int_{{l_{AD}}} {(M + N{w_i})} {\theta _{AD}}{\rm{d}}{l_{AD}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 4\int_{{l_{AE}}} {(M + N{w_i})} {\theta _{AE}}{\rm{d}}{l_{AE}} + \int_{{l_{EF}}} {(M + N{w_i})} {\theta _{EF}}{\rm{d}}{l_{EF}}} \end{array} $ | (12) |
其中θAB、θAD、θAE和θEF的值取为:
| $ \begin{array}{*{20}{l}} {{\theta _{AB}} = \frac{{2w}}{{b{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }},{\theta _{AD}} = \frac{{2w}}{b},{\theta _{EF}} = \frac{{4w}}{b},}\\ {{\theta _{AE}} = {\theta _{AB}}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi + {\theta _{AD}}{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi = \frac{{2w}}{{b{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \end{array} $ | (13) |
将式(13)代入式(12),可得夹层板变形时在铰线处的总耗散能为:
| $ {E_p} = \left( {\frac{{4a}}{b} + \frac{{2{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \right)N{w^2} + \left( {\frac{{8a}}{b} + \frac{{8{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right)Mw $ | (14) |
板的屈服函数可由膜力和弯矩来描述,对于夹层板而言,其屈服面的形式与截面形状以及面板和芯层的相对强度和厚度有关,因此与普通平板有所不同,可表示为:
| $ \frac{{|M|}}{{{M_0}}} + \frac{{|N|}}{{{N_0}}} = 1 $ | (15) |
式中:M0为夹层板的极限弯矩;N0为夹层板的极限膜力。
对于Ⅰ型夹层板(图 3),垂直于芯层方向(X轴方向)的极限弯矩可表示为:
| $ \begin{array}{*{20}{l}} {{M_{0x}} = {\sigma _f}{t_f}[({h_c} - {w_{mn}}) + {t_f}] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\sigma _c}{t_c}{{({h_c} - {w_{mn}})}^2}/4({d_p} - {d_f})} \end{array} $ | (16) |

|
Download:
|
| 图 3 Ⅰ型折叠式夹层板及几何参数 Fig. 3 Ⅰ-type folded sandwich panel and geometric parameters | |
极限膜力可表示为:
| $ {N_{0x}} = 2{\sigma _f}{t_f} + {\sigma _c}{t_c}({h_c} - {w_{mn}})/({d_p} - {d_f}) $ | (17) |
对于U型夹层板(图 4),垂直于芯层方向(X轴方向)的极限弯矩可表示为:
| $ \begin{array}{*{20}{l}} {{M_{0x}} = {\sigma _f}{t_f}[({h_c} - {w_{mn}}) + {t_f}] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\sigma _c}{{({h_c} - {w_{mn}})}^2}({d_p} - 2{d_f})/4{d_p}} \end{array} $ | (18) |

|
Download:
|
| 图 4 U型折叠式夹层板及几何参数 Fig. 4 U-type folded sandwich panel and geometric parameters | |
极限膜力可表示为:
| $ {N_{0x}} = 2{\sigma _f}{t_f} + {\sigma _c}({h_c} - {w_{mn}})({d_p} - 2{d_f})/{d_p} $ | (19) |
对于离散型芯层折叠式夹层板(图 3、图 4)平行于芯层方向(Y轴方向)的极限弯矩可表示为:
| $ {M_{0y}} = {\sigma _f}{t_f}[({h_c} - {w_{mn}}) + {t_f}] + {\sigma _c}{({h_c} - {w_{mn}})^2}/4 $ | (20) |
极限膜力可表示为:
| $ {N_{0y}} = 2{\sigma _f}{t_f} + {\sigma _c}({h_c} - {w_{mn}}) $ | (21) |
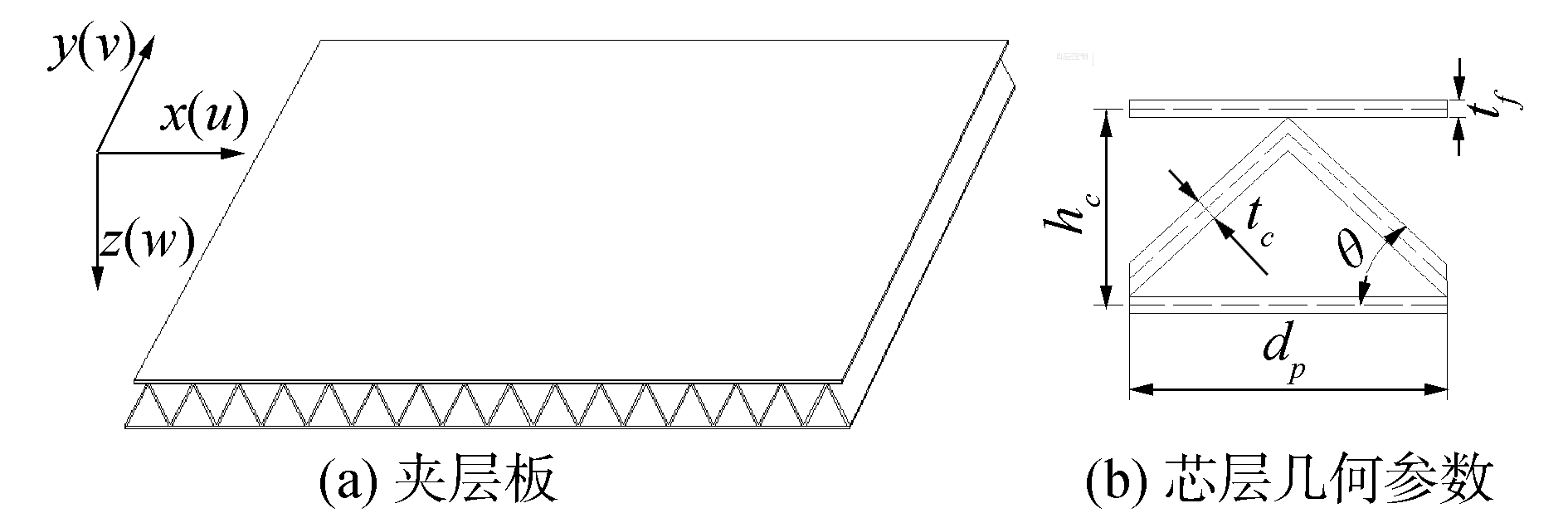
对于连续型芯层折叠式夹层板(图 5、图 6),垂直于芯层方向(X轴方向)和平行于芯层方向(Y轴方向)的极限弯矩和极限膜力相等,可表示为:
| $ {M_0} = {\sigma _f}{t_f}[({h_c} - {w_{mn}}) + {t_f}] + {\sigma _c}{({h_c} - {w_{mn}})^2}/4 $ | (22) |
|
Download:
|
| 图 5 V型折叠式夹层板及几何参数 Fig. 5 V-type folded sandwich panel and geometric parameters | |

|
Download:
|
| 图 6 Uc型折叠式夹层板及几何参数 Fig. 6 Uc-type folded sandwich panel and geometric parameters | |
极限膜力可表示为:
| $ {N_0} = 2{\sigma _f}{t_f} + {\sigma _c}({h_c} - {w_{mn}}) $ | (23) |
计算4种折叠式夹层板的相对密度系数ρ:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\bar \rho }_I} = 2{t_c}/{d_p}}\\ {{{\bar \rho }_U} = {t_c}({d_p} - 2{d_f})/{h_c}{d_p}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {{{\bar \rho }_V} = {t_c}/({h_c} - {t_c}){\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta }\\ {{{\bar \rho }_{Uc}} = {t_c}(2{d_f}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta + {d_p} - 2{d_f})/{h_c}{d_p}{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \theta } \end{array}} \right. $ | (24) |
对于夹层板的动态响应问题,一般很难得到其最终变形的封闭形式解,为了尽可能准确地表示其变形量,本文采用屈服函数的外接方形和内接方形作为其屈服面进行求解,如图 7所示。

|
Download:
|
| 图 7 夹层板屈服曲线 Fig. 7 The yield curve of the sandwich panel | |
外接方形屈服面:
| $ |N| = {N_0},|M| = {M_0} $ | (25) |
内接方形屈服面:
| $ |N| = 0.5{N_0},|M| = 0.5{M_0} $ | (26) |
从理论上来说,采用外接方形作为屈服函数,求得的最终变形量会小于实际的最终变形量;而采用内接方形作为屈服函数,求得的最终变形量会大于实际的最终变形量。因此,在求得结果之后,为尽可能的减少误差,应取其平均值作为夹层板最终变形量的计算值。
1.3.2 变形计算当屈服曲面为外接方形屈服面时,总耗散能为:
| $ \begin{array}{*{20}{l}} {{E_p} = \left( {\frac{{4a}}{b} + \frac{{2{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \right){N_0}{w^2} + }\\ {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{{8a}}{b} + \frac{{8{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_0}w} \end{array} $ | (27) |
当屈服曲面为内接方形屈服面时,总耗散能为:
| $ \begin{array}{*{20}{l}} {{E_p} = \left( {\frac{{2a}}{b} + \frac{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - \frac{{{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{2}} \right){N_0}{w^2} + }\\ {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{{4a}}{b} + \frac{{4{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_0}w} \end{array} $ | (28) |
夹层板芯层压缩完成之后,在整体变形的过程中,其初始动能最终由其塑性变形能所耗散,因此:
| $ {E_p} = {E_k} $ | (29) |
把式(26)和式(27)分别代入式(28),得:
| $ \begin{array}{*{20}{c}} {\left( {\frac{{4a}}{b} + \frac{{2{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \right){N_0}{w^2} + }\\ {\left( {\frac{{8a}}{b} + \frac{{8{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_0}w = {E_k}} \end{array} $ | (30) |
| $ \begin{array}{*{20}{c}} {\left( {\frac{{2a}}{b} + \frac{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - \frac{{{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{2}} \right){N_0}{w^2} + }\\ {\left( {\frac{{4a}}{b} + \frac{{4{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_0}w = {E_k}} \end{array} $ | (31) |
把M0x、N0x、M0y、N0y分别代入式(30)和式(31),舍去负值解,可得:
| $ {w_{1x}} = \frac{{\sqrt {{{\left[ {\left( {\frac{{8a}}{b} + \frac{{8{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0x}}} \right]}^2} + 4{E_k}{N_{0x}}\left( {\frac{{4a}}{b} + \frac{{2{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \right)} - \left( {\frac{{8a}}{b} + \frac{{8{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0x}}}}{{2{N_{0x}}\left( {\frac{{4a}}{b} + \frac{{2{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \right)}} $ | (32) |
| $ {w_{2x}} = \frac{{\sqrt {{{\left[ {\left( {\frac{{4a}}{b} + \frac{{4{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0x}}} \right]}^2} + 4{E_k}{N_{0x}}\left( {\frac{{2a}}{b} + \frac{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - \frac{{{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{2}} \right)} - \left( {\frac{{4a}}{b} + \frac{{4{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0x}}}}{{2{N_{0x}}\left( {\frac{{2a}}{b} + \frac{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - \frac{{{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{2}} \right)}} $ | (33) |
| $ {w_{1y}} = \frac{{\sqrt {{{\left[ {\left( {\frac{{8a}}{b} + \frac{{8{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0y}}} \right]}^2} + 4{E_k}{N_{0y}}\left( {\frac{{4a}}{b} + \frac{{{\rm{2cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \right)} - \left( {\frac{{8a}}{b} + \frac{{8{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0y}}}}{{2{N_{0y}}\left( {\frac{{4a}}{b} + \frac{{{\rm{2cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - {\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi } \right)}} $ | (34) |
| $ {w_{2y}} = \frac{{\sqrt {{{\left[ {\left( {\frac{{4a}}{b} + \frac{{4{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0y}}} \right]}^2} + 4{E_k}{N_{0y}}\left( {\frac{{2a}}{b} + \frac{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - \frac{{{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{2}} \right)} - \left( {\frac{{4a}}{b} + \frac{{4{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}} \right){M_{0y}}}}{{2{N_{0y}}\left( {\frac{{2a}}{b} + \frac{{{\rm{cos}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{{{\rm{sin}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }} - \frac{{{\rm{tan}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \varphi }}{2}} \right)}} $ | (35) |
取上述解的平均值,即可得到折叠式夹层板在爆炸冲击载荷作用下塑性变形的最终计算值:
| $ w = \frac{1}{4}({w_{1x}} + {w_{2x}} + {w_{1y}} + {w_{2y}}) $ | (36) |
取4种典型折叠式夹层板计算其在爆炸冲击载荷作用下的位移响应,同时利用ABAQUS对空中爆炸载荷进行数值仿真模拟,把有限元计算结果与理论计算结果对比分析,验证本文理论方法的可行性。
本文所述误差计算方法:
| $ E = \frac{{|{w_T} - {w_s}|}}{{{w_T}}} \times 100\% $ | (37) |
为了便于分析和比较,爆炸载荷冲量用无量纲参数表示:
| $ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{I}=\frac{I}{M\sqrt{{{\sigma }_{f}}/{{\rho }_{f}}}} $ | (38) |
式中:M=2ρftc+hcρc表示单位面积夹层板的质量,kg。
计算时选取合理的结构尺寸,并假定弹性模量E=2.10×105 MPa,泊松比μ=0.3,材料密度ρf=7 850 kg/m3,材料屈服强度σf=235 MPa,最大等效塑性应变取为0.3。用shell单元建立有限元模型(图 8所示),单元类型取4节点减缩积分四边形单元(S4R),结构四周刚性固定。具体几何参数见表 1。

|
Download:
|
| 图 8 四种典型折叠式夹层板有限元模型 Fig. 8 The finite element model of four typical folded sandwich panels | |
| 表 1 折叠式夹层板几何参数 Table 1 Geometric parameters of the folded sandwich panels |
为了验证本文提出的理论预报公式的可行性,选择5中爆炸载荷进行对比分析。各工况炸药量me依次选取1.2、3.6、6.0、9.6、14.4 kg,系数Ai取平均值225,考虑近场爆炸,爆距r取1.0 m。
在有限元数值模拟中,材料类型为理想弹塑性材料(供有限元仿真输入使用),计算不同冲量作用下,折叠式夹层板的最大塑性变形量。由于背爆面中心点可以反映整个夹层板的最大塑性变形,因此在有限元数值分析中选取夹层板背爆面中心点为典型测点,研究不同夹层板的变形量。
2.2 中心位移对比分析从图 9中可以看出,在冲击载荷作用下,4种夹层板的位移曲线变化趋势相同,均随着载荷冲量的增加而逐渐增大,且随着冲量的继续增大,理论解的增长趋势较仿真解更大。比较分析外接屈服面和内接屈服面的理论值可以发现,采用外接方形屈服函数求解得到的夹层板最大塑性变形比仿真值大,采用内接屈服函数得到的最大塑性变形比仿真值小;取外接值和内接值的平均值作为理论值与仿真值吻合度较高。而从图形变化趋势可以看出,如果继续增加炸药量,理论值与仿真值的差距将会增大,该理论公式将不再适用。4种夹层板的理论解和仿真结果如表 2所示。

|
Download:
|
| 图 9 4种典型折叠式夹层板冲量-位移曲线 Fig. 9 Impulse-displacement curves of four typical folded sandwich panel | |
| 表 2 不同折叠式夹层板的理论解与仿真值 Table 2 Theoretical solution and simulation value of different folded sandwich panels |
从表 2中可以看出,在同一爆炸冲量作用下,Uc型折叠式夹层板的位移最小,这是由于Uc型夹层板与上下面板存在接触区域,接触面积较大,一定程度上相当于增加了夹层板面板的厚度,因此抗冲击能力较强。
在不同爆炸冲量作用下,本文的计算解与仿真解在数值大小和整体趋势上吻合度较好,理论值与仿真值误差均在20%以内,并且大多数在10%以内,这说明本文提出的简化计算方法在一定冲量范围内具有可行性和实用性。
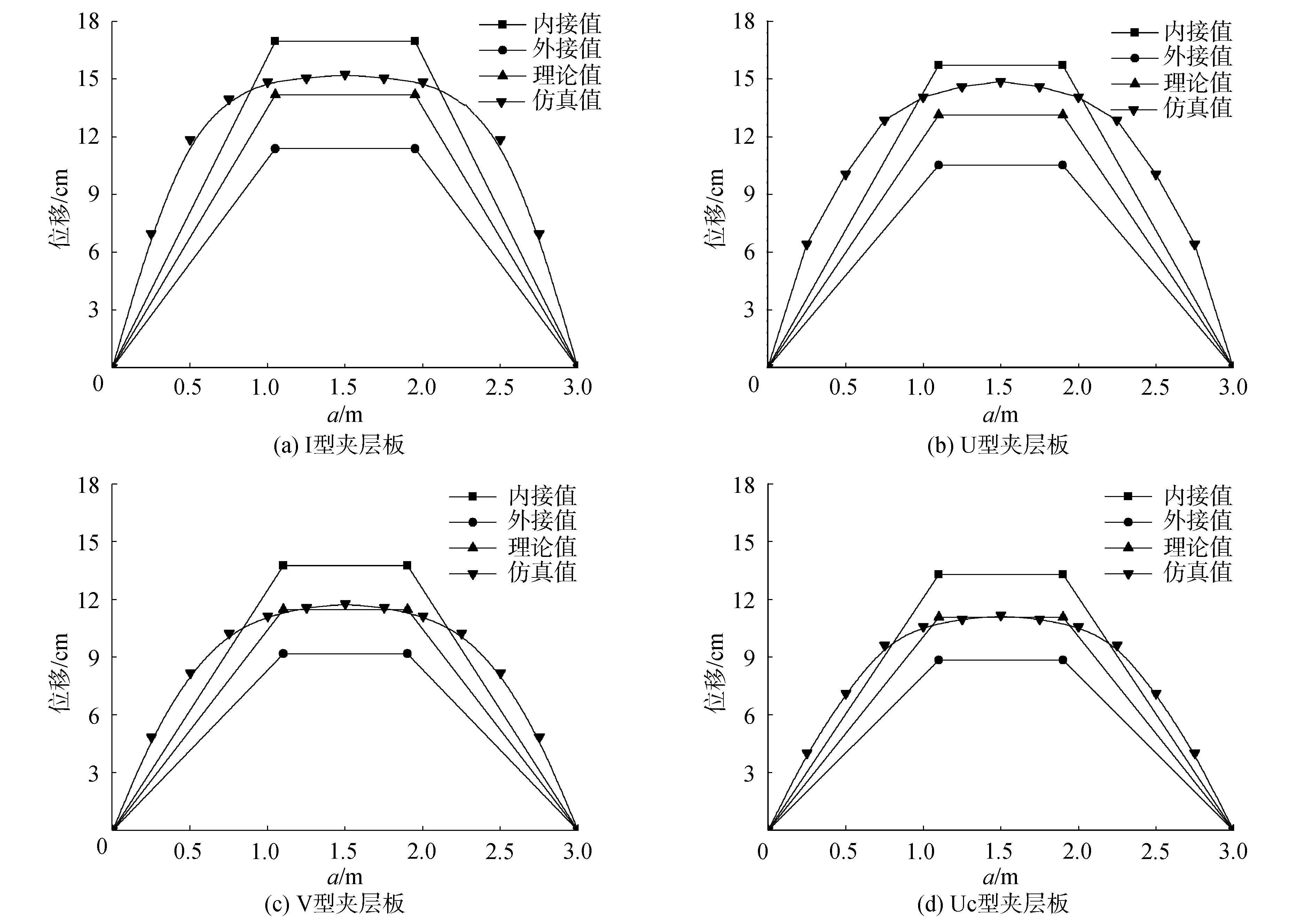
2.3 变形模式对比分析为了研究折叠式夹层板的整体变形情况,选取相同冲量(I=0.184 5)下长、宽2个方向中部典型剖面处夹层板的结构位移进行分析。夹层板沿X轴和Y轴方向中心线的位移分布分别如图 10和图 11所示。
|
Download:
|
| 图 10 X轴方向中心线位移 Fig. 10 Displacement curves of the center line in X axis | |

|
Download:
|
| 图 11 Y轴方向中心线位移 Fig. 11 Displacement curves of the center line in Y axis | |
从图 10、11中可以看出,夹层板的中部变形量与理论值较为接近,但在靠近中部区域的两侧,夹层板变形量基本大于理论值。利用内接屈服面函数求得的位移值与夹层板两侧变形值较为接近,但最大值偏大。利用外接屈服面函数求得的位移值在整个结构中均小于仿真值。由于简化解析采用刚塑性材料模型,位移曲线具有明显的折点,因此与实际变形模式相比这种偏差不可避免,但本文简化解析方法也能在一定程度上反映结构的变形情况,具有一定的参考价值。
总体来说,在夹层板的整体变形过程中,理论值与仿真值的变化趋势基本一致,沿X轴方向均存在一定程度的平台区,而沿Y轴方向则并不明显,两者峰值吻合较好,但在边缘区域仿真值大于理论值。利用内接屈服面函数求解,能更好地反映其部分区域的变形情况,但峰值偏大;而利用外接屈服面函数求解则始终小于仿真值,且两者偏差较大。
3 结论1) 将折叠式夹层板在爆炸冲击载荷作用下的动态响应分成3个阶段,结合每一阶段的响应特点,采用动能定理、能量守恒定律和刚塑性材料模型简化分析响应过程,研究夹层板在冲击载荷作用下的塑性响应求解方法,并推导出适用于多种折叠式夹层板的塑性变形简化计算公式。
2) 在小计算量内,计算不同冲量作用下多种形式折叠式夹层板的塑性变形,并与有限元仿真结果进行对比,发现2种结果吻合较好,证明了所得理论预报公式的可行性与实用性,并为夹层板的工程设计提供参考。
3) 在芯层数量相同的情况下Uc连续型夹层板结构具有更优的抗爆性能,并且利用内接屈服面函数能更好的反映夹层板局部区域的变形情况。
| [1] |
张晓君, 杜志鹏, 谢永和. 夹层板在舰艇冲击防护中的研究进展[J]. 中国造船, 2011, 52(4): 270-281. ZHANG Xiaojun, DU Zhipeng, XIE Yonghe. Advances in study of sandwich plates for ship shock mitigating[J]. Shipbuilding of China, 2011, 52(4): 270-281. DOI:10.3969/j.issn.1000-4882.2011.04.032 (  0) 0)
|
| [2] |
LOK T S, CHENG Qianhua. Dynamic behavior of truss-core sandwich panel as an orthotropic thick plate[C]//Proceedings of the Seventh International Conference and Exposition on Engineering, Construction, Operations, and Business in Space. New Mexico: American Society of Civil Engineers, 2000: 342-348.
(  0) 0)
|
| [3] |
LOK T S, CHENG Q H. Bending and forced vibration response of a clamped orthotropic thick plate and sandwich panel[J]. Journal of sound and vibration, 2001, 245(1): 63-78. (  0) 0)
|
| [4] |
梁军, 刘均, 程远胜. 冲击载荷作用下方形蜂窝夹层板塑性动力响应分析[J]. 船舶力学, 2010, 14(10): 1165-1172. LIANG Jun, LIU Jun, CHENG Yuansheng. Dynamic plastic response of sandwich plates with square honeycomb cores subjected to shock loading[J]. Journal of ship mechanics, 2010, 14(10): 1165-1172. DOI:10.3969/j.issn.1007-7294.2010.10.013 (  0) 0)
|
| [5] |
尹群, 李舒, 王珂. 冲击毁伤载荷作用下新型舰船舱壁结构型式研究[J]. 舰船科学技术, 2017, 39(6): 6-11. YIN Qun, LI Shu, WANG Ke. Research on new ship bulkhead structure under impact damage load[J]. Ship science and technology, 2017, 39(6): 6-11. DOI:10.3404/j.issn.1672-7619.2017.06.002 (  0) 0)
|
| [6] |
LI Wei, HUANG Guangyan, BAI Yang, et al. Dynamic response of spherical sandwich shells with metallic foam core under external air blast loading-Numerical simulation[J]. Composite structures, 2014, 116: 612-625. DOI:10.1016/j.compstruct.2014.05.038 (  0) 0)
|
| [7] |
ZHU Feng, ZHAO Longmao, LU Guoxing, et al. A numerical simulation of the blast impact of square metallic sandwich panels[J]. International journal of impact engineering, 2009, 36(5): 687-699. DOI:10.1016/j.ijimpeng.2008.12.004 (  0) 0)
|
| [8] |
LANGDON G S, KARAGIOZOVA D, VON KLEMPERER C J, et al. The air-blast response of sandwich panels with composite face sheets and polymer foam cores:experiments and predictions[J]. International journal of impact engineering, 2013, 54: 64-82. DOI:10.1016/j.ijimpeng.2012.10.015 (  0) 0)
|
| [9] |
俞鞠梅.金属折叠式夹层板上层建筑防护性能分析[D].镇江: 江苏科技大学, 2014. YU Jumei. Research on protective mechanism of superstructure applying folded core sandwich panels[D]. Zhenjiang: Jiangsu University of Science and Technology, 2014. (  0) 0)
|
| [10] |
XIA Zhicheng, WANG Xihao, FAN Hualin, et al. Blast resistance of metallic tube-core sandwich panels[J]. International journal of impact engineering, 2016, 97: 10-28. DOI:10.1016/j.ijimpeng.2016.06.001 (  0) 0)
|
| [11] |
XIANG X M, LU G, MA G W, et al. Blast response of sandwich beams with thin-walled tubes as core[J]. Engineering structures, 2016, 127: 40-48. DOI:10.1016/j.engstruct.2016.08.034 (  0) 0)
|
| [12] |
LIM J Y, BART-SMITH H. High velocity compressive response of metallic corrugated core sandwich columns[J]. International journal of mechanical sciences, 2016, 106: 78-94. DOI:10.1016/j.ijmecsci.2015.12.010 (  0) 0)
|
| [13] |
邓磊, 王安稳, 毛柳伟, 等. 方孔蜂窝夹层板在爆炸载荷下的吸能特性[J]. 振动与冲击, 2012, 31(17): 186-189. DENG Lei, WANG Anwen, MAO Liuwei, et al. Energy absorption characteristics of a square hole honeycomb sandwich plate under blast loading[J]. Journal of vibration and shock, 2012, 31(17): 186-189. DOI:10.3969/j.issn.1000-3835.2012.17.034 (  0) 0)
|
| [14] |
朱锡, 李朝晖. 非接触爆炸载荷作用下舰船板架的塑性动力响应[J]. 武汉造船, 1998(6): 1-4. ZHU Xi, LI Chaohui. Plastic dynamic response of shipboard under non-contact explosion loading[J]. Wuhan shipbuilding, 1998(6): 1-4. (  0) 0)
|
| [15] |
吴有生, 彭兴宁, 赵本立. 爆炸载荷作用下舰船板架的变形与破损[J]. 中国造船, 1995(4): 55-61. WU Yousheng, PENG Xingning, ZHAO Benli. Plastic deformation and damage of naval panels subjected to explosion loading[J]. Shipbuilding of China, 1995(4): 55-61. (  0) 0)
|
| [16] |
FLECK N A, DESHPANDE V S. The resistance of clamped sandwich beams to shock loading[J]. Journal of applied mechanics, 2003, 71(3): 386-401. DOI:10.1115/1.1629109 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


