光谱解混在高光谱图像应用中扮演着重要角色。解混算法依赖于预先假设的线性或非线性的光谱混合模型,由于线性混合模型在实际应用中具有灵活、易于实现等优点,当前大部分光谱解混算法均基于线性混合模型(linear mixing model, LMM)[1]。稀疏解混算法将高光谱图像中每个混合像元建模为预先可获得的光谱库中地物光谱的线性组合,其目的是在光谱库中找到最优的端元子集并求解该端元子集所对应的丰度[2]。
由于参与混合像元的端元数量远小于库中涉及的原子数量,在求解稀疏解混欠定方程时,需要基于稀疏诱导正则项的有效稀疏回归技术。Bioucas-Dias等[3]提出变量分离与增广拉格朗日(sparse unmixing algorithm via variable splitting and augmented Lagrangian, SUnSAL)算法,该算法通常假设参与每个像元的端元数量较少,尽管该方法具有低复杂度,但它没有在解混模型中考虑端元的分布情况,解混性能较差。Iordache等[4]提出的协同变量分离与增广拉格朗日(the collaborative SUnSAL, CLSUnSAL)算法是在假设高光谱图像中的所有像元共享相同的活越端元的情况下开发的。这意味着如果光谱库原子的丰度被收集在矩阵中,则丰度矩阵中应该只有少数几个非零行。但CLSUnSAL算法却没有考虑到端元总是出现在空间均匀区域而并非均匀分布在整个高光谱图像场景中,根据这一分析,Zhang等[4]等提出了局部协同稀疏回归算法。研究表明,稀疏解混中包含的空间信息对估计的丰度的准确性有积极的影响[5]。Iordache等[6]提出的全变差正则化变量分离与增广拉格朗日(sparse unmixing via variable splitting augmented Lagrangian and total variation, SUnSAL-TV)算法将空间信息作为全变差(total variation, TV)正则项应用于稀疏解混数学模型。该TV项假设2个空间相邻的像元对同一种地物端元具有相似的丰度。然而,地物分布总是充满了复杂性,对于那些地物分布边界上的像元来说,在TV正则项的作用下,SUnSAL-TV算法可能会产生过平滑与边缘模糊的现象。
Lefkimmiatis等[7]提出的结构张量全变差(structure tensor total variation, STV)正则项族能够很好地描述图像内局部邻域周围的变化度量,将该正则项族应用于灰度和矢量值图像的去噪与去模糊中已取得了很显著的效果。受此启发,本文提出了一种结构张量全变差再优化变量分离与增广拉格朗日(SUnSAL-TV-STV)的稀疏解混算法。该算法通过将STV正则项引入到SUnSAL-TV模型中约束求解的丰度矩阵,自适应地校正相邻像元所对应的丰度向量之间的平滑性,该算法具有良好的鲁棒性与解混性能。
1 线性稀疏解混模型LMM中每个像元的光谱由端元光谱的线性混合来近似表达。在这种情况下,令L维向量y表示具有L个光谱带的高光谱图像的像元向量。观测像元yi可以以光谱库A中的光谱特征的线性组合的形式给出:
| $ {\mathit{\boldsymbol{y}}_i} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i} + {\mathit{\boldsymbol{n}}_i} $ | (1) |
式中:m×1维向量xi表示被估计的丰度;L×1维向量ni表示影响每个光谱带测量的误差。在线性混合模型中,丰度向量满足非负限制(ANC):xi≥0与和为1限制(ASC)
由于在光谱库中只有少数的端元原子参与观测像元光谱的混合,式(1)中的丰度向量xi是稀疏的。通过上面的这些定义,可以将解混问题写成P0问题:
| $ \mathop {{\rm{min}}}\limits_{{x_i}} {\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|_0}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left\| {{\mathit{\boldsymbol{y}}_i} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i}} \right\|_2} \le \delta ,{\mathit{\boldsymbol{x}}_i} \ge 0 $ | (2) |
式中:‖xi‖0代表丰度向量xi中非零数值的个数;δ是根据噪声和建模误差设置的容忍误差。由于P0问题是非凸优化问题,正交匹配追踪算法(orthogonal matching pursuit, OMP)是一种成熟的贪婪算法来解决P0问题[9]。字典A的稀疏度定义为A中最小线性相关的原子个数,它给定一个简单而直接的方式计算P0问题的解的唯一性,然而计算一个矩阵的稀疏度与求解P0问题同样困难。已经证明,在受限等距特性(restricted isometry property, RIP)的某种条件下,丰度向量的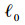

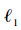
| $ \mathop {{\rm{min}}}\limits_{{x_i}} \frac{1}{2}{\kern 1pt} \left\| {{\mathit{\boldsymbol{y}}_i} - \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{x}}_i}} \right\|_2^2 + \lambda {\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|_1}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{x}}_i} \ge 0 $ | (3) |
式中: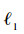
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{AX}} + \mathit{\boldsymbol{N}} $ | (4) |
这种方法将丰度矩阵X转换到Sobolev空间W1, 2(R2,Rm)。令n为任意二维空间内的单位方向向量,丰度X中任意像元点x处沿着方向n的方向导数定义为:
| $ \frac{{\partial \mathit{\boldsymbol{X}}}}{{\partial \mathit{\boldsymbol{n}}}}(x) = ({\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{X}}}(x))\mathit{\boldsymbol{n}} $ | (5) |
式中:JX是X的雅克比(Jacobian)矩阵,定义为:
| $ {\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{X}}}(\mathit{\boldsymbol{x}}) = [\nabla {\mathit{\boldsymbol{X}}_1}(\mathit{\boldsymbol{x}}), \cdots ,\nabla {\mathit{\boldsymbol{X}}_m}(\mathit{\boldsymbol{x}})] $ | (6) |
方向导数的大小‖∂X/∂n‖2描述了丰度X中像元点x沿n的变化量。为了更加有效地捕获与x相邻的像元的丰度差异,本文计算3×3窗口中‖∂X/∂n‖2的加权均方根(root mean square, RMS),其中像素点x位于该窗口的中心。RMSK{‖∂X/∂n‖2}就是所谓的方向变化量:
| $ \begin{array}{*{20}{c}} { {\rm{RM}}{{\rm{S}}_K}\{ {{\left\| {\partial \mathit{\boldsymbol{X}}/\partial \mathit{\boldsymbol{n}}} \right\|}_2}\} = \sqrt {\mathit{\boldsymbol{K}}*\left\| {\partial \mathit{\boldsymbol{X}}/\partial \mathit{\boldsymbol{n}}} \right\|_2^2} = }\\ {\sqrt {{\mathit{\boldsymbol{n}}^{\rm{T}}}({S_k}\mathit{\boldsymbol{X}})\mathit{\boldsymbol{n}}} } \end{array} $ |
式中:K(x)代表非负旋转对称的高斯卷积核;SKX代表像元点x所对应的结构张量,可表示为:
| $ {S_K}\mathit{\boldsymbol{X}}(x) = \mathit{\boldsymbol{K}}*[\mathit{\boldsymbol{J}}_\mathit{\boldsymbol{X}}^{\rm{T}}\mathit{\boldsymbol{JX}}](x) $ | (7) |
式中:SKX(x)是一个实对称2×2矩阵,令λ+=λ+(SKX(x)),λ-=λ-(SKX(x))为SKX(x)的2个特征值且有λ+≥λ-,θ+和θ-为2个特征值所对应的单位特征向量。令ω∈(-π, π]表示方向向量n与特征向量θ+之间的夹角,利用矩阵的特征分解对式(7)进行展开分析,可以得出2个重要结论:
1) 特征向量θ+和θ-的方向描述了最大和最小矢量变化的方向,特征值的算术平方根
2) 结构张量的特征值能够反映某一像元点相对于周围像元点的丰度的几何特征。当
由上面的分析,根据文献[7]中定义,将结构张量正则项定义为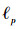
| $ {\rm{ST}}{{\rm{V}}_p}(\mathit{\boldsymbol{X}}) = \int_{{{\bf{R}}^2}} {{{\left\| {(\sqrt {{\lambda ^ + }} ,\sqrt {{\lambda ^ - }} )} \right\|}_p}{\rm{d}}x} $ | (8) |
在式(8)的基础上,引入基于补丁的Jacobian算子[11], 则STV正则项的离散形式可以表示为:
| $ {{{[{\mathit{\boldsymbol{J}}_K}\mathit{\boldsymbol{X}}]}_n}} $ | (9) |
式中:JK是扮演着线性映射JK:RNx×Ny×m→χ (Nx×Ny=N代表图像平面)的基于补丁的Jacobian算子,χ
| $ {\left\| \mathit{\boldsymbol{M}} \right\|_{{S_p}}} = {(\sum\limits_{n = 1}^{{\rm{min}}({N_1},{N_2})} {\sigma _n^p} )^{\frac{1}{p}}} $ |
式中σn是矩阵M(M∈RN1×N2)的第n个奇异值。
2.2 解混模型与ADMM优化算法 2.2.1 SUnSAL-TV-STV解混模型SUnSAL-TV-STV属于一种“两步法”算法,先通过SUnSAL-TV算法求解丰度矩阵,再利用STV正则项来探索丰度的分片平滑结构。这个再优化的过程可表示为丰度降噪模型[13]:
| $ \mathit{\boldsymbol{\hat S}} = \mathop {{\rm{ argmin }}}\limits_{\mathit{\boldsymbol{\hat S}} \in {{\bf{R}}^{m \times N}}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{S}} - \mathit{\boldsymbol{X}}} \right\|_F^2 + {\lambda _{{\rm{STV}}}} {\rm{STV}} (\mathit{\boldsymbol{S}})} \right\} $ | (10) |
式中:X表示SUnSAL-TV算法求解的丰度矩阵;
综上,本文提出SUnSAL-TV-STV求解优化问题:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{c}} {\mathop {{\rm{min}}}\limits_X \frac{1}{2}\left\| {\mathit{\boldsymbol{AX}} - \mathit{\boldsymbol{Y}}} \right\|_F^2 + \lambda {{\left\| \mathit{\boldsymbol{X}} \right\|}_{1,1}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _{TV}}{{\left\| {\mathit{\boldsymbol{HX}}} \right\|}_{1,1}} + {\iota _{R + }}(\mathit{\boldsymbol{X}})} \end{array}\\ \begin{array}{*{20}{r}} {\mathit{\boldsymbol{\hat S}} = \mathop {{\rm{argmin }}}\limits_{\hat S \in {{\bf{R}}^{m \times N}}} \frac{1}{2}\left\| {\mathit{\boldsymbol{\hat S}} - \mathit{\boldsymbol{X}}} \right\|_F^2 + }\\ {{\lambda _{{\rm{STV}}}}{\rm{ST}}{{\rm{V}}_P}(\mathit{\boldsymbol{\hat S}}) + {\iota _C}(\mathit{\boldsymbol{\hat S}})} \end{array} \end{array} \right. $ | (11) |
式中:
乘子交替法(the alternating direction method of multipliers, ADMM)是求解上述优化问题的一个简单而有效的算法。对于给定的目标函数(11),有如下约束优化问题:
| $ \left\{ \begin{array}{l} \mathop {{\rm{min}}}\limits_{U,{V_1},{V_2},{V_3},{V_4},{V_5}} \frac{1}{2}\left\| {{\mathit{\boldsymbol{V}}_1} - \mathit{\boldsymbol{Y}}} \right\|_F^2 + \lambda {\left\| {{\mathit{\boldsymbol{V}}_2}} \right\|_{1,1}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _{{\rm{TV}}}}{\left\| {{\mathit{\boldsymbol{V}}_4}} \right\|_{1,1}} + {\iota _{R + }}({\mathit{\boldsymbol{V}}_5})\\ \hat U = \mathop {{\rm{min}}}\limits_{\hat U \in {{\bf{R}}^{m \times N}}} \frac{1}{2}\left\| {\hat U - U} \right\|_F^2 + {\lambda _{{\rm{STV}}}} {\rm{STV}}{ _P}(\hat U) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\iota _C}(\hat U) \end{array} \right. $ |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}\left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{V}}_1} = \mathit{\boldsymbol{AU}}}\\ {{\mathit{\boldsymbol{V}}_2} = \mathit{\boldsymbol{U}}}\\ {{\mathit{\boldsymbol{V}}_3} = \mathit{\boldsymbol{U}}}\\ {{\mathit{\boldsymbol{V}}_4} = \mathit{\boldsymbol{H}}{\mathit{\boldsymbol{V}}_3}}\\ {{\mathit{\boldsymbol{V}}_5} = \mathit{\boldsymbol{U}}} \end{array}} \right. $ |
令L(U, V, D)≡g(U, V)+(μ/2)‖GU-BV-D‖F2为增广拉格朗日乘子形式:
| $ \mathop {{\rm{min}}}\limits_{U,V} g (\mathit{\boldsymbol{U}},\mathit{\boldsymbol{V}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{GU}} + \mathit{\boldsymbol{BV}} = 0 $ | (12) |
μ是一个正数,D/μ是关联于限制GU+ BV=0的拉格朗日乘子。V、G、B可表示为:
| $ \mathit{\boldsymbol{V}} = ({\mathit{\boldsymbol{V}}_1},{\mathit{\boldsymbol{V}}_2},{\mathit{\boldsymbol{V}}_3},{\mathit{\boldsymbol{V}}_4},{\mathit{\boldsymbol{V}}_5}) $ |
| $ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}\\ \mathit{\boldsymbol{I}}\\ \mathit{\boldsymbol{I}}\\ {\bf{0}}\\ \mathit{\boldsymbol{I}} \end{array}} \right]\;\:\mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - \mathit{\boldsymbol{I}}}&0&0&0&0\\ 0&{ - \mathit{\boldsymbol{I}}}&0&0&0\\ 0&0&{ - \mathit{\boldsymbol{I}}}&0&0\\ 0&0&H&{ - \mathit{\boldsymbol{I}}}&0\\ 0&0&0&0&{ - \mathit{\boldsymbol{I}}} \end{array}} \right] $ |
至于优化问题:
| $ \hat U = \mathop {{\rm{min}}}\limits_{\hat U \in {{\bf{R}}^{m \times N}}} \frac{1}{2}\left\| {\mathit{\boldsymbol{\hat U}} - \mathit{\boldsymbol{U}}} \right\|_F^2 + {\lambda _{{\rm{STV}}}} {\rm{STV}}{ _P}(\mathit{\boldsymbol{\hat U}}) + {\iota _C}(\mathit{\boldsymbol{\hat U}}) $ | (13) |
本文采用文献[7]中介绍的迭代方案求解优化问题(13)。ADMM算法中的停止迭代条件设置为‖GU(k)+BV(k)‖F≤ε,该优化算法的收敛速度依赖于选择一个合适的参数μ。试验仿真将采用文献[14-15]中描述的一个自适应方案来自动调整参数μ。
3 合成数据实验在2个不同的合成数据集上,我们通过实验来主要对比SUnSAL、CLSUnSAL、SUnSAL-TV算法以及本文提出的SUnSAL-TV-STV算法的解混性能。所有对比算法根据在调整正则项参数后各算法的信号重建误差(signal-to-reconstruction error, SRE)值改变量不超过0.001时来选择最佳参数。所有对比试验均使用MATLAB R2012b在配备G2030 CPU(3.2 GHz)和2 GB RAM台式机上实现。
信号重建误差(SRE)用于评估解混精度。令
| $ {\rm{SRE}} ({\mathit{\boldsymbol{x}}_i}) = 10{\rm{lg}}\left( {\frac{{{\rm{E}}(\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|_2^2)}}{{{\rm{E}}(\left\| {{\mathit{\boldsymbol{x}}_i} - {{\mathit{\boldsymbol{\hat x}}}_i}} \right\|_2^2)}}} \right) $ |
SRE的值越大,解混结果越精确。此外,合成数据试验还采用了成功概率(Ps)的指标来评估解混性能。Ps定义为:
| $ {P_s} = P({\left\| {{{\mathit{\boldsymbol{\hat x}}}_i} - {\mathit{\boldsymbol{x}}_i}} \right\|^2}/{\left\| {{\mathit{\boldsymbol{x}}_i}} \right\|^2} \le T) $ |
这是对相对误差功率小于等于某个阈值T的概率估计[16]。为了缩短算法的运行时间,本文采用HySime(hyperspectral signal subspace estimation)算法[17]来估计试验数据的信号子空间,在此基础上采用多信号分类(multi-signal classification, MUSIC)算法来修剪光谱库以识别光谱库的子集,该子集包含端元信号[18]。
3.1 合成数据实验1第1个实验中使用的光谱库是USGS数字光谱库splib06a[19]的第1章(A1∈R224×498)。该实验随机选择5个光谱原子作为端元集并根据狄利克雷(Dirichlet)分布[19]模拟丰度矩阵来生成含有64×64个像元的合成数据集1(DC1)。为模拟噪声环境,在上述生成的DC1中,本实验加入了不同信噪比(SNR=E‖Ax‖2/E‖n‖22)(20 dB,30 dB,40 dB)的高斯白噪声。采用HySime-MUSIC算法修剪光谱库库以保留10个光谱原子。
表 1给出的是不同SNR环境下各解混算法获得的SRE(dB)值。图 1对30 dB(DC1)下各解混算法的解混成功率进行了可视化对比。
| 表 1 DC1下各算法所得最优SRE值及参数 Table 1 Optimal SRE values obtained by various algorithms under DC1 and the parameters |

|
Download:
|
| 图 1 30 dB DC1下不同算法的解混成功率曲线 Fig. 1 Unmixing successful probability for DC1 with SNR=30 dB | |
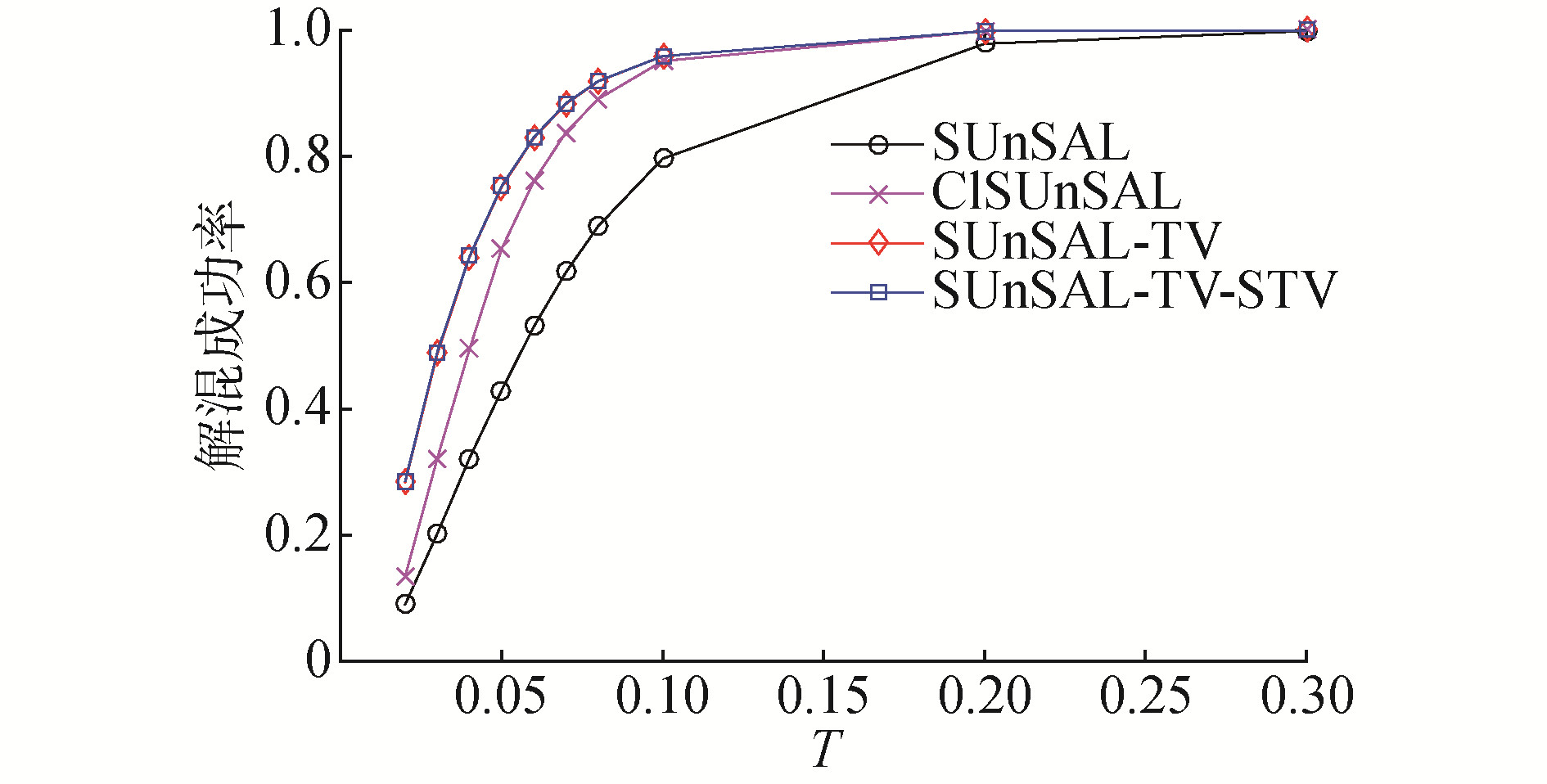
第2个实验使用的光谱库是由USGS库中随机选择的498种地物光谱生成(A2∈R224×498)。本实验从光谱库A2中随机选择9个光谱原子作为端元信号并根据Drichlet分布模拟丰度矩阵来合成具有75×75个像元的合成数据集DC2。在生成的DC2中同样加入了不同SNR(30、40、50 dB)的高斯白噪声。此外,该实验修剪光谱库后保留了20个光谱原子。表 2给出了不同SNR环境下各解混算法获得的SRE(dB)值。图 2描绘了30 dB(DC2)下各解混算法的解混成功率曲线。
|
Download:
|
| 图 2 30 dB DC2下不同算法的解混成功率曲线 Fig. 2 Unmixing successful probability for DC2 with SNR=30 dB | |
本文统计了SNR=20 dB的DC1实验中所有解混算法的计算处理时间,对应于SUnSAL、CLSUnSAL、SUnSAL-TV以及SUnSAL-TV-STV算法的处理时间分别为0.590 2、15.317 9、15.103 8、53.650 0 s。
SUnSAL算法的计算复杂度是最低的,但由于该算法并没有考虑到图像所包含的空间先验信息,解混精度也是所有算法中最低的。CLSUnSAL算法只是简单地假设所有像元共享光谱库中少数活跃的端元集,对空间信息的利用仍然不够充分。SUnSAL-TV-STV算法由于引入了新的空间正则项而提高了计算复杂度,但该算法采用STV正则项约束SUnSAL-TV算法所求解的丰度矩阵,自适应地修正了丰度矩阵的过平滑与边缘模糊问题,因此该算法能够以更高的可信度估计端元子集以及丰度矩阵。对比表 1和表 2中给出的SRE值可有力支持这一理论分析,同时也验证了本文所提出算法的优越性。此外,从图 1与图 2中可以观察到,在同一阈值T下SUnSAL-TV-STV算法具有最高的解混成功率。
| 表 2 DC2下各算法所得最优SRE值及参数 Table 2 Optimal SRE values obtained by various algorithms under DC2 and the parameters |
使用AVIRIS Cuprite开源数据集来进行真实高光谱数据试验。该实验使用的是一个非常具有代表性的250×191的像元子集,224个光谱带的光谱波长均匀分布在0.4~2.5 μm内。本实验移除了受吸水性与较低信噪比干扰的36个光谱带。该实验使用3.1节的数字光谱库A1作为本实验的光谱库,并相应的移除所对应的36个光谱带。此外,为提高解混精度,避免计算微小的误差值,将大于0.001的丰度估计值设为非零丰度并采用HySime-MUSIC算法人工修剪光谱库A1以保留54个光谱原子。最后要说明的是,在实际高光谱图像应用中,测试图像与预先获得的光谱库中的端元光谱之间由于成像条件不同总是存在一些差异[20],但本文将其视作统一控制因素,不予讨论上述差异对解混结果造成的影响。
真实数据试验采用原始高光谱图像与重建图像(通过被修剪光谱库及其相应的丰度矩阵重建)之间的绝对重建误差(ARE)来评估解混性能。ARE定义为:
| $ {\rm{ARE}} = {\left\| {\mathit{\boldsymbol{\hat Y}} - \mathit{\boldsymbol{Y}}} \right\|_1} $ |
式中Ŷ表示重建图像。图 3对应用各解混算法求得的真实数据集中明矾岩、芽化石和玉髓3种矿物的丰度图(从左到右)进行了定性的比较。表 3给出了在真实高光谱数据上应用各解混算法后计算所得的最优ARE值。

|
Download:
|
| 图 3 由SUnSAL,CLSUnSAL,SUnSAL-TV和SUnSAL-TV-STV算法估计的AVIRIS Cuprite矿区250×191像元子集的丰度 Fig. 3 Fractional abundance maps estimated by SUnSAL, CLSUnSAL, SUnSAL-TV, and SUnSAL-TV-STV(from top to bottom)for the considered 250×191 pixel subset of the AVIRIS Cuprite scene | |
从表 3中各解混算法计算所得ARE值的对比中可以看出,SUnSAL-TV-STV算法具有最低的重建误差。此外,上述各解混算法估计的每个像元中丰度值大于0.01的平均端元数分别为5.041 8、5.091 4、5.437 3、5.520 9。这些微小的差异反映出SUnSAL-TV-STV能够使用光谱库中少量的端元光谱来解释每个混合像元,从而强调了解的稀疏性。定量地评估真实高光谱数据的解混结果是不充分的,还可以定性地观察到在明矾岩的丰度估计图中SUnSAL-TV-STV算法自适应地修正了由SUnSAL-TV算法产生的过平滑与边缘模糊问题。综上所述,可以得出结论,SUnSAL-TV-STV算法是一种包含空间信息的有效的高光谱图像稀疏解混算法。
| 表 3 真实数据下各算法所得最优ARE值及参数 Table 3 Optimal ARE values obtained by various algorithms under the real hyperspectral data and the parameters |
1) 本文提出了一种包含空间信息的高光谱图像稀疏解混算法SUnSAL-TV-STV。相对于SUnSAL-TV模型,该算法引入了结构张量全变差空间正则项,该空间正则项可根据丰度向量所对应的像元的空间几何特征,自适应地对SUnSAL-TV算法所求解的丰度矩阵进行降噪处理,有效地改善其边缘模糊与过平滑问题。
2) 与现阶段的其他稀疏解混算法相比,该算法在合成数据与真实高光谱数据的试验仿真中均获得了较好的解混性能。
虽然该算法在解混性能上得到了提高,但由于添加了新的空间正则项而牺牲了算法复杂度,未来工作将进一步改进算法以降低算法复杂度。此外,受空间非局部相似性的启发,未来工作也将考虑在解混模型中引入能够更充分挖掘图像空间信息的非局部结构张量全变差[21]正则项来有效提高解混性能。
| [1] |
BIOUCAS-DIAS J M, PLAZA A, DOBIGEON N, et al. Hyperspectral unmixing overview:geometrical, statistical, and sparse regression-based approaches[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2012, 5(2): 354-379. (  0) 0)
|
| [2] |
IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Sparse unmixing of hyperspectral data[J]. IEEE transactions on geoscience and remote sensing, 2011, 49(6): 2014-2039. DOI:10.1109/TGRS.2010.2098413 (  0) 0)
|
| [3] |
IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Collaborative sparse regression for hyperspectral unmixing[J]. IEEE transactions on geoscience and remote sensing, 2014, 52(1): 341-354. (  0) 0)
|
| [4] |
ZHANG Shaoquan, LI Jun, LIU Kai, et al. Hyperspectral unmixing based on local collaborative sparse regression[J]. IEEE geoscience and remote sensing letters, 2016, 13(5): 631-635. (  0) 0)
|
| [5] |
TONG Lei, ZHOU Jun, LI Xue, et al. Region-based structure preserving nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2017, 10(4): 1575-1588. DOI:10.1109/JSTARS.2016.2621003 (  0) 0)
|
| [6] |
IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Total variation spatial regularization for sparse hyperspectral unmixing[J]. IEEE transactions on geoscience and remote sensing, 2012, 50(11): 4484-4502. DOI:10.1109/TGRS.2012.2191590 (  0) 0)
|
| [7] |
LEFKIMMIATIS S, ROUSSOS A, MARAGOS P, et al. Structure tensor total variation[J]. SIAM journal on imaging sciences, 2015, 8(2): 1090-1122. DOI:10.1137/14098154X (  0) 0)
|
| [8] |
AKHTAR N, SHAFAIT F, MIAN A. Futuristic greedy approach to sparse unmixing of hyperspectral data[J]. IEEE transactions on geoscience and remote sensing, 2015, 53(4): 2157-2174. (  0) 0)
|
| [9] |
AKHTAR N, SHAFAIT F, MIAN A. SUnGP: a greedy sparse approximation algorithm for hyperspectral unmixing[C]//Proceedings of the 22nd International Conference on Pattern Recognition. Stockholm, Sweden: IEEE, 2014: 3726-3731.
(  0) 0)
|
| [10] |
LAI Mingjun. On sparse solutions of underdetermined linear systems[J]. Journal of concrete and applicable mathematics, 2010, 8(2): 296-327. (  0) 0)
|
| [11] |
WU Zhaojun, WANG Qiang, JIN Jing, et al. Structure tensor total variation-regularized weighted nuclear norm minimization for hyperspectral image mixed denoising[J]. Signal processing, 2017, 131: 202-219. DOI:10.1016/j.sigpro.2016.07.031 (  0) 0)
|
| [12] |
LEFKIMMIATIS S, WARD J P, UNSER M. Hessian schatten-norm regularization for linear inverse problems[J]. IEEE transactions on image processing, 2013, 22(5): 1873-1888. (  0) 0)
|
| [13] |
HE Wei, ZHANG Hongyan, ZHANG Liangpei. Total variation regularized reweighted sparse nonnegative matrix factorization for hyperspectral unmixing[J]. IEEE Transactions on geoscience and remote sensing, 2017, 55(7): 3909-3921. DOI:10.1109/TGRS.2017.2683719 (  0) 0)
|
| [14] |
HE B S, YANG H, WANG S L. Alternating direction method with self-adaptive penalty parameters for monotone variational inequalities[J]. Journal of optimization theory and applications, 2000, 106(2): 337-356. (  0) 0)
|
| [15] |
WANG S L, LIAO L Z. Decomposition method with a variable parameter for a class of monotone variational inequality problems[J]. Journal of optimization theory and applications, 2001, 109(2): 415-429. (  0) 0)
|
| [16] |
LI Y, ZHANG S, DENG C, et al. Reweighted local collaborative sparse regression for hyperspectral unmixing[J]. Infrared physics & technology, 2019, 97: 277-286. (  0) 0)
|
| [17] |
BIOUCAS-DIAS J M, NASCIMENTO J M P. Hyperspectral subspace identification[J]. IEEE transactions on geoscience and remote sensing, 2008, 46(8): 2435-2445. DOI:10.1109/TGRS.2008.918089 (  0) 0)
|
| [18] |
IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Dictionary pruning in sparse unmixing of hyperspectral data[C]//Proceedings of the 4th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing. Shanghai, China: IEEE, 2012: 1-4.
(  0) 0)
|
| [19] |
TANG Wei, SHI Zhenwei, WU Ying. Regularized simultaneous forward-backward greedy algorithm for sparse unmixing of hyperspectral data[J]. IEEE transactions on geoscience and remote sensing, 2014, 52(9): 5271-5288. DOI:10.1109/TGRS.2013.2287795 (  0) 0)
|
| [20] |
YUAN Yuan, FENG Yachuang, LU Xiaoqiang. Projection-based NMF for hyperspectral unmixing[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2015, 8(6): 2632-2643. DOI:10.1109/JSTARS.2015.2427656 (  0) 0)
|
| [21] |
LEFKIMMIATIS S, OSHER S. Nonlocal structure tensor functionals for image regularization[J]. IEEE transactions on computational imaging, 2015, 1(1): 16-29. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


