2. 哈尔滨工程大学 计算机科学与技术学院, 黑龙江 哈尔滨 150001
2. College of Computer Science and Technology, Harbin Engineering University, Harbin 150001, China
近年来,随着传感器、无线射频识别标签(RFID)以及机器对机器(machine-to-machine, M2M)等相关技术的快速发展,对可穿戴设备等应用领域需求的提高,物联网(internet of things, IOT)己经成为当今学术研究领域和工业制造领域的一项热门技术,并在未来新型互联网世界中占有重要地位[1]。自2005年国际电信联盟正式提出物联网概念以来,物联网产业发展迅猛,目前被广泛应用于环境监测与保护、智能交通、移动医疗、食品安全和物流供应链管理等诸多领域。根据Statistic门户网站最新统计数据,2017年物联网的互联设备数量约为203.5亿,预计2020年增长至307.3亿,市场规模将达7.1万亿美元。
WSNs作为物联网参与信息感知的重要组成部分发挥着越来越重要的作用。WSNs是一种分布式无线网络,由部署在感知区域的数量庞大的低功耗传感器节点通过无线通信链路通信所构成。传感器节点是一种微型计算单元,具有存储容量小,计算能力有限和电池供能等特点。由于无线网络的开放性以及传感器节点自身的限制,WSNs面临着多种多样的安全威胁。引入密钥管理和身份认证机制作为保护WSNs的第一道防线,可以有效防御来自WSNs外部的攻击。然而,攻击者通过捕获节点可以获得节点内部的秘密消息,进而发动内部攻击。第一道防线无法抵抗WSNs的内部攻击。入侵检测技术作为安全防御的第二道防线能够从根源上发现安全威胁,降低攻击带来的损失。由于WSNs的局限性,传统的入侵检测技术不能直接应用于WSNs环境中。研究一种适合WSNs入侵检测技术成为研究热点,引起了国内外专家学者的广泛关注。
根据检测入侵的实现细节可以将入侵检测系统分为基于特征的入侵检测技术和基于异常的特征检测技术[2]。基于特征的入侵检测技术使用一组预定义恶意行为模式和攻击特征进行入侵检测,而基于异常的入侵检测系统使用异于正常的行为作为特征检测入侵行为[3]。WSNs应用场景多种多样,基于预定义攻击特征的入侵检测是不切实际的,基于异常的入侵检测系统能够在缺少预定义攻击特征的前提下检测未知攻击。基于异常的入侵检测系统主要包括:基于统计学的入侵检测技术和基于机器学习的入侵检测技术。
张玲等[4]引入粗糙集方法对基于人工免疫的入侵检测模型进行改进,将异常检测和误用检测有机结合,提出一种入侵检测方法,该方法能够在不终止入侵检测行为的前提下实现疫苗的注入。粗糙集优化了疫苗,进而提高了入侵检测方法的检测性能。疫苗的注入有效降低了检测器的长度,提高了检测速度。然而,基于免疫的入侵检测方法在训练初期存在检测率低的问题。
杜辉等[5]提出一种K-means算法解决了聚类数目预先设定和算法陷入局部最优的问题。该算法在样本空间均匀地防止若干数目的探测器,使用万有引力定律牵引探测器,当探测器之间的距离足够近时,进行合并。算法最终包含的探测器的数目就是聚类中心的数目。但是该方法对样本数据的离群点效果不佳,由于离群点与聚类中心距离较远,万有引力产生的作用微乎其微。
为了解决数据量过大造成入侵检测效率低的问题,江颉等[6]将自适应AP算法于聚类算法相结合,提出自适应AP聚类算法,并将其应用于入侵检测。该算法仅对基准数据和距离聚类中心较远的样本进行聚类,其余样本数据进行直接关联操作,减少了进行聚类的样本数量,降低了聚类的时间,同时根据关联结果对模型不断调整。数据压缩提高了聚类的效率,但是不可避免地造成了精度的下降。
刘绪崇[7]针对传统模糊C均值聚类算法的缺陷,提出一种改进算法:采用Mercer核定义优化FCM算法的目标函数提高了FCM的寻优能力,使用Lagrange乘子法分别计算聚类中心和隶属度矩阵,提高了算法收敛的速度。但是该算法没有解决不平衡聚类和噪声点对聚类结果的影响。
许勐璠等[8]针对现有入侵检测方法对未知类型攻击检测率低的问题,提出了基于半监督学习和信息增益率的入侵检测方案:训练阶段,借助半监督学习算法将少量标记数据扩展为大规模训练数据;检测阶段,借助信息增益率量化不同特征对检测性能的影响,提高了模型对未知类型攻击的识别能力。
任家东等[9]针对Probe(probing),U2R(user to root)和R2L(remote to local)的检测率比较低这一问题,提出一种混合多层次入侵检测模型:首先,使用KNN剔除离群样本数据,构造一个质量高且规模小的训练集;然后,针对不同类型的攻击,提出一种类别划分方法;最终构建多层次随机森林模型进行网络异常的检测。实验表明该方法能够提高Probe、U2R和R2L等网络攻击行为的检测效果。
现有的入侵检测方法取得一定成果的同时,存在一定的问题:针对已知攻击类型的攻击检测率较高,但是未知类型的攻击效果不佳;由于应用场景的复杂多变,实际应用中的入侵检方案受到恶劣环境的影响存在误报率偏高的现象;为了提高检测率,一些入侵检测算法引入复杂的数学模型,增加了计算复杂度,不适合资源受限的应用场景。本文针对WSNs资源高度受限的特性,提出一种基于机器学习的WSNs入侵检测方法,用来抵抗WSNs常见的攻击行为。
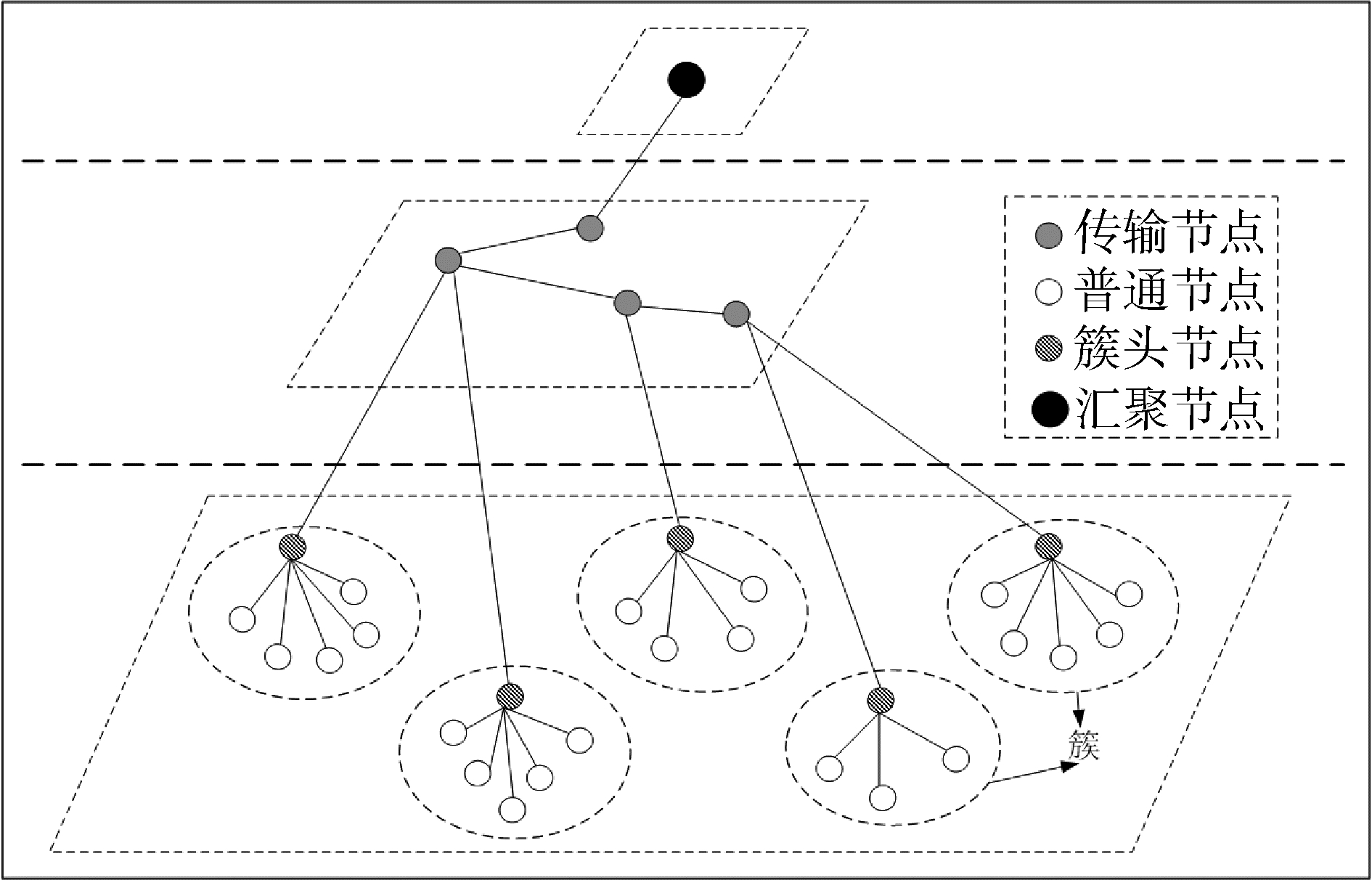
1 WSNs网络结构及威胁模型 1.1 网络结构本文的提出的入侵检测方法基于3层WSNs网络。网络包含4种节点类型:传感器节点部署在监控区域,在组网初期根据分簇算法形成簇,负责采集监控区域的状态信息,形成感知数据并发送给簇头节点;簇头节点是每个簇的管理者负责将传感器节点采集的感知数据进行数据聚合发送给传输节点;传输节点将数据以无线多跳的形式传输至汇聚节点;汇聚节点负责进一步处理数据并呈现给用户。网络结构如图 1所示。
|
Download:
|
| 图 1 分层WSNs网络模型 Fig. 1 Cluster-based WSNs network model | |
本文提出的入侵检测方法主要针对黑洞攻击、灰洞攻击、洪泛攻击和调度攻击等类型的主动攻击行为,具体如下所示。
黑洞攻击:攻击节点在每个工作周期的开始阶段将自己是簇头节点的消息通过广播的方式发送给其他节点。因此,一些节点会错误地加入伪簇头节点进而将数据包发送给伪簇头节点。真正的簇头节点会将数据包转发至基站,发起黑洞攻击的伪簇头节点会持续地丢弃数据包并不会转发给基站。
灰洞攻击:与黑洞攻击相同的是,攻击节点在每个工作周期的开始阶段将自己是簇头节点的消息通过广播的方式发送给其他节点。一些节点会错误地加入伪簇头节点进而将数据包发送给伪簇头节点。与黑洞攻击不同的是,发起灰洞攻击的伪簇头节点随机丢弃数据包或者丢弃特定类型的数据包并阻止数据包转发给基站。
洪泛攻击:洪泛攻击主要发送大量簇头广播消息占用大量网络带宽资源。感知节点收到大量的簇头广播消息不仅耗费了感知层节点的能源供给,而且导致感知节点耗费大量时间决定加入具体的簇头节点。除此之外,攻击节点会尝试欺骗感知节点并伪装成伪簇头,令远距离感知节点加入自己导致其能源耗费严重。
调度攻击:调度攻击发生在LEACH协议的初始化阶段,簇头节点实现分时复用调度策略为感知节点确定数据传输时间戳。攻击者假装簇头节点,赋予所有感知节点相同的发送数据时间戳。攻击者将广播调度行为修改为单播调度行为,最终导致数据冲突进而数据丢失。
2 基于机器学习的检测算法 2.1 基于密度感知的初始数据集划分算法假设数据集为X={x1, x2, …, xN},数据集中的每个数据点表示为xi={xi1, xi2, …, xiM},其中,M表示数据样本属性的数目。数据点聚类中心通常被具有低局部密度的邻居样本点包围,具有高局部密度的数据点之间保持较大的距离。
定义1 样本数据xi的局部密度表示为ρi:
| $ {\rho _i} = \sum\limits_{j = 1}^N {{\rm{exp}}} \left[ { - {{\left( {\frac{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|}}{{{d_c}}}} \right)}^2}} \right] $ | (1) |
式中:‖ xi- xj‖表示xi和xj之间的欧式距离;dc为预定义的截断距离,通常为所有样本截断距离的前1%~2%。局部密度ρi表示样本数据xi之间距离小于dc的数据点个数。与样本数据xi之间距离小于dc的数据点越多,密度值ρi越大。本文选择连续型高斯核计算样本数据的局部密度避免不同样本数据的局部密度值相同。
定义2 特征距离表示样本数据xi与具有更高局部密度的样本数据之间的最小距离:
| $ {\delta _i} = \mathop {{\rm{min}}}\limits_{{x_j}:{\rho _j} > {\rho _i}} (\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|) $ | (2) |
式中:δi表示样本数据xi与其他高密度样本数据的最短距离。具有较大局部密度和较大特征距离的样本数据成为聚类中心的可能性更大。
定义3 直接邻居q表示样本数据p的直接邻居定义为:
| $ q = {\rm{arg}}{\kern 1pt} {\kern 1pt} \mathop {{\rm{min}}}\limits_{j:{\rho _p} > {\rho _i}} (\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_p}} \right\|) $ | (3) |
拥有最大密度的样本数据xs没有直接邻居,这类样本数据的特征距离为:
| $ {\delta _s} = \mathop {{\rm{max}}}\limits_{s \ne i} (\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_s}} \right\|) $ | (4) |
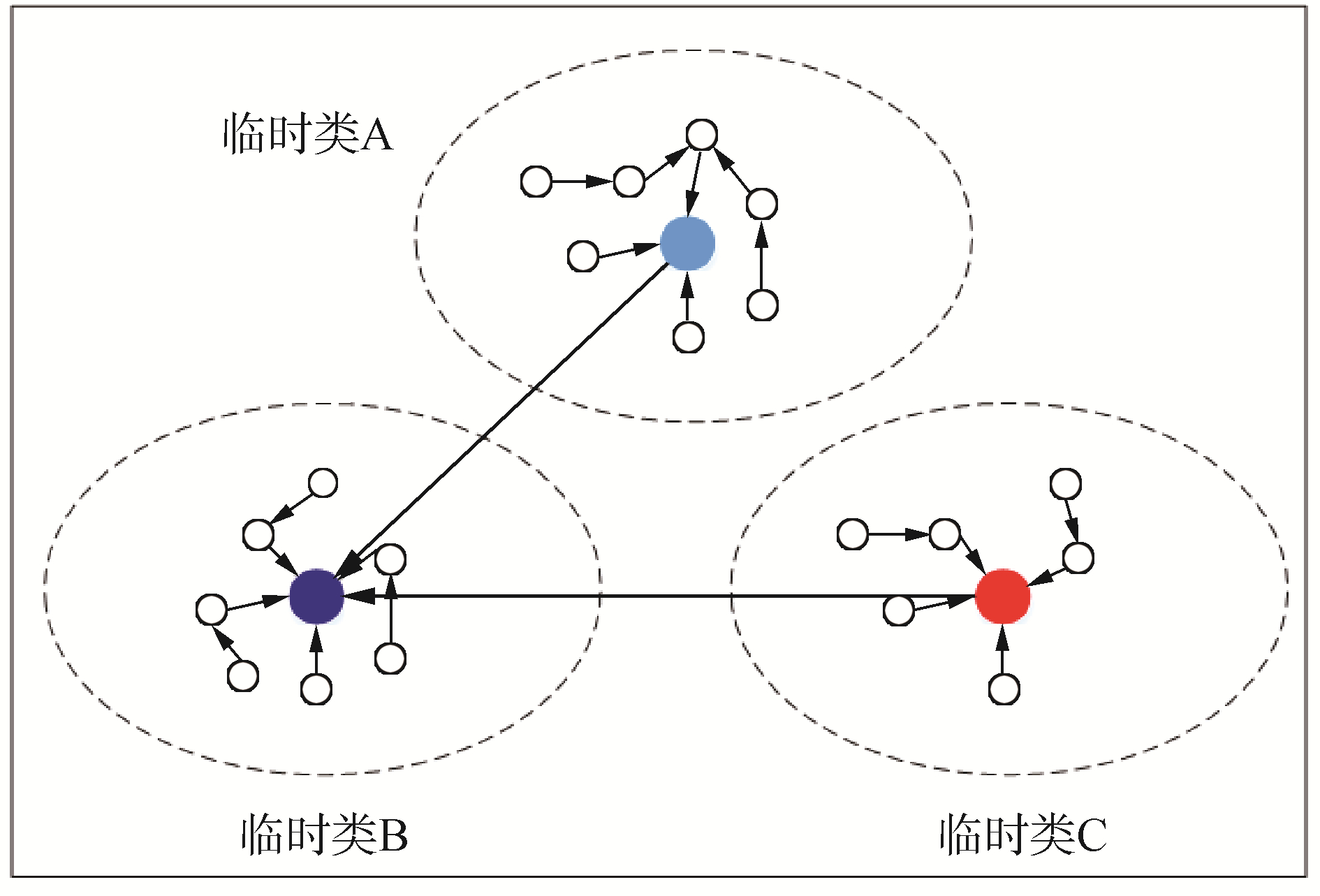
构造有向无环图(directed acycline graph,DAG)根据特征距离对数据集进行划分。DAG的顶点表示数据点,DAG的有向边表示数据点之间的邻居关系。需要注意一点,直接邻居关系是不可逆的,如果数据点p的直接邻居是数据点q,那么数据点q的直接邻居不是数据点p。使用特征距离作为DAG有向边的权重。特征距离可以有效描述数据分布密度,拥有较小特征距离的数据样本与它的直接邻居处在同一类内,拥有较大特征距离的特征点与它的直接邻居不在同一类内。因此,经过若干次迭代后,数据集划分成若干临时类,如图 2所示。
|
Download:
|
| 图 2 基于DAG的临时类划分 Fig. 2 Temporary class division based on DAG | |
采用同时具备较大局部密度和特征距离的点作为潜在聚类中心可以避免dc选取不当导致特征距离大于dc的高局部密度数据无法正确聚类的问题。兼顾数据局部密度和特征距离二者的优点,选取二者的乘积作为最终决定聚类中心的值,记为γ,其中γi=ρiδi。
假设基于DAG的临时类划分产生的临时类的数目为M,临时类表示为:tClustk∩tClustq=∅,tClustk={x1k, x2k, …, xtk, …, xnkk}⊂X,其中k和nk分别表示临时类的索引号和第k个临时类包含的样本数据的个数。临时类的聚类中心表示为:tCen={tc1, tc2, …, tck, …, tcM}⊂X。根据模糊聚类算法最终聚类个数C,对产生的M个临时类进行融合,形成数据集基于密度的初始划分。临时类合并算法具体描述如下所示:
1) 根据公式γi=ρiδi计算临时类聚类中心的γ,并将M个临时类聚类中心按照γ降序排列;
2) 根据γ选择前C个临时类的聚类中心作为模糊聚类的初始聚类中心;
3) 将余下临时类内的样本合并到其直接邻居所在的前C个临时类内,完成临时类的合并,形成数据集的初始划分。
数据集初始划分表示样本数据经过临时类合并算法形成数据集的初始划分,数据集初始划分定义为FC×N=[f1, 1, f2, 1, …, fC, 1; …; f1, N, f2, N, …, fC, N]。
其中C表示临时类个数,N表示数据样本的总个数。设数据集的初始划分共包含C个子类,函数f满足:
| $ {f_{i,j}} = \left\{ {\begin{array}{*{20}{l}} {1,}&{{\rm{ 数据 }}j{\rm{ 属于子类 }}i}\\ {0,}&{{\rm{其他}}} \end{array}} \right. $ | (5) |
聚类中心一般处于数据点密度高的区域,处于高密度区域的数据点应该在聚类中心更新时具备更大的权重,将局部数据密度引入模糊聚类的中心计算,聚类中心计算公式更新为:
| $ v_i = \frac{{(\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p{x_j}{f_{i,j}}{\rho _j})}}{{(\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p{f_{i,j}}{\rho _j})}} $ | (6) |
将局部密度应用于更新聚类中心,仅使用聚类中心相关的数据点进行聚类中心更新的计算,能保证聚类中心总是处在高密度区域附近而非随机移动。由于聚类中心总是处在高密度区域,经过较少的迭代次数目标函数完成收敛,提高了算法的效率。
2.2 基于密度感知的模糊聚类算法在初始数据集划分算法的基础上,本文提出了基于密度感知的核模糊聚类算法(density- awared kernel based fuzzy c-means clustering algorithm, DKFCM)。输入的样本经过核函数映射到高维特征空间,解决低维空间线性不可分的问题。DKFCM的目标函数定义[10]:
| $ \begin{array}{*{20}{l}} {{J_{{\rm{ DKFCM }}}}(\mathit{\boldsymbol{T}},\mathit{\boldsymbol{U}},\mathit{\boldsymbol{V}}) = \sum\limits_{i = 1}^c {\sum\limits_{j = 1}^n {u_{ij}^m} } t_{ij}^p{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j} - \mathit{\boldsymbol{v}}_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }})} \right\|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^c {{\eta _i}} \sum\limits_{j = 1}^n {u_{ij}^m} {{(1 - {t_{ij}})}^p}} \end{array} $ | (7) |
式中:xj∈Rd(j=1, 2, …, n)表示训练样本;Φ(xj)是样本xj在高维特征空间的映射;viΦ是高维特征空间中第i类的聚类中心; T表示绝对度矩阵,tij表示第j个样本属于第i个类的绝对度;U表示模糊隶属度矩阵,uij表示第j个样本属于第i个类的相对度;V是高维特征空间中聚类中心的矩阵;m和p分别表示模糊隶属度和概率隶属度的典型值。R一般取值为1,ηi表示为:
| $ {\eta _i} = R(\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j} - \mathit{\boldsymbol{v}}_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }})} \right\|^2}) \cdot {(\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p)^{ - 1}} $ | (8) |
DKFCM算法的目标函数达到最优,绝对度矩阵T和相对度矩阵U需要分别满足:
| $ {{t_{ij}} = {{\left[ {1 + {{\left( {\frac{{{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}) - \mathit{\boldsymbol{v}}_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right\|}^2}}}{{{\eta _i}}}} \right)}^{\frac{1}{{p - 1}}}}} \right]}^{ - 1}}} $ | (9) |
| $ {{u_{ij}} = {{\left[ {\sum\limits_{k = 1}^c {{{\left( {\frac{{t_{ij}^{p - 1}{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}) - \mathit{\boldsymbol{v}}_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right\|}^2}}}{{t_{kj}^{p - 1}{{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}) - \mathit{\boldsymbol{v}}_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right\|}^2}}}} \right)}^{\frac{1}{{m - 1}}}}} } \right]}^{ - 1}}} $ | (10) |
式(10)中的隶属度矩阵满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{u_{ij}} \in [0,1],i = 1,2, \cdots ,n,j = 1,2, \cdots ,c}\\ {\sum\limits_{i = 1}^c {{u_{ij}}} = 1,i = 1,2, \cdots ,n} \end{array}} \right. $ |
将数据局部密度和数据集初始划分引入模糊聚类算法,更新聚类中心的计算公式为:
| $ v_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = (\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({x_j}){f_{i,j}}{\rho _j}) \cdot {(\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p{f_{i,j}}{\rho _j})^{ - 1}} $ | (11) |
数据样本xj和聚类中心vi在特征空间分别映射为Φ(xj)和viΦ,Φ(xj)和viΦ的距离:
| $ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D_{ij}^2 = {{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}) - \mathit{\boldsymbol{v}}_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}} \right\|}^2} = }\\ {K({\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{x}}_j}) - 2K({\mathit{\boldsymbol{x}}_j},{{\mathit{\boldsymbol{\tilde v}}}_i}) + 2K({{\mathit{\boldsymbol{\tilde v}}}_i},{{\mathit{\boldsymbol{\tilde v}}}_i})} \end{array} $ | (12) |
| $ K({\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{x}}_j}) = {\rm{exp}}\left( {\frac{{{{\left\| {{\mathit{\boldsymbol{x}}_j} - {\mathit{\boldsymbol{x}}_j}} \right\|}^2}}}{{2{\sigma ^2}}}} \right) = 1 $ | (13) |
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} K({\mathit{\boldsymbol{x}}_j},{{\mathit{\boldsymbol{\tilde v}}}_i}) = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}) \cdot \mathit{\boldsymbol{v}}_i^\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} = \\ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}) \cdot (\sum\limits_{k = 1}^n {u_{ik}^m} t_{ik}^p\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}){f_{i,k}}{\rho _k}) \cdot {(\sum\limits_{k = 1}^n {u_{ij}^m} t_{ij}^p{f_{i,k}}{\rho _k})^{ - 1}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (\sum\limits_{k = 1}^n {u_{ik}^m} t_{ik}^pK({\mathit{\boldsymbol{x}}_j},{\mathit{\boldsymbol{x}}_k}){f_{i,j}}{\rho _j}) \cdot {(\sum\limits_{k = 1}^n {u_{ik}^m} t_{ik}^p{f_{i,j}}{\rho _j})^{ - 1}} \end{array} $ | (14) |
| $ \begin{array}{l} K({{\mathit{\boldsymbol{\tilde v}}}_i},{{\mathit{\boldsymbol{\tilde v}}}_i}) = {\left( {\frac{{\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}({\mathit{\boldsymbol{x}}_j}){f_{i,j}}{\rho _j}}}{{\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p{f_{i,j}}{\rho _j}}}} \right)^2} = \\ \frac{{(\sum\limits_{j = 1}^n {\sum\limits_{k = 1}^n {u_{ij}^m} } t_{ij}^pu_{ik}^mt_{ik}^pK({x_j},{x_k}){f_{i,j}}{\rho _j}{f_{i,k}}{\rho _k})}}{{{{(\sum\limits_{j = 1}^n {u_{ij}^m} t_{ij}^p{f_{i,j}}{\rho _j})}^2}}} \end{array} $ | (15) |
DKFCM算法的描述,远离聚类中心的点被视为离群点,赋予离群点较小的绝对度,例如tij < ε,ε是非常接近0的正数。算法的描述具体如下:
1) 计算各个数据样本的局部密度和特征距离,根据截断距离dc对数据集进行基于DAG的临时类划分;
2) 执行临时类合并算法得到模糊聚类的初始聚类中心tCen以及样本数据与临时聚类之间的关系FC×N=[f1, 1, f2, 1, …, fC, 1; …; f1, N, f2, N, …, fC, N];
3) 将数据样本的局部数据密度和关系矩阵引入模糊聚类的中心计算,更新聚类中心计算公式;
4) 将tCen作为聚类中心V(0)的初始值,运行KFCM算法,获得模糊隶属度矩阵、绝对度矩阵,同时初始化核函数;
5) 确定c、m、p的值,最大迭代次数为rmax,停止阈值ε,根据式(12)~(15)不断地更新聚类中心,模糊隶属度矩阵和绝对度矩阵直到收敛。
2.3 模糊支持向量机实际应用中,训练集中的样本数据对模型的训练做出的贡献有所不同,一些样本数据比另外一些样本数据更重要。有意义的样本数据期望被正确分类,而像噪声这种无意义的样本数据是否正确分类影响不大。这就意味着一些样本数据可能不仅属于一个类也可能属于多个类:样本数据90%的可能属于某一个类、10%的可能无实际意义或者20%的可能属于一个类、80%的可能无实际意义。换言之,每个样本数据存在模糊隶属度0 < si≤1。si可以表示训练点属于一个类的倾向,1-si表示训练点无实际意义的倾向。
假设存在l对数据点{xi, yi, si}i=1l,对数据点进行二分类,其中xi∈ Rn,yi∈{+1, -1}是数据点对应的类标签,si∈(0, 1]是模糊隶属度,表示样本xi属于yi的倾向。
模糊支持向量机(fuzzy support vector machine, FSVM)模型求解最优分类超平面转换成基于不等式约束的二次规划问题:
| $ \mathop {{\rm{min}}}\limits_{w,b,\xi } J(\mathit{\boldsymbol{w}},b,\xi ) = \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + C\sum\limits_{i = 1}^l {{s_i}} {\xi _i} $ | (16) |
满足约束条件:
| $ \left\{ {\begin{array}{*{20}{l}} {{y_i}[{\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi ({\mathit{\boldsymbol{x}}_i}) + b] \ge 1 - {\xi _i},{\xi _i} \ge 0,i = 1, \cdots ,l}\\ {\left\{ {\begin{array}{*{20}{l}} {s_j^ + = {u_{ij}}}\\ {s_j^ - = 1 - {u_{ij}}} \end{array}} \right.} \end{array}} \right. $ |
式中:w是分类超平面向量;b是偏移量;φ (xi)是将样本xi映射到高维空间的非线性核函数;ξi是分类错误率,C是控制分类边际与分类错误率之间的正则化常数;si由DKFCM算法完成聚类后,所得的模糊隶属度uij确定,能够降低分类错误率对目标函数的影响,降低了噪声和孤立点的影响力。
构造拉格朗日乘子对式(16)进行优化:
| $ \begin{array}{*{20}{c}} {L(\mathit{\boldsymbol{w}},b,\xi ,\alpha ,\beta ) = \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + C\sum\limits_{i = 1}^t {{s_i}} {\xi _i} - }\\ {\sum\limits_{i = 1}^l {{\alpha _i}} ({y_i}({\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi ({x_i}) + b) - 1 + {\xi _i}) - \sum\limits_{i = 1}^l {{\beta _i}} {\xi _i}} \end{array} $ | (17) |
使用SMO优化算法对式(17)进行求解获得最优判别式:
| $ y(x) = {\rm{sgn}} [\sum\limits_{j = 1}^l {{\alpha _j}} {y_j}K(x,{x_j}) + b] $ | (18) |
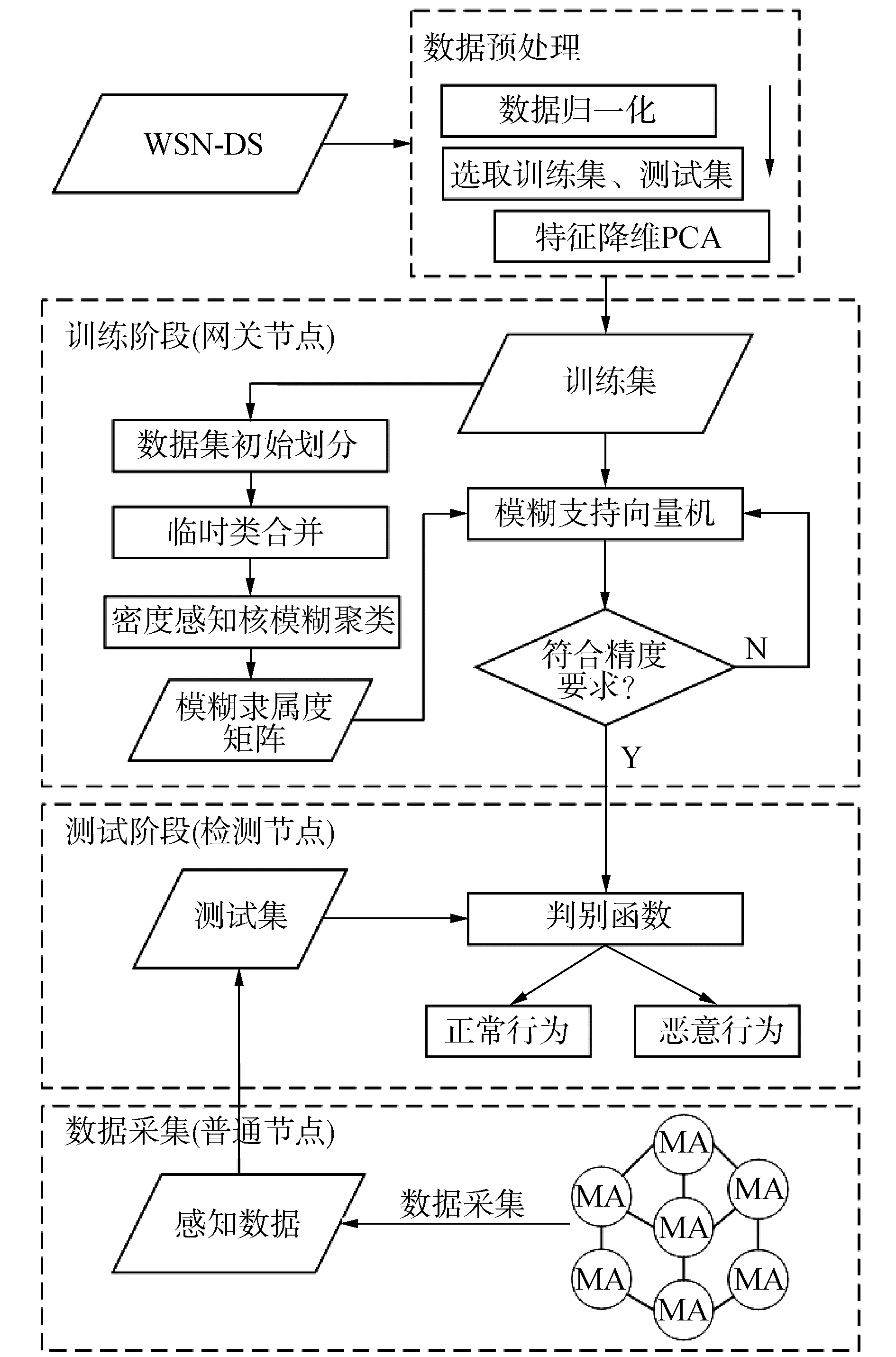
在DKFCM与FSVM的基础上本文提出一种应用于WSNs的基于机器学习的入侵检测模型DKFCM-FSVM,如图 3所示。
|
Download:
|
| 图 3 入侵检测模型 Fig. 3 Intrusion detection model | |
模型包含的实体包括汇聚节点、检测节点和普通节点,具体分工如下。
1) 汇聚节点。
汇聚节点的主要功能是训练检测器,主要包括样数据预处理、训练分类器和分发分类器3个功能。
数据预处理:与普通节点不同的是,网关节点具有充足的能源供给和强大的运算能力,能够处理大规模样本数据库。基站选取WSN-DS(针对无线传感器网络入侵检测设计的数据集)作为训练集训练DKFCM-FSVM模型。数据预处理的2个重要过程是归一化和特征降维。
训练检测器:检测器的训练是入侵检测模型的关键部分。首先,网关节点对训练集进行数据预处理;计算样本数据的数据密度和特征距离,使用临时类合并算法形成数据集初始划分,挖掘训练集中数据点潜在的分布特征;使用DKFCM算法计算模糊隶属度矩阵U(r);根据式(18)训练模糊支持向量机,计算参数α和b。根据式(18)进行样本的预测并验证提出方法的准确度。检测结果以正常或异常的形式输出。
发布检测器:基站将验证过的检测器发送至各个检测节点,供检测节点进行入侵行为的检测。
2) 检测节点。
一定数量的检测节点被分配到网络内对普通节点提取的测试样本进行检测以便发现入侵行为。相比于普通节点,检测节点具备更大的存储空间和强大的运算能力,可以存储检测模型和运行入侵检测算法。检测节点的主要功能是实时检测入侵行为:
检测节点运行基站发布的检测器,主要依据公式(18)对网络行为进行检测,结果为正常和异常;检测节点一旦发现异常行为向基站发送告警信息;检测节点向基站发送新的样本并更新基站样本数据库,通知基站重新训练检测器保证检测器的实效性。
3) 普通节点。
普通节点运行监测代理(monitor agent, MA)获取感知层网络中感知节点获取的感知数据,并发送至检测节点进行入侵检测。
3 实验与分析 3.1 实验环境在入侵检测实验中,感知层网络的覆盖范围是100 m×100 m,100个感知节点:使用笔记本计算机作为网关节点,检测节点10个,普通节点90个。仿真参数如表 1所示。每次仿真的持续时间设置为200 s,实验结果采用20次仿真结果的平均值。
| 表 1 仿真模型的参数和值 Table 1 Parameters and Values of simulation model |
本节采用NS-2进行仿真实验验证本文提出的入侵检测算法的有效性。为了验证提出方法在感知层网络环境下入侵检测的效果,本小节采用的数据集WSN-DS。WSN-DS数据集是专门针对WSNs入侵检测所设计。在使用低能量感知集群层次结构(LEACH)路由协议的感知层网络环境收集数据并形成数据集。WSN-DS数据集包含374 661条记录,数据集的每个样本包含23个属性,文献[11]介绍了每个属性的具体含义。分别将WSN-DS数据集的60%和40%作为训练集和测试集,每种类型的攻击具体如表 2所示。
| 表 2 数据集随机分配训练集60%和测试集40% Table 2 The random distribution of data set 60% of training set and 40% of test set data sets |
入侵检测系统的检测结果包含下面四种:真阳性(true positive,TP)表示异常行为被正确识别为异常行为所占的比例;假阳性(false positive,FP)表示正常行为被错误识别为异常行为所占的比例;真阴性(true negative,TN)表示正常行为被正确识别为正常行为所占的比例;假阴性(false negative,FN)表示异常行为被错误识别为正常行为所占的比例。根据上述4种检测结果进一步演化出准确率、误报率、漏报率和受试者工作特性曲线下方面积,作为本文入侵检测技术采用的评价指标。
1) 准确率(precision)表示正确识别异常行和正常行为为占有的比例,计算公式为:
| $ P = \frac{{{\rm{TP}}}}{{{\rm{TP + FP}}}} $ | (19) |
2) 误报率(false positive rate, FPR)表示将正常行为识别为异常行为占有的比例为:
| $ {\rm{FPR}} = \frac{{{\rm{FP}}}}{{{\rm{FP}} + {\rm{TN}}}} $ | (20) |
3) 漏报率(false negative rate, FNR)表示将异常行为识别为正常行为占有的比例:
| $ {\rm{FNR}} = \frac{{{\rm{FN}}}}{{{\rm{TP}} + {\rm{FN}}}} $ | (21) |
为了验证提出方法的有效性,本节选择SVM、FCM-SVM、FCM-FSVM和KFCM-FSVM算法作为对比算法分别对比。算法的核函数采用高斯核函数,FCM-FSVM、KFCM-FSVM和DKFCM-FSVM的参数m取典型值2,ε取典型值0.01,使用随机矩阵作为初始矩阵,根据文献[12]设置模糊隶属度,其中核函数的参数σ取值为0.01,正则化常数C取值为2。在训练集上训练本文提出的算法和对照组算法,训练完成后在测试集上完成算法的验证。采用10-fold交叉验证方式,取实验结果的平均值进行对比。
图 4给出了DKFCM-FSVM与对照算法之间在准确率上的对比结果。同对照算法相比,本文提出的DKFCM-FSVM算法检测5种行为的平均准确率分别为0.998、0.993、0.905、0.997和0.947,在不同行为的检测上准确率均达到最优。SVM算法耗时短,检测率最差,其次是FCM-SVM算法,优于SVM算法。FCM-FSVM和KFCM-FSVM的检测率相近,DKFCM-FSVM略优于KFCM-FSVM。

|
Download:
|
| 图 4 5种分类算法的准确率对比 Fig. 4 Comparison of precision rates of five classification algorithms | |
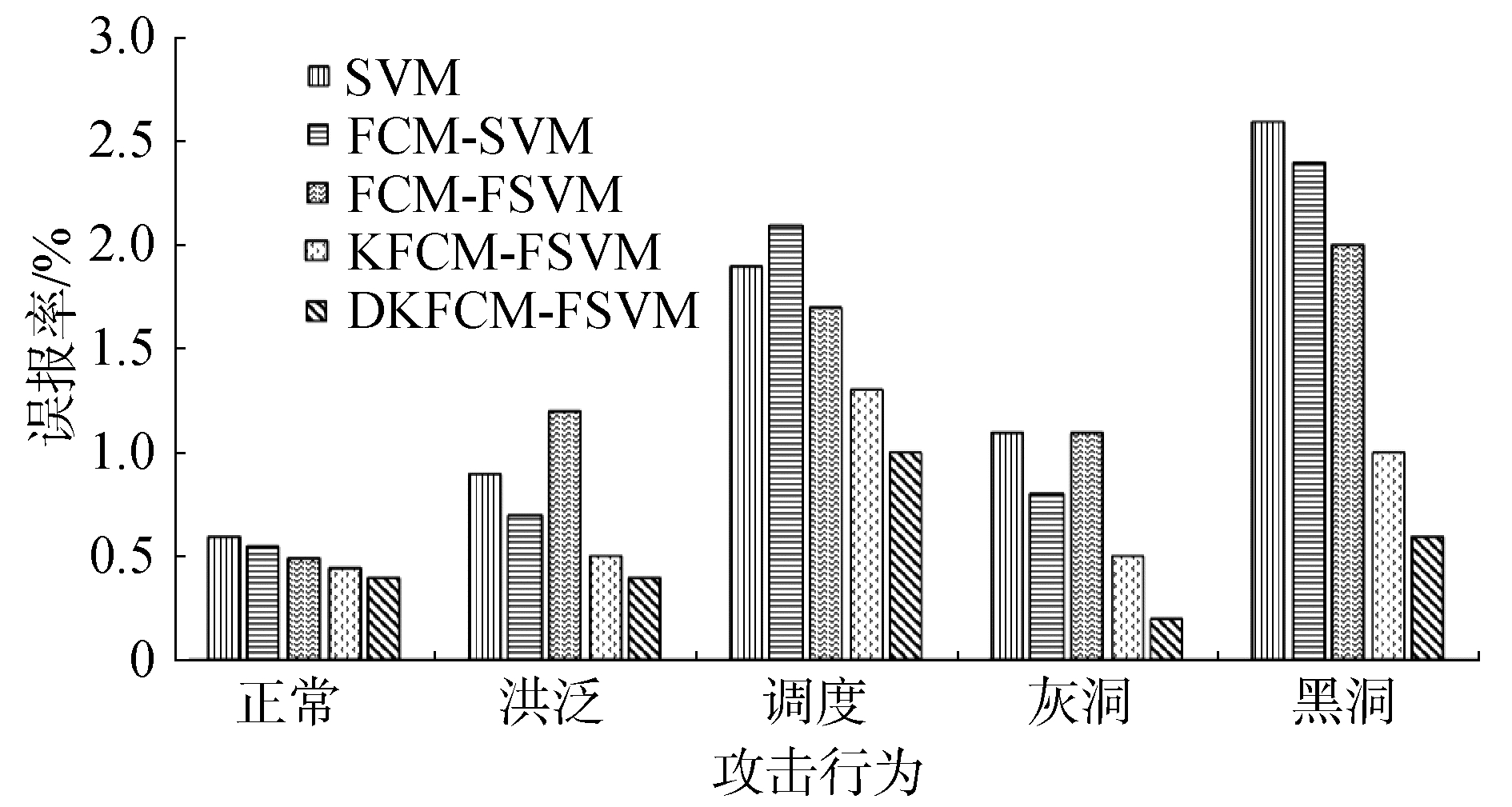
图 5给出了DKFCM-FSVM与对照算法之间在误报率上的对比结果。同对照算法相比,本文提出的DKFCM-FSVM算法检测5种行为的平均误报率分别为0.004、0.004、0.01、0.002和0.006,在不同行为的检测上达到最低的误报率。SVM算法的误报率最高,其次是FCM-SVM算法,优于SVM算法。FCM-FSVM和KFCM-FSVM的误报率相近,DKFCM-FSVM优于KFCM-FSVM。
|
Download:
|
| 图 5 5种分类算法的误报率对比 Fig. 5 Comparison of false positive rates of five classification algorithms | |
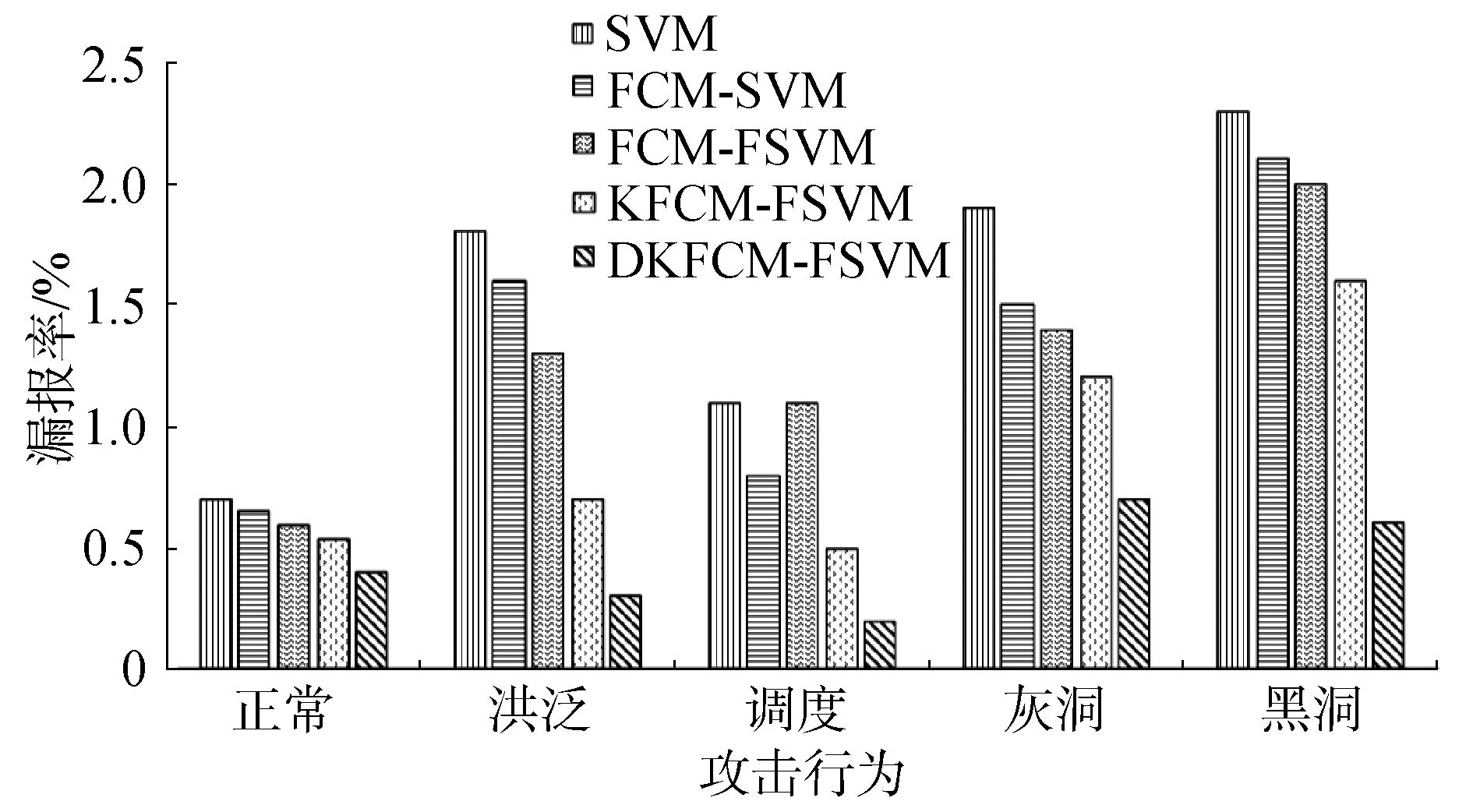
图 6给出了DKFCM-FSVM与对照算法之间在漏报率上的对比结果。同对照算法相比,本文提出的DKFCM-FSVM算法检测5种行为的平均漏报率分别为0.004、0.003、0.002、0.007和0.006,在不同行为的检测上达到最低的漏报率。SVM算法的漏报率较高,其次是FCM-SVM算法,优于SVM算法。FCM-FSVM和KFCM-FSVM的漏报率相近,DKFCM-FSVM优于KFCM-FSVM。
|
Download:
|
| 图 6 5种分类算法的漏报率对比 Fig. 6 Comparison of underreporting rates of five classification algorithms | |
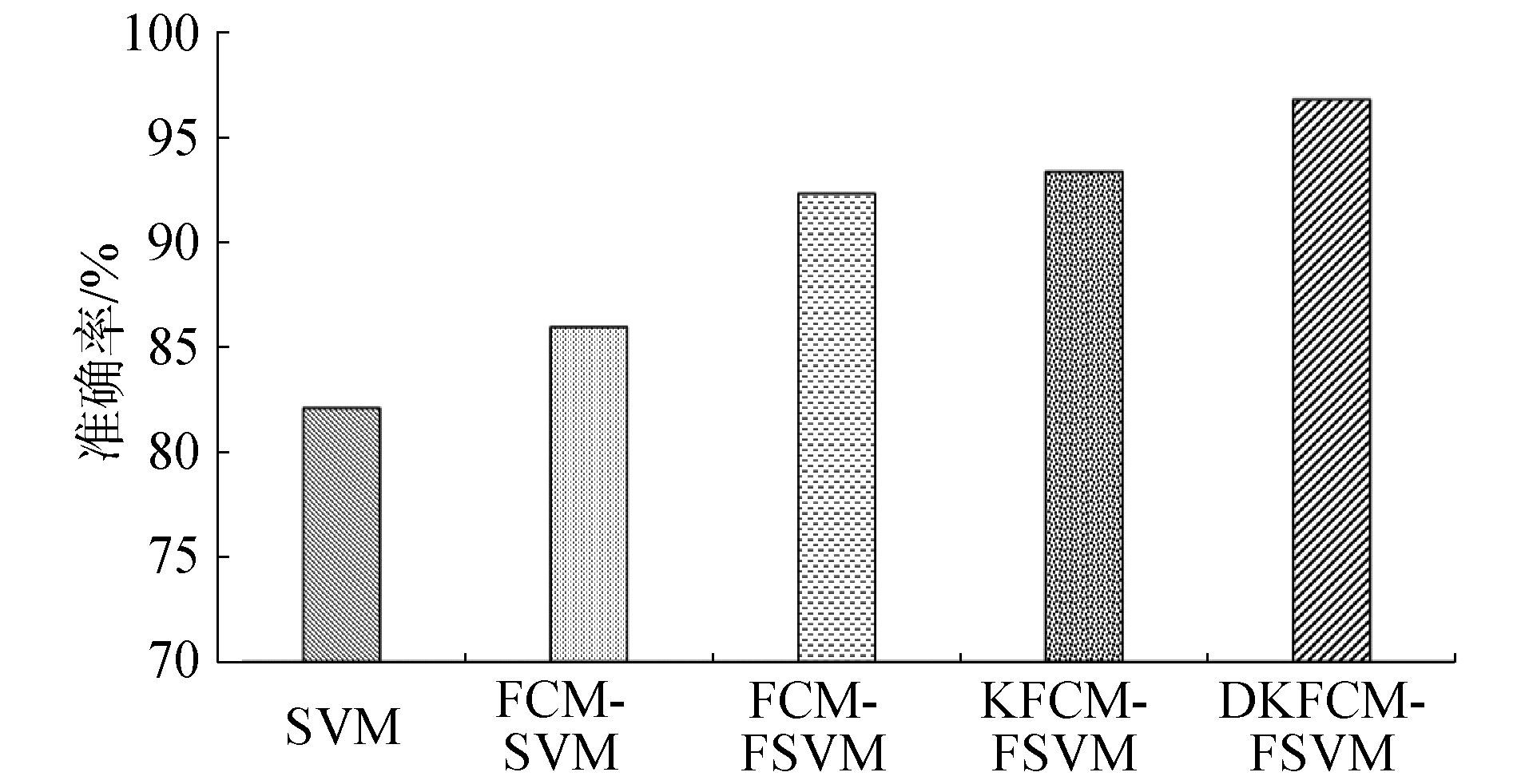
图 7给出了DKFCM-FSVM与对照算法之间在总体检测准确率的对比结果,各算法你总体检测准确率分别为0.820 8、0.859 6、0.923 6、0.933 2和0.968。因此,本文提出的DKFCM-FSVM优于对比算法。
|
Download:
|
| 图 7 5种分类算法的总体检测准确率对比 Fig. 7 Comparison of the overall detection accuracy of five classification algorithms | |
实验结果分析:WSNs环境下,正常数据和入侵数据的比例不平衡,多数行为是正常行为,由入侵攻击产生的异常数据占有极少数,除此之外正常行为和入侵行为在多数情况下线性不可分,需要使用核函数映射到高维空间,SVM的检测效果不佳。FCM对初始聚类的选取和不平衡的数据集敏感,同样效果不佳。即使使用核函数将样本映射到高维空间,噪声数据和离群点对聚类产生的影响也是不容忽视的,引入数据密度和特征距离能有效避免噪声数据和离群点对分类结果的影响,达到最优分类结果。误报率和漏报率低也说明本文提出的算法更适合不平衡数据集,能有效应对离群点和噪声数据。
4 结论1) DKFCM引入数据密度和特征距离对模糊聚类进行改进,降低了噪声点和离群点对聚类算法影响的同时加快了聚类算法的收敛速度;FSVM使用DKFCM所得的模糊隶属度作为模糊因子,增强了模糊因子选取的客观性,提高了分类准确度,显著提高了WSNs场景下入侵检测的效果。
2) 实验结果表明,在WSN-DS数据集下,DKFCM-FSVM入侵检测各项评价指标与对照算法相比均达到最优,其能源消耗仅比SVM略高。因此,DKFCM-FSVM可以应用到实际的WSNs场景中,从而提升WSNs抵抗网络内部攻击的能力。
3) 传统机器学习处理大规模数据具有检测精度低和检测速度慢等问题。深度学习在模式识别、图像处理和恶意流量分析等方面取得显著成功,为入侵检测领域提供了一种思路。
| [1] |
BERTONI G, DAEMEN J et al. Duplexing the sponge: single-pass authenticated encryption and other applications[C]// International Workshop on Selected Areas in Cryptography. Springer, Berlin, Heidelberg, 2011. https://www.researchgate.net/publication/221274795_Duplexing_the_Sponge_Single-Pass_Authenticated_Encryption_and_Other_Applications
(  0) 0)
|
| [2] |
BHUYAN M H, BHATTACHARYYA D K, KALITA J K. Network anomaly detection: methods, systems and tools[J]. IEEE communications surveys & tutorials, 2014, 16(1): 303-336. (  0) 0)
|
| [3] |
OSANAIYE O, CHOO K K R, DLODLO M. Distributed denial of service (DDoS) resilience in cloud: Review and conceptual cloud DDoS mitigation framework[J]. Journal of network & computer applications, 2016, 67(2): 147-165. (  0) 0)
|
| [4] |
张玲, 白中英, 罗守山, 等. 基于粗糙集和人工免疫的集成入侵检测模型[J]. 通信学报, 2013, 34(9): 166-176. ZHANG Lin, BAI Zhongying, LUO Shoushan, et al. Integrated intrusion detection model based on rough set and artificial immune[J]. Journal on communications, 2013, 34(9): 166-176. (  0) 0)
|
| [5] |
杜辉, 王宇平, 董晓盼. 采用万有引力定律自动确定类数的K均值算法[J]. 西安交通大学学报, 2014, 48(10): 115-119. DU Hui, WANG Yuping, DONG Xiaopan. An improved k-means algorithm with auto-determined clustering number by using gravity[J]. Journal of Xi'an Jiaotong University, 2014, 48(10): 115-119. DOI:10.7652/xjtuxb201410018 (  0) 0)
|
| [6] |
江颉, 王卓芳, 陈铁明, 等. 自适应AP聚类算法及其在入侵检测中的应用[J]. 通信学报, 2015, 36(11): 118-126. JIANG Jie, WANG Zhuofang, CHEN Tieming, et al. Adaptive AP clustering algorithm and its application on intrusion detection[J]. Journal on communications, 2015, 36(11): 118-126. DOI:10.11959/j.issn.1000-436x.2015242 (  0) 0)
|
| [7] |
刘绪崇, 陆绍飞, 赵薇, 等. 基于改进模糊C均值聚类算法的云计算入侵检测方法[J]. 中南大学学报(自然科学版), 2016, 47(7): 2320-2325. LIU Xuchong, LU Shaofei, ZHAO Wei, et al. A cloud computing intrusion detection with objective function optimization based on fuzzy C-means clustering algorithm[J]. Journal of Central South University (science and technology), 2016, 47(7): 2320-2325. (  0) 0)
|
| [8] |
许勐璠, 李兴华, 刘海, 等. 基于半监督学习和信息增益率的入侵检测方案[J]. 计算机研究与发展, 2017, 54(10): 2255-2267. XU Mengfan, LI Xinghua, LIU Hai, et al. An intrusion detection scheme based on semi-supervised learning and information gain ratio[J]. Journal of computer research and development, 2017, 54(10): 2255-2267. DOI:10.7544/issn1000-1239.2017.20170456 (  0) 0)
|
| [9] |
任家东, 刘新倩, 王倩, 等. 基于KNN离群点检测和随机森林的多层入侵检测方法[J]. 计算机研究与发展, 2019, 56(3): 566-575. REN Jiadong, LIU Xinqian, WANG Qian, et al. An multi-level intrusion detection method based on knn outlier detection and random forest[J]. Journal of computer research and development, 2019, 56(3): 566-575. (  0) 0)
|
| [10] |
LIU Y, HOU T, KANG B, et al. Unsupervised binning of metagenomic assembled contigs using improved fuzzy C-Means method[J]. IEEE/ACM transactions on computational biology and bioinformatics, 2016, 14(6): 1459-1467. (  0) 0)
|
| [11] |
ALMOMANI I, AL-KASASBEH B, AL-AKHRAS M. AL-Akhras. WSN-DS: A Dataset for Intrusion Detection Systems in Wireless Sensor Networks [J]. Journal of sensors, 2016, 12(6): 158-175.
(  0) 0)
|
| [12] |
JIANG X, YI Z, LYU J C. Fuzzy SVM with a new fuzzy membership function[J]. Neural computing & applications, 2006, 15(3-4): 268-276. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


