2. 长沙理工大学 水沙科学与水灾害防治湖南省重点实验室, 湖南 长沙 116024
2. Key Laboratory of Water-Sediment Sciences and Water Disaster Prevention of Hu'nan Province, Changsha University of Science and Technology, Changsha 410114, China
Level set方法[1]、VOF方法[2]、波前追踪法(front-tracking method)[3]和相场方法(phase-field method)[4]是追踪自由表面的4种常用方法。Level set方法的最大优势是能够容易处理自由表面的拓扑变化,但在相同网格分辨率下其计算精度不如显式的波前追踪法,其质量守恒性弱于VOF法[5]。为弥补level set方法的上述不足,主要的措施包括采用高精度的离散格式(如空间上5阶WENO格式、时间上3阶TVD Runge-Kutta格式)[6-8]、重构level set方程的解[9-11]等。重构将强制level set方程的解符合符号距离函数条件。为实现重新初始化,一种方式是迭代求解伪时间瞬态重构方程[9-12],另一种是直接求解Eikonal方程。现阶段,Eikonal方程的快速求解方法有快速步进法(fast marching method)[13-15]、快速扫描法(fast sweeping method)[16-18]2类。对于几何特征简单的交界面,快速扫描法的计算速度要快于快速步进法[19]。不过,快速扫描法需要对计算全域进行遍历,而快速步进法只需遍历自由表面附近的区域。为进一步提高快速步进重构的效率,Herrmann[20]提出了基于区域分解的快速步进并行算法。Tugurlan[21]和Yang等[22]又分别改进了信息传递方式以提高分布式内存架构下并行计算的效率。黄筱云等[23-24]则提出了基于共享内存架构的快速步进重构算法,解决了相互重叠内边界节点重构值传递问题。在此基础上,夏波等[25]提出了一种自适应分区策略,确保各分区计算荷载平衡,进一步提高并行重构效率。
在level set方法中,重新初始化会定期实施,甚至是每一步都需进行level set函数的重构。若采用文献[25]的自适应分区技术,区域分解将会带来额外的计算开销。因此,本文将充分利用共享内存架构的优势,提出一种隐式分区并行策略,避免区域分解带来额外开销。
1 显式分区并行重构 1.1 快速步进分区并行重构Level set函数的重构(又称为重新初始化)被认为是求解如下问题:
| $ \left\{\begin{array}{ll} |\nabla \phi(x, y)|=1, & (x, y) \in \varOmega \backslash \varGamma \\ \phi(x, y)=0, & (x, y) \in \varGamma \end{array}\right. $ | (1) |
式中:Ω表示整个计算区域;Γ为交界面。快速步进重构采用1阶迎风格式离散方程(1),即节点(i, j)上фi, j的空间导数由该节点与ф < фi, j的相邻节点所决定[26]。离散后的方程(1)则变成一个关于фi, j的二次方程。若给定那些ф < фi, j相邻节点的值,即可求出фi, j的值。因此,选择从交界面开始,向外依次求解每个节点上的二次方程,便能求出整个域内所有节点的值。具体操作时,先采用文献[27]中的方法重构交界面周围网格节点,将其作为起始边界;再试算起始边界外侧所有网格节点的值,并将这些节点根据其值放置到最小堆中,其中,处于根节点的网格节点被认为满足方程(1),或者说重构成功;然后,将根节点上的节点取出,试算其相邻未重构的节点,并将这些节点放置到最小堆中,或调整它们在最小堆中的位置;最后,将根节点的子孙节点中的网格节点依次向上递补。
基于区域分解的并行重构预先将整个计算区域划分成p个子区域,并分配给对应的线程,每个线程独立完成各自子区域内的重构。这时,需要求解的问题形式为:
| $ \left\{\begin{array}{ll} \left|\nabla \phi^{p}(x, y)\right|=1, & (x, y) \in \varOmega^{p} \backslash \varGamma^{p} \\ \phi^{p}(x, y)=0, & (x, y) \in \varGamma^{p} \\ \phi=\cup \phi^{p} \end{array}\right. $ | (2) |
在文献[23-25]中,计算区域将沿网格线进行分割,故子区域边界节点将相互重叠。每个子区域独自实施重构无法确保这些重叠的内边界节点的重构值一致,故需要采取同步措施。在显式分区并行算法中,当重构到边界节点时,该节点重构值将与相邻子区域重叠节点比较,若其值小于重叠节点,则将该值传递给相邻子区域。每个子区域在接收到传递值后,除了更新重叠节点的值外,还将其作为基准,回滚域内重构过的网格节点。当所有子区域内所有节点都重构完毕后,整个区域的重构过程才算结束。具体过程见文献[24]。
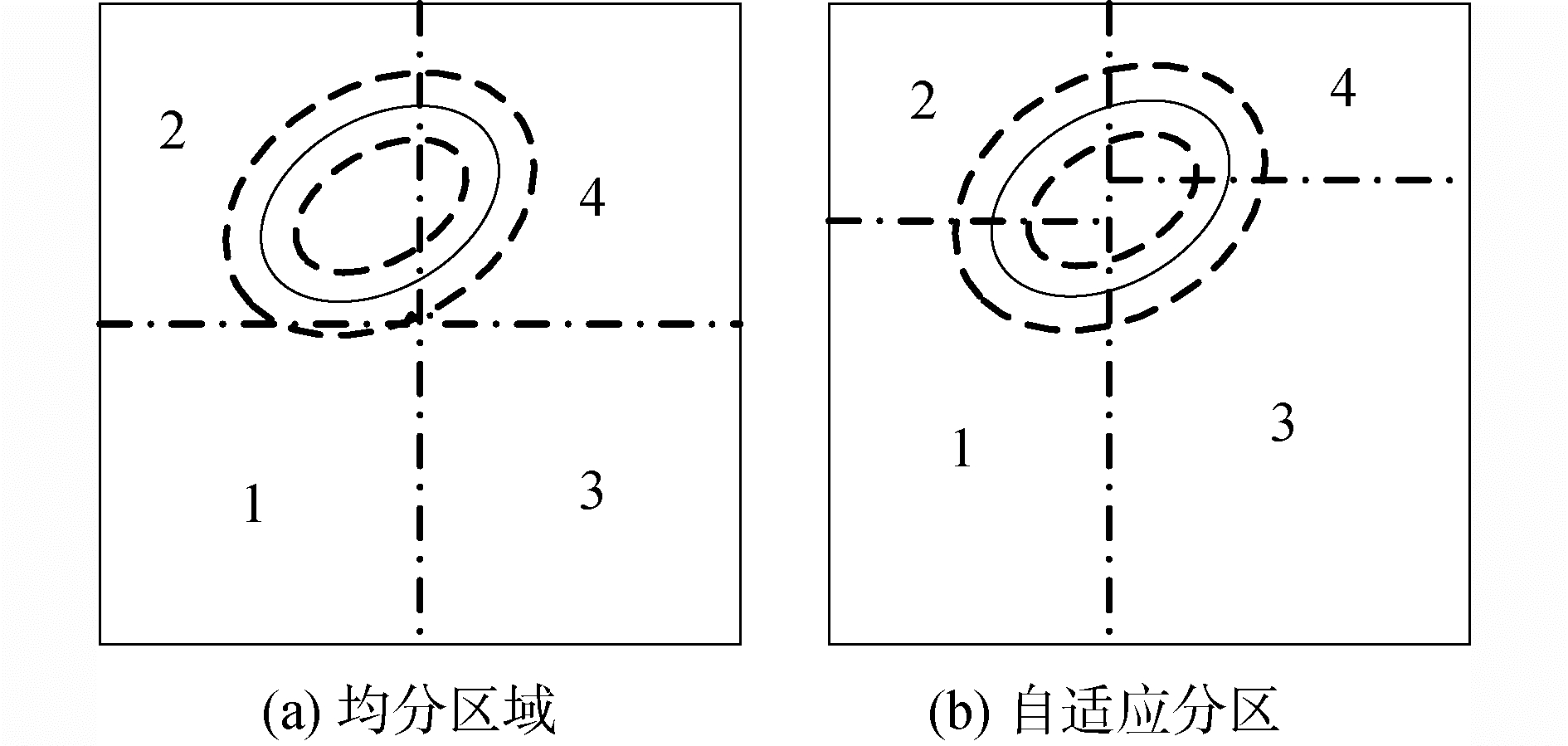
1.2 自适应分区策略Level set方法的重新初始化只需在交界面周围一定范围内执行,传统均分计算区域的策略可能导致子区域间重构计算开销不一致,如图 1(a)所示。自适应分区策略则通过平分交界面长度(或面积)来划分计算区域,保证子区域间开销基本一致,如图 1(b)所示。
|
Download:
|
| 图 1 2种显式分区策略的比较 Fig. 1 Comparison between two explicit domain decompositions | |
自适应分区是一种递归剖分过程。即先将计算区域分成2个子区域,再分别将子区域分成2个更小的子区域,然后继续将这些更小的子区域分成2块,直至划分子区域的数量与线程数量相同。此外,文献[25]中的自适应分区策略还根据沿不同坐标轴方向划分所产生需要重构内边界节点的数量来确定子区域一分为二的操作。这是因为需要重构的内边界节点数量越少,子区域间信息传递次数以及域内节点回滚的次数也越少。
2 隐式分区并行重构上面所述的并行算法需提前将整个计算区域沿网格线显式地划分成多个子区域。为保存重叠节点在不同线程下的计算值,实现相互重叠节点间的信息比较和传递,需要为这些节点分配额外的存储空间。当频繁地实施自适应分区并行重构时,存储空间的分配和回收操作会造成不小的计算开销。
本文提出的隐式分区并行重构不直接划分计算区域,而是划分交界面,将问题(1)将变成:
| $ \left\{\begin{array}{ll} \left|\nabla \phi^{p}(x, y)\right|=1, & (x, y) \in \varOmega \backslash \varGamma^{p} \\ \phi^{p}(x, y)=0, & (x, y) \in \varGamma^{p} \\ \phi=\min \phi^{p} \end{array}\right. $ | (3) |
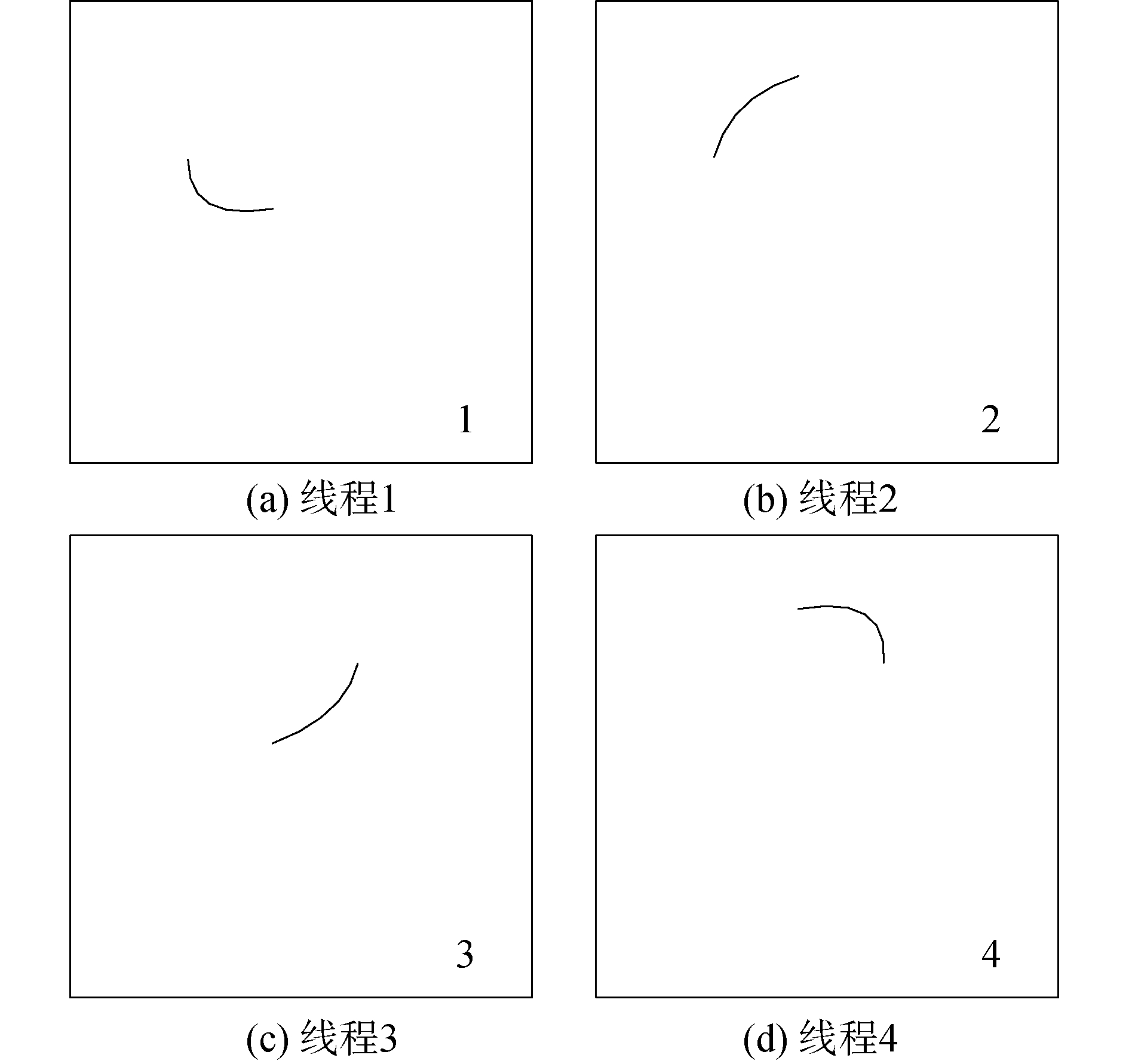
这意味着将一个以交界面为起始边界的重构问题变成以交界面一部分为起始边界的重构问题的集合。每个线程将独立求解一个交界面部分的重构问题。图 1所描述的椭圆形交界面边界重构问题若按照隐式分区并行策略处理,将变成图 2所示的情况。即将交界面分成长度一致的4个部分,每个线程完成以交界面的一部分为起始边界的重构。
|
Download:
|
| 图 2 图 1重构的隐式分区并行策略 Fig. 2 Implicit domain decomposition method for the problem shown in Fig. 1 | |
在具体的操作时,无需为每个线程复制整个计算区域,而是允许每个线程均能获取所有节点。在线程更新网格节点值之前,应预先比较写入值与节点既有值的大小,若写入值更小,则更新该节点,当多个线程更新同一节点出现冲突时,可通过OpenMP中的原子操作解决;若节点值更小,写入值将不被采纳,而且线程将不能通过该节点向外继续求解其他未重构的节点。此时,线程自动将该节点作为其子区域的边界节点。
与显式分区并行重构比较,隐式分区并行重构没有子区域间节点值传递环节和回滚环节。隐式分区并行重构方法的特点是允许线程重构其他线程重构过的节点,其中,节点被重新重构称为重演。
在快速步进重构法中,节点根据重构状态分为3类:Far表示未重构、Close表示重构中、Alive表示已重构。而在新的隐式分区并行重构算法中,节点状态将被设定为线程私有。这样,被一个线程重构过的节点可以被另一个线程继续重构。当一个线程重构结束时,所有节点会被标记成Alive或保留Far标记。节点保留Far标记是因为该节点在其他线程下的重构值更小。当重构结束时,重构的节点势必属于某个线程,即以某个线程的计算结果作为其重构值,而属于某个线程重构节点的集合构成该线程控制的区域,这样,整个重构区域分解成多个子区域。
为了保证线程间重构开销平衡,减小节点重复重构的次数,隐式分区并行重构同样采用自适应策略划分交界面。定义交界面为Γ,线程总数为NP,具体步骤如下:
1) 令o=1, n=Np, Γo=Γ。
2) 确定交界面Γo的坐标中值(xc, yc)。
3) 确定交界面Γ0分别与x=xc及y=yc相交的交点个数mx和my。
4) 当mx < my,Γ0上的x>xc部分移到Γ0+n/2,其余部分保留在Γ0中;否则,将交界面中y>yc的部分移给Γ0+n/2。
5) 若n>2,则o←o, n←n/2, Γo←Γo和o←o+n/2, n←n/2, Γo←Γo+n/2,
6) 返回步骤2)执行递归操作。
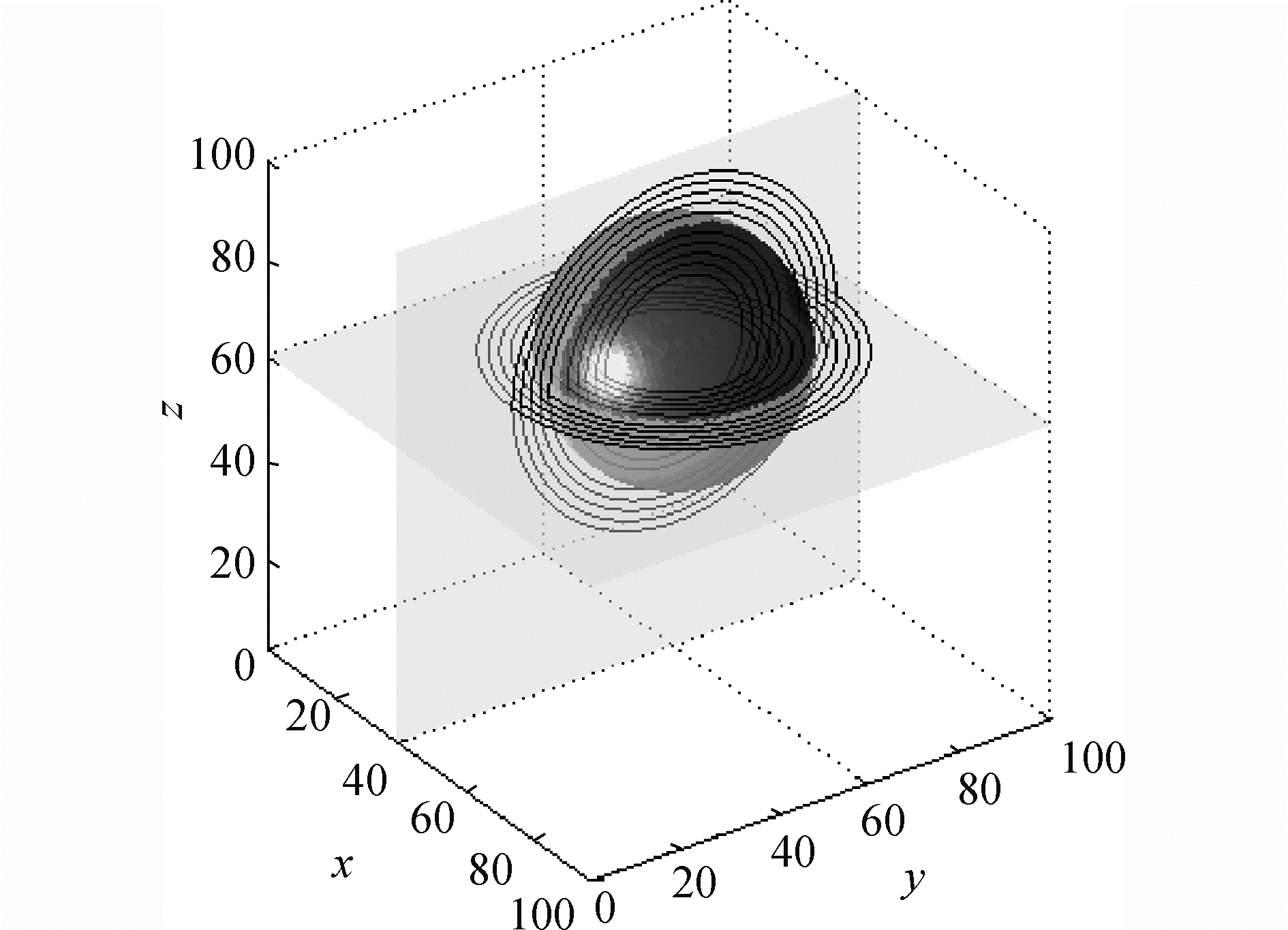
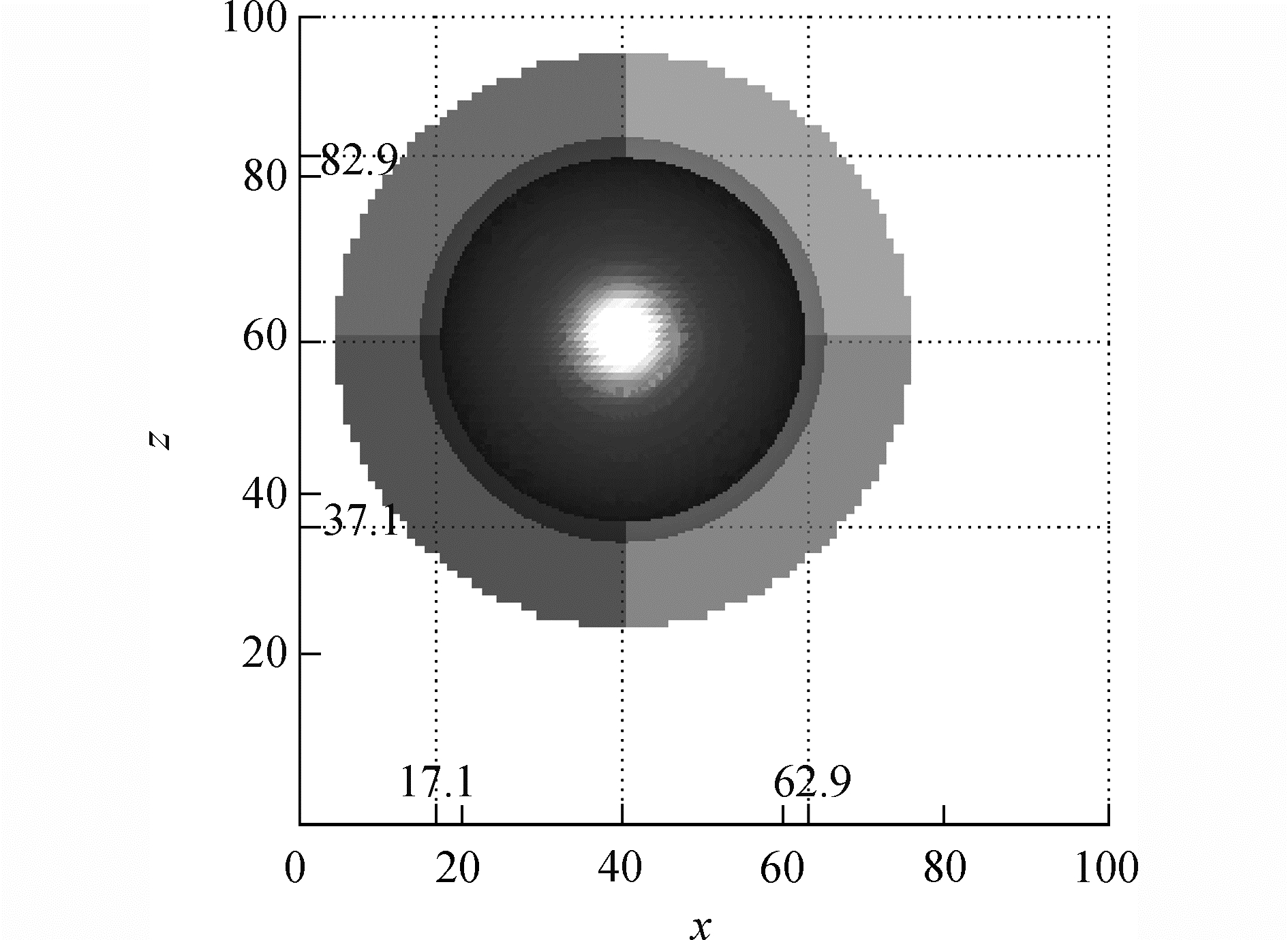
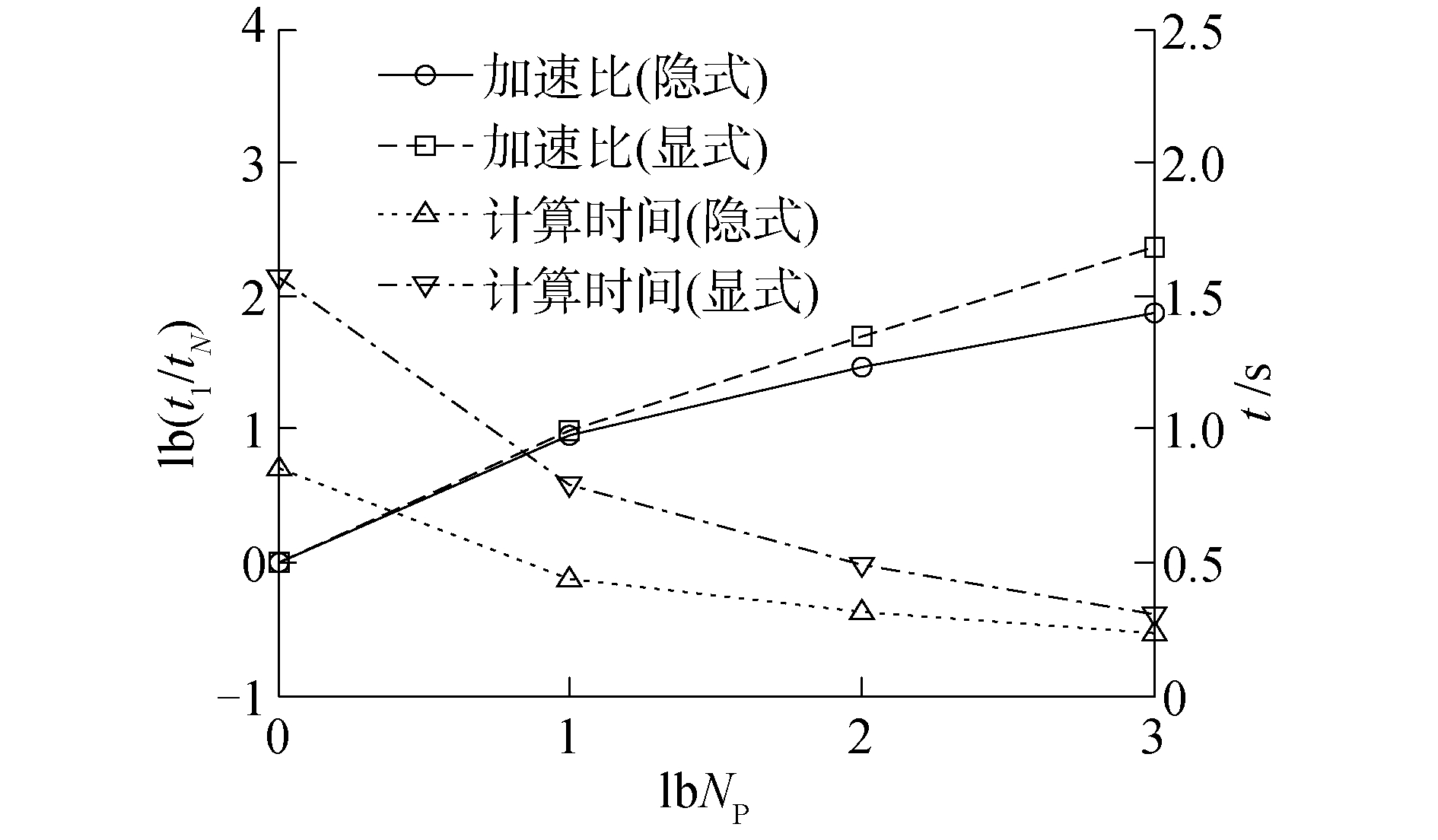
3 算例及讨论 3.1 圆球圆球位于尺寸为100×100×100的计算区域内,其球心位置为(40, 60, 60),半径为25。重构区域的范围设定为ф∈[-12, 12]。图 3为8线程下重构等值面f=-10, -8, -6, -4, -2, 2, 4, 6, 8, 10与平面x=40以及平面z=60的交线。图 4给出了y=50平面上不同线程控制的分区,可以看出,分区大小基本相等,且其边界垂直于交界面边界,这是因为信息沿交界面法向方向传播。表 1给出ф=10等值面所包围的体积以及重构的计算误差,其中,体积计算和误差估计采用文献[25]中的方法,整体计算精度为1阶。图 5比较了隐式分区和显式分区下不同线程数量带来的加速比。8线程下显式分区并行的加速比达到5,而隐式分区并行的加速比接近4。虽然相同线程数量下隐式分区并行重构加速比略小于显式分区计算,但前者实际计算时间要小于后者。
|
Download:
|
| 图 3 8线程下不同等值面的重构结果与平面x=40和平面z=60的交线(圆球) Fig. 3 Intersections between sphere′s reconstructed isosurfaces and two planes of x=40 & z=60 under 8 threads (sphere) | |
|
Download:
|
| 图 4 平面y=50上不同线程控制的区域(圆球) Fig. 4 Regions governed by different threads at the plane of y=50(sphere) | |
| 表 1 圆球等值面ф=10并行重构的计算损失和误差 Table 1 Computational loss and error of the parallel reconstructed sphere isosurface of ф=10 |
|
Download:
|
| 图 5 隐式与显式分区下圆球并行重构加速比与耗时比较 Fig. 5 Comparison of speedup & runtime between the implicit and explicit domain decomposition methods in parallel reconstruction of the sphere | |
实际上,隐式分区并行重构中的节点重演和显式分区并行算法中的节点回滚都是为了保证线程间计算的同步。在显式分区并行算法中,定义了回滚参数:
| $ F_{r}= \frac{{ N_{t}}}{{M}} $ | (4) |
式中:Nt节点回滚操作总次数; M计算区域内重构节点总数。
本文同样定义一个节点重演参数,也用Fr表示,即:
| $ F_{r}= \frac{{ M_{r}}}{{M}} $ | (5) |
式中Mr节点重演操作总次数。
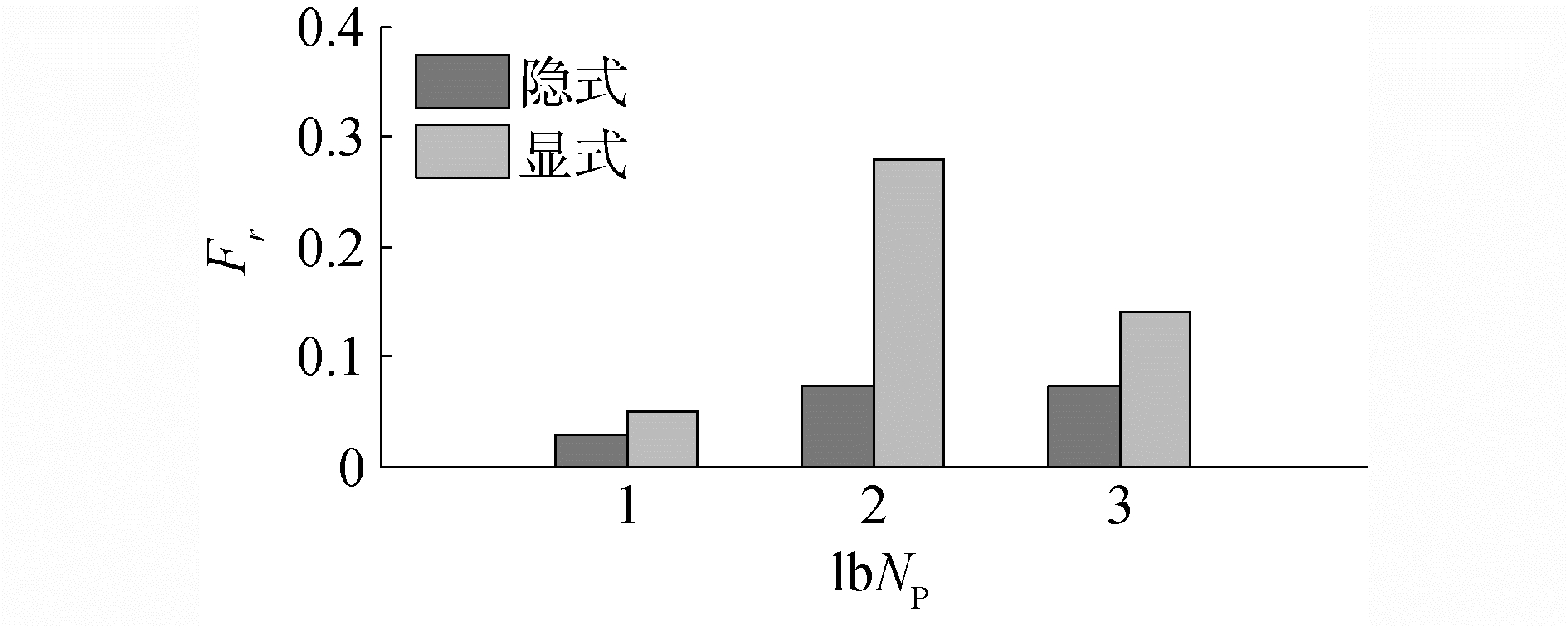
图 6给出了采用隐式和显式分区在不同线程数量下的Fr值。可以看出,采用隐式分区算法,节点重演的比例明显低于显式分区算法。
|
Download:
|
| 图 6 隐式与显式分区下圆球并行重构Fr值的对比 Fig. 6 Comparison of the Fr value between the implicit and explicit domain decomposition methods in parallel reconstruction of the sphere | |
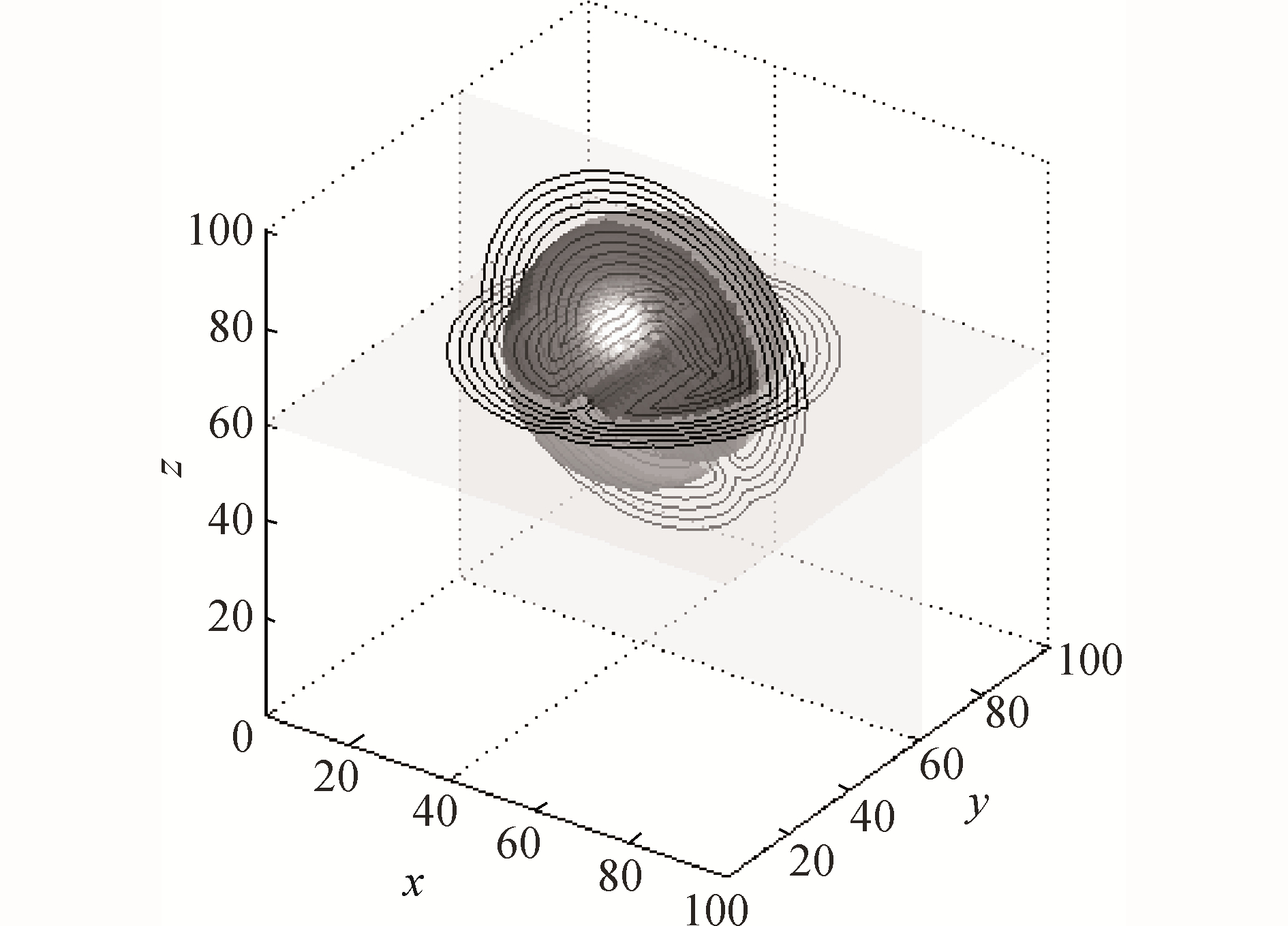
同样在100×100×100计算区域的(40, 60, 60)位置上,放置半径为25、缺口宽度为10,深度为25, 缺口在y平面上的投影与x轴夹角呈-45°的Zalesak球,如图 7所示。本算例的整个重构范围仍取ф∈[-12, 12]。图 7给出了8线程下重构等值面f=-10, -8, -6, -4, -2, 2, 4, 6, 8, 10与平面y=60以及平面z=60的交线。
|
Download:
|
| 图 7 8线程下不同等值面的重构结果与平面y=60和平面z=60的交线(Zalesak圆球) Fig. 7 Intersections between Zalesak sphere′s reconstructed isosurfaces and two planes of y=60 & z=60 under 8 threads (Zalesak sphere) | |
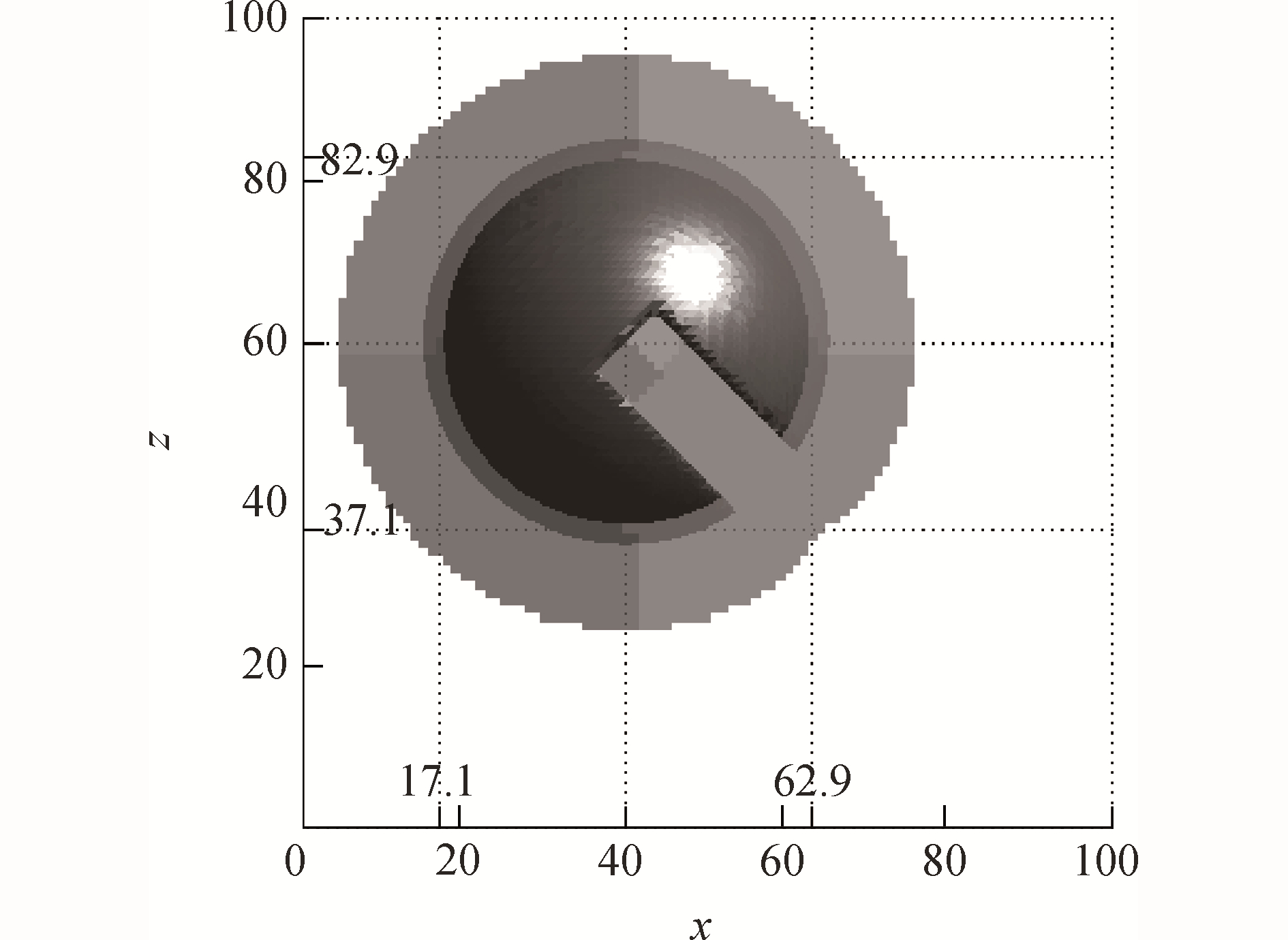
不同线程在y=50平面上的控制分区如图 8所示,可以看出,与圆球算例同一平面上线程控制区域分布(图 4)相比,本算例中不同线程控制区域分布存在差异。ф=5等值面所包围的体积以及重构值的计算误差见表 2。
|
Download:
|
| 图 8 平面y=50上不同线程控制的区域(Zalesak球) Fig. 8 Regions governed by different threads at the plane of y=50(Zalesak sphere) | |
| 表 2 Zalesak球等值面ф=10并行重构的计算损失和误差 Table 2 Computational loss and error of parallel reconstruction of the Zalesak′s sphere isosurface of ф=5 |
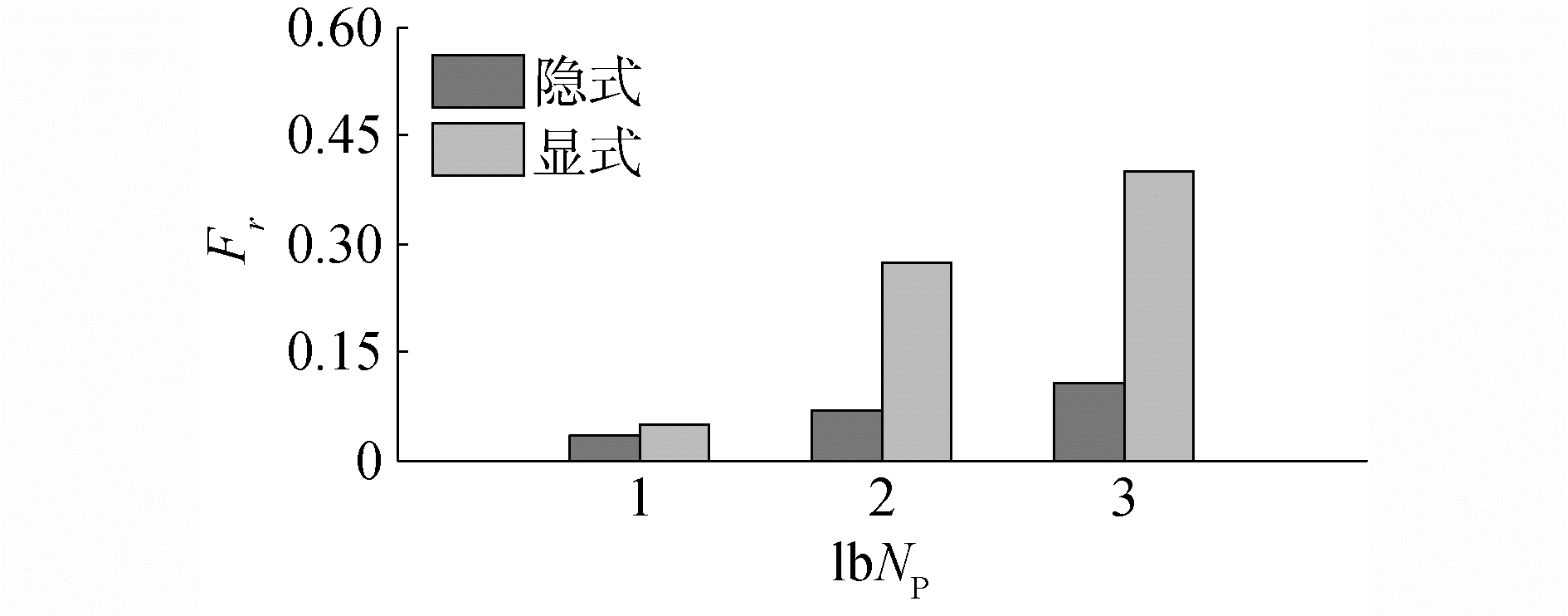
Zalesak球隐式与显式分区并行重构的加速比和计算时间如图 9所示,容易看出,2种并行算法的加速比相近,8线程下的加速比均接近4,但隐式分区并行重构算法的计算时间明显要少于显式分区,几乎只有前者耗时的1/2。从图 10中同样可以看出,在Zalesak球等值面的并行重构中,隐式分区的节点重演次数也少于显式算法的节点回滚次数,前者的Fr值不到后者的1/3。

|
Download:
|
| 图 9 隐式与显式分区下Zalesak球并行重构加速比与耗时比较 Fig. 9 Comparison of speedup & runtime between the implicit and explicit domain decomposition methods in parallel reconstruction of the Zalesak sphere | |
|
Download:
|
| 图 10 隐式与显式分区下Zalesak球并行重构Fr值的对比 Fig. 10 Comparison of the Fr value between the implicit and explicit domain decomposition methods in parallel reconstruction of the Zalesak sphere | |
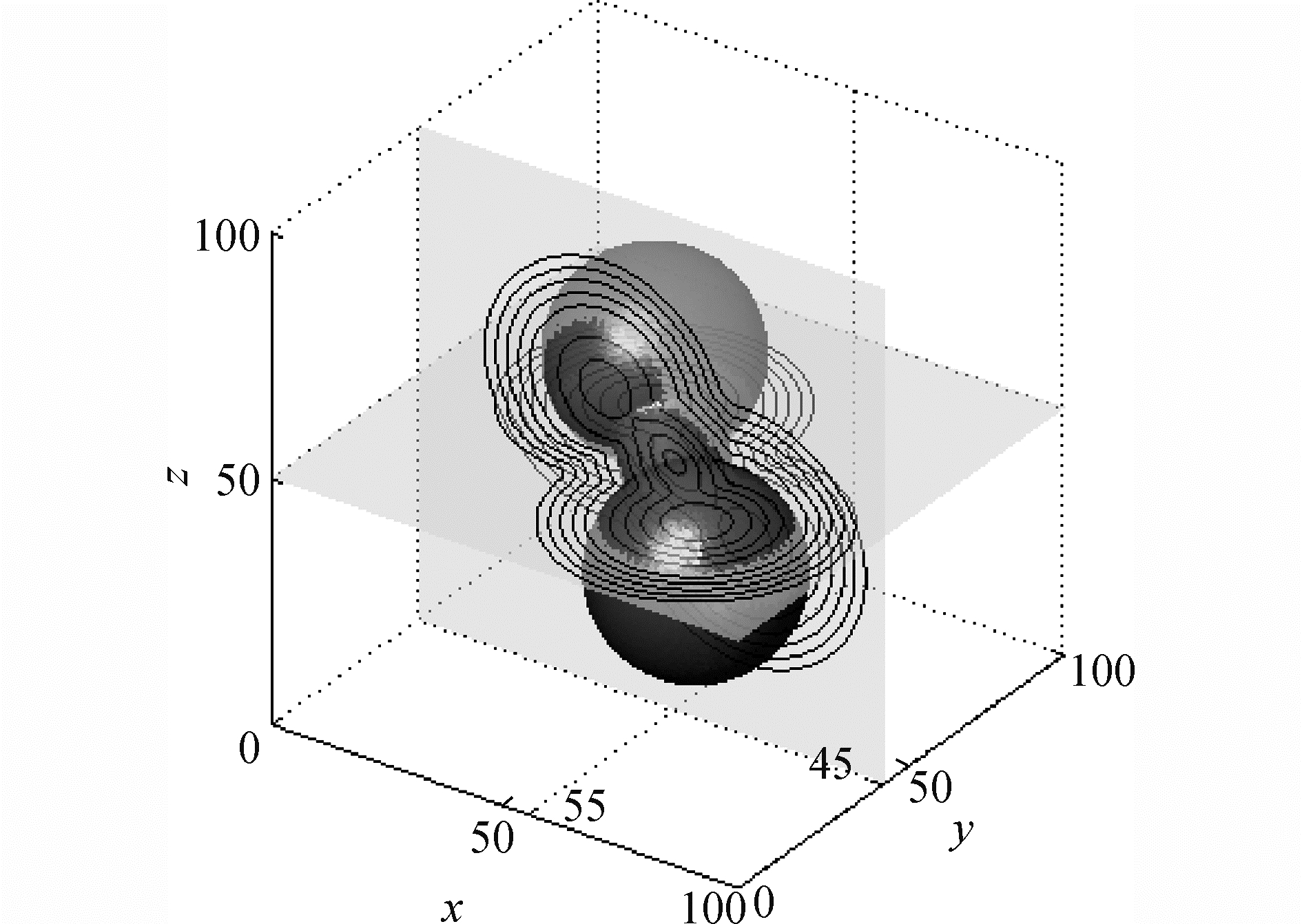
放置在100×100×100计算区域内的哑铃由半径相同的2个球体和1个圆柱体构成。2个球体分别位于(40, 60, 60)和(70, 30, 40)处,半径为20,连接2个球心的圆柱的横截面半径为10。哑铃等值面同样采用8个线程重构,其重构范围依然限制在ф∈[-12, 12]。图 11给出8线程下哑铃重构等值面f=-10, -8, -6, -4, -2, 2, 4, 6, 8, 10与平面y=45以及平面z=50的交线。图 12显示平面y=50上不同线程控制的计算区域。
|
Download:
|
| 图 11 8线程下不同等值面的重构结果与与平面y=45和平面z=50的交线(哑铃) Fig. 11 Intersections between dumbbell′s reconstructed isosurfaces and two planes of y=45 & z=50 under 8 threads (dumbbell) | |

|
Download:
|
| 图 12 平面y=50上不同线程控制的区域(哑铃) Fig. 12 Regions governed by different threads at the plane of y=50(dumbbell) | |
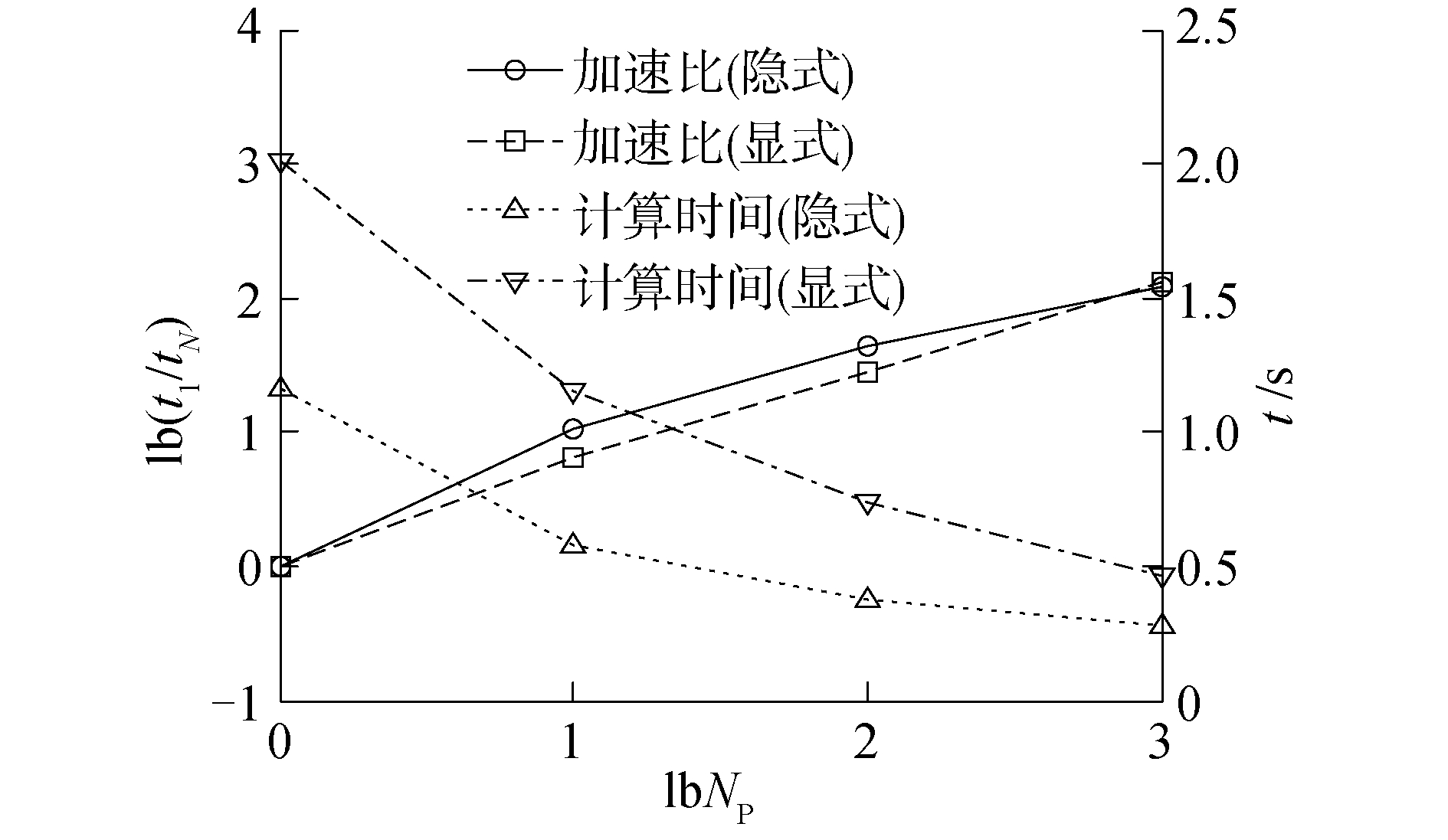
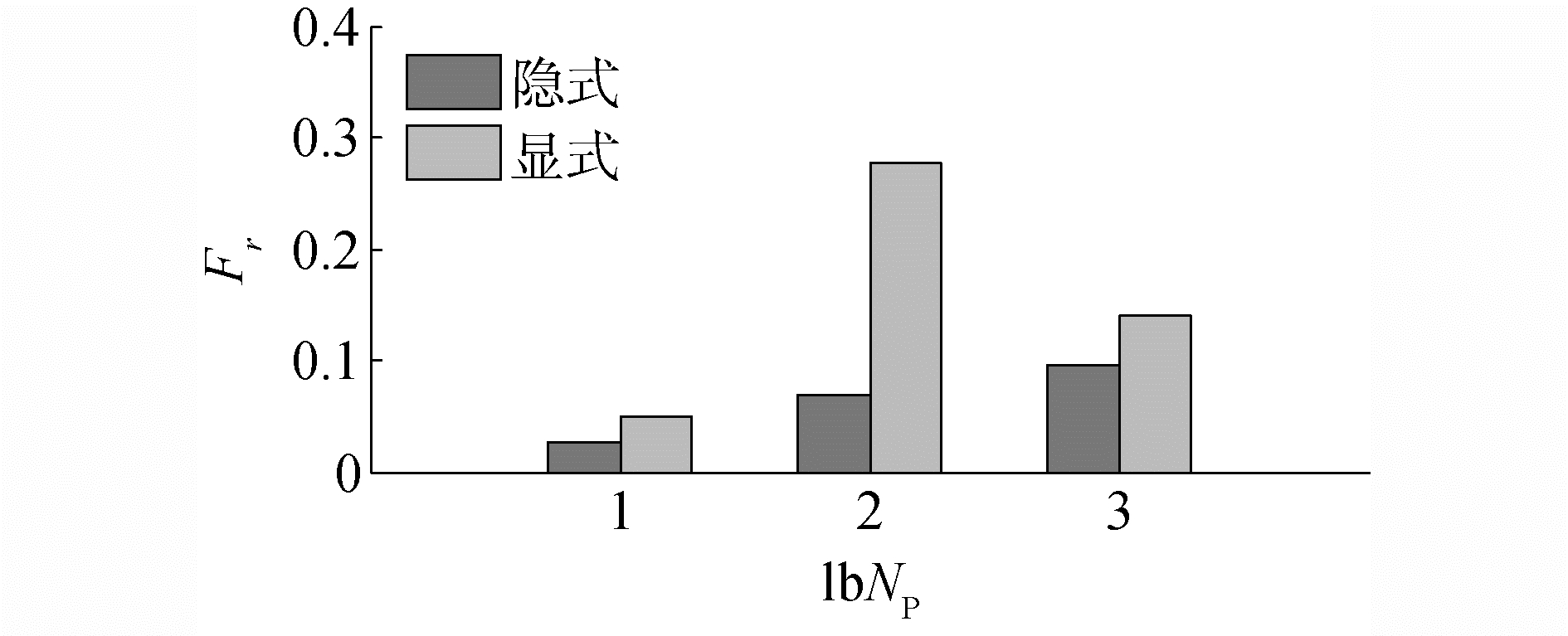
表 3给出了ф=5等值面所包围体积以及重构的计算误差。从图 13可以看出,相同线程数量下隐式分区并行计算的加速比略大于显式分区,且隐式分区并行计算耗时几乎只有显式分区的1/2。如图 14所示,在哑铃等值面的并行重构中,隐式分区的节点重演次数也少于显式算法的节点回滚次数。
| 表 3 哑铃等值面ф=5并行重构的计算损失和误差 Table 3 Computational loss and error of the parallel isosurface reconstruction of the dumbbell isosurface of ф=5 |
|
Download:
|
| 图 13 隐式与显式分区下哑铃并行重构加速比与耗时比较 Fig. 13 Comparison of speedup & runtime between the implicit and explicit domain decomposition methods in parallel reconstruction of the dumbbell | |
|
Download:
|
| 图 14 隐式与显式分区下哑铃并行重构Fr值的对比 Fig. 14 Comparison of the Fr value between the implicit and explicit domain decomposition methods in parallel reconstruction of the dumbbell | |
1) 基于共享内存架构的隐式分区并行算法能够有效节约计算时间。
2) 相同线程数量下,隐式分区并行算法的加速比与显式分区并行算法基本一致,8线程下并行算法的加速比接近4。
3) 在相同线程数量下,隐式分区并行算法的实际耗时要小于显式分区并行算法。
4) 隐式分区并行重构的节点重演次数要少于显式分区并行重构的节点回滚次数。
| [1] |
S SETHIAN J A, SMEREKA P. Level set methods for fluid interfaces[J]. Annual review of fluid mechanics, 2003, 35: 341-372. (  0) 0)
|
| [2] |
HIRT C W, NICHOLS B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J]. Journal of computational physics, 1981, 39(1): 201-225. (  0) 0)
|
| [3] |
UNVERDI S O, TRYGGVASON G. A front-tracking method for viscous, incompressible, multi-fluid flows[J]. Journal of computational physics, 1992, 100(1): 25-37. (  0) 0)
|
| [4] |
BADALASSI V E, CENICEROS H D, BANERJEE S. Computation of multiphase systems with phase field models[J]. Journal of computational physics, 2003, 190(2): 371-397. (  0) 0)
|
| [5] |
GIBOU F, FEDKIW R, OSHER S. A review of level-set methods and some recent applications[J]. Journal of computational physics, 2018, 353: 82-109. (  0) 0)
|
| [6] |
PENG Danping, MERRIMAN B, OSHER S, et al. A PDE-based fast local level set method[J]. Journal of computational physics, 1999, 155(2): 410-438. (  0) 0)
|
| [7] |
ENRIGHT D, FEDKIW R, FERZIGER J, et al. A hybrid particle level set method for improved interface capturing[J]. Journal of computational physics, 2002, 183(1): 83-116. (  0) 0)
|
| [8] |
MCSHERRY R J, CHUA K V, STOESSER T. Large eddy simulation of free-surface flows[J]. Journal of hydrodynamics, ser. B, 2017, 29(1): 1-12. (  0) 0)
|
| [9] |
SUSSMAN M, SMEREKA P, OSHER S. A level set approach for computing solutions to incompressible two-phase flow[J]. Journal of computational physics, 1994, 114(1): 146-159. (  0) 0)
|
| [10] |
ENRIGHT D, LOSASSO F, FEDKIW R. A fast and accurate semi-Lagrangian particle level set method[J]. Computers & structures, 2005, 83(6/7): 479-490. (  0) 0)
|
| [11] |
JIANG Liang, LIU Fengbin, CHEN Darong. A fast particle level set method with optimized particle correction procedure for interface capturing[J]. Journal of computational physics, 2015, 299: 804-819. (  0) 0)
|
| [12] |
MIRZADEH M, GUITTET A, BURSTEDDE C, et al. Parallel level-set methods on adaptive tree-based grids[J]. Journal of computational physics, 2016, 322: 345-364. (  0) 0)
|
| [13] |
SETHIAN J A. Fast marching methods[J]. SIAM review, 1999, 41(2): 199-235. (  0) 0)
|
| [14] |
CHOPP D L. Some improvements of the fast marching method[J]. SIAM journal on scientific computing, 2001, 23(1): 230-244. (  0) 0)
|
| [15] |
HASSOUNA M S, FARAG A A. Multistencils fast marching methods: a highly accurate solution to the Eikonal equation on Cartesian domains[J]. IEEE transactions on pattern analysis and machine intelligence, 2007, 29(9): 1563-1574. (  0) 0)
|
| [16] |
RICHARD TSAI Y H, CHENG L T, OSHER S, et al. Fast sweeping algorithms for a class of Hamilton-Jacobi equations[J]. SIAM journal on numerical analysis, 2003, 41(2): 673-694. (  0) 0)
|
| [17] |
QIAN Jianliang, ZHANG Yongtao, ZHAO Hongkai. Fast sweeping methods for Eikonal equations on triangular meshes[J]. SIAM journal on numerical analysis, 2007, 45(1): 83-107. (  0) 0)
|
| [18] |
LI Fengyan, SHU Chiwang, ZHANG Yongtao, et al. A second order discontinuous Galerkin fast sweeping method for Eikonal equations[J]. Journal of computational physics, 2008, 227(17): 8191-8208. (  0) 0)
|
| [19] |
GREMAUD P A, KUSTER C M. Computational study of fast methods for the Eikonal equation[J]. SIAM journal on scientific computing, 2006, 27(6): 1803-1816. (  0) 0)
|
| [20] |
HERRMANN M. A domain decomposition parallelization of the fast marching method[R]. Stanford, CA: Center for Turbulence Research, Stanford University, 2003: 253-261. https://www.researchgate.net/publication/235144798_A_Domain_Decomposition_Parallelization_of_the_Fast_Marching_Method
(  0) 0)
|
| [21] |
TUGURLAN M C. Fast marching methods-parallel implementation and analysis[D]. Baton Rouge, LA: Louisiana State University, 2008. https://www.researchgate.net/publication/277056975_Fast_Marching_Methods_-_Parallel_Implementation_and_Analysis
(  0) 0)
|
| [22] |
YANG Jianming, STERN F. A highly scalable massively parallel fast marching method for the Eikonal equation[J]. Journal of computational physics, 2017, 332: 333-362. (  0) 0)
|
| [23] |
黄筱云, 董国海, 赵利平, 等. Level set函数重新初始化的并行快速步进法[J]. 哈尔滨工程大学学报, 2016, 37(5): 666-671, 689. HUANG Xiaoyun, DONG Guohai, ZHAO Liping, et al. A parallelized fast marching method for reinitialization of level set function[J]. Journal of Harbin Engineering University, 2016, 37(5): 666-671, 689. (  0) 0)
|
| [24] |
黄筱云, 董国海, 常佳夫, 等. Level set函数快速步进重构并行算法的改进[J]. 哈尔滨工程大学学报, 2017, 38(6): 836-842. HUANG Xiaoyun, DONG Guohai, CHANG Jiafu, et al. Improvement of parallel fast marching method for reconstruction of level set function[J]. Journal of Harbin Engineering University, 2017, 38(6): 836-842. (  0) 0)
|
| [25] |
夏波, 黄筱云, 陈同庆, 等. Level set函数快速步进并行重构的分区优化[J]. 哈尔滨工程大学学报, 2019, 40(9): 1601-1607. XIA Bo, HUANG Xiaoyun, CHEN Tongqing, et al. Optimized domain decomposition for parallel reconstruction of the level set function by fast marching method[J]. Journal of Harbin Engineering University, 2019, 40(9): 1601-1607. (  0) 0)
|
| [26] |
SETHIAN J A. A fast marching level set method for monotonically advancing fronts[J]. Proceedings of the national academy of sciences of the United States of America, 1996, 93(4): 1591-1595. (  0) 0)
|
| [27] |
LOSASSO F, FEDKIW R, OSHER S. Spatially adaptive techniques for level set methods and incompressible flow[J]. Computers & fluids, 2006, 35(10): 995-1010. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


