2. 西北工业大学 无人机特种技术国防科技重点实验室, 陕西 西安 710072;
3. 西北工业大学 自动化学院, 陕西 西安 710072
2. National Key Laboratory of Special Technology on UAV, Northwestern Polytechnical University, Xi'an 710072, China;
3. School of Automation, Northwestern Polytechnical University, Xi'an 710072, China
目标识别技术(target identification technique, TIT)可以理解为将未知含义的目标对象判别为一组已知目标集的某一类或某一个,该技术一般使用目标特征间的相似性来描述目标对象间的相似性。因此,目标识别方法的优劣可由其描述目标的特点决定,特定的识别任务决定着描述特征的选择。
图像不变矩可分为复数矩、旋转矩、几何矩和正交矩等4类,其中正交矩又可分为连续正交矩与离散正交矩,而用于二值图或灰度图二维密度分布描述的不变连续正交矩称为图像不变连续正交矩(简称图像矩)[1-2]。图像矩在目标图像经过平移、缩放或旋转之后,仍保持不变,因此可用于目标图像的特征描述[3-4]。在图像矩的研究与应用中,一部分研究关注图像矩的构造与快速计算[5],而另一部分研究则围绕着图像矩在图像处理、识别、配准等领域的应用[6-8],这2个方向相互影响相互制约。目前,有关图像矩的快速计算多以傅里叶变换为基础展开,如圆谐傅里叶矩、雅可比-傅里叶矩、指数矩等。然而傅里叶变换以正弦-余弦函数系作为变换核,计算过程中进行了复数运算,在高分辨率数字图像的图像矩计算处理效率上并非最优。本文依据不变矩理论,结合沃尔什变换构造了一种基于沃尔什变换的图像矩,并利用快速沃尔什变换实现了该图像矩的快速计算。
1 沃尔什变换及图像矩构造过程简介沃尔什变换[9-10]的变换核只取+1和-1这2个值,其变换过程中只需进行实数加、减运算,没有乘、除运算,其逆变换仅有一个1/N因子。由于变换核的二值性符合计算机处理机制,故沃尔什变换具有更快的计算效率,整个计算过程误差积累小可以被忽略。
图像矩在构造过程中[11-12],为保证其旋转不变性以及伸缩不变性,常针对直角坐标系进行归一化与极坐标的处理与转换。归一化的实现方法又可分为外接圆法和内切圆法,从集合的角度来看IA⊂I⊂IB,其中IA为内切圆归一化后的图像点集,I为原图像像素点集,IB为外接圆归一化后图像点集。归一化处理后,通过极坐标转换获得原图的极坐标图像,进而利用单位圆所在方形区域进行图像矩的构造。
2 基于沃尔什变换的图像矩 2.1 二维沃尔什变换设自变量为n1、n2,且n1∈[0, N1-1],n2∈[0, N2-1]的二维离散信号为x(n1, n2)其二维沃尔什变换与逆变换的计算式分别为式(1)、(2),矩阵形式为式(3)、(4):
| $ \begin{array}{l} X\left( {{k_1}, {k_2}} \right) = \sum\limits_{{n_2} = 0}^{{N_2} - 1} {\sum\limits_{{n_1} = 0}^{{N_1} - 1} x } \left( {{n_1}, {n_2}} \right){\rm{Wa}}{{\rm{l}}_w}\left( {{k_1}, {n_1}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;{\rm{Wa}}{{\rm{l}}_w}\left( {{k_2}, {n_2}} \right)/{N_1}{N_2} \end{array} $ | (1) |
式中:k1∈[0, N1-1],Walw(k, n)表示第k个沃尔什函数的第n个采样点。
| $ \begin{array}{l} x\left( {{n_1}, {n_2}} \right) = \sum\limits_{{k_2} = 0}^{{N_2} - 1} {\sum\limits_{{k_1} = 0}^{{N_1} - 1} X } \left( {{k_1}, {k_2}} \right){\rm{Wa}}{{\rm{l}}_w}\left( {{k_1}, {n_1}} \right)\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\rm{Wa}}{{\rm{l}}_w}\left( {{k_2}, {n_2}} \right) \end{array} $ | (2) |
式中,n1∈[0, N1-1],n2∈[0, N2-1]。
| $ \begin{array}{l} \left[ {X\left( {{k_1}, {k_2}} \right)} \right] = \left[ {{\rm{Wa}}{{\rm{l}}_w}\left( {{p_1}} \right)} \right]\left[ {x\left( {{n_1}, {n_2}} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{\rm{Wa}}{{\rm{l}}_w}\left( {{p_2}} \right)} \right]/{N_1}{N_2} \end{array} $ | (3) |
| $ \begin{array}{l} \left[ {x\left( {{n_1}, {n_2}} \right)} \right] = \left[ {{\rm{Wa}}{{\rm{l}}_w}\left( {{p_1}} \right)} \right]\left[ {X\left( {{k_1}, {k_2}} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{\rm{Wa}}{{\rm{l}}_w}\left( {{p_2}} \right)} \right] \end{array} $ | (4) |
| $ 式中, \left\{ {\begin{array}{*{20}{l}} {{k_1}, {n_1} = 0, 1, \cdots {N_1} - 1, }&{{N_1} = {2^{p1}}}\\ {{k_2}, {n_2} = 0, 1, \cdots {N_2} - 1, }&{{N_2} = {2^{p2}}} \end{array}} \right., {\rm{Wa}}{{\rm{l}}_w}\left( {{p_1}} \right) $ |
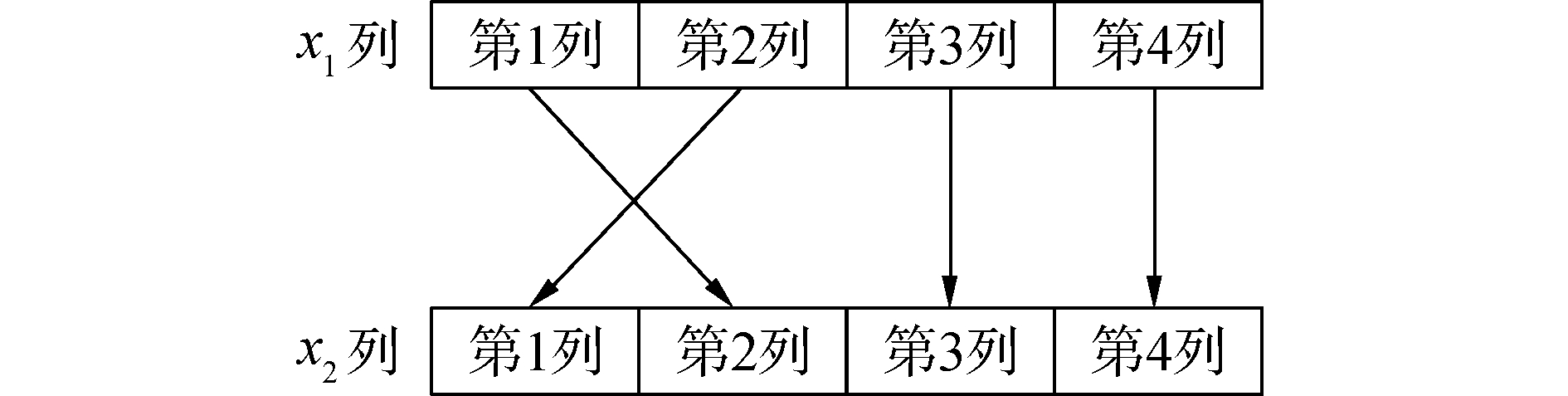
与Walw(p2)为沃尔什排列下沃尔什变换矩阵。由变换矩阵组成以及矩阵运算可知,二维沃尔什变换结果与x(n1, n2)的数据排列有关,当二维离散信号x(n1, n2)列数据间发生交换时,其所得沃尔什变换结果的列方向数据组成完全相同,但列方向数据顺序位置并不相同。例如,x1、x2为列方向数据组成但排列不同的2个矩阵,其位置关系如图 1所示。针对x1、x2进行沃尔什变换的计算结果如下:
| $ {\mathit{\boldsymbol{x}}_1} = \left[ {\begin{array}{*{20}{c}} 1&2&3&4\\ 5&6&7&8\\ 9&{10}&{11}&{12}\\ {13}&{14}&{15}&{16} \end{array}} \right] \Rightarrow {\mathit{\boldsymbol{X}}_1} = \left[ {\begin{array}{*{20}{c}} {8.5}&{ - 1}&0&{0.5}\\ { - 4}&0&0&0\\ 0&0&0&0\\ { - 2}&0&0&0 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{x}}_2} = \left[ {\begin{array}{*{20}{c}} 2&1&3&4\\ 6&5&7&8\\ {10}&9&{11}&{12}\\ {14}&{13}&{15}&{16} \end{array}} \right] \Rightarrow {\mathit{\boldsymbol{X}}_2} = \left[ {\begin{array}{*{20}{c}} {8.5}&{ - 1}&{0.5}&0\\ { - 4}&0&0&0\\ 0&0&0&0\\ { - 2}&0&0&0 \end{array}} \right] $ |
|
Download:
|
| 图 1 矩阵x1与x2位置关系 Fig. 1 Positional relationship diagram matrix x1 and x2 | |
依据上述沃尔什变换矩阵计算的结果,为便于理解在此引入柱面图像。
当直角坐标系下的图像发生旋转时,对应的极坐标下图像,仅沿极角方向做平移变换。故可将极坐标二维图像的极角方向首尾相接看作环形数据,即将极坐标二维图像转换至三维空间的柱面图像,如图 2所示。
由图 2可知,lena图像逆时针旋转60°后,图(e)相对图(b)向左平移;柱面图中,在图像方位角与俯视角相同的情况下,图(f)相对图(c)围绕中心轴(z轴)顺时针方向发生旋转。结合图 2结果,当二维离散信号x(n1, n2)发生环形平移时,可看作其所对应的数字图像绕中心轴旋转。
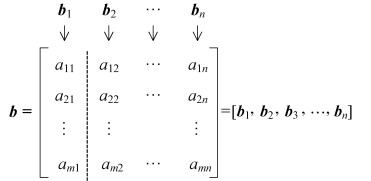
2.3 沃尔什变换的图像矩构建令b=[b1b2…bn],具体形式见式(5)。由上面的分析可知,b1, b2, …, bn的排列顺序将直接影响沃尔什变换的结果,若通过一定的运算将b1, b2, …, bn的排列顺序保持相对不变,那么沃尔什变换的结果也会保持相对不变[13-15]。结合图 2中(c)、(f)图,假设沿z轴方向可找到具有强分辨力的一条裁剪线,将(c)、(f)图展开为相同的二维平面图像,可以得到相对不变的沃尔什变换值。

|
Download:
|
| 图 2 三维柱面图像的形成 Fig. 2 Formation process of a three-dimensional cylindrical image | |
|
(5) |
结合式(3)构造沃尔什图像矩,计算公式为:
| $ \begin{array}{l} \left[ {W\left( {{k_1}, {k_2}} \right)} \right] = \left[ {{\rm{Wa}}{{\rm{l}}_w}(N)} \right]\left[ {{g_p}\left( {{n_1}, {n_2}} \right)} \right]\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {{\rm{Wa}}{{\rm{l}}_w}(N)} \right]/{N^2} \end{array} $ | (6) |
| $ {\mathit{\boldsymbol{g}}_n}\left( {{n_1}, {n_2}} \right) = \mathit{\boldsymbol{g}}\left( {{n_1}, {n_2}} \right)\mathit{\boldsymbol{P}}\left( {{n_1}, {n_2}} \right) $ | (7) |
式中:k1, n1, k2, n2=0, 1, …, N-1,N=2p,P(n1, n2)为置换矩阵;g(n1, n2)为极坐标图像矩阵;Walw(N)为N阶沃尔什排列的沃尔什正交函数矩阵;W(k1, k2)为目标图像的沃尔什图像矩。根据正交理论可知,可由有限沃尔什图像矩近似重构图像函数,矩阵形式计算式为:
| $ {\mathit{\boldsymbol{g}}_n}\left( {{n_1}, {n_2}} \right) = {\rm{Wa}}{{\rm{l}}_w}(N)\mathit{\boldsymbol{W}}\left( {{k_1}, {k_2}} \right){\rm{Wa}}{{\rm{l}}_w}(N) $ | (8) |
| $ \mathit{\boldsymbol{g}}\left( {{n_1}, {n_2}} \right) = {\mathit{\boldsymbol{g}}_p}\left( {{n_1}, {n_2}} \right)\mathit{\boldsymbol{P}}{\left( {{n_1}, {n_2}} \right)^{ - 1}} $ | (9) |
由沃尔什图像矩的构造过程可知,置换矩阵可将极坐标图像按固有特征转换至顺序空间,顺序空间的极坐标图像映射相对不变,而极坐标图像的固有特征有很多,最大值、最小值、均值、极值、阶跃、分位数等,也可以是一个加密算法,或是一个人造的强特征,但需要考虑极坐标图像的纹理特征。
在矩阵论中,置换矩阵是由0、1组成的方阵,在沃尔什图像矩计算中,置换矩阵P(n1, n2),可由单位矩阵E(n1, n2)通过列交换得到。本文选取基于序列加权的特征来构造置换矩阵,N×N极坐标图像的每一点g(n1, n2)的加权计算式为:
| $ {g_W}\left( {{n_1}, {n_2}} \right) = \frac{{{n_1}}}{N}g\left( {{n_1}, {n_2}} \right) $ | (10) |
进而求取gw矩阵的列方向之和最大值对应的序号,以此序号对单位矩阵E(n1, n2)进行列交换,便可获得基于序列加权的置换矩阵P(n1, n2)。
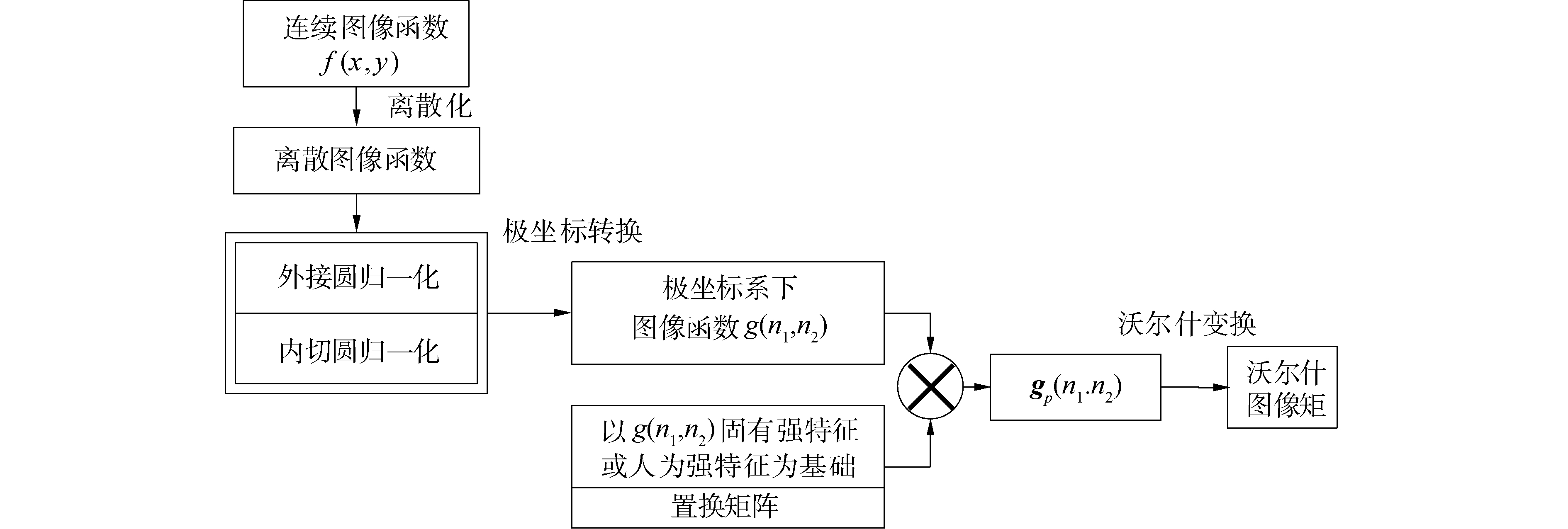
通过以上分析与推导可知,沃尔什图像矩的计算流程如图 3所示。
3 沃尔什图像矩不变性实验 3.1 图像矩不变性简单评价图像矩在数学形式上为矩阵,原图像的图像矩与发生平移、旋转、缩放等操作后图像的图像矩,可利用矩阵间的相对误差进行简单定量评价,定义图像发生变换前后的沃尔什图像矩分别为w与w′,则w与w′间的相对误差为:
| $ \delta = \sqrt {\frac{{\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{\left( {{w_{ij}} - w_{ij}^\prime } \right)}^2}} } }}{{\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {w_{ij}^2} } }}} $ | (11) |
沃尔什图像矩的计算过程,可先计算目标图像质心(xi, yi),再将直角坐标系下的数字图像中心移至其质心,最后计算沃尔什图像矩。图像平移并不改变其质心,故沃尔什图像矩具有平移不变性,此处不再单独设计实验。
|
Download:
|
| 图 3 沃尔什图像矩计算流程 Fig. 3 Calculation process of walsh image moment | |
由式(6)可知,N阶沃尔什排列的沃尔什正交函数矩阵Walw(N)在旋转变换中并不发生变化,当目标图像一定时,gp(n1, n2)的构造主要取决置换矩阵,而置换矩阵是以极坐标图像的强特征通过单位阵置换而成,该特征并不随原图像的旋转而变化,故沃尔什图像矩具有旋转不变性。
实验设计及结果:
针对2组8幅旋转图像进行沃尔什图像矩的计算与验证,仿真实验中旋转变换均采用双线性插值。
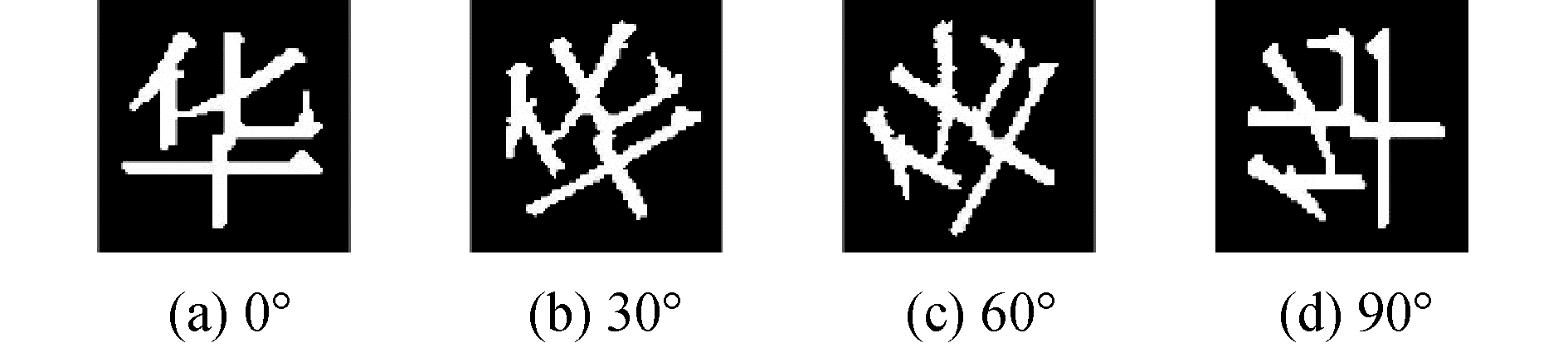
第1组为64×64大小的汉字二值图像仿真实验,旋转方向如图 4所示。
|
Download:
|
| 图 4 二值图像实验 Fig. 4 Experimental results on binary image | |
以内切圆归一化法将图 4转化至极坐标,利用式(6)分别计算每幅图的沃尔什图像矩,数据如表 1所示,比较各组数据可知,旋转后沃尔什图像矩近似相等,其误差主要由旋转插值算法引起。当旋转90°时,双线性插值算法引入误差为零,故图 4(a)与图 4(d)沃尔什图像矩相等。
| 表 1 沃尔什图像矩部分数据 Table 1 Walsh image moment part data |
以图 4(a)的沃尔什图像矩为理论值,利用式(11)分别计算图 4(b)~(d)内切圆归一化法沃尔什图像矩的相对误差,其结果为8.02%、8.04%和0。
第2组为128×128大小的lena灰度图像,计算过程归一化法选择外接圆法,图 5中的旋转均按逆时针方向旋转。

|
Download:
|
| 图 5 Lena灰度图像 Fig. 5 Lena grayscale image | |
利用式(6)计算每幅图的沃尔什图像矩,数据如表 2所示,比较各组数据可知,Lena灰度图像旋转后沃尔什图像矩近似相等。
| 表 2 沃尔什图像矩部分数据 Table 2 Walsh image moment part data |
以图 5 (a)的沃尔什图像矩为理论值,利用式(11)分别计算图 5 (b)~(d)外接圆归一化法沃尔什图像矩的相对误差,其结果为8.32%、6.72%和0。
3.2.3 缩放不变性首先,原图像的缩放变化依旧不会改变置换矩阵的构成,其次,当目标图像一定时其图像函数是一定的,而针对图像函数,无论图像缩放系数如何改变,其归一化图像函数均是不变的,故可对归一化处理后的图像进行沃尔什图像矩的计算,故沃尔什图像矩具有缩放不变性。
实验设计及结果:
针对128×128大小Lena灰度图像分别做0.8倍、1.2倍、2倍缩放,缩放变换中均采用双线性插值。利用式(6)分别计算上述缩放比例下的Lena图像的沃尔什图像矩,数据如表 3所示。
| 表 3 缩放变换下沃尔什图像矩部分数据 Table 3 Walsh image moment partial data under scaling transformation |
以系数为1.0的lena沃尔什图像矩为理论值,利用式(11)分别计算缩放系数为0.8、1.5、2.0下的沃尔什图像矩间的相对误差,其结果为2.36%、1.33%和0.77%。
由以上实验数据可知,图像发生变换前后对应的沃尔什图像矩存在一定的相对误差,但进一步分析可知,仿真中所用缩放图像,均由图像旋转、图像缩放等计算公式所得,当计算中所使用的插值算法不同时,计算所得的相对误差也将有所不同。例如:当采用最邻近元插值法时,以图 5(a)的沃尔什图像矩为理论值,利用式(11)分别计算图 5(b)~(d)外接圆归一化法沃尔什图像矩的相对误差,其结果为10.68%、9.80%和0。
综上可见,图像的沃尔什矩相对误差主要由插值算法与计算舍入误差引起。因此,由仿真结果可进一步验证沃尔什图像矩具有平移、旋转、缩放不变等特性。
3.3 重构实验沃尔什变换核为正交函数系,因此可由有限的沃尔什图像矩重构原图像,计算式如式(8)、(9)所示,定义[fR(n1, n2)]为重构后直角坐标系下的图像,与原图像的误差为e计算式如式(12)所示:
| $ e = \frac{{\sum\limits_{{n_1}} {\sum\limits_{{n_2}} {{{\left[ {f\left( {{n_1}, {n_2}} \right) - {f_R}\left( {{n_1}, {n_2}} \right)} \right]}^2}} } }}{{\sum\limits_{{n_1}} {\sum\limits_{{n_2}} f } {{\left( {{n_1}, {n_2}} \right)}^2}}} $ | (12) |
在UCID图库[16]中随机选取25幅图,分别利用同阶次指数矩[17]、沃尔什图像矩进行重构实验,并利用式(12)计算重构后边缘的误差,结果如6所示,横坐标为图像抽取的序号,纵坐标为对应序号的重构图像边缘误差e。

|
Download:
|
| 图 6 重构图像边缘误差 Fig. 6 Reconstructed image edge error | |
由边缘误差曲线可知,计算过程累计误差较小的沃尔什图像矩,其重构图像边缘误差远小于由指数矩重构的图像边缘误差。
4 结论1) 以不变矩理论为依据,结合沃尔什变换,给出了沃尔什图像矩的定义及计算方法。在沃尔什图像矩的计算过程中,引入置换矩阵并借助柱面图像的思想对其进行构造,其构造可依据普通已有的图像特征,也可以是私有的加密算法,因此沃尔什图像矩还具有一定的隐匿性。
2) 由仿真实验数据的分析可知:沃尔什图像矩对图像具有一定的描述能力,且具有平移、缩放、旋转等不变特性;沃尔什图像矩计算中的误差主要来源于插值算法以及离散化目标图像自身,其计算效率优于基于傅里叶变换的图像矩快速计算。
| [1] |
HU M K. Visual pattern recognition by moment invariants[J]. IRE transactions on information theory, 1962, 8(2): 179-187. DOI:10.1109/TIT.1962.1057692 (  0) 0)
|
| [2] |
PROKOP R J, REEVES A P. A survey of moment-based techniques for unoccluded object Representation and recognition[J]. CVGIP:graphical models and image processing, 1992, 54(5): 438-460. DOI:10.1016/1049-9652(92)90027-U (  0) 0)
|
| [3] |
KARAKASIS E G, AMANATIADIS A, GASTERATOS A, et al. Image moment invariants as local features for content based image retrieval using the Bag-of-Visual-Words model[J]. Pattern recognition letters, 2015, 55: 22-27. DOI:10.1016/j.patrec.2015.01.005 (  0) 0)
|
| [4] |
WU Haiyong, YAN Senlin. Computing invariants of Tchebichef moments for shape based image retrieval[J]. Neurocomputing, 2016, 215: 110-117. DOI:10.1016/j.neucom.2015.05.147 (  0) 0)
|
| [5] |
UPNEJA R. Accurate and fast Jacobi-Fourier moments for invariant image recognition[J]. Optik, 2016, 127(19): 7925-7940. DOI:10.1016/j.ijleo.2016.05.097 (  0) 0)
|
| [6] |
WANG Xue, LI Baoqiong, XU Minli, et al. Quality assessment of Traditional Chinese Medicine using HPLC-PAD combined with Tchebichef image moments[J]. Journal of chromatography B, 2017, 1040: 8-13. DOI:10.1016/j.jchromb.2016.11.026 (  0) 0)
|
| [7] |
GILMORE C, PETERS S, LOVETRI J, et al. GPR target detection using a neural network classifier of image moments as invariant features[C]//Proceedings of 2004 International Symposium on Antenna Technology and Applied Electromagnetics and URSI Conference. Ottawa, Canada: IEEE, 2004: 1-4.
(  0) 0)
|
| [8] |
KUSHWAHA A, SINGH A, SHRIVASTAV S K. Signature classification using image moments[M]//SA P K, SAHOO M N, MURUGAPPAN M, et al. Progress in Intelligent Computing Techniques: Theory, Practice, and Applications. Singapore: Springer, 2018: 235-244.
(  0) 0)
|
| [9] |
关肇直, 陈文德. 沃尔什函数与沃尔什变换[M]. 北京: 国防工业出版社, 1984.
(  0) 0)
|
| [10] |
郭黎利, 张昕, 林继华, 等. 沃尔什(Walsh)码的频谱特性分析[J]. 哈尔滨工程大学学报, 2003, 24(5): 552-555, 570. GUO Lili, ZHANG Xin, LIN Jihua, et al. Spectrum characteristic analysis of Walsh code[J]. Journal of Harbin Engineering University, 2003, 24(5): 552-555, 570. DOI:10.3969/j.issn.1006-7043.2003.05.019 (  0) 0)
|
| [11] |
XIAO Bin, CUI Jiangtao, QIN Hongxing, et al. Moments and moment invariants in the Radon space[J]. Pattern recognition, 2015, 48(9): 2772-2784. DOI:10.1016/j.patcog.2015.04.007 (  0) 0)
|
| [12] |
REN Haiping, PING Ziliang, BO W, et al. Multidistortion-invariant image recognition with radial harmonic Fourier moments[J]. Journal of the Optical Society of America A, 2003, 20(4): 631-637. DOI:10.1364/JOSAA.20.000631 (  0) 0)
|
| [13] |
BESPALOV M S, GOLUBEV A S, POCHENCHUK A S. Derivation of fast algorithms via binary filtering of signals[J]. Problems of information transmission, 2016, 52(4): 359-372. DOI:10.1134/S0032946016040049 (  0) 0)
|
| [14] |
郭黎利, 刘明夺, 姜晓斐. 沃尔什序列组的两个新性质及其推论[J]. 华南理工大学学报(自然科学版), 2013, 41(6): 35-41. GUO Lili, LIU Mingduo, JIANG Xiaofei. Two new properties and corresponding deductions of Walsh sequence set[J]. Journal of South China University of Technology (Natural Science Edition), 2013, 41(6): 35-41. DOI:10.3969/j.issn.1000-565X.2013.06.007 (  0) 0)
|
| [15] |
XIE Zhengwei, QIU Daowen, CAI Guangya. Quantum algorithms on Walsh transform and Hamming distance for Boolean functions[J]. Quantum information processing, 2018, 17(6): 139. DOI:10.1007/s11128-018-1885-y (  0) 0)
|
| [16] |
SCHAEFER G, STICH M. UCID: an uncompressed color image database[C]//Proceedings of Storage and Retrieval Methods and Applications for Multimedia. San Jose, California, United States: SPIE, 2003: 472-480.
(  0) 0)
|
| [17] |
赖玥聪, 黄添强, 蒋仁祥. 采用指数矩的图像区域复制粘贴篡改检测[J]. 中国图象图形学报, 2015, 20(9): 1212-1221. LAI Yuecong, HUANG Tianqiang, JIANG Renxiang. Image region copy-move forgery detection based on Exponential-Fourier moments[J]. Journal of image and graphics, 2015, 20(9): 1212-1221. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


