2. 大连理工大学 运载工程与力学学部工程力学系, 工业装备结构分析国家重点实验室, 辽宁 大连 116024;
3. 大连理工大学 海洋科学与技术学院, 工业装备结构分析国家重点实验室, 辽宁 盘锦 124000
2. Department of Engineering Mechanics, State key Laboratory of Analysis of Industrial Equipment, Dalian University of Technology, Dalian 116024, China;
3. School of Ocean Science and Technology, State key Laboratory of Analysis of Industrial Equipment, Dalian University of Technology, Panjin 124000, China
浮式生产储卸油装置(floating production storage offloading, FPSO[1],由于其兼有生产和储油的功能、水深适应能力强、抗风浪能力强、移动性能优良等优点,近年来被广泛应用于海洋油气开发。通常,FPSO船体依靠系泊系统将其限制在固定海域开展生产运输工作。软刚臂单点系泊系统具有系泊-浮体分离、多铰接连接方式和全水上系泊方式等优点,受到了国内外越来越多的重视。Mamoun等[2]对于SBM公司所研发的软刚臂系泊系统对FLNG在极端海况的输运过程进行水动力学分析。苏方磊[3]基于物理模型试验对浅水水上软刚臂系泊FPSO的运动与系泊力响应特性进行研究,并对影响船体运动与系泊塔水平系泊力响应的各种参数进行了敏感度分析。吕柏呈等[4]结合数值模拟与模型试验针对软刚臂单点系泊系统横向振动问题开展研究并进行了TLD减振设计,实验结果表明TLD减振系统能够有效减小YOKE横向振动行为。武文华等[5]依托于真实海洋平台建立了原型监测系统,提出现场监测的理念,得到了多年现场实测数据。
可以看出,水动力学仿真分析和模型实验是海洋工程装备结构的标准设计方法。同时,对于多体连接特征的海洋装备结构还需要开展描述其多铰连接特性的多体动力学分析。目前已经有一些学者就海洋工程装备进行了该方面的分析研究。Wang等[6]采用多体动力学方法建立了FPSO软刚臂系泊系统数值模型并进行了耦合动力分析。吕柏呈等[7]建立了软刚臂多体动力学方程,构造了系泊系统受到的荷载和各铰节点运动姿态的对应关系,对分析长期服役的系泊系统易损性评估提供了依据。Ha等[8]开发了一种多体系统动力学仿真器,用于船舶和近海结构建造和运输的过程模拟。另一方面,当采用绝对坐标法对多体动力学系统建模时会得到微分-代数方程组,约束违约问题带来了数值求解过程中的积分困难。Kane等[9]提出了构造保辛算法的一般性方法。戈新生等[10]分别对广义质量阵,约束方程和广义力阵在平衡位置附近进行泰勒展开,提出了一种线性化求解方法。张乐等[11]基于向后差分法提出了一种求解微分-代数方程组的双循环隐式积分方法。钟万勰等[12, 13]提出的祖冲之类保辛方法能够有效地解决约束方程违约问题。研究表明,祖冲之类方法求解过程中约束方程不必处处满足,只需要在时间格点处精确满足即可,依据这一理论,微分-代数方程组求解过程变得简单,而且不存在约束方程违约的问题。此外,该方法可自动满足哈密顿体系的保辛特性,做到同时保约束和保能量,具有较高的计算精度。
本文对于软刚臂系泊系统建立了多体动力学模型,得到描述其各单体运动状态的微分-代数方程组,进而应用了祖冲之类保辛算法进行数值模拟。本文选取了2组现场实测数据分别计算了软刚臂系泊系统的系泊回复力。计算结果表明,相较于传统的静力学数值分析,多体动力学模拟可得到动力特性更加明显的计算结果。同时,本文还针对系泊腿及YOKE等结构的位移和受力响应进行分析,从而更加全面地评估软刚臂系泊系统的工作状态。
1 FPSO软刚臂单点系泊系统软刚臂单点系泊系统由系泊塔架、系泊腿、软刚臂(YOKE)、旋转接头和FPSO支撑构架组成,通过13个铰节点互相连接构成。
YOKE与左、右系泊腿下端分别通过万向节连接(如图 1(a)),释放沿万向节转轴方向的2个旋转自由度,可将其模型化为万向节模型。左、右系泊腿上端与系泊构架分别通过万向节和一个止推轴承相连接(如图 1(b)),联合释放3个方向的旋转自由度,可将3者模型化成球铰模型。YOKE通过一个回转支撑、一个旋转铰和单点转塔的滑环相连接(如图 1(c)),分别释放3个方向的旋转自由度,可将3者联合模型化为球铰模型。因此,软刚臂单点系泊系统在建模过程中可视为由5个单体和5个铰组成的多体系统。

|
Download:
|
| 图 1 各铰简化模型 Fig. 1 Simplified model of each hinge joint | |
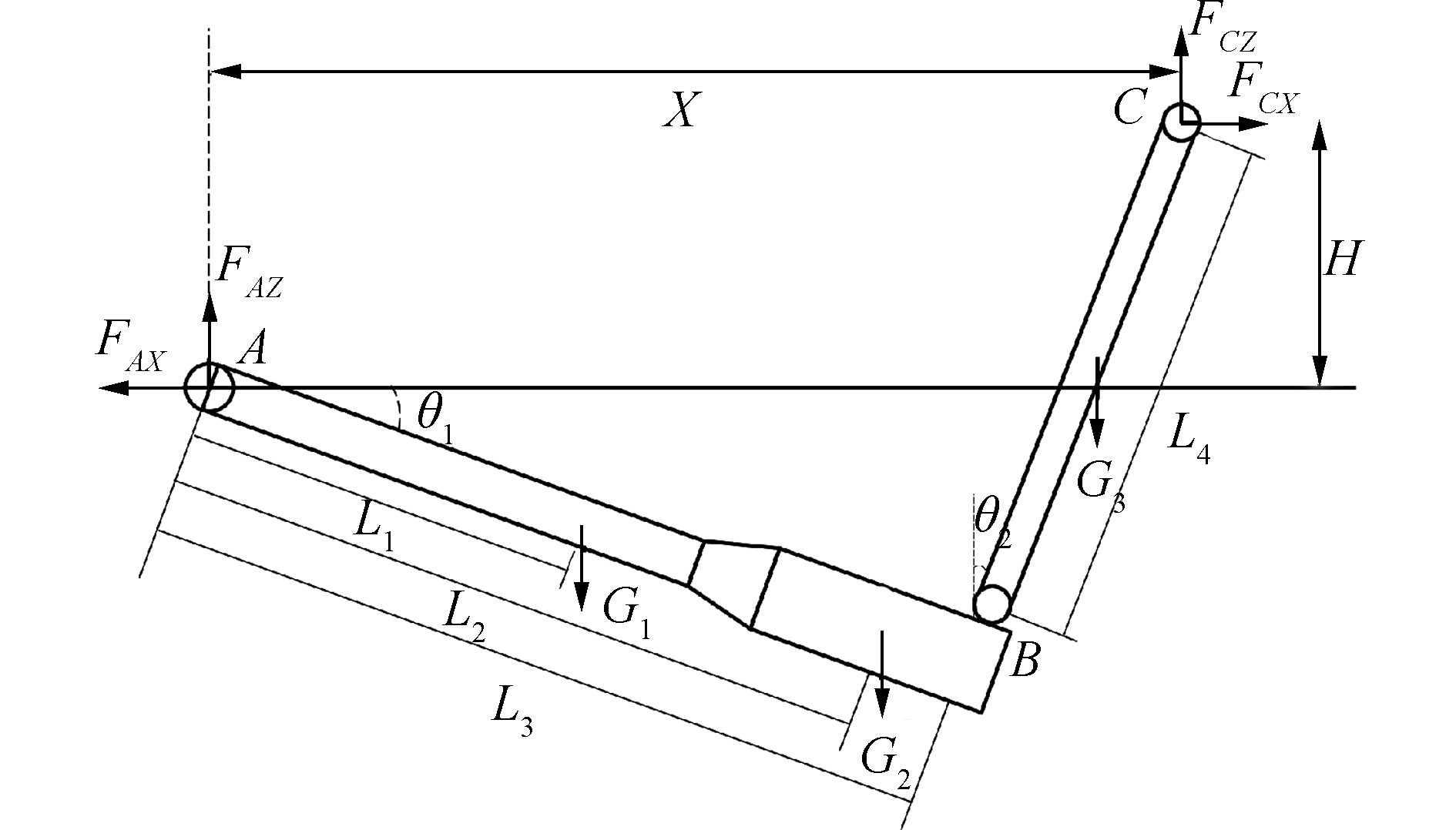
系泊系统系泊性能主要是由系泊刚度来决定。通常系泊刚度是一个非线性值,依赖于理论分析和模型实验决定。计算系泊刚度时一般将系泊系统模型化成如图 2的力学模型。
|
Download:
|
| 图 2 软刚臂系泊系统静力分析模型 Fig. 2 Static analysis model of the SYMS | |
以单点转塔处为坐标原点建立如图 2所示的坐标系统,根据几何关系可得:
| $ \left\{ \begin{array}{l} X = {L_3}\cos {\theta _1} + {L_4}\sin {\theta _2}\\ H = {L_4}\cos {\theta _2} - {L_3}\sin {\theta _1} \end{array} \right. $ | (1) |
式中:X为FPSO船体与单点转塔的水平距离;H为FPSO船体与单点转塔的高度差;L3为软刚臂长度;L4为系泊腿长度;θ1为软刚臂与水平面夹角;θ2为系泊腿与水平面法向的夹角。
根据力平衡关系可得:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{F}}_{AX}} = {\mathit{\boldsymbol{F}}_{CX}}}\\ {{\mathit{\boldsymbol{F}}_{AZ}} + {\mathit{\boldsymbol{F}}_{CZ}} = {\mathit{\boldsymbol{G}}_1} + {\mathit{\boldsymbol{G}}_2} + {\mathit{\boldsymbol{G}}_3}} \end{array}} \right. $ | (2) |
式中:FAX、FAZ分别为YOKE与单点转塔连接处X和Z方向受力;FCX、FCZ为系泊腿受到系泊支架在X和Z方向的拉力;G1、G2和G3分别为YOKE、水箱及系泊腿的重力。
根据力矩平衡关系可得:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_1}{R_1}\cos {\theta _1} + {\mathit{\boldsymbol{G}}_2}{R_2}\cos {\theta _2} + {\mathit{\boldsymbol{G}}_3}\left( {{R_3}\cos {\theta _1} + \frac{{{R_4}}}{2}\sin {\theta _2}} \right)}\\ { + {\mathit{\boldsymbol{F}}_{CX}} \cdot H - {\mathit{\boldsymbol{F}}_{CZ}}\left( {{R_3}\cos {\theta _1} + {R_4}\sin {\theta _2}} \right) = 0} \end{array} $ | (3) |
联立公式(1)~(3),即可求得C点处的系泊回复力FCX:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{CX}} = \frac{{{\mathit{\boldsymbol{G}}_1}{R_1}\cos {\theta _1} + {\mathit{\boldsymbol{G}}_2}{R_2}\cos {\theta _2} + {\mathit{\boldsymbol{G}}_3}\left( {{L_3}\cos {\theta _1} + \frac{{{L_4}}}{2}\sin {\theta _2}} \right)}}{{\frac{{{L_3}\cos {\theta _1} + {L_4}\cos {\theta _2}}}{{\tan {\theta _2}}} - H}} - }\\ {\frac{{\frac{{{\mathit{\boldsymbol{G}}_3}}}{2}\left( {{L_3}\cos {\theta _1} + {L_4}\sin {\theta _2}} \right)}}{{\frac{{{L_3}\cos {\theta _1} + {L_4}\cos {\theta _2}}}{{\tan {\theta _2}}} - H}}}\\ {K = \frac{{{\mathit{\boldsymbol{F}}_{CX}}}}{S}} \end{array} $ | (4) |
式中S为FPSO船体偏离平衡位置的距离。
基于上述分析能够计算系泊系统的等效系泊刚度K和静态系泊回复力FCX。但是由于软刚臂系泊结构的多铰连接特性,仅开展二维状态下软刚臂系泊系统受力分析无法全面准确描述其真实服役状态,因此开展软刚臂系泊系统多体动力学行为分析十分必要。
2.2 软刚臂单点系泊系统多体动力学模型在软刚臂系泊系统多体建模过程中,设单点转塔作为0号物体处于静止状态;YOKE为1号物体;左、右系泊腿分别为2、3号物体;与船体固接的系泊支架为4号物体。具体连接形式如图 3所示。由于软刚臂系泊系统为典型的非树型系统,建模过程中将铰H5作切断铰处理。

|
Download:
|
| 图 3 软刚臂系泊系统结构形式 Fig. 3 The structure of the SYMS | |
定义笛卡尔坐标下软刚臂系泊系统的广义坐标向量为:
| $ \mathit{\boldsymbol{Q}} = \left[ {{\mathit{\boldsymbol{q}}_{11}},{\mathit{\boldsymbol{q}}_{12}},{\mathit{\boldsymbol{q}}_{13}},{\mathit{\boldsymbol{q}}_{21}},{\mathit{\boldsymbol{q}}_{22}},{\mathit{\boldsymbol{q}}_{31}},{\mathit{\boldsymbol{q}}_{32}},{\mathit{\boldsymbol{q}}_{41}},{\mathit{\boldsymbol{q}}_{42}},{\mathit{\boldsymbol{q}}_{43}}} \right] $ |
式中:q1i(i=1, 2)为YOKE绕单点转塔的转动角度;q2i(i=1, 2)和q3i(i=1, 2)分别为左、右系泊腿绕下铰节点的转动角度;q4i(i=1,2,3)为右系泊腿上铰节点的转动角度。
建立系泊系统各物体的随体坐标系:YOKE、左系泊腿、右系泊腿和系泊支架分别对应e1、e2、e3和e4。各铰点转轴矢量可表示为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_1} = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{p}}_1^1}\\ {\mathit{\boldsymbol{p}}_2^1}\\ {\mathit{\boldsymbol{p}}_3^1} \end{array}} \right] = }\\ {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{g}}_1}}\\ {\cos \left( {{\mathit{\boldsymbol{q}}_{11}}} \right){\mathit{\boldsymbol{g}}_2} + \sin \left( {{\mathit{\boldsymbol{q}}_{11}}} \right){\mathit{\boldsymbol{g}}_3}}\\ {\sin \left( {{\mathit{\boldsymbol{q}}_{12}}} \right){\mathit{\boldsymbol{g}}_1} - \sin \left( {{\mathit{\boldsymbol{q}}_{11}}} \right)\cos \left( {{\mathit{\boldsymbol{q}}_{12}}} \right){\mathit{\boldsymbol{g}}_2} + \cos \left( {{\mathit{\boldsymbol{q}}_{11}}} \right)\cos \left( {{\mathit{\boldsymbol{q}}_{12}}} \right){\mathit{\boldsymbol{g}}_3}} \end{array}} \right]} \end{array} $ |
| $ {\mathit{\boldsymbol{P}}_2} = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{p}}_1^2}\\ {\mathit{\boldsymbol{p}}_2^2} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{e}}_1^1}\\ {\mathit{\boldsymbol{e}}_2^2} \end{array}} \right]\;\;\;\;\;{\mathit{\boldsymbol{P}}_3} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{p}}_1^3}\\ {\mathit{\boldsymbol{p}}_2^3} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}_1^1}\\ {\mathit{\boldsymbol{e}}_2^3} \end{array}} \right] $ |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_4} = \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{p}}_1^4}\\ {\mathit{\boldsymbol{p}}_2^4}\\ {\mathit{\boldsymbol{p}}_2^4} \end{array}} \right\} = }\\ {\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}_1^3}\\ {\cos \left( {{\mathit{\boldsymbol{q}}_{11}}} \right)\mathit{\boldsymbol{e}}_2^3 + \sin \left( {{\mathit{\boldsymbol{q}}_{11}}} \right)\mathit{\boldsymbol{e}}_3^3}\\ {\sin \left( {{\mathit{\boldsymbol{q}}_{12}}} \right)\mathit{\boldsymbol{e}}_1^3 - \sin \left( {{\mathit{\boldsymbol{q}}_{11}}} \right)\cos \left( {{\mathit{\boldsymbol{q}}_{12}}} \right)\mathit{\boldsymbol{e}}_2^3 + \cos \left( {{\mathit{\boldsymbol{q}}_{11}}} \right)\cos \left( {{\mathit{\boldsymbol{q}}_{12}}} \right)\mathit{\boldsymbol{e}}_3^3} \end{array}} \right]} \end{array} $ | (5) |
式中(g1, g2, g3)为大地坐标系基矢量。
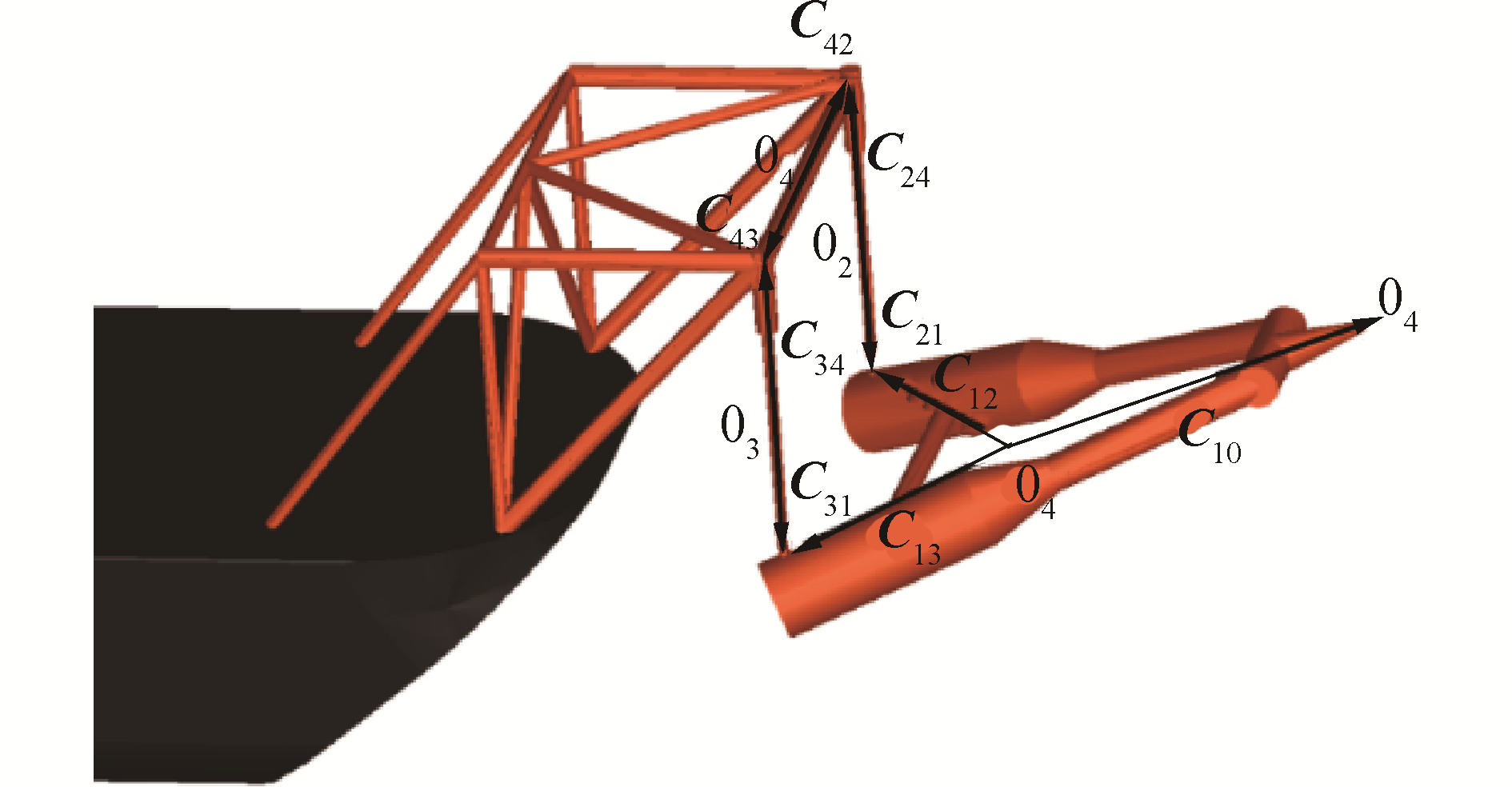
图 4给出了软刚臂单点系泊系统各物体质心位置及其体铰矢量。图中,Oi(i=1, 2, 3, 4)为各物体质心位置,Cij(i=1, 2, 3, 4,j=1, 2, 3, 4)为物体i到物体j的体铰矢量。
|
Download:
|
| 图 4 软刚臂系泊系统体铰矢量 Fig. 4 Body-hinge vector of the SYMS | |
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{r}}_1} = - {\mathit{\boldsymbol{C}}_{10}}}\\ {{\mathit{\boldsymbol{r}}_2} = {\mathit{\boldsymbol{r}}_1} + {\mathit{\boldsymbol{C}}_{12}} - {\mathit{\boldsymbol{C}}_{21}}}\\ {{\mathit{\boldsymbol{r}}_3} = {\mathit{\boldsymbol{r}}_1} + {\mathit{\boldsymbol{C}}_{13}} - {\mathit{\boldsymbol{C}}_{31}}}\\ {{\mathit{\boldsymbol{r}}_4} = {\mathit{\boldsymbol{r}}_3} + {\mathit{\boldsymbol{C}}_{34}} - {\mathit{\boldsymbol{C}}_{43}}} \end{array}} \right. $ | (6) |
式中ri(i=1-4)为各物体质心位置矢量。
球铰H5作切断铰处理,与铰H5相连接的2个物体相对位移为零,可以得到软刚臂单点系泊系统相对加速度约束方程表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\ddot h}}}_5} \cdot \mathit{\boldsymbol{e}}_3^1 = 0}\\ {{{\mathit{\boldsymbol{\ddot h}}}_5} \cdot \mathit{\boldsymbol{e}}_3^2 = 0}\\ {{{\mathit{\boldsymbol{\ddot h}}}_5} \cdot \mathit{\boldsymbol{e}}_3^3 = 0} \end{array}} \right. $ | (7) |
式中,
| $ {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_5} \cdot \mathit{\boldsymbol{\ddot Q}} + {\mathit{\boldsymbol{t}}_5} = 0 $ | (8) |
式中t5为由广义速率引起的加速度。
由虚功率原理可以得到软刚臂系泊系统的多体动力学方程:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{M}} \cdot \mathit{\boldsymbol{\ddot Q}} - \mathit{\boldsymbol{F}} = \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_5^{\rm{T}} \cdot \mathit{\boldsymbol{\lambda }}}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_5} \cdot \mathit{\boldsymbol{\ddot Q}} + {\mathit{\boldsymbol{t}}_5} = 0} \end{array}} \right. $ | (9) |
式中:M为系统广义质量阵;F为系统的广义外力向量;Φ5为约束雅克比矩阵;λ为拉格朗日乘子向量。
3 多体动力学方程数值求解基于笛卡尔坐标描述建立的多体动力学微分-代数方程组,约束违约问题是造成数值积分困难的重要原因之一。钟万勰等所提出的祖冲之类保辛方法能够有效地解决约束方程违约问题,本文基于祖冲之类方法构造了保辛算法[14],并应用到软刚臂系泊系统多体动力学方程的求解过程中。
3.1 祖冲之类保辛算法构造式(9)中Q为系统所受外力向量,包括海洋环境荷载引起的真实外力
| $ {\mathit{\boldsymbol{Q}}^{\rm{a}}}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right) = \mathit{\boldsymbol{Q}} - \frac{1}{2}\frac{{\partial \left[ {{{\mathit{\boldsymbol{\dot q}}}^{\rm{T}}}\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)} \right]}}{{\partial \mathit{\boldsymbol{q}}}}\mathit{\boldsymbol{\dot q}} + \frac{{\partial \left[ {\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\dot q}}} \right]}}{{\partial \mathit{\boldsymbol{q}}}}\mathit{\boldsymbol{q}} $ | (10) |
根据祖冲之类方法思想,在典型区段[0, η]内建立作用量[12]:
| $ \begin{array}{*{20}{c}} {\delta S = \delta \int_0^\eta {\left( {\frac{1}{2}{{\mathit{\boldsymbol{\dot q}}}^{\rm{T}}}\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\dot q}} - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( \mathit{\boldsymbol{q}} \right)\lambda } \right){\rm{d}}t} + }\\ {\int_0^\eta {\delta {\mathit{\boldsymbol{q}}^{\rm{T}}}{\mathit{\boldsymbol{Q}}^a}\left( {\mathit{\boldsymbol{q}},\mathit{\boldsymbol{\dot q}}} \right){\rm{d}}t} = \delta \int_0^\eta {\left( {\frac{1}{2}{{\mathit{\boldsymbol{\dot q}}}^{\rm{T}}}\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\dot q}} - {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\left( \mathit{\boldsymbol{q}} \right)\lambda } \right){\rm{d}}t} + }\\ {\int_0^\pi \delta {\mathit{\boldsymbol{q}}^{\rm{T}}} \cdot \left( {\mathit{\boldsymbol{Q}} - \frac{1}{2}\frac{{\partial \left[ {{{\mathit{\boldsymbol{\dot q}}}^{\rm{T}}}\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)} \right]}}{{\partial \mathit{\boldsymbol{q}}}}\mathit{\boldsymbol{\dot q}} + \frac{{\partial \left[ {\mathit{\boldsymbol{M}}\left( \mathit{\boldsymbol{q}} \right)\mathit{\boldsymbol{\dot q}}} \right]}}{{\partial \mathit{\boldsymbol{q}}}}\mathit{\boldsymbol{q}}} \right){\rm{d}}t} \end{array} $ | (11) |
式中:M为广义质量阵;q为广义坐标向量;λ为约束的拉格朗日乘子。对广义坐标q进行线性差值:
| $ \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{q}} = \left( {1 - t/\eta } \right){\mathit{\boldsymbol{q}}_0} + \left( {t/\eta } \right){\mathit{\boldsymbol{q}}_1}}\\ {\mathit{\boldsymbol{\dot q}} = \left( {{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}} \right)/\eta } \end{array}} \right. $ | (12) |
根据离散区间的哈密顿正则方程:
| $ \left\{ {\begin{array}{*{20}{c}} { - {\mathit{\boldsymbol{p}}_0} = \partial S/\partial {\mathit{\boldsymbol{q}}_0}}\\ {{\mathit{\boldsymbol{p}}_1} = \partial S/\partial {\mathit{\boldsymbol{q}}_1}} \end{array}} \right. $ | (13) |
将作用量和广义坐标代入可得:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{p}}_0} - \frac{\mathit{\boldsymbol{M}}}{\mathit{\boldsymbol{\eta }}}\left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2}} \right)\left( {{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}} \right) - \\ \frac{\eta }{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q^ \top \left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2}} \right)\lambda + \frac{\eta }{2} \cdot \mathit{\boldsymbol{Q}}\left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2},\frac{{{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}}}{\eta }} \right) + \\ \frac{G}{2}\left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2},\frac{{{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}}}{\eta }} \right)\;\;\;\;\;\left( {{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}} \right) = 0\\ - {\mathit{\boldsymbol{P}}_1} + \frac{\mathit{\boldsymbol{M}}}{\eta }\left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2}} \right)\left( {{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}} \right) - \\ \frac{\eta }{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_q^ \top \left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2}} \right)\lambda + \frac{\eta }{2} \cdot \mathit{\boldsymbol{Q}}\left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2},\frac{{{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}}}{\eta }} \right) + \\ \frac{G}{2}\left( {\frac{{{\mathit{\boldsymbol{q}}_0} + {\mathit{\boldsymbol{q}}_1}}}{2},\frac{{{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}}}{\eta }} \right)\;\;\;\;\;\left( {{\mathit{\boldsymbol{q}}_1} - {\mathit{\boldsymbol{q}}_0}} \right) = 0 \end{array} \right. $ | (14) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{q}}_0},\mathit{\boldsymbol{\eta }}} \right) = 0 $ | (15) |
式中p0和p1分别代表区间两端的广义动量。式(14)与约束方程(15)联立求解即可得到位移、速度、加速度和受力等信息。
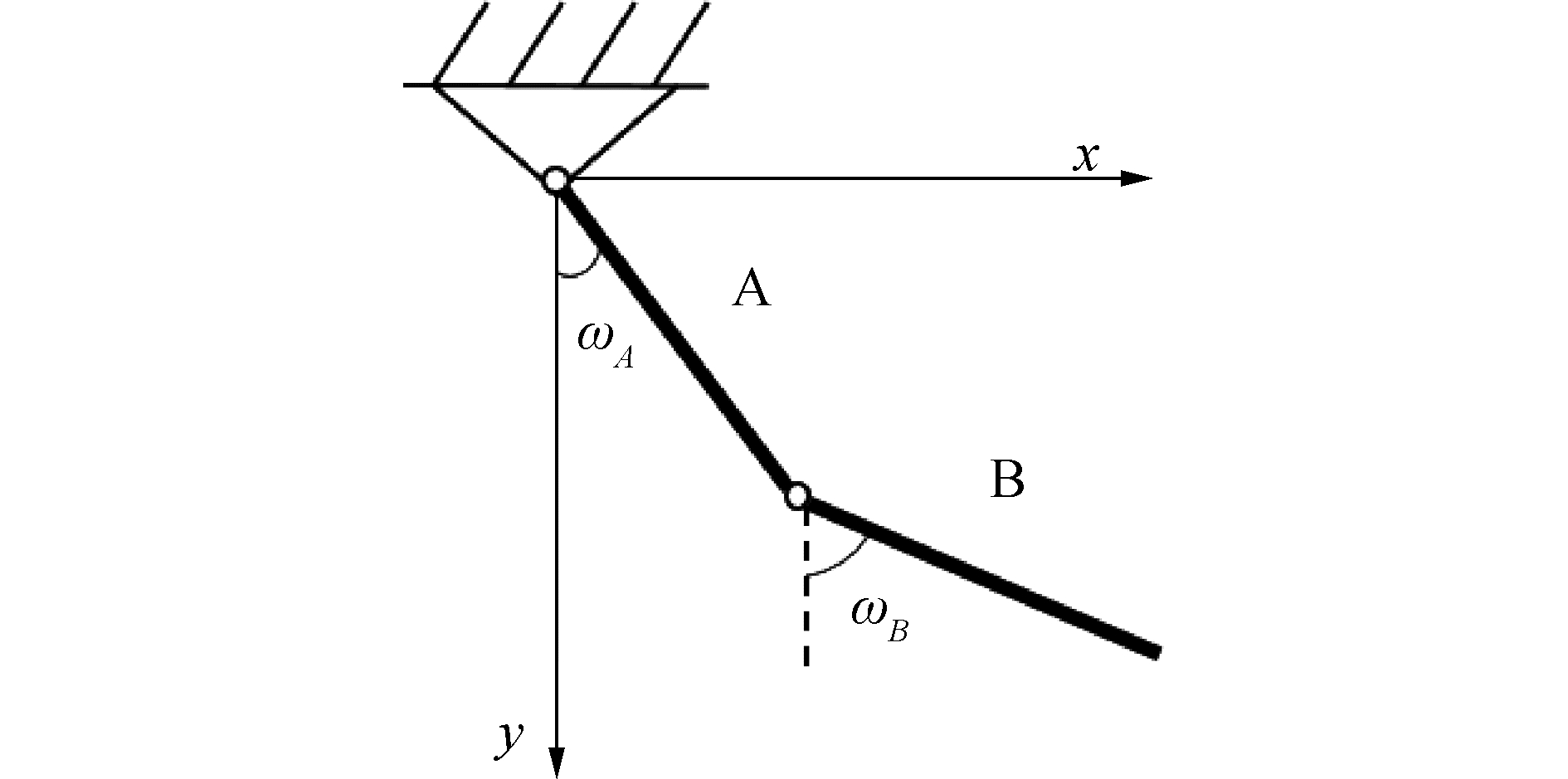
3.2 祖冲之类保辛算法的保约束保能量验证选取一双摆系统作为数值算例证明祖冲之类保辛算法在保约束保能量方面的特性。如图 5所示的平面双摆系统,两杆长度均为1 m,质量均为1 kg。杆A左端铰接固定,右端与杆B左端相铰接,杆B右端为自由端。初始状态时,杆A和杆B垂直悬挂,在初始角速度ωA=2 πrad/s,ωB=-πrad/s的作用下开始运动。取重力加速度为9.8 m/s2,仿真时间为5 s,积分步长为0.005 s。
|
Download:
|
| 图 5 平面双摆系统 Fig. 5 Planar double pendulum system | |
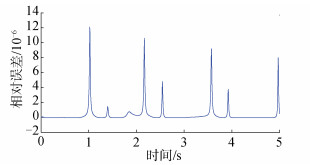
图 6和7分别给出了双摆系统中约束相对误差和能量相对误差随时间的变化趋势。可以看出约束相对误差的量级为10-11,能量相对误差的量级为10-6,表明了保辛算法可以良好地保证双摆系统的约束条件和能量守恒特性。

|
Download:
|
| 图 6 双摆系统约束相对误差 Fig. 6 Relative error of constraints of system | |
|
Download:
|
| 图 7 双摆系统能量相对误差 Fig. 7 Relative error of constraints of system | |
2011年,大连理工大学在渤海某FPSO建立了一套软刚臂原型监测系统,全面监测了海洋环境(风、波浪、海流)荷载因子、FPSO浮体运动响应、软刚臂系泊系统的运动姿态。基于原型监测数据开展了软刚臂系泊系统动力特性及运动行为研究。
4.1 基于原型监测数据的系泊回复力分析分别选取2组典型工况的FPSO六自由度实测数据作为输入量,计算了软刚臂系泊系统在不同海况下系泊回复力变化,如表 1所示。工况1为相对温和的海况,工况2为在极端环境载荷引起的FPSO纵向剧烈运动的海况。
| 表 1 2种工况的环境参数及FPSO运动姿态 Table 1 The environmental parameters and FPSO motion attitude of the two working cases |
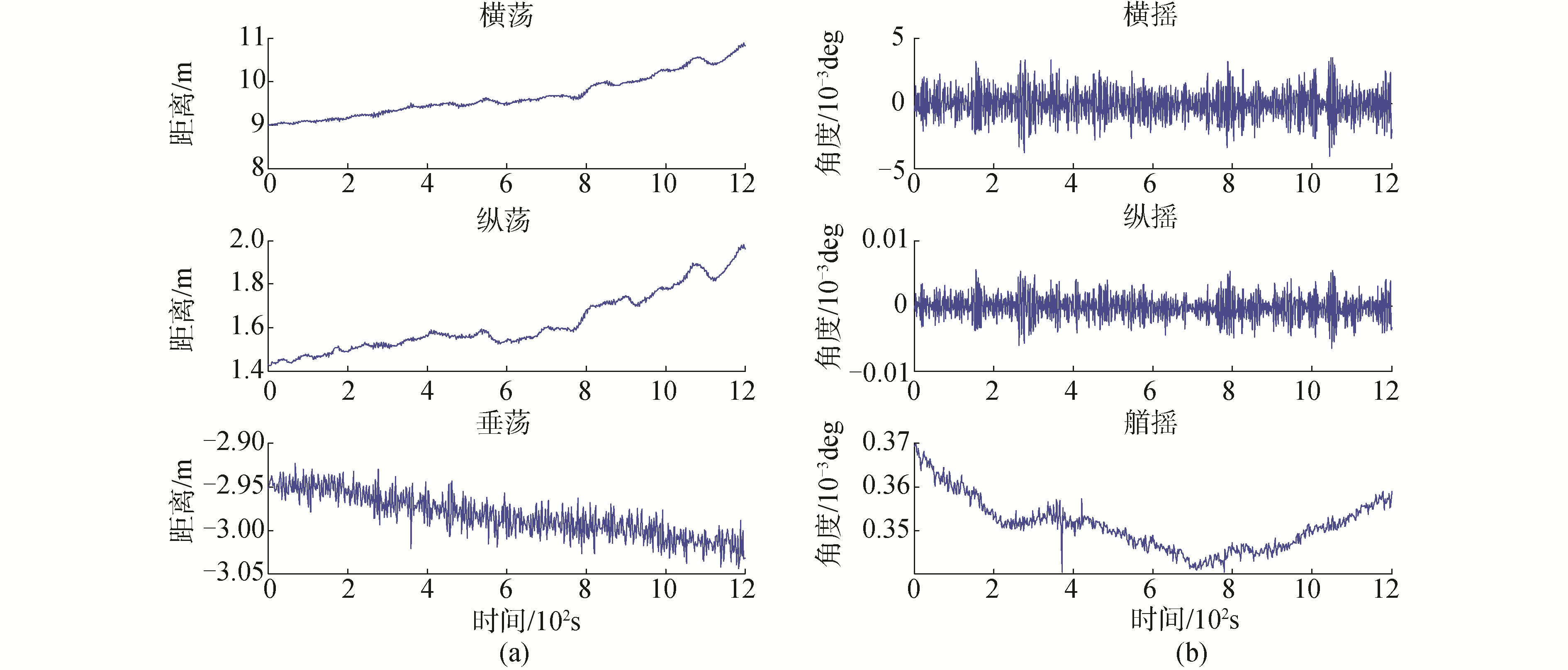
工况1:FPSO浮体六自由度时程数据如图 8所示,可以看出FPSO始终处于缓慢运动状态,本工况主要用于分析平稳低速状态下静力法与本文动力法的差别。
|
Download:
|
| 图 8 FPSO船体六自由度数据(工况1) Fig. 8 Data of six degrees of freedom (DOF) of FPSO (working case 1) | |
根据所建立的软刚臂系泊系统多体动力学模型,对工况1条件下FPSO平台开展动力学分析,系泊回复力的计算结果如图 9所示。

|
Download:
|
| 图 9 动力法与静力法计算系泊力对比(工况1) Fig. 9 Comparison of mooring force calculated by dynamic method and static method(working case 1) | |
可以看出,在较为温和的海况下,动力法与静力法计算得到的系泊回复力均稳定在25 kN附近,两者保持较为一致的变化趋势。但是通过保辛算法得到的多体动力学结果具有较为明显的动力效果,且系泊力幅值比静力法偏大约7%。
工况2:选取监测过程中较为剧烈海况下FPSO船体的六自由度数据作为输入条件。图 10同时给出了FPSO船体六自由度数据时程曲线和对应的频域分析结果。可以看出,横荡、纵荡和艏摇主要集中在低频区域,而横摇、纵摇和垂荡则具有明显的波频效应,表明了本文选取数据的代表性。

|
Download:
|
| 图 10 FPSO船体六自由度数据及其频谱分析 Fig. 10 Data of six degrees of freedom of FPSO and its spectrum analysis | |
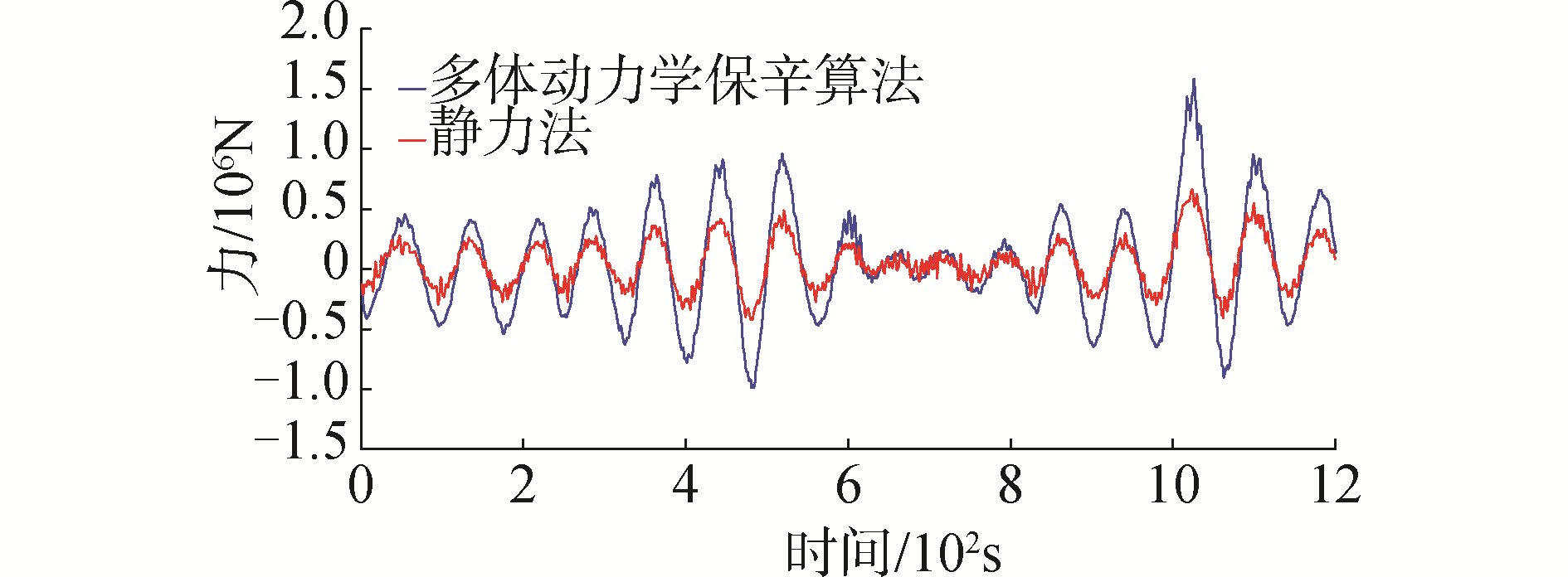
工况2下软刚臂动力学分析结果和对应的静力学结果如图 11所示。可以看出,在较为剧烈海况下,多体动力学保辛算法与静力法结果差别明显。除在600~800 s区间动力法与静力法结果相对接近外,其他时刻下动力法回复力幅值可接近静力法计算结果的2倍。说明当FPSO在受到较大环境荷载作用呈现出大幅运动时,静力法计算得到的结果偏小,无法真实反应出系泊结构在受到的动力响应下的受力行为,对于海洋工程结构设计带来了危险性。
|
Download:
|
| 图 11 动力法与静力法计算系泊力对比(工况2) Fig. 11 Comparison of mooring force calculated by dynamic method and static method(working case 2) | |
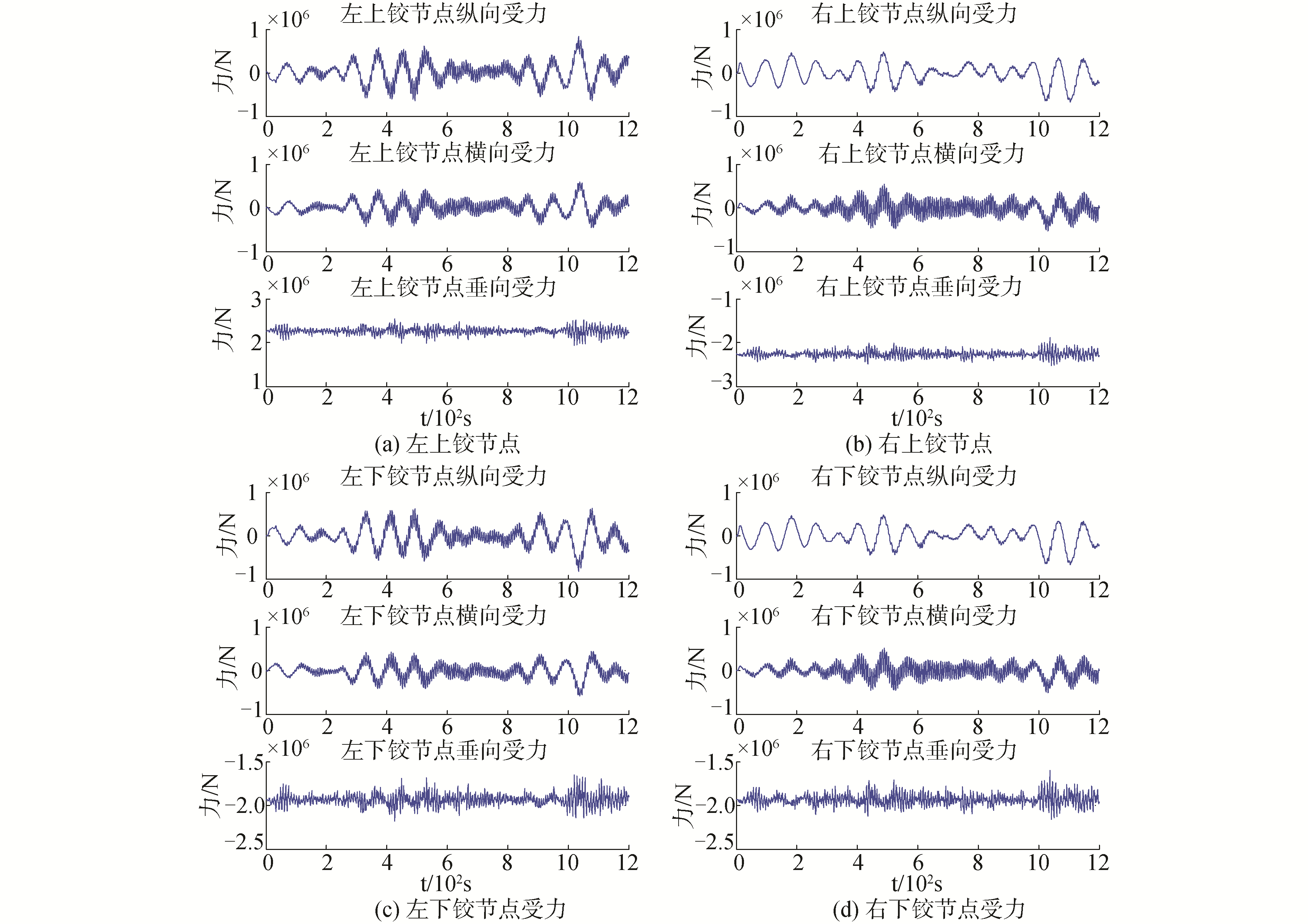
多体动力学保辛方法同时还可以得到各单体的姿态、受力等信息。以工况二为例,分别计算了软刚臂系泊系统各铰节点的受力时程(图 12)。其中,上铰节点受力可用于计算系泊回复力,下铰节点及单点转塔受力可为铰结构疲劳损伤研究提供数据支持。
|
Download:
|
| 图 12 软刚臂系泊系统各铰结构受力时程 Fig. 12 Internal force of each hinge joints of the SYMS | |
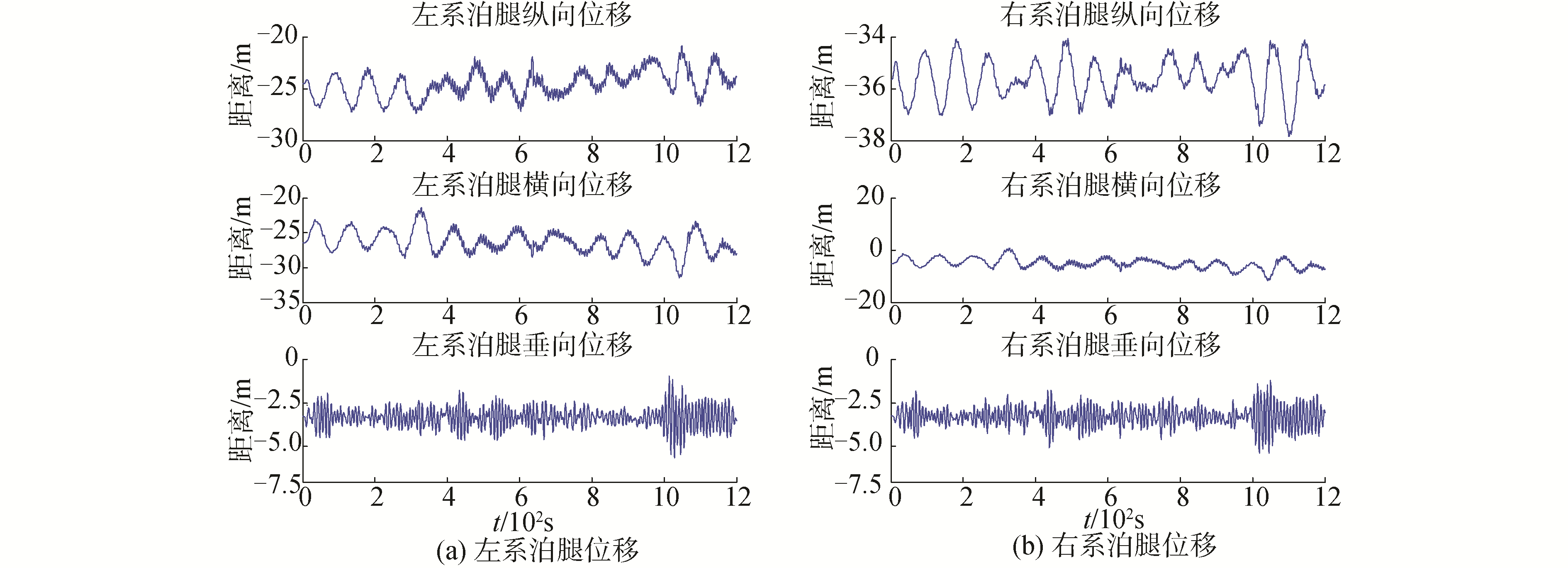
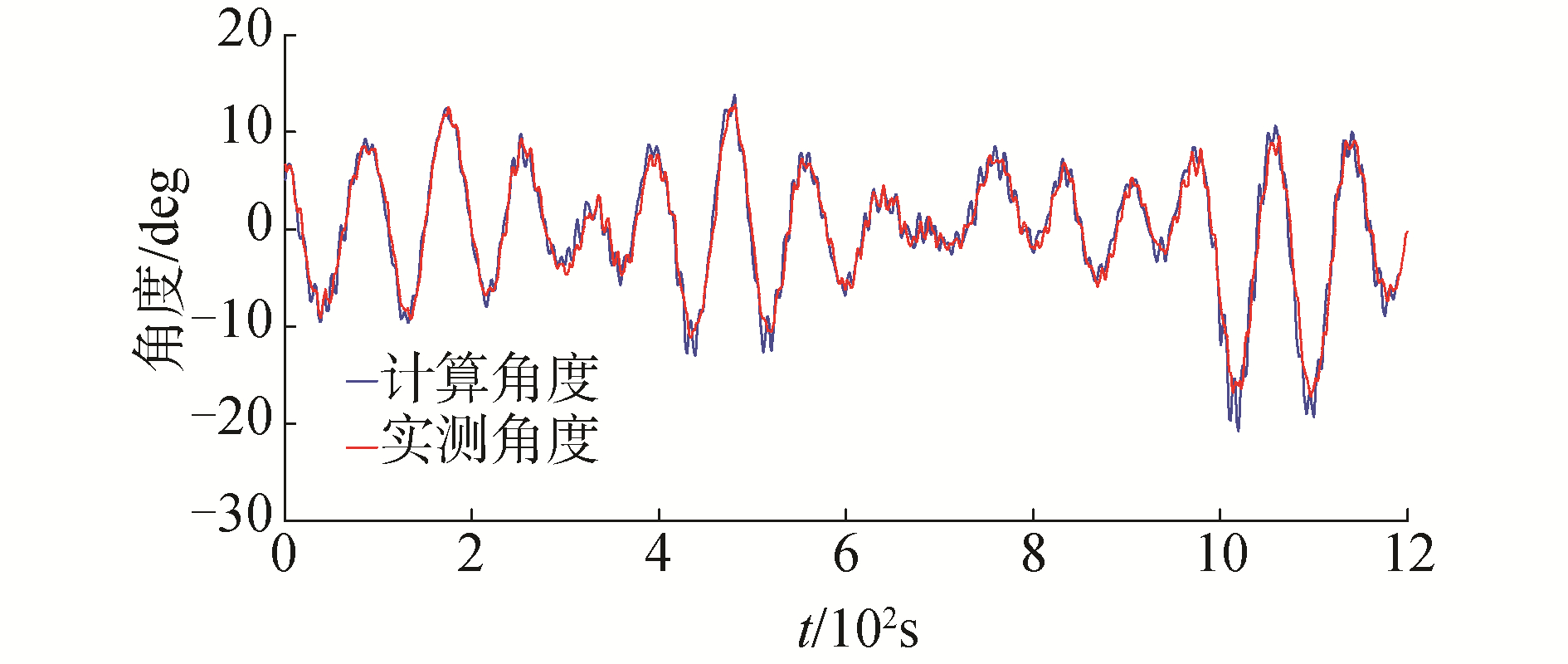
图 13给出了各单体位移及铰结构转动量随时间的变化规律,并给出了左、右系泊腿的位移时程曲线,其中左系泊腿最大纵向摆动幅值超过3 m,此时需要密切考虑系泊系统与FPSO浮体的位置关系,避免发生YOKE与船艏的碰撞事故。图 14给出了下铰节点的纵向转动量时程曲线,其中蓝色曲线为本文计算所得的角度变化,红色曲线为监测系统布设倾角传感器的实测角度变化。可以看出,下铰节点的计算结果与实测结果吻合良好,再次证明本文计算模型的准确性。
|
Download:
|
| 图 13 系泊腿位移 Fig. 13 Displacement of the mooring legs | |
|
Download:
|
| 图 14 铰结构转动量 Fig. 14 Rotation of the hinge joints | |
1) 依据多体动力学理论,本文建立了描述软刚臂系泊系统运动行为的多体动力学模型。针对微分-代数方程组求解过程中遇到的约束违约问题,应用祖冲之类保辛算法进行数值求解。在保辛的基础上得到了保能量、计算精度高的仿真计算结果。
2) 系泊回复力是软刚臂系泊系统设计中的重要指标。与传统的静力方法相比,本文所采用的多体动力学方法计算结果具有明显的动力效果,尤其在较为恶劣的海况下,其受力幅值接近静力法计算结果的2倍。依赖于多体动力学方法的受力分析可为FPSO作业方提供更加准确地预警方案。
3) 基于保辛方法计算了软刚臂系泊系统各组成结构的动力响应。计算结果与实测信息的一致性表明了本文计算方法能够更好地还原软刚臂系泊系统的真实运动状态。各单体的受力时程可为软刚臂系泊系统的易损性分析提供直接的输入条件。
| [1] |
吴家鸣. FPSO的特点与现状[J]. 船舶工程, 2012, 32(S2): 1-4, 102. WU Jiaming. Distinguishing feature and existing circumstances of FPSO[J]. Ship engineering, 2012, 32(S2): 1-4, 102. (  0) 0)
|
| [2] |
NACIRI M, MAUREL W, QUÉAU J P. Passive disconnection of an SPM-moored LNG carrier in waves[C]//Proceedings of 24th International Conference on Offshore Mechanics and Arctic Engineering. Halkidiki, Greece: ASME, 2005: 963-973.
(  0) 0)
|
| [3] |
苏方磊.水上软刚臂系泊FPSO水动力响应特性试验研究[D].大连: 大连理工大学, 2015. SU Fanglei. Experimental study of an overwater soft yoke moored FPSO's hydrodynamic response characteristics[D]. Dalian: Dalian University of Technology, 2015. (  0) 0)
|
| [4] |
吕柏呈, 武文华, 姚伟岸, 等.软刚臂单点系泊系统横向振动分析和TLD减振设计[C]//中国海洋工程学会.第十七届中国海洋(岸)工程学术讨论会论文集.南宁: 中国海洋工程学会, 2015.
(  0) 0)
|
| [5] |
武文华, 唐达, 岳前进, 等.海洋平台结构原型监测及其现场应用[C]//第十六届中国海洋(岸)工程学术讨论会论文集(上册).大连: 中国海洋工程学会, 2013.
(  0) 0)
|
| [6] |
WANG S Q, LI S Y, CHEN X H. Dynamical analysis of a soft yoke moored FPSO in shallow waters[M]//LEE J H W. Asian and Pacific Coasts 2011. World Scientific, 2011:956-963.
(  0) 0)
|
| [7] |
LYU Baicheng, WU Wenhua, YAO Weian, et al. Multibody dynamical modeling of the FPSO soft yoke mooring system and prototype validation[J]. Applied ocean research, 2019, 84: 179-191. DOI:10.1016/j.apor.2019.01.011 (  0) 0)
|
| [8] |
HA S, KU N K, ROH M I, et al. Multibody system dynamics simulator for process simulation of ships and offshore plants in shipyards[J]. Advances in engineering software, 2015, 85: 12-25. DOI:10.1016/j.advengsoft.2015.02.008 (  0) 0)
|
| [9] |
KANE C, MARSDEN J E, ORTIZ M, et al. Variational integrators and the Newmark algorithm for conservative and dissipative mechanical systems[J]. International journal for numerical methods in engineering, 2000, 49(10): 1295-1325. DOI:10.1002/1097-0207(20001210)49:10<1295::AID-NME993>3.0.CO;2-W (  0) 0)
|
| [10] |
戈新生, 赵维加, 陈立群. 基于完全笛卡尔坐标的多体系统微分-代数方程符号线性化方法[J]. 工程力学, 2004, 21(4): 106-111. GE Xinsheng, ZHAO Weijia, CHEN Liqun. Symbolic linearization of differential/algebraic equation for multibody system based on fully Cartesian coordinates[J]. Engineering mechanics, 2004, 21(4): 106-111. DOI:10.3969/j.issn.1000-4750.2004.04.019 (  0) 0)
|
| [11] |
张乐, 章定国.求解微分-代数方程的双循环隐式积分方法[C]//第九届全国多体系统动力学暨第四届全国航天动力学与控制学术会议论文摘要集.武汉: 中国力学学会, 2015.
(  0) 0)
|
| [12] |
钟万勰, 高强, 彭海军. 经典力学辛讲[M]. 大连: 大连理工大学出版社, 2013. ZHONG Wanxie, GAO Qiang, PENG Haijun. Classical mechanics-its symplectic description[M]. Dalian: Dalian University of Technology Press, 2013. (  0) 0)
|
| [13] |
钟万勰, 高强. 约束动力系统的分析结构力学积分[J]. 动力学与控制学报, 2006, 4(3): 193-200. ZHONG Wanxie, GAO Qiang. Integration of constrained dynamical system via analytical structural mechanics[J]. Journal of dynamics and control, 2006, 4(3): 193-200. DOI:10.3969/j.issn.1672-6553.2006.03.001 (  0) 0)
|
| [14] |
阚子云, 彭海军, 陈飙松, 等. 开放式多体系统动力学仿真算法软件研发(Ⅱ)DAEs求解算法对比[J]. 计算力学学报, 2015, 32(6): 707-715, 721. KAN Ziyun, PENG Haijun, CHEN Biaosong, et al. Study of open simulation algorithm software for multibody system dynamics (Ⅱ) comparison of algorithms for solving DAEs[J]. Chinese journal of computational mechanics, 2015, 32(6): 707-715, 721. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


