斜齿轮在传动过程中的接触应力是造成齿面点蚀和疲劳破坏的主要因素。为延长齿轮使用寿命和降低疲劳破坏,精确计算每一啮合位置的最大接触应力是其基础保证[1-3]。现有齿轮加工技术可满足齿面精度要求,然而在实际齿轮装配过程中安装误差往往很难避免,在安装误差作用下轮齿进入和退出啮合阶段常发生边缘接触,使得初始接触点偏离接触线中心,造成此时接触椭圆不完整[4]。现有接触应力计算方法主要依据有限元法、赫兹理论及ISO标准,其中有限元法是国内外学者常采用的数值计算方法,龙慧[5]、杨生华[6]、唐进元等[5]利用有限元软件对圆柱齿轮的网格密度、接触应力分布规律、应力计算精度及收敛性问题进行了详细的研究和探讨。SantoshS.Pat[8]、Tribhuwan Singh等[9]在弹性静力学基础上建立渐开线圆柱齿轮的三维有限元模型,计算并分析了摩擦系数、螺旋角、齿宽等因素对轮齿表面接触应力分布的影响,并引入了AGMA标准进行对比。以上研究成果是基于标准齿轮采用有限元法计算其接触应力,对于安装误差导致边缘接触及接触椭圆不完整的啮合状况并没有涉及,同时由文献[10]可知有限元法求解接触应力的精度依赖于齿轮模型单元数和节点数,高精确的数值解往往需要更多节点和更细化的单元,从而易造成齿轮接触计算量偏大、求解过程耗时长,给工程应用带来很大不便。赫兹理论计算接触应力需求得接触椭圆长短轴尺寸,然而由轮齿几何接触分析(TCA)[11]可知含安装误差的齿轮副由于边缘接触造成当前接触椭圆不完整,即无法计算接触面内长轴和短轴的大小,此时赫兹理论无法用于求解椭圆面上应力分布的[12]。ISO标准虽然计算简便,但其主要基于实验和理论相结合的方法给出的是整个啮合过程中最大接触应力及其设计参考值,不能反映含安装误差的齿轮在不同啮合位置的最大接触应力以及其在整个啮合周期内的变化规律[13-14]。
斜齿轮安装误差包括中心距误差、空间轴交角误差以及轴平面内轴交角误差。由于以上安装误差均可导致轮齿啮合时发生边缘接触和接触椭圆不完整,故本文仅以轴平面内含轴交角安装误差的斜齿轮为例,对接触应力计算中存在的边缘接触、接触椭圆不完整、有限元法计算耗时长以及ISO标准不能反映不同啮合位置最大接触应力变化规律的问题,提出一种混合赫兹和Winkler模型相结合的最大接触应力精确计算方法。该方法不考虑齿轮轴变形、润滑及摩擦因素的影响,利用轮齿几何接触分析(TCA)和承载接触分析(LTCA)结果,通过计算初始接触点在齿面上的不同位置、接触点的主曲率、接触椭圆长轴大小和实际接触线上离散点载荷分布,利用经典赫兹理论和Winkler模型精确计算和分析了轴平面内含轴交角安装误差的斜齿轮在不同啮合位置的最大接触应力及其变化规律,并与ANSYS有限元软件计算结果进行对比分析。
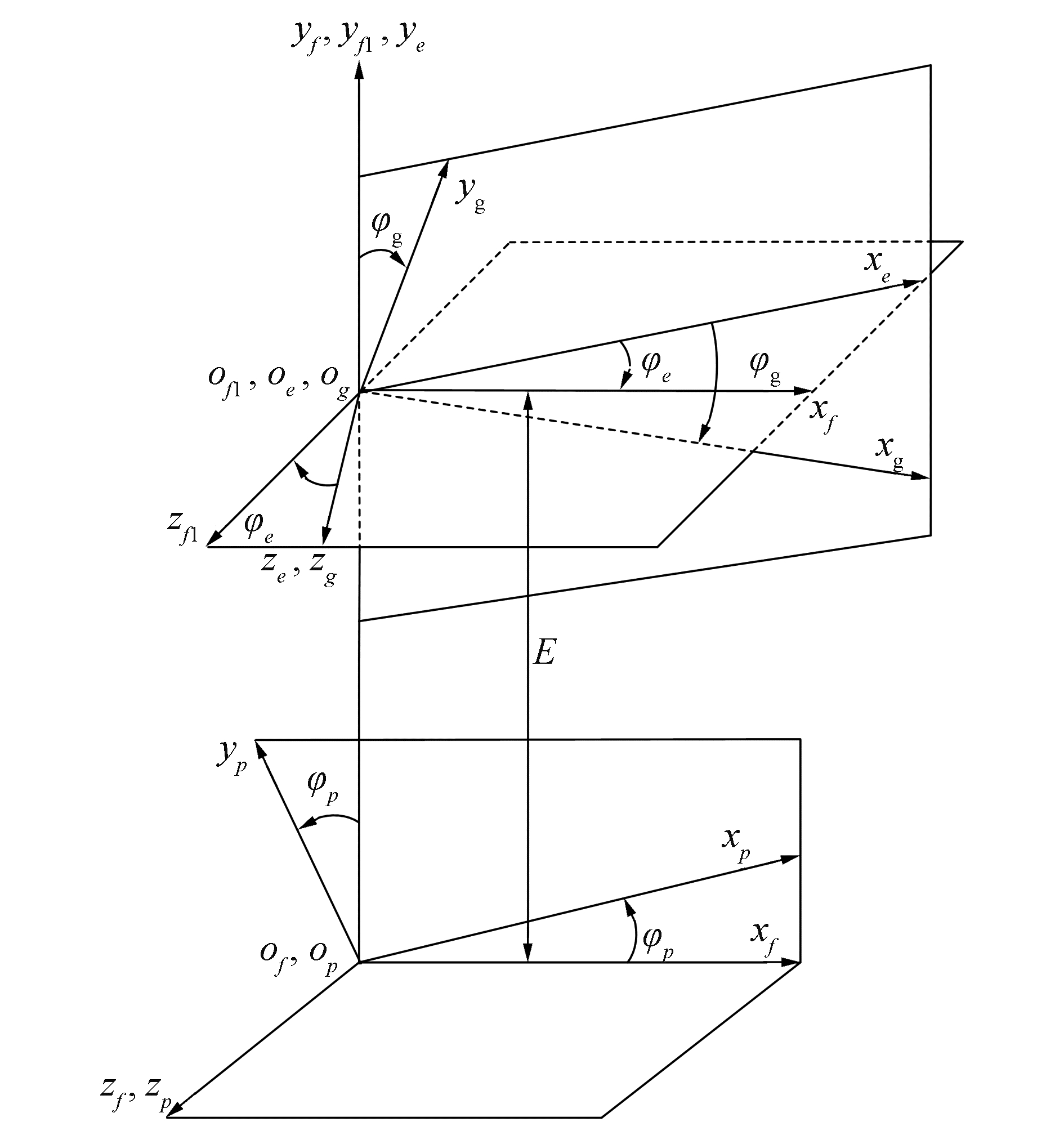
1 含安装误差斜齿轮几何接触分析斜齿轮在承载接触时,每一啮合位置的最大接触应力必然发生在几何初始接触点上,为此须对含安装误差的斜齿轮进行几何接触分析(TCA)以确定齿面的几何初始接触点和啮合印痕。文中斜齿轮安装误差为轴平面内轴交角误差,斜齿轮采用渐开线齿面,大小轮啮合坐标系如图 1所示,其中动坐标系Op、Og分别与小轮、大轮固连,φp、φg为其相应转角。Oe为误差坐标系,将大小轮轴平面内轴交角安装误差归纳到大轮上,φe为轴平面内大轮的轴交角安装误差,E表示中心距。采用Rp(up, lp)和Rg(ug, lg)分别表示小轮和大轮在自身动坐标系Op和Og下的齿面方程,根据齿面方程并利用式(1)可求得小轮和大轮在自身动坐标系下的齿面单位法矢量np(up, lp)、ng(ug, lg)。
|
Download:
|
| 图 1 啮合坐标系 Fig. 1 Mating coordinate system | |
| $ \left\{ \begin{array}{l} {n_p}\left( {{u_p},{l_p}} \right) = \frac{{\frac{{\partial {R_p}\left( {{u_p},{l_p}} \right)}}{{\partial {u_p}}} \times \frac{{\partial {R_p}\left( {{u_p},{l_p}} \right)}}{{\partial {l_p}}}}}{{\left| {\frac{{\partial {R_p}\left( {{u_p},{l_p}} \right)}}{{\partial {u_p}}} \times \frac{{\partial {R_p}\left( {{u_p},{l_p}} \right)}}{{\partial {l_p}}}} \right|}}\\ {n_g}\left( {{u_g},{l_g}} \right) = \frac{{\frac{{\partial {R_g}\left( {{u_g},{l_g}} \right)}}{{\partial {u_g}}} \times \frac{{\partial {R_g}\left( {{u_g},{l_g}} \right)}}{{\partial {l_g}}}}}{{\left| {\frac{{\partial {R_g}\left( {{u_g},{l_g}} \right)}}{{\partial {u_g}}} \times \frac{{\partial {R_g}\left( {{u_g},{l_g}} \right)}}{{\partial {l_g}}}} \right|}} \end{array} \right. $ | (1) |
由斜齿轮连续切触条件可知大小轮齿面需转换到固定坐标系Of下进行几何接触分析(TCA),斜齿轮齿面连续切触方程如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{M}}_{{f_p}}}\left( {{\varphi _p}} \right){\mathit{\boldsymbol{R}}_p}\left( {{u_p},{l_p}} \right) = {\mathit{\boldsymbol{M}}_{fe}}\left( {{\varphi _g}} \right){\mathit{\boldsymbol{M}}_{eg}}{\mathit{\boldsymbol{R}}_g}\left( {{u_g},{l_g}} \right)}\\ {{\mathit{\boldsymbol{L}}_{fp}}\left( {{\varphi _p}} \right){\mathit{\boldsymbol{n}}_p}\left( {{u_p},{l_p}} \right) = {\mathit{\boldsymbol{L}}_{fe}}\left( {{\varphi _g}} \right){\mathit{\boldsymbol{L}}_{eg}}{\mathit{\boldsymbol{n}}_g}\left( {{u_g},{l_g}} \right)} \end{array}} \right. $ | (2) |
式中:Rp、Rg和np、ng分别为小轮、大轮在各自固连坐标系Op、Og下的齿面几何方程和齿面单位法矢量;Mfp为坐标系Op到Of的4×4变换矩阵;Meg和Mfe分别为坐标系Og转换到Oe和坐标系Oe转换到固定坐标系Of的4×4变换矩阵。Lfp、Lfe和Leg表示矩阵Mfp、Mfe和Meg去掉最后一行和最后一列形成的3×3矩阵。由式(2)可导出含有6个未知量的5个独立方程,在求解此方程组时通过给定小轮转角φp并以一定步长连续转动即可求得齿面初始接触点和接触印痕。
| $ {\mathit{\boldsymbol{M}}_{eg}} = \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _g}}&{\sin {\varphi _g}}&0&0\\ { - \sin {\varphi _g}}&{\cos {\varphi _g}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_{fe}} = \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _e}}&0&{\sin {\varphi _e}}&0\\ 0&{1|}&0&E\\ { - \sin {\varphi _e}}&0&{\cos {\varphi _e}}&0\\ 0&0&0&1 \end{array}} \right] $ |
| $ {\mathit{\boldsymbol{M}}_{fp}} = \left[ {\begin{array}{*{20}{c}} {\cos {\varphi _p}}&{ - \sin {\varphi _p}}&0&0\\ {\sin {\varphi _p}}&{\cos {\varphi _p}}&0&0\\ 0&0&1&0\\ 0&0&0&1 \end{array}} \right] $ |
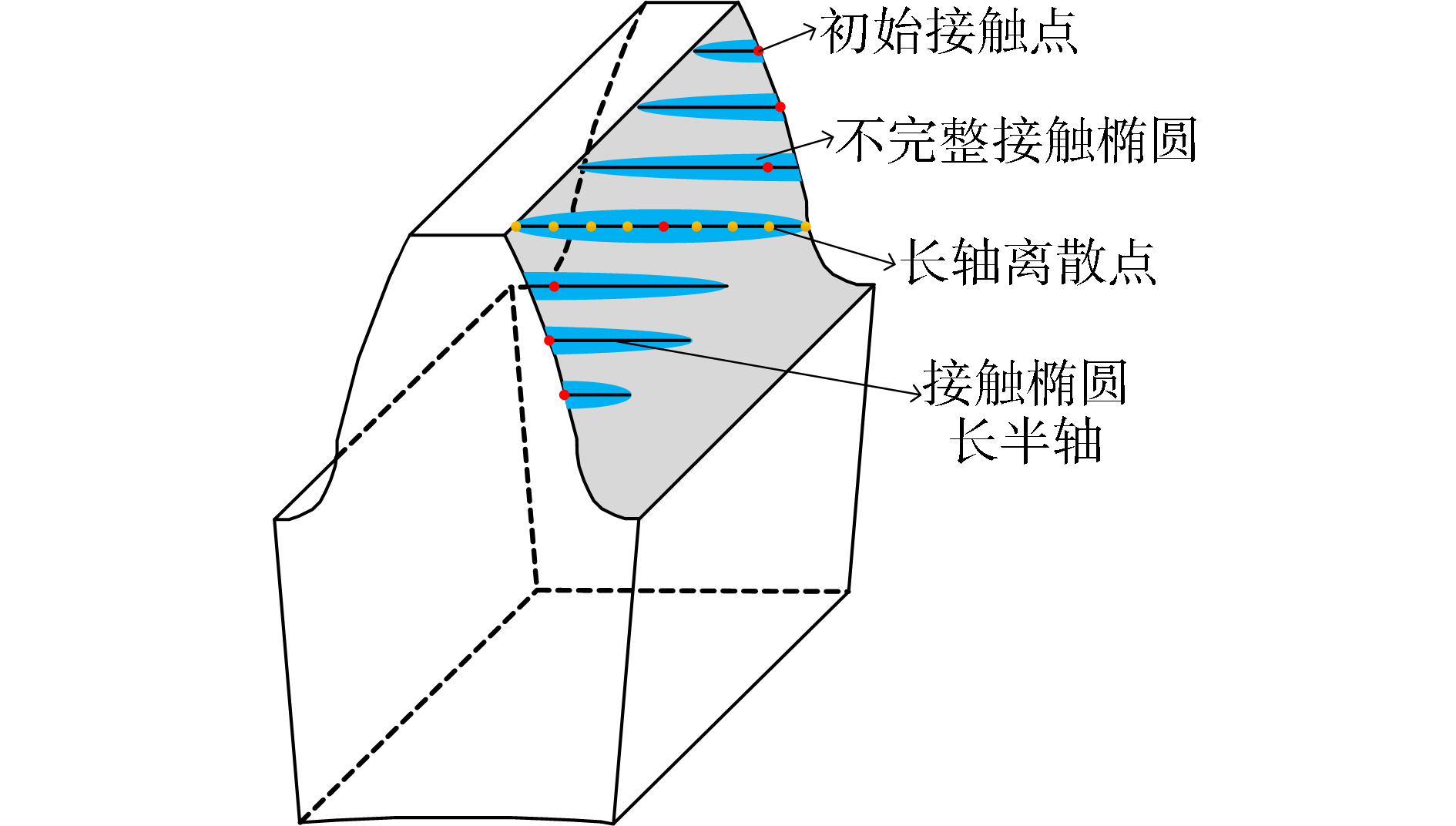
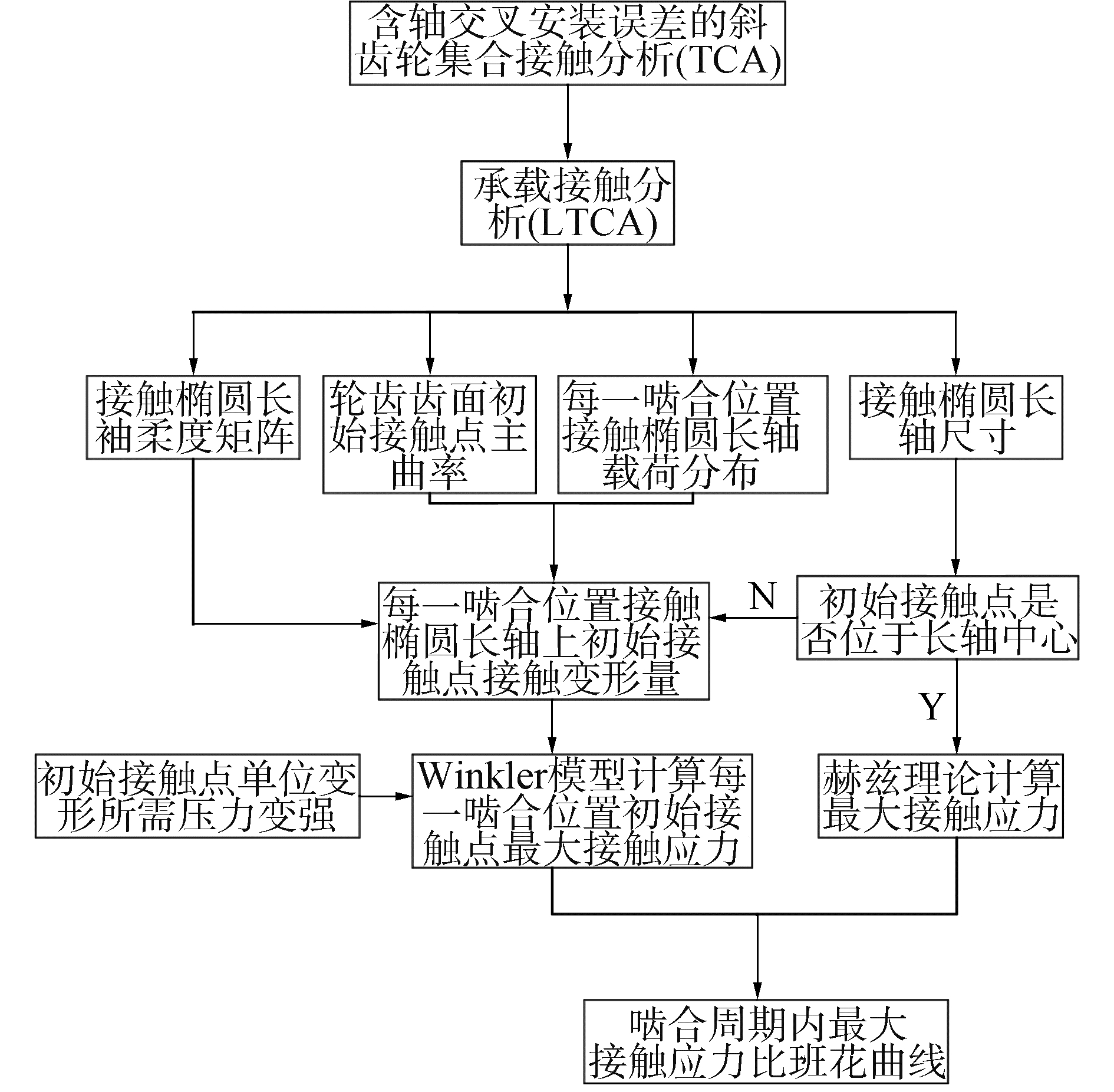
轴平面内含轴交角安装误差的斜齿轮由理论上的线接触转换为点接触,当齿轮受载时齿面接触印痕呈现为完整或不完整的细长接触椭圆面。特别在齿轮进入和退出啮合阶段边缘接触的发生使得接触印痕完全表现为半个接触椭圆,具体如图 2所示。对于这种接触椭圆不完整的啮合位置,经典赫兹理论无法用于最大接触应力的求解,为此,在TCA分析基础上提出一种混合分析法用于求解斜齿轮不同啮合位置的最大接触应力。同时由于接触印痕为细长的完整或不完整接触椭圆面,为便于求解载荷在齿面上的分布,将该细长接触印痕简化为载荷只在椭圆长轴上分布。图 3为轴平面内含轴交角安装误差的斜齿轮接触应力计算流程图。
|
Download:
|
| 图 2 不完整接触椭圆示意 Fig. 2 Incomplete contact ellipse on tooth surface | |
|
Download:
|
| 图 3 接触应力计算流程 Fig. 3 Flowchart for calculating contact stress | |
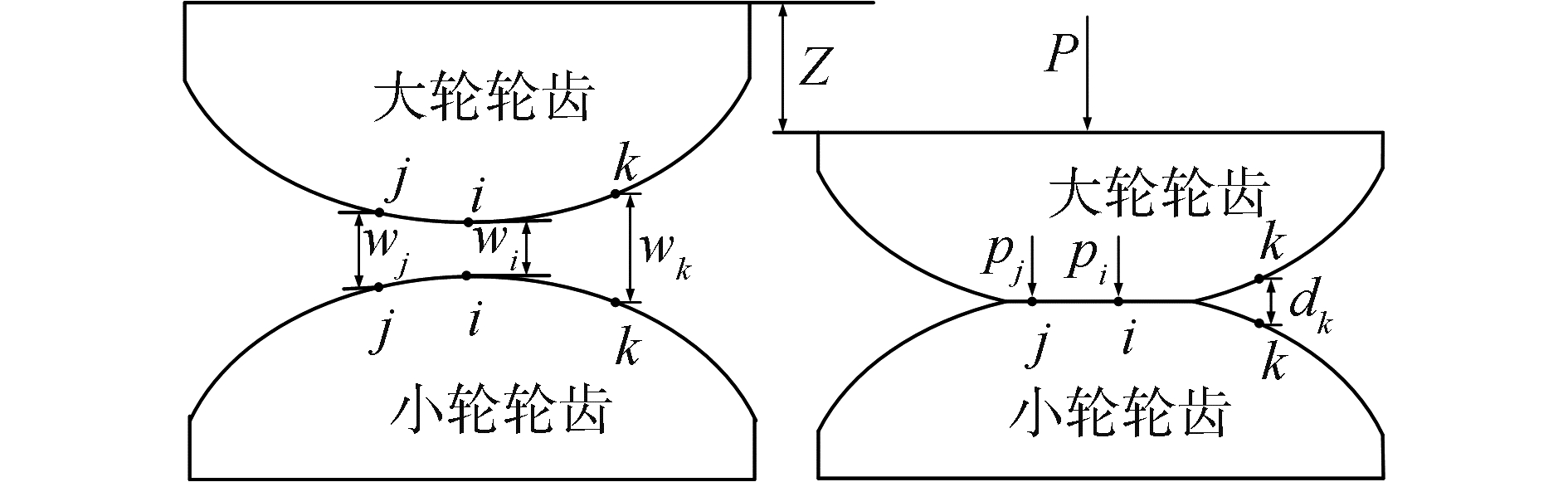
斜齿轮承载接触示意图如图 4所示,利用弹性接触变形协调方程和力平衡方程,建立如式(3)所示轮齿承载接触数学规划。
|
Download:
|
| 图 4 轮齿接触示意 Fig. 4 Schematic diagram of tooth contact under load | |
| $ \left\{ {\begin{array}{*{20}{l}} {\min \sum\limits_{t = 1}^{n + 1} {{\mathit{\boldsymbol{X}}_{\rm{t}}}} ,P = \frac{\mathit{\boldsymbol{T}}}{{{\mathit{\boldsymbol{R}}_{\rm{b}}}\cos {\beta _{\rm{b}}}}}}\\ {\mathit{\boldsymbol{W}} = - {\mathit{\boldsymbol{F}}_{pg}}\mathit{\boldsymbol{p}} + \mathit{\boldsymbol{Z}} + \mathit{\boldsymbol{d}} + \mathit{\boldsymbol{X}}}\\ {P = {\mathit{\boldsymbol{e}}^{\rm{T}}}\mathit{\boldsymbol{p}} + {\mathit{\boldsymbol{X}}_{n + 1}},{: \mathit{\boldsymbol{p}}_t} = 0{\rm{||}}{: \mathit{\boldsymbol{d}}_t} = 0}\\ {{\rm{ s}}{\rm{.t}}{\rm{. }}{\mathit{\boldsymbol{p}}_t} \ge 0,{\mathit{\boldsymbol{d}}_t} \ge 0,{\mathit{\boldsymbol{Z}}_t} \ge 0,{\mathit{\boldsymbol{X}}_t} \ge 0} \end{array}} \right. $ | (3) |
式中:Z为齿轮副综合法向变形量;p为接触椭圆长轴上离散点载荷;d为受载后瞬时接触椭圆长轴离散点法向间隙,以上3者为待求量。T为负载扭矩, Rb和βb分别为负载轮基圆半径和基圆螺旋角,W为TCA中求得的齿面法向间隙。采用改进的单纯形法求解该非线性接触问题,根据承载后间隙大小判断接触与否,规划目标是变形能最小,式中Xt(t=1, 2, …,n+1)为人工变量,Fpg为的斜齿轮齿面综合法向柔度矩阵,该柔度矩阵具体计算方法参考文献[15],X为列向量[X1 X2 X3…Xn]T,n维向量e的各个元素均为1,P为总法向啮合力,s.t.为约束条件。
对于齿轮副在第j个啮合位置的载荷分配系数Lj可由式(4)得出
| $ {L_j} = \frac{{\sum\limits_{i = 1}^n {{p_{ji}}} }}{P} $ | (4) |
式中:pji为LTCA求解出的第j个啮合位置上接触椭圆长轴上第i个离散点载荷;n表示第j个啮合位置的接触椭圆长轴共有n个离散点;P为总啮合力。
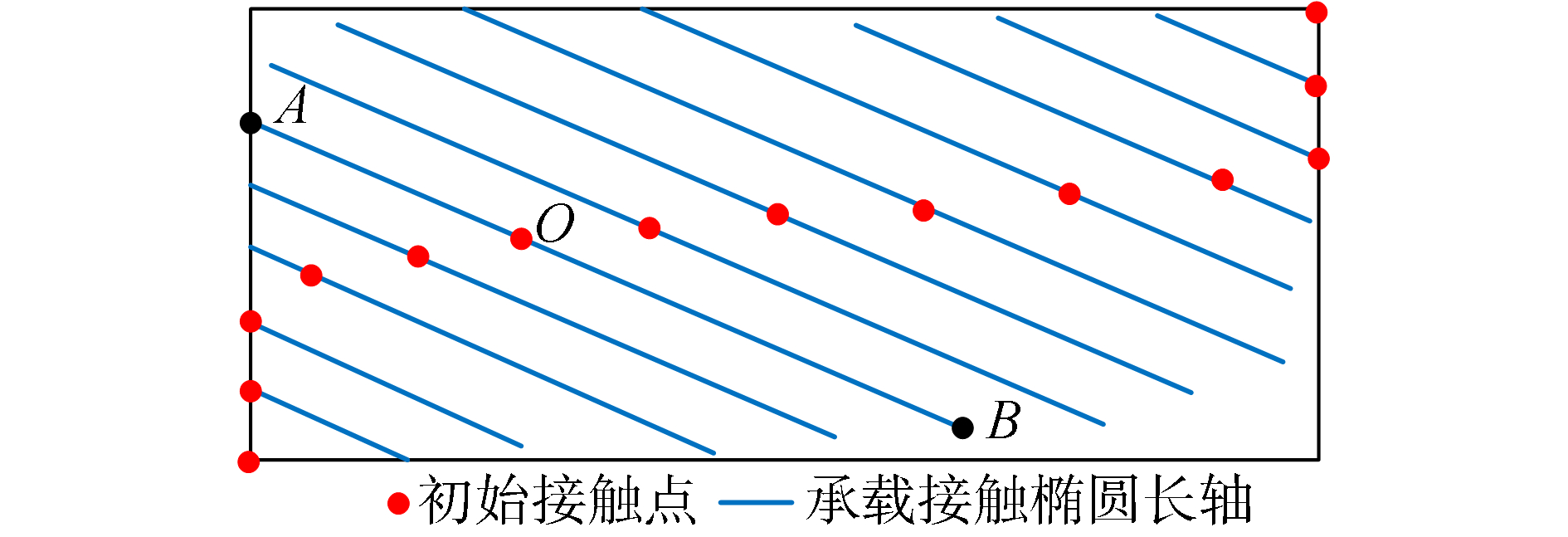
为便于判断初始接触点是否在实际接触椭圆长轴对称中心,采用如图 5所示小轮旋转投影面上的接触椭圆长轴两端离散点坐标与初始接触点的距离进行对比。
|
Download:
|
| 图 5 小轮旋转投影面示意 Fig. 5 Schematic diagram of the rotary projection of pinion tooth surface | |
设某一瞬时接触椭圆长轴两端点在旋转投影面上的坐标分别为A(x1, y1)和B(x2, y2),其相对初始接触点位置O(x0, y0)的距离分别为S1和S2,则为S1、S2可用下式进行计算:
| $ \left\{ {\begin{array}{*{20}{l}} {{S_1} = \sqrt {{{\left( {{x_1} - {x_0}} \right)}^2} + {{\left( {{y_1} - {y_0}} \right)}^2}} }\\ {{S_2} = \sqrt {{{\left( {{x_2} - {x_0}} \right)}^2} + {{\left( {{y_2} - {y_0}} \right)}^2}} } \end{array}} \right. $ |
若S1=S2,则初始接触点位长轴中心,否则初始接触点位于非长轴中心,即此时接触椭圆是不完整的。
2.2 赫兹接触应力针对以上分离的初始接触点位于接触椭圆长轴中心的啮合位置,由于其具有完整的椭圆长短轴故可采用赫兹理论直接计算出该啮合位置的最大接触应力,初始接触点位于长轴中心时接触应力σj计算表达式如下:
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{A_j} = \frac{1}{2}\left( {{k_{j11}} + {k_{j12}} + {k_{j21}} + {k_{j22}}} \right)}\\ {{B_j} = \frac{1}{2}\sqrt {C_j^2 + D_j^2 + 2C_j^2D_j^2\sin \left( {2{\varphi _j}} \right)} } \end{array}\\ \begin{array}{*{20}{l}} {{C_j} = {k_{j11}} - {k_{j12}}}\\ {{D_j} = {k_{j21}} - {k_{j22}}} \end{array}\\ \begin{array}{*{20}{l}} {{a_j} = {\alpha _j}{{\left[ {\frac{{3{L_j}P_j^*}}{{4{A_j}}}\left( {\frac{{1 - v_1^2}}{{{E_1}}} + \frac{{1 - v_2^2}}{{{E_2}}}} \right)} \right]}^{\frac{1}{3}}}}\\ {{b_j} = {\beta _j}{{\left[ {\frac{{3{L_j}P_j^*}}{{4{A_j}}}\left( {\frac{{1 - v_1^2}}{{{E_1}}} + \frac{{1 - v_2^2}}{{{E_2}}}} \right)} \right]}^{\frac{1}{3}}}} \end{array}\\ {\sigma _j} = \frac{{3{L_j}P}}{{2\pi {a_j}{b_j}}} \end{array} \right. $ | (5) |
式中:kj11、kj12和kj21、kj22为小轮和大轮齿面上第j个啮合位置几何初始接触点的主曲率,其可通过齿轮空间几何理论求解出,具体计算方法参考第2.3节;E1、E2和ν1、ν2分别表示小轮及大轮的弹性模量和泊松比;αj、βj和aj、bj分别表示在第j个啮合位置接触椭圆长短半轴系数及长短半轴大小,其中αj、βj可利用θj计算值通过文献[16]查询得到;φj是大小轮齿面几何初始接触点主方向之间的夹角,该值通过TCA得到;Lj为式(4)计算的载荷分配系数。
对于含安装误差的斜齿轮接触应力,工程上主要关心每一啮合位置的最大接触应力以及每个啮合位置的最大接触应力是否在合理范围内,因此当齿面接触椭圆完整时,只需利用式(5)计算得此时第j个啮合位置的最大接触应力σj,而对于初始接触点并不位于接触椭圆长轴中心,即具有不完整椭圆形接触面,此时最大接触应力计算可采用Winkler弹性模型。
2.3 Winkler模型计算接触应力由于含轴交角安装误差的斜齿轮在进入和退出啮合阶段常发生边缘接触,且齿轮在受载时接触变形属于小变形,受压后的接触平面呈现为一个长轴很长、短轴很短的不完整接触椭圆面,具体如图 6所示。

|
Download:
|
| 图 6 含安装误差斜齿轮接触印痕示意 Fig. 6 Schematic diagram of contact for helical gear with assembly error | |
不完整的接触椭圆面不能参照上一节赫兹理论进行接触应力的计算。由于接触面为一细长的接触印痕,因此将载荷在该细长接触面上的分布简化为载荷只在长轴上分布,此时结合LTCA并利用Winkler模型可进行最大接触应力的求解。
图 7为Winkler弹性基本模型,该模型假定接触体由许多相互独立且互不影响的弹簧组成,即接触表面任意点所受到的接触应力只与该点的变形量成正比,且该点的接触应力不影响除该点以外的其他位置的变形。

|
Download:
|
| 图 7 Winkler弹性基础模型 Fig. 7 Model of Winkler elastic basic foundation | |
Winkler模型接触应力σj计算表达式如下。由于大小轮齿面接触应力近似相等,故本节以小轮齿面为例用于计算接触椭圆不完整时的最大接触应力。
| $ {\sigma _j} = {k_j}{\delta _j} $ | (6) |
式中:δj为小轮第j个啮合位置上初始接触点的接触变形量;kj表示第j个啮合位置小轮初始接触点产生单位变形所需要的压力强度,且δj和kj均为未知量,其中δj的求解需利用LTCA中接触椭圆长轴离散点柔度矩阵,而kj则需利用TCA中齿面初始接触点的4个主曲率求得。
基于Winkler模型、TCA及LTCA含轴交角安装误差的斜齿轮接触应力求解分以下4个步骤:
1) 分离出整个啮合周期内初始接触点不在接触椭圆长轴中心的啮合点;2)基于TCA结果,利用空间几何理论计算第j个啮合位置初始接触点在大小轮齿面上的4个主曲率并利用kj定义求解其数值;3)对以上分离的初始接触点,利用LTCA中求得的第j个啮合位置接触椭圆长轴柔度矩阵及其对应初始接触点上的离散载荷Pj计算出j点的接触位移δj;4)结合δj、kj,利用式(6)计算第j啮合位置的最大接触应力σj。
综合以上分析并由kj定义可知其数值的大小为空间曲面上一点产生单位变形所需要的压力强度,利用空间几何和弹性半空间理论可推导出其数值,求解小轮齿面主曲率的计算方法如下:
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{R}}_u} = \frac{{\partial {\mathit{\boldsymbol{R}}_p}\left( {{u_p},{l_p}} \right)}}{{\partial {u_p}}}\\ {{\bf{R}}_l} = \frac{{\partial {\mathit{\boldsymbol{R}}_p}\left( {{u_p},{l_p}} \right)}}{{\partial {l_p}}}\\ {\mathit{\boldsymbol{R}}_{ul}} = \frac{{\partial {\mathit{\boldsymbol{R}}_p}\left( {{u_p},{l_p}} \right)}}{{\partial {u_p}\partial {l_p}}}\\ {\mathit{\boldsymbol{R}}_{uu}} = \frac{{{\partial ^2}{\mathit{\boldsymbol{R}}_p}\left( {{u_p},{l_p}} \right)}}{{\partial u_p^2}}\\ {\mathit{\boldsymbol{R}}_{ll}} = \frac{{{\partial ^2}{\mathit{\boldsymbol{R}}_p}\left( {{u_p},{l_p}} \right)}}{{\partial l_p^2}}\\ {\mathit{\boldsymbol{n}}_p} = \frac{{{\mathit{\boldsymbol{R}}_u} \times {\mathit{\boldsymbol{R}}_p}}}{{\left| {{\mathit{\boldsymbol{R}}_u} \times {\mathit{\boldsymbol{R}}_p}} \right|}} \end{array} \right. $ | (7) |
式中:Ru、Ruu和Rl、Rll分别表示小轮齿面方程Rp(up, lp)对参数up和lp的一阶导数和二阶导数;np为小轮齿面单位法矢。
令L、M、N和E、F、G的计算表达式为式(8):
| $ \left\{ {\begin{array}{*{20}{l}} {L = {\mathit{\boldsymbol{R}}_{uu}} \cdot {\mathit{\boldsymbol{n}}_p}}\\ {M = {\mathit{\boldsymbol{R}}_{ul}} \cdot {\mathit{\boldsymbol{n}}_p}}\\ {N = {\mathit{\boldsymbol{R}}_{ul}} \cdot {\mathit{\boldsymbol{n}}_p}}\\ {E = {\mathit{\boldsymbol{R}}_u} \cdot {\mathit{\boldsymbol{R}}_u}}\\ {F = {\mathit{\boldsymbol{R}}_u} \cdot {\mathit{\boldsymbol{R}}_l}}\\ {G = {\mathit{\boldsymbol{R}}_l} \cdot {\mathit{\boldsymbol{R}}_l}}\\ {L{d_u} + M{d_l} = {k_{j1r}}\left( {E{d_u} + F{d_l}} \right),r = 1,2}\\ {M{d_u} + N{d_l} = {k_{j1r}}\left( {F{d_u} + G{d_l}} \right),r = 1,2} \end{array}} \right. $ | (8) |
则根据空间几何理论中Rodrigue公式可计算得小轮齿面上初始接触点的主曲率kj11和kj12。同理可求解得初始接触点在大轮齿面上的主曲率kj21和kj22。
基于以上求解出的大小轮齿面几何初始接触点主曲率及TCA中求解出的主方向夹角,利用式(9)并依据kj含义可求解出斜齿轮在第j个啮合位置初始接触点产生单位变形所需要的压力强度kj。
| $ \left\{ {\begin{array}{*{20}{l}} {1 = {\gamma _j}\left[ {\frac{{9{P_*}{{\left( {{k_{j11}} + {k_{j12}} + {k_{j21}} + {k_{j22}}} \right)}^{\frac{1}{3}}}}}{{128}}} \right.}\\ {\left. {{{\left( {\frac{{1 - v_1^2}}{{{E_1}}} + \frac{{1 - v_2^2}}{{{E_2}}}} \right)}^2}} \right]}\\ {{k_j} = \frac{{3{P_*}}}{{2{\rm{ \mathsf{ π} }}{a_j}{b_j}}}} \end{array}} \right. $ | (9) |
式中:γj为弹性接触变形系数,它同样通过查询文献[16]得到;P*表示斜齿轮在第j个啮合位置上初始接触点处产生1 mm变形所需的压力,为中间变量。
设图 6所示斜齿轮在第j个啮合位置接触椭圆长轴上共有n个离散点,那么该长轴离散点组成的接触柔度矩阵可用进行表述。
| $ {\mathit{\boldsymbol{f}}_j} = \left[ {\begin{array}{*{20}{c}} {{\omega _{11}}}& \cdots &{{\omega _{1m}}}& \cdots &{{\omega _{1n}}}\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {{\omega _{m1}}}& \cdots &{{\omega _{mm}}}& \cdots &{{\omega _{mn}}}\\ \vdots &{{\omega _{pq}}}& \vdots & \vdots & \vdots \\ {{\omega _{n1}}}& \cdots &{{\omega _{nm}}}& \cdots &{{\omega _{nn}}} \end{array}} \right] $ | (10) |
矩阵中任一元素ωpq表示在椭圆长轴上第q个节点施加单位法向集中力载荷时,对长轴上第p个离散点产生的变形量;柔度矩阵斜对角元素ωmm表示在长轴离散点m上施加单位法向集中力载荷时该节点自身产生的变形量,n表示第j个啮合位置上接触椭圆长轴共有n个离散点。
利用式(6)中求得的第j个啮合位置接触椭圆长轴每个离散点载荷pj(j=1, 2,…,n), 并结合下式可求出斜齿轮在第j个啮合位置上接触椭圆长轴初始接触点j的综合接触变形量δj和最大接触应力σj。
| $ \left\{ {\begin{array}{*{20}{l}} {{\delta _j} = {\omega _{j1}}{p_1} + {\omega _{j2}}{p_2} + \cdots + {\omega _{jn}}{p_n}}\\ {{\sigma _j} = {k_j}{\delta _j}} \end{array}} \right. $ |
斜齿轮参数列于表 1中,该模型不考虑摩擦、润滑和轴的影响。
| 表 1 斜齿轮基本参数 Table 1 Basic parameter of helical gear |
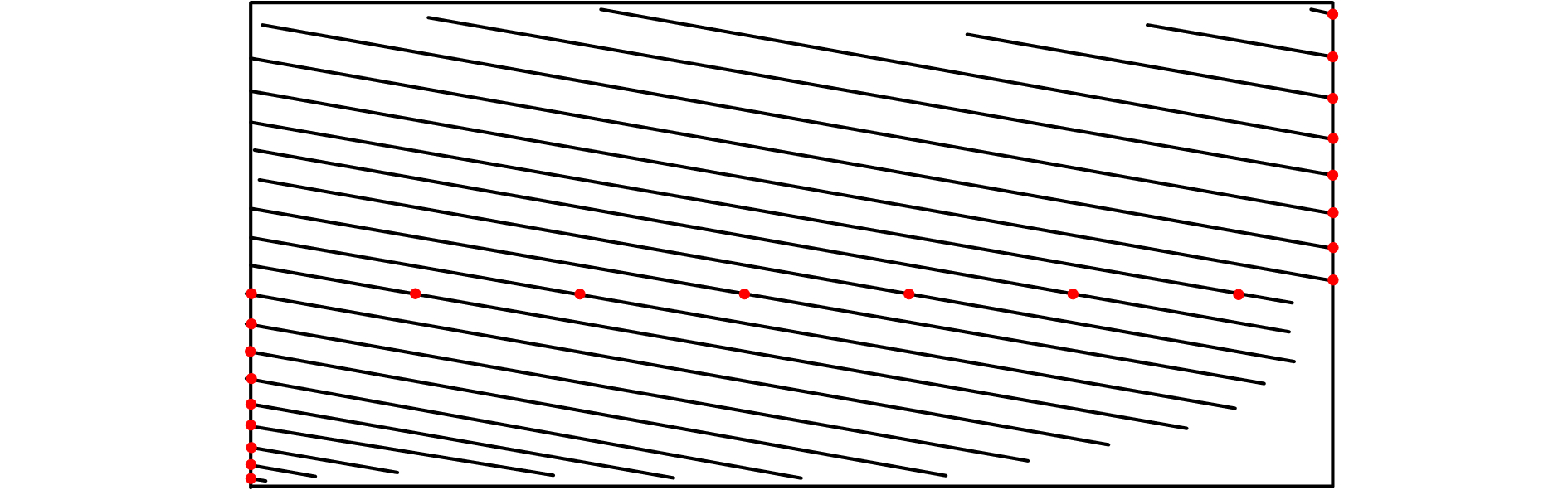
将啮合周期划分为23个啮合位置,通过TCA仿真分析可得图 8所示小轮齿面接触印痕。从图中可以看出轴平面含轴交角安装误差的斜齿轮多数啮合位置处于接触椭圆长轴不完整的啮合状态。
|
Download:
|
| 图 8 小轮齿面接触印痕 Fig. 8 Contact trace of pinion tooth surface | |
图 9为齿面载荷分配系数(不同载荷下该系数几乎不变),该曲线变化规律呈现为中间大两边小,这是由于表 1所示参数的斜齿轮理论重合度为2.25,即在相同负载下斜齿轮首先进入三齿啮合区,再进入双齿啮合区,最后再次进入三齿啮合区,且在三齿啮合区单个轮齿承受的载荷比两齿啮合区所承受的载荷要小,故曲线呈中间大两边小的变化规律。

|
Download:
|
| 图 9 载荷分配系数 Fig. 9 Load distribution factor of helical gear | |
图 10为负载在100、400、700和1 000 N·m时混合分析法求解出的不同啮合位置最大接触应力变化曲线。从图中可以看出4组接触应力曲线均呈中凹变化规律,这是由2个方面原因所致:1) 图 8所示小轮齿面接触印痕前8个和后8个啮合位置均处于边缘接触状态,在啮合时会产生应力集中效应,而中间7个啮合位置则未发生边缘接触;2) 图 9中前8个啮合位置载荷分配系数随啮合位置依次增大,而后8个啮合位置载荷分配系数则随啮合位置依次降低,在发生边缘接触时载荷的增大和减小会相应的扩大和降低应力集中现象,故4组应力变化曲线呈中凹变化规律。同时从图 10中还可看出发生边缘接触的第8个啮合位置接触应力比第16个啮合位置处的接触应力偏大,这是由于图 9中第8个啮合位置的载荷分配系数大于第16个啮合位置的载荷分配系数,且图 8中接触印痕表明第8个啮合位置的接触椭圆长半轴更小,故接触应力曲线呈现为左边高右边低。此外,在4种载荷下整个啮合周期内的最大接触应力分别为663、995、1 180和1 308 MPa,即啮合周期内最大接触应力随载荷增加表现为非线性增长,但增幅逐渐降低。

|
Download:
|
| 图 10 不同负载下接触应力变化曲线 Fig. 10 Curves of contact stress under multi-loads | |
有限元法是计算轮齿接触的一种可靠数值方法,为验证本文提出的混合分析法计算出的轴平面内含轴交角安装误差斜齿轮接触应力及其变化规律是否可靠,采用与ANSYS有限元软件计算结果进行对比。在考虑斜齿轮重合度及边界条件的基础上,ANSYS采用八节点六面体单元和五齿网格模型来计算齿轮在整个啮合周期内的最大接触应力变化规律,并将该计算结果与图 10中混合分析法计算数值进行对比分析。基于大小轮齿面方程Rg(ug, lg)和Rp(up, lp)建立ANSYS有限元网格模型,并创建相应接触对,具体有限元网格模型如图 11所示,模型中共有468 842个节点和420 000个八节点六面体单元,其中小轮内圈及两侧为固定约束。负载的施加利用MPC184刚性梁单元,首先在大轮回转中心建立一个编号为N的节点,再利用MPC184单元与大轮内圈所有节点进行刚性连接,最后通过在节点N上施加负载扭矩传递到啮合轮齿上。

|
Download:
|
| 图 11 斜齿轮副有限元网格模型 Fig. 11 Finite element model of helical gear | |
为使计算结果具有可比性,同样将ANSYS求解接触应力的啮合周期均划分为23个啮合位置,并利用ANSYS批处理功能将小轮和大轮分别每间隔φp、φg转角计算一次轮齿的接触应力,φp、φg计算如式(11)。
| $ \left\{ \begin{array}{l} \Delta \varphi = \frac{{2{\rm{ \mathsf{ π} }}}}{{22{Z_p}}}\\ {\varphi _p} = \Delta \varphi (n - 1),n = 1,2, \cdots ,23\\ {\varphi _g} = \frac{{{\varphi _p}{Z_p}}}{{{Z_g}}} \end{array} \right. $ | (11) |
式中Zp、Zg分别为小轮和大轮齿数。
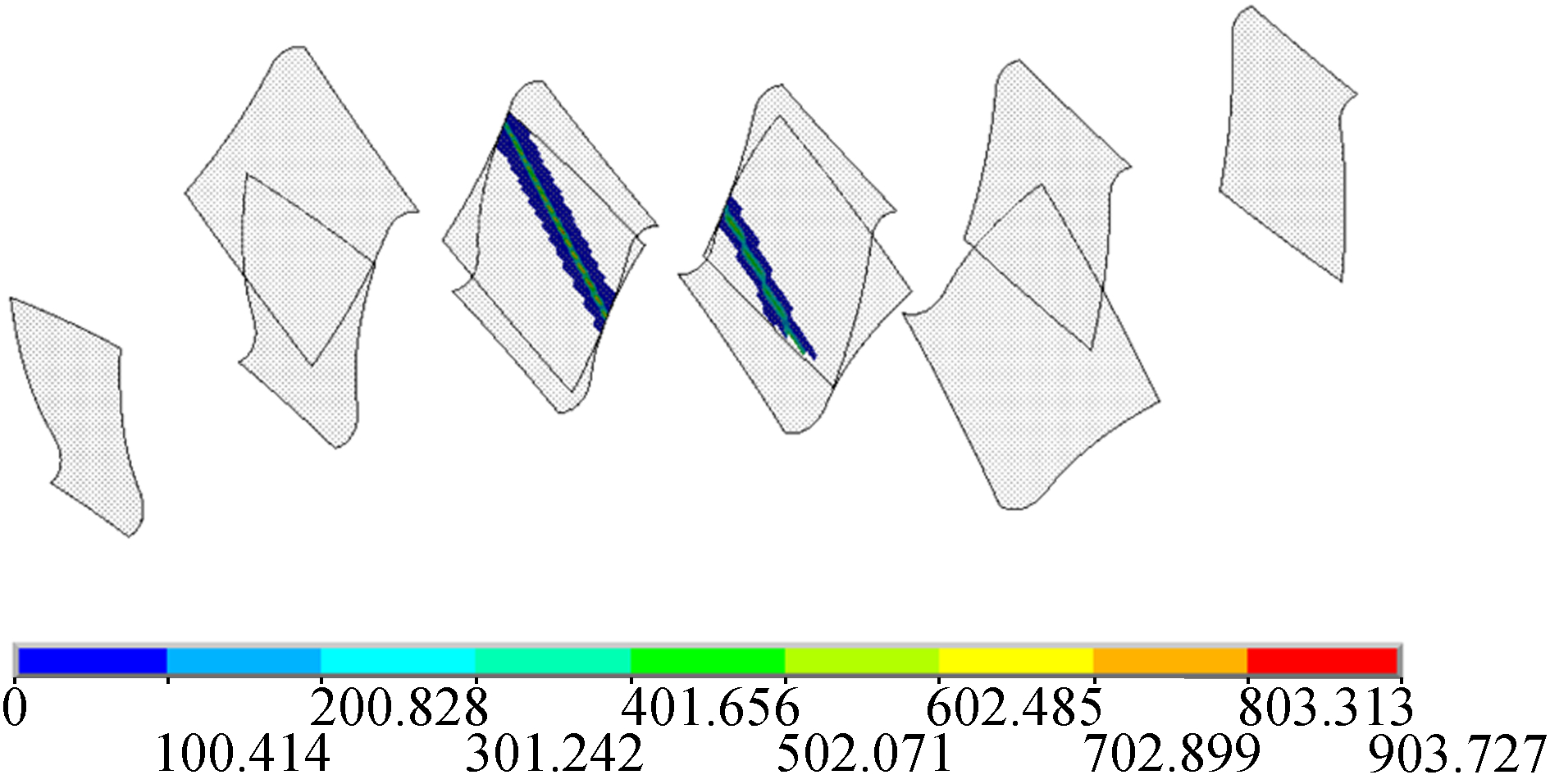
图 11所示有限元模型左右2个轮齿的接触应力计算误差较大,故提取中间轮齿在每个啮合位置的最大接触应力,即可绘制不同啮合位置的最大接触应力变化曲线。图 12为φp=12Δφ,负载为1 000 N·m时ANSYS计算出的齿面接触应力云图,从图中可知ANSYS计算的接触印痕接近于线接触,因此本文将齿面载荷在细长椭圆面上的分布简化为在椭圆长轴的分布是合理的。
|
Download:
|
| 图 12 有限元接触对接触应力云 Fig. 12 Contact stress nephogram by ANSYS | |
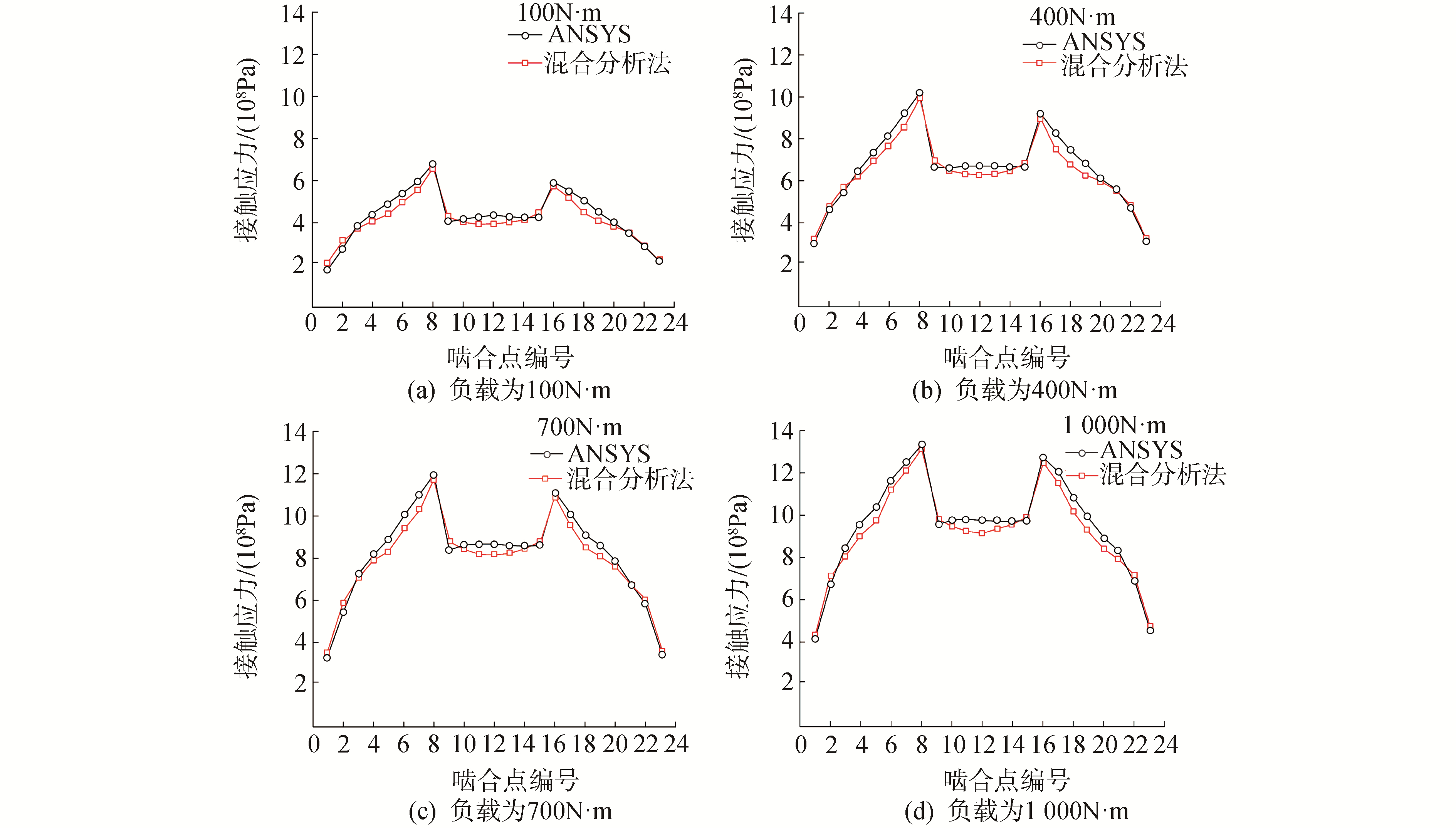
图 13为4种负载作用下混合分析法和ANSYS计算的最大接触应力变化规律对比图,从图 13可知基于混合分析法的斜齿轮接触应力在ANSYS计算数值上下波动,且2者计算出的接触应力曲线变化规律相似,与ANSYS计算数值相比最大相对误差分别约为6.38%、6.52%、6.78%和5.88%,这表明接触应力波动幅值较小。这种无规律的波动由2个方面原因造成:1)在运用Winkler模型计算不同啮合位置初始接触点处的接触变形系数kj时,很难准确的排除接触区域的影响而单独计算j点的系数kj,即计算出的kj存在一定的误差;2)由于Winkler模型是忽略接触点之间的剪切作用,这会导致计算出的接触应力偏离理论数值,即该模型本身会造成计算数值偏差。综合分析以上2种方法计算结果,表明混合分析法在计算轴平面内含轴交角安装误差的斜齿轮接触应力方法是合理的,计算结果是可靠的。
|
Download:
|
| 图 13 混合法和有限元法接触应力对比 Fig. 13 Comparison of contact stress between proposed method and finite element method | |
为比较混合法和有限元法的计算效率,分别列出了2种方法求解接触应力的总耗时和内存占用量,具体如表 2所示,计算机为八核心,主频为3.7 GHz,内存总量为32 G。混合分析法程序采用Fortran编制,由于程序中TCA和LTCA只需计算一次即可得求得斜齿轮齿面接触柔度矩阵和初始接触点位置,在负载一定的情况下可一次性计算得23个啮合位置的最大接触应力,在计算其他负载对应的接触应力时只需在LTCA中更改负载数值即可。而ANSYS有限元软件则采用的是将大小轮每转动如式(11)所示角度后需重新计算一次接触应力,因而总耗时约为单个啮合位置计算耗时的23倍。从表 2中可知混合分析法相较于ANSYS有限元软件, 计算耗时缩短了约38.7倍,同时内存占用量节省了约15倍,这表明基于混合分析法的接触应力计算相较于ANSYS有限元软件具有更高的效率。
| 表 2 计算效率对比 Table 2 Efficiency of calculation |
1) 针对含安装误差的斜齿轮齿面易发生边缘接触及接触椭圆不完整时经典赫兹理论无法求解接触应力的问题,提出了混合赫兹、Winkler模型的接触应力计算方法,并以轴平面内含轴交角安装误差的斜齿轮为例,推导了该混合分析法的求解过程。
2) 对含安装误差的斜齿轮采用混合分析法求解接触应力时应力曲线均呈现中凹变化规律;在发生边缘接触的位置应力集中导致接触应力增幅较大。因此在装配时应尽可能减小安装误差以避免产生过多的边缘接触位置。
3) 在相同条件下对混合分析法和ANSYS计算的结果进行了对比研究,结果表明2者所求解的接触应力变化规律类似,相对误差在6.78%以内,从而验证了本文所提方法的合理性和可靠性,同时对该误差产生的原因进行了具体分析。此外,在求解速度方面混合分析法相较于ANSYS具有更高的计算效率。
4) 本文主要以齿轮几何学、弹性接触力学和Winkler模型为基础,分析了含安装误差的齿轮副接触应力变化规律,该推导过程和所用理论具有一般性和通用性。因此,对于更加普遍存在的空间轴交角误差以及中心距误差造成的齿面接触椭圆不完整和边缘接触问题,该混合分析法同样适用。
| [1] |
佟操, 孙志礼, 柴小冬, 等. 基于响应面和MCMC的齿轮接触疲劳可靠性[J]. 东北大学学报(自然科学版), 2016, 37(4): 532-537. TONG Cao, SUN Zhili, CHAI Xiaodong, et al. Gear contact fatigue reliability based on response surface and MCMC[J]. Journal of Northeastern University (Natural Science), 2016, 37(4): 532-537. DOI:10.3969/j.issn.1005-3026.2016.04.018 (  0) 0)
|
| [2] |
王运知. 直齿轮承载接触分析与强度计算[J]. 机械传动, 2016, 40(3): 74-77. WANG Yunzhi. Load contact analysis and strength calculation of spur gear[J]. Journal of mechanical transmission, 2016, 40(3): 74-77. (  0) 0)
|
| [3] |
朱有利, 王燕礼, 边飞龙, 等. 渐开线直齿圆柱齿轮接触疲劳失效成因再分析[J]. 摩擦学学报, 2014, 34(6): 722-728. ZHU Youli, WANG Yanli, BIAN Feilong, et al. Re-examining the origins of contact fatigue failure of involute cylindrical spur gears[J]. Tribology, 2014, 34(6): 722-728. (  0) 0)
|
| [4] |
唐进元, 陈兴明, 罗才旺. 考虑齿向修形与安装误差的圆柱齿轮接触分析[J]. 中南大学学报(自然科学版), 2012, 43(5): 1703-1709. TANG Jinyuan, CHEN Xingming, LUO Caiwang. Contact analysis of spur gears based on longitudinal modification and alignment errors[J]. Journal of Central South University (Science and Technology), 2012, 43(5): 1703-1709. (  0) 0)
|
| [5] |
杨生华. 齿轮接触有限元分析[J]. 计算力学学报, 2003, 20(2): 189-194. YANG Shenghua. Finite element analysis of gear contact[J]. Chinese journal of computational mechanics, 2003, 20(2): 189-194. DOI:10.3969/j.issn.1007-4708.2003.02.012 (  0) 0)
|
| [6] |
龙慧, 张光辉, 罗文军. 旋转齿轮瞬时接触应力和温度的分析模拟[J]. 机械工程学报, 2004, 40(8): 24-29. LONG Hui, ZHANG Guanghui, LUO Wenjun. Modelling and analysis of transient contact stress and temperature of involute gears[J]. Chinese journal of mechanical engineering, 2004, 40(8): 24-29. DOI:10.3321/j.issn:0577-6686.2004.08.005 (  0) 0)
|
| [7] |
唐进元, 刘艳平. 直齿面齿轮加载啮合有限元仿真分析[J]. 机械工程学报, 2012, 48(5): 124-131. TANG Jinyuan, LIU Yanping. Loaded Meshing simulation of face-gear drive with spur involute pinion based on finite element analysis[J]. Journal of mechanical engineering, 2012, 48(5): 124-131. (  0) 0)
|
| [8] |
PATIL S S, KARUPPANAN S, ATANASOVSKA I, et al. Contact stress analysis of helical gear pairs, including frictional coefficients[J]. International journal of mechanical sciences, 2014, 85: 205-211. DOI:10.1016/j.ijmecsci.2014.05.013 (  0) 0)
|
| [9] |
SINGH T, PARVEZ M. Comparative study of stress analysis of helical gear using AGMA Standards and FEM[J]. International journal of engineering sciences & research technology, 2013, 2(7): 1836-1841. (  0) 0)
|
| [10] |
钱德拉佩特拉T R, 贝莱冈度A D.工程中的有限元方法[M].曾攀, 雷丽萍, 译. 4版.北京: 机械工业出版社, 2015: 353-360. CHANDRUPATLA T R, BELEGUNDU A D. Introduction to finite elements in engineering[M]. ZENG Pan, LEI Liping, trans. 4th ed. Beijing: China Machine Press, 2015: 353-360. (  0) 0)
|
| [11] |
LITVIN F L, FAN Qi, VECCHIATO D, et al. Computerized generation and simulation of meshing of modified spur and helical gears manufactured by shaving[J]. Computer methods in applied mechanics and engineering, 2001, 190(39): 5037-5055. DOI:10.1016/S0045-7825(00)00362-5 (  0) 0)
|
| [12] |
铁摩辛柯S P, 古地尔J N.弹性理论[M].徐芝纶, 译. 3版.北京: 高等教育出版社, 2013: 377-379. TIMOSHENKO S P, GOODIER J N. Theory of elasticity[M]. XU Zhilun, trans. 3rd ed. Beijing: Higher Education Press, 2013: 377-379. (  0) 0)
|
| [13] |
International Organization for Standardization. ISO 6336-2, Calculation of load capacity of spur and helical gears[S]. Geneva: International Organization for Standardization, 2006.
(  0) 0)
|
| [14] |
PEDRERO J I, PLEGUEZUELOS M, MUÑOZ M. Critical stress and load conditions for pitting calculations of involute spur and helical gear teeth[J]. Mechanism and machine theory, 2011, 46(4): 425-437. DOI:10.1016/j.mechmachtheory.2010.12.001 (  0) 0)
|
| [15] |
方宗德, 刘更, 沈允文. 圆柱齿轮传动的三维接触分析[J]. 西北工业大学学报, 1992, 10(1): 74-79. (  0) 0)
FANG Zongde, LIU Geng, SHEN Yunwen. 3-D tooth contact analysis of helical gears[J]. Journal of Northwestern Polytechnical University, 1992, 10(1): 74-79. (  0) 0)
|
| [16] |
COOPER D H. Hertzian contact-stress deformation coefficients[J]. Journal of applied mechanics, 1969, 36(2): 296-303. DOI:10.1115/1.3564624 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


