行星齿轮传动系统因具有高刚性、高精度、高传动效率、高扭矩体积比等特点而广泛应用于航空、汽车及航海领域。其中,人字齿行星传动系统因传动平稳、传动扭矩高等特点被应用在更为严苛的环境中,因此,近年来对人字齿行星传动系统的研究更加深入。Kahraman[1]建立了斜齿行星传动系统动力学模型,指出无论在静态还是动态条件下,传动误差激励都不可以被忽略。朱增宝等[2-3]考虑偏心及齿频误差对两级人字齿行星传动系统均载特性和非线性动力学特性的影响,得出差动级均载系数对齿频误差及偏心误差敏感的结论。蒋立冬等[4]在定坐标系下建立了功率分流人字齿行星传动系统动力学模型,对系统固有模态特性进行了研究。Sondkar等[5]研究了双斜齿行星齿轮系统的振动特性,并分析了双斜齿左右齿轮相位差和太阳轮支撑条件对模态的影响。Ajmi等[6-7]对宽面直齿和斜齿进行研究,指出齿轮的变形对系统静态和动态分析的重要性。沈稼耕[8]研究了啮合相位对人字齿行星传动系统动力学特性的影响。张丽娜[9]通过将包含齿侧间隙非线性的时变啮合刚度描述为傅里叶谐波形式研究了行星传动系统的动态特性,为功率分流式行星传动系统的减振降噪奠定理论基础。陈国辉[10]建立了两级封闭差动轮系动力学模型并分析了系统的固有特性,参数灵敏度及动态响应。
目前,对人字齿行星传动系统的动力学模型的研究越来越完善,对系统动静态特性的研究也更加全面,最有效的办法就是使太阳轮处于浮动状态以改善均载特性,但尚未解决工程实际应用中出现的在空载或轻载状态下此类行星齿轮系统产生输出轴转频多倍频及其谐频的频率响应成分问题。因此,本文根据行星齿轮系统的结构特点,建立其在空载或者轻载条件下的非线性动力学模型,研究该特征频率的产生机理,并分析其在不同行星轮数与载荷条件下的变化规律。
1 人字齿行星传动模型 1.1 封闭差动轮系建模本文研究对象是两级封闭差动轮系(如图 1所示),系统主要由以下2部分组成:差动级、封闭级行星齿轮,组合齿圈Ⅰ、Ⅱ及浮动齿圈。前后部分通过3种齿式联轴器联接,即直齿联轴器、斜齿联轴器和鼓形齿联轴器。

|
Download:
|
| 图 1 两级封闭差动轮系示意 Fig. 1 Schematic diagram of two stage closed differential gear train | |
采用集中参数法建立人字齿行星齿轮系统的动力学模型。模型考虑系统各构件的2个横向自由度x、y及绕z轴的扭转自由度θz。其中,除了因为轴承参数的特殊性导致需要进行坐标变换外,所有构件均采用固定坐标系。下面分别建立各子结构动力学方程。
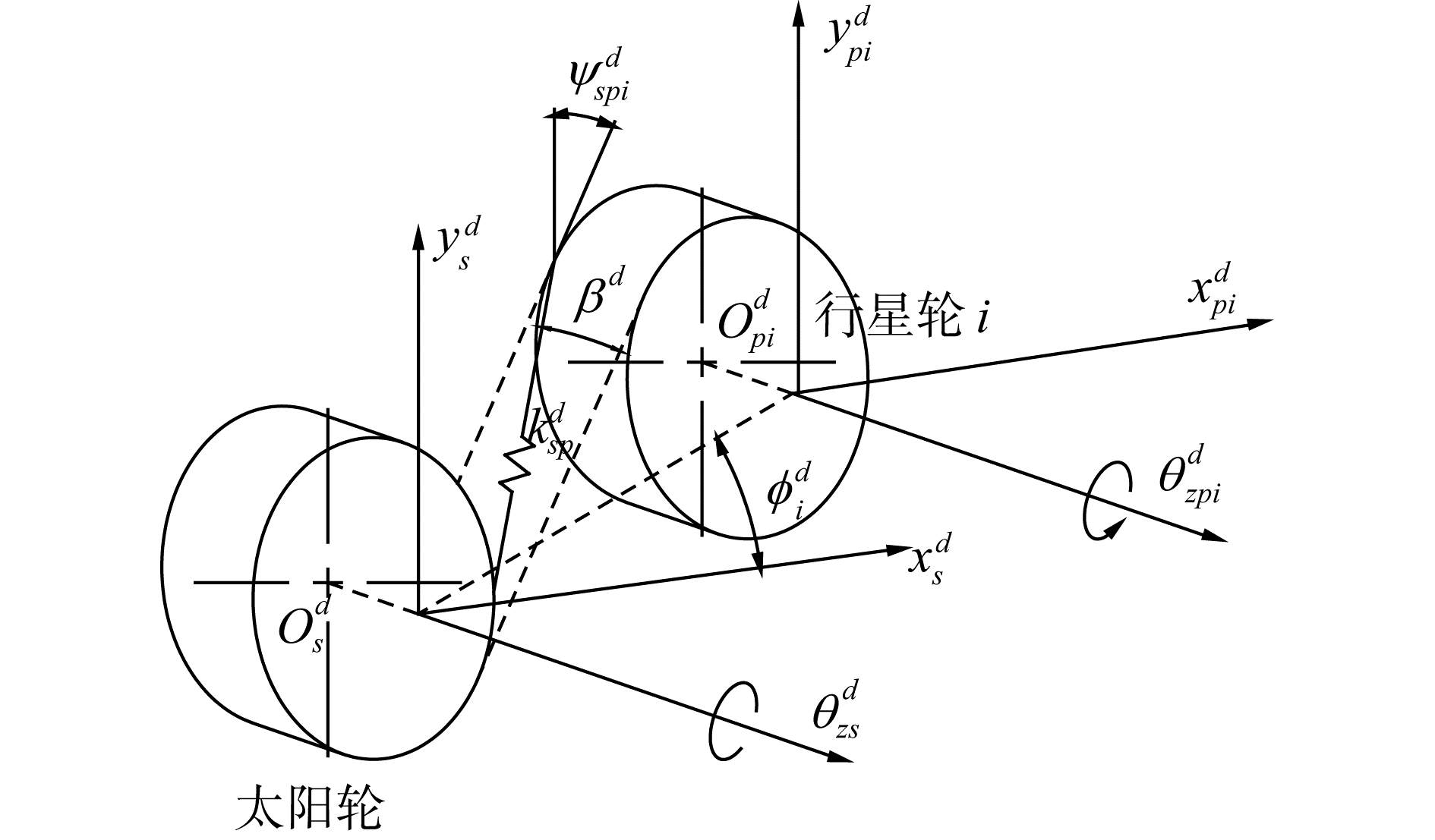
1.1.1 太阳轮—行星轮啮合对动力学模型基于集中参数法建立太阳轮—行星轮啮合对动力学模型如图 2所示。
|
Download:
|
| 图 2 太阳轮—行星轮啮合对动力学模型 Fig. 2 Dynamic model of the meshing pair of sun gear and planetary gear | |
定义啮合面与y轴夹角为:
| $ \mathit{\Psi }_{{\rm{spi}}}^d = \left\{ {\begin{array}{*{20}{c}} {{\alpha ^d} - \phi _i^d,}&{ {\rm sun} :ccw}\\ { - {\alpha ^d} - \phi _i^d,}&{ {\rm sun} :cw} \end{array}} \right. $ |
左侧的太阳轮—行星轮啮合对中太阳轮和行星轮的动力学方程分别为:
| $ \left\{ \begin{array}{l} m_s^d\ddot y_s^d + c_{sp}^d\dot p_{{\rm{spi}}}^d\cos {\beta ^d}\cos \psi _{{\rm{spi}}}^d + k_{sp}^dp_{{\rm{spi}}}^d\cos {\beta ^d}\cos \psi _{{\rm{spi}}}^d = 0\\ m_s^d\ddot x_s^d + c_{sp}^d\dot p_{{\rm{spi}}}^d\cos {\beta ^d}\sin \psi _{{\rm{spi}}}^d + k_{sp}^dp_{{\rm{spi}}}^d\cos {\beta ^d}\sin \psi _{{\rm{spi}}}^d = 0\\ J_{zs}^d\ddot \theta _{zs}^d + c_{sp}^d\dot p_{spi}^d\cos {\beta ^d}r_{bs}^d + k_{sp}^dp_{spi}^d\cos {\beta ^d}r_{bs}^d = {T_i}/{N^d} \end{array} \right. $ | (1) |
| $ \left\{ \begin{array}{l} m_p^d\ddot y_{pi}^d + c_{sd}^d\dot p_{{\rm{spi}}}^d\cos {\beta ^d}\cos \psi _{{\rm{spi}}}^d + k_{sp}^dp_{{\rm{spi}}}^d\cos {\beta ^d}\cos \psi _{{\rm{spi}}}^d = 0\\ m_p^d\ddot x_{{\rm{pi}}}^d + c_{sp}^d\dot p_{{\rm{spi}}}^d\cos {\beta ^d}\sin \psi _{{\rm{spi}}}^d + k_{sp}^dp_{{\rm{spi}}}^d\cos {\beta ^d}\sin \psi _{{\rm{spi}}}^d = 0\\ J_{{\rm{zp}}}^d\ddot \theta _{{\rm{zpi}}}^d + c_{sp}^d\dot p_{{\rm{spi}}}^d\cos {\beta ^d}r_{bp}^d + k_{sp}^dp_{{\rm{spi}}}^d\cos {\beta ^d}r_{{\rm{bp}}}^d = 0 \end{array} \right. $ | (2) |
定义啮合弹簧压缩变形为正,由图 2所示,则弹簧的变形量可表示为:
| $ \begin{array}{*{20}{c}} {p_{{\rm{spi}}}^d = \left[ {\left( {y_s^d - y_{pi}^d} \right)\cos \psi _{{\rm{spi}}}^d + \left( {x_s^d - x_{{\rm{pi}}}^d} \right)} \right.}\\ {\left. { + \left( {r_{{\rm{bs}}}^d\theta _{{\rm{zs}}}^d - r_{{\rm{bp}}}^d\theta _{{\rm{zpi}}}^d} \right)} \right]\cos \beta - e_{{\rm{spi}}}^d} \end{array} $ | (3) |
将式(3)代入式(1)和(2)可得太阳轮—行星轮啮合对的动力学方程。
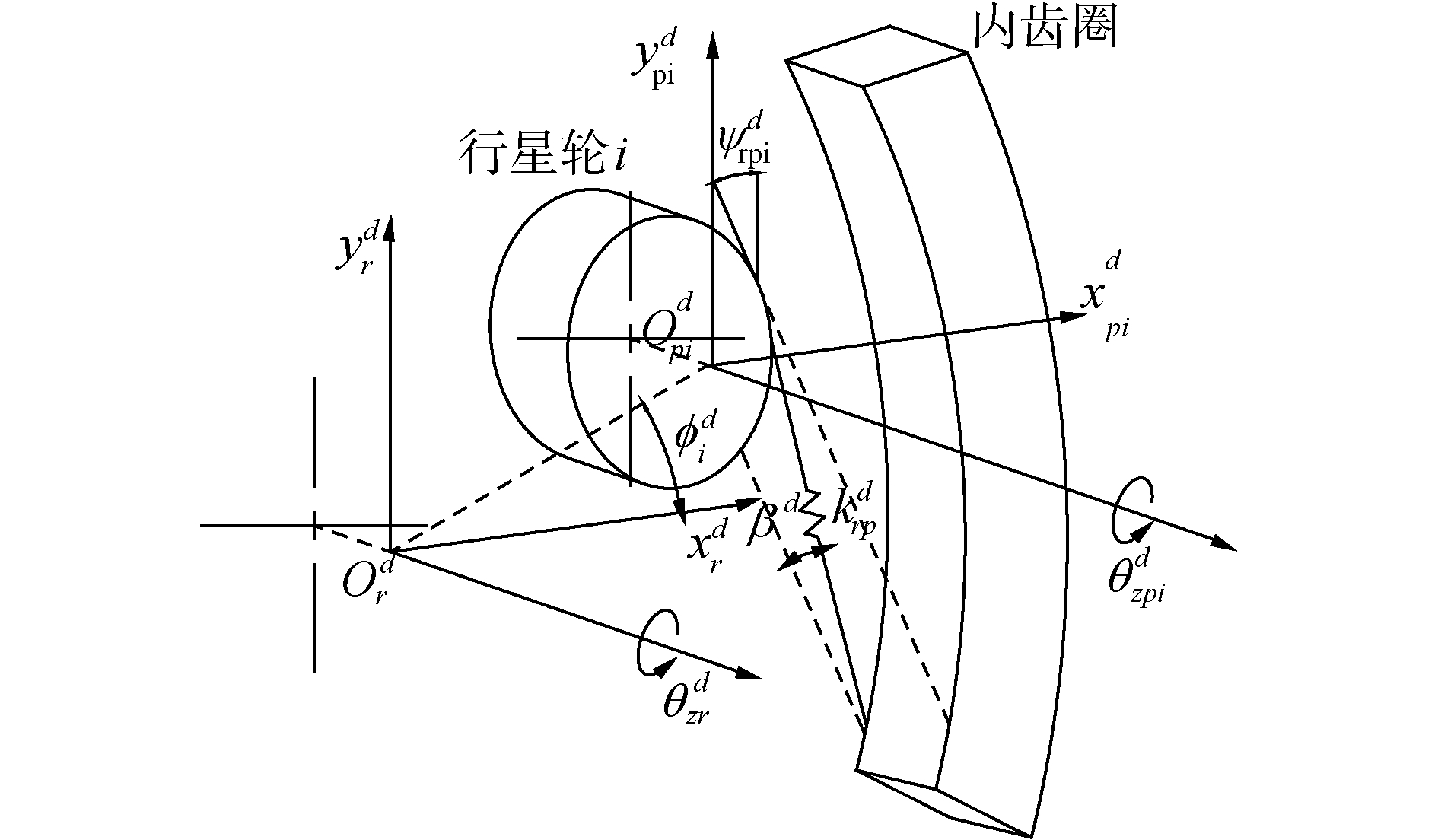
1.1.2 内齿圈—行星轮啮合对动力学模型建立内齿圈—行星轮啮合对动力学模型,如图 3所示。
|
Download:
|
| 图 3 内齿圈—行星轮啮合对动力学模型 Fig. 3 Dynamic model of the meshing pair of ring gear and planetary gear | |
定义作用平面与y轴的夹角为:
| $ \psi _{rpi}^d\left\{ {\begin{array}{*{20}{l}} {{\alpha ^d} + \phi _i^d}&{{\rm{ sun : }}ccw}\\ { - {\alpha ^d} + \phi _i^d}&{{\rm{ sun }}:cw} \end{array}} \right. $ |
式中:ccw表示太阳轮逆时针旋转,cw表示顺时针旋转。
得到内齿圈—行星轮啮合对的内齿圈和行星轮动力学方程分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {m_r^d\ddot y_r^d + c_{rp}^d\dot p_{{\rm{rpi}}}^d\cos {\beta ^d}\cos \psi _{rpi}^d + k_{rp}^dp_{{\rm{rpi}}}^d\cos {\beta ^d}\cos \psi _{{\rm{rpi}}}^d = 0}\\ {m_r^d\ddot x_r^d - c_{rp}^d\dot p_{{\rm{rpi}}}^d\cos {\beta ^d}\sin \psi _{{\rm{rpi}}}^d - k_{rp}^dp_{{\rm{rpi}}}^d\cos {\beta ^d}\sin \psi _{{\rm{rpi}}}^d = 0}\\ {J_r^d\ddot \theta _{zr}^d + c_{rp}^d\dot p_{{\rm{rpi}}}^d\cos {\beta ^d}r_{br}^d + k_{rp}^dp_{{\rm{rpi}}}^d\cos {\beta ^d}r_{br}^d = 0} \end{array}} \right. $ | (4) |
| $ \left\{ {\begin{array}{*{20}{l}} {m_p^d\ddot y_{pi}^d - c_{rp}^d\dot p_{{\rm{rpi}}}^d\cos {\beta ^d}\cos \alpha _{{\rm{rpi}}}^d - k_{rp}^dp_{{\rm{rpi}}}^d\cos {\beta ^d}\cos \alpha _{{\rm{rpi}}}^d = 0}\\ {m_p^d\ddot x_{pi}^d + c_{rp}^d\dot p_{{\rm{rpi}}}^d\cos {\beta ^d}\sin \alpha _{{\rm{rpi}}}^d + k_{rp}^dp_{{\rm{rpi}}}^d\cos {\beta ^d}\sin \alpha _{{\rm{rpi}}}^d = 0}\\ {J_p^d\ddot \theta _{{\rm{zpi}}}^d - c_{rp}^d\dot p_{{\rm{rpi}}}^d\cos {\beta ^d}r_{bp}^d - k_{rp}^dp_{{\rm{rpi}}}^d\cos {\beta ^d}r_{bp}^d = 0} \end{array}} \right. $ | (5) |
啮合弹簧的变形量为:
| $ \begin{array}{*{20}{c}} {p_{{\rm{spi}}}^d = \left( {y_r^d - y_{pi}^d} \right)\cos \psi _{{\rm{spi}}}^d + \left( { - x_r^d + x_{pi}^d} \right) + }\\ {\left( {r_{br}^d\theta _{zr}^d - r_{bp}^d\theta _{{\rm{zpi}}}^d} \right) - e_{{\rm{rpi}}}^d} \end{array} $ | (6) |
将式(6)代入(式4)和(5),可得太阳轮—行星轮啮合对的动力学方程。
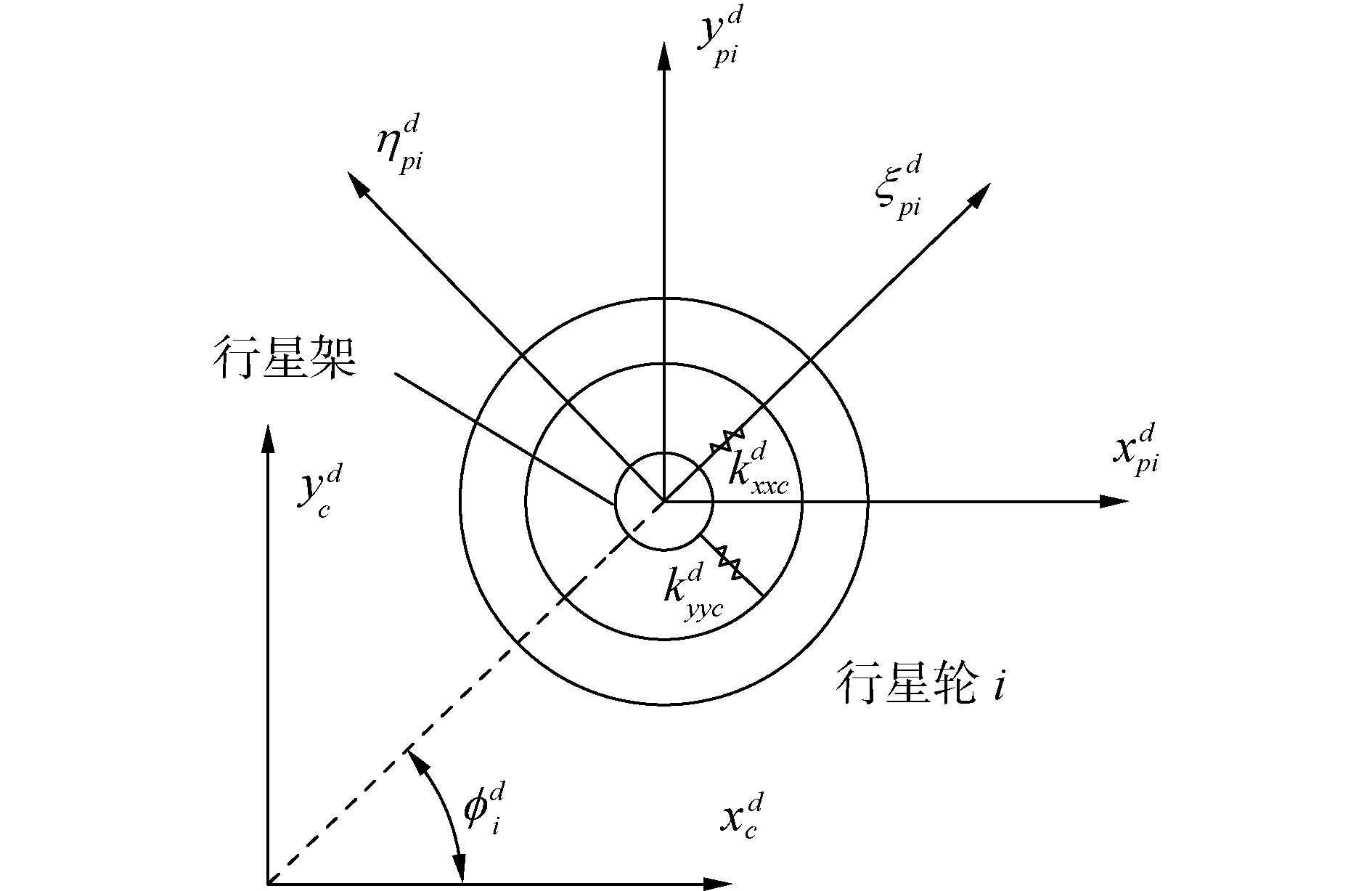
1.1.3 行星架—行星轮啮合对动力学模型行星架—行星轮耦合对动力学模型如图 4所示。
|
Download:
|
| 图 4 行星架—行星轮耦合对动力学模型 Fig. 4 Dynamic model of the coupling pair of carrier and planetary gear | |
行星架与处于任意位置ϕid的行星轮通过轴承耦合。轴承等效为2个平移刚度参数[kyypd kxxpd]和平移阻尼参数[cyypd cxxpd]。考虑到轴承参数与载荷方向有关,而通常状态下计算轴承参数的坐标系与系统定坐标系不同,因此,需要将弹簧变形量由系统定坐标系变换至图 4所示的随行星轮相位角变化的轴承坐标系ξpidOpidηpid:
| $ \left[ {\begin{array}{*{20}{l}} {\eta _i^d}\\ {\xi _i^d} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {c\phi _i^d}&{ - s\phi _i^d}\\ {s\phi _i^d}&{c\phi _i^d} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\left( {y_c^d - y_{pi}^d} \right)}&{ + r_c^d\theta _{zc}^d\cos \phi _i^d}\\ {\left( {x_c^d - x_{pi}^d} \right)}&{ - r_c^d\theta _{zc}^d\sin \phi _i^d} \end{array}} \right] $ |
通过坐标变换,可得轴承在系统定坐标系下所受的垂向力Fycpid与横向力Fxcpid为:
| $ \left[ {\begin{array}{*{20}{c}} {F_{{\rm{ycpi}}}^d}\\ {F_{{\rm{xcpi}}}^d} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {c\phi _i^d}&{s\phi _i^d}\\ { - s\phi _i^d}&{c\phi _i^d} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {k_{yyp}^d\eta _i^d + c_{yyp}^d\dot \eta _i^d}\\ {k_{xxp}^d\xi _i^d + c_{xxp}^d\dot \xi _i^d} \end{array}} \right] $ |
式中:Fycpid为通过坐标变换得到的轴承在y向所受的力;Fxcpid为轴承在x向所受的力。cxxpd、cyypd、kxxpd和kyypd为行星轮轴承横向和垂向阻尼系数和刚度系数。
得到行星架—行星轮耦合对动力学方程为:
| $ \left\{ \begin{array}{l} m_c^d\ddot y_c^d + F_{{\rm{ycpi}}}^d = 0\\ m_c^d\ddot x_c^d + F_{{\rm{xcpi}}}^d = 0\\ J_{zc}^d\ddot \theta _{zc}^d + F_{{\rm{ycpi}}}^dr_c^d\cos \phi _i^d - F_{{\rm{xcpi}}}^dr_c^d\sin \phi _i^d = {T_o}\\ m_p^d\ddot y_{pi}^d - F_{{\rm{ycpi}}}^d = 0\\ m_p^d\ddot x_{pi}^d - F_{{\rm{xcpi}}}^d = 0 \end{array} \right. $ |
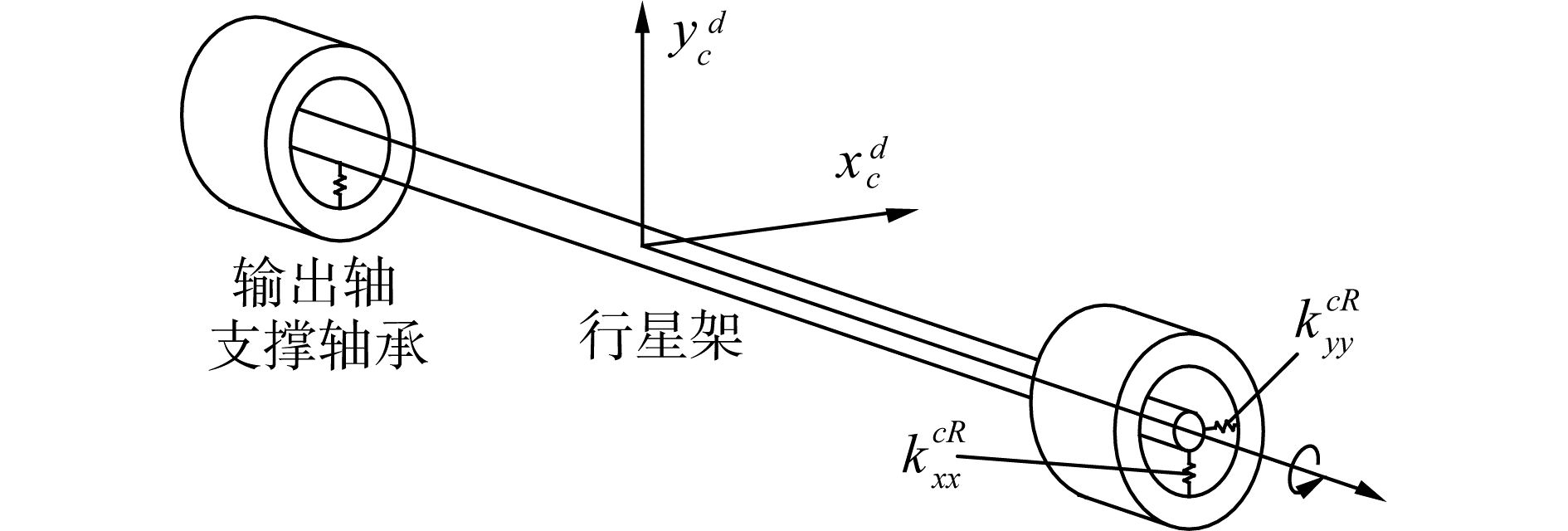
行星架支撑轴承动力学模型如图 5所示。
|
Download:
|
| 图 5 行星架—支承轴承动力学模型 Fig. 5 Dynamic model of carrier and bearings | |
将左右轴承等效为2个横向刚度和阻尼参数,在动态位移和动态速度的作用下,弹簧的受力为:
| $ \left\{ {\begin{array}{*{20}{l}} {F_{yc}^{dL} = k_{yy}^{cL}y_c^d + c_{yy}^{cL}\dot y_c^d}\\ {F_{yc}^{dR} = k_{yy}^{cR}y_c^d + c_{yy}^{cR}\dot y_c^d}\\ {F_{xc}^{dL} = k_{xx}^{cL}x_c^d + c_{xx}^{cL}\dot x_c^d}\\ {F_{xc}^{dR} = k_{xx}^{cR}x_c^d + c_{yy}^{cR}\dot x_c^d} \end{array}} \right. $ |
式中:cxxcL、cyycL、cxxcR和cyycR分别为行星架左侧和右侧轴承阻尼系数。
行星架支撑轴承的行星架的动力学方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {m_c^d\ddot y_c^d + F_{ycL}^{dL} + F_{ycR}^{dR} = 0}\\ {m_c^d\ddot x_c^d + F_{xcL}^{dL} + F_{xcR}^{dR} = 0}\\ {J_{zc}^d\ddot \theta _{zc}^d + k_{\theta zc}^d\theta _{zc}^d = 0} \end{array}} \right. $ |
基于切片法及迭代法分别求得各联轴器的刚度和阻尼矩阵如下所示。
直齿联轴器的刚度矩阵为:
| $ {K_{{\rm{spur}}}} = \frac{{\partial {F_{spur}}}}{{\partial {q_{spur}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{k_{spur}}{z_{spur}}}}{2}}&{\frac{{{T_0}}}{{2{L_{spur}}{R_{spur}}}}}&0\\ {\frac{{ - {T_0}}}{{2{L_{spur}}{R_{spur}}}}}&{\frac{{{k_{spur}}{z_{spur}}}}{2}}&0\\ 0&0&{r_{spur}^2{k_{spur}}{z_{spur}}} \end{array}} \right] $ |
直齿联轴器的阻尼矩阵为:
| $ {C_{spur}} = \frac{{\partial {F_{spur}}}}{{\partial {q_{spur}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{c_{spur}}{z_{spur}}}}{2}}&0&0\\ 0&{\frac{{{c_{spur}}{z_{spur}}}}{2}}&0\\ 0&0&{r_{bs}^2{c_{spur}}{z_{spur}}} \end{array}} \right] $ |
斜齿联轴器的刚度矩阵为:
| $ {K_{hel}} = \frac{{\partial {F_{hel}}}}{{\partial {q_{hel}}}} = \frac{{{k_{hel}}{z_{hel}}}}{4}\left[ {\begin{array}{*{20}{c}} {2c{\beta ^2}}&0&0\\ 0&{2c{\beta ^2}}&0\\ 0&0&{4r_b^2c{\beta ^2}} \end{array}} \right] $ |
斜齿联轴器的阻尼矩阵为:
| $ {C_{hel}} = \frac{{\partial {F_{hel}}}}{{\partial {q_{hel}}}} = \frac{{{c_{hel}}{z_{hel}}}}{4}\left[ {\begin{array}{*{20}{c}} {2c{\beta ^2}}&0&0\\ 0&{2c{\beta ^2}}&0\\ 0&0&{4r_b^2c{\beta ^2}} \end{array}} \right] $ |
鼓形齿联轴器的刚度矩阵为:
| $ {K_{cro}} = \frac{{\partial {F_{cro}}}}{{\partial {q_{cro}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{k_{cro}}{z_{cro}}}}{2}}&{\frac{{{T_0}}}{{2{L_{cro}}{R_{cro}}}}}&0\\ { - \frac{{{T_0}}}{{2{L_{cro}}{R_{cro}}}}}&{\frac{{{k_{cro}}{z_{cro}}}}{2}}&0\\ 0&0&{r_{cro}^2{k_{cro}}{z_{cro}}} \end{array}} \right] $ |
鼓形齿联轴器的阻尼矩阵为:
| $ {C_{cro}} = \frac{{\partial {F_{cro}}}}{{\partial {q_{cro}}}} = \left[ {\begin{array}{*{20}{c}} {\frac{{{c_{cro}}{z_{cro}}}}{2}}&0&0\\ 0&{\frac{{{c_{cro}}{z_{cro}}}}{2}}&0\\ 0&0&{r_{bc}^2{c_{cro}}{z_{cro}}} \end{array}} \right] $ |
其中,cβ2表示cos2β。
根据以上建立的动力学方程,得到了封闭差动人字齿行星传动系统在系统坐标系下的动力学方程,如下:
| $ M\mathit{\boldsymbol{\ddot q}} + C\mathit{\boldsymbol{\dot q}} + K\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{f}} $ | (7) |
式中:M为系统质量矩阵;C为系统阻尼矩阵;K为系统刚度矩阵;f为系统激励列向量,仅包括重力和输入扭矩;q为系统自由度向量,包括2个平移自由度y、x和一个轴向扭转自由度θz。
1.2 考虑齿隙及重力作用的齿轮啮合模型在空载或者轻载工况下,行星齿轮系统传递扭矩较小,因而齿轮静态啮合力相对较小。因为行星齿轮系统差动级太阳轮采用浮动布置方案,其在重力作用下,兼之齿轮间隙的影响,可能出现轮齿脱离现象。因此,本节根据行星传动系统的结构特点,考虑齿轮间隙和重力作用,建立其在空载或轻载条件下的非线性动力学模型。如图 6所示,由于齿轮间隙的影响,齿轮啮合存在三种状态:正向啮合、反向啮合和楔形啮合状态。在正常工作条件下,行星齿轮啮合对的某一侧将保持啮合状态(传递载荷),则将该状态下的啮合称之为正向啮合。与此相对应,出现另外一侧的啮合称为反向啮合,当齿轮对两侧同时进入啮合状态时,称之为楔形啮合。
|
Download:
|
| 图 6 齿轮正向啮合和反向啮合几何示意 Fig. 6 Geometric schematic of the gear forward meshing and reverse meshing | |
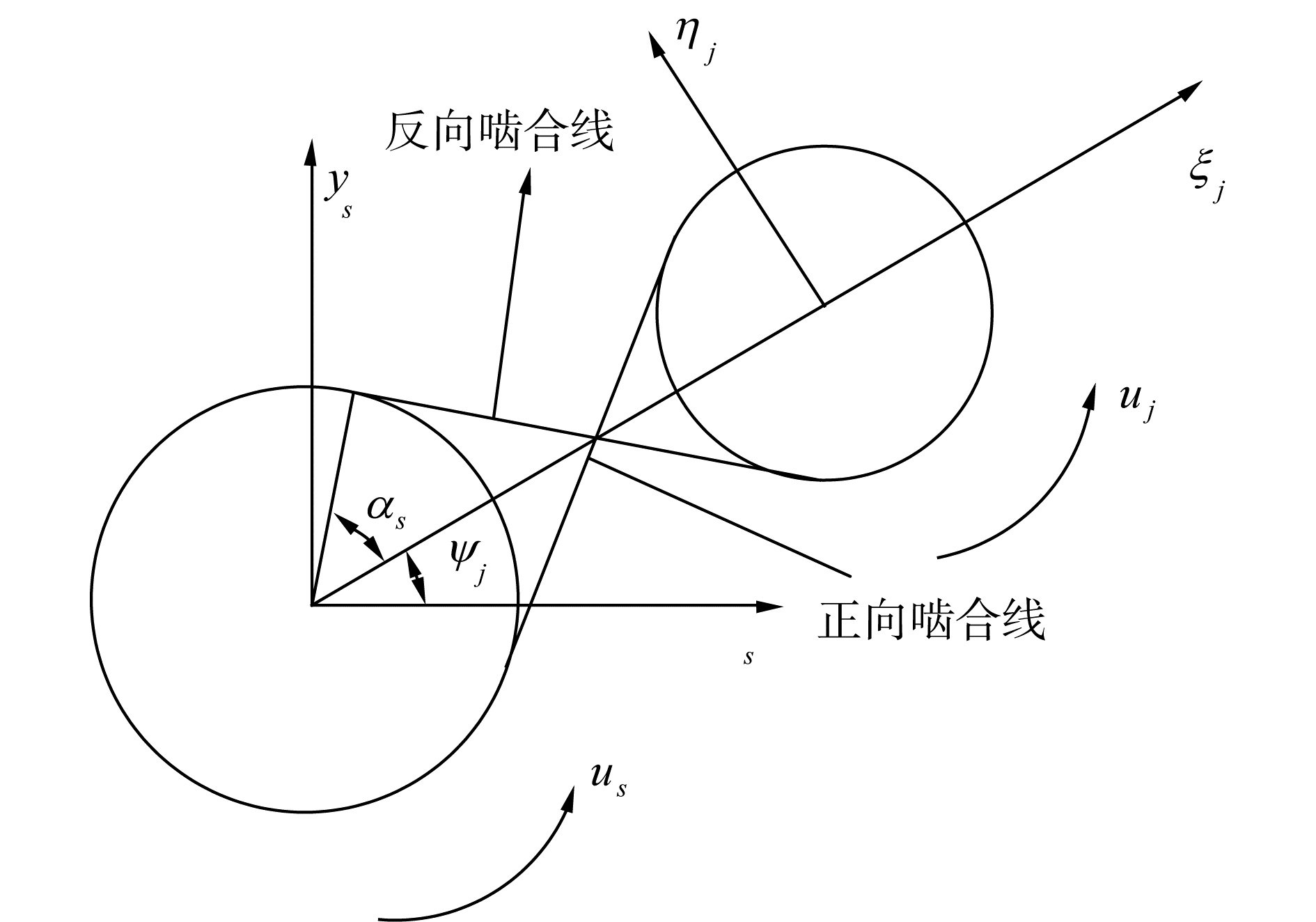
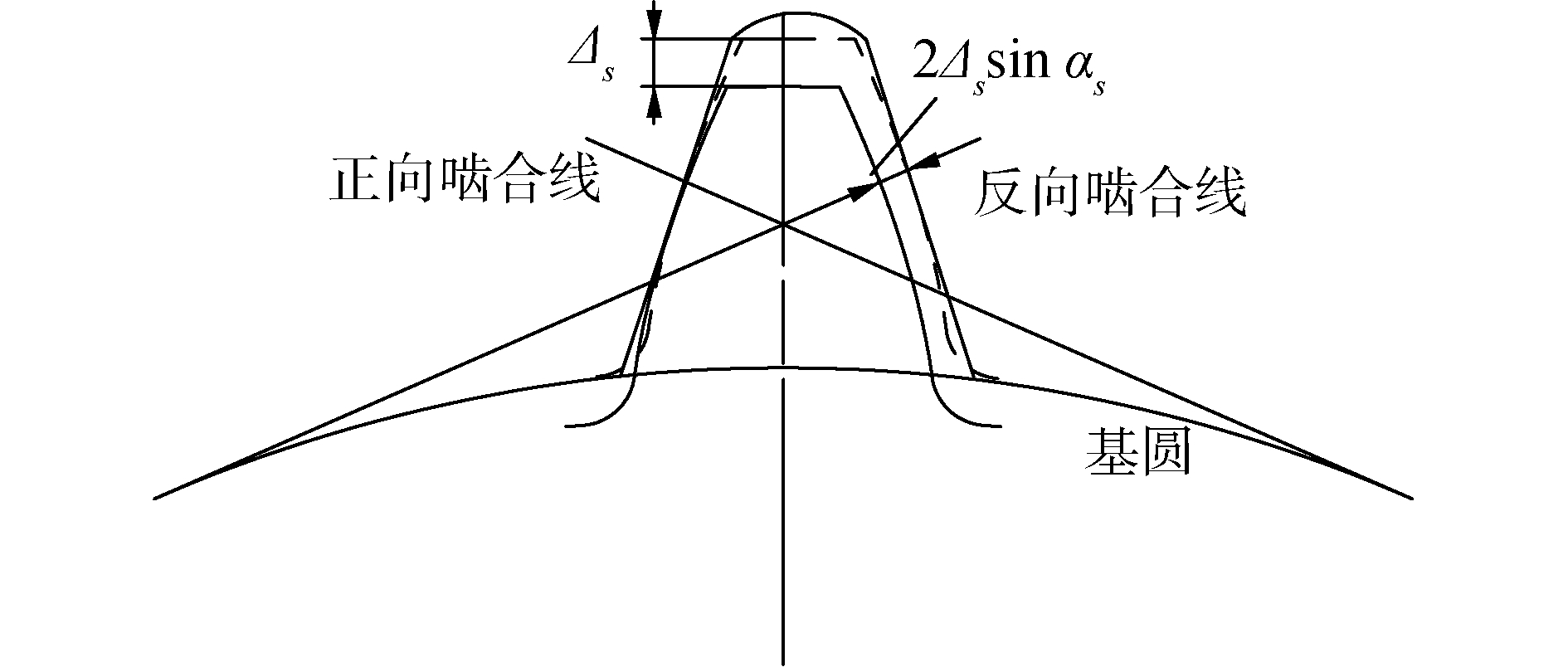
如图 7所示,对于正向啮合,定义太阳轮-行星轮啮合对、内齿圈-行星轮啮合对的正向啮合线上的变形量函数分别为:
|
Download:
|
| 图 7 太阳轮-行星轮啮合对变形量 Fig. 7 Deformation of sun gear and planetary gear meshing pair | |
| $ \begin{array}{*{20}{c}} {\delta _{sj}^d = - {x_s}\sin \psi _{sj}^d + {y_s}\cos \psi _{sj}^d - {\xi _j}\sin {\alpha _s} - }\\ {{\eta _j}\cos {\alpha _s} + {u_j} + {u_s}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\delta _{rj}^d = - {x_r}\sin \psi _{rj}^d + {y_r}\cos \psi _{rj}^d + {\xi _j}\sin {\alpha _r} - }\\ {{\eta _j}\cos {\alpha _r} - {u_j} + {u_r}} \end{array} $ |
式中:ψsjd=ψj-αs,ψrjd=ψj+αr,u为齿轮沿作用线微位移,u=rbθz。
正向啮合的作用力fqjd(q=s, r)可以表示为:
| $ f_{qj}^d = h_{qj}^dk_{qj}^d\left( t \right)\delta _{qj}^d $ |
| $ h_{qj}^d = \left\{ \begin{array}{l} 1,\;\;\;\;\;\delta _{qj}^d > 0\\ 0,\;\;\;\;\delta _{qj}^d \le 0 \end{array} \right.,j = 1,2, \cdots ,N $ |
式中hqjd是跟踪正向啮合状态的变量,即当正向啮合变形量为正值时,存在作用力;反之则作用力为零。
与正向啮合同理,定义太阳轮-行星轮啮合对、内齿圈-行星轮啮合对的反向啮合线上的变形量函数分别为:
| $ \begin{array}{*{20}{c}} {\delta _{sj}^b = {x_s}\sin \psi _{sj}^b - {y_s}\cos \psi _{sj}^b - {\xi _j}\sin {\alpha _s} + }\\ {{\eta _j}\cos {\alpha _s} - {u_j} - {u_s}} \end{array} $ |
| $ \begin{array}{*{20}{c}} {\delta _{rj}^b = {x_r}\sin \psi _{rj}^b - {y_r}\cos \psi _{rj}^b - {\xi _j}\sin {\alpha _r} + }\\ {{\eta _j}\cos {\alpha _r} + {u_j} - {u_r}} \end{array} $ |
式中:ψsjb=ψj+αs;ψrjb=ψj-αr
反向啮合的作用力fqjb(q=s, r)可以表示为:
| $ f_{qj}^b = h_{qj}^bk_{qj}^b\left( {\delta _{qj}^b - {b_q}} \right) $ |
| $ h_{qj}^b = \left\{ {\begin{array}{*{20}{l}} {1,}&{\delta _{qj}^b > {b_q}}\\ {0,}&{\delta _{qj}^b \le {b_q}} \end{array},j = 1,2, \cdots ,N} \right. $ |
式中:hqjb是跟踪反向啮合状态的变量,即当反向啮合变形量大于齿隙时,存在作用力;反之则作用力为零。bq表示齿轮间隙,齿隙定义为端平面上理想齿厚与实际齿厚之差,可依据JIS B 1703-76计算。其存在关系(如图 6所示):
| $ {\Delta _q} = {b_q}/\left( {2\tan {\alpha _q}} \right) $ |
如图 6所示,对于太阳轮-行星轮啮合对和内齿圈—行星轮啮合对,其齿轮中心距变化量δqjR(q=s, r)可表示为:
| $ \delta _{rj}^R = - {x_r}\cos {\psi _j} - {y_r}\sin {\psi _j} + {\eta _j} $ |
| $ \delta _{sj}^R = {x_s}\cos {\psi _j} + {y_s}\sin {\psi _j} - {\xi _j} $ |
计算楔形啮合时反向啮合线上的变形量,需要减去由于中心距变化引起的反向啮合线上的相应变形量,即反向啮合修正变形量δqjb, m(q=s, r)可表示为:
| $ \delta _{qj}^{b,m} = \delta _{qj}^b - 2{\Delta _q}\sin {\alpha _q} $ |
楔形啮合状态下,正向啮合力和反向啮合力可以表示为:
| $ f_{qj}^d = h_{qj}^wk_{qj}^d\left( t \right)\delta _{qj}^d,f_{qj}^b = h_{qj}^wk_{qj}^b\delta _{qj}^{b,m} $ |
| $ h_{qj}^w = \left\{ {\begin{array}{*{20}{l}} {1,}&{\delta _{qj}^R > {\Delta _q}}\\ {0,}&{\delta _{qj}^R \le {\Delta _q}} \end{array},j = 1,2, \cdots ,N} \right. $ |
式中hqjw是跟踪楔形啮合状态的变量,即当齿轮中心距变化量大于Δq时,进入楔形啮合状态。
2 系统动力学特性分析根据第一部分建立的行星齿轮系统在空载或轻载状态下的非线性动力学模型,对式(7)进行无量纲化运算,令:
| $ \tilde \omega = \sqrt {K_{sp}^d/M_{sp}^d} $ |
定义无量纲时间尺度τ和无量纲激励频率Ω:
| $ \left\{ {\begin{array}{*{20}{l}} {\tau = \tilde \omega t}\\ {\mathit{\Omega } = \omega /\tilde \omega } \end{array}} \right. $ |
令b为位移标称尺度,则无量纲位移向量:
| $ \mathit{\boldsymbol{\tilde X}}\left( \tau \right) = \frac{{X\left( {\tau /\tilde \omega } \right)}}{b} $ | (8) |
由式(8)可得:
| $ X\left( t \right) = \tilde X\left( \tau \right)b $ | (9) |
对式(9)进行微分,可得无量纲化的行星系统动力学方程为:
| $ M{\mathit{\boldsymbol{{\ddot {\tilde q}}}}} + \frac{C}{{\tilde \omega }}{\mathit{\boldsymbol{{\dot {\tilde q}}}}} + \frac{K}{{{{\tilde \omega }^2}}}{\mathit{\boldsymbol{{\tilde q}}}} = \frac{{\mathit{\boldsymbol{{f}}}}}{{b{{\tilde \omega }^2}}} $ | (10) |
采用无条件收敛且具有较高精度的Newmark-β法求解式(10)可得输出轴的振动响应特性,系统参数详见表(1),取系统输入轴扭矩Ti=1 000 N·m,输出轴转频fo=1.8 Hz时,计算分析输出轴的垂向振动响应特性,并计算差动级行星轮个数对输出轴垂向振动特性的影响。
| 表 1 系统参数表 Table 1 System parameter table |
式中,差动级的啮合刚度参数为kspd=2.67×109 N·m,kspd=2.93×109 N·m。封闭级的啮合刚度参数为kspc=4.28×109 N·m,krpc=4.51×109 N·m。联轴器的啮合刚度参数为:kcc1=3.22×108 N·m,kcc2=3.96×108 N·m,kcc3=2.92×108 N·m,kcc4=4.08×108 N·m,kcc5=4.89×108 N·m。差动级行星轮个数为3,封闭级行星轮个数为5。
2.1 轻载时系统输出轴振动特性分析当差动级行星轮个数为3时,考虑行星系统差动级太阳轮采用浮动布置方案,且系统处于空载或轻载工况时,行星齿轮系统传递扭矩较小,导致齿轮静态啮合力相对较小。在重力作用下,考虑齿轮间隙的影响,可能出现轮齿脱离现象。即系统动力学方程中(如式20所示),激励向量仅考虑重力和传递的扭矩。此状态下,考虑1.2节所示的齿轮脱离方程,通过求解封闭差动人字齿行星传动系统动力学方程,得到输出轴的无量纲垂向振动位移

|
Download:
|
| 图 8 Ti=1 000 N·m, Nd=3时,输出轴的垂向响应特性 Fig. 8 Vertical response characteristics of the output axis when Ti=1 000 N·m, Nd=3 | |
图 9所示为差动级行星轮个数为4时,得到输出轴的无量纲垂向振动响应特性。由图 9可见,当系统处于空载或轻载工况时,由于齿轮重力及间隙的影响,输出轴存在输入轴转频的4倍频及其谐频的频率响应成分。

|
Download:
|
| 图 9 Ti=1 000 N·m, Nd=4时,输出轴的垂向响应特性 Fig. 9 Vertical response characteristics of the output axis when Ti=1 000 N·m, Nd=4 | |
当差动级行星轮个数提高到5个,行星传动系统处于轻载状态下,得到输出轴的垂向振动响应特性如图 10所示,此时输出轴存在输入轴转频的5倍频及其谐频的频率响应成分。

|
Download:
|
| 图 10 Ti=1 000 N·m, Nd=5时,输出轴的垂向响应特性 Fig. 10 Vertical response characteristics of the output axis when Ti=1 000 N·m, Nd=5 | |
由图 8至图 10所示的计算结果可得:当行星传动系统处于空载或轻载工况时,系统输出轴存在输入轴转频的倍频及其谐频的频率响应成分,频率的倍数与差动级行星轮个数相等。这是因为行星传动系统在此状态下齿轮静态啮合力相对较小,且行星齿轮系统差动级太阳轮采用浮动布置方案,在重力作用及齿轮间隙的影响下,出现了轮齿脱离现象。
2.2 重载时系统输出轴振动特性分析提高输入轴扭矩,使行星传动系统处于重载条件下,此时取输入轴扭矩,取差动级行星轮个数为3,考虑齿轮重力和间隙的影响,计算行星传动系统处于重载运行工况时输出轴的垂向振动响应,计算结果如图 11所示。由图 11可得,当行星传动系统处于重载工况时,即使考虑齿轮重力和间隙的影响,系统输出轴的振动响应特性也不含有输入轴的倍频及其谐频的频率响应成分,因为在重载工况下,齿轮的静态啮合力较大,行星齿轮系统不会出现轮齿脱离现象。即,在重载工况下,可忽略齿轮重力和间隙对系统振动响应的影响。

|
Download:
|
| 图 11 Ti=1×105 N·m, Nd=3时,输出轴的垂向响应特性 Fig. 11 Vertical response characteristics of the output axis when Ti=1×105 N·m, Nd=3 | |
1) 当差动级太阳轮采用浮动布置方案时,在空载或者轻载工况下,行星齿轮系统传递扭矩较小,齿轮静态啮合力相对较小,在重力作用及齿轮间隙的影响下,会出现轮齿脱离现象,导致输出轴产生输入轴的多倍频及其谐频的频率响应成分。
2) 当系统输入扭矩较小时,行星齿轮系统产生的倍频成分和差动级行星轮个数有直接关系,当行星轮个数为N时,系统会产生输入轴的N倍频及其谐频的频率响应成分。当输入扭矩增大时至重载时,输出轴的倍频响应成分消失。
3) 在实际运行过程中,行星齿轮系统应尽量避免空载或轻载工况,以降低系统的振动,降低传动噪音,提高行星减速器系统的稳定性。
| [1] |
KAHRAMAN A. Planetary gear train dynamics[J]. Journal of mechanical design, 1994, 116(3): 713-720. DOI:10.1115/1.2919441 (  0) 0)
|
| [2] |
朱增宝, 朱如鹏, 鲍和云, 等. 偏心与齿频误差对封闭差动人字齿轮传动系统动态均载特性的影响分析[J]. 航空动力学报, 2011, 26(11): 2601-2609. ZHU Zengbao, ZHU Rupeng, BAO Heyun, et al. Impact of run-out and meshing-frequency errors on dynamic load sharing for encased differential herringbone train[J]. Journal of aerospace power, 2011, 26(11): 2601-2609. (  0) 0)
|
| [3] |
朱增宝, 朱如鹏, 王传礼, 等. 封闭差动人字齿轮传动系统均载及动力学特性分析研究[M]. 北京: 国防工业出版社, 2015.
(  0) 0)
|
| [4] |
蒋立冬, 王冀, 岳彦炯, 等. 功率分流人字齿行星传动系统的固有特性研究[J]. 机械传动, 2013, 37(12): 54-58. JIANG Lidong, WANG Ji, YUE Yanjiong, et al. Study on the intrinsic characteristic of power split double helical tooth planetary transmission system[J]. Journal of mechanical transmission, 2013, 37(12): 54-58. (  0) 0)
|
| [5] |
SONDKAR P, KAHRAMAN A. A dynamic model of a double-helical planetary gear set[J]. Mechanism and machine theory, 2013, 70: 157-174. DOI:10.1016/j.mechmachtheory.2013.07.005 (  0) 0)
|
| [6] |
AJMI M, VELEX P. A model for simulating the quasi-static and dynamic behaviour of solid wide-faced spur and helical gears[J]. Mechanism and machine theory, 2005, 40(2): 173-190. DOI:10.1016/j.mechmachtheory.2003.06.001 (  0) 0)
|
| [7] |
VELEX P, MAATAR M. A mathematical model for analyzing the influence of shape deviations and mounting errors on gear dynamic behaviour[J]. Journal of sound and vibration, 1996, 191(5): 629-660. DOI:10.1006/jsvi.1996.0148 (  0) 0)
|
| [8] |
沈稼耕.计入啮合相位的人字齿行星齿轮系统动力学研究[D].南京: 南京航空航天大学, 2014. SHEN Jiageng. Research on dynamics of herringbone planetary gear trains based on mesh phasing[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D565803 (  0) 0)
|
| [9] |
张丽娜.功率分流式行星齿轮传动系统建模及动态特性研究[D].济南: 山东大学, 2017. ZHANG Li'na. Modeling and dynamic behavior analysis of the power-split planetary gear train[D]. Jinan: Shandong University, 2017 http://cdmd.cnki.com.cn/Article/CDMD-10422-1017079722.htm (  0) 0)
|
| [10] |
陈国辉.舰船用两级封闭差动轮系动力学特性分析[D].哈尔滨: 哈尔滨工业大学, 2015. CHEN Guohui. Research on two stage differential planetary gear train used in ship[D]. Harbin: Harbin Institute of Technology, 2015. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


