多机器人任务分配和路径规划是多机器人系统研究的核心问题之一,它是多机器人系统应用的基础[1-4]。目前有关多机器人任务分配的研究成果已有不少[5-12],然而这些研究并没有考虑到现实任务分配的环境中存在障碍物的情况。基于多机器人任务分配与自组织神经网络的相似性原理,许多学者将自组织神经网络应用到多机器人任务分配中。自组织神经网络算法[13-16]由Kohonen[14]于20世纪80年代提出,这类算法主要应用于对输入层的输入数据进行分类。之后,许多学者将这类算法应用到了多机器人任务分配中。文献[17-19]采用SOM实现在无障碍物的二维平面下多水下机器人(autonomous underwater vehicle, AUV)任务分配与路径规划。文献[20]将SOM与旅行商问题相结合,有效地将SOM应用到无人水面艇(unmanned surface vessel, USV)的多任务分配和路径规划中,提出的算法能够保证USV以较少的消耗在避开障碍物的情况下遍历所有任务的情况。文献[21]将SOM算法与栅格信度函数相结合,有效地实现了三维自主水下机器人的任务分配和路径规划。
综合以上,目前多机器人系统任务分配需要解决以下问题:1)在二维的工作空间中不存在障碍物,因此多机器人的任务分配算法不具备实际效益;2)没有考虑机器人移动的方向角问题,在实际环境中原始的SOM算法直接使用机器人的当前位置与环境中目标位置的偏差来规划机器人的路径,这可能会出现横穿障碍物的情况,以至于机器人无法到达相对应的任务目标点,从而无法顺利完成任务分配。
本文针对以上问题,通过引入矢量方向对传统的SOM算法进行改进,提出了一种更加实用可行的多机器人任务分配与路径规划算法,机器人利用矢量方向成功的避开了环境中的障碍物,在克服可能横穿障碍物问题的同时成功进行了任务分配。改进后的VDSOM算法能够很好地适应具有障碍物的环境,具有较强的实用性与自适应性。
1 基于改进的SOM的多机器人任务分配和路径规划在多机器人系统中,经常会遇到多个机器人之间的协调、合作问题。无论从单个机器人角度出发,还是从多个机器人角度出发,多任务分配研究的主要问题是在完成所分配任务的前提下消耗的能量最少。多机器人任务分配和路径规划是研究如何有效地分配任务目标,以便于移动机器人能够沿着较优的路径访问在有障碍物的工作区域内的所有目标。多机器人系统任务分配的目标是区域内的所有任务目标点都有对应的机器人访问,且总代价尽可能小。对于单个机器人而言,代价是由从起始点到其所经过的所有目标点的距离来衡量,而对于整个多机器人系统而言,代价是所有单个机器人代价的总和。为了完成对工作区域中所有目标的访问,首先是考虑将任务目标分配给不同的移动机器人;其次,在完成任务分配后要进行路径规划,由于工作区域内存在障碍物,因此每个机器人都必须具有避障的能力;最后,在移动到相应目标的过程中移动机器人需要智能地调整运动方向,进而保证每个机器人的路径规划都能实现。任务分配完成的标准为所有的任务即目标点都被机器人访问过。为了简化描述,将工作空间用二维平面表示,在这个工作空间中随机分布一定数量的障碍物、移动机器人、任务目标点。这里假设移动机器人的所有性能相同,即具备相同的导航、避障、位置识别功能,且所有机器人的能量储备相同,能量消耗速率也相同。因此,只需要研究如何进行任务分配即可,即如何应用VDSOM进行多机器人任务分配,并使其总工作量最小。
假设工作区域内随机分布K=(1, 2, …, K)台机器人和M=(1, 2, …, M)个任务,图 1所示的多机器人系统的SOM模型有两层神经元:1)输入层包含所有的任务目标点,共有M个,所有任务目标点的坐标依次排列以构成神经网络的输入数据集合;2)竞争层共包括KM个神经元,若工作区域用W表示,则这KM个神经元的表示为(W11, W12, …, W1M, WK1, WK2, …, WKM),代表着K台机器人的坐标和相对应的运动轨迹。由于共有M个任务目标点和K台机器人,故机器人将这M个任务的分配和路径规划的结果分成K组。输出神经元的初始权值是由机器人的初始位置坐标来初始化。任务分配完成后,M个任务目标点从KM个输出神经元中选出M个神经元,即共有M个获胜神经元,且这M个获胜神经元是由K台机器人组成。因此,K台机器人形成了K条路径,从起始位置出发,经过若干个目标,最终K台机器人访问的目标和为M个。
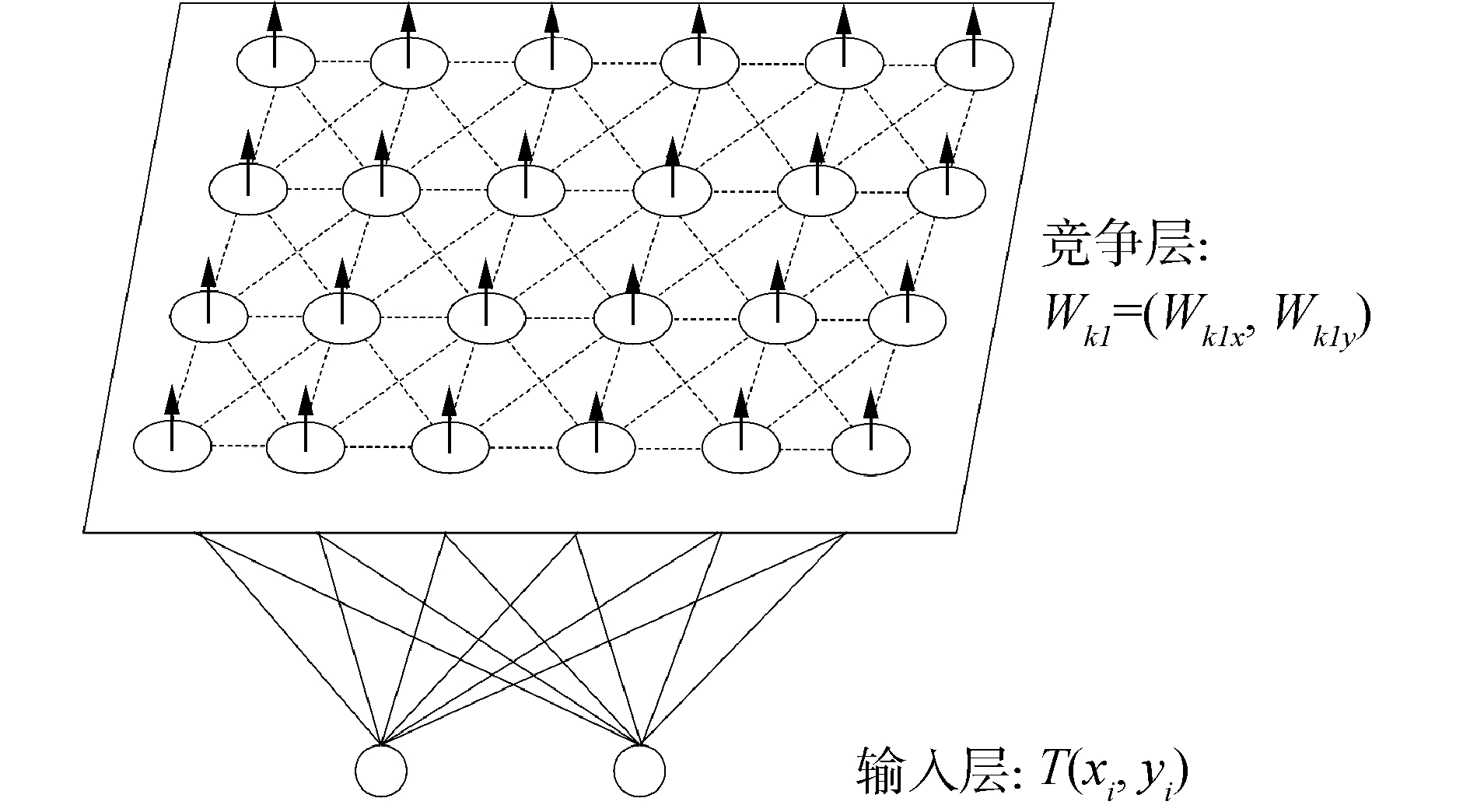
|
Download:
|
| 图 1 SOM神经网络 Fig. 1 SOM neural network diagram | |
在SOM神经网络中,输入层的输入数据为任务目标点的坐标,输入数据用Ti=(xi, yi)表示。Wkm=(wkmx, wkmy)是输出神经元的位置坐标(其中k=1, 2, …, K; m=1, 2, …, M)。[Nk, Nm]表示从第k组输出神经元中选出的第m个神经元是获胜神经元:
| $ \begin{array}{l}{\left[N_{k}, N_{m}\right] \Leftarrow \min \left\{D_{ikm}, i=1, 2, \cdots, M\right.} \\ {k=1, 2, \cdots, K, m=1, 2, \cdots, M \&\& \{k, m\} \in U\}}\end{array} $ | (1) |
式中:U表示在一次迭代中没有成为获胜者的神经元集;Dikm表示的是某一时刻某2个神经元之间的加权距离:
| $\begin{array}{c}{D_{i k m}=\left|T_{i}-W_{k m}\right|(1+L)=} \\ {\sqrt{\left(x_{i}-w_{k m x}\right)^{2}+\left(y_{i}-w_{k m y}\right)^{2}}(1+L)=} \\ {\sqrt{\left(x_{i}-w_{k m x}\right)^{2}+\left(y_{i}-w_{k m y}\right)^{2}}\left(\frac{S_{i}-\bar{s}}{1+\bar{s}}\right)}\end{array} $ | (2) |
式中:
当获胜神经元被选出后,下一步是设计邻域函数,进而确定下一次的获胜神经元。邻域函数的作用是确定获胜神经元和邻域神经元之间的影响,获胜神经元受到的影响力即强度越大,与获胜神经元相邻的神经元所受到的影响力就越低,直到没有影响。如果没有影响,则说明该神经元已非获胜神经元的邻域神经元,即称为非邻域神经元。在工作区域内,获胜神经元的邻域是一个圆形,其圆心的坐标是获胜神经元的位置坐标,随着更新迭代的过程,圆心一直在变化,直到该获胜神经元到达了与其相对应的任务目标点。优胜邻域函数如下:
| $ f(E, h)=\left\{\begin{array}{ll}{E^{2} / H^{2}(t), } & {E<\lambda} \\ {0, } & {其他}\end{array}\right. $ | (3) |
式中:f(E, h)∈[0, 1];E代表邻域内获胜神经元m与其他神经元之间的距离;Em(t)代表获胜神经元m的优胜邻域;γ是邻域半径;H(t)=εtH0;t为迭代次数;ε是变化率;ε越大,总的计算时间便越长,故而机器人运动的总路径就越短,H0是一个常数。
1.1.3 权值修改在获胜神经元以及其优胜邻域确定后,获胜神经元(获胜的机器人)和其邻居神经元(在领域半径内的其余机器人)需要向与获胜神经元对应的输入神经元(任务目标点)运动。将这个运动的过程映射到SOM网络,不仅是在SOM学习的过程中不断地调整权值的坐标进而将目标合理地分配给机器人,并为每个机器人规划出一条路径。权值的更新规则为:
| $ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ W_{k m}(t)=\\ \left\{\begin{array}{ll}{T_{i}, } & {D_{i k m} \leqslant D_{0}} \\ {W_{k m}(t-1)+\eta \mathrm{e}^{-f}\left(T_{i}-W_{k m}(t-1)\right), } & {D_{i k m}>D_{0}}\end{array}\right. $ | (4) |
D0是一个常数也是一个终止条件,若Dikm∈D0则认为输出神经元的权值(机器人)已经到达了其任务目标点,将该机器人的坐标置为其相对应的任务目标点的坐标。学习率η的一般规律为:
| $t \uparrow \rightarrow \eta \downarrow $ | (5) |
为了克服传统的SOM算法的缺点,使移动机器人能够自动避开障碍物,引入矢量方向的概念对传统的SOM权值进行调节,提出了一种矢量方向自组织映射算法VDSOM。机器人需要确定一个策略,以帮助在避开环境中障碍物的情况下到达任务目标点。
1.2.1 基于VD的路径规划假设机器人从当前位置出发,可到达其相邻的8个位置中的一个位置,8个位置基于8个方向,方向包括东(E)、东南(NE)、南(N)、西南(NW)、西(W)、西北(SW)、北(S)和东北(SE)。在环境中,机器人的位置可以看成是一个统一的网格,通过这样一种表示方法,障碍物是机器人不能到达的单元,而剩余单元机器人均可访问。图 2为机器人可以移动的下一个区域的方向。
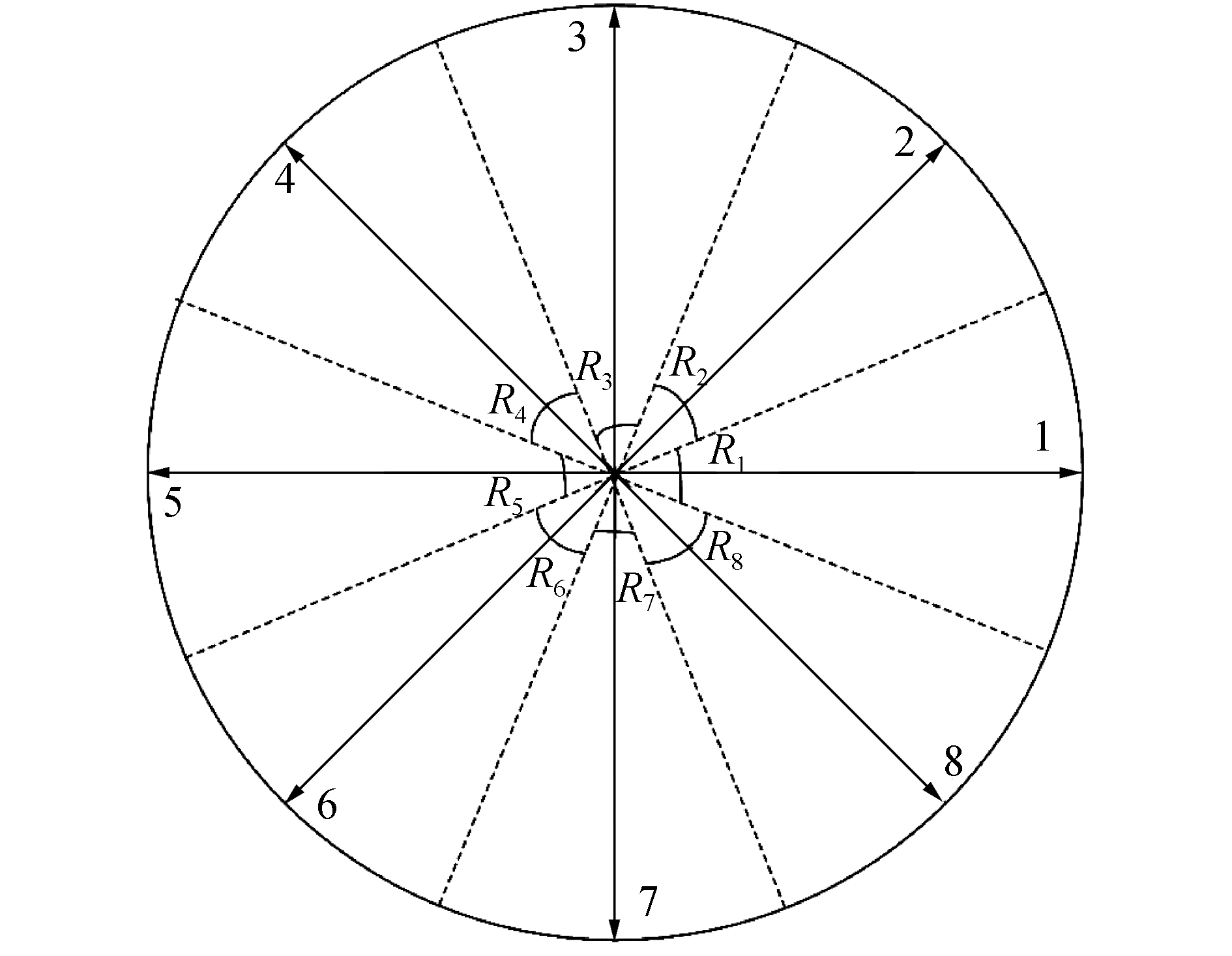
|
Download:
|
| 图 2 机器人可选的下个区域的方向 Fig. 2 The direction of the next area that the robot can select | |
假设Wk1=(wk1x, wk1y)为机器人当前所处的位置,则机器人从当前位置到其对应的目标位置的矢量为Wk1Ti,其移动方向角θ由下式给出:
| $ \theta=\arctan \frac{y-w_{k 1 y}}{x-w_{k 1 x}} $ | (6) |
若成功到达其对应的任务目标点,则θ=NaN。
由于假设机器人从当前位置出发,下一个位置可由8个方向选择,因此将区间R=(-π, π]平分为8个区间为:
| $ R = \left\{ {\begin{array}{*{20}{l}} {{R_1} = ( - {\rm{ \mathsf{ π} }}/8, {\rm{ \mathsf{ π} }}/8]}\\ {{R_2} = ({\rm{ \mathsf{ π} }}/8, 3{\rm{ \mathsf{ π} }}/8]}\\ {{R_3} = (3{\rm{ \mathsf{ π} }}/8, 5{\rm{ \mathsf{ π} }}/8]}\\ {{R_4} = (5{\rm{ \mathsf{ π} }}/8, 7{\rm{ \mathsf{ π} }}/8]}\\ {{R_5} = (7{\rm{ \mathsf{ π} }}/8, {\rm{ \mathsf{ π} }}] \cup ( - {\rm{ \mathsf{ π} }}, - 7{\rm{ \mathsf{ π} }}/8]}\\ {{R_6} = ( - 7{\rm{ \mathsf{ π} }}/8, - 5{\rm{ \mathsf{ π} }}/8]}\\ {{R_7} = ( - 5{\rm{ \mathsf{ π} }}/8, - 3{\rm{ \mathsf{ π} }}/8]}\\ {{R_8} = ( - 3{\rm{ \mathsf{ π} }}/8, - {\rm{ \mathsf{ π} }}/8]} \end{array}} \right. $ | (7) |
这8个动作形成了一组矢量集,用A(w)表示坐标w处可选择的矢量集,矢量集选择规则为:
| $\boldsymbol{A}(\boldsymbol{w})=\left\{\boldsymbol{d}_{1}, \boldsymbol{d}_{2}, \boldsymbol{d}_{3}, \boldsymbol{d}_{4}, \boldsymbol{d}_{5}, \boldsymbol{d}_{6}, \boldsymbol{d}_{7}, \boldsymbol{d}_{8}\right\} $ | (8) |
与矢量d1、d2、d3、d4、d5、d6、d7、d8相对应的机器人的移动方向为E、NE、N、NW、W、SW、S和SE,其表示如图 2。在图 2中每个方向角对应一个矢量标号,故机器人的方向选择规则为,首先判断由式(6)所得的方向角θ属于式(7)的哪个区域角,其次通过式(8)选择对应的矢量标号,最后通过标号对应的方向确定下一步行驶方向。如果根据以上步骤,机器人不能顺利到达目标,即机器人碰到障碍物,则修改θ,修改公式为:
| $ \theta=\theta+\beta \frac{\pi}{4}, \beta \in[-3, 4] 且 \beta \in Z $ | (9) |
其中θ的修改规则为:
1) 若机器人的移动方向为矢量d1,则β=0;
2) 若机器人遇到障碍物且其任务目标位于障碍物的左上方,则判断机器人当前位置到障碍物上方最高点的矢量角属于式(7)中哪个区间。若属于R2则机器人移动方向为矢量d2,即β=1,若属于R3则机器人移动方向为矢量d3,β=2;
3) 其余障碍物方向同理2),只需改变相对应的β即可。
在运动方向确定后,估算出机器人的下一个位置坐标Gi。假设2个横向单元间的距离为c(c为一常数),下一位置坐标Gi如下:
| $ {G_i} = \left\{ \begin{array}{l} \left( {\left( {{w_{k1x}} + c} \right), {w_{k1y}}} \right), 移动方向为矢量{\mathit{\boldsymbol{d}}_1}\\ \left( {\left( {{w_{k1x}} + c} \right), \left( {{w_{k1y}} + c} \right)} \right), 移动方向为矢量{\mathit{\boldsymbol{d}}_2}\\ \left( {{w_{k1x}}, \left( {{w_{k1y}} + c} \right)} \right), 移动方向为矢量{\mathit{\boldsymbol{d}}_3}\\ \left( {\left( {{w_{k1x}} - c} \right), \left( {{w_{k1y}} + c} \right)} \right), 移动方向为矢量 {\mathit{\boldsymbol{d}}_4}\\ \left( {\left( {{w_{k1x}} - c} \right), {w_{k1y}}} \right), 移动方向为矢量{\mathit{\boldsymbol{d}}_5}\\ \left( {\left( {{w_{k1x}} - c} \right), \left( {{w_{k1y}} - c} \right)} \right), 移动方向为矢量{\mathit{\boldsymbol{d}}_6}\\ \left( {{w_{k1x}}, \left( {{w_{k1y}} - c} \right)} \right), 移动方向为矢量{\mathit{\boldsymbol{d}}_7}\\ \left( {\left( {{w_{k1x}} + c} \right), \left( {{w_{k1y}} - c} \right)} \right., 移动方向为矢量{\mathit{\boldsymbol{d}}_8} \end{array} \right. $ | (10) |
式中:c一般取0.5。
将工作区域离散化后,路径规划问题就演变成为寻找机器人的下一个行驶位置,只有准确找到这个位置,才能使机器人自主规划出一条切实可行的无碰撞路径。如图 3所示为VDSOM算法中路径规划部分的流程图。
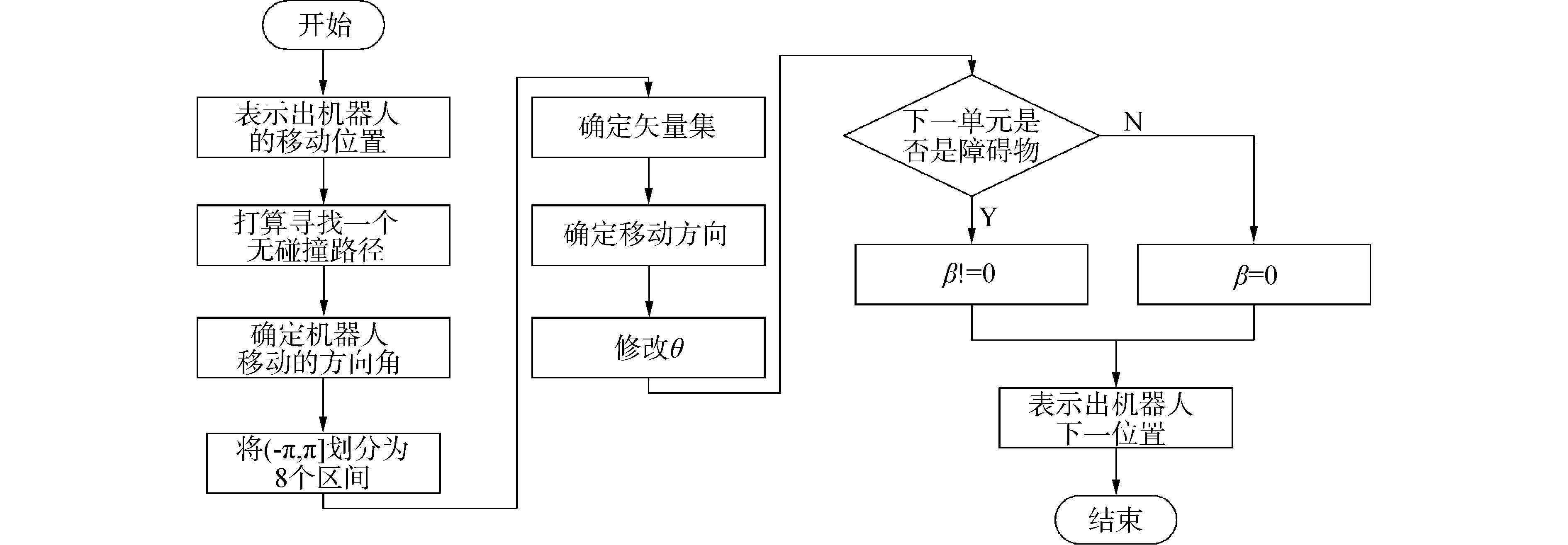
|
Download:
|
| 图 3 基于VD的路径规划 Fig. 3 Detailed flow chart of path planning based on VD | |
在获胜神经元以及其优胜领域确定后,获胜神经元(获胜的机器人)和其邻居神经元(在领域半径内的其余机器人),需要向与获胜神经元对应的输入神经元(任务目标点)运动。将这个运动的过程映射到VDSOM网络,旨在VDSOM学习的过程中不断地调整权值的坐标,由于权值即为移动机器人的坐标,故而权值的改变即对应机器人位置的改变。权值的更新规则如下:
| $ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ W_{k m}(t)=\\ \left\{\begin{array}{ll}{T_{i}, } & {D_{ikm} \leqslant D_{0}} \\ {W_{t m}(t-1)+\eta \mathrm{e}^{-f}\left(G_{i}-W_{km}(t-1)\right), } & {D_{ikm}>D_{0}}\end{array}\right. $ | (11) |
1) 初始化数据,对竞争层也就是输出层的各神经元权重随机赋值,在输入层中输入任务目标点的坐标,并建立初始化优胜领域Em(0),之后给学习率和变化率赋初值,VDSOM网络形成;
2) 判断是否仍有未输入到VDSOM网络的任务目标点;
3) 如果有,转到步骤4;否则,转到步骤5;
4) 随机地将第Ti个目标输入进VDSOM网络;
5) 竞争确定获胜神经元m(即寻找到一个获胜机器人),通过式(1)、(2)确定获胜神经元(机器人);
6) 计算邻域函数,定义优胜邻域Em(t),以m为中心,确定t时刻的权值调整域。通常初始邻域Em(0)较大,Em(t)随着t的增大而逐渐缩小,从而确定最终第t次迭代的优胜邻域Em(t)。图 4所示为邻域的收缩过程。
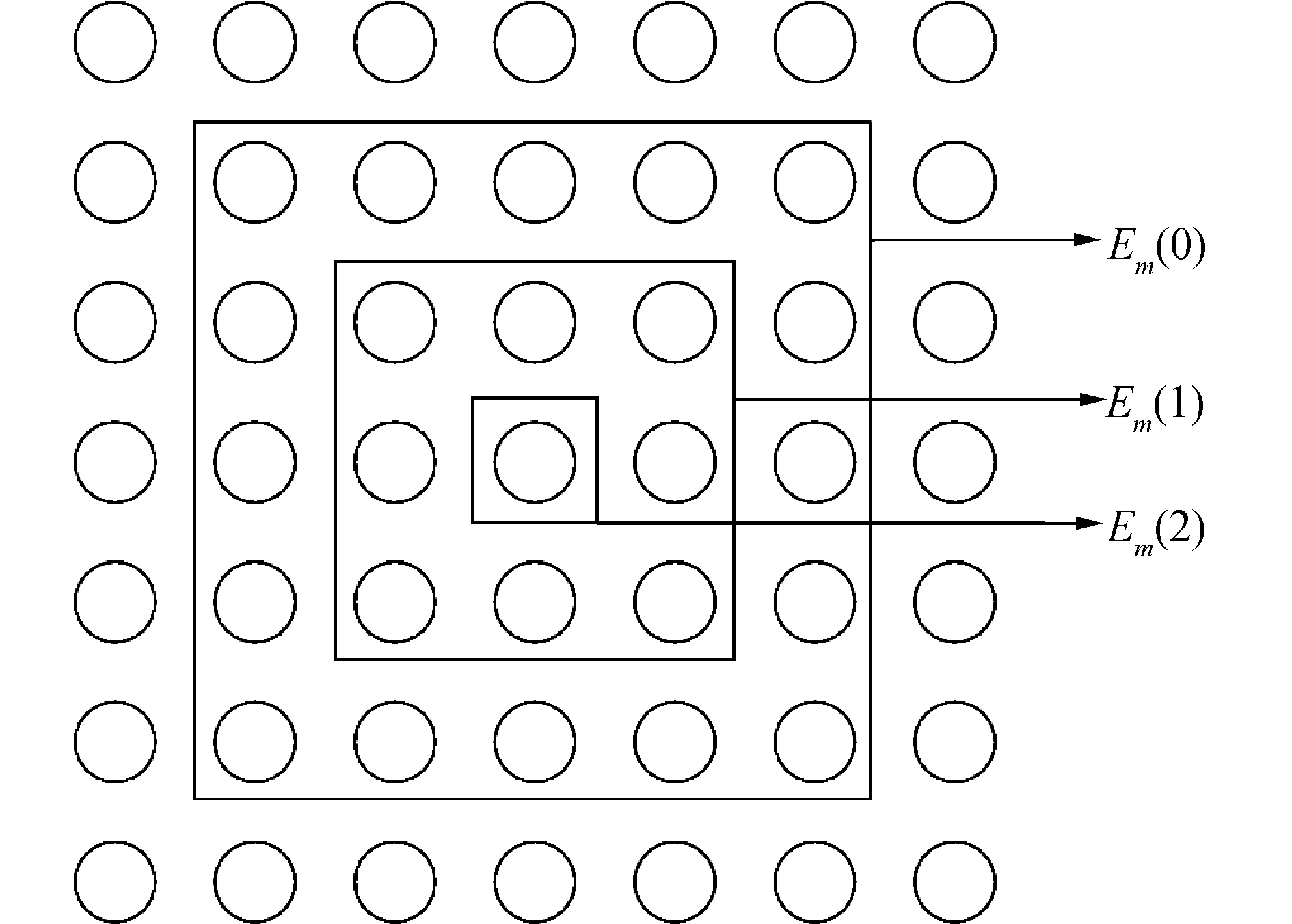
|
Download:
|
| 图 4 优胜邻域收缩 Fig. 4 Winning neighborhood shrinkage diagram | |
7) 确定优胜邻域内获胜神经元的邻居神经元;
8) 使用VD方法进行路径规划,优胜邻域内的所有神经元向对应任务目标点移动一定距离;
9) 修改获胜者及其邻居权重值;
10) 判断权值是否改变;
11) 若权值发生改变,转到步骤2;否则,转到步骤12;
12) 分配任务结束。
2 仿真实验分析障碍物、目标点和机器人随机地分布在仿真实验环境中。机器人都用菱形表示,不考虑其真实的形状和大小,并且假设每个机器人都是相同的,且机器人配备必须的传感器以识别障碍物。采用圆形表示任务目标点而障碍物则用正方形表示。具体算法设计中,取参数ε=0.1,学习率η=0.5,邻域半径γ=3。ε和η为0~1之间的常数,由于本文主要研究VDSOM算法在多机器人任务分配与路劲规划中的应用,并没有深入研究参数对于VDSOM的效率的影响,因此主要通过选取不同的参数进行试验,多次仿真试验后,选取ε=0.1,η=0.5,虽然这个参数的选择并不一定是最优,但是这并不影响任务分配的结果。由于本文竞争层的机器人个数在15以内,所以选择邻域半径γ=2。
2.1 机器人与目标数量相同图 5所示为机器人与目标数量相同时,多机器人系统任务分配与路径规划的过程。图 5(a)为初始状态,在工作区域x∈[0, 80]、y∈[0, 80]中分别随机地分布11个移动机器人和任务目标点,任务分配完成后所有的任务目标点均有机器人访问。如图 5(b)所示,此时系统已处于稳定状态。
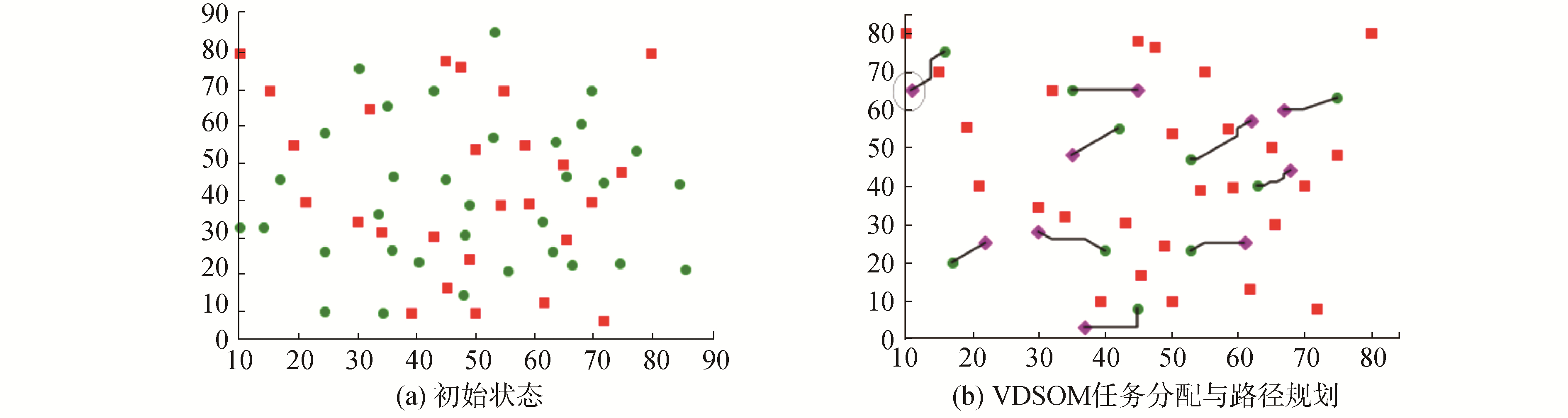
|
Download:
|
| 图 5 机器人与目标数量相同的任务分配与路径规划 Fig. 5 Task allocation and path planning with the same number of robot and target | |
与传统的SOM算法比较,本文所提出的VDSOM算法能够在成功避开障碍物的情况下将每次迭代的移动方向角表示出来。表 1表示图 5(b)中虚线圈中的机器人使用SOM和VDSOM到达任务目标点的移动方向角的对比数据。
| 表 1 1对1时SOM与VDSOM的移动方向偏移角的比较 Table 1 Comparison of the moving direction offset angles of SOM and VDSOM in 5(b) |
从数据的对比情况可知,如果使用传统的SOM算法,机器人在迭代10次后会与障碍物发生碰撞继而无法到达对应的目标点。而本文所提出的VDSOM算法具备避障功能,能避过障碍物成功到达对应的任务目标点。
2.2 机器人数量少于目标数量图 6(a)为初始状态,在工作区域x∈[0, 90]、y∈[0, 90]中分别随机地分布4个移动机器人和33个任务目标点,任务分配完成后所有的任务目标点均有机器人访问。如图 6(b)所示,此时系统已处于稳定状态。通过使用VDSOM算法对4个机器人进行任务分配与路径规划,4个机器人最终自组织地到达各自的目标点,且总能耗最小。
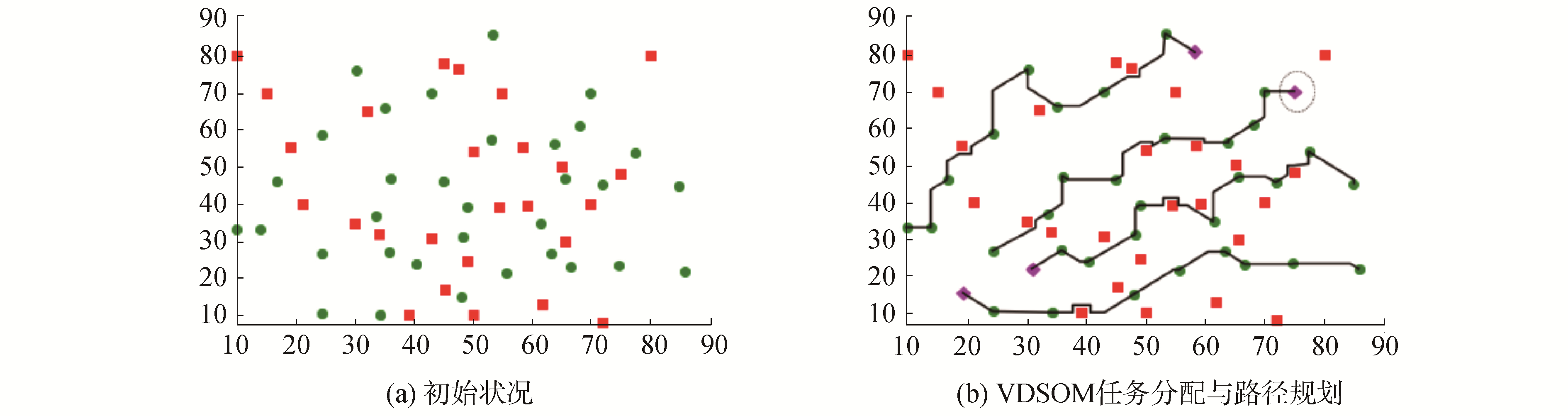
|
Download:
|
| 图 6 机器人与目标数量不同时的任务分配与路径规划 Fig. 6 Task allocation and path planning with different number of robot and target | |
同样,表 2表示图7(b)中虚线圈中的机器人使用SOM和VDSOM到达任务目标点的移动方向角的对比数据可知,如果使用传统的SOM算法,机器人在迭代30次后会与障碍物发生碰撞,继而无法到达对应的任务目标点。而本文所提出的VDSOM算法具备避障功能,能够绕过障碍物到达对应的任务目标点,算法的实效性更高。而本文所提出的VDSOM算法具备避障功能,能够绕过障碍物到达对应的任务目标点,算法的实效性更高。
| 表 2 1对多时SOM与VDSOM的移动方向偏移角的比较 Table 2 Comparison of the moving direction offset angles of SOM and VDSOM in 7(b) |
1) 本文所提出的算法在二维平面上,能够很好的通过方向角选择对应的动作,进而避开环境中的障碍物,成功的克服了传统的SOM算法的不足。
2) 与现有的二维工作环境中的多机器人任务分配算法相比,解决了因没有障碍物而不符合实际需求与在有障碍物的情况下如何自动避开障碍物的问题。
3) 本文所提出的VDSOM算法具备较强的鲁棒性、实用性和自适应性,能够在具有目标和障碍物的二维平面上进行大规模的任务分配问题,如地震救援、军事等实际应用价值很高的分配问题。
目前尚未完成多机器人协作解决任务分配问题,在今后的研究中,会将重点转向于多机器人协作上,以解决需要同时由多个机器人协作处理的复杂任务。
| [1] |
黎萍, 杨宜民. 多机器人系统任务分配的研究进展[J]. 计算机工程与应用, 2008, 44(17): 201-205, 227. LI Ping, YANG Yimin. Progress of task allocation in multi-robot systems[J]. Computer engineering and applications, 2008, 44(17): 201-205, 227. DOI:10.3778/j.issn.1002-8331.2008.17.060 (  0) 0)
|
| [2] |
李相民, 颜骥, 刘波, 等. 多智能体协同任务分配问题研究综述[J]. 计算机与数字工程, 2014, 42(12): 2443-2450. LI Xiangmin, YAN Ji, LIU Bo, et al. A survey of multi-agents cooperative task allocation research[J]. Computer and digital engineering, 2014, 42(12): 2443-2450. DOI:10.3969/j.issn1672-9722.2014.12.049 (  0) 0)
|
| [3] |
ZHANG Yunzhi, WANG Gang, TAO Li. Research on task allocation based on quantum particle swarm and hybrid algorithm of cuckoo[J]. Computer science and engineering, 2017. (  0) 0)
|
| [4] |
苏丽颖, 李小鹏, 杜峰, 等. 多机器人系统任务分配问题的建模与求解[J]. 中南大学学报(自然科学版), 2013, 44(S2): 122-125. SU Liying, LI Xiaopeng, DU Feng, et al. Modeling and solution for assignment problem of multiple robots system[J]. Journal of Central South University (Science and Technology), 2013, 44(S2): 122-125. (  0) 0)
|
| [5] |
SCHNEIDER E, SKLAR E I, PARSONS S, et al. Auction-based task allocation for multi-robot teams in dynamic environments[C]//Proceedings of the 16th Conference Towards Autonomous Robotic Systems. Liverpool, UK: Springer, 2015: 246-257.
(  0) 0)
|
| [6] |
AKBARIMAJD A, SIMZAN G. Application of artificial capital market in task allocation in multi-robot foraging[J]. International journal of computational intelligence systems, 2014, 7(3): 401-417. DOI:10.1080/18756891.2014.922814 (  0) 0)
|
| [7] |
LI Juntao, DONG Tingting, LI Yuanyuan. Research on task allocation in multiple logistics robots based on an improved ant colony algorithm[C]//Proceedings of 2016 International Conference on Robotics and Automation Engineering. Jeju, South Korea: IEEE, 2016: 17-20.
(  0) 0)
|
| [8] |
秦新立, 宗群, 李晓瑜, 等. 基于改进蚁群算法的多机器人任务分配[J]. 空间控制技术与应用, 2018, 44(5): 55-59. QIN Xinli, ZONG Qun, LI Xiaoyu, et al. Task allocation of multi-robot based on improved ant colony algorithm[J]. Aerospace control and application, 2018, 44(5): 55-59. DOI:10.3969/j.issn.1674-1579.2018.05.008 (  0) 0)
|
| [9] |
刘瑞轩, 张永林. 基于改进蚁群算法的多自主式水下机器人任务分配[J]. 中国舰船研究, 2018, 13(6): 107-112. LIU Ruixuan, ZHANG Yonglin. Task allocation of multiple autonomous underwater vehicles based on improved ant colony algorithm[J]. Chinese journal of ship research, 2018, 13(6): 107-112. (  0) 0)
|
| [10] |
DOU Jiajia, CHEN Chunlin, YANG Pei. Genetic scheduling and reinforcement learning in multirobot systems for intelligent warehouses[J]. Mathematical problems in engineering, 2015, 2015: 597956. (  0) 0)
|
| [11] |
LI Siding, XU Xin, ZUO Lei. Task assignment of multi-robot systems based on improved genetic algorithms[C]//Proceedings of 2015 IEEE International Conference on Mechatronics and Automation. Beijing: IEEE, 2015: 1430-1435.
(  0) 0)
|
| [12] |
段勇, 王宇, 喻祥尤. 基于免疫遗传算法的多机器人环境探索[J]. 沈阳工业大学学报, 2018, 40(3): 299-303. DUAN Yong, WANG Yu, YU Xiangyou. Multi-robot environment exploration based on immune genetic algorithm[J]. Journal of Shenyang University of Technology, 2018, 40(3): 299-303. (  0) 0)
|
| [13] |
KOHONEN T. Essentials of the self-organizing map[J]. Neural networks, 2013, 37: 52-65. DOI:10.1016/j.neunet.2012.09.018 (  0) 0)
|
| [14] |
KOHONEN T. Self-organized formation of topologically correct feature maps[J]. Biological cybernetics, 1982, 43(1): 59-69. DOI:10.1007/BF00337288 (  0) 0)
|
| [15] |
徐少华, 何新贵, 李盼池. 自组织过程神经网络及其应用研究[J]. 计算机研究与发展, 2003, 40(11): 1612-1615. XU Shaohua, HE Xingui, LI Panchi. Research and applications of self-organization process neural networks[J]. Journal of computer research and development, 2003, 40(11): 1612-1615. (  0) 0)
|
| [16] |
KOHONEN T. Analysis of a simple self-organizing process[J]. Biological cybernetics, 1982, 44(2): 135-140. DOI:10.1007/BF00317973 (  0) 0)
|
| [17] |
朱大奇, 李欣, 颜明重. 多自治水下机器人多任务分配的自组织算法[J]. 控制与决策, 2012, 27(8): 1201-1205, 1210. ZHU Daqi, LI Xin, YAN Mingzhong. Task assignment algorithm of multi-AUV based on self-organizing map[J]. Control and decision, 2012, 27(8): 1201-1205, 1210. (  0) 0)
|
| [18] |
FAIGL J. An application of self-organizing map for multirobot multigoal path planning with minmax objective[J]. Computational intelligence and neuroscience, 2016, 2016: 2720630. (  0) 0)
|
| [19] |
ZHU Daqi, HUANG Huan, YANG S X. Dynamic task assignment and path planning of multi-AUV system based on an improved self-organizing map and velocity synthesis method in three-dimensional underwater workspace[J]. IEEE transactions on cybernetics, 2013, 43(2): 504-514. DOI:10.1109/TSMCB.2012.2210212 (  0) 0)
|
| [20] |
LIU Yuanchang, BUCKNALL R. Efficient multi-task allocation and path planning for unmanned surface vehicle in support of ocean operations[J]. Neurocomputing, 2018, 275: 1550-1566. DOI:10.1016/j.neucom.2017.09.088 (  0) 0)
|
| [21] |
朱大奇, 曹翔. 多个水下机器人动态任务分配和路径规划的信度自组织算法[J]. 控制理论与应用, 2015, 32(6): 762-769. ZHU Daqi, CAO Xiang. An improved self-organizing map method for multiple autonomous underwater vehicle teams in dynamic task assignment and path planning[J]. Control theory & applications, 2015, 32(6): 762-769. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


