概率可靠性理论和技术自上世纪中叶出现以来,发展迅速,发挥了巨大的作用。但随着科学水平和工业技术的提高,新的要求不断被提出。为考虑非概率性不确定性因素的影响,出现了模糊可靠性理论[1],凸集或Info-Gap可靠性理论[2];考虑对象的复杂性,新的可靠性分析方法[3]不断的发展。近年来,理论的积累和技术的发展的需求,使考虑可靠性问题中不确定性因素本身的复杂性逐渐成为研究的热点。其中随机性和模糊性共存的结构可靠性问题受到越来越多学者的关注。这类问题中最为基本的是,在概率可靠性问题中考虑失效准则的模糊性,出现了随机变量和模糊失效准则混合的PROFUST可靠性模型[4]。进一步,考虑基本变量的复杂性不确定性,出现了模糊变量和随机变量混合的可靠性模型[5-6];以及基本变量中模糊性和随机性耦合的可靠性模型[7-8];随机或模糊变量与凸集或Info-Gap变量混合的可靠性模型[9-11]等。这些进展也证实了发展考虑复杂性不确定性综合作用的可靠性统一理论具有重要意义。
基本变量同时与概率分布函数和模糊隶属函数相关联是结构可靠性问题中模糊性和随机性结合的一种特殊情况。本文称之为模糊-随机联合可靠性问题。早期有学者开展过相关研究,李云贵等[12]基于对概率密度函数和模糊隶属函数的积分,定义了可靠性指标,建立一种结构可靠性模型;吕震宙等[13]基于一种自定义的测度函数,提出了一种新的可靠性指标建立了相应的分析模型。这些模型中可靠性评价指标并不具备严格的概率或模糊测度属性,相对孤立,难以与已有的概率或模糊可靠性理论相容。
本文在前人研究的基础上,依据模糊事件的条件概率理论,发展了一种模糊-随机联合可靠性方法,该方法能与本文作者课题组[14]建立的POFUST、模糊和随机变量混合、模糊随机耦合等结构可靠性模型相统一。以推动模糊性和随机性复杂作用的结构可靠性统一理论的发展。
1 变量取值约束的结构可靠性问题对于一般的应力~强度双变量结构可靠性问题,应力S和强度R均为随机变量,相应的概率密度函数分别为fS(s)和fR(r),由概率可靠性理论,结构的失效概率和可靠度分别为:
| $ {P_f} = \int\limits_{r < s} {{f_R}(r){f_S}(s){\rm{d}}r{\rm{d}}s} $ | (1) |
| $ {P_s} = \int\limits_{r \ge s} {{f_R}(r){f_S}(s){\rm{d}}r{\rm{d}}s = 1 - {P_f}} $ | (2) |
对于上述一般性问题,考虑已知S和R服从以上概率分布时,又获知S≥s0,R≤r0。此时结构失效成为条件概率问题。由条件概率原理:
| $ {P_f} = \frac{{\int\limits_{r < s, r \le {r_0}, s \ge {s_0}} {{f_R}(r){f_S}(s){\rm{d}}r{\rm{d}}s} }}{{\int\limits_{r \le {r_0}, s \ge {s_0}} {{f_R}(r){f_S}(s){\rm{d}}r{\rm{d}}s} }} $ | (3) |
| $ {P_s} = \frac{{\int\limits_{r \ge s, r \le {r_0}, s \ge {s_0}} {{f_R}(r){f_s}(s){\rm{d}}r{\rm{d}}s} }}{{\int\limits_{r \le {r_0}, s \ge {s_0}} {{f_R}(r){f_S}(s){\rm{d}}r{\rm{d}}s} }} = 1 - {P_f} $ | (4) |
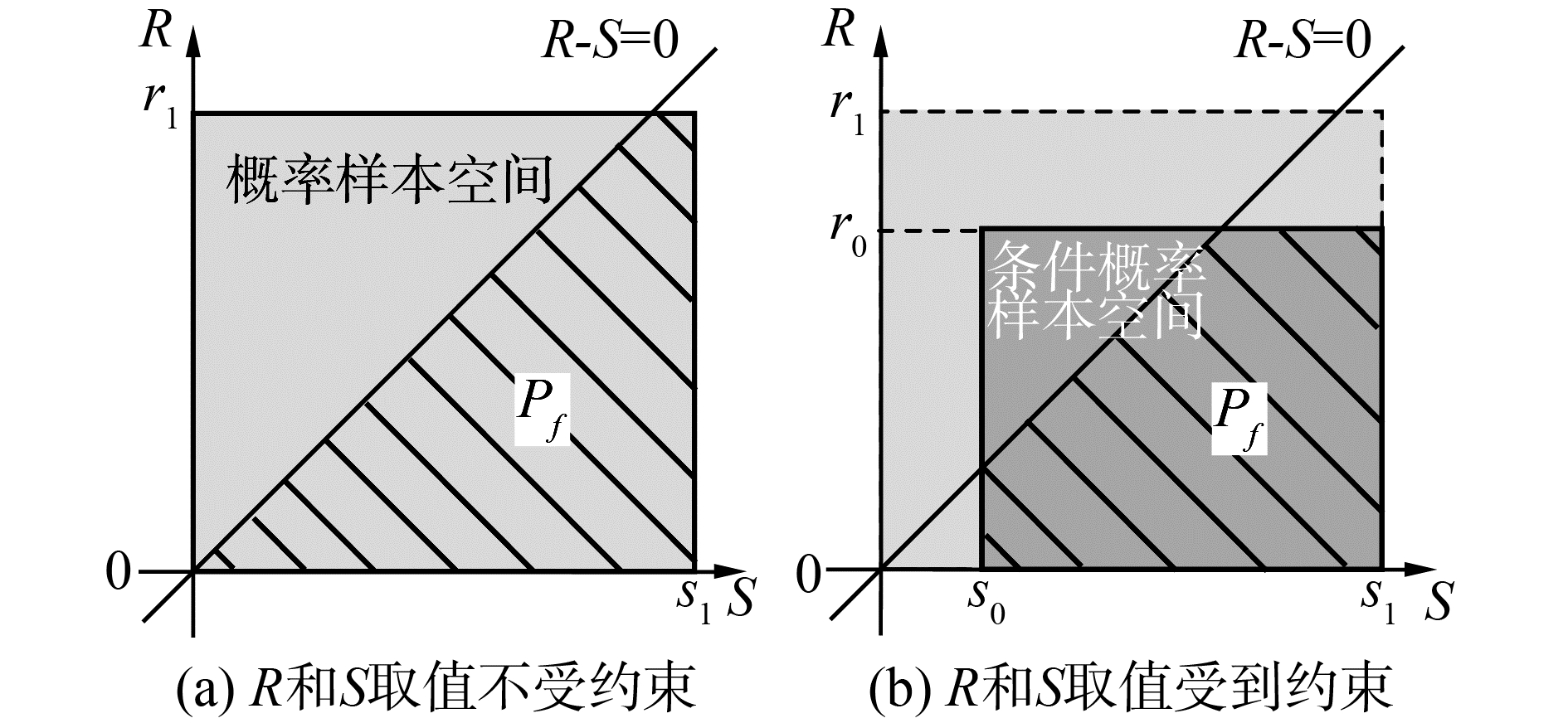
以上2个公式表明,较式(1)、(2),附加了S和R的取值约束信息后,结构的失效概率和可靠度会发生变化。这是概率样本空间的变化导致的。图 1展示了S和R服从相互独立的均匀分布时,取值约束下,概率样本空间和失效概率的变化情况。
|
Download:
|
| 图 1 变量取值约束下概率空间和失效概率的变化 Fig. 1 Variations of probability space and failure probability under constrained variable value | |
结构模糊-随机联合可靠性问题的特征是:基本变量具有随机性,同时又对某一概念有一定的模糊隶属度。这导致其不确定性需用概率密度函数和模糊隶属函数共同描述。如对于强度R,由概率密度函数fR(r)和隶属函数μR(r)分别决定其随机性和模糊性。即R以一定的概率取实现值r0,由fR(r)表征;同时r0对于某一概念有隶属度μR(r0)。文献[12]给出了该情况的一种实例解释:地震载荷中,“大震载荷”同时具有模糊性和随机性,载荷的取值是随机的;而载荷对“大震作用”这一概念具有一定的隶属度。
2.1 变量取值约束问题的特征函数形式记式(3)、(4)中随机向量[R, S]T在二维实数空间R2中的取值约束域为Ωsub,失效域为Ωf={[r, s]T:r < s}。将2者写为特征函数形式:
| $ \varphi_{\mathrm{sub}}(r, s)=\left\{\begin{array}{ll}{1, } & {[r, s]^{\mathrm{T}} \in \mathit{\Omega}_{\mathrm{sub}}} \\ {0, } & {[r, s]^{\mathrm{T}} \notin \mathit{\Omega}_{\mathrm{sub}}}\end{array}\right.和\\ \varphi_{f}(r, s)=\left\{\begin{array}{ll}{1, } & {[r, s]^{\mathrm{T}} \in \mathit{\Omega}_{f}} \\ {0, } & {[r, s]^{\mathrm{T}} \notin \mathit{\Omega}_{f}}\end{array}\right. $ | (5) |
则式(3)可转化为:
| $ {P_f} = \frac{{\int\limits_{{{\rm{R}}^2}} {{f_R}(r){f_S}(s){\varphi _{{\rm{sub }}}}(r, s){\varphi _f}(r, s){\rm{d}}r{\rm{d}}s} }}{{\int\limits_{{{\rm{R}}^2}} {{f_R}(r){f_S}(s){\varphi _{{\rm{sub}}}}(r, s){\rm{d}}r{\rm{d}}s} }} $ | (6) |
依据模糊事件的概率测度理论[15],上式本质上是模糊事件条件概率的特殊形式。
模糊事件的条件概率具体为:设A和B为概率空间Ω上的模糊集,隶属函数分别为μA(ω)和μB(ω),则B发生条件下A发生的概率为:
| $ P(A|B) = \frac{{P(AB)}}{{P(B)}} = \frac{{\int\limits_\Omega {{\mu _A}(\omega ){\mu _B}(\omega ){\rm{d}}P} }}{{\int\limits_\Omega {{\mu _B}(\omega ){\rm{d}}P} }} $ | (7) |
需要特别指出的是:与普通事件的条件概率不同,式(7)中,AB并非模糊事件的交,即AB≠A∩B,而是表示隶属度为μA×μB的模糊集。
2.2 取值约束在模糊集上的推广将2.1节应力强度可靠性问题中(R, S)T的取值约束域Ωsub推广为模糊集Fsub,其联合隶属函数为μsub(r, s)。这种情况下,自然可用μsub(r, s)替代式(6)中的特征函数φsub(r, s),得到:
| $ {P_f} = \frac{{\int\limits_{{{\rm{R}}^2}} {f_R(r){f_S}(s){\mu _{{\rm{sub }}}}(r, s){\varphi _f}(r, s){\rm{d}}r{\rm{d}}s} }}{{\int\limits_{{{\rm{R}}^2}} {{f_R}(r){f_S}(s){\mu _{{\rm{sub}}}}(r, s){\rm{d}}r{\rm{d}}s} }} $ | (8) |
| $ {P_s} = \frac{{\int\limits_{{{\rm{R}}^2}} {{f_R}(r){f_S}(s){\mu _{{\rm{sub}}}}(r, s){\varphi _s}(r, s){\rm{d}}r{\rm{d}}s} }}{{\int\limits_{{{\rm{R}}^2}} {{f_R}(r){f_S}(s){\mu _{{\rm{sub}}}}(r, s){\rm{d}}r{\rm{d}}s} }} = 1 - {P_f} $ | (9) |
式中:φs(r, s)为安全域Ωs={(r, s)T:r < s}的特征函数;Pf和Ps是模糊事件的概率测度,仍有概率的含义和性质,在理论基础和运算方法上与现有的基于概率测度的可靠性方法相容。
3 任意变量情况下模型的推广不失一般性,设结构的基本向量,X=[X1 X2 … Xn]T,具有随机性,其联合概率密度函数为f(x),x=[x1 x2 … xn]T∈Rn;X又与联合隶属函数μ(x)关联。结构的极限状态函数为G(x)=0,G(x) < 0表示失效。
记Ωf={x:G(x) < 0}和Ωs={x:G(x)≥0}的特征函数分别φf(x)和φs(x)。依据式(8)、(9)的条件概率意义,将其推广到n个变量的情况,得到:
| $ {P_f} = \frac{{\int\limits_{{{\rm{R}}^n}} {f(x)\mu (x){\varphi _f}(x){\rm{d}}x} }}{{\int\limits_{{{\rm{R}}^n}} {f(x)\mu (x){\rm{d}}x} }} $ | (10) |
| $ {P_s} = \frac{{\int\limits_{{{\rm{R}}^n}} {f(x)\mu (x){\varphi _s}(x){\rm{d}}x} }}{{\int\limits_{{{\rm{R}}^n}} {f(x)\mu (x){\rm{d}}x} }} = 1 - {P_f} $ | (11) |
若X的各分量相互独立,则有:
| $ {P_f} = \frac{{\int\limits_{{{\rm{R}}^n}} {\left[ {\prod\limits_{i = 1}^n {{f_i}} \left( {{x_i}} \right)} \right]\left[ {\mathop \wedge \limits_{i = 1}^n {\mu _i}\left( {{x_i}} \right)} \right]{\varphi _f}(x){\rm{d}}x} }}{{\int\limits_{{{\rm{R}}^n}} {f(x)\mu (x){\rm{d}}x} }} $ | (12) |
式中fi(xi)和μi(xi)分别是与Xi相关联的概率密度函数和隶属函数。
由式(12)可知,式(10)、(11)中各积分的被积函数中本质上混合了代数运算和模糊运算,这一特征是由模糊事件的条件概率原理决定的。
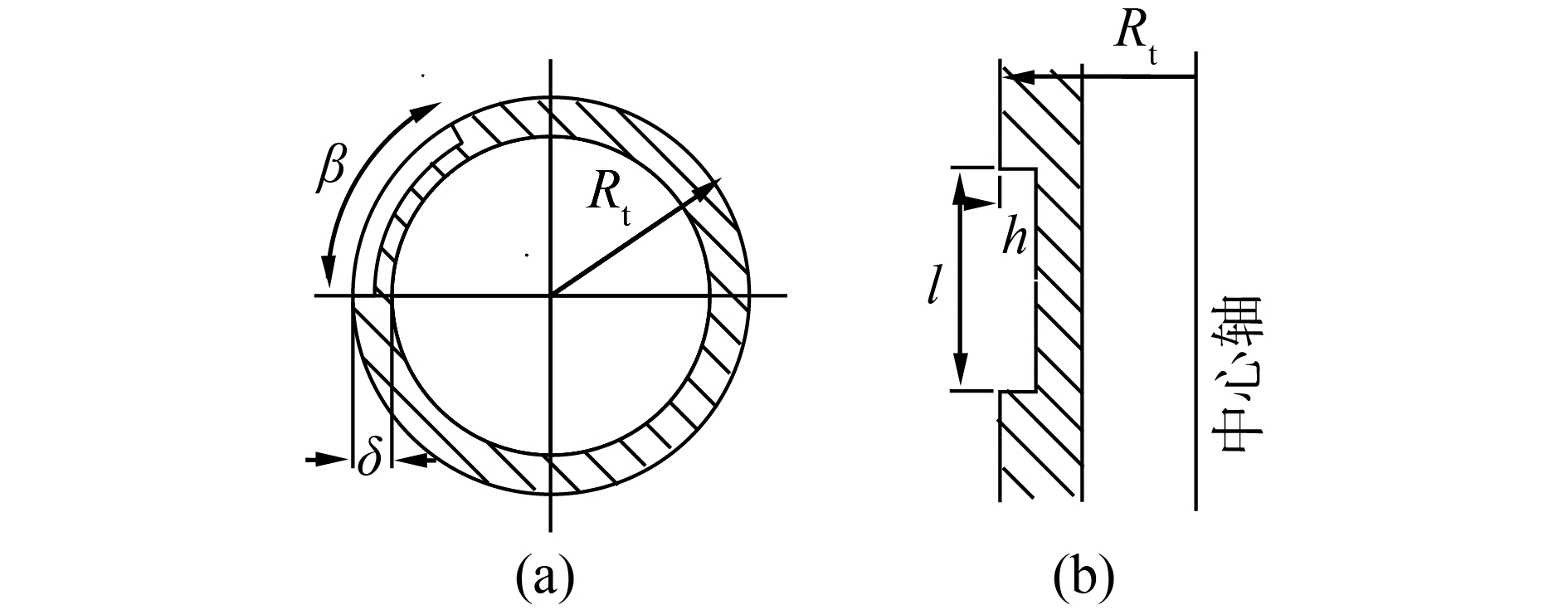
4 工程实例某在役换热器传热管内,出现管壁局部减薄的体积缺陷,经规范化后转化为瓦片状缺陷,如图 2所示。传热管内部工作压力为p,外半径为Rt=7.5 mm,壁厚为δ=1.35 mm,缺陷张角记为β、高度为l=10 mm、深度为h。在工作温度下,材料弹性模量E=1.95×105 MPa,泊松比为0.30。由于探伤误差和材料老化等影响,p、β、h和材料屈服强度σs可视为正态随机变量,分布参数如表 1。
|
Download:
|
| 图 2 传热管局部减薄体积缺陷 Fig. 2 Heat transfer tube with local thinned volume defect | |
| 表 1 基本变量的分布参数 Table 1 Distribution parameters of the basic variables |
p和σs又具有模糊性,相应的隶属函数分别为:
| $ {\mu _p}(p) = \left\{ {\begin{array}{*{20}{l}} {0, }&{p < 13, }\\ {\min (p - 13, 1)}&{p \ge 13} \end{array}} \right. $ | (13) |
| $ \mu_{\sigma}(\sigma)=\left\{\begin{array}{ll}{0, } & {\sigma \geqslant 255} \\ {\min (0.1(\sigma-255), 1), } & {\sigma<255}\end{array}\right. $ | (14) |
在通用有限元软件中对上述传热管参数化建模,对不同的缺陷进行了试分析,验证了分析结果与网格划分的无关性。然后进行静力学有限元分析,计算不同缺陷下的最大等效应力σmax,无量纲化后得到Σmax=σmaxδ/(2pRt)。β=50°时的有限元网格和等效应力云图如图 3所示。

|
Download:
|
| 图 3 1/4含缺陷传热管的网格划分和等效应力云图 Fig. 3 Meshing and equivalent stress nephograms of a quarter tube model | |
不同缺陷尺寸下的Σmax如表 2。将β和h无量纲化,h*=h/δ和β*=β/90,采用多项式对表 2数据进行拟合,得到三次多项式Σmax=fΣ(h*, β*),其各项系数见表 3。
| 表 2 不同缺陷的最大无量纲等效应力Σmax Table 2 The maximum dimensionless equivalent stress Σmax for varying defects |
| 表 3 拟合多项式fΣ(h*, β*)的各项系数 Table 3 The coefficients of fitting polynomial fΣ(h*, β*) |
考虑σs为管材的流变应力,得到极限状态函数:
| $ {G_{\rm{t}}}\left( {p, h, \beta , {\sigma _{\rm{s}}}} \right) = {\sigma _{\rm{s}}} - 2p{R_{\rm{t}}}{f_\Sigma }\left( {{h^*}, {\beta ^*}} \right)/\delta $ |
考虑到h和σs为单纯的随机变量,认为其取值范围不受约束(注:< 0的取值对失效概率影响很小),故与之相关联的隶属函数应恒等于1。采用Monte-Carlo方法求解失效概率。
| $ {P_f} = \frac{{\sum\limits_{i = 1}^N {\left[ {{\mu _p}\left( {{p_i}} \right) \wedge {\mu _\beta }\left( {{\beta _i}} \right)} \right]} {\mathop{\rm sgn}} \left[ {{G_\text{t}}(x)} \right]}}{{\sum\limits_{i = 1}^N {\left[ {{\mu _p}\left( {{p_i}} \right) \wedge {\mu _\beta }\left( {{\beta _i}} \right)} \right]} }} $ |
式中:N为抽样次数,N>100/Pf;x=[p β h σs]T;Gt>0时,sgn(Gt)=1,否则sgn(Gt)=0。
在MATLAB平台中编制程序,计算得到不同缺陷深度下的失效概率如表 4所示。
| 表 4 不同深度缺陷对应的失效概率 Table 4 Failure probabilities for varying defects |
对表 4中数据进处理并差值计算,依“3σ”准则,要使3倍标准差内传热管不失效,缺陷深度应满足h < 0.334δ。
若不考虑p和β的模糊取值约束,即p、β、h和σs为单纯的随机变量,计算得到不同缺陷深度下(注:方差不变)的失效概率如表 5所示。
| 表 5 不考虑变量模糊性时不同缺陷深度的失效概率 Table 5 Failure probabilities for varying defects ignoring the fuzziness of basic variables |
对比上述计算结果,若不考虑变量的模糊取值约束,计算失效概率将降低,这是概率样本空间扩大导致的。如此会产生偏危险的评价结果。
5 结论1) 本文方法运用了模糊事件的条件概率理论,能有效解决基本变量同时与概率分布函数和模糊隶属函数相关联的结构可靠性评估问题。
2) 本文模型同样采用概率方法和概率测度度量可靠性,与经典的概率可靠性理论、其它采用概率测度的结构可靠性理论和以及本文作者课题组提出的模糊性和随机性复杂结合的可靠性新理论相容。为发展模糊性和随机性复杂作用的结构可靠性统一理论奠定了部分理论基础。
3) 算例显示,在一些问题中,忽视随机变量的模糊取值约束可能会给出偏危险的分析结论。
4) 文中失效概率的求解采用了Monte-Carlo方法,其计算效率较低,在失效概率较小时该问题尤为突出,须进一步发展高效的可靠度计算方法。
| [1] |
CAI Kaiyuan, WEN Chuanyuan, ZHANG Minglian. Fuzzy variables as a basis for a theory of fuzzy reliability in the possibility context[J]. Fuzzy sets and systems, 1991, 42(2): 145-172. DOI:10.1016/0165-0114(91)90143-E (  0) 0)
|
| [2] |
李昆锋, 杨自春. 基于Info-Gap理论的结构非概率可靠性方法研究[J]. 机械强度, 2013, 35(2): 174-178. LI Kunfeng, YANG Zichun. Study on non-probabilistic structural reliability method based on Info-Gap decision theory[J]. Journal of mechanical strength, 2013, 35(2): 174-178. (  0) 0)
|
| [3] |
ZHAO Wei, FAN Feng, WANG Wei. Non-linear partial least squares response surface method for structural reliability analysis[J]. Reliability engineering & system safety, 2017, 161: 69-77. (  0) 0)
|
| [4] |
HUANG Hongzhong. Structural reliability analysis using fuzzy sets theory[J]. Eksploatacja I niezawodność, 2012, 14(4): 284-294. (  0) 0)
|
| [5] |
ADDURI P R, PENMETSA R C. System reliability analysis for mixed uncertain variables[J]. Structural safety, 2009, 31(5): 375-382. DOI:10.1016/j.strusafe.2009.02.001 (  0) 0)
|
| [6] |
YANG Zichun, LI Kunfeng, CAI Qi. Universal reliability method for structural models with both random and fuzzy variables[J]. Computer modeling in engineering and sciences, 2013, 95(2): 143-171. (  0) 0)
|
| [7] |
李昆锋, 杨自春, 蔡琦. 二态失效的结构模糊随机可靠性统一模型[J]. 华中科技大学学报(自然科学版), 2015, 43(6): 55-59, 65. LI Kunfeng, YANG Zichun, CAI Qi. Fuzzy random reliability unified model for structures based on binary state failure[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2015, 43(6): 55-59, 65. (  0) 0)
|
| [8] |
LI Haibin, NIE Xiaobo. Structural reliability analysis with fuzzy random variables using error principle[J]. Engineering applications of artificial intelligence, 2018, 67: 91-99. DOI:10.1016/j.engappai.2017.08.015 (  0) 0)
|
| [9] |
李昆锋, 杨自春, 孙文彩. 结构凸集-概率混合可靠性分析的新方法[J]. 机械工程学报, 2012, 48(14): 192-198. LI Kunfeng, YANG Zichun, SUN Wencai. New hybrid convex model and probability reliability method for structures[J]. Journal of mechanical engineering, 2012, 48(14): 192-198. (  0) 0)
|
| [10] |
李昆锋, 杨自春, 孙文彩. 结构非概率-模糊混合可靠性分析方法[J]. 华中科技大学学报(自然科学版), 2012, 40(8): 67-71. LI Kunfeng, YANG Zichun, SUN Wencai. Analyzing hybrid non-probabilistic and fuzzy reliability of structures[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2012, 40(8): 67-71. (  0) 0)
|
| [11] |
WANG Chong, QIU Zhiping, XU Menghui, et al. Novel reliability-based optimization method for thermal structure with hybrid random, interval and fuzzy parameters[J]. Applied mathematical modelling, 2017, 47: 573-586. DOI:10.1016/j.apm.2017.03.053 (  0) 0)
|
| [12] |
李云贵, 赵国藩. 基于模糊随机概率理论的可靠度分析模型[J]. 大连理工大学学报, 1995, 35(4): 528-531. LI Yungui, ZHAO Guofan. Unified model for structural reliability analysis based on fuzzy random probabilistic theory[J]. Journal of Dalian University of Technology, 1995, 35(4): 528-531. (  0) 0)
|
| [13] |
吕震宙, 岳珠峰. 模糊随机可靠性分析的统一模型[J]. 力学学报, 2004, 36(5): 533-539. LÜ Zhenzhou, YUE Zhufeng. Unified reliability model for fuzziness and randomness of the basic variables and state variables in structure[J]. Acta mechanica sinica, 2004, 36(5): 533-539. DOI:10.3321/j.issn:0459-1879.2004.05.004 (  0) 0)
|
| [14] |
李昆锋, 杨自春, 孙文彩. 模糊失效准则下的结构非概率可靠性分析方法[J]. 工程力学, 2013, 30(5): 36-41. LI Kunfeng, YANG Zichun, SUN Wencai. Non-probabilistic structural reliability method based on fuzzy failure criterion[J]. Engineering mechanics, 2013, 30(5): 36-41. (  0) 0)
|
| [15] |
ZADEH L A. Probability measures of fuzzy events[J]. Mathematical analysis and applications, 1968, 23(2): 421-427. DOI:10.1016/0022-247X(68)90078-4 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


