2. 海洋信息获取与安全工信部重点实验室(哈尔滨工程大学) 工业和信息化部, 黑龙江 哈尔滨 150001;
3. 哈尔滨工程大学, 水声工程学院, 黑龙江 哈尔滨 150001
2. Key Laboratory of Marine Information Acquisition and Security(Harbin Engineering University), Ministry of Industry and Information Technology, Harbin 150001, China;
3. College of Underwater Acoustic Engineering, Harbin Engineering University, Harbin 150001, China
卷积/反卷积是信号处理中的基本问题,反卷积是指通过测量输出和已知输入重构未知输入的过程。反卷积技术在语音信号处理、通信信道均衡[1]、图像处理、地震勘探[2]、空气声源定位[3-4]等多个领域的研究已得到了迅猛发展,其在稳健高分辨和抗噪处理方面性能卓越。在这一过程中涌现出很多经典的反卷积求解方法,例如共轭梯度法、Landweber迭代法[5]、维纳滤波法[6],增量维纳滤波法、DAMAS2(deconvolution approach for the mapping of acoustic sources 2)[7]、DAMAS3[7]算法以及基于傅里叶变换的非负最小二乘[8]、Richardson-Lucy(R-L)[9]算法等。
声呐技术发展对具有稳健、高分辨和高增益处理能力的水下阵列信号处理技术需求迫切。本质上利用时间采样与空间采样的对偶性,可将时间序列反卷积技术用于空间阵列信号处理,这为阵列稳健高分辨信号处理提供了一种可能的解决途径。由此,反卷积技术在阵处理领域得到了广泛关注。常规波束形成空间谱输出可以看作阵列方向图函数与点目标方位信息的卷积结果,因而通过反卷积可以得到目标的方位信息,进而有效改善目标方位估计精度。关于反卷积技术在水下阵列信号处理技术中应用研究工作有限,Yang[10]将反卷积技术应用于水下均匀声压阵和圆阵信号处理中[11],并利用水下声压阵海试数据对反卷积波束形成的稳健性、分辨率和增益方面进行了验证,改善效果显著,Yang指出其文中方法限于点扩散函数(pint spread function, PSF)移不变阵列模型,开展移变模型阵列的反卷积波束形成研究是下一步研究工作。
矢量阵与传统声压阵相比,因具有良好的左右舷分辨能力以及额外的信号处理增益正逐步成为水下阵列的发展趋势,针对矢量阵的高分辨信号处理方法种类繁多[12-13],但稳健性欠佳,为了提高稳健型进行了修正的高分辨处理方法其分辨力和抑制噪声能力又会降低。反卷积波束形成的出现为此提供了一种可能解决途径。很多经典的卷积模型都是建立在线性移不变系统的基础上的,矢量阵阵列指向性函数不具有移不变性。解决反卷积波束形成在PSF移变模型阵列中的应用是有必要的。本文研究了利用非负最小二乘(nonnegative least-squares, NNLS)进行矢量阵移变PSF反卷积求解的方法,实现了矢量阵的稳健高分辨波束形成处理。利用NNLS算法对上述模型的反卷积问题进行了仿真验证,并对矢量阵反卷积波束形成和最小方差无畸变响应(minimum variance distortionless response,MVDR)、多重信号分类(multiple signal classification,MUSIC)高分辨算法进行了对比,对主瓣宽度、主旁瓣比、少快拍信号和存在阵型误差模型时的性能进行了对比分析。
1 矢量阵反卷积波束形成理论分析 1.1 时域卷积/反卷积模型对于一般线性系统,系统的输出可以被写为输入信号与系统单位冲击响应的广义卷积形式,即叠加积分:
| $ y\left( t \right) = \int_{ - \infty }^{ + \infty } {h\left( {t\left| \tau \right.} \right)x\left( \tau \right){\rm{d}}\tau } + n\left( t \right) $ | (1) |
式中:x(τ)是系统τ时刻的输入值;y(t)是系统的输出即获得的观测值;h(t|τ)表示系统在τ时刻系统的单位冲击响应函数;n(t)表示系统噪声。
如果将h(t)视为系统在0时刻的单位冲击响应函数,当它满足线性移不变性质,则τ时刻的脉冲响应函数h(t|τ)只是0时刻单位脉冲响应在时间上τ个延迟,h(t|τ)=h(t-τ),此时,叠加积分就可以表示成卷积。忽略系统噪声的情况下,式(1)可以被表示为:
| $ \begin{array}{l} y\left( t \right) = \int_{ - \infty }^{ + \infty } {h\left( {t\left| \tau \right.} \right)x\left( \tau \right){\rm{d}}\tau } = \\ \;\;\;\;\;\;\;\;\;\;\int_{ - \infty }^{ + \infty } {h\left( {t - \tau } \right)x\left( \tau \right){\rm{d}}\tau } = h\left( t \right) * x\left( t \right) \end{array} $ | (2) |
脉冲响应函数不具有移不变性质时,叠加积分不可等效为卷积。实际中很多系统都无法保证时不变/移不变性。
1.2 时空卷积/反卷积类比阵处理中,多目标情况下的阵列的常规波束形成空间谱输出可以看成每一个角度的指向性图和该角度的源强度乘积之和,可以用一个叠加积分来表示:
| $ P\left( \theta \right) = \int {R\left( {\theta \left| \vartheta \right.} \right)S\left( \vartheta \right){\rm{d}}\vartheta } $ | (3) |
式中:ϑ表示目标所在方位,S(ϑ)是表示目标函数,反映目标方位和强度信息,理想情况下是δ函数,这里等效为时域系统的输入信号x(t); R(θ|ϑ)表示ϑ方向的阵列指向性函数,它是阵列指向ϑ方向时的指向性函数,等效为时域中的系统单位脉冲响应h(t),也被称作反卷积中的PSF; P(θ)表示常规波束形成空间谱输出,等效为系统的输出y(t),其值可等效于各个目标方向的阵列指向性函数经过目标强度加权后的叠加积分。如果阵列的指向性函数R(θ|ϑ)具有移不变性,则有R(θ|ϑ)=R(θ-ϑ),此时叠加积分可以表示为如下卷积过程:
| $ P\left( \theta \right) = \int {R\left( {\theta \left| \vartheta \right.} \right)S\left( \vartheta \right){\rm{d}}\vartheta } = R\left( \theta \right) * S\left( \theta \right) $ | (4) |
因此,对常规波束输出空间谱P(θ)和自然指向性函数R(θ)反卷积可以得到目标函数S(θ),其理想情况下是δ函数,因此具有高分辨效果。
1.3 矢量阵卷积模型及点扩散函数特点等间距矢量阵的几何模型如图 1所示,假定阵列的所有阵元沿z轴等间距排列,每个矢量传感器由一个声压传感器、一个分布在x轴的振速传感器、一个分布在z轴的振速传感器组成。
|
Download:
|
| 图 1 矢量阵的几何模型 Fig. 1 Uniform line vector array geometry | |
假设平面波声源从(ϑ, φ)入射到基阵,ϑ和φ分别是水平方位角和极角(与阵列所在平面夹角),常规波束方位谱可以被表示为基阵的指向性函数和声源目标函数的叠加积分:
| $ P\left( {\theta ,\phi } \right) = \int_0^{2{\rm{ \mathsf{ π} }}} {\int_0^{\rm{ \mathsf{ π} }} {R\left( {\theta ,\phi \left| {\vartheta ,\varphi } \right.} \right)S\left( {\vartheta ,\varphi } \right)\sin \varphi {\rm{d}}\varphi {\rm{d}}\vartheta } } $ | (5) |
式中:R(θ, ϕ|ϑ, φ)表示当声源位于(ϑ, φ)时,在所有θ和ϕ方向形成的能量响应输出,是(ϑ, φ)方向目标形成的指向性函数。基阵的指向性函数可以由阵列的几何参数计算而得。如果只考虑二维情况,假设信号以平面波入射,即φ=π/2,则:
| $ \begin{array}{*{20}{c}} {{R_V}\left( {\theta \left| \vartheta \right.} \right) = {{\left| {\frac{{\left( {1 + \cos \left( {\theta - \vartheta } \right)} \right)}}{2}} \right|}^2} \cdot }\\ {{{\left| {\frac{{\sin \left( {\frac{{N{\rm{ \mathsf{ π} }}d}}{\lambda }\left( {\cos \theta - \cos \vartheta } \right)} \right)}}{{N\sin \left( {\frac{{{\rm{ \mathsf{ π} }}d}}{\lambda }\left( {\cos \theta - \cos \vartheta } \right)} \right)}}} \right|}^2} = \mathit{\boldsymbol{U}}{\mathit{\boldsymbol{R}}_H}} \end{array} $ | (6) |
式中:RH(ϑ)为声压阵的自然指向性函数,由上式可以看出,矢量阵的自然指向性函数RV(θ|ϑ)为声压阵自然指向性函数RH(ϑ)与一个角度指向因子U(ϑ)=(1+cosθ)/2的乘积。则式(5)变为:
| $ P\left( \theta \right) = \int_0^{2{\rm{ \mathsf{ π} }}} {{R_v}\left( {\theta \left| \vartheta \right.} \right)S\left( \vartheta \right)\sin \vartheta {\rm{d}}\vartheta } $ | (7) |
式中RV(θ|ϑ)是ϑ方向形成的矢量阵的指向性函数。矢量阵自然指向性的移位为:
| $ \begin{array}{*{20}{c}} {{R_V}\left( {\theta - \vartheta } \right) = {{\left| {\frac{{\left( {1 + \cos \left( {\theta - \vartheta } \right)} \right)}}{2}} \right|}^2} \cdot }\\ {{{\left| {\frac{{\sin \left( {\frac{{N{\rm{ \mathsf{ π} }}d}}{\lambda }\cos \left( {\theta - \vartheta } \right)} \right)}}{{N\sin \left( {\frac{{{\rm{ \mathsf{ π} }}d}}{\lambda }\cos \left( {\theta - \vartheta } \right)} \right)}}} \right|}^2}} \end{array} $ | (8) |
比较式(6)和式(8),显然RV(θ|ϑ)≠RV(θ-ϑ),无法利用常规移不变模型方法进行求解。分析可知,U(θ)=(1+cosθ)是关于θ移不变的函数,而RH(θ)是关于cosθ的移不变函数,二者相乘后无法通过简单的变量代换将其等效为某个统一变量的移不变模型。其时间域上的等效应为移变系统,即:
| $ h\left( {t\left| \tau \right.} \right) \ne h\left( {t - \tau } \right) $ | (9) |
如果将这一问题进行空时等效, 则可写为:
| $ \begin{array}{l} y\left( t \right) = \int_{ - \infty }^{ + \infty } {h\left( {t\left| \tau \right.} \right)x\left( \tau \right){\rm{d}}\tau } = \\ \;\;\;\;\;\;\;\;\;\left( {{h_1}\left( {t\left| \tau \right.} \right){h_2}\left( {t\left| \tau \right.} \right)} \right) * x\left( t \right) \end{array} $ | (10) |
其中:
| $ h\left( {t\left| \tau \right.} \right) = \left( {{h_1}\left( {t\left| \tau \right.} \right){h_2}\left( {t\left| \tau \right.} \right)} \right) $ |
式中:h1(t|τ)是关于t的时不变/移不变系统,h2(t|τ)是关于cost的时不变/移不变系统。因此整个系统不能等效为移不变系统。因此无法直接利用现有的常规反卷积方法求解,尤其是转换到变换域的基于FFT的快速算法求解,也无法利用简单映射为移不变系统的方法求解。但是矢量阵的波束输出依然可以被写作目标函数和矢量阵指向性函数的叠加积分的形式。因此可以进行移变反卷积求解。
1.4 NNLS反卷积求解方法NNLS是一种在多个领域广泛应用的线性方程组求解方法。求解最小二乘问题,经典的方法是构造方程组,根据该方法求解的特点,可以将其应用于移变反卷积模型的求解。Ehrenfried利用NNLS求解噪声源定位的反卷积问题[8]。褚志刚[14]将该方法用于提高识别发动机噪声源的定位精度中。其基本原理可以推广到矢量阵反卷积处理,具体方法是在常规波束输出、矢量阵点扩散函数字典、声源目标函数之间建立差函数方程组,通过最小化差函数的原则来实现对目标函数S的求解,获取声源的分布,写做矩阵形式的表达式如下:
| $ \mathit{\boldsymbol{\varphi }} = {\left\| {\mathit{\boldsymbol{RS}} - \mathit{\boldsymbol{P}}} \right\|_2} $ | (11) |
式中:P是矢量阵常规波束形成输出空间谱; R是所有角度矢量阵的指向性函数形成的指向性函数字典矩阵,即矢量阵点扩散函数字典;S是反映声源方位和强度信息的目标函数;‖‖2表示2范数。对于上述方程组求解可以采用梯度投影法,该方法的核心是负梯度方向指向标量场下降最快的方向,通过在ϕ关于S的负梯度方向上按特定步长反复迭代搜索来求得S。计算过程中,初始化S(0)=0,由第i次迭代计算结果S(i)到i+1次迭代计算结果S(i+1)的具体步骤为:
1) 由迭代得到的S(i)计算残差向量:
| $ \boldsymbol{r}^{(i)}=\boldsymbol{R} \boldsymbol{S}^{(i)}-\boldsymbol{P} $ | (12) |
2) 计算ϕ在S空间的负梯度向量:
| $ \boldsymbol{w}^{(i)}=-\boldsymbol{R}^{\mathrm{T}} \boldsymbol{r}^{(i)} $ | (13) |
3) 计算投影梯度w,定义搜索路径:
| $ {\mathit{\boldsymbol{\bar w}}^{\left( i \right)}} = \left\{ \begin{array}{l} 0,\;\;\;\;\;\;\;{w^{\left( i \right)}} < 0,{\mathit{\boldsymbol{S}}^{\left( i \right)}} = 0\\ {\mathit{\boldsymbol{w}}^{\left( i \right)}},\;\;\;\;其他 \end{array} \right. $ | (14) |
4) 计算辅助向量:
| $ \boldsymbol{g}^{(i)}=\boldsymbol{R} \overline{w}^{(i)} $ | (15) |
5) 计算最优搜索步长:
| $ \lambda=-\frac{\boldsymbol{g}^{(i)} \cdot \boldsymbol{r}^{(i)}}{\boldsymbol{g}^{(i)} \cdot \boldsymbol{g}^{(i)}} $ | (16) |
6) 计算S(i+1)迭代结果:
| $ {\mathit{\boldsymbol{S}}^{\left( {i + 1} \right)}} = \max \left( {{\mathit{\boldsymbol{S}}^{\left( i \right)}} + \lambda {{\bar w}^{\left( i \right)}},0} \right) $ | (17) |
NNLS算法并不局限于移不变反卷积模型求解,只需要获得阵列所有方位的指向性函数矩阵即可。需要注意的是,对于移不变模型采用NNLS算法时可采用FFT变换域计算的方式实现快速计算,但这并不适用于移变模型阵列。该方法并不局限于矢量阵,对结构固定不变的阵列该方法都适用。
2 仿真分析仿真条件:20元均匀矢量阵,阵间距为信号频率半波间距,信号频率500 Hz。不同角度的指向性函数如图 2所示,可以看出不同角度的矢量阵指向性函数不同,不是自然指向性函数的移位,因此是移变的。虽然抗左右模糊作用,但是其效果与方位有关,在端射方向附近效果较差,存在伪峰。

|
Download:
|
| 图 2 指向不同角度的矢量阵指向性函数 Fig. 2 The beam power distribution for a vector sensor line array for a signal at different degrees | |
图 3是预存的矢量阵PSF矩阵即指向性函数矩阵伪彩图。图 4是矢量阵CBF与dCv的仿真对比结果。

|
Download:
|
| 图 3 预存PSF矩阵 Fig. 3 The predefined PSF | |

|
Download:
|
| 图 4 矢量阵CBF和dCV的波束输出对比 Fig. 4 Comparison of dCv and CBF in vector array | |
通过图 4可以看出,该方法适用于矢量阵这种PSF移变模型阵。与CBF相比,dCv有更窄的主瓣和低旁瓣级,同时具有更好的左右舷分辨能力,改善了线阵的左右舷分辨问题。该算法也可以推广到宽带信号的方位估计中,针对宽带信号只要将其划分为若干个窄带,针对每个窄带信号做dCv,最后再将反卷积的结果综合累加即可。
2.1 阵增益仿真阵增益定义为整个阵的输出端信噪比和阵的单个阵元输出的信噪比。对于一个点源来说,如果噪声是各向同性的,则阵增益可以写为:
| $ \begin{array}{l} {\rm{DI}} = \frac{{4{\rm{ \mathsf{ π} }}\sigma _n^2}}{{\sigma _n^2\int_0^{\rm{ \mathsf{ π} }} {\int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {R\left( {\theta ,\phi \left| {\vartheta ,\varphi } \right.} \right){\rm{d}}\varphi \sin \vartheta {\rm{d}}\vartheta } } }} = \\ \;\;\;\;\;\frac{4}{{\int_0^{{\rm{2 \mathsf{ π} }}} R (\theta |\vartheta )\sin \vartheta {\rm{d}}\vartheta }} \end{array} $ | (18) |
反卷积波束形成的增益与常规波束形成的增益之比被称为反卷积增益(deconvolution gain, DG),是衡量反卷积波束比常规波束形成器输出信噪比提高多少的参数,即:
| $ {\rm{DG}} = \frac{{{\rm{D}}{{\rm{I}}_{{\rm{dGv}}}}}}{{{\rm{D}}{{\rm{I}}_{{\rm{CBF}}}}}} = \frac{{\int_0^{\rm{ \mathsf{ π} }} {{R_{{\rm{CBF}}}}\left( {\theta \left| \vartheta \right.} \right)\sin \vartheta {\rm{d}}\vartheta } }}{{\int_{ - {\rm{ \mathsf{ π} }}}^{\rm{ \mathsf{ π} }} {{R_{{\rm{dCv}}}}\left( {\theta \left| \vartheta \right.} \right)\sin \vartheta {\rm{d}}\vartheta } }} $ | (19) |
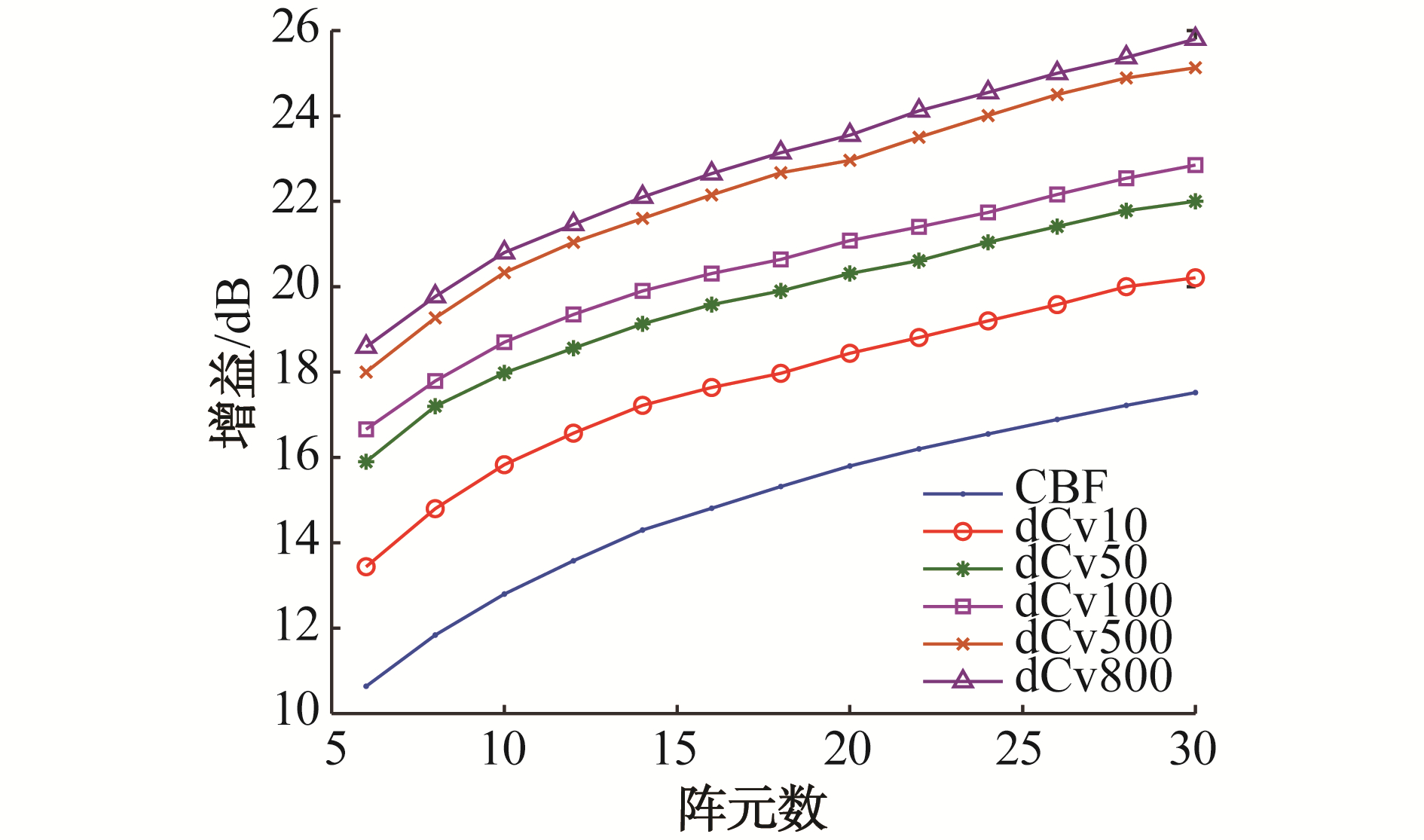
图 5为矢量阵常规波束形成与迭代不同次数的NNLS反卷积波束形成的对比分析图,在计算过程中,R(θ|ϑ)由常规波束形成和反卷积波束形成的方位谱代替。由图 5可见,随着NNLS的迭代次数增加,dCv的增益逐渐增加,这是因为随着迭代次数的增加,主瓣宽度逐渐变窄。但当迭代次数超过500次时,阵增益增加的很小,这是因为NNLS算法接近收敛。
|
Download:
|
| 图 5 矢量阵CBF和dCV的增益对比分析 Fig. 5 Directivity index comparison of CBF and dCV as a function of the number of elements | |
左右舷分辨的能力通常由左右舷抑制比来衡量,也叫左右舷抑制增益,是衡量阵列左右舷分辨能力的定量参数,单位是dB,定义为一对映像方位的响应之比[15],即:
| $ G\left( {\theta ,{\theta _0}} \right) = 10\lg {\left| {\frac{{R\left( {\theta ,{\theta _0}} \right)}}{{R\left( { - \theta ,{\theta _0}} \right)}}} \right|^2} $ | (20) |
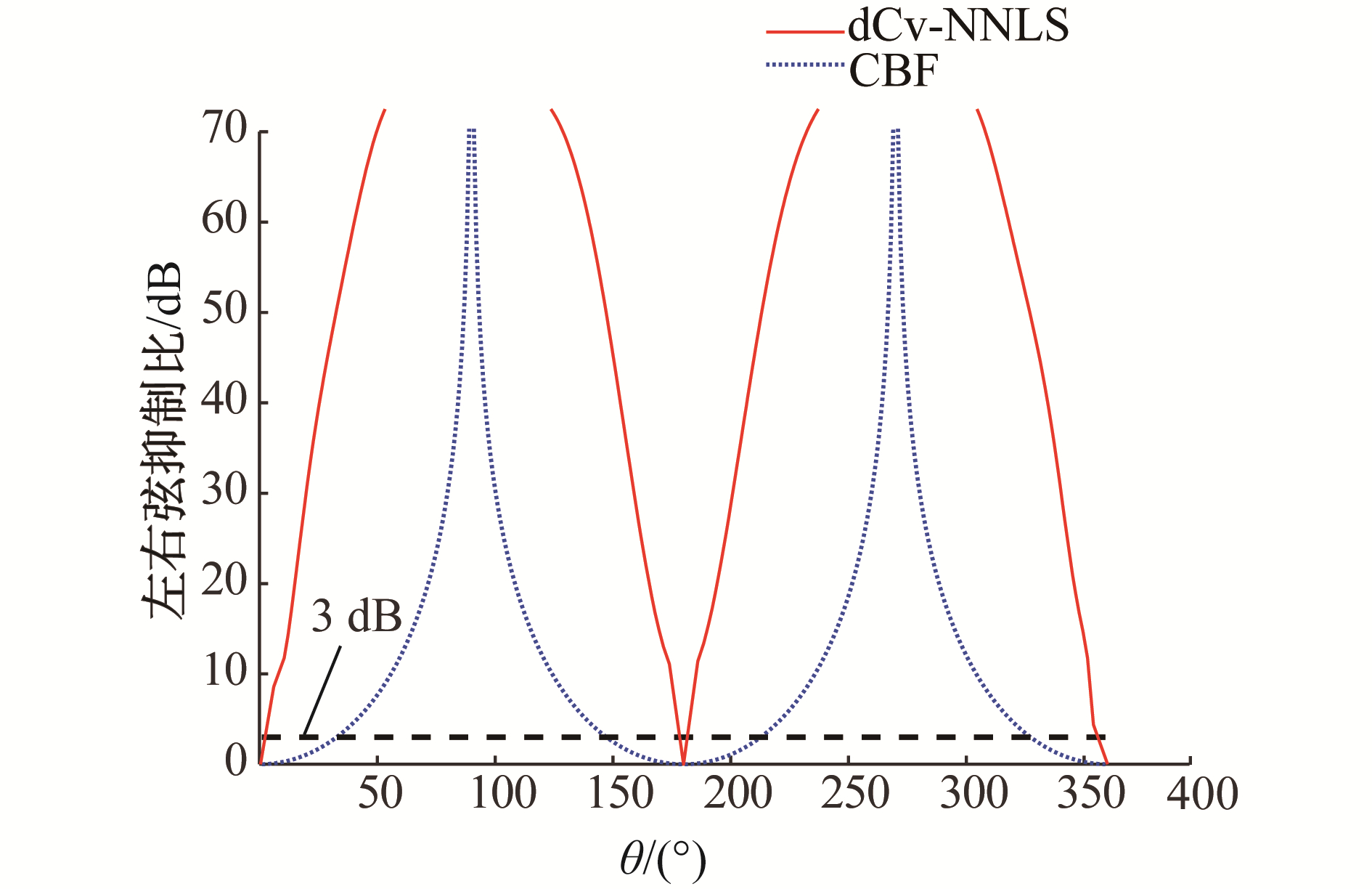
左右舷抑制比是波束图中目标方位谱峰与映像方位谱峰相差的分贝数,左右舷抑制比越高表示左右舷分辨的效果越好。针对来自不同方位的信号在不同信噪比条件下的左右舷抑制比进行了仿真对比,仿真参数同上,常规波束形成和反卷积的左右舷抑制比真结果如图 6。
|
Download:
|
| 图 6 矢量阵CBF和dCV的左右舷抑制比 Fig. 6 The left/right suppression ratio of dCv and CBF | |
图 6中的虚线为3 dB的门限。由图可见,矢量波束形成左右舷分辨能力不均匀,在阵列的法向附近左右舷分辨能力最优,当目标靠近阵列端射方向附近时,左右舷分辨能力迅速下降,对于常规波束形成端射方向附近很大范围内的角度左右舷分辨能力小于3 dB。反卷积波束形成结果的左右舷抑制比明显优于常规波束形成,有更好的左右舷抑制效果,数值仿真获得的小于3 dB的左右舷抑制比的角度范围为仅有17°。
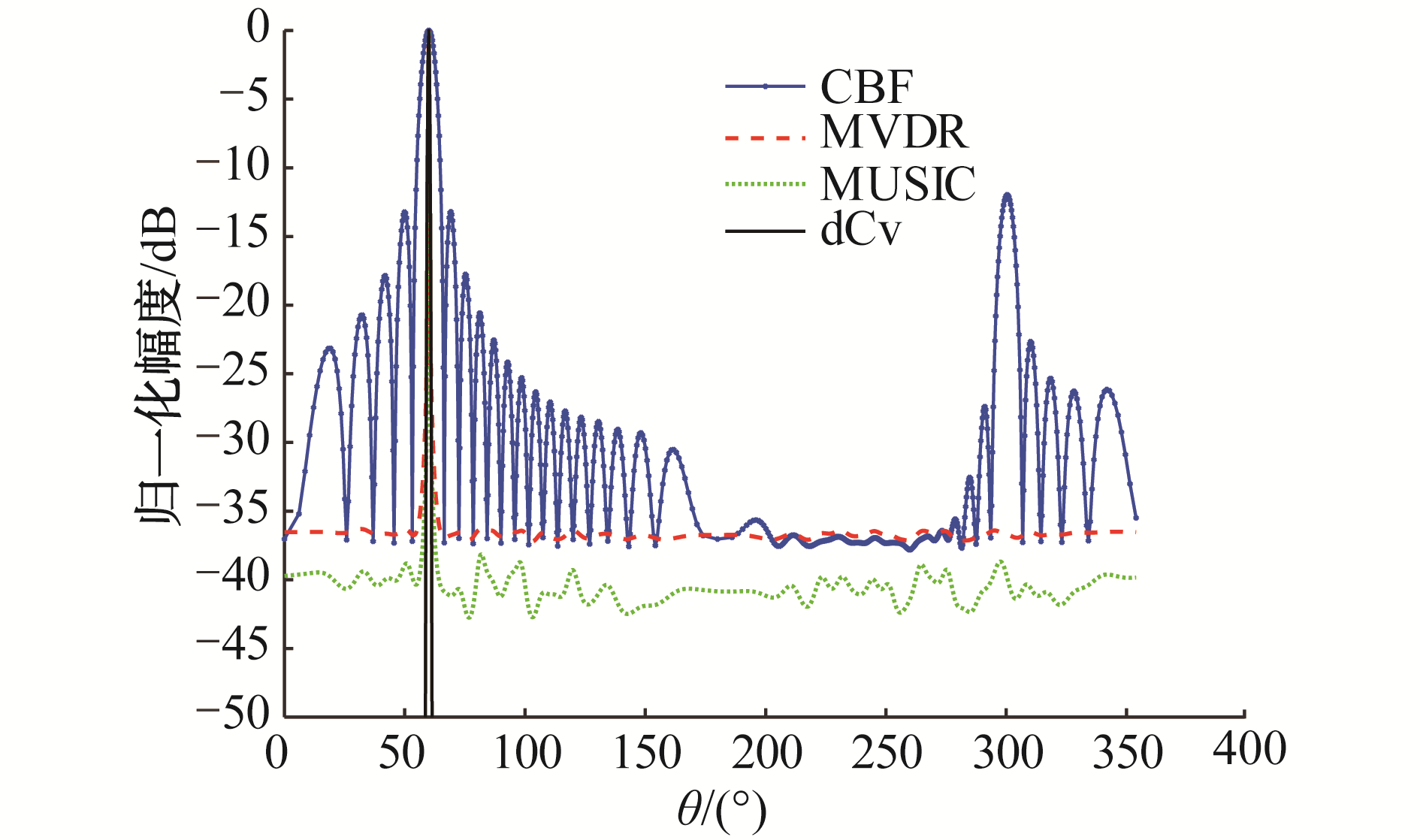
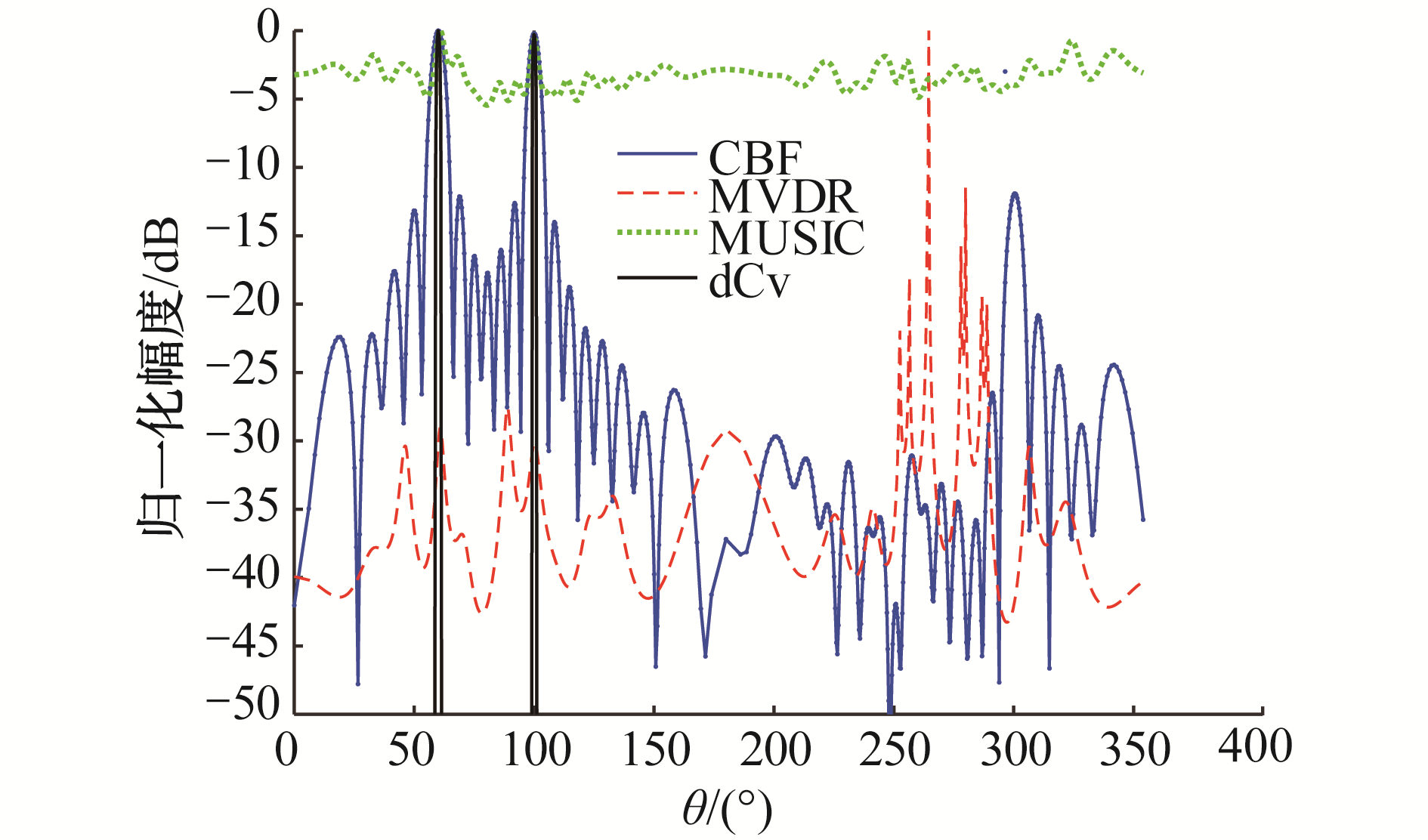
2.3 矢量阵反卷积与多种波束形成算法性能对比仿真条件:20元矢量阵,信号频率500 Hz,入射角度,输入信噪比为20 dB。仿真比较CBF、MVDR、MUSIC、和NNLS-dCv几种算法对信号的DOA估计性能,结果如图 7。由图 7可见,3种方法的分辨率都明显优于CBF,与MUSIC和MVDR方法相比,dCv方法主瓣窄的同时旁瓣级最低。
|
Download:
|
| 图 7 矢量阵波束输出空间谱DOA估计性能比较 Fig. 7 Beam power distribution using different DOA algorithms | |
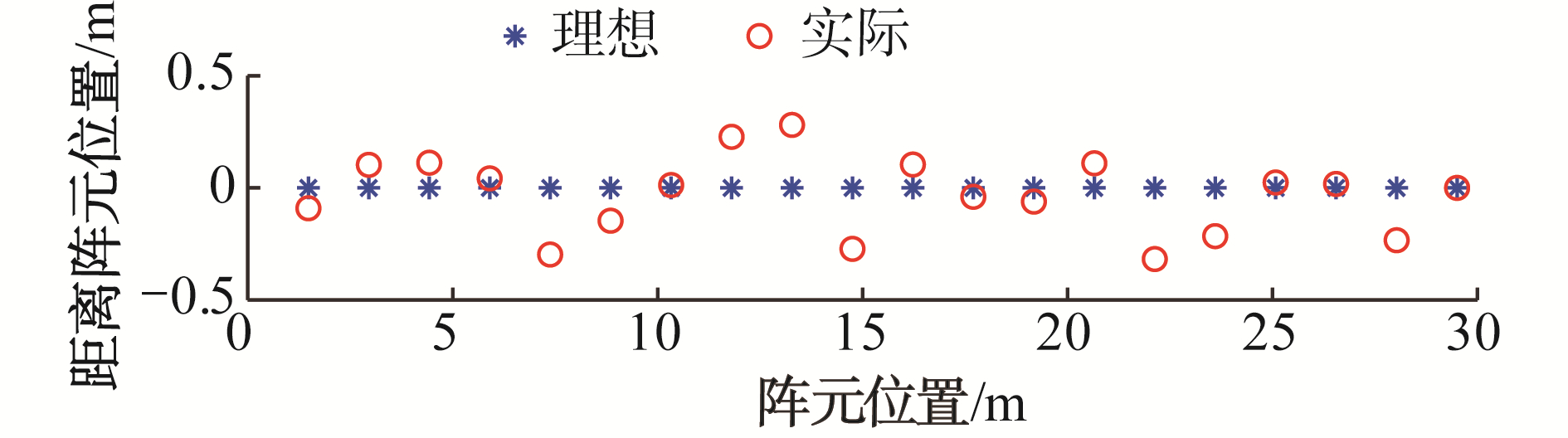
假设阵元位置存在随机误差,方差为0.15倍阵元间距,阵元位置示意图如图 8所示。
|
Download:
|
| 图 8 无阵元位置与有阵元位置对比 Fig. 8 The array configuration with and without position error | |
图 9为有阵元位置误差时矢量阵CBF和dCV的波束输出对图。由图 9可见,当存在阵元位置误差时,MVDR及MUSIC方法的性能明显下降。dCV波束形成也存在一定的旁瓣级升高现象,但整体抗阵位误差的能力仍然优于另外2种算法。

|
Download:
|
| 图 9 有阵元位置误差时矢量阵CBF和dCV的波束输出对比 Fig. 9 Beam output power comparison of CBF and dCV with array position | |
图 10为相同条件下双目标仿真结果,信号频率为500 Hz和800 Hz,入射角度分别为60°、100°,快拍数K=1。由图 10可见,由于MVDR和MUSIC算法无法适应单快拍模型,此时方法已经失效。CBF和dCv仍能准确估计目标方位。因此,dCv算法在实际应用时适用于小样本少快拍数据处理,对快速运动目标的方位跟踪效果更好。
|
Download:
|
| 图 10 单快拍波束输出空间谱估计性能比较 Fig. 10 Beam output power comparison for single snapshot data | |
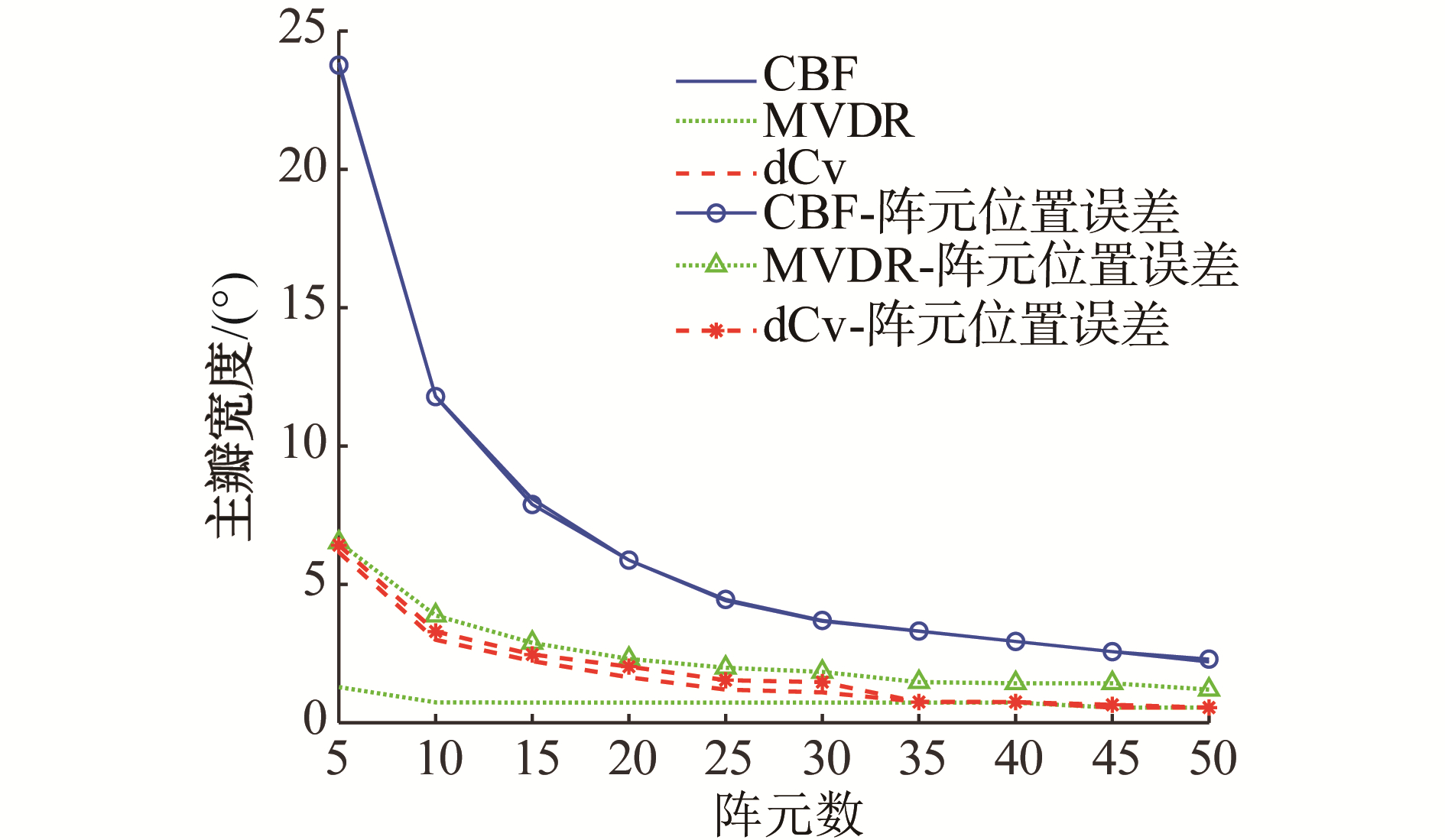
图 11显示了20元阵CBF,MVDR和dCv-NNLS的-3 dB主瓣宽度对比图,由于MVDR和MUSIC的主瓣宽度非常接近,所以在这里只比较了MVDR的主瓣宽度。信号从60°入射的500 Hz单频信号,信噪比为20 dB时。由图 11可见,CBF的主瓣宽度随着阵元数的增加而减少。3条没有标记的曲线代表了阵列结构为理想情况下的主瓣宽度曲线。在理想情况下,MVDR波束形成器有最窄的主瓣。有标记的3条曲线代表存在阵列误差时的主瓣宽度,阵列误差条件同图 8。存在阵列误差时,dCv-NNLS的主瓣宽度比MVDR和CBF的窄, dCv的主瓣宽度约是CBF的1/4。存在阵元位置误差时,CBF和dCv的主瓣宽度几乎不变,但是MVDR的主瓣宽度明显变宽。可见CBF和dCv算法更为稳健。
|
Download:
|
| 图 11 不同阵元数的主瓣宽度对比图 Fig. 11 Beam width as a function of the number of elements | |
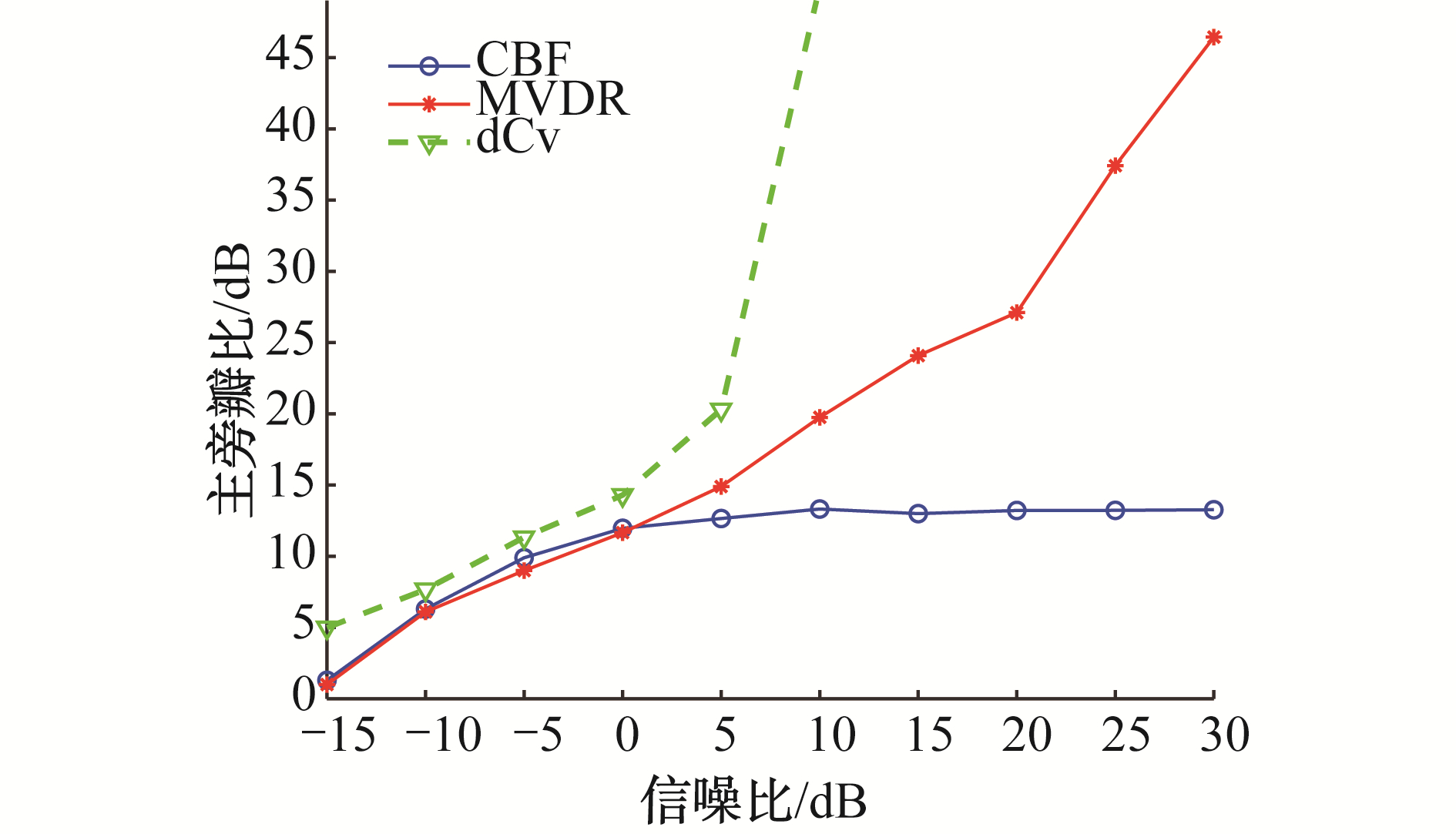
图 12显示了CBF、MVDR和dCv-NNLS在不同输入信噪比下的主旁瓣比,波束的主旁瓣比代表的是波束图中主瓣与最大旁瓣的比值。信号为从60°入射的500 Hz单频信号。从图 12可以看出,在所有的情况下,dCv-NNLS的主旁瓣均比高于CBF,有利于弱目标检测。在高信噪比情况下(SNR>0),dCv的主旁瓣比最高,然后是MVDR,最后是CBF;在低信噪比的情况(SNR < 0),dCv的主旁瓣比最高,然后是CBF,最后是MVDR。这是由于MVDR的稳健性差,在低信噪比时性能有所退化。dCv-NNLS在低信噪比时仍能取得较好的旁瓣抑制效果。
|
Download:
|
| 图 12 不同输入信噪比下的主旁瓣对比 Fig. 12 The peak-to-sidelobe ratio as a function of input SNR | |
1) 针对固定阵的阵列信号处理模型PSF可预测的特点,将噪声源定位中的非负最小二乘方法应用到矢量阵中,使反卷积波束形成算法可以应用到PSF是移变的阵列模型中。
2) 以矢量阵为例仿真证明了该算法的可行性,仿真结果表明,方法与矢量阵CBF和其他高分辨算法相比具有更好的增益、更窄的主瓣和低的旁瓣,且适用于快拍数少和存在阵元位置误差的情况下,具有良好的稳健性。
目前我们只考虑目标了在阵列的远场的模型,把入射信号假设成平面波,如果目标在阵列的近场,则PSF函数是与距离和方位有关的二维变量,事实上, 该方法在水声信号处理中近场声源被动定位的应用问题也是非常值得研究的方向。
| [1] |
DE CASTRO F C F, DE CASTRO M C F, ARANTES D S. Concurrent blind deconvolution for channel equalization[C]//Proceedings of IEEE International Conference on Communications. Helsinki, Finland, 2001: 366-371. https://ieeexplore.ieee.org/document/936964/
(  0) 0)
|
| [2] |
NSIRI B, CHONAVEL T, BOUCHER J M, et al. Blind submarine seismic deconvolution for long source wavelets[J]. IEEE journal of oceanic engineering, 2007, 32(3): 729-743. DOI:10.1109/JOE.2007.899408 (  0) 0)
|
| [3] |
LYLLOFF O, FERNÃNDEZ-GRANDE E, AGERKVIST F, et al. Improving the efficiency of deconvolution algorithms for sound source localization[J]. The journal of the acoustical society of America, 2015, 138(1): 172-180. DOI:10.1121/1.4922516 (  0) 0)
|
| [4] |
ZHONG Di, YANG Dong, ZHU Min. Improvement of sound source localization in a finite duct using beamforming methods[J]. Applied acoustics, 2016, 103: 37-46. DOI:10.1016/j.apacoust.2015.10.007 (  0) 0)
|
| [5] |
VONESCH C, UNSER M. A fast thresholded landweber algorithm for wavelet-regularized multidimensional deconvolution[J]. IEEE transactions on image processing, 2008, 17(4): 539-549. (  0) 0)
|
| [6] |
SEKKO E, THOMAS G, BOUKROUCHE A. A deconvolution technique using optimal Wiener filtering and regularization[J]. Signal processing, 1999, 72(1): 23-32. (  0) 0)
|
| [7] |
DOUGHERTY R. Extensions of DAMAS and benefits and limitations of deconvolution in beamforming[C]//Proceedings of the 11th AIAA/CEAS Aeroacoustics Conference. Monterey, California, 2005. https://www.researchgate.net/publication/260624421_Extensions_of_DAMAS_and_Benefits_and_Limitations_of_Deconvolution_in_Beamforming
(  0) 0)
|
| [8] |
EHRENFRIED K, KOOP L. Comparison of iterative deconvolution algorithms for the mapping of acoustic sources[J]. AIAA journal, 2012, 45(7): 1584-1595. (  0) 0)
|
| [9] |
BLAHUT R E. Theory of remote image formation[M]. Cambridge: Cambridge University Press, 2004.
(  0) 0)
|
| [10] |
YANG T C. Deconvolved conventional beamforming for a horizontal line array[J]. IEEE journal of oceanic engineering, 2018, 43(1): 160-172. DOI:10.1109/JOE.2017.2680818 (  0) 0)
|
| [11] |
YANG T C. Performance analysis of superdirectivity of circular arrays and implications for sonar systems[J]. IEEE journal of oceanic engineering, 2019, 44(1): 156-166. DOI:10.1109/JOE.2018.2801144 (  0) 0)
|
| [12] |
梁国龙, 马巍, 范展, 等. 矢量声纳高速运动目标稳健高分辨方位估计[J]. 物理学报, 2013, 62(14): 144302. LIANG Guolong, MA Wei, FAN Zhan, et al. A high resolution robust localization approach of high speed target based on vector sonar[J]. Acta physica sinica, 2013, 62(14): 144302. DOI:10.7498/aps.62.144302 (  0) 0)
|
| [13] |
时洁, 杨德森, 时胜国. 基于最差性能优化的运动声源稳健聚焦定位识别方法研究[J]. 物理学报, 2011, 60(6): 064301. SHI Jie, YANG Desen, SHI Shengguo. Robust localization and identification method of moving sound sources based on worst-case performance optimization[J]. Acta physica sinica, 2011, 60(6): 064301. (  0) 0)
|
| [14] |
褚志刚, 杨洋. 基于非负最小二乘反卷积波束形成的发动机噪声源识别[J]. 振动与冲击, 2013, 32(23): 75-81. CHU Zhigang, YANG Yang. Noise source identification for an engine based on FFT-non-negative least square (NNLS) deconvolution beamforming[J]. Journal of vibration and shock, 2013, 32(23): 75-81. DOI:10.3969/j.issn.1000-3835.2013.23.014 (  0) 0)
|
| [15] |
张宾, 孙贵青, 李启虎. 阵形畸变对拖曳双线阵左右舷分辨性能的影响[J]. 声学学报, 2008, 33(4): 294-299. ZHANG Bin, SUN Guiqing, LI Qihu. Effects of shape distortion upon left/right discrimination of towed twin-line array[J]. Acta acustica, 2008, 33(4): 294-299. DOI:10.3321/j.issn:0371-0025.2008.04.002 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


