2. 广东省新能源和可再生能源研究开发与应用重点实验室, 广东 广州 510640;
3. 中国科学院 可再生能源重点实验室, 广东 广州 510640;
4. 中国科学院大学, 北京 100049;
5. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. Guangdong Provincial Key Laboratory of New and Renewable Energy Research and Development, Guangzhou 510640, China;
3. Chinese Academy of Sciences Key Laboratory of Renewable Energy, Guangzhou 510640, China;
4. University of Chinese Academy of Sciences, Beijing 100049, China;
5. Collage of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
波浪能是一种分布广、蕴藏量丰富的可再生能源。波浪能利用技术种类繁多,振荡水柱技术是其中一种重要的方式。振荡水柱式技术是利用腔体将波浪能转化为气室中的气动能量(一级转换),然后通过空气透平将气室内的气动能量转化成为电能(二级转换)。在振荡水柱技术中,后弯管振荡水柱技术能量转换性能表现突出。目前实验研究表明,在规则波中,后弯管技术的一级转换(俘获宽度比)最高达到了204.5%,在随机波中,一级转换最高也达到了87.1%[1]。而振荡水柱中空气透平的转换效率较低,一般不超过60%[2]。因此,透平的低转换效率是制约振荡水柱技术发展的一个主要瓶颈。
由于振荡水柱中气流来回往复运动的特点,振荡水柱中的空气透平设计方法与常规单向稳定工况透平存在着一定的区别。在过去的文献中,主要对3类透平进行了研究以适用于这类双向流动气流,分别是Wells透平[3]、冲动式透平[4]、径向透平[5]。其中,Wells透平由于具有结构简单,制造方便,便于运行控制的特点,已广泛运用于在波浪能发电站中。如:1989年,日本坂田港口的防波提就安装了5个配有Wells透平的振荡水柱装置[6];1991-2000年,苏格兰Islay岛的波浪能示范发电站使用的是直径1.2 m的双叶轮Wells透平[7];1993年,葡萄牙皮考岛上的波浪能发电站使用的是直径2.3 m的Wells透平[8];2000年至今,苏格兰Islay岛新建的波浪能发电站使用的是2台250 kW的Wells透平发电机组[9]。
Wells透平工作在不稳定气流中。目前对Wells透平进行研究的文献,一般是基于准稳态分析的方法进行研究Wells透平在不稳定气流中的流动特性。准稳态分析方法一般先对Wells透平在不同流量系数下的稳定流动特性进行测试。非稳定流动下的流动特性则视为多个不同稳定流动状态的叠加,相互之间没有影响。这一方法在许多方法中广泛使用。文献[11-13]使用这一方法对Wells透平在非稳定流动中的流动特性进行分析。这一方法简单方便,只需测量Wells透平在稳定流动状态的流动特性,即可得到同一Well透平在任何不稳定流中的流动特性。但与真实运行状况是否一致仍然有待验证。
本文通过实验测试结合计算流体力学(computation fluid dynamic, CFD)分析的方法对Wells透平在稳定和不稳定流的流动特性进行研究。Wells透平在不稳定流中流动特性的研究有利于确定适合的Wells透平控制方法,进一步提升Wells透平实际运行的转换效率。
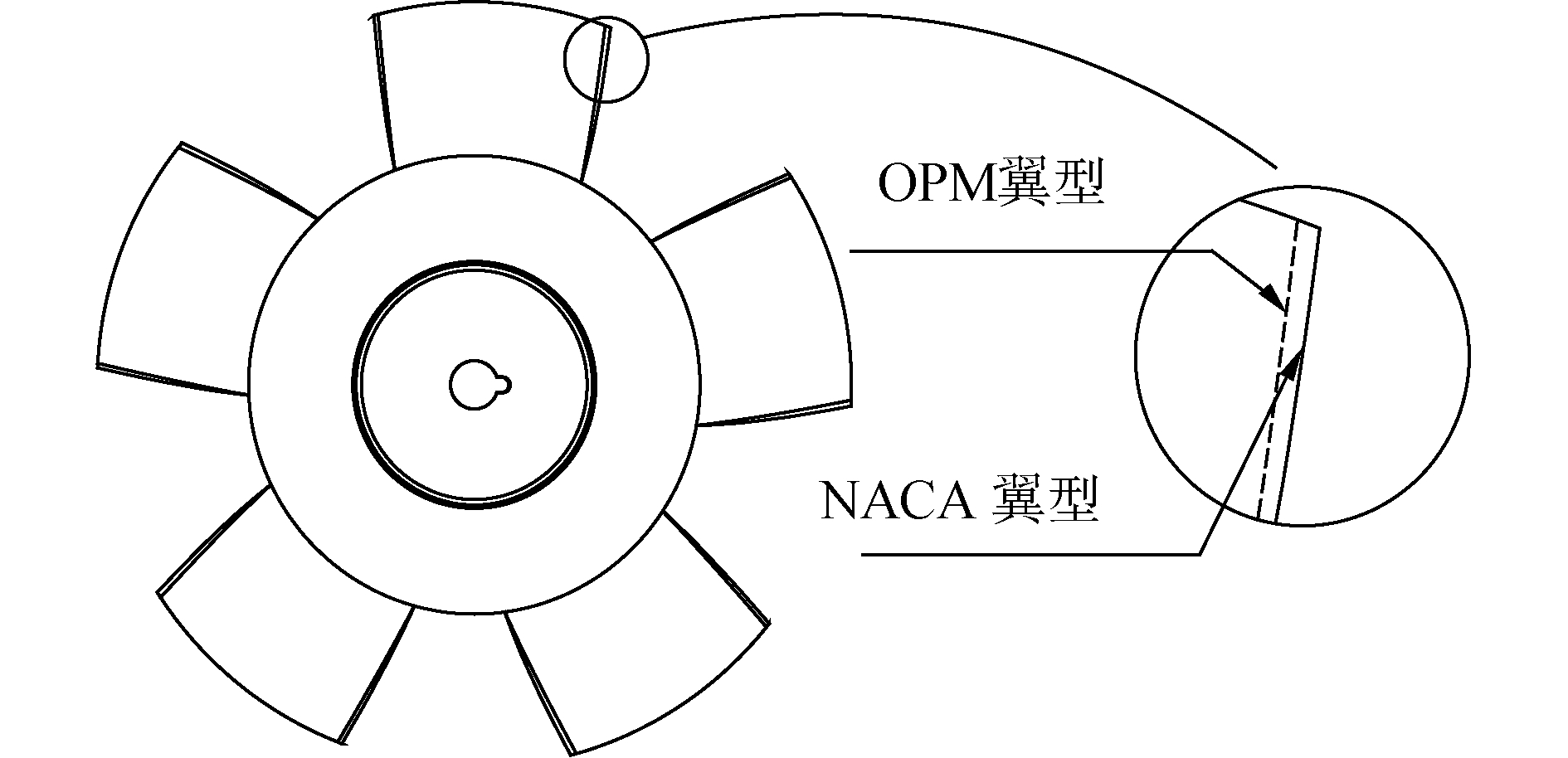
1 实验模型和研究方法 1.1 实验透平与实验测试方法本文对2个Wells透平在稳定流和不稳定流中的流动特性进行测试。2个Wells透平叶轮的外径均为200 mm。本文测试的2个Wells透平,一个使用NACA0020翼型进行设计,另一个使用遗传算法优化得到的翼型进行设计,优化翼型记作OPM翼型。2个翼型的形状以及曲率分布如图 1所示。2个透平使用同样的设计方法得到,设计方法见文献[14-15]。设计得到的透平示意图如图 2所示。2个透平叶栅稠度沿半径方向的叶栅稠度分布如表 1所示。

|
Download:
|
| 图 1 NACA0020翼型和OPM翼型在翼型表面的曲率分布 Fig. 1 Curvature radius distribution of NACA airfoil and OPM airfoil on the airfoil surface | |
|
Download:
|
| 图 2 OPM翼型和NACA翼型Wells透平的示意 Fig. 2 Wells turbine with the optimal airfoil and NACA airfoil | |
| 表 1 2个叶轮的叶栅稠度分布 Table 1 Distribution of solidity of two impellers |
为了了解不稳定气流对Wells透平的影响,应该得到Wells透平的内部流动的流场分布。目前,CFD方法可以得到透平的内部流场。但是,具体CFD结果的可靠性有待验证。一般,使用实验结果对CFD结果进行可靠性验证。如果数值计算结果与实验结果比较吻合,则可以把CFD结果视作是可靠的。
本文将通过实验测试结果来验证CFD计算方法的可靠性。在实验结果与数值模拟结果吻合的前提下,对透平内部的流动进行分析,得到不稳定流中Wells透平的流动特性。
本文所使用的实验测试装置主要由气缸、透平、扭矩仪、伺服电机等组成。测试装置结构图如图 3所示,现场布置图 4所示。

|
Download:
|
| 图 3 实验测试装置 Fig. 3 Test devices | |

|
Download:
|
| 图 4 实验测试装置现场布置 Fig. 4 Photograph of experimental test device | |
本文分别在稳定气流工况和不稳定下,对2组叶轮进行了性能测试。稳定气流工况下,驱动活塞的位移随时间以三角波的方式运动,产生速度大小恒定、但方向周期性变化的气流。不稳定气流工况下,驱动活塞的位移随时间以正弦波方式运动,产生方向和大小都不断变化的正弦波气流。实验时,伺服电机将Wells透平的转速控制在恒定转速,通过改变活塞运动速度的方法来测得不同流量系数下的透平转换效率。本文实验主要采用的测试转速为3 000 r/min,当流量系数过大,透平输出扭矩超出扭矩仪量程后,则采用2 000 r/min。实验过程中,每个工况进行3次实验。
实验过程中测量的变量包括:透平前后压差Δp,活塞的位移s,透平转速n,透平输出力矩M。其中,透平前后压差Δp通过采集卡采集,采集频率为8 Hz,压力传感器的量程为:-1~1 kPa,精度等级为0.5% FS;活塞的位置s通过统计旋转编码不同方向的脉冲数来测量,采集频率为8 Hz,每圈的脉冲数为2 000 Hz;透平转速n和透平输出力矩M通过扭矩传感器采集,采集频率为8 Hz,扭矩传感器的量程为:-0.1~+0.1 N·m,精度等级0.5% FS,适用范围为转速小于6 000 r/min。
1.2 数值计算模型为了减少计算量,本文只针对Wells透平单流道内流动进行CFD计算,在计算区域的周向设置2个周期性边界。计算区域的上游和下游长度均为叶顶处弦长的6倍长度。计算模型的网格如图 5所示。近壁网格与壁面的距离为0.01 mm,使得壁面y+的值约为1。

|
Download:
|
| 图 5 模型的网格划分 Fig. 5 The mesh of the model | |
本文计算过程中,透平的转速为3 000 r/min。采用为标准SST湍流模型计算。在稳定流动中,设置的边界条件主要包括:一个速度进口条件,进口速度随计算的工况而改变;一个压力出口条件,相对静压为0;叶片表面为无滑移壁面边界条件;轮毂和流道的外壁面则设为相对于绝对坐标系静止的无滑移壁面边界条件;在周向的2个边界条件则为旋转的周期性边界条件。在不稳定流动中,壁面边界条件和周期性边界条件不变,出口设为压力开放边界条件,入口设为开放速度边界条件,速度以正弦波的方式随时间变化。
2 结果与讨论 2.1 稳定流中实验结果与CFD结果对比根据实验测量结果,即可整理得到Wells透平压力系数Cp、功率系数ψ和透平转换效率η与流量系数ϕ的关系:
| $ C_{p}=\overline{\Delta p} /\left(\frac{1}{2} \rho U^{2}\right) $ | (1) |
| $ \psi=P_{\text { sharp }} /\left(\frac{1}{2} \rho U^{3} S_{\text { tur }}\right) $ | (2) |
| $ \eta=P_{\text { sharp }} / P_{\text { air }} $ | (3) |
| $ \phi=v / U $ | (4) |
式中:
| $ \overline{\Delta p}=\frac{1}{T} \int_{0}^{\mathrm{T}}|\Delta p| \mathrm{d} t $ | (5) |
| $ P_{\mathrm{air}}=\frac{1}{T} \int_{0}^{\mathrm{T}}|\dot{V} \cdot \Delta p| \mathrm{d} t $ | (6) |
| $ P_{\text { sharp }}=\frac{1}{T} \int_{0}^{\mathrm{T}}(M \cdot \omega) \mathrm{d} t $ | (7) |
| $ S_{\mathrm{tur}}=\frac{\pi}{4}\left(D_{\mathrm{tip}}^{2}-d^{2}\right) $ | (8) |
| $ v=\frac{\overline{\dot{V}}}{S_{\mathrm{tur}}} $ | (9) |
式中:Δp为透平前后压差,测量得到;
|
Download:
|
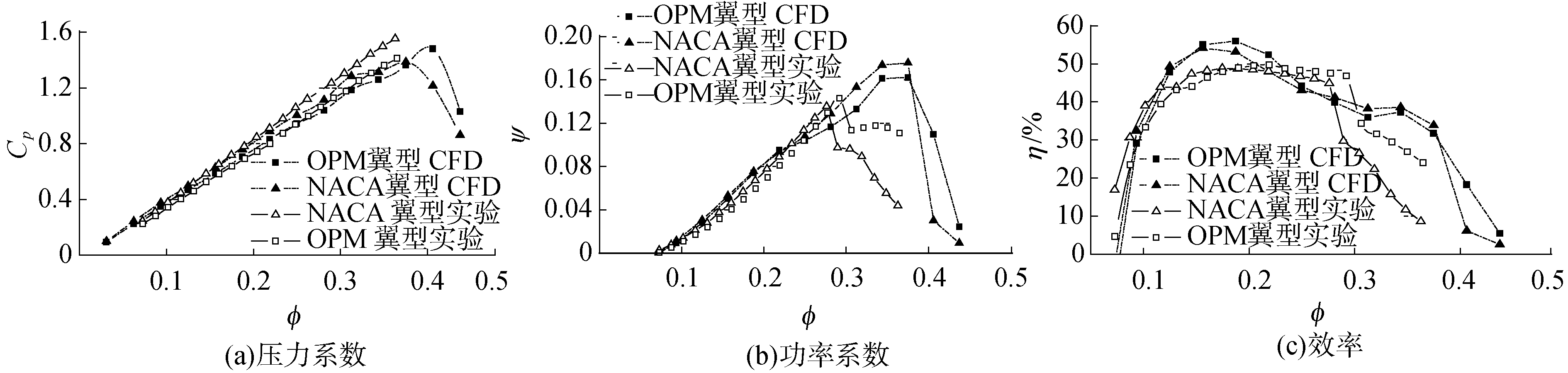
| 图 6 2个叶轮的实验结果和CFD结果 Fig. 6 Experimental results and CFD results for of two impellers | |
由图 6(a)、(b)可知,2个叶轮压力系数曲线和功率系数曲线的CFD结果与实验结果比较吻合。当ϕ>0.3,功率系数的CFD结果与实验结果出现比较大的误差。这因为当ϕ>0.3时,叶轮的输出力矩超过了扭矩仪的量程,本文的实验测试转速从3 000 r/min调整至2 000 r/min,但数值计算设置转速仍为3 000 r/min。总体来看,当实验条件与CFD条件一致时,CFD结果是可信的。
此外,由图 6(c)可知,OPM翼型叶轮的最高转换效率略高于NACA翼型。根据实验结果,NACA翼型叶轮的最高转换效率为48.85%,3次试验的标准差为0.129 0%。OPM翼型叶轮的最高转换效率为49.74%,3次试验的标准差为0.133 1%。CFD结果中,NACA翼型叶轮的最高转换效率为54.08%,OPM翼型叶轮的最高转换效率为55.96%。实验结果和CFD结果都表明,OPM翼型拓宽了Wells透平正常运行的流量系数范围。
综合图 6,本文的CFD结果对压力系数和功率系数的计算都是比较准确的,对于效率的计算定量上与实验结果误差比较大,但定性上与实验结果相符。
2.2 不稳定气流对Wells透平流动的影响与其他透平相比,Wells透平内部流动的最大特点是通过透平的气流速度是不定向、不稳定的,气流反复进入和流出Wells透平,透平的进口也是透平的出口。一个典型通过Wells透平的气流是透平的进口速度以正弦波的规律变化。其他不规则气流则可以看作是多个正弦波的叠加。
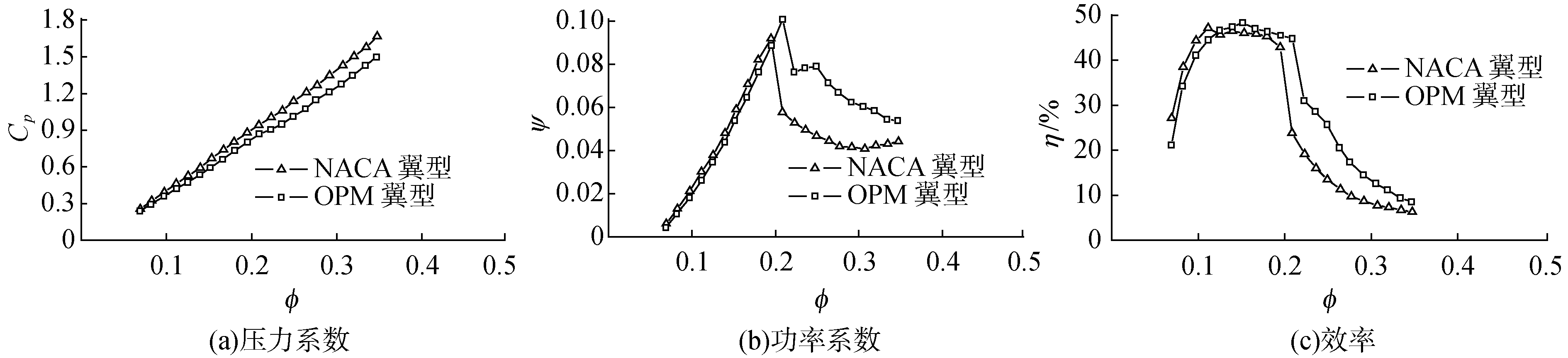
为了研究Wells透平在不稳定气流下的流动特性,通过实验测量了Wells透平在不同正弦波中的流动特性。图 7显示了2种翼型透平在不同振幅正弦波中压力系数、功率系数,以及效率与流量系数的关系。
|
Download:
|
| 图 7 2个叶轮在不稳定流中的性能曲线 Fig. 7 The experimental performance of two impellers in unsteady flow | |
由图 7可以看出,在不稳定气流中,2个不同翼型Wells透平的曲线呈现与稳定流中曲线同样的规律,但数值上有所差别。OPM翼型叶轮的最高转换效率略高于NACA翼型叶轮的最高转换效率。根据实验结果,在不稳定流动中,NACA翼型叶轮的最高转换效率为47.17%,而优化翼型叶轮的最高转换效率为48.32%。
为了对比Wells透平在不稳定流中的流动特性与稳态流动的差别,可以对实验测得的输出扭矩曲线和准稳态分析结果进行对比。准稳态分析结果是根据稳定流测试结果,以气流速度进行插值得到。
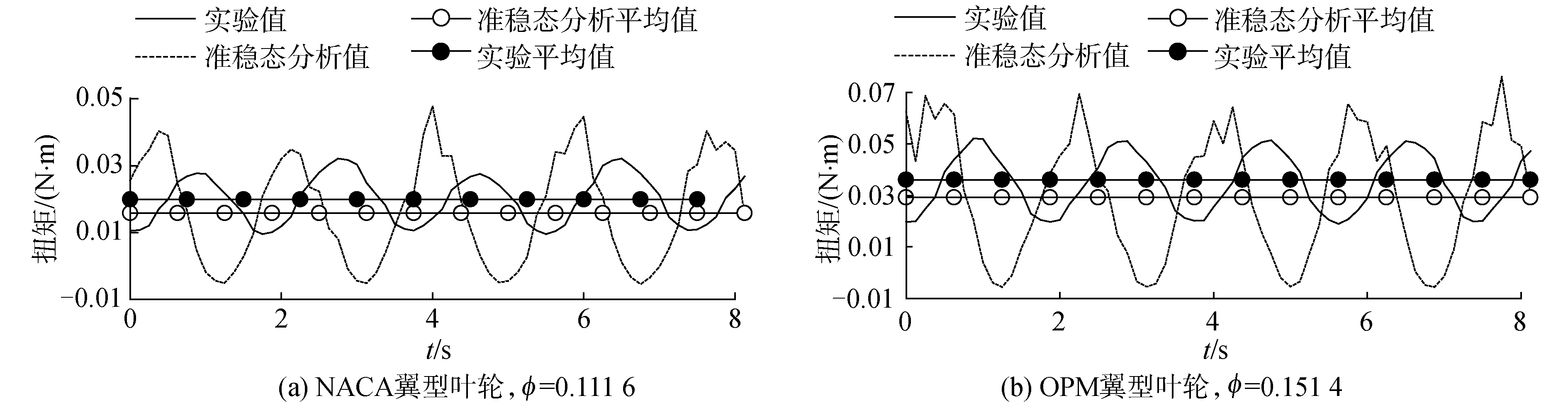
图 8(a)显示了NACA翼型叶轮在流量系数ϕ=0.111 6时的输出扭矩准稳态分析曲线和实验曲线。图 8(b)显示了OPM翼型叶轮在流量系数ϕ=0.151 4时的输出扭矩准稳态分析曲线和实验曲线。2个叶轮分别在这2个流量系数下的转换效率最高。
|
Download:
|
| 图 8 2个叶轮的输出扭矩曲线 Fig. 8 Output torque of two impellers | |
在图 8中,准稳态分析曲线与实验曲线相差很大。图 8中扭矩仪测量的并不是叶轮的瞬时输出扭矩,而是叶轮传递到负载的扭矩。由于实验过程中叶轮转速一直小范围波动,且负载是可以自动调控输出扭矩的伺服电机,因此测量得到的扭矩并不是叶轮的瞬时输出扭矩。
图 8测量的扭矩虽然不是叶轮的瞬时输出扭矩。但一段时间内扭矩仪传递的能量等于叶轮的输出功。假设实验过程中叶轮的转速等于恒定值,则实验测得输出扭矩的平均值等于叶轮输出扭矩的平均值。
观察图 8可知,实验测量输出扭矩的平均值高于理论分析输出扭矩的平均值。其中,图 8(a)的实验测量平均值是理论分析平均值的1.26倍;图 8(b)的实验测量平均值是理论分析平均值的1.23倍。这一实验结果表明,气流的不稳定性能提高Wells透平的输出力矩。
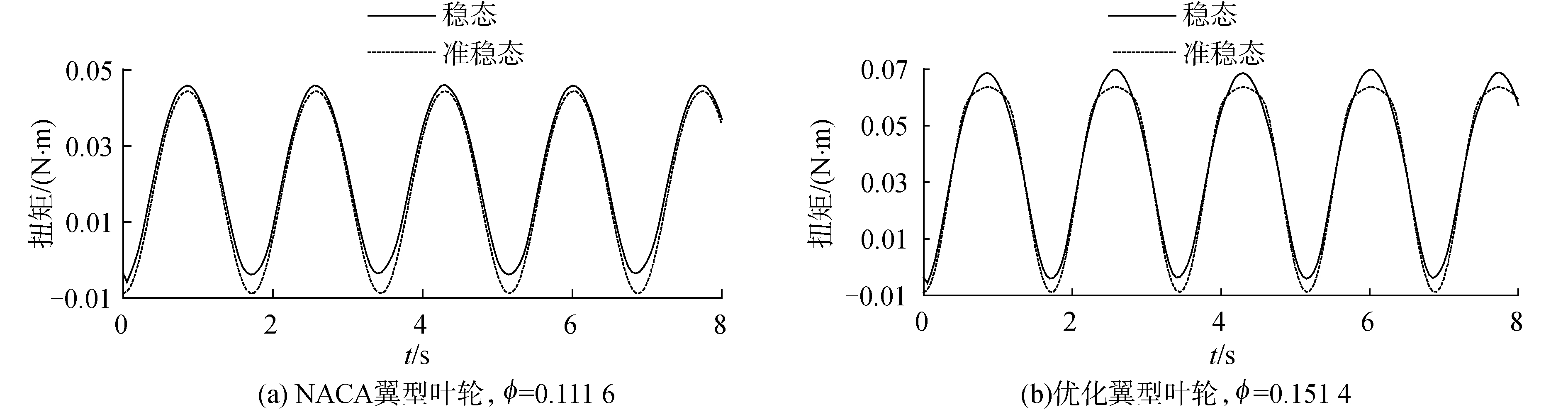
由于负载端惯性的影响,Wells透平在不稳定流中的瞬时输出扭矩是非常难直接测量得到。因此,实验结果不能显示出Wells透平在不稳定流中的瞬时输出扭矩和准稳态输出扭矩有何区别。为此,本文对Wells透平进行了非稳态的CFD分析,以研究不稳定流对Wells透平内部流动的影响。图 9显示了Wells透平输出扭矩的非稳态CFD结果,以及根据稳态CFD结果插值得到的准稳态分析结果。
|
Download:
|
| 图 9 2个叶轮输出扭矩的CFD结果 Fig. 9 CFD results of two impellers′ output torque | |
图 9的规律与实验测试结果基本一致,但数值上与实验测试结果略有差距。图 9(a)的非稳态计算平均值是准稳态分析平均值的1.27倍。图 9(b)的非稳态计算平均值是准稳态分析平均值的1.05倍。
由图 9可知,不稳定流动中,Wells透平的输出力矩高于准稳态理论分析结果的主要原因在于:不稳定流中,Wells透平的输出力矩的最大值和最小值一般高于同样流速下稳态流动的输出扭矩,但大小与具体翼型有关系。实际上,当Wells透平的输出力矩是最大值时,通过Wells透平的进口速度正好处于正弦波的波峰或波谷。Wells透平的输出力矩是最小值时,通过Wells透平的速度正好等于0。
由本文2种翼型Wells透平在不稳定流中的研究结果可知,Wells透平在不稳定流中的流动特性与稳定流不同。直接使用目前常用的准稳态分析方法可能得到错误的结果。
3 结论1) 稳定流的实验测试结果和CFD结果都表明,OPM翼型提高了Wells透平的最高转换效率,拓宽了正常运行流量系数范围。实验结果表明在稳定流中,NACA叶轮的最高转换效率为48.85%,OPM翼型的最高转换效率为49.74%。不稳定流的实验结果表明同样的结论。
2) 不稳定流的输出力矩测试结果表明:气流的不稳定性可以提高Wells透平的输出力矩。不稳定流的CFD结果表明,在进口速度同样为0的前提下,不稳定流中的阻力矩更小。在进口速度达到峰值时,一般情况下,Wells透平输出力矩大于稳定流中同样进口速度时的输出力矩。但不同翼型的提升效果不一样,OPM翼型输出力矩的提升幅度低于NACA翼型。
根据本文的结果,Wells透平在不稳定流中的流动特性与稳定流的流动特性不完全一样,直接使用目前文献常用的准稳态分析方法可能得到错误的结果。但如何考虑不稳定流对Wells透平的影响,是一个有待研究的问题。
| [1] |
WU Bijun, LI Meng, WU Rukang, et al. Experimental study on primary efficiency of a new pentagonal backward bent duct buoy and assessment of prototypes[J]. Renewable energy, 2017, 113: 774-783. DOI:10.1016/j.renene.2017.06.010 (  0) 0)
|
| [2] |
STARZMANN R, CAROLUS T H, TEASE K, et al. Effect of design parmeters on aero-acoustic and aerodynamic performance of Wells turbines[C]//Proceedings of the ASME 201130th International Conference on Ocean, Offshore and Arctic Engineering. Rotterdam, Netherlands, 2011: 1-10. https://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1624875
(  0) 0)
|
| [3] |
RAGHUNATHAN S, TAN C P, OMBAKA O O. Performance of the Wells self-rectifying air turbine[J]. The aeronautical journal, 1985, 89(890): 369-379. (  0) 0)
|
| [4] |
SETOGUCHI T, KANEKO K, MAEDA H, et al. Impulse turbine with self-pitch-controlled guide vanes for wave power conversion:performance of mono-vane type[J]. International journal of offshore and polar engineering, 1993, 3(1): 73-78. (  0) 0)
|
| [5] |
MCCORMICK M E, REHAK J G, WILLIAMS B D. An experimental study of a bidirectional radial turbine for pneumatic wave energy conversion[C]//Proceedings of Mastering the Oceans Through Technology. Newport, RI, USA, 1992: 866-870. https://journals.sagepub.com/doi/abs/10.1243/095765002760024917
(  0) 0)
|
| [6] |
OHNEDA H, IGARASHI S, SHINBO O, et al. Construction procedure of a wave power extracting caisson breakwater[C]//Proceedings of the 3rd Symposium on Ocean Energy Utilization. Tokyo, 1991: 171-179.
(  0) 0)
|
| [7] |
WHITTAKER T J T, MCILWAINE S J, RAGHUNATHAN S. A review of the Islay shoreline wave power plant[C]//Proceedings of the 1st European Wave Energy Symposium. Edinburgh, 1993: 283-286.
(  0) 0)
|
| [8] |
FALCÃO A F D O. The shoreline OWC wave power plant at the Azores[C]//Proceedings of the 4th European Wave Energy Conference. Denmark, 2000: 42-47.
(  0) 0)
|
| [9] |
HEATH T, WHITTAKER T J T, BOAKE C B. The design, construction and operation of the LIMPET wave energy converter[C]//Proceedings of the 4th European Wave Energy Conference. Aalborg, 2000: 49-55.
(  0) 0)
|
| [10] |
SETOGUCHI T, SANTHAKUMAR S, TAKAO M, et al. A modified Wells turbine for wave energy conversion[J]. Renewable energy, 2003, 28(1): 79-91. DOI:10.1016/S0960-1481(02)00006-X (  0) 0)
|
| [11] |
TAKAO M, SETOGUCHI T, NAGATA S, et al. A study on the effects of blade profile and non-uniform tip clearance of the wells turbine[C]//Proceedings of the ASME 200827th International Conference on Offshore Mechanics and Arctic Engineering. Estoril, Portugal, 2008: 1-8. http://proceedings.asmedigitalcollection.asme.org/proceeding.aspx?articleid=1634269
(  0) 0)
|
| [12] |
CUI Ying, HYUN B S. Numerical study on Wells turbine with penetrating blade tip treatments for wave energy conversion[J]. International journal of naval architecture and ocean engineering, 2016, 8(5): 456-465. DOI:10.1016/j.ijnaoe.2016.05.009 (  0) 0)
|
| [13] |
黄忠洲, 余志, 蒋念东, 等. 规则往复流中Wells透平自起动过程的数值模拟和实验研究[J]. 太阳能学报, 2006, 27(3): 284-288. HUANG Zhongzhou, YU Zhi, JIANG Niandong, et al. Self-starting performance of wells turbine in regular reciprocating airflow[J]. Acta energiae solaris sinica, 2006, 27(3): 284-288. DOI:10.3321/j.issn:0254-0096.2006.03.014 (  0) 0)
|
| [14] |
STARZMANN R, CAROLUS T. Effect of blade skew strategies on the operating range and aeroacoustic performance of the Wells turbine[J]. Journal of turbomachinery, 2014, 136(1): 011003. (  0) 0)
|
| [15] |
STARZMANN R, CAROLUS T, TEASE K, et al. Wells turbine rotors: a comparison of the predicted and measured aerodynamic performance[C]//Proceedings of the 9th European Turbomachinery Conference. Istanbul, Turkey, 2011: 1085-1095.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


