2. 北京航天长征飞行器研究所, 北京 100076;
3. 中集海洋工程有限公司, 广东 深圳 518000
2. Beijing Institute of Space Long March Vehicle, Beijing 100076, China;
3. China International Marine Containers Offshore Engineering Co. Ltd., Shenzhen 518000, China
现代海战不仅是武器装备之间的比拼,优秀的作战策略更是保证获胜的重要一环,其中海上封锁已经成为各海军强国夺取制海权的常用方式。在目标水域和洋区,采用海上封锁获取海洋控制权是一种有效且易实施的军事手段[1-2],发生海战时,针对重要军事水域的防御和关键航道的封锁是确保作战胜利的必要条件。水下爆炸尤其是近场水下爆炸会对舰船结构造成严重毁伤,通过对水下爆炸载荷特性分析不断发展,舰船毁伤特性研究进一步完善[3-7],因此,可通过水雷的水下爆炸载荷对舰船造成严重毁伤来实现水域封锁的目的。
国内针对水雷布阵作战封锁最优策略的研究成果十分匮乏。衡辉等[8]建立了服从均匀分布和正态分布目标舰船通过雷障正面宽度时毁伤概率的数学模型,并对数学模型进行了仿真计算;尚奇等[9]采用二维数学分析及统计的方法,建立了符合水雷攻击模式的数学模型,对小子样条件下的弹点散布方差进行研究;冷相文等[10]运用概率论多维随机变量分布理论,构建了目标舰船毁伤概率模型;朱红波等[11]根据自航水雷的散布特性,以水雷障碍对目标舰船平均毁伤概率为评估指标,建立了自航水雷障碍期望雷位配置优化模型;王威等[12]运用柔性仿真方法和理论对常规潜艇攻势布雷作战进行了研究,设计出了一个柔性仿真框架,为常规潜艇攻势布雷效能评估提供了一种方法和思路。目前研究主要集中在雷阵对单艘舰船的封锁概率问题,并未对多艘舰船进行毁伤概率评估,且对于布雷数量的优化问题缺乏探究。本文以某目标水域为研究对象,建立计及水雷散布特性的雷阵封锁概率评估模型,运用压缩粒子群算法探索多种因素控制下的水雷布阵优化方案,为制定海上水雷封锁策略提供技术依据。
1 数学模型 1.1 水雷布放模型通常自航水雷的布设方式主要以扇面齐射为主,以期望雷位与射击平台所在方位为扇面中线,根据水雷数量、雷线长度向期望雷位齐射[13]。水雷并非可以准确到达指定的雷位,受各种外界因素的影响,会导致实际雷位与期望雷位存在一定的散布误差[14-15]。
为描述方便,以雷障区域中心为坐标原点,以原点向右平行于雷障宽度定为X轴正向,以原点垂直于X轴向上为Y轴正向,建立自航水雷障碍坐标系,如图 1所示。设雷障正面宽度为L,布设n枚水雷,其中空心原点代表期望雷位,坐标为(

|
Download:
|
| 图 1 自航水雷障碍坐标系 Fig. 1 Self-propelled mine barrier coordinate system | |
在图 1雷障坐标系所布设的二维水雷,都可投影至垂直于目标舰船航向的一条雷线,即将二维雷阵转化为单维雷线,且两者的封锁概率相同,简化了分析。图 2表示目标舰船以攻角α驶入雷障区,图 3表示水雷经过投影后在雷线上的布置图。

|
Download:
|
| 图 2 目标舰船以攻角α驶入雷区 Fig. 2 The target warship enters the mine barrier at the angle of attack α | |

|
Download:
|
| 图 3 投影后的雷线示意 Fig. 3 Schematic diagram of projected mine line | |
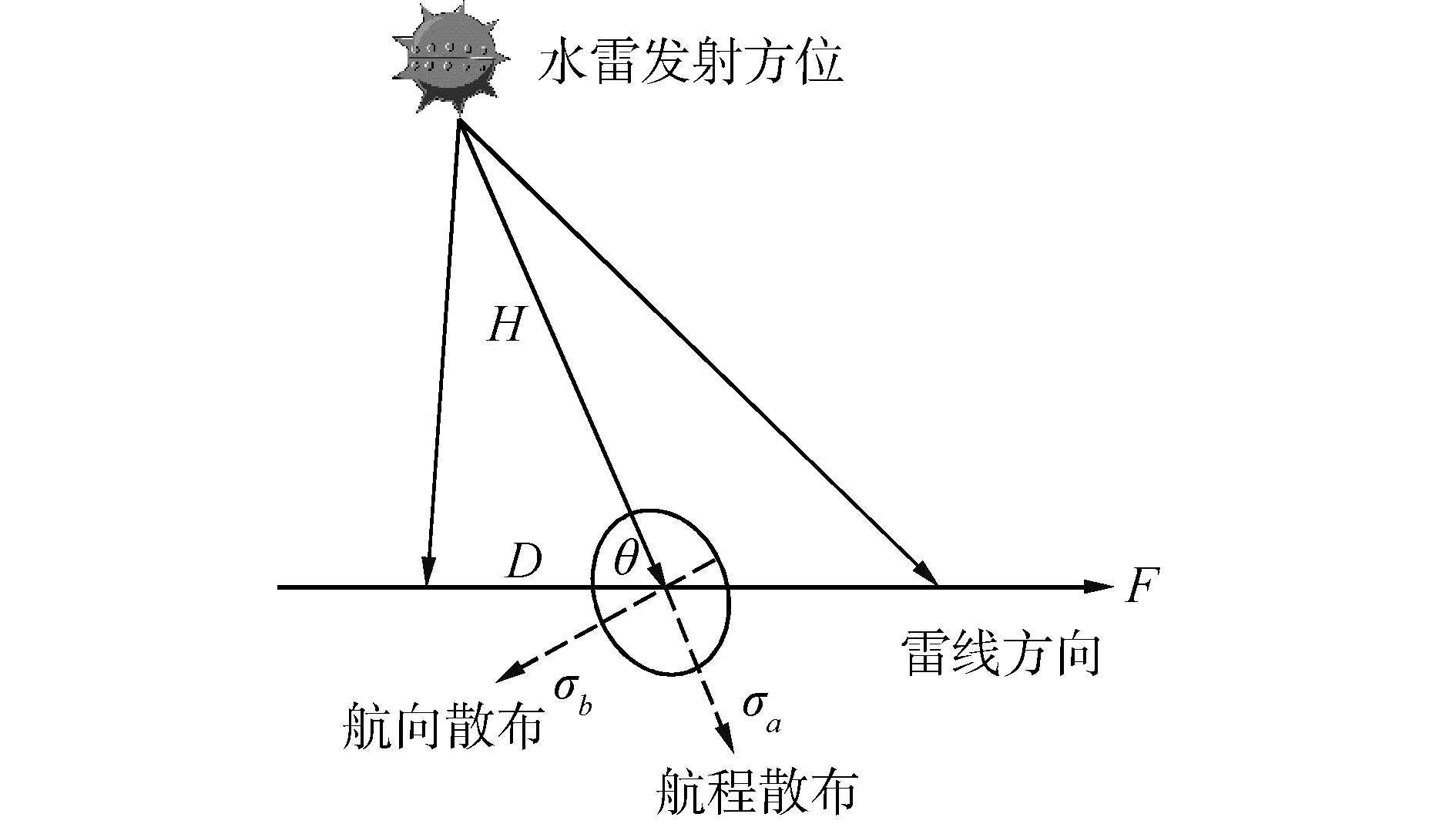
综合各种影响水雷布设的误差,将水雷散布误差主要分为航程误差和航向误差[16],2个方向分布密度函数均呈正态分布,航程散布误差与水雷发射方向一致,航向散布误差方向垂直于水雷发射方向,如图 4所示。
|
Download:
|
| 图 4 水雷布设散布误差椭圆示意 Fig. 4 The error ellipse diagram of dispersion during the laying of mine | |
假设某一水雷的航程散布均方差为σa,航向散布均方差为σb,期望雷位横坐标为x,航程误差分布概率为f1,航向误差分布概率为f2,则:
| $ \left\{\begin{array}{l}{f_{1} \sim N\left(\overline{x}, \sigma_{a}^{2}\right)} \\ {f_{2} \sim N\left(\overline{x}, \sigma_{b}^{2}\right)}\end{array}\right. $ | (1) |
σa与σb主要受航程的影响较大,一般认为它们与水雷航程之间存在线性关系[17]:
| $ \left\{\begin{array}{l}{\sigma_{a}=K_{a} S_{0}} \\ {\sigma_{b}=K_{b} S_{0}}\end{array}\right. $ | (2) |
式中:S0为水雷发射点至落点间的距离;Ka为航程偏差率;Kb为航向偏差率。
已知任意一枚水雷的实际落点与期望落点的距离都满足雷位散布椭圆规律,发射方向H与雷线方向F的夹角为θ, 则该枚水雷位于雷线上的分布概率密度函数f为:
| $ f \sim N\left(\overline{x}, \sigma_{m}^{2}\right) $ | (3) |
其中σm2=σa2cos2θ+σb2sin2θ。
1.2 雷阵封锁概率评估模型假设目标舰船以攻角90°通过雷障区,雷障区域宽度即为计算时的雷线长度L,取坐标原点为雷线中点,实际航线与X轴的交点坐标为xs,由于其航线未知,可假设随机变量xs服从某一概率分布p(xs)。此外共有N枚水雷均匀分布于雷区,第i枚水雷在雷线上的实际坐标为xi,期望坐标为xi,且xi服从均值为xi、散布均方差为σim的正态分布,则可推导出第i枚水雷在雷线方向上的散布概率密度函数pfi[18]:
| $ \left\{\begin{array}{l}{p_{f i}=\delta \eta} \\ {\delta=\frac{1}{\sqrt{2 {\rm{ \mathsf{ π} }}} \sigma_{i m}}} \\ {\eta=\exp \left(\frac{-\left(x_{i}-\overline{x}_{i}\right)^{2}}{2 {\sigma_{i m}}^{2}}\right)}\end{array}\right. $ | (4) |
其中:
| $ \sigma_{i m}^{2}=\sigma_{i a}^{2} \cos ^{2} \theta+\sigma_{i b}^{2} \sin ^{2} \theta $ |
| $ \overline{x}_{i}=L i /(N+1)-L / 2 $ |
式中:i是水雷在雷线上投影后,依次从雷线负半轴到正半轴的编号,i=1, 2, …, N。
只有目标舰船位于水雷动作半径Wr内,水雷才有可能被引爆,即需要满足条件:
| $ \left|x_{\mathrm{s}}-x_{\mathrm{i}}\right| \leqslant W_{r} $ |
计及布放完好概率pb和水雷的正常起爆概率pr的影响,当目标舰船经过时,第i枚水雷引爆的概率为:
| $ p_{\mathrm{g} i}\left(x_{\mathrm{s}}\right)=p_{\mathrm{r}} p_{\mathrm{b}} \int_{x_{\mathrm{s}}-W_{\mathrm{r}}}^{x_{\mathrm{s}}+W_{\mathrm{r}}} p_{\mathrm{f}i} \mathrm{d} x_{i} $ | (5) |
目标舰船通过雷阵并引爆水雷的过程中,能否失去战斗能力是一个概率事件,本文以pm代表舰船毁伤的概率,其大小主要取决于舰船排水量、尺寸、吃水深度以及水雷破坏半径等因素[19-20],则第i枚水雷对舰船造成毁伤,使其失去战斗力的概率为:
| $ p_{\mathrm{h}i}\left(x_{\mathrm{s}}\right)=p_{\mathrm{g} i}\left(x_{\mathrm{s}}\right) p_{\mathrm{m}} $ | (6) |
对于某射击平台同一时刻发射出去的水雷,其受外界影响基本一致,具有相同的散布性质,即航程误差和航向误差具有相同的分布规律,那么:
| $ \sigma_{1 a} \approx \sigma_{i a} \cdots \approx \sigma_{n a} $ |
| $ {\sigma}_{1 b} \approx {\sigma}_{i b} \cdots \approx {\sigma}_{n b} $ |
即推得σ1 m≈σim…≈σnm≈σm。
而雷阵封锁概率是指在舰船通过目标水域时,至少有一枚水雷引爆并造成舰船毁伤的概率。对于上述雷线布设N枚水雷时,雷阵的封锁概率pn为:
| $ p_{n}=1-\prod\limits_{i=1}^{n}\left(1-p_{\mathrm{h}i}\right) $ | (7) |
雷阵封锁概率主要分为水雷散布概率和舰船目标触雷概率,由雷阵封锁概率模型式(7),可根据舰船的通过方式计算雷阵封锁概率。假设目标舰船的计划航线在雷线上任意一点通过的概率为pxs,则可计算出整个雷线的封锁概率P为:
| $ P=\int_{-\frac{L}{2}}^{\frac{L}{2}} p_{n} p_{x_{s}} \mathrm{d} x_{s} $ | (8) |
由于舰船通过雷障的方式复杂多变,导致pxs的求解十分复杂。为便于计算,本文以目标舰船均匀概率通过雷障时为研究对象,其航线与雷线上的交点xs在雷线上服从均匀分布,即
| $ P_{\mathrm{u}}=\frac{1}{L} \int_{-\frac{L}{2}}^{\frac{L}{2}} p_{n} \mathrm{d} x_{s} $ | (9) |
为验证雷阵封锁概率评估模型的准确性,根据水下近场爆炸作用下舰船的毁伤特性设置工况[21-22],确定水雷的毁伤半径,并采用蒙特卡罗算法对舰船通过目标水域时的封锁概率进行仿真计算[23],最后通过理论公式计算结果与仿真结果对比验证数值模型的有效性。
在水雷散布概率验证中,取水雷航程S0为7 km,散布误差率Ka和Kb为0.01[17],由式(2)可得航程散布均方差σa与航向散布均方差σb均为70 m;发射方向与雷线方向的夹角θ=90°,水雷作用半径32.7 m,正常起爆概率为pr=0.95,布放完好率为pb=0.95,造成舰船破坏率为pm=0.95,水雷数量N分别取4、6、8、10枚。分别应用理论公式和蒙特卡罗算法对上述工况进行计算,理论与仿真结果如图 5所示。从图 5中可以发现蒙特卡罗仿真结果与理论计算结果曲线吻合良好,验证了雷阵封锁概率评估模型的准确性。

|
Download:
|
| 图 5 理论与仿真结果对比 Fig. 5 Comparison of theoretical and simulated results | |
粒子群算法(particle swarm optimization,PSO)是数学上一种具有代表性的优化算法,具有易于实现、结果准确等优点[24],常被应用于求解实际工程问题。为有效控制粒子的飞行速度使得算法达到全局探测与局部开采两者间的有效平衡,Clerc等[25]构造了引入收缩因子的PSO算法,即压缩粒子群算法(particle swarm optimization with compression factor,CFPSO),其速度更新公式为:
| $ v_{i d}^{k+1}=\varphi\left\{v_{i d}^{k}+c_{1} r_{1}\left(p_{i d}-x_{i d}^{k}\right)+c_{2} r_{2}\left(p_{g d}-x_{i d}^{k}\right)\right\} $ | (10) |
| $ \varphi=\frac{2}{\left|2-C-\sqrt{C^{2}-4 C}\right|}, \quad C=c_{1}+c_{2} $ |
式中:k为当前迭代次数;vidk是当前k次迭代下的速度;φ为收缩因子;c1和c2为学习因子;r1和r2为[0, 1]范围内的随机数;pid是第i个粒子迄今为止搜索到的最优位置称为个体极值;xid是第i个粒子的向量;pgd是整个粒子群迄今为止搜索到的最优位置为全局极值。
粒子群算法的优化速度受2个方面的影响[26],即迭代步数M和粒子数N,总共循环数为M×N。为比较PSO和CFPSO 2种算法在迭代步数M和粒子数N选取方面的优劣,结合实际数学问题,通过算例进行具体分析:求解
本文先选取40个粒子,分别选取100、1 000和10 000迭代步,以5次计算结果平均值作为f(x)的最优解。本文在PSO算法中学习因子通常取c1=c2=2,权重为0.5,而CFPSO通常取c1=c2=2.05,权重为0.729[27],本算例2种算法的具体参数设置如表 1所示。目标函数优化结果如表 2所示。
| 表 1 在40个粒子数时PSO和CFPSO参数设置 Table 1 The parameter settings for the PSO and CFPSO When the numbers of particles is 40 |
| 表 2 不同迭代步fmin(x)计算结果比较 Table 2 Comparison of fmin(x) calculation results for different iterative steps |
由表 2可知,在低迭代步数情况下,CFPSO可优先得到比较好的结果。而在大迭代步数下,PSO效果要比CFPSO收敛的好。
为比较PSO和CFPSO 2种算法在粒子个数选取方面的优劣,本文分别选取10、20和40个粒子,以5次计算结果平均值作为目标函数的最优解,2种算法的具体参数设置如表 3所示。目标函数优化结果如表 4所示。
| 表 3 在1 000迭代步数下PSO和CFPSO参数设置 Table 3 The parameter settings for the PSO and CFPSO when the numbers of iterative steps is 1 000 |
| 表 4 不同粒子数fmin(x)计算结果比较 Table 4 Comparison of fmin(x) calculation results for different numbers of particles |
由表 4可知,在1 000迭代步的情况下,不论是低粒子数还是高粒子数,计算结果显示CFPSO算法均优于PSO算法。
综上所述,相对于基本粒子群法,带压缩因子的粒子群优化算法能在较低迭代数、较低粒子数情况下快速得到较理想的结果。
3 水雷布阵策略优化 3.1 水雷布阵方位优化传统的布雷方式主要为均匀布设与集中布设[11]。均匀布设即水雷均匀布设于雷线,以保证水雷能够散布整个雷线;集中布设即考虑了水雷自身的散布特性,发射点均选取雷线中点,形成自然雷障。在保证基本条件相同的情况下,分别用均匀布设、集中布设及CFPSO算法优化雷位3种布雷方式,对雷阵封锁概率进行对比分析。
以水雷封锁作战概率模型式(8)为目标函数,使用CFPSO算法对其进行优化。其参数设定如下:粒子数40,迭代步200,学习因子c1=2.05,c2=2.05,收缩因子φ=0.729,P代表目标函数求解结果。本文使用40个粒子,维度为6,初始化参数设置为随机化的标准正态分布。以目标水域宽度500 m,雷线上布设6枚水雷,毁伤半径R=32.7 m为研究基准,对于不同取值的雷位散布均方差σm,采用CFPSO算法优化期望水雷坐标,结果如表 5所示。
| 表 5 CFPSO算法迭代雷位布设优化 Table 5 Iterative optimization of mines layout based on CFPSO algorithm |
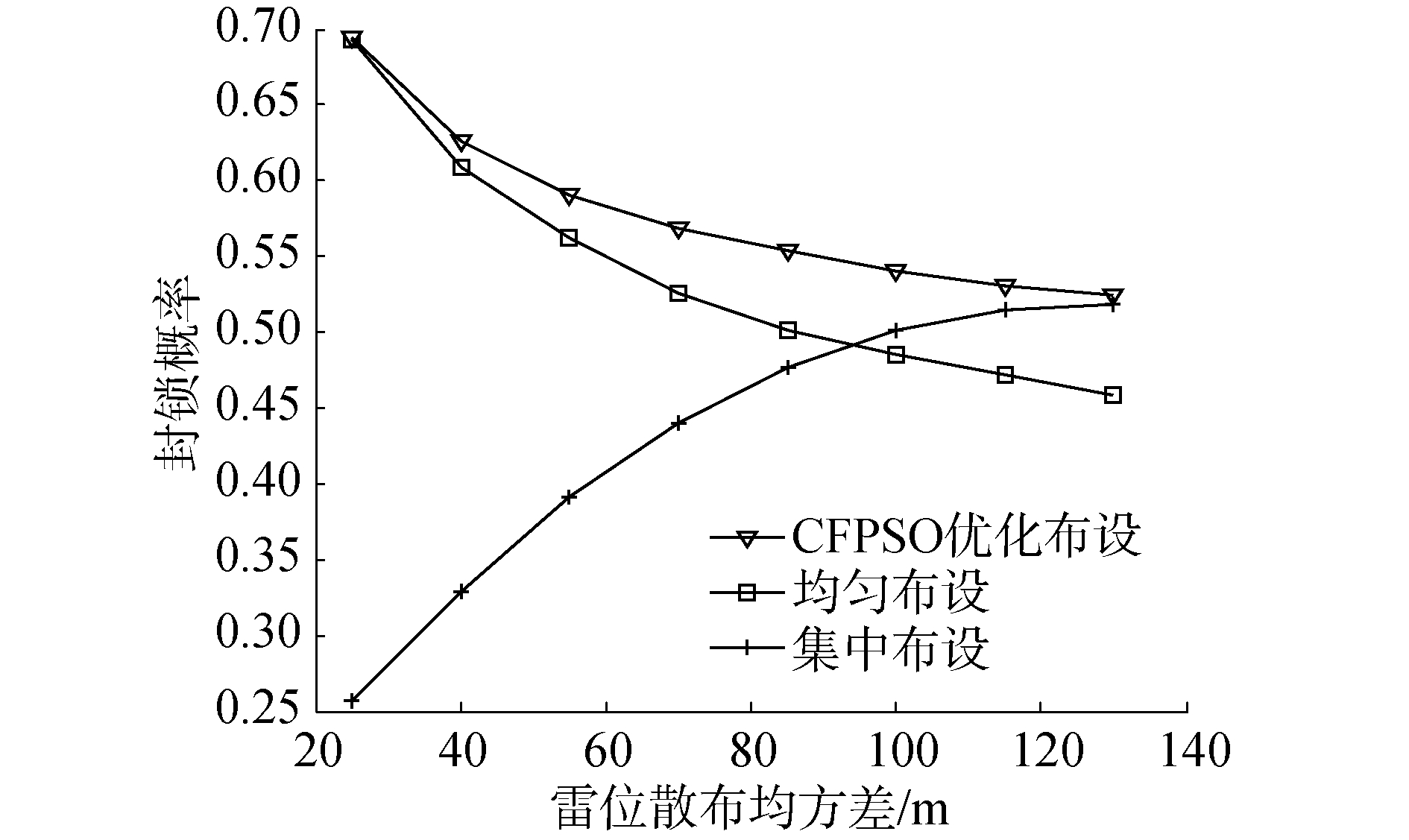
由图 6所示,CFPSO算法优化后的布设与均匀布设、集中布设相比可知:当目标舰船以均匀概率方式通过雷障时,对于不同雷位散布均方差,采用CFPSO算法优化后的水雷布设方式可使雷阵封锁概率最优。
|
Download:
|
| 图 6 3种布设方案结果对比 Fig. 6 Comparison of the results of three deployment schemes | |
假设封锁概率达到0.6时满足封锁需求,即期望封锁概率为0.6,目标水域宽度为500 m,以水雷毁伤半径R=32.7 m为研究基准,分别采用CFPSO算法优化布设、均匀布设和集中布设3种方式确定期望雷位,并得出不同水雷数量下封锁概率,从而可以确定目标水域达到所需封锁概率时的水雷布设数量。
已知条件:雷线宽度L=500 m,雷位散布均方差为70 m,正常起爆概率为pr=0.95,布放完好率为pb=0.95,造成舰船毁伤率为pm=0.95,本节研究某当量水雷的毁伤半径32.7 m下的雷阵封锁概率。选取水雷数目1~9,以CFPSO算法优化程序,对单艘舰船以均匀概率方式通过雷障时雷阵的封锁概率进行计算。
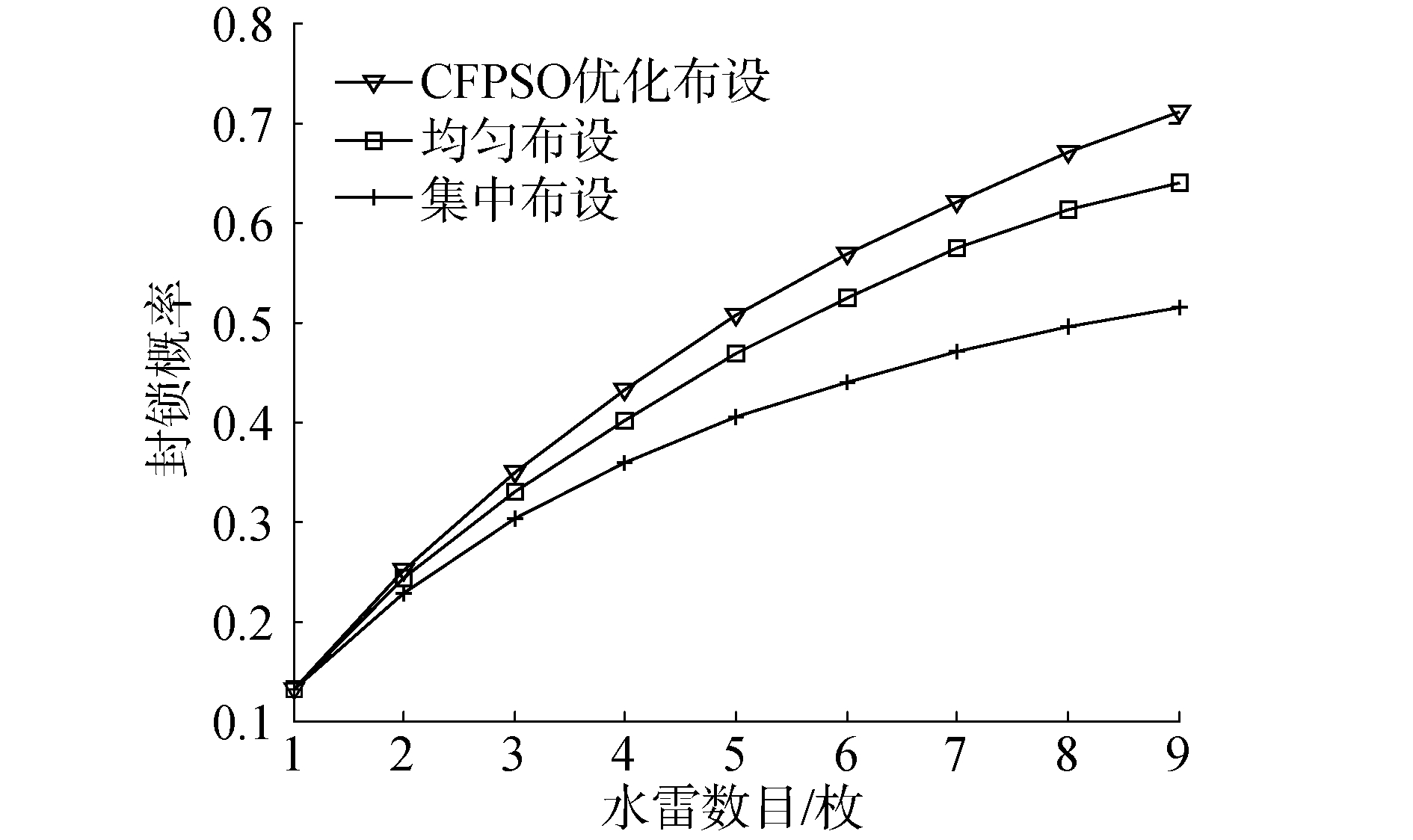
由表 6和图 7可知,3种布设方式下,雷阵封锁概率都随着水雷数量的增加而增大,CFPSO算法优化后的封锁概率均大于均匀布设和集中布设的情况。当目标舰船以均匀概率方式通过雷障区时,利用CFPSO算法优化后的布雷方式,布设7枚水雷可使雷阵封锁概率达到0.621,而采用均匀布设的布雷方式,需要布设8枚水雷才可达到期望封锁概率,因此相比均匀布设方式,采用CFPSO算法优化后的雷位可使水雷的利用率提升12.5%。表 7为CFPSO算法优化后的水雷发射坐标。
| 表 6 3种布设方案下不同水雷数目的雷阵封锁概率 Table 6 The blockading probability of mine arrays with different numbers of mines based on the three deployment schemes |
|
Download:
|
| 图 7 不同水雷数目下3种方案结果对比 Fig. 7 Comparison of the results of three deployment schemes with different numbers of mines | |
| 表 7 达到期望封锁概率时水雷的发射坐标 Table 7 The mines′ launch coordinates when the desired blockage probability is reached |
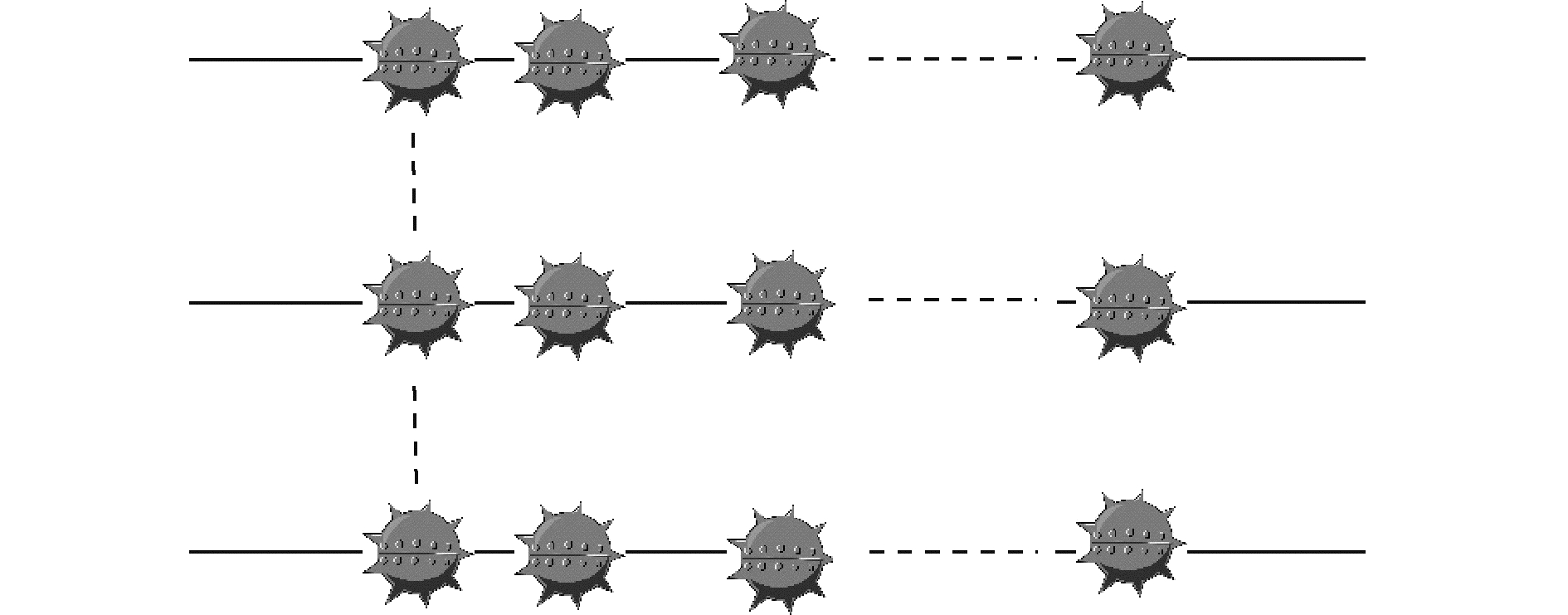
针对舰船编队通过雷障时,所有舰船全部毁伤即为封锁成功。现假设编队中舰船依次相关通过目标水域,雷阵封锁概率Pm即为全部舰船毁伤的概率。在舰船以编队航行时,所谓相关性通过雷阵,即后方舰船均以前方舰船通过雷阵时的航线为目标航线,故每条雷线最多可封锁一艘舰船。通过在目标水域长度方向均匀布设多重雷线进行封锁,每条雷线均以3.2.1节优化出的单雷线进行布设,其多雷线示意图如图 8所示。
|
Download:
|
| 图 8 多雷线示意 Fig. 8 The diagram of multi mine lines | |
假设舰船编队有舰船m艘,雷阵布有n条雷线,且n≥m。每条雷线均采用CFPSO算法优化后的布雷方式,其封锁概率均为P,则雷阵封锁概率为
| $ \sum\limits_{k=m}^{n} C_{k-1}^{m-1} P^{m}(1-P)^{k-m} \geqslant 0.6, \quad n \geqslant m $ | (11) |
为对雷阵水雷总数目进行优化,取m=3,即编队有3艘舰船,n的取值为3≤n≤8,即雷阵中布设3~8条雷线,则整个雷阵的封锁概率P3为:
| $ P_{3}=\sum\limits_{k=3}^{n} C_{k-1}^{2} P^{3}(1-P)^{k-3}, \quad 3 \leqslant n \leqslant 8 $ | (12) |
通过n取不同的值,由式(11)求得达到期望雷阵封锁概率时的单条雷线封锁概率的最小值Pmin,由表 6选取CFPSO优化后的最适概率Pb,并由式(12)得出雷阵封锁概率P3,且其对应雷线上的水雷数目为d,求得雷阵总雷数N=nd。其中,一条雷线上布设13枚水雷时,通过CFPSO算法优化后,封锁概率可达0.821;布设14枚时,雷线封锁概率为0.851。具体计算结果如表 8所示。
| 表 8 不同雷线数目下的各参数结果 Table 8 The various parameters with different numbers of mine lines |
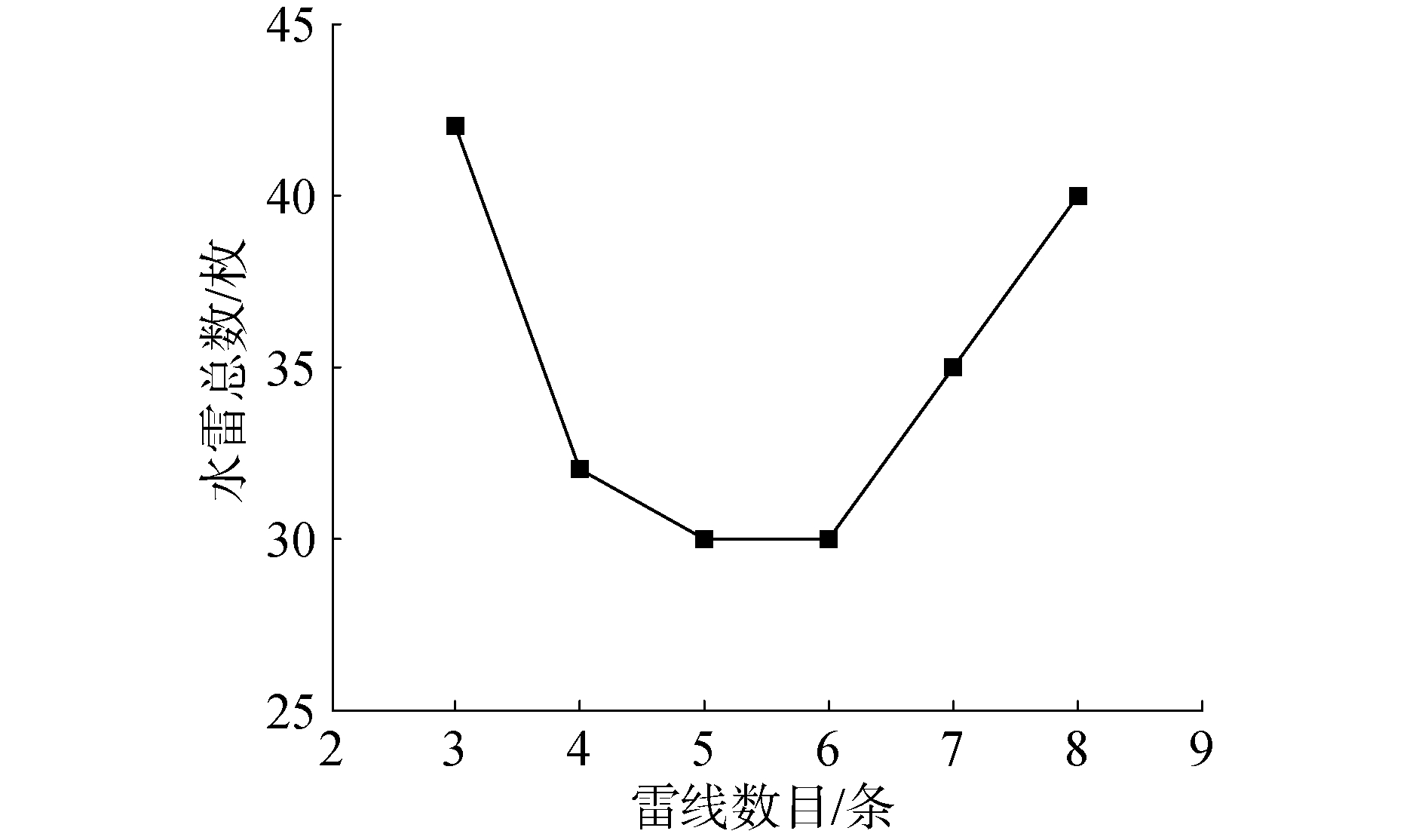
由图 9可知,最少布设的水雷数目为30枚,而以均匀布设方式布雷时,基于相同原理易得出,在满足雷阵期望封锁概率时最少布雷数目为35枚,因此在多雷线水雷数目优化方面,采用CFPSO算法优化后的雷位,可使水雷的利用率提升14.3%。
|
Download:
|
| 图 9 不同雷线数目下的水雷总数 Fig. 9 The total number of mines based on different numbers of mine lines | |
当N=30时,有2种布设方案,方案1为n=5时,即有5条雷线,每条雷线有6枚水雷;方案2为n=6时,即布设6条雷线,每条雷线有5枚水雷。由表 8的2种布设方案的雷阵封锁概率可知,在相同水雷数目情况下,方案1雷阵的封锁概率为0.628,方案2雷阵的封锁概率为0.667。故为能达到目标水域期望封锁概率0.6且使水雷总数最少,优先选择方案2的布阵方式。其中方案2中每条雷线上水雷的发射坐标x1~x5分别为-133.8、-133.8、0.04、133.8、133.8。
4 结论1) 针对单雷线模型,选取雷位散布均方差作为变量时,CFPSO算法对雷线上水雷发射坐标优化后的雷线封锁概率均比均匀布设和集中布设的方式高;选取水雷数目作为变量时,基于CFPSO算法优化后的布雷策略能够在较少的水雷数目下达到期望封锁概率。
2) 针对多雷线水雷数量优化,采用多条雷线等间距分布且每条雷线均利用CFPSO算法优化后的单雷线布雷策略进行布设,可使目标水域达到期望封锁概率的基础上,得出水雷总数最少的布设方案,节约了布设成本。
本文主要针对水面舰船进行布雷策略优化,故可将二维优化问题转为单维问题分析,在后续研究中进一步探究针对水下潜器的布雷封锁优化方案,即可将三维优化问题转化为二维问题分析。
| [1] |
傅金祝. 防御布雷和攻势布雷[J]. 水雷战与舰船防护, 2008, 16(4): 62-68. FU Jinzhu. Defensive and offensive mining[J]. Mine warfare & ship self-defence, 2008, 16(4): 62-68. (  0) 0)
|
| [2] |
王诗平, 孙士丽, 张阿漫, 等. 冲击波和气泡作用下舰船结构动态响应的数值模拟[J]. 爆炸与冲击, 2011, 31(4): 367-372. WANG Shiping, SUN Shili, ZHANG Aman, et al. Numerical simulation of dynamic response of warship structures subjected to underwater explosion shockwaves and bubbles[J]. Explosion and shock waves, 2011, 31(4): 367-372. (  0) 0)
|
| [3] |
ZHANG A M, WU W B, LIU Y L, et al. Nonlinear interaction between underwater explosion bubble and structure based on fully coupled model[J]. Physics of fluids, 2017, 29(8): 082111. DOI:10.1063/1.4999478 (  0) 0)
|
| [4] |
MING F R, ZHANG A M, XUE Y Z, et al. Damage characteristics of ship structures subjected to shockwaves of underwater contact explosions[J]. Ocean engineering, 2016, 117: 359-382. DOI:10.1016/j.oceaneng.2016.03.040 (  0) 0)
|
| [5] |
ZONG Zhi, ZHAO Yanjie, LI Haitao. A numerical study of whole ship structural damage resulting from close-in underwater explosion shock[J]. Marine structures, 2013, 31: 24-43. DOI:10.1016/j.marstruc.2013.01.004 (  0) 0)
|
| [6] |
CAO X Y, MING F R, ZHANG A M, et al. Multi-phase SPH Modelling of air effect on the dynamic flooding of a damaged cabin[J]. Computers & fluids, 2018, 163: 7-19. (  0) 0)
|
| [7] |
ZHANG Aman, YANG Wenshan, HUANG Chao, et al. Numerical simulation of column charge underwater explosion based on SPH and BEM combination[J]. Computers & fluids, 2013, 71: 169-178. (  0) 0)
|
| [8] |
衡辉, 李雪, 杨迎化, 等. 自航水雷雷障宽度对舰船毁伤概率影响[J]. 水雷战与舰船防护, 2015, 23(2): 35-38. HENG Hui, LI Xue, YANG Yinghua, et al. Influence of slmm obstacles 'width on warships' destroy probability[J]. Mine warfare & ship self-defence, 2015, 23(2): 35-38. (  0) 0)
|
| [9] |
尚奇, 李兵, 胡敏. 水雷小子样弹点散布方差估计[J]. 水雷战与舰船防护, 2005, 13(1): 30-32. SHANG Qi, LI Bing, HU Min, et al. Small sample placement of mines scattered variance estimation[J]. Mine warfare & ship self-defence, 2005, 13(1): 30-32. (  0) 0)
|
| [10] |
冷相文, 朱红波, 张旭. 自航水雷障碍对舰船目标流毁伤效能评估方法[J]. 南京理工大学学报, 2014, 38(3): 371-374. LENG Xiangwen, ZHU Hongbo, ZHANG Xu. Estimate method for damage effectiveness of mobile mine obstacles attacking warship target flows[J]. Journal of Nanjing University of Science and Technology, 2014, 38(3): 371-374. DOI:10.3969/j.issn.1005-9830.2014.03.011 (  0) 0)
|
| [11] |
朱红波, 张旭, 冷相文. 基于遗传算法的自航水雷障碍雷位配置[J]. 弹箭与制导学报, 2012, 32(2): 162-164. ZHU Hongbo, ZHANG Xu, LENG Xiangwen. Configuration of planting locations in mobile mine obstacle based on genetic algorithm[J]. Journal of projectiles, rockets, missiles and guidance, 2012, 32(2): 162-164. DOI:10.3969/j.issn.1673-9728.2012.02.045 (  0) 0)
|
| [12] |
王威, 罗朝晖, 王树宗. 常规潜艇攻势布雷效能评估的柔性仿真框架设计[J]. 微计算机信息, 2006, 22(10): 283-285, 108. WANG Wei, LUO Zhaohui, WANG Shuzong. Framework layout of flexible simulation model on efficacy evaluation in submarine-laying-mine[J]. Control & automation, 2006, 22(10): 283-285, 108. DOI:10.3969/j.issn.1008-0570.2006.10.105 (  0) 0)
|
| [13] |
徐晓明, 颜冰, 刘群杰. 基于ADC模型的无人布雷系统布雷阶段效能评估[J]. 水雷战与舰船防护, 2016, 24(1): 32-38. XU Xiaoming, YAN Bing, LIU Qunjie. Mine laying effectiveness evaluation of underwater unmanned mine laying system based on ADC model[J]. Mine warfare & ship self-defence, 2016, 24(1): 32-38. (  0) 0)
|
| [14] |
NGUYEN B, HOPKIN D, YIP H. Considering mine countermeasure exploratory operations conducted by autonomous underwater vehicles[J]. Military operations research, 2014, 19(2): 19-34. (  0) 0)
|
| [15] |
朱红波, 冷相文, 张旭. 一种自航水雷障碍毁伤舰船概率计算方法[J]. 鱼雷技术, 2013, 21(4): 313-316. ZHU Hongbo, LENG Xiangwen, ZHANG Xu. A calculation method for of surface warship damage probability of by mobile mine obstacle[J]. Torpedo technology, 2013, 21(4): 313-316. DOI:10.3969/j.issn.1673-1948.2013.04.015 (  0) 0)
|
| [16] |
刘剑, 黄文斌. 一种自航水雷散布概率的计算方法[J]. 鱼雷技术, 2005, 13(3): 43-45. LIU Jian, HUANG Wenbin. A calculation method of the dispersion probability of self-propelled mine[J]. Torpedo technology, 2005, 13(3): 43-45. DOI:10.3969/j.issn.1673-1948.2005.03.012 (  0) 0)
|
| [17] |
倪永杰, 王建国. 潜布自航水雷障碍的效力计算方法[J]. 水雷战与舰船防护, 2007, 15(1): 8-10. NI Yongjie, WANG Jianguo. Effectiveness calculation method of sub-laid self-propelled mine[J]. Mine warfare & ship self-defence, 2007, 15(1): 8-10. (  0) 0)
|
| [18] |
衡辉, 王新华, 杨迎化. 联合封锁作战中水雷综合运用模式研究[J]. 水雷战与舰船防护, 2017, 25(4): 25-27, 33. HENG Hui, WANG Xinhua, YANG Yinghua. Research on integrated application mode of mine in joint blockade war[J]. Mine warfare & ship self-defence, 2017, 25(4): 25-27, 33. (  0) 0)
|
| [19] |
ZHANG A M, MING F R, WANG S P. Coupled SPHS-BEM method for transient fluid-structure interaction and applications in underwater impacts[J]. Applied ocean research, 2013, 43: 223-233. DOI:10.1016/j.apor.2013.10.002 (  0) 0)
|
| [20] |
金辉, 贾则, 周学滨, 等. 水面舰船结构在水下近场爆炸作用下冲击响应研究[J]. 兵工学报, 2016, 37(Suppl): 91-95. JIN Hui, JIA Ze, ZHOU Xuebin, et al. Research on shock response of surface ship structure under underwater near field explosion[J]. Acta armamentarii, 2016, 37(Suppl): 91-95. (  0) 0)
|
| [21] |
XIAO W, ZHANG A M, WANG S P. The whipping response of a fluid filled cylindrical shell subjected to an underwater explosion[J]. Marine structures, 2017, 52: 82-93. DOI:10.1016/j.marstruc.2016.12.002 (  0) 0)
|
| [22] |
ZHANG Aman, ZHOU Weixing, WANG Shiping, et al. Dynamic response of the non-contact underwater explosions on naval equipment[J]. Marine structures, 2011, 24(4): 396-411. DOI:10.1016/j.marstruc.2011.05.005 (  0) 0)
|
| [23] |
蔡尚.水下爆炸作用下舰船毁伤效能评估及水雷布阵策略优化研究[D].哈尔滨: 哈尔滨工程大学, 2018. CAI Shang. Research on evaluation of warship damage and optimization of mine strategy subjected to underwater explosion[D]. Harbin: Harbin Engineering University, 2018. (  0) 0)
|
| [24] |
VAN DEN BERGH F, ENGELBRECHT A P. A cooperative approach to particle swarm optimization[J]. IEEE transactions on evolutionary computation, 2004, 8(3): 225-239. (  0) 0)
|
| [25] |
CLERC M, KENNEDY J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space[J]. IEEE transactions on evolutionary computation, 2002, 6(1): 58-73. (  0) 0)
|
| [26] |
DELICE Y, AYDOĞAN E K, ÖZCAN U, et al. A modified particle swarm optimization algorithm to mixed-model two-sided assembly line balancing[J]. Journal of intelligent manufacturing, 2017, 28(1): 23-36. (  0) 0)
|
| [27] |
VENTER G, SOBIESKI J S. Particle swarm optimization[C]//Proceedings of the 9-th AIAA/USAF/NASA/ISSMO Symposium on Multidisciplinary Analysis and Optimization Conference. Reston, VA, 2002, 4: 129-132.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


