圆柱壳结构在船舶工程、航空航天及土木工程领域应用广泛。开展复杂边界条件下圆柱壳结构振动特性分析,明确其振动规律,对丰富圆柱壳结构基础理论及指导工程应用具有重要意义。Rayleigh[1]基于壳体弯曲变形和拉伸变形的可分离性,对光壳圆柱壳的拉伸振动和弯曲振动分别进行了研究,给出了无限长圆柱壳在真空中的自振频率公式。Leissa[2]采用壳体理论对圆柱壳进行了系统深入的分析,为解析法求解圆柱壳振动问题奠定了基础。骆东平[3]采用迭代法求解Flügge方程,以两端固定、两端简支、一端固定另一端自由和两端自由4种常见的边界条件为基础,考察了边界条件变化对圆柱壳自由振动的影响,Yu[4]讨论了简支和固支边界条件下有限长圆柱壳的自由振动特性,Cheng等[5]以圆柱壳-圆板为模型,采用Rayleigh-Ritz法求解特征值方程从而求解其自由振动特性,并采用数值法对结果进行验证。Qu等[6]提出基于区域分解的方法,研究了力激励下变截面圆柱壳自由振动及力激励下响应特性。Pang等[7]和LI等[8]依据Flügge薄壳理论建立振动分析模型,采用Jacobi-Ritz法分析了均厚度以及变厚度圆柱壳、球壳等组合壳体结构的自由及受迫振动特性。汪志强等[9]采用Flügge经典薄壳理论讨论了正交各向异性圆柱壳的自由振动问题,且所提出方法可考虑正交各向异性圆柱壳在复杂和受外力的情况。
综合以上,目前多是针对经典边界条件对圆柱壳结构自由振动特性开展研究,而对复杂边界条件下圆柱壳结构瞬态振动特性研究较少。而在实际工程应用中,柱壳结构往往会受到瞬态载荷的作用,例如设备的突然开关、武器的发射等,结构在激励载荷作用下会产生剧烈的振动,可能会导致结构的疲劳破坏、机械故障等。此外,结构所处边界条件也是复杂多样的。因此,本文基于区域能量分解法,开展复杂边界条件下圆柱壳瞬态振动特性分析,旨在为复杂边界条件下圆柱壳结构瞬态振动特性分析提供数据积累和方法依据。
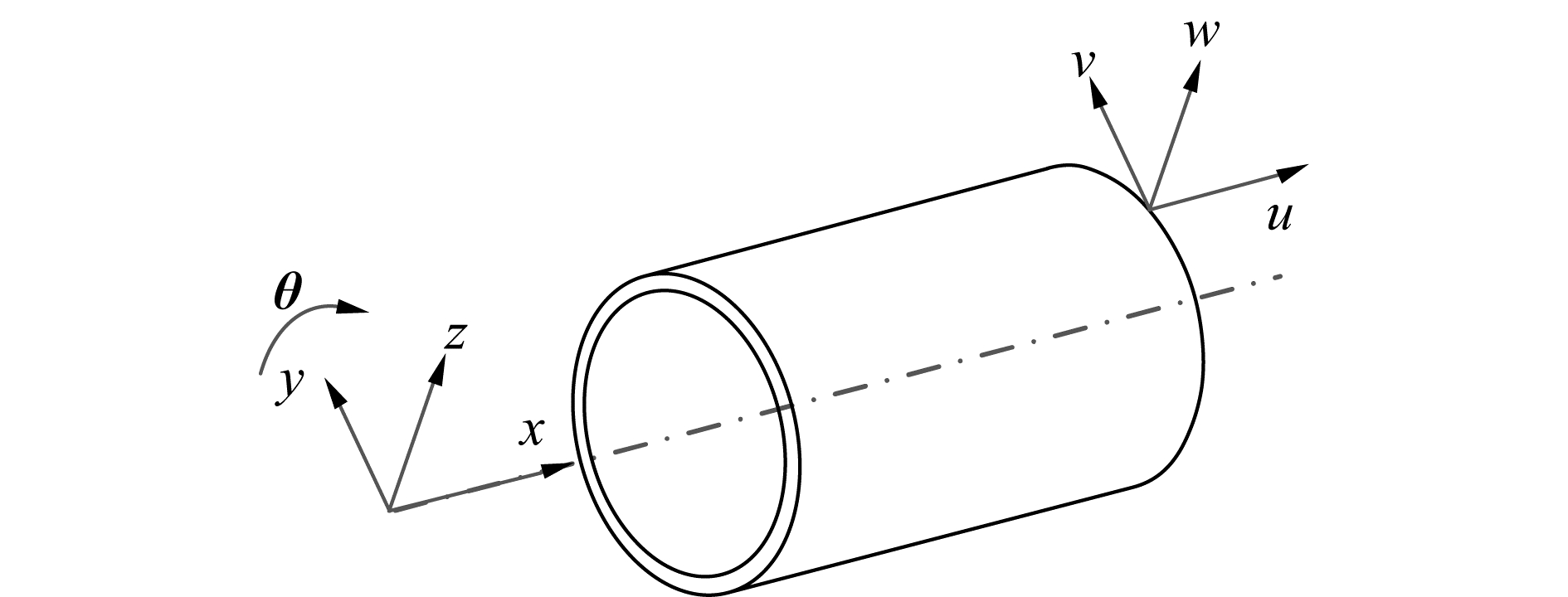
1 柱壳结构区域能量分析模型建立圆柱壳结构长为L,半径为R,厚度为h,结构模型及坐标系统如图 1所示。
|
Download:
|
| 图 1 圆柱壳结构理论模型 Fig. 1 Theoretical model of cylindrical shell structure | |
将圆柱壳体沿轴线方向均匀地截断成NL段,即每一段的长度Li=L/NL。根据修正的Hamilton原理[10-11],考虑到每一段的能量和相邻两段之间的影响,圆柱壳体的总势能为:
| $ {\mathit{\Pi }_{{\rm{Tol}}}} = \int_{{t_0}}^{{t_1}} {\sum\limits_{i = 1}^{{N_L}} {\left( {{T_{L,i}} - {U_{L,i}} + {W_{L,i}}} \right){\rm{d}}t} } + \int_{{t_0}}^{{t_1}} {\sum\limits_{i,i + 1} {{\mathit{\Pi }_{K,L}}{\rm{d}}t} } $ | (1) |
式中:TL, i、UL, i、WL, i分别为圆柱壳体的第i段的动能、应变能、外力功和附加能量泛函;ΠK, L为相邻分段i和i+1之间的附加界面势能。
当忽略圆柱壳体旋转惯性的条件下,圆柱壳体第i段的动能可以表示为:
| $ T_{L, i}=\frac{1}{2} \iint_{S_{i}} \rho h_{i}\left[\left(\frac{\partial \boldsymbol{u}_{i}}{\partial t}\right)^{2}+\left(\frac{\partial \boldsymbol{v}_{i}}{\partial t}\right)^{2}+\left(\frac{\partial \boldsymbol{w}_{i}}{\partial t}\right)^{2}\right] R \mathrm{d} \boldsymbol{x} \mathrm{d} \boldsymbol{\theta} $ | (2) |
式中:ui、vi、wi分别为不同方向位移矢量;ρ为结构质量密度;hi为第i段结构厚度;Si为结构中面面积。
根据Reissner-Naghdi′s线性薄壳理论[12-14],i分段的最大结构应变能可以表示为:
| $ \begin{gathered} {U_{L,i}} = \frac{1}{2}\iiint {\left( {{\mathit{\boldsymbol{\sigma }}_1} \times {\mathit{\boldsymbol{\varepsilon }}_1} + {\mathit{\boldsymbol{\sigma }}_2} \times {\mathit{\boldsymbol{\varepsilon }}_2} + \mathit{\boldsymbol{\tau }} \times {\mathit{\boldsymbol{\varepsilon }}_3}} \right){\text{d}}V} = \hfill \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\iint_{{S_i}} {\left[ {\int_{ - \frac{h}{2}}^{\frac{h}{2}} {\left( {\frac{E}{{1 - {\mu ^2}}}\left[ {\left( {{\mathit{\boldsymbol{\varepsilon }}_1} + \mu {\mathit{\boldsymbol{\varepsilon }}_2}} \right) + } \right.} \right.} } \right.} \hfill \\ \;\;\;\;\;\;\;\;\;z\left( {{\mathit{\boldsymbol{\chi }}_1} + \mu {\mathit{\boldsymbol{\chi }}_2}} \right)] \times \left( {{\mathit{\boldsymbol{\varepsilon }}_1} + z{\mathit{\boldsymbol{\chi }}_1}} \right) + \hfill \\ \;\;\;\;\;\;\;\;\;\frac{E}{{1 - {\mu ^2}}}\left[ {\left( {{\mathit{\boldsymbol{\varepsilon }}_2} + \mu {\mathit{\boldsymbol{\varepsilon }}_1}} \right) + z\left( {{\mathit{\boldsymbol{\chi }}_2} + \mu {\mathit{\boldsymbol{\chi }}_1}} \right)} \right] \times \hfill \\ \;\;\;\;\;\;\;\;\;\left( {{\mathit{\boldsymbol{\varepsilon }}_2} + z{\mathit{\boldsymbol{\chi }}_2}} \right) + \frac{E}{{2(1 + \mu )}}\left[ {{\mathit{\boldsymbol{\varepsilon }}_3} + z\left( {{\mathit{\boldsymbol{\chi }}_3} + {\mathit{\boldsymbol{\chi }}_4}} \right)} \right] \times \hfill \\ \;\;\;\;\;\;\;\;\;\left[ {{\mathit{\boldsymbol{\varepsilon }}_3} + z\left( {{\mathit{\boldsymbol{\chi }}_3} + {\mathit{\boldsymbol{\chi }}_4}} \right)} \right]){\text{d}}z]R{\text{d}}\mathit{\boldsymbol{x}}{\text{d}}\mathit{\boldsymbol{\theta }} \hfill \\ \end{gathered} $ | (3) |
考虑到z的奇数次幂和其他相乘在对称区间的积分为0,可以得到:
| $ \begin{gathered} {U_{L,i}} = \frac{1}{2}\iint_{{S_i}} {{K_i}}\left[ {{{\left( {\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial \mathit{\boldsymbol{x}}}}} \right)}^2} + \frac{{2\mu }}{R}\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial \mathit{\boldsymbol{x}}}}\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}} + {\mathit{\boldsymbol{w}}_i}} \right) + } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\left. {\frac{1}{{{R^2}}}{{\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}} + {\mathit{\boldsymbol{w}}_i}} \right)}^2} + \frac{{1 - \mu }}{2}{{\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{x}}}} + \frac{1}{R}\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}}} \right)}^2}} \right]R{\text{d}}\mathit{\boldsymbol{x}}{\text{d}}\mathit{\boldsymbol{\theta }} + \hfill \\ \;\;\;\;\;\;\;\;\;\frac{1}{2}\iint_{{S_i}} {{D_i}}\left[ {{{\left( {\frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial {\mathit{\boldsymbol{x}}^2}}}} \right)}^2} + \frac{{2\mu }}{{{R^2}}}\frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial {\mathit{\boldsymbol{x}}^2}}}\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}} + \frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial {\mathit{\boldsymbol{\theta }}^2}}}} \right) + } \right. \hfill \\ \;\;\;\;\;\;\;\;\;\left. {\frac{1}{{{R^4}}}{{\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}} - \frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial {\mathit{\boldsymbol{\theta }}^2}}}} \right)}^2} + \frac{{1 - \mu }}{{2{R^2}}}{{\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{x}}}} - 2\frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial \mathit{\boldsymbol{x}}\partial \mathit{\boldsymbol{\theta }}}}} \right)}^2}} \right] \cdot \hfill \\ \;\;\;\;\;\;\;\;\;R{\text{d}}\mathit{\boldsymbol{x}}{\text{d}}\mathit{\boldsymbol{\theta }} \hfill \\ \end{gathered} $ | (4) |
式中:
假设外部载荷全部作用在中面位置处,圆柱壳结构的第i分段分布着沿x方向、θ方向、z方向外力fu, i、fv, i、fw, i,此时结构第i分段的外力作功为:
| $ {W_{L,i}} = \frac{1}{2}\iint_{{S_i}} {\left( {{\mathit{\boldsymbol{f}}_{u,i}}{\mathit{\boldsymbol{u}}_i} + {\mathit{\boldsymbol{f}}_{v,i}}{\mathit{\boldsymbol{v}}_i} + {\mathit{\boldsymbol{f}}_{w,i}}{\mathit{\boldsymbol{w}}_i}} \right)}R{\text{d}}\mathit{\boldsymbol{x}}{\text{d}}\mathit{\boldsymbol{\theta }} $ | (5) |
圆柱壳体的第i段、第i+1段的界面上的附加能量泛函为:
| $ {\mathit{\Pi }_{\lambda ,L}} = \int_l {\left( {\lambda {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_u} + \beta {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_v} + \vartheta {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_w} + \psi {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_r}} \right)} R{\text{d}}\mathit{\boldsymbol{\theta }} $ | (6) |
其中λ、β、
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_u} = {\mathit{\boldsymbol{u}}_i} - {\mathit{\boldsymbol{u}}_{i + 1}},{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_v} = {\mathit{\boldsymbol{v}}_i} - {\mathit{\boldsymbol{v}}_{i + 1}},\\ {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_w} = {\mathit{\boldsymbol{w}}_i} - {\mathit{\boldsymbol{w}}_{i + 1}},{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_r} = \frac{{\partial {\mathit{\boldsymbol{w}}_i}}}{{\partial \mathit{\boldsymbol{x}}}} - \frac{{\partial {\mathit{\boldsymbol{w}}_{i + 1}}}}{{\partial \mathit{\boldsymbol{x}}}} \end{array} \right. $ | (7) |
将式(2)、(4)~(6)代入式(1),并根据广义变分原理,对ui、vi、wi、ui、vi+1、wi+1、
| $ \lambda = {K_i}\left[ {\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial \mathit{\boldsymbol{x}}}} + \frac{\mu }{R}\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}} + {\mathit{\boldsymbol{w}}_i}} \right)} \right] $ | (8) |
| $ \begin{array}{l} \beta = \frac{{\left( {1 - \mu } \right){K_i}}}{2}\left( {\frac{1}{R}\frac{{\partial {\mathit{\boldsymbol{u}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}} + \frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{x}}}}} \right) + \\ \;\;\;\;\;\;\;\;\frac{{\left( {1 - \mu } \right){D_i}}}{2}\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{x}}}} - 2\frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial \mathit{\boldsymbol{x}}\partial \mathit{\boldsymbol{\theta }}}}} \right) \end{array} $ | (9) |
| $ \vartheta = {D_i}\left( {\frac{1}{{{R^2}}}\frac{{{\partial ^2}{\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{x}}\partial \mathit{\boldsymbol{\theta }}}} - \frac{{{\partial ^3}{\mathit{\boldsymbol{w}}_i}}}{{\partial {\mathit{\boldsymbol{x}}^3}}} - \frac{{2 - \mu }}{{{R^2}}}\frac{{{\partial ^3}{\mathit{\boldsymbol{w}}_i}}}{{\partial \mathit{\boldsymbol{x}}\partial {\mathit{\boldsymbol{\theta }}^2}}}} \right) $ | (10) |
| $ \psi = {D_i}\left[ {\frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial {\mathit{\boldsymbol{x}}^2}}} - \frac{\mu }{{{R^2}}}\left( {\frac{{\partial {\mathit{\boldsymbol{v}}_i}}}{{\partial \mathit{\boldsymbol{\theta }}}} - \frac{{{\partial ^2}{\mathit{\boldsymbol{w}}_i}}}{{\partial {\mathit{\boldsymbol{\theta }}^2}}}} \right)} \right] $ | (11) |
将式(8)~(11)代入式(1)后得到新的能量泛函:
| $ \begin{array}{l} {{\mathit{\bar \Pi }}_{{\rm{Tol}}}} = \int_{{t_0}}^{{t_1}} {\sum\limits_{i = 1}^{{N_L}} {\left( {{T_{L,i}} - {U_{L,i}} + {W_{L,i}}} \right){\rm{d}}t} } + \\ \;\;\;\;\;\;\;\;\;\;\int_{{t_0}}^{{t_1}} {\sum\limits_{i,i + 1} {\int_l {\left( {{N_x}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_u} + {N_\theta }{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_v} + {Q_x}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_w} - {M_x}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_r}} \right)R{\rm{d}}\mathit{\boldsymbol{\theta }}{\rm{d}}t} } } \end{array} $ | (12) |
式中:Nx=λ,Nθ=β,
为保证数值算法的计算稳定性,在式(12)的基础上添加一项子结构交界面位移连续方程的最小二乘加权参数残值Πκ, L,此时,结构的完整能量泛函表示为:
| $ {\mathit{\tilde \Pi }_{{\rm{Tol}}}} = {\mathit{\bar \Pi }_{{\rm{Tol}}}} + {\mathit{\Pi }_{\kappa ,L}} $ | (13) |
| $ \begin{array}{*{20}{c}} {{\mathit{\Pi }_{\kappa ,L}} = - \frac{1}{2}\sum\limits_{i,i + 1} {\int_l {\left( {{\kappa_u}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_u^2 + {\kappa_v}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_v^2 + } \right.} } }\\ {\left. {{\kappa_w}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_w^2 + {\kappa_r}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_r^2} \right)R{\rm{d}}\mathit{\boldsymbol{\theta }}} \end{array} $ | (14) |
式中:κu、κv、κw和κr为柱壳分段后第i段和第i+1段分区界面加权参数。
引入边界条件控制参数ζu、ζv、ζw、ζr,此时的能量泛函可以表示为:
| $ \begin{array}{l} {{\mathit{\tilde \Pi }}_{{\rm{Tol}}}} = \int_{{t_0}}^{{t_1}} {\sum\limits_{i = 1}^{{N_L}} {\left( {{T_{L,i}} - {U_{L,i}} + {W_{L,i}}} \right){\rm{d}}t} } + \\ \;\;\;\;\;\;\;\;\;\;\int_{{t_0}}^{{t_1}} {\sum\limits_{i,i + 1} {\int_l {\left( {{\zeta _u}{N_x}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_u} + {\zeta _v}{N_\theta }{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_v} + {\zeta _w}{\theta _x}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_w} - } \right.} } } \\ \;\;\;\;\;\;\;\;\;\;\left. {{\zeta _r}{M_x}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_r}} \right)R{\rm{d}}\mathit{\boldsymbol{\theta }} - \frac{1}{2}\sum\limits_{i,i + 1} {\int_l {\left( {{\zeta _u}{\kappa _u}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_u^2 + {\zeta _v}{\kappa _v}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_v^2 + } \right.} } \\ \;\;\;\;\;\;\;\;\;\;\left. {{\zeta _w}{\kappa _w}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_w^2 + {\zeta _r}{\kappa _r}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}_r^2} \right)R{\rm{d}}\mathit{\boldsymbol{\theta }} \end{array} $ | (15) |
表 1给出了多种边界条件下的控制权参数,可通过选择不同权参数模拟不同的边界条件。
| 表 1 不同边界条件对应的控制参数ζt(t=u, v, w, r) Table 1 Control parameters ζt(t=u, v, w, r) corresponding to different boundary conditions |
在上述理论中建立了柱壳结构的广义能量泛函,在此基础上采用Newmark积分方法[15],求解结构的瞬态振动响应。其主要的求解方程为:
| $ \mathit{\boldsymbol{M}}{\ddot \delta _{t + \Delta t}} + \mathit{\boldsymbol{C}}{\dot \delta _{t + \Delta t}} + \mathit{\boldsymbol{K}}{\delta _{t + \Delta t}} = {\mathit{\boldsymbol{F}}_{t + \Delta t}} $ | (23) |
该方程显然还需要补充2组方程才能够进行求解。Newmark法假设t+Δt时刻的速度和位移为:
| $ {\dot \delta _{t + \Delta t}} = {\dot \delta _t} + \left[ {\left( {1 - \gamma } \right){{\ddot \delta }_t} + \gamma {{\ddot \delta }_{t + \Delta t}}} \right]\Delta t,\;\;\;\;\;0 \le \gamma \le 1 $ | (24) |
| $ \begin{array}{*{20}{c}} {{\delta _{t + \Delta t}} = {\delta _t} + {{\dot \delta }_t}\Delta t + \left[ {\left( {1/2 - \beta } \right){{\ddot \delta }_t} + \beta {{\ddot \delta }_{t + \Delta t}}} \right]\Delta {t^2},}\\ {0 \le 2\beta \le 1} \end{array} $ | (25) |
由式(23)~(25)可知,Newmark方法计算的收敛性与计算精度与参数γ和β的选取关系较大。由文献[10-11]可知,当γ≥0.5,β≥(1/2+γ)/2时,算法无条件稳定,这时候可以根据精度来选择时间步长Δt,在本文中γ=0.5,β=0.25。
2.2 最小二乘参数与分段数收敛性在结构的瞬态振动特性研究展开之前,对最小二乘加权参数收敛性进行分析,得出最佳的最小二乘加权参数。根据前面所定义的边界条件,选取F-E边界条件,即柱壳结构的左端为自由边界,结构的右端为弹性边界,弹性参数取值为ku=kv=2×108 N/m,结构参数为:L=6 m,R=1 m,h/R=0.01,E=210 GPa,ρ=7 800 kg/m3,μ=0.3。位移容许函数在母线方向上的切比雪夫正交多项式的截断值为8,结构分段数NL=2。频率无量纲化计算公式为:
| $ \mathit{\Omega } = \omega R{\left( {\rho \left( {1 - {\mu ^2}} \right)/E} \right)^{1/2}} $ | (26) |
表 2给出了不同周向波数下,不同最小加权参数对结构前5阶无量纲化固有频率的影响,可以看出,当加权参数增大时,结构的固有频率也随之增大,当加权参数达到某一个临界值时,结构的计算结果趋于稳定。在实际数值计算中,加权参数的取值不可能无穷大,同时为保证计算的绝对数值稳定性,根据表 2结果,在后续的计算中,最小二乘残差加权系数取值为κ=1×1014。
| 表 2 最小二乘加权参数收敛性分析 Table 2 Convergence analysis of least squares weighted parameters |
在对加权参数分析的基础上,由本文的计算模型可知,只有选取合理的分段数,才能保证数值计算的计算效率和精度,因此需对分段数的收敛性进行分析。结构参数与表 2所用计算模型保持一致,并且加权参数κ取值为1×1014。表 3给出了不同分段数下对结构不同阶数的无量纲化固有频率Ω的影响,无量纲化公式与表 2保持一致,为了验证收敛性分析的正确性,有限元计算所得的结果作为参照值也在表 3中列出。
| 表 3 区域分段数的收敛性分析 Table 3 The convergence analysis of the number of regional segments |
由表 3可以看出,当NL=8时,其计算结果与已经保持在小数点后6位保持一致,因此,在后续的计算中,如不做特别说明,柱壳分段数取值为NL=8。
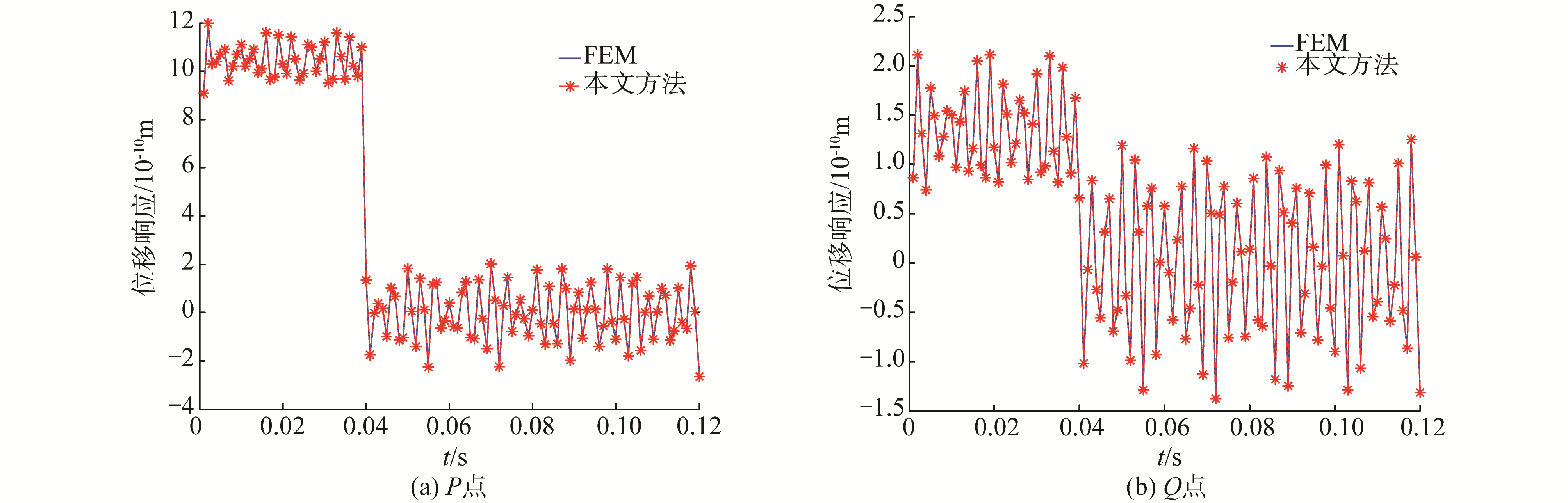
3 柱壳结构瞬态振动响应研究 3.1 模型验证圆柱壳的瞬态振动响应分析参数:L=6 m,R=1 m,h/R=0.04,ρ=7 800 kg/m3,μ=0.3。为研究结构损耗因子的影响,将采用复杨氏模量E(1+jη)的形式引入结构损耗因子[18]。选取2个响应点,位置分别为点P(x1=L/2, θ=0°)与Q(x1=3L/4, θ=30°)。图 3给出了结构在P点作用阶跃载荷,实际作用时间为t0=0.04 s,整个分析时间为0.12 s,时间间隔分析步为Δt=0.000 1 s,γ=0.5,β=0.25,载荷作用方向为径向。作为验证对比,有限元仿真的数据结构在图 3中给出。图 4给出了结构在P点位置处受相同的阶跃载荷时结构的瞬态响应曲线,此时载荷的作用方向为P点的轴向位置处。通过图 2、3可以看出,本文方法计算的瞬态响应与FEM计算所得结果一致吻合,验证了本文方法的正确性,在本文中只给出了阶跃载荷的瞬态响应。

|
Download:
|
| 图 2 圆柱壳在C-C边界条件下受径向阶跃载荷下圆柱壳瞬态位移响应曲线 Fig. 2 Transient displacement response of cylindrical shell under radial load with C-C boundary | |
|
Download:
|
| 图 3 圆柱壳在C-C边界条件下受轴向阶跃载荷下圆柱壳瞬态位移响应曲线 Fig. 3 Transient displacement response of cylindrical shell under axis load with C-C boundary | |
|
Download:
|
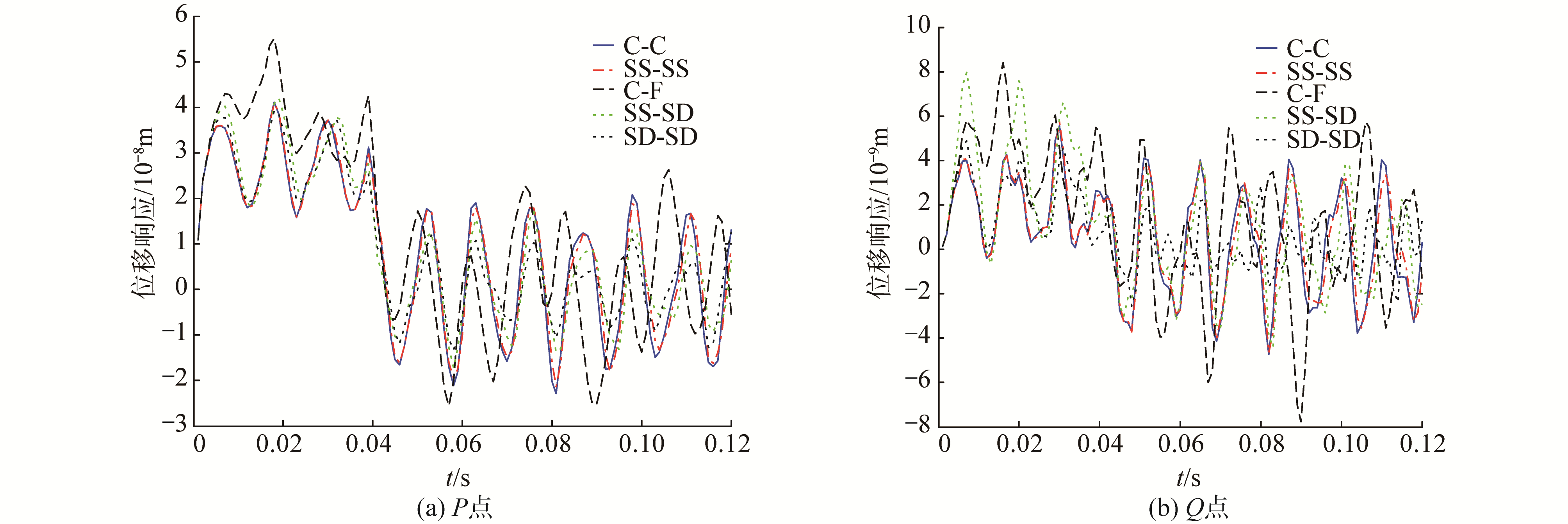
| 图 4 圆柱壳在不同边界条件下受轴向阶跃载荷下圆柱壳瞬态位移响应曲线 Fig. 4 Transient displacement response of cylindrical shell under axis load with various boundaries | |
图 4给出了不同边界条件下圆柱壳在相同径向载荷下结构的瞬态位移响应曲线,载荷形式如图 2所示。由图 4可知,边界条件对结构的瞬态响应影响较大,但在趋势上基本保持一致。对于P点,C-F边界下的瞬态响应的共振频率与其他的边界条件具有较大的差异,而其余边界条件的共振频率峰值相差不大。对于Q点,其变化趋势与P点不一致,其在SS-SD、C-F以及软边界SD-SD与其他的边界条件的响应曲线变化较大。
3.3 结构参数对瞬态响应的影响图 5给出了结构在相同长度、半径以及阻尼损耗因子下改变结构的厚度时结构的瞬态位移响应曲线,为更清晰的显示在瞬态载荷作用前后结构响应的变化,柱壳结构损耗因子η=0.003。

|
Download:
|
| 图 5 厚度改变时C-C边界受轴向阶跃载荷圆柱壳瞬态位移响应曲线 Fig. 5 Transient displacement response of cylindrical shell subjected to axial step load at the C-C boundary with various thickness | |
图 6给出相同的结构参数下,只改变阻尼损耗因子下的瞬态位移响应曲线,为更清晰的显示损耗因子对结构振动响应的影响, 损耗因子分别选取0.01、0.04以及0.1。图 5与图 6边界条件都为C-C边界条件,作用载荷都为阶跃载荷。

|
Download:
|
| 图 6 结构损耗因子改变时C-C边界受轴向阶跃载荷圆柱壳瞬态位移响应曲线 Fig. 6 Transient displacement response of cylindrical shell subjected to axial step load at the C-C boundary with various loss factor | |
从图 5可以看出,结构的厚度发生变化时,结构的整个瞬态响应曲线发生了较大的变化,在相同的频率范围内,随着结构厚度的增加,其波峰数量逐渐减少,且响应峰值也随之降低;同时也可看出,改变结构的厚度,会使结构在瞬态载荷作用完成后响应曲线峰值发生偏移,在载荷作用阶段,仅改变响应曲线峰值,不同厚度结构频率特征基本相似,这也是在实际工程中比较关注基频的原因。从图 6可以看出,结构的损耗因子增大时,很多波峰几乎都被消除,说明结构损耗因子对于短时的瞬态响应控制具有重要的作用。从波峰值能够看出,结构损耗因子仅影响结构响应曲线的峰值点,对于结构的固有频率影响较小。
4 结论1) 本文方法的柱壳分段数在NL=8时收敛,最小二乘残差加权系数取值达到κ=1×1014时结构的数值计算具有良好的稳定性;
2) 不同边界条件下,圆柱壳在相同的径向载荷作用时,结构的瞬态位移响应随边界条件的改变而发生变化,且发生变化的趋势保持一致;
3) 相同频率范围内,结构厚度越小,其位移响应曲线波峰的数量越多,并且其瞬态响应值越大;对于结构损耗因子的变化,只影响结构的共振峰值,对于结构固有频率影响较小。
| [1] |
RAYLEIGH J. The theory of sound[M]. New York: Dover Publications, 1945.
(  0) 0)
|
| [2] |
LEISSA A W. Vibration of shells[M]. New York: Acoustic Society of America, 1993.
(  0) 0)
|
| [3] |
骆东平. 任意边界条件下圆柱壳体振动特性分析[J]. 固体力学学报, 1990, 11(1): 86-96. LUO Dongping. Vibration characteristics of cylindrical shells with arbitrary boundary conditions[J]. Acta mechnica solida sinica, 1990, 11(1): 86-96. (  0) 0)
|
| [4] |
YU Y Y. Free vibrations of thin cylindrical shells having finite lengths with freely supported and clamped edges[J]. Journal of applied mechanics, 1955, 22: 547-552. (  0) 0)
|
| [5] |
CHENG L, NICOLAS J. Free vibration analysis of a cylindrical shell-circular plate system with general coupling and various boundary conditions[J]. Journal of sound and vibration, 1992, 155(2): 231-247. (  0) 0)
|
| [6] |
QU Yegao, CHEN Yong, LONG Xinhua, et al. Free and forced vibration analysis of uniform and stepped circular cylindrical shells using a domain decomposition method[J]. Applied acoustics, 2013, 74(3): 425-439. DOI:10.1016/j.apacoust.2012.09.002 (  0) 0)
|
| [7] |
PANG Fuzhen, LI Haichao, CHOE K, et al. Free and forced vibration analysis of airtight cylindrical vessels with doubly curved shells of revolution by using Jacobi-Ritz method[J]. Shock and vibration, 2017, 2017: 4538540. (  0) 0)
|
| [8] |
LI Haichao, PANG Fuzhen, MIAO Xuhong, et al. A semi-analytical method for vibration analysis of stepped doubly-curved shells of revolution with arbitrary boundary conditions[J]. Thin-walled structures, 2018, 129: 125-144. (  0) 0)
|
| [9] |
汪志强, 李学斌, 黄利华. 基于波传播方法和多元分析的正交各向异性圆柱壳振动特性研究[J]. 振动与冲击, 2018, 37(7): 227-232. WANG Zhiqiang, LI Xuebin, HUANG Lihua. Vibration characteristics of orthotropic circular cylindrical shells based on wave propagation approach and multi-variate analysis[J]. Journal of vibration and shock, 2018, 37(7): 227-232. (  0) 0)
|
| [10] |
薛开, 王久法, 李秋红, 等. Mindlin矩形板在任意弹性边界条件下的振动特性分析[J]. 哈尔滨工程大学学报, 2014(4): 477-481. XUE Kai, WANG Jiufa, LI Qiuhong, et al. Vibration behavior analysis of Mindlin rectangular plates with arbitrary elastic boundary conditions[J]. Journal of Harbin Engineer University, 2014(4): 477-481. (  0) 0)
|
| [11] |
周海军, 李玩幽, 吕秉琳, 等. 弹性支撑及连接边界的多跨曲梁面内自由振动分析[J]. 哈尔滨工程大学学报, 2012(6): 696-701. ZHOU Haijun, LI Wanyou, LYU Binglin, et al. In-plane free vibration analysis of multi-span curved beams with elastic support and connecting boundary conditions[J]. Journal of Harbin Engineer University, 2012(6): 696-701. DOI:10.3969/j.issn.1006-7043.201107007 (  0) 0)
|
| [12] |
庞福振, 李海超, 霍瑞东, 等. 基于Jacobi-Ritz法的旋转组合结构自由振动特性分析[J]. 振动工程学报, 2018, 31(5): 105-114. PANG Fuzhen, LI Haichao, HUO Ruidong, et al. Free Vibration Analysis of Rotating Composite Structures Based on Jacobi-Ritz Method[J]. Journal of Vibration Engineering, 2018, 31(5): 105-114. (  0) 0)
|
| [13] |
LI H, PANG F, MIAO Xuhong, et al. Jacobi-Ritz method for free vibration analysis of uniform and stepped circular cylindrical shells with arbitrary boundary conditions:A unified formulation[J]. Computers & mathematics with applications, 2019, 77(2): 427-440. (  0) 0)
|
| [14] |
PANG F, LI H, et al. Application of flügge thin shell theory to the solution of free vibration behaviors for spherical-cylindrical-spherical shell:A unified formulation[J]. European journal of mechanics-A/solids, 2019, 74: 381-393. DOI:10.1016/j.euromechsol.2018.12.003 (  0) 0)
|
| [15] |
李鸿晶, 王通, 廖旭. 关于Newmark-β法机理的一种解释[J]. 地震工程与工程振动, 2011, 31(2): 55-62. LI Hongjing, WANG Tong, LIAO Xu. An interpretation on Newmark beta methods in mechanism of numerical analysis[J]. Journal of earthquake engineering and engineering vibration, 2011, 31(2): 55-62. (  0) 0)
|
| [16] |
JAFARI A A, BAGHERI M. Free vibration of non-uniformly ring stiffened cylindrical shells using analytical, experimental and numerical methods[J]. Thin-walled structures, 2006, 44(1): 82-90. DOI:10.1016/j.tws.2005.08.008 (  0) 0)
|
| [17] |
PELLICANO F. Vibrations of circular cylindrical shells:theory and experiments[J]. Journal of sound and vibration, 2007, 303(1/2): 154-170. (  0) 0)
|
| [18] |
杜敬涛.任意边界条件下结构振动, 封闭声场及其耦合系统建模方法研究[D].哈尔滨: 哈尔滨工程大学, 2009. DU Jingtao. Study on modeling methods for structural vibration, enclosed sound field and their coupling system subject to general boundary conditions[D]. Harbin: Harbin Engineering University, 2009. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y1655598 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


