2. 中国科学院 声学研究所, 北京 100190;
3. 哈尔滨工程大学 水声技术重点实验室, 黑龙江 哈尔滨 150001
2. Institute of Acoustics, Chinese Academy of Sciences, Beijing 100190, China;
3. Acoustic Science and Technology Laboratory, Harbin Engineering University, Harbin 150001, China
纵向换能器是换能器的基本结构形式之一,广泛应用于水声领域、超声领域,对其振动分析的研究工作比较多,一些经典专著也常从纵向换能器分析入手,展开换能器基本问题的分析与讨论,基于等效电路方法给出的纵向换能器频率方程,分别对应节点两侧振动部分进行描述和求解计算[1-2]。文献[3-4]基于等效电路基本理论对纵向超声换能器进行了优化设计并研究了双激励工作模式;文献[5]利用一维振动理论分析了前盖板带圆台凹孔的纵向换能器带宽特性;文献[6]利用等效电路方法对所设计的三共振带宽纵向换能器进行分析;文献[7]利用等效电路方法研究了夹心式复合变幅杆换能器频率方程。以上文献都没有给出纵向换能器频率方程的直接参数化表达式。目前由于有限元方法的广泛应用[8],计算精度更高,使得许多研究工作缺失了频率方程的推导,但在讨论振动声辐射、耦合作用机理,或指导直接工程应用时,有限元方法就显得物理图像不够清晰,因此有必要针对典型结构换能器的振动特性进行进一步的理论分析,得到精确表达的数学模型,再用高精度有限元方法进行验证。本文针对这一基础研究课题,以纵向换能器为研究对象,从一维振动的振动位移函数出发,考虑部件截面参数,利用能量分析方法,经过数学推导得到描述纵向换能器频率特性的数学表达式。
1 基于能量法的纵向换能器等效模型能量法是从能量的观点出发, 根据能量守恒、功能关系等物理原理,进行等效关系建模,在机械系统等效模型中,等效弹性元件参数利用位能等效关系确定,等效质量元件参数利用动能等效关系确定,例如应用于壳体结构振动的建模分析等。
1.1 纵向换能器等效模型纵向换能器结构上由压电堆、尾质量、前盖板等部分组成,本文忽略预应力螺杆和压电陶瓷中心孔,并简化成连续结构体,满足细棒近似条件,如图 1所示,压电陶瓷堆长度le,密度ρe,纵波声速ve,直径de,截面积Se;尾质量长度l1,密度ρ1,纵波声速v1,直径d1,截面积S1;前盖板长度l2,密度ρ2,纵波声速v2,细端直径d2,细端截面积S2,喇叭口直径dT;换能器沿z轴方向做一维纵振动,并且假设垂直于z轴的任意截面内振动位移相等,基频模态下,振动节点位于M点,将压电陶瓷堆分割成后振段le1和前振段le2,选节点M为坐标原点。

|
Download:
|
| 图 1 纵向换能器结构示意 Fig. 1 The structure of longitudinal transducer | |
换能器各部分的振动位移函数表达为:
压电陶瓷堆:
| $ {\xi _{\rm{e}}} = {A_{\rm{e}}}\sin \left( {{k_{\rm{e}}}z} \right) $ |
尾质量:
| $ {\xi _1} = {A_1}\sin \left( {{k_1}z + {\varphi _1}} \right) $ | (1) |
前盖板:
| $ \xi_{2}=A_{2} \frac{1}{z+F l_{2}-l_{\mathrm{e}_{2}}} \sin \left(k_{2} z+\varphi_{2}\right) $ | (2) |
其中h为喇叭形前盖板收缩得到的圆锥的高:
| $ h=\frac{d_{T}}{d_{T}-d_{2}} l_{2} $ |
引用文献[1]中的延展系数F,得:
| $ h=(F+1) l_{2} $ |
根据半波振子条件,节点两侧各为1/4振子,端部振动位移为极大值,则有:
| $ \left\{\begin{array}{l}{\left.\frac{\partial \xi_{1}}{\partial z}\right|_{z=-l_{1}-l_{e_{1}}}=0} \\ {\left.\frac{\partial \xi_{2}}{\partial z}\right|_{z=l_{e_{2}}+l_{2}}=0}\end{array}\right. $ |
代入式(1)、(2),得:
| $ \left\{ {\begin{array}{*{20}{l}} {\cos \left( {{k_1}\left( { - {l_1} - {l_{{{\rm{e}}_1}}}} \right) + {\varphi _1}} \right) = 0}\\ {\cos \left( {{k_2}\left( {{l_{{{\rm{e}}_2}}} + {l_2}} \right) + {\varphi _2} + {\varphi _0}} \right) = 0} \end{array}} \right. $ |
其中:
| $ \varphi_{0}=\arcsin \frac{1}{\sqrt{k_{2}^{2} l_{2}^{2}(F+1)^{2}+1}} $ | (3) |
得到:
| $ \left\{ {\begin{array}{*{20}{l}} {{\varphi _1} = - \frac{{\rm{ \mathsf{ π} }}}{2} + {k_1}\left( {{l_1} + {l_{{{\rm{e}}_1}}}} \right)}\\ {{\varphi _2} = \frac{{\rm{ \mathsf{ π} }}}{2} - {k_2}\left( {{l_2} + {l_{{{\rm{e}}_2}}}} \right) - {\varphi _0}} \end{array}} \right. $ |
將φ1、φ2代入式(1)、(2),得到位移函数表达式:
| $ \left\{ \begin{array}{l} {\xi _e} = {A_e}\sin \left( {{k_{\rm{e}}}z} \right)\\ {\xi _1} = - {A_1}\cos \left( {{k_1}\left( {z + {l_1} + {l_{{{\rm{e}}_1}}}} \right)} \right)\\ {\xi _2} = {A_2}\frac{1}{{z + F{l_2} + {l_{{{\rm{e}}_2}}}}}\cos \left( {{k_2}\left( {z - {l_2} - {l_{{{\rm{e}}_2}}}} \right) - {\varphi _0}} \right) \end{array} \right. $ |
其中Ae、A2可以根据位移连续边界条件用A1表示出来:
| $ \left\{ \begin{array}{l} {A_{\rm{e}}} = \frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}{A_1}\\ {A_2} = \frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}} \cdot \frac{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}} \right)}}{{\cos \left( {{k_2}{l_2} + {\varphi _0}} \right)}}F{l_2}{A_1} \end{array} \right. $ |
将换能器从振动节点处分为尾端支路和前端支路2个部分,选择最简单的等效模型,即在每个支路分别用一个质量元件和一个弹性元件串联的“质量-弹簧”模型表达各个结构,每个结构之间是机械串联关系。于是对换能器的压电堆(分后振段和前振段)、尾质量、前盖板进行等效,可以得到图 2所示的集总参数机电等效电路图。

|
Download:
|
| 图 2 纵向换能器集总参数机电等效电路 Fig. 2 The lumped parameter equivalent diagram of longitudinal transducer | |
图 2中,De1、me1分别为压电堆后振段le1的等效弹性系数和等效质量,De2、me2分别为压电堆前振段le2的等效弹性系数和等效质量,D1、m1分别为尾质量的等效弹性系数和等效质量,D2、m2分别为前盖板的等效弹性系数和等效质量,F1、F2驱动力,其中F1为压电堆后振段le1对尾质量提供的驱动力、F2为压电堆前振段le2对前盖板提供的驱动力,R1为尾部1/4振子的机械阻尼,R2为前部1/4振子的机械阻尼(包括辐射阻分量)。下面将尾端支路和前端支路分别利用能量法计算图 2中各等效质量、等效弹性系数,为了便于表达,计算等效参数时取换能器的尾端作为参考点。
1.2 尾端支路等效参数尾端支路压电陶瓷元件的位能:
| $ \frac{1}{2}{D_{{{\rm{e}}_1}}}A_1^2 = \frac{1}{2}\int\limits_{ - {l_{{{\rm{e}}_1}}}}^0 {{E_{\rm{e}}}{S_{\rm{e}}}{{\left( {\frac{{\partial {\xi _{\rm{e}}}}}{{\partial z}}} \right)}^2}{\rm{d}}z} $ |
计算得到尾端支路压电陶瓷元件的等效弹性系数:
| $ {D_{{{\rm{e}}_1}}} = {\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2}{E_{\rm{e}}}{S_{\rm{e}}}{k_{\rm{e}}}\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}}}{2} + \frac{1}{4}\sin \left( {2{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)} \right] $ |
尾端支路压电陶瓷元件的动能:
| $ \frac{1}{2}{m_{{{\rm{e}}_1}}}{\omega ^2}A_1^2 = \frac{1}{2}\int\limits_{ - {l_{{{\rm{e}}_1}}}}^0 {{\rho _{\rm{e}}}S{\omega ^2}\xi _{\rm{e}}^2{\rm{d}}z} $ |
计算得到尾端支路压电陶瓷元件的等效质量:
| $ {m_{{{\rm{e}}_1}}} = {\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2}\frac{{{\rho _{\rm{e}}}{S_{\rm{e}}}}}{{{k_{\rm{e}}}}}\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}}}{2} - \frac{1}{4}\sin \left( {2{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)} \right] $ |
尾端支路尾质量元件的位能:
| $ \frac{1}{2}{D_1}A_1^2 = \frac{1}{2}\int\limits_{ - \left( {{l_{{{\rm{e}}_1}}} + {l_1}} \right)}^{ - {l_{{{\rm{e}}_1}}}} {{E_1}{S_1}{{\left( {\frac{{\partial {\xi _1}}}{{\partial z}}} \right)}^2}{\rm{d}}z} $ |
计算得到尾端支路尾质量元件的等效弹性系数:
| $ {D_1} = {E_1}{S_1}{k_1}\left[ {\frac{{{k_1}{l_1}}}{2} - \frac{1}{4}\sin \left( {2{k_1}{l_1}} \right)} \right] $ |
尾端支路尾质量元件的动能:
| $ \frac{1}{2}{m_1}{\omega ^2}A_1^2 = \frac{1}{2}\int\limits_{ - \left( {{l_{{{\rm{e}}_1}}} + {l_1}} \right)}^{ - {l_{{{\rm{e}}_1}}}} {{\rho _1}{S_1}{\omega ^2}\xi _1^2{\rm{d}}z} $ |
计算得到尾端支路尾质量元件的等效质量:
| $ m_{1}=\frac{\rho_{1} S_{1}}{k_{1}}\left[\frac{k_{1} l_{1}}{2}+\frac{1}{4} \sin \left(2 k_{1} l_{1}\right)\right] $ |
前端支路压电陶瓷元件的位能:
| $ \frac{1}{2}{D_{{{\rm{e}}_2}}}A_1^2 = \frac{1}{2}\int\limits_0^{{l_{{{\rm{e}}_2}}}} {{E_{\rm{e}}}{S_{\rm{e}}}{{\left( {\frac{{\partial {\xi _{\rm{e}}}}}{{\partial z}}} \right)}^2}{\rm{d}}z} $ |
计算得到前端支路压电陶瓷元件的等效弹性系数:
| $ {D_{{{\rm{e}}_2}}} = {\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2}{E_{\rm{e}}}{S_{\rm{e}}}{k_{\rm{e}}}\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}}}{2} + \frac{1}{4}\sin \left( {2{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}} \right)} \right] $ |
前端支路压电陶瓷元件的动能:
| $ \frac{1}{2}{m_{{{\rm{e}}_2}}}{\omega ^2}A_1^2 = \frac{1}{2}\int\limits_0^{{l_{{{\rm{e}}_2}}}} {{\rho _{\rm{e}}}{S_{\rm{e}}}{\omega ^2}\xi _{\rm{e}}^2{\rm{d}}z} $ |
计算得到前端支路压电陶瓷元件的等效质量:
| $ {m_{{{\rm{e}}_2}}} = {\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2}\frac{{{\rho _{\rm{e}}}{S_{\rm{e}}}}}{{{k_{\rm{e}}}}}\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}}}{2} - \frac{1}{4}\sin \left( {2{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}} \right)} \right] $ |
前端支路前盖板元件的位能:
| $ \frac{1}{2}{D_2}A_1^2 = \frac{1}{2}\int\limits_{{l_{{{\rm{e}}_2}}}}^{{l_{{{\rm{e}}_2}}} + {l_2}} {{E_2}{{\left( {\frac{{z + F{l_2} - {l_{{{\rm{e}}_2}}}}}{{F{l_2}}}} \right)}^2}{S_2}{{\left( {\frac{{\partial {\xi _2}}}{{\partial z}}} \right)}^2}{\rm{d}}z} $ |
将位移函数ξ2代入上式:
| $ \begin{array}{l} \frac{1}{2}{D_2}A_1^2 = \frac{1}{2}\int\limits_{{l_{{{\rm{e}}_2}}}}^{{l_{{{\rm{e}}_2}}} + {l_2}} {{E_2}{{\left( {\frac{{z + F{l_2} - {l_{{{\rm{e}}_2}}}}}{{F{l_2}}}} \right)}^2}{S_2}A_2^2} \times \\ \;\;\;\;\;\;\left( {\frac{1}{{{{\left( {z + F{l_2} - {l_{{{\rm{e}}_2}}}} \right)}^2}}}\cos \left( {{k_2}\left( {z - {l_2} - {l_{{{\rm{e}}_2}}}} \right) - {\varphi _0}} \right.} \right) + \\ \;\;\;\;\;\;\frac{{{k_2}}}{{z + F{l_2} - {l_{{{\rm{e}}_2}}}}}\sin {\left( {{k_2}\left( {z - {l_2} - {l_{{{\rm{e}}_2}}}} \right) - {\varphi _0}} \right)^2}{\rm{d}}z \end{array} $ |
为了推导方便,令:
| $ y = z + F{l_2} - {l_{{{\rm{e}}_2}}} $ |
则
| $ z - {l_2} - {l_{{{\rm{e}}_2}}} = y - \left( {F + 1} \right){l_2} $ |
得到前端支路前盖板元件的等效弹性系数的积分表示:
| $ \begin{array}{*{20}{c}} {{D_2} = \frac{{A_2^2{E_2}{S_2}}}{{A_1^2{F^2}l_2^2}}\int\limits_{F{l_2}}^{\left( {F + 1} \right){l_2}} {\left( {\frac{1}{y}\cos \left( {{k_2}\left( {y - \left( {F + 1} \right){l_2}} \right) - {\varphi _0}} \right) + } \right.} }\\ {{{\left. {{k_2}\sin \left( {{k_2}\left( {y - \left( {F + 1} \right){l_2}} \right) - {\varphi _0}} \right)} \right)}^2}{\rm{d}}y} \end{array} $ |
令:
| $ \theta = 2\left( {F + 1} \right){k_2}{l_2} + 2{\varphi _0} $ |
化简积分式:
| $ \begin{array}{l} I = \int\limits_{F{l_2}}^{\left( {F + 1} \right){l_2}} {\left( {\frac{1}{{2{y^2}}}\cos \left( {2{k_2}y - \theta } \right) + \frac{{{k_2}}}{y}\sin \left( {2{k_2}y - \theta } \right)} \right){\rm{d}}y} - \\ \;\;\;\;\;\;\;\frac{{{k_2}}}{4}\left[ {\sin \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) - \sin \left( {2{\varphi _0}} \right)} \right] + \frac{1}{2}k_2^2{l_2} + \\ \;\;\;\;\;\;\;\frac{1}{{2F\left( {F + 1} \right){l_2}}} \end{array} $ |
利用关系式:
| $ \begin{array}{l} \frac{1}{{2{y^2}}}\cos \left( {2{k_2}y - \theta } \right) + \frac{{{k_2}}}{y}\sin \left( {2{k_2}y - \theta } \right) = \\ \;\;\;\;\;\;\;\;\;\;\frac{{\cos \theta }}{2}\left[ {\frac{1}{{{y^2}}}\cos \left( {2{k_2}y} \right) + \frac{{2{k_2}}}{y}\sin \left( {2{k_2}y} \right)} \right] + \\ \;\;\;\;\;\;\;\;\;\;\frac{{\sin \theta }}{2}\left[ {\frac{1}{{{y^2}}}\sin \left( {2{k_2}y} \right) - \frac{{2{k_2}}}{y}\cos \left( {2{k_2}y} \right)} \right] \end{array} $ |
再利用积分公式:
| $ \int\left(\frac{\sin (\alpha x)}{x^{2}}-\alpha \frac{\cos (\alpha x)}{x}\right) \mathrm{d} x=-\frac{\sin (\alpha x)}{x} $ |
| $ \int\left(\frac{\cos (\alpha x)}{x^{2}}+\alpha \frac{\sin (\alpha x)}{x}\right) \mathrm{d} x=-\frac{\cos (\alpha x)}{x} $ |
化简得:
| $ \begin{array}{l} I = \frac{1}{2}k_2^2{l_2} + \frac{1}{{2F{l_2}}}\cos \left( {2{k_2}{l_2} + 2{\varphi _0}} \right) - \\ \;\;\;\;\;\;\frac{{{k_2}}}{4}\sin \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) + \frac{1}{{2F(F + 1){l_2}}} + \frac{{{k_2}}}{4}\sin {(2\varphi )_0} - \\ \;\;\;\;\;\;\frac{1}{{2(F + 1){l_2}}}\cos \left( {2{\varphi _0}} \right) = \frac{1}{2}k_2^2{l_2} + \\ \;\;\;\;\;\;\frac{1}{{2F{l_2}}}\cos \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) - \frac{{{k_2}}}{4}\sin \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) + \\ \;\;\;\;\;\;\frac{1}{{2F(F + 1){l_2}}} + \frac{1}{{2(F + 1){l_2}}} - \frac{{{k_2}}}{4}\sin \left( {2{\varphi _0}} \right) \end{array} $ |
求得前端支路前盖板元件的等效弹性系数:
| $ \begin{array}{l} {D_2} = \frac{{A_2^2{E_2}{S_2}{k_2}}}{{A_1^2{F^2}l_2^2}}\left( {\frac{1}{2}{k_2}{l_2} + \frac{1}{{2F{k_2}{l_2}}}\cos \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) - } \right.\\ \;\;\;\;\;\;\;\;\frac{1}{4}\sin \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) + \frac{1}{{2F\left( {F + 1} \right){k_2}{l_2}}} + \\ \;\;\;\;\;\;\;\;\left. {\frac{1}{{2\left( {F + 1} \right){k_2}{l_2}}} - \frac{1}{4}\sin \left( {2{\varphi _0}} \right)} \right) \end{array} $ |
前端支路前盖板元件的动能:
| $ \frac{1}{2}{m_2}{\omega ^2}A_1^2 = \frac{1}{2}\int\limits_{{l_{{{\rm{e}}_2}}}}^{{l_{{{\rm{e}}_2}}} + {l_2}} {{\rho _2}{{\left( {\frac{{z + F{l_2} - {l_{{{\rm{e}}_2}}}}}{{F{l_2}}}} \right)}^2}{S_2}{\omega ^2}\xi _2^2{\rm{d}}z} $ |
计算得前端支路前盖板元件的等效质量:
| $ \begin{array}{l} {m_2} = \frac{{A_2^2{\rho _2}{S_2}}}{{A_1^2{F^2}{k_2}l_2^2}}\left[ {\frac{{{k_2}{l_2}}}{2} + \frac{1}{4}\sin \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) - } \right.\\ \;\;\;\;\;\;\;\;\frac{1}{4}\sin \left( {2{\varphi _0}} \right)] \end{array} $ |
根据尾端支路机械抗分量等于0:
| $ \omega {m_{{{\rm{e}}_1}}} + \omega {m_1} - \frac{1}{\omega }{D_{{{\rm{e}}_1}}} - \frac{1}{\omega }{D_1} = 0 $ |
将ω=v1k1=veke,ω2=E1/ρ1=Ee/ρe代入上式,得:
| $ \begin{array}{l} {\rho _1}{v_1}{S_1}\left[ {\frac{{{k_1}{l_1}}}{2} + \frac{1}{4}\sin \left( {2{k_1}{l_1}} \right)} \right] + {\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}{\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2} \cdot \\ \;\;\;\;\;\;\;\;\;\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}}}{2} - \frac{1}{4}\sin \left( {2{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)} \right] - \\ \;\;\;\;\;\;\;\;\;{\rho _1}{v_1}{S_1}\left[ {\frac{{{k_1}{l_1}}}{2} - \frac{1}{4}\sin \left( {2{k_1}{l_1}} \right)} \right] - \\ \;\;\;\;\;\;\;\;\;{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}{\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2}\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}}}{2} + \frac{1}{4}\sin \left( {2{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)} \right] = 0 \end{array} $ |
化简得:
| $ \tan \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right) = \frac{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}{{{\rho _1}{v_1}{S_1}}}\cot \left( {{k_1}{l_1}} \right) $ | (4) |
根据前端支路机械抗分量等于0:
| $ \omega {m_{{{\rm{e}}_2}}} + \omega {m_2} - \frac{1}{\omega }{D_{{{\rm{e}}_2}}} - \frac{1}{\omega }{D_2} = 0 $ |
代入等效参数:
| $ \begin{array}{l} \omega {\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2}\frac{{{\rho _{\rm{e}}}{S_{\rm{e}}}}}{{{k_{\rm{e}}}}}\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}}}{2} - \frac{1}{4}\sin \left( {2{k_{{{\rm{e}}_2}}}{l_{{{\rm{e}}_2}}}} \right)} \right] + \\ \;\;\;\omega \frac{{A_2^2{\rho _2}{S_2}}}{{A_1^2{F^2}{k_2}l_2^2}}\left[ {\frac{{{k_2}{l_2}}}{2} + \frac{1}{4}\sin \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) - \frac{1}{4}\sin \left( {2{\varphi _0}} \right)} \right] - \\ \;\;\;\frac{1}{\omega }{\left( {\frac{{\cos \left( {{k_1}{l_1}} \right)}}{{\sin \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right)}}} \right)^2}{E_{\rm{e}}}{S_{\rm{e}}}{k_{\rm{e}}}\left[ {\frac{{{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}}}{2} + \frac{1}{4}\sin \left( {2{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}} \right)} \right] - \\ \;\;\;\frac{1}{\omega }\frac{{A_2^2{E_2}{S_2}{k_2}}}{{A_1^2{F^2}l_2^2}}\left( {\frac{1}{2}{k_2}{l_2} + \frac{1}{{2F{k_2}{l_2}}}\cos \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) - } \right.\\ \;\;\;\frac{1}{4}\sin \left( {2\left( {{k_2}{l_2} + {\varphi _0}} \right)} \right) + \frac{1}{{2F(F + 1){k_2}{l_2}}} + \\ \;\;\;\frac{1}{{2(F + 1){k_2}{l_2}}} - \frac{1}{4}\sin \left( {2{\varphi _0}} \right)) = 0 \end{array} $ |
化简得:
| $ \tan \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_{\rm{2}}}}}} \right) = \frac{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}{{{\rho _2}{v_2}{S_2}}}\frac{1}{{\tan \left( {{k_2}{l_2} + {\varphi _0}} \right) - \frac{1}{{F{k_2}{l_2}}}}} $ | (5) |
其中φ0由式(3)描述。再将式(5)与式(4)联合,利用公式:
| $ \begin{array}{l} \cot \left( {{k_{\rm{e}}}\left( {{l_{{{\rm{e}}_1}}} + {l_{{{\rm{e}}_2}}}} \right)} \right) = \frac{1}{{\tan \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right) + \tan \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}} \right)}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{\cot \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_1}}}} \right) + \cot \left( {{k_{\rm{e}}}{l_{{{\rm{e}}_2}}}} \right)}} \end{array} $ |
得:
| $ \begin{array}{*{20}{c}} {\cot \left( {{k_{\rm{e}}}{l_{\rm{e}}}} \right) = \frac{{F{k_2}{l_2}\tan \left( {{k_2}{l_2} + {\varphi _0}} \right) - 1}}{{\frac{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}{{{\rho _{\rm{1}}}{v_{\rm{1}}}{S_{\rm{1}}}}}F{k_2}{l_2}\cot \left( {{k_1}{l_1}} \right)\tan \left( {{k_2}{l_2} + {\varphi _0}} \right) - \frac{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}{{{\rho _{\rm{1}}}{v_{\rm{1}}}{S_{\rm{1}}}}}\cot \left( {{k_1}{l_1}} \right) + \frac{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}{{{\rho _{\rm{2}}}{v_{\rm{2}}}{S_{\rm{2}}}}}F{k_2}{l_2}}} - }\\ {\frac{{F{k_2}{l_2}}}{{\frac{{{\rho _{\rm{1}}}{v_{\rm{1}}}{S_{\rm{1}}}}}{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}F{k_2}{l_2}\tan \left( {{k_1}{l_1}} \right) + \frac{{{\rho _{\rm{2}}}{v_{\rm{2}}}{S_{\rm{2}}}}}{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}F{k_2}{l_2}\tan \left( {{k_2}{l_2} + {\varphi _0}} \right) - \frac{{{\rho _{\rm{2}}}{v_{\rm{2}}}{S_{\rm{2}}}}}{{{\rho _{\rm{e}}}{v_{\rm{e}}}{S_{\rm{e}}}}}}}} \end{array} $ | (6) |
经典文献[1-2]利用等效电路法并通过一些函数近似得到了频率方程,可以证明,式(4)、(5)经过一些近似处理也可以化简成与文献[1-2]一致的频率方程表达式。本文推导过程不曾利用数学近似,因此式(6)表达的频率方程适用范围将更广。
3 纵向换能器谐振频率计算分析利用式(6)表示的纵向换能器的频率方程可以直接由结构参数求出纵向换能器的谐振频率,公式中包含了尾质量截面积S1、前盖板细端截面积S2、压电堆截面积Se,本文得出的频率方程具有更宽泛的适用性,不要求部件等截面和截面的具体形状,也不需要预先假定节点位置,再进行逼近处理。由式(6)求出频率参数后,可以再用式(4)计算节点位置。
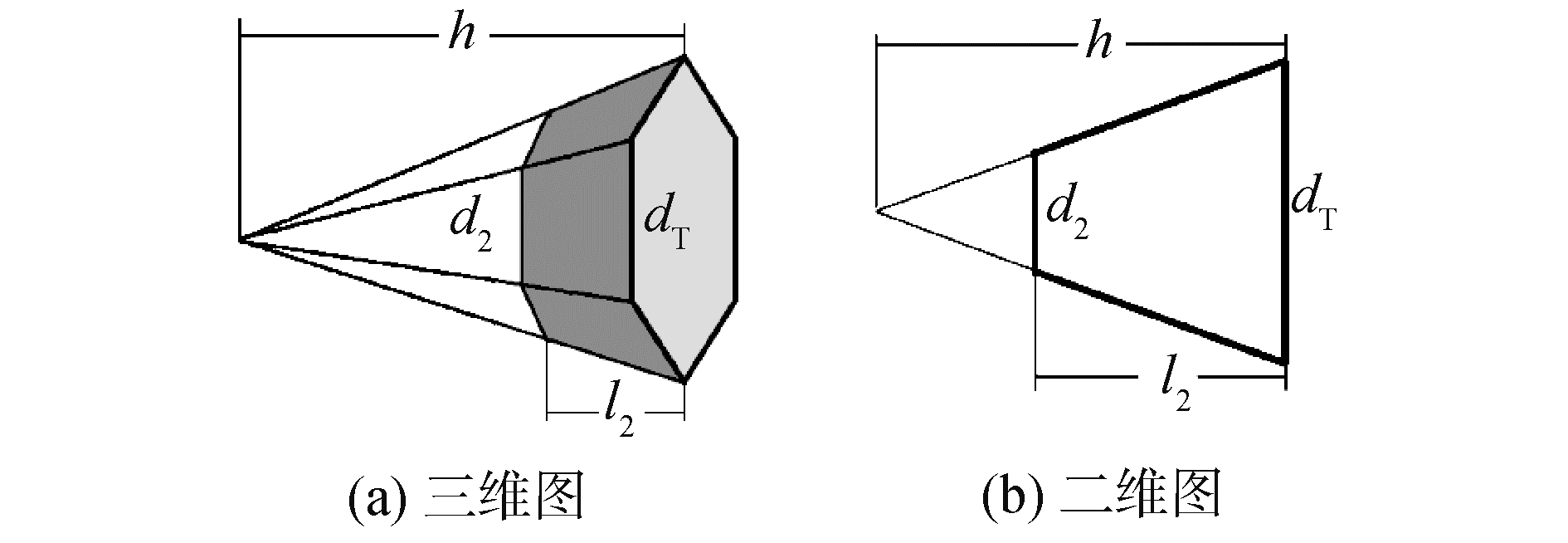
上述推导中没有刻意规定截面一定为圆形,因此式(6)也适用于其他多边形(或椭圆形)截面的情况,下面以辐射面为多边形情形为例进行计算,算例中依据延展系数F的定义原则,假定多边形台体是棱锥的一部分(如图 3所示)。为了证明理论模型的有效性,我们同时建立了有限元模型,通过模态分析和振型求出谐振频率及节点位置,有限元分析换能器是相对成熟的技术[8],具体过程在此从略,仅在表 1中给出结果数据进行对比。
|
Download:
|
| 图 3 多边形前盖板示例 Fig. 3 The example of polygon front cover | |
| 表 1 纵向换能器谐振频率计算比较 Table 1 Comparsion of longitudinal frequency calculation of longitudinal transducer |
从表 1可以看出,频率方程式(6)可以有效计算纵向换能器的谐振频率和节点位置,谐振频率计算误差在2%左右,节点位置偏差在1 mm(约占换能器总长度1%)左右。当换能器的前盖板截面尺寸与压电堆相比明显变大时(如算例3),计算结果的误差增大。再举算例4,将前盖板横向尺寸变成算例2的2倍,计算结果的偏差变得更大。这里给出的4个算例,主要为了突出模型方法对不等截面和多种截面形状的适用性,算例中le、l1、l2均保持不变,如果依据经典计算方法则不能得到差异性结果。
在前盖板和后盖板采用特殊结构时,如前盖板设计成大尺寸薄板并利用弯曲模振动耦合实现宽带辐射[9-15]、为了减小换能器纵向长度将尾质量块设计成反包嵌套形式[14-15]等,本文频率方程不再适用,有限元方法可以给出较准确结果;如果前盖板采用截面直径逐渐变小的反向喇叭(锥形变幅杆)形状[16],可以借鉴本文处理方法推导频率方程,在此不做赘述。
4 结论1) 从一维纵振动理论出发,建立纵向换能器的最简机电等效模型,利用能量法推导等效模型和元件参数表达式,进一步推导得到频率方程。
2) 通过与有限元方法相比,验证了频率方程对纵向换能器基频谐振特性描述的准确性,可用于部件不等截面情形和多种截面形状纵向换能器谐振频率的计算,具有更广的适用性。
3) 由于该方程直接给出了参数化表达式,方便直接解算频率参数,不需要预先假定节点位置的逼近处理。
4) 在前盖板截面尺寸与压电堆相比差异悬殊时,计算结果偏差增大,其原因主要是本文的推导仍然基于一维振动模型的假设,而随着前盖板截面尺寸与压电堆相比变大时,这一假设偏离实际情况就越远。
后续工作将考虑横向振动耦合效应,修改模型,使分析方法的适用性更加广泛,计算的准确性得到进一步提高。
| [1] |
周福洪. 水声换能器及基阵[M]. 北京: 国防工业出版社, 1984: 62-84.
(  0) 0)
|
| [2] |
栾桂冬, 张金铎, 金欢阳. 传感器及其应用[M]. 西安: 西安电子科技大学出版社, 2002: 161-165.
(  0) 0)
|
| [3] |
林书玉. 夹心式压电陶瓷功率超声换能器的优化设计[J]. 压电与声光, 2003, 25(3): 199-202. LIN Shuyu. Optimization design of the sandwich piezoelectric ceramic ultrasonic transducer[J]. Piezoelectrics & acoustooptics, 2003, 25(3): 199-202. DOI:10.3969/j.issn.1004-2474.2003.03.007 (  0) 0)
|
| [4] |
林书玉. 双激励源压电陶瓷超声换能器的共振频率特性分析[J]. 电子学报, 2009, 37(11): 2504-2509. LIN Shuyu. Analysis on the resonance frequency of sandwich ultrasonic transducers with two sets of piezoelectric ceramic elements[J]. Acta electronica sinica, 2009, 37(11): 2504-2509. DOI:10.3321/j.issn:0372-2112.2009.11.026 (  0) 0)
|
| [5] |
贺西平, 胡静. 穿单孔型宽频带换能器[J]. 声学学报, 2007, 32(3): 221-225. HE Xiping, HU Jing. Study on the wide-band sandwich transducer with single hole[J]. Acta acustica, 2007, 32(3): 221-225. DOI:10.3321/j.issn:0371-0025.2007.03.004 (  0) 0)
|
| [6] |
秦雷, 王丽坤, 唐会彦, 等. 夹心式复合变幅杆换能器频率方程的推导[J]. 振动与冲击, 2011, 30(7): 188-191. QIN Lei, WANG Likun, TANG Huiyan, et al. Frequency equation of a sandwich transducer with complex transformer[J]. Journal of vibration and shock, 2011, 30(7): 188-191. DOI:10.3969/j.issn.1000-3835.2011.07.035 (  0) 0)
|
| [7] |
BUTLER S C. Triple-resonant transducers[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 2012, 59(6): 1292-1300. DOI:10.1109/TUFFC.2012.2320 (  0) 0)
|
| [8] |
莫喜平. ANSYS软件在模拟分析声学换能器中的应用[J]. 声学技术, 2007, 26(6): 1279-1290. MO Xiping. Simulation and analysis of acoustics transducers using the ANSYS software[J]. Technical acoustics, 2007, 26(6): 1279-1290. DOI:10.3969/j.issn.1000-3630.2007.06.042 (  0) 0)
|
| [9] |
李英明, 莫喜平, 潘耀宗, 等. 铁镓驱动弯曲圆盘换能器设计及振动特性研究[J]. 应用声学, 2016, 35(6): 471-479. LI Yingming, MO Xiping, PAN Yaozong, et al. Flexural vibration of bender disk transducer driven by Galfenol[J]. Journal of applied acoustics, 2016, 35(6): 471-479. (  0) 0)
|
| [10] |
周天放, 蓝宇, 桑永杰. 空腔式前盖板宽带纵向换能器研究[J]. 哈尔滨工程大学学报, 2016, 37(9): 1215-1219. ZHOU Tianfang, LAN Yu, SANG Yongjie. Research on longitudinal broadband transducer with cavity-type front cover[J]. Journal of Harbin Engineering University, 2016, 37(9): 1215-1219. (  0) 0)
|
| [11] |
HAWKINS D W, GOUGH P T. Multiresonance design of a Tonpilz transducer using the Finite Element Method[J]. IEEE transactions on ultrasonics, ferroelectrics, and frequency control, 1996, 43(5): 782-790. DOI:10.1109/58.535479 (  0) 0)
|
| [12] |
CHARLES D, GREG W, LISA N, et al. Analyses and measurements of acoustically matched, air-coupled tonpilz transducers[C]//1999 IEEE ultrasonics symposium, 1045-1048.
(  0) 0)
|
| [13] |
ZHANG Kai. The study of 33 mode single crystal longitudinal transducer[C]//2015 Symposium on Piezoelectricity, Acoustic waves, and device applications, Jinan, China, 282-284.
(  0) 0)
|
| [14] |
莫喜平, 刘永平, 崔政, 等. 宽带宽波束纵向水声换能器研究[J]. 应用声学, 2006, 25(5): 270-272. MO Xiping, LIU Yongping, CUI Zhen, et al. A broadband and wide-beam longitudinal underwater transducer[J]. Journal of applied acoustics, 2006, 25(5): 270-272. DOI:10.3969/j.issn.1000-310X.2006.05.003 (  0) 0)
|
| [15] |
GOU Yue, DAI Yuyu. Simulation study on wideband transducer with longitudinal-flexural coupling vibration[C]//2019 Symposium on Piezoelectrcity, Acoustic Waves and Device Applications (SPAWDA), 2019: 1-4.
(  0) 0)
|
| [16] |
LIU Yingxiang, CHEN Weishan, LU Di, et al. Study on the vibration coupling of ultrasonic motor using longitudinal transducers[C]//2012 Symposium on Piezoelectricity, Acoustic Waves, and Device, Shanghai, China, 2012.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


