2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
水声学研究中,声场的正确预报及海底声学参数的准确反演都需要预知海底浅层沉积层的等效分层结构[1-7]。由于沉积层等效分层结构获取的困难性,在最新的一些基于模式选择[8]和跨维度贝叶斯算法[9-11]的地声参数反演技术中,沉积层层数及参数也作为未知变量进行估计。这些技术由于计算量大、难以有效用于实际工程应用中,另外,跨维度贝叶斯技术得到的沉积层结构极其复杂而难为常用的声场预报模型所利用。通过分析浅层剖面仪的走航测量结果来获取实验区域浅层沉积层的等效分层结构是目前最常用的方法[12-13]。目前浅剖数据处理大都通过人工观察的方式进行,无法将沉积层的等效结构与GPS位置信息有效结合起来,故而无法直接用于水下三维声场准确建模和预测的应用中, 也无法与其他测绘系统协同合作。本文利用混合联合信号处理方法,从浅层剖面结果中自动提取沉积层的等效垂直分层结构,为声场预报和地声参数反演提供可靠的沉积层先验信息。
1 沉积层的影响及浅层剖面仪作为水下声传播的下边界,浅层沉积层的结构及声学参数对声传播有着显著的影响。图 1给出了3种不同沉积层结构类型下简正波传播模型[14]预测的声场分布图。仿真计算中,声源频率为300 Hz,声源深度为10 m,海水深度为65 m,水中声速为1 500 m/s。

|
Download:
|
| 图 1 仿真不同沉积层分层结构下的声场分布 Fig. 1 Predicted sound pressure field for different sediment layering conditions | |
图 1给出了利用不同沉积层分层的海底地声模型计算得到的声场二维分布图,其中图 1(a)为半无限海底模型,其声学参数纵波声速、密度和吸收系数分别为1 550 m/s、1.8 g/cm3和0.15 dB/波长。图 1(b)为一层10 m的沉积层覆盖在图 1(a)的半无限空间的计算结果,其中沉积层的声学参数纵波声速、密度和吸收系数分别为1 475 m/s、1.6 g/cm3和0.06 dB/波长。图 1(c)的环境在图 1(b)的沉积层下面加入了一厚度为5 m的沉积层,新加入的沉积层声学参数纵波声速、密度和吸收系数为1 590 m/s、1.8 g/cm3和0.8 dB/波长,海底半无限空间的声学参数不变。
从图 1可以看出,海底沉积层结构及声学参数的不同,导致仿真的水中声场空间结构存在明显差别。在地声参数反演中,沉积层模型经常假设为一固定模型,如果模型与实际情况不符,则由匹配场反演技术得到的声学参数可能无法为声呐性能评估等应用提供可靠的环境信息。
在实际海洋环境中,表层沉积层会受到河流冲积、沉积化过程等影响,其垂直结构及空间分布十分复杂,为获得可靠的声场预报和地声参数反演结果,通过一定的信号处理方法获得沉积层等效结构的先验信息是十分必要的。
浅层剖面仪是在海水深度回声探测仪的基础上发展而来的,后来在港口建设、海底管道铺设及航道疏浚中等海岸工程中得到广泛应用[15-16]。根据发射信号频率、声源级及沉积层底质的不同,浅层剖面仪的探测深度范围一般为十几米至几十米不等。图 2给出了海上浅层剖面仪拖曳工作示意图。一般情况下,浅层剖面仪的拖体部分随测量船移动,在设置了一定的信号频率、脉冲宽度、增益等参数后,拖体上的发射换能器会向水下垂直发射声波信号。通过累积接收到的海底反射回波的时间和强度,进而获得可用来描绘浅层沉积层的剖面图。如何从剖面中自动提取可以表征沉积层等效分层结构的信息是本文研究的重要目的。
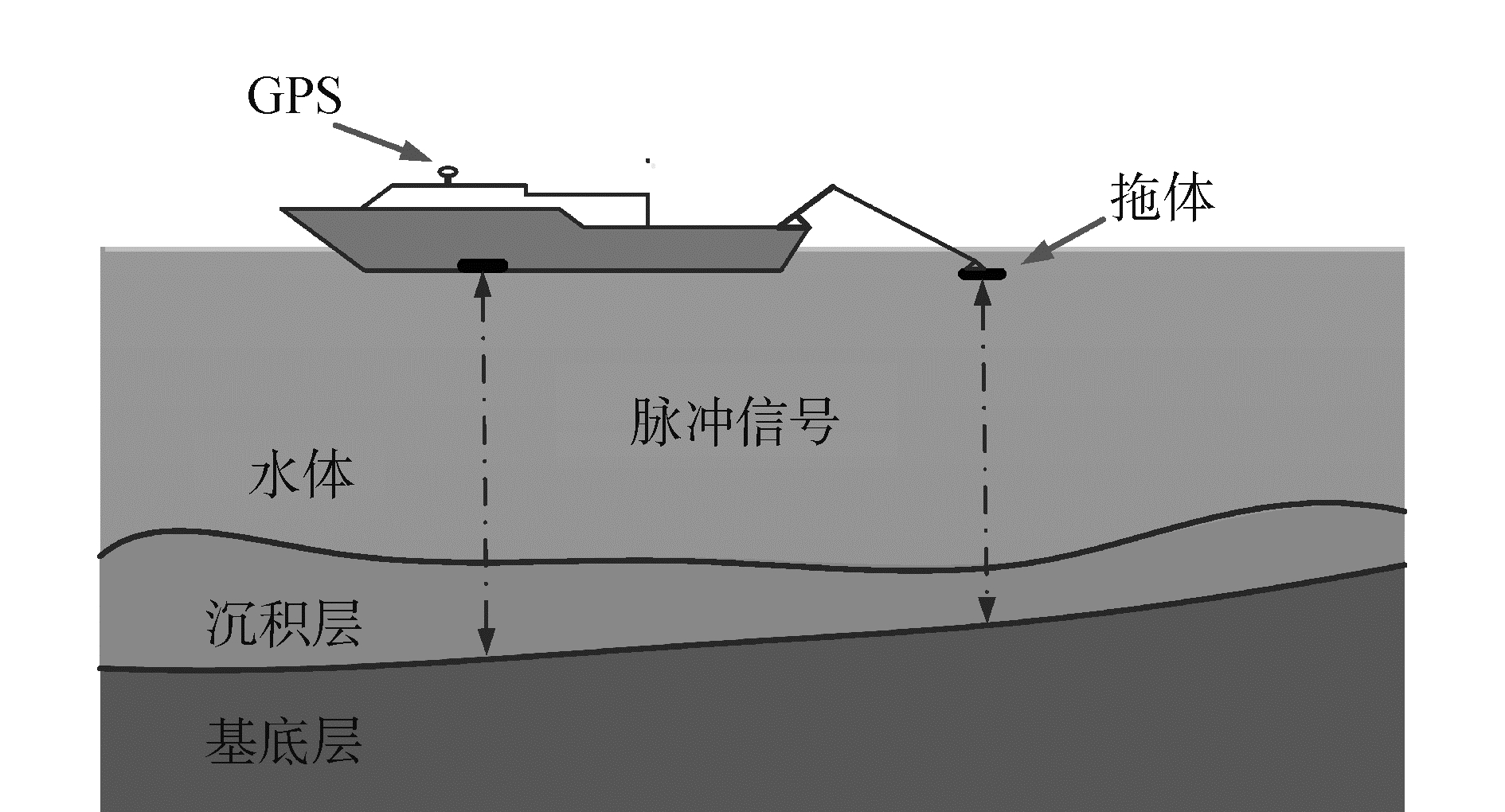
|
Download:
|
| 图 2 浅层剖面仪海上拖曳作业 Fig. 2 Demonstration of an at-sea seismic survey | |
2016年,开展了利用浅层剖面仪进行沉积层结构获取的海上综合实验。实验所用的浅层剖面仪为Edgetech 3100p,测量船按照4~6 kn的速度沿设定航线航行,浅层剖面仪拖体拖曳深度大致维持在水下5 m,发射信号脉冲形式为2~12 kHz的线性调频信号。
2 多处理方法联合提取沉积层结构浅层剖面仪用于海上测量时会与海水深度仪和GPS记录同时进行。现有浅层剖面结果一般由专业人士通过手动调节增益进行沉积层结构信息的观察提取,无法与水深测量结果及位置信息相结合,因而很难描述沉积层的空间分布规律,也难以直接用于地声模型的建模中。本文通过联合图像统计增强、多尺度线条滤波、小波分解及重构和图像二值化的处理方式,从浅层剖面仪的输出图像中自动提取浅层沉积层的等效结构信息。
2.1 图像统计增强技术由于环境噪声、海底界面混响、接收灵敏度等多种影响,浅层剖面仪的输出的浅剖图像中的结构会通常会比较模糊。这种模糊对于具有多分层结构海底的浅剖图像会更加明显,由于界面深度越深,其反射的能量越少,这导致接收到图像信息的能量在界面处与临近深度的对比度很低。
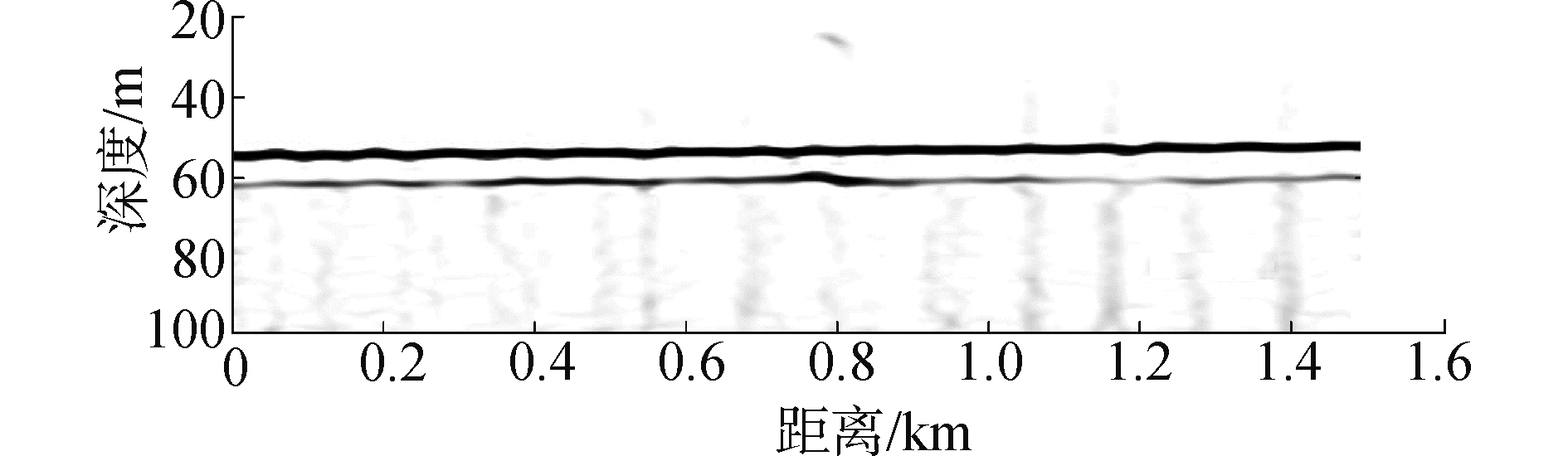
图 3(a)为浅层剖面仪的原始输出数据图像,图中可以看出在深度为55 m处有一较强的黑色线条,在63 m处有一较为不明显的灰色线条。这2个线条分别为海水与沉积层的交界面和沉积层与基底层的交界面。这些水平线条的识别和提取是获得沉积层垂直分层结构的重要前提,提高线条与图像其他位置上的对比度是需要进行预处理。为获得更加清晰的剖面图像,首先利用统计理论的图像均衡技术[17]以增强界面的对比度:

|
Download:
|
| 图 3 浅层剖面仪原始数据图像统计增强 Fig. 3 Seismic profile image statistics enhancement | |
| $ P = \min \left| {{c_1}\left( {T\left( k \right)} \right)-{c_0}\left( k \right)} \right| $ | (1) |
式中:c0是原始图像的累积统计直方图;c1是在所有强度下图像的累积统计直方图;T代表对图像灰度的一种线性处理。
图 3(b)为经过统计均衡后的浅剖图像,相比于图 3(a)的原始图像,统计均衡后的图像在界面处有更强的能量聚积并且线条连续。这些连续的线条为后续线条提取提供了更好的图像输入,利于沉积层结构的准确提取。
2.2 多尺度线条滤波器沉积层的分层结构大致呈水平分布的连续线条。由于海底体积混响和界面阻抗差的距离非均匀性,浅剖图像中的水平线条的宽度随深度和距离在发生着一定的变化,而且存在间断点,这为线条识别和提取的信号处理增加了一定的难度。
为应对浅剖图像中表征沉积层结构线条变化的特点,利用一种可以在一定尺度范围内检测线性结构的多尺度线性滤波器[18]。该滤波器可以在给定尺度范围内输出对处理图像L中线性结构的最大响应:
| $ M = \mathop {\max }\limits_{{s_{\min }} \le s \le {s_{\max }}} M\left( s \right) $ | (2) |
式中smin和smax是设定的最小和最大的滤波器尺度。二维多尺度线条滤波器通过计算Hessian矩阵在尺度s下的本征值来计算局部结构的响应:
| $ \begin{array}{l} M\left( s \right) = \\ \left\{ \begin{array}{l} 0, \;\;\;{\lambda _2} < 0\\ \exp \left( {-\frac{{{R^2}}}{{2{\alpha ^2}}}} \right)\left( {1-\exp \left( {-\frac{{{S^2}}}{{2{\beta ^2}}}} \right)} \right), \;\;\;\;其他 \end{array} \right. \end{array} $ | (3) |
式中:参数α和β用来调节滤波器对R(椭圆比)和S(信噪比)的敏感度,R和S分别为:
| $ R = \frac{{A/\pi }}{{{l^2}}} = \frac{{\left| {{\lambda _1}} \right|}}{{\left| {{\lambda _2}} \right|}} $ | (4) |
| $ S = {\left\| L \right\|_F} = \sqrt {\lambda _1^2 + \lambda _2^2} $ | (5) |
式中:λ1和λ2是Hessian矩阵的本征值,而且满足λ1>λ2;参数A和l分别是是用来描述结构特征的最大的椭圆截面积和椭圆长轴距离。S是图像L的F范数,可以看作图像结构信息和图像背景噪声的比值。式(3)所检测的为图像中能量高点的线条结构,如果需要检测图像中能量低点组成的线条结构,只需调整λ2的正负值。需要指出的是,尺度范围目前是根据数据的采样频率和线条厚度变化设定的,需要根据浅地剖面仪的参数设置进行选择。
图 4为图 3(b)的多尺度滤波后的输出结果,其中滤波器的尺度参数为smin=2和smax=16,增加量为2。相比于滤波前的图像,多尺度线条滤波器可有效检测出图像中不同宽度的条纹,并输出界面对比度更高的图像。需要指出的是,滤波后的图像中也出现了许多垂直方向上的线条结构,这部分条纹可能是多尺度滤波器同时检测各方向线条的结果,是水平线条提取的干扰。
|
Download:
|
| 图 4 对图 3(b)处理结果的多尺度滤波的输出 Fig. 4 Multi-scale line filtering results of Fig. 3 (b) | |
由于垂直干扰的尺度范围与水平线条相近,为了在干扰环境下准确地提取沉积层的垂直分层结构,本文利用二维小波变换的方法[19-20]滤除图 4中垂直方向的干扰线条并保留和增强表征沉积层分层界面的水平线条。
二维小波变换是一种成熟、有效的图像处理手段,将图像逐层分解成一系列互相独立的、表示不同细节的子图像。利用双正交小波滤波器组的二维小波变换将二维的图像分解为互相独立的方向(水平方向、垂直方向和对角方向)细节子图和平滑的低频图像:
| $ {f_0} = {c_A} + {c_H} + {c_V} + {c_D} $ |
式中,cA、cH、cV和cD分别表示低频子图像、水平子图像、垂直子图像和对角子图像,如图 5所示。垂直子图像中包含了垂直方向线条的干扰,而水平线条的结构则在水平方向的细节子图像中被保留了下来。
图 5为对图 4的二维小波变换分解的结果,图 5(a)为低频分量子图表示原始图中的低频分量,这一分量中保存了沉积层的主要结构,保证了分层界面在重建时的连续性;图 5(b)为水平分量子图表示原始图中的具有水平分量的部分,这一分量包含了待增强的水平分层界面结构;图 5(c)和(d)分别表示原始图中的垂直和交叉方向的分量子图,这一分量表示沉积层结构中的非水平分层分量与垂直告饶,在对分层结构的重构和提取时是待滤除的干扰。在二维小波变换对多尺度滤波器输出结果进行分解后,对分解子图处理,最后输出利用逆二维小波变换重建图像的流程图如图 6所示。

|
Download:
|
| 图 6 对子图处理的二维小波变换分解与重构示意 Fig. 6 2-D wavelet transform decomposition and reconstruction for sub-image processing | |
对水平方向子图像所进行的阈值增强处理如下:
| $ {c'_1} = \left\{ \begin{array}{l} 0, \;\;\;\;{c_1} < {T_1}\\ {P_1}, \;\;\;{c_1} \ge {T_1} \end{array} \right. $ | (6) |
式中:阈值T1=c1P1,P1为水平细节子图像的最大灰度值,阈值系数0 < c1 < 1,将水平细节子图像中灰度值小于阈值T1的点设置为0,灰度值大于阈值T1的点设置为P1。
对低频子图像、垂直方向子图像和交叉方向子图像进行的阈值滤波处理如下:
| $ {c'_2} = \left\{ \begin{array}{l} 0, \;\;\;\;{c_2} \le {T_2}\\ {c_2}, \;\;\;{c_2} > {T_1} \end{array} \right. $ | (7) |
式中:阈值T2=c2P2,其中P2为所处理子图像的最大灰度值,阈值系数0 < c2 < 1,将所处理子图中灰度值小于阈值T2的点设置为0,灰度值大于阈值T2的点保持不变。
在采用阈值滤波和阈值增强对4个子图进行处理后,利用逆二维小波变换对子图进行重建。图 7(a)为逆二维小波变换重建后的结果,相比于图 4,垂直条纹的干扰被完全抑制,图中只保留了表征沉积层垂直分层结构的水平线条,并且线条能量得到增强。

|
Download:
|
| 图 7 逆二维小波重建与二值化处理 Fig. 7 Inverse 2-D wavelet reconstruction and binarization processing | |
为了方便提取等效分层结构参数,需要先将经过上述信号处理的输出图像(图 7(a))进行二值化处理。二值化处理结果如图 7(b)所示,用“1”表示沉积层分层界面(黑色),其他区域用“0”表示(白色)。因为二值化的图像中水层和海底基底层均用“0”来表示,因而在任意一距离上的沉积层分层界面边界可以通过这一距离上深度方向的循环移位相减来求得。
如图 8所示,二值化后的深度向量可以通过对距离r0处列向量(深度方向)循环移位相减,得到水平线条区域的边界列向量(参数向量):

|
Download:
|
| 图 8 深度向量的二值化结果与循环移位相减 Fig. 8 The depth vector binarization results and cyclic shift subtraction processing | |
| $ {\mathit{\boldsymbol{b}}_{{r_0}}} = \left| {{\mathit{\boldsymbol{a}}_{{r_0}}}-{{\mathit{\boldsymbol{a'}}}_{{r_0}}}} \right| $ | (8) |
式中:ar0是距离r0处深度方向向量;a′r0是ar0循环移位后的结果。那么分层沉积层在每一个水平距离上的等效分层数目n可以通过下式求得:
| $ n = \frac{N}{2} $ | (9) |
式中N表示参数向量br0中非零值的个数,即沉积层分层界面的边界数。利用沉积层等效分层数可以对某一区域的海底进行统计建模。而分层沉积层中各分层界面的等效深度di可以表示为:
| $ {d_i} = \frac{{{L_{{\rm{even}}}} + {L_{{\rm{odd}}}}}}{2} $ | (10) |
式中:Leven表示参数向量br0中偶数项位置,即分层界面上边界的位置;Lodd表示向量br0中奇数项位置,即分层界面下边界的位置。那么分层沉积层中各分层界面的等效厚度tj表示为:
| $ {t_j} = {L_{{\rm{even}}}}-{L_{{\rm{odd}}}} $ | (11) |
这一厚度信息通常与沉积层界面混响有关,因而可以进一步寻求分层界面厚度与沉积层介质参数之间的关系,也可以用来计算沉积层分层界面处的反射能量。
3 典型沉积层结构的提取结果利用上述联合处理方法,对实验中获得的浅剖测线数据进行处理。图 9~11分别给出了3种典型沉积层结构的海底浅剖原始输出图像和等效分层界面提取结果:无明显沉积层分层海底、覆盖单层沉积层的海底和覆盖复杂的多层沉积层的海底。从原始输出图中可以看出,沉积层结构随距离非均匀变换,特别是深层的沉积层结构。而处理结果中,原始图像中可用来表征沉积层界面的特征均能够被准确地提取出来,尤其是在原始图像中不易直观观察到的模糊界面(如图 11所示),这为海底地声模型的建立提供了更准确的先验信息。

|
Download:
|
| 图 9 无明显沉积层分层海底的处理结果 Fig. 9 Processing results of bottom without obvious sedimentary layer | |

|
Download:
|
| 图 10 单层沉积层结构海底处理结果 Fig. 10 Processing results of bottom with single-layer sediment structure | |

|
Download:
|
| 图 11 复杂沉积层结构海底处理 Fig. 11 Processing results of bottom with complex-layer sediment structure | |
在水下声场预报和地声参数反演中,图 9所示的海底可作为半无限空间海底声学模型,图 10所示的海底可近似作为单层沉积层覆盖在半无限空间的海底声学模型。图 11所示的海底沉积层结构比较复杂,沉积层分层数随距离发生一定的变化,这就需要进行分段地声模型建模才能获得准确的声传播预报和地声参数反演结果。
4 结论1) 采用图像统计增强对浅剖输出数据进行预处理,然后利用多尺度线条滤波提取到多种尺度下的沉积层分层界面结构。
2) 结合数据特点,对子图处理的二维小波分解与重构方法,抑制了浅剖测量结果中会出现的垂直方向干扰,增强了深层界面的能量。
3) 二值化与移位相减处理自动提取到沉积层等效分层结构参数,包括沉积层等效分层数、沉积层等效深度和沉积层等效厚度。
4) 海上实测数据表明该方法可以在几种典型海底沉积层分层环境下均能准确提取沉积层的等效分层界面。
在下一步研究中,需要结合沉积物沉积过程和海洋环境因素对局部海域沉积层特性做进一步研究。
| [1] |
YANG Jie, JACKSON D R, TANG Dajun. Mid-frequency geoacoustic inversion using bottom loss data from the shallow water 2006 experiment[J]. The journal of the acoustical society of America, 2012, 131(2): 1711-1721. DOI:10.1121/1.3666009 (  0) 0)
|
| [2] |
GUILLON L, DOSSO S E, CHAPMAN N R, et al. Bayesian geoacoustic inversion with the image source method[J]. IEEE journal of oceanic engineering, 2016, 41(4): 1035-1044. DOI:10.1109/JOE.2016.2516421 (  0) 0)
|
| [3] |
任群言, 朴胜春, 马力, 等. 利用渔船噪声矢量场对地声参数的估计[J]. 哈尔滨工程大学学报, 2018, 39(2): 236-240. REN Qunyan, PIAO Shengchun, MA Li, et al. Geoacoustic inversion using ship noise vector field[J]. Journal of Harbin Engineering University, 2018, 39(2): 236-240. (  0) 0)
|
| [4] |
江鹏飞, 林建恒, 马力, 等. 一种海洋环境噪声分步反演地声参数方法[J]. 声学学报, 2016, 41(1): 59-66. JIANG Pengfei, LIN Jianheng, MA Li, et al. A multi-step method of geo-acoustic inversion by ambient noise[J]. Acta acustica, 2016, 41(1): 59-66. (  0) 0)
|
| [5] |
过武宏, 笪良龙, 赵建昕. 地声参数及传播损失不确定性估计与建模[J]. 应用声学, 2015, 33(1): 71-78. GUO Wuhong, DA Lianglong, ZHAO Jianxin. Estimation and modeling of geoacoustic parameters and transmission loss uncertainty[J]. Journal of applied acoustics, 2015, 33(1): 71-78. (  0) 0)
|
| [6] |
翁晋宝, 李风华, 郭永刚. 深海近距离声场频率-距离干涉结构反演海底声学参数[J]. 声学学报, 2015, 40(2): 207-215. WENG Jinbao, LI Fenghua, GUO Yonggang. Geoacoustic inversion based on near-field frequency-range interference patter in deep water[J]. Acta acustica, 2015, 40(2): 207-215. (  0) 0)
|
| [7] |
郭永刚, 王宁, 高大治. 由垂直入射脉冲和海底回波反演海底声参数[J]. 中国海洋大学学报, 2006, 36(1): 112-118. GUO Yonggang, WANG Ning, GAO Dazhi. Sea bottom acoustic parameters inversing by normal incidence and reflection[J]. Periodical of ocean university of china, 2006, 36(1): 112-118. (  0) 0)
|
| [8] |
DOSSO S E, DONG Hefeng, DUFFAUT K. Model selection for profile structure in Bayesian geoacoustic inversion[J]. The journal of the acoustical society of America, 2017, 141(5): 3470. (  0) 0)
|
| [9] |
DOSSO S E, DETTMER J. Bayesian matched-field geoacoustic inversion[J]. Inverse problems, 2011, 27(5): 055009. DOI:10.1088/0266-5611/27/5/055009 (  0) 0)
|
| [10] |
TOLLEFSEN D, DOSSO S E. Bayesian geoacoustic inversion of ship noise on a horizontal array[J]. The journal of the acoustical society of America, 2008, 124(2): 788-795. DOI:10.1121/1.2940581 (  0) 0)
|
| [11] |
DOSSO S E, DETTMER J, STEININGER G, et al. Efficient trans-dimensional Bayesian inversion for geoacoustic profile estimation[J]. The journal of the acoustical society of America, 2014, 136(11): 114018. (  0) 0)
|
| [12] |
THEUILLON G, STEPHAN Y, PACAULT A. High-resolution geoacoustic characterization of the seafloor using a subbottom profiler in the gulf of Lion[J]. IEEE journal of oceanic engineering, 2008, 33(3): 240-254. DOI:10.1109/JOE.2008.926958 (  0) 0)
|
| [13] |
YANG T C, YOO K, FIALKOWSKI L T. Subbottom profiling using a ship towed line array and geoacoustic inversion[J]. The journal of the acoustical society of America, 2007, 122(6): 3338-3352. DOI:10.1121/1.2799495 (  0) 0)
|
| [14] |
莫亚枭, 朴胜春, 张海刚, 等. 一种能量守恒的双向耦合简正波水声传播模型[J]. 声学学报, 2016, 41(2): 154-162. MO Yaxiao, PIAO Shengchun, ZHANG Haigang, et al. An energy-conserving two-way coupled mode model for underwater acoustic propagation[J]. Acta acustica, 2016, 41(2): 154-162. (  0) 0)
|
| [15] |
曹双, 罗红雨, 曾飞. 浅地层剖面仪在近海航道工程中的应用[J]. 海岸工程, 2010, 29(2): 70-75. CAO Shuang, LUO Hongyu, ZENG Fei. Application of subbottom profiler in engineering for waterway in near-shore sea[J]. Coastal engineering, 2010, 29(2): 70-75. DOI:10.3969/j.issn.1002-3682.2010.02.011 (  0) 0)
|
| [16] |
王继立, 黄潘阳, 胡涛骏, 等. 浅地层剖面仪在海底管道检测中的应用[J]. 船海工程, 2013, 42(3): 161-163. WANG Jili, HUANG Panyang, HU Taojun, et al. Application of sub-bottom profiler in submarine pipeline inspection[J]. Ship & ocean engineering, 2013, 42(3): 161-163. DOI:10.3963/j.issn.1671-7953.2013.03.043 (  0) 0)
|
| [17] |
李乐鹏, 孙水发, 夏冲, 等. 直方图均衡技术综述[J]. 计算机系统应用, 2014, 23(3): 1-8. LI Lepeng, SUN Shuifa, XIA Chong, et al. Survey of histogram equalization technology[J]. Computer systems & applications, 2014, 23(3): 1-8. DOI:10.3969/j.issn.1003-3254.2014.03.001 (  0) 0)
|
| [18] |
FRANGI A F, NIESSEN W J, VINCKEN K L, et al. Multiscale vessel enhancement filtering[C]//Proceedings of the First International Conference on Medical Image Computing and Computer-Assisted Intervention. Cambridge, MA, USA, 1998: 130-137.
(  0) 0)
|
| [19] |
FENG L, SUEN C Y, TANG Y Y, et al. Edge extraction of images by reconstruction using wavelet decomposition details at different resolution levels[J]. International journal of pattern recognition and artificial intelligence, 2000, 14(6): 779-793. DOI:10.1142/S0218001400000519 (  0) 0)
|
| [20] |
李金, 高尚伟, 吕普轶, 等. 基于二维小波变换的双彩色图像数字水印算法[J]. 哈尔滨工程大学学报, 2002, 23(5): 97-101. LI Jin, GAO Shangwei, LYU Puyi, et al. Dual color images watermarking algorithm based on wavelet transform[J]. Journal of Harbin Engineering University, 2002, 23(5): 97-101. DOI:10.3969/j.issn.1006-7043.2002.05.023 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40



