深度学习从大类上可以归入神经网络,不过在具体实现中有许多变化。深度学习的核心是特征学习,旨在通过分层网络获取分层次的特征信息,从而解决以往需要人工设计特征的重要难题[1-2]。深度学习是一个框架,包含卷积神经网络、稀疏编码器、自动编码器等多个重要算法。针对不同问题,需要选取的网络模型达到的处理效果也各不相同[3]。
由于图像特征数目过少,可能无法精确地实现分类,即欠拟合,也不会由于提取的特征数目过多,导致分类过程中过于注重某个特征出现分类错误,即过拟合。卷积神经网络不需要做大量的特征提取和特征选择工作,只需要在其训练完成后,将需要处理的问题输入,即可得到一个较好的拟合效果[4-5]。
针对当前方法在图像识别领域应用过程中容易受到物体形状、位移、尺度、光照、背景等因素的影响导致识别准确率不高,鲁棒性较低、方法可移植性较差的缺点,本文提出了基于多层卷积神经网络深度学习算法的图像识别方法,并分析了该方法在图像识别领域的可移植性。
1 多层卷积神经网络深度学习算法下的图像识别 1.1 模型训练过程多层卷积神经网络深度学习模型是由多层感知机演变而来的,主要包括输入图像局部感受野、图像权值共享及图像时间/空间下采样3个部分,这3部分操作的最终目的是为了保证多层卷积神经网络能够学习到输入图像的更多细节特征,大大减少了神经元个数,使得输入图像具有形状、尺度及位移不变性,同时又能够减少输入图像的分辨率,降低计算复杂性,缩小搜索空间,更有利于图像识别[6-7]。
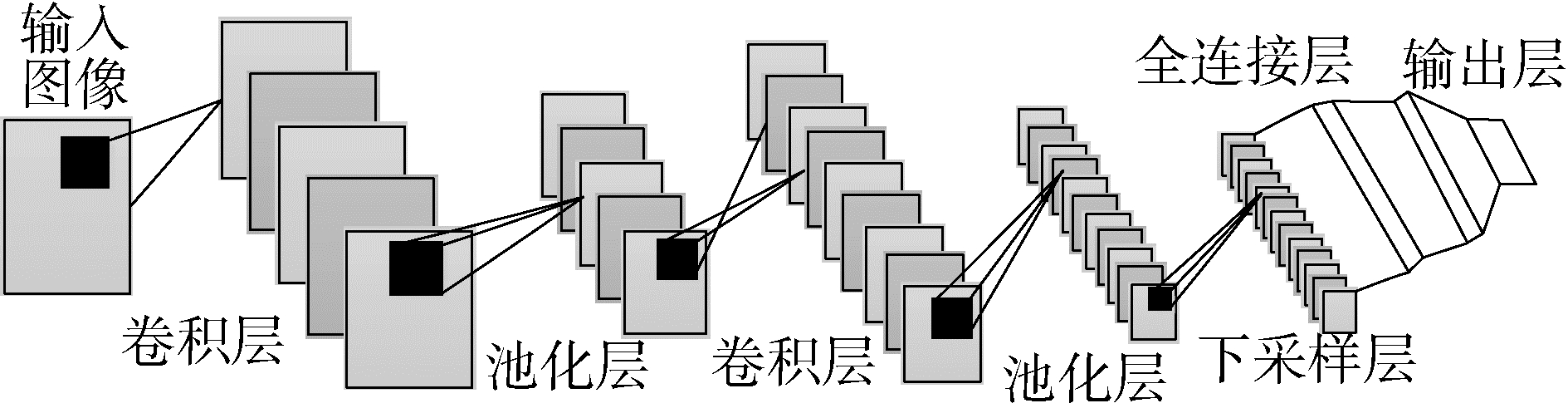
本文使用了6层卷积神经模型,包括卷积层、池化层、卷积层、池化层、下采样层、全连接层以及输出层,如图 1所示。并采用3×3的卷积核进行了10次迭代。
|
Download:
|
| 图 1 卷积神经网络结构 Fig. 1 Structure of convolutional neural network | |
训练过程包括数据训练和对应的类别标签训练。在模型初始化设置过程中,多层卷积神经网络深度学习模型的参数多为一些较小的、各部分相同的随机数,不仅能够保证模型不会进入过于饱和状态,而且还能保证模型具有较强的学习能力。多层卷积神经网络深度学习模型的训练方法与BP神经网络(BP neural network)模型的训练方法类似,主要分为2步:1)模型的前向传播,将训练图像数据中的任意一个样本(Xp, Yp)输入模型中,通过多层卷积神经网络深度学习,计算得到模型输出层的实际输出值,即最终的识别结果[8-9],具体计算公式描述为:
| $ {O_p} = {F_n}(L({F_2}({F_1}({O_p}{W_1}){W_2}))L{W_n}) $ | (1) |
式中:F1、F2、LFn和W1、W2、LWn分别表示多层卷积神经网络深度学习模型中的一组滤波器及其对应权值;n为模型中包含的训练数据个数。
根据式(1)计算得到模型输出层的实际输出值Op与期望输出值Yp之间的误差大小,采用极小化规则反向传播方法调整多层卷积神经网络深度学习模型中的对应参数。具体过程如下:
1) 极小化规则反向传播方法。
① 前向传播。
采用平方误差代价函数计算模型输出层的实际输出值Op与期望输出值Yp之间的误差大小。假设训练的输入图像数据有N个,对应的类别标签有C个,则可得模型训练整体误差En的计算公式:
| $ {E^n} = \frac{1}{2}\sum\limits_{n = 1}^N {\sum\limits_{k = 1}^C {{{(t_k^n - y_k^n)}^2}} } $ | (2) |
式中:tkn为多层卷积神经网络深度学习模型中第n个训练数据期望输出的第k维数据;ykn为多层卷积神经网络深度学习模型中第n个训练数据实际输出的第k维数据。
如果只考虑单个训练数据,则可得多层卷积神经网络深度学习模型中第n个训练数据的误差为:
| $ {E^n} = \frac{1}{2}\sum\limits_{n = 1}^N {{{(t_k^n - y_k^n)}^2}} = \frac{1}{2}\left\| {{\mathit{\boldsymbol{t}}^n} - {\mathit{\boldsymbol{y}}^n}} \right\|_2^2 $ | (3) |
根据上述计算可得当前模型第l层的输出值为:
| $ {{X^l} = f({u^l})} $ | (4) |
| $ {{u^l} = {\mathit{\boldsymbol{W}}^l}{X^{l - 1}} + b} $ | (5) |
式中:f(g)为模型输出激活函数,用于获得待识别图像特征图;Wl为模型第l层训练数据的权值矩阵;Xl-1为当前模型第l-1层的输出;b为模型偏置项。
② 模型反向传播过程中,模型中每个神经元对于误差偏置项的灵敏度计算公式:
| $ {\frac{{\partial E}}{{\partial b}} = \frac{{\partial E}}{{\partial u}}\frac{{\partial u}}{{\partial b}} = \delta } $ | (6) |
| $ {\frac{{\partial u}}{{\partial b}} = 1} $ | (7) |
式中:∂E/∂u为模型误差对于输入图像数据u的导数。则可得模型反向传播过程中第l层神经元偏置项灵敏度计算公式为:
| $ {\delta ^l} = {({\mathit{\boldsymbol{W}}^{l + 1}})^T}{\delta ^{l + 1}} \odot f({u^l}) $ | (8) |
式中:δl+1为模型第l+1层神经元偏置项灵敏度;⊙表示模型中每个元素相乘。
对于误差函数,模型输出层的偏置项灵敏度与上述计算略有不同,表示为:
| $ {\delta ^l} = f({u^l}) \odot ({y^n} - {t^n}) $ | (9) |
在上述计算基础上,采用delta法则,实时更新多层卷积神经网络深度学习模型的各神经元权值,计算公式为:
| $ {\varDelta {\mathit{\boldsymbol{W}}^l} = - \eta \frac{{\partial E}}{{\partial {\mathit{\boldsymbol{W}}^l}}}} $ | (10) |
| $ {\frac{{\partial E}}{{\partial {\mathit{\boldsymbol{W}}^l}}} = {\mathit{\boldsymbol{X}}^{l - 1}}{{({\mathit{\boldsymbol{\delta }}^l})}^{\rm{T}}}} $ | (11) |
式中η为模型的学习率。
2) 模型中下采样层权值更新。
对于模型中的下采样层,输入的特征图数目与输出的特征图数目相等,即:
| $ x_j^l = f(\beta {\rm{down}} (x_j^{l - 1}) + b) $ | (12) |
下采样层神经元偏置项灵敏度,即对输入图像做降采样处理:
| $ \delta _j^l = f(\beta {\rm{down}} (x_j^{l - 1}) + b) $ | (13) |
式中down(·)表示下采样函数。
模型中下采样层权值更新方法与卷积层权值更新方法类似,计算公式为:
| $ \frac{{\partial E}}{{\partial \beta }} = \sum\nolimits_{u,v} {{{(\delta _j^l{\rm{down}} (x_j^{l - 1}))}_{u,v}}} $ | (14) |
在上述多层卷积神经网络深度学习模型训练完成基础上,为了提高该模型在图像识别过程中的准确率,引入Fisher准则,提出了基于类内距离和类间距离的能量函数[10-11],计算公式为:
| $ J = R + \gamma {J_1} - \eta {J_2} $ | (15) |
式中:R为多层卷积神经网络深度学习模型的代价函数;γ为能量函数调节参数;J1为待识别图像样本之间的相似度函数;J2为待识别图像类别标签之间的相似度函数。
在充分考虑类内距离J1和类间距离能量函数J2的基础上,计算模型输出层各个输出单元的残差,使得模型权值能更加快速收敛到有利于图像识别的最优值[12],计算公式为:
| $ \left\{ {\begin{array}{*{20}{l}} {\varepsilon = \frac{{\partial {J_1}}}{{\partial \delta _j^l}} = \frac{\partial }{{\partial \delta _j^l}}\frac{1}{2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{\left\| {{\mathit{\boldsymbol{Y}}_p} - {\mathit{\boldsymbol{M}}^{({i^\prime })}}} \right\|}^2}} } }\\ {\varepsilon = \frac{{\partial {J_2}}}{{\partial \delta _j^l}} = \frac{\partial }{{\partial \delta _j^l}}\frac{1}{2}\sum\limits_{i = 1}^m {\sum\limits_{j = 1}^n {{{\left\| {{\mathit{\boldsymbol{Q}}_p} - {\mathit{\boldsymbol{M}}^{({i^\prime })}}} \right\|}^2}} } } \end{array}} \right. $ | (16) |
| $ {M^{({i^\prime })}} = \frac{{\sum\limits_{j = 1}^n {{Y_p}} }}{n} $ | (17) |
式中M(i′)为待识别图像第i′类样本的均值。根据式(17)即可找到有利于图像识别的最优权值,将该权值计算结果代入式(17)中,即可获得图像识别结果,该理论分析结果证明多层卷积神经网络深度学习算法具有可移植性。
2 可移植性测试硬件环境:3.4 GHz双核处理器,4 GB内存,M40显卡,Ubuntu14.04操作系统。
软件环境:C++编译器。
为检验多层卷积神经网络深度学习算法在图像识别领域应用的可移植性,随机选取PASCAL VOC2007数据库中的2 750张图片,6个类别标签作为测试集,如表 1所示。
| 表 1 实验测试数据集 Table 1 Experimental test data set |
选取识别准确率、鲁棒性、以及识别耗时3项指标作为评价指标,识别表 1中的6种图像类型,测试基于多层卷积神经网络深度学习算法的图像识别方法的有效性,测试结果如表 2所示。
| 表 2 测试结果统计 Table 2 Test results statistics |
从表 2中可以看出,采用多层卷积神经网络深度学习算法识别6种不同类型图像的平均准确率为96.3%;识别6种不同类型图像的平均鲁棒性为96.8%;识别6种不同类型图像的平均耗时为17.8 ms。这是由于所提方法在训练完多层卷积神经网络深度学习模型基础上,引入Fisher准则,并提出了基于类内距离和类间距离的能量函数,使得模型权值能够更加快速收敛到有利于图像识别的最优值,大大提高了6种不同类型图像识别准确率和鲁棒性,同时加快了识别速度,平均识别耗时均达到毫秒级。假设道路上发生交通事故,所提方法具有毫秒级处理速度,有利于决策者及时作出应对措施,避免交通事故造成的经济损失和人员伤亡。
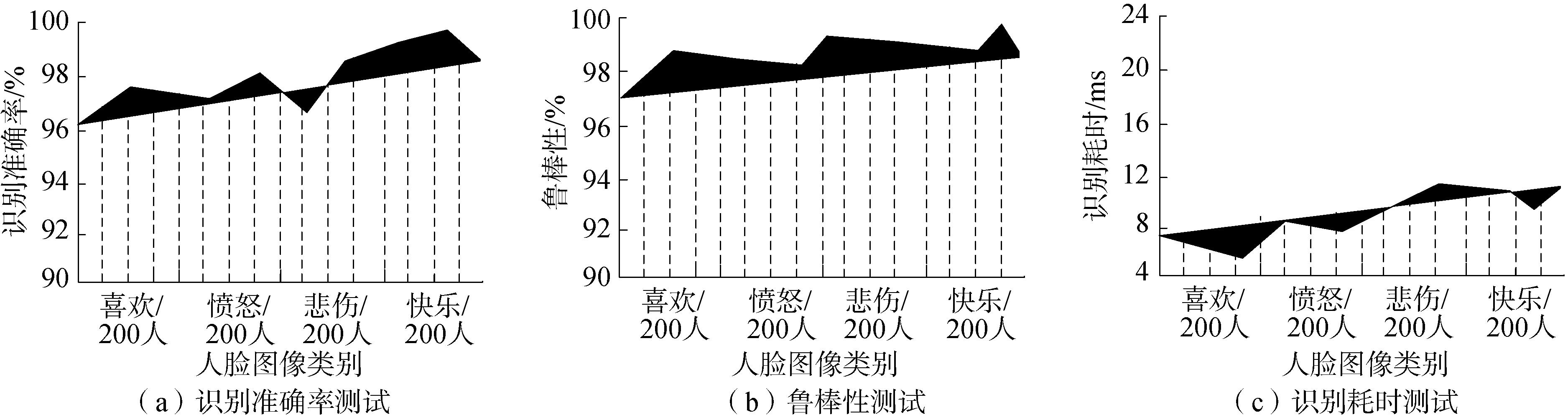
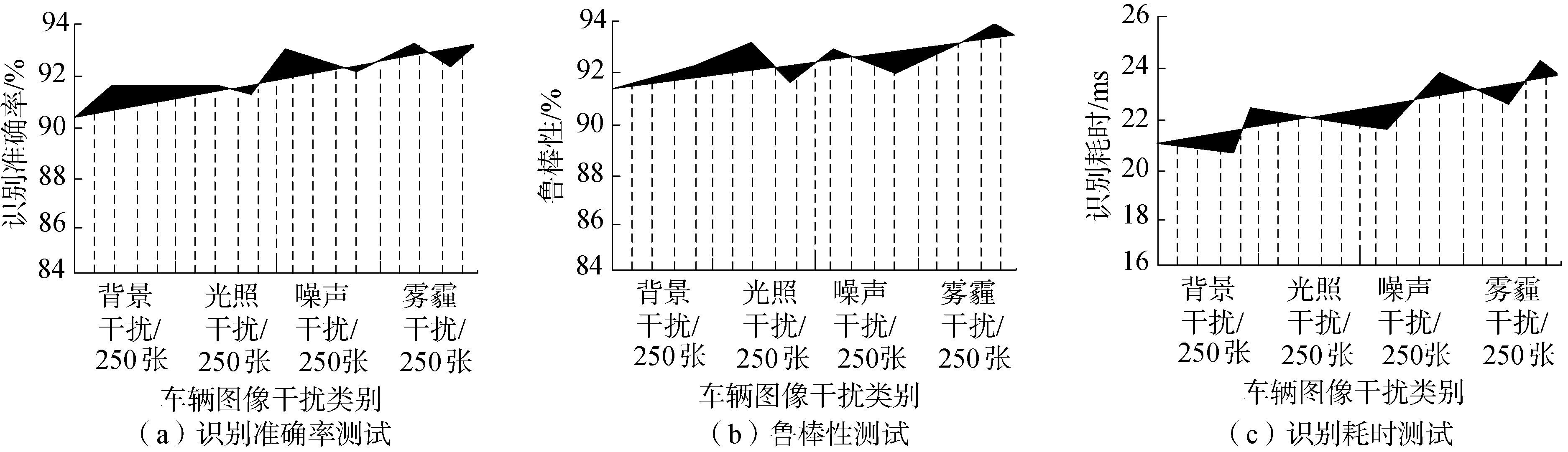
为了进一步检验所提方法的有效性和可移植性,选取比较复杂的人脸图像和容易受光照、背景、位移等影响的车辆图像作为训练样本,训练样本中喜欢、愤怒、悲伤、快乐4种表情各200张,受背景干扰、光照干扰、噪声干扰和雾霾干扰的车辆各250张,其中部分样本示例如图 2和图 3所示,采用所提方法识别4类人脸图像和4类不同类型干扰车辆图像,测试结果如图 4和图 5所示。

|
Download:
|
| 图 2 人脸图像训练样本 Fig. 2 Face image training sample | |

|
Download:
|
| 图 3 车辆图像训练样本 Fig. 3 Vehicle image training sample | |
|
Download:
|
| 图 4 人脸图像训练样本的识别结果 Fig. 4 Recognition results of face image training samples | |
|
Download:
|
| 图 5 车辆图像训练样本的识别结果 Fig. 5 Recognition results of vehicle image training samples | |
分析图 4和图 5的实验结果可以发现,采用所提方法无论是识别具有复杂表情的人脸图像训练样本, 还是具有各种干扰因素影响的车辆图像训练样本均取得了较好的成果,识别准确率和鲁棒性均较高,识别耗时较少。这是由于所提方法构建的识别模型中包括输入图像局部感受野、图像权值共享以及图像时间/空间下采样3个部分,这3部分操作保证了多层卷积神经网络能够学习到输入图像的更多细节特征,大大减少神经元个数,使得输入图像具有形状、尺度以及位移不变性,同时又能够减少输入图像的分辨率、降低计算复杂性、缩小搜索空间,更有利于识别。通过多层卷积神经网络深度学习算法对样本数据进行多次迭代训练,通过分类器输出训练后的实验样本,降低了原始数据的偏置程度,以提高实验结果的准确性。
上述实验结果表明,多层卷积神经网络深度学习算法应用在图像识别领域具有可移植性,这与上述理论分析结果一致。
3 结论1) 本文提出了基于多层卷积神经网络深度学习算法的图像识别方法,利用模型权值共享、更新、下采样等操作对输入图像做降采样处理,有效降低了计算复杂度。
2) 利用delta法则、Fisher准则以及基于类内距离和类间距离的能量约束函数实时调整多层卷积神经网络深度学习模型参数,计算模型输出层各个输出单元的残差,让模型权值能够更加快速收敛到有利于图像识别的最优值。
3) 本文实现了所提出的算法,并随机选取PASCAL VOC2007数据库中的图片,从理论和实验两方面证明了所提方法的可移植性。
| [1] |
刘万军, 梁雪剑, 曲海成. 不同池化模型的卷积神经网络学习性能研究[J]. 中国图象图形学报, 2016, 21(9): 1178-1190. LIU Wanjun, LIANG Xuejian, QU Haicheng. Learning performance of convolutional neural networks with different pooling models[J]. Journal of image and graphics, 2016, 21(9): 1178-1190. (  0) 0)
|
| [2] |
朱威, 屈景怡, 吴仁彪. 结合批归一化的直通卷积神经网络图像分类算法[J]. 计算机辅助设计与图形学学报, 2017, 29(9): 1650-1657. ZHU Wei, QU Jingyi, WU Renbiao. Straight convolutional neural networks algorithm based on batch normalization for image classification[J]. Journal of computer-aided design & computer graphics, 2017, 29(9): 1650-1657. DOI:10.3969/j.issn.1003-9775.2017.09.008 (  0) 0)
|
| [3] |
常玲玲, 马丙鹏, 常虹, 等. 深度网络结构在行人检测任务中的性能对比[J]. 计算机仿真, 2017, 34(7): 373-377, 411. CHANG Lingling, MA Ruipeng, CHANG Hong, et al. Comparative study on deep network architectures in pedestrian detection task[J]. Computer simulation, 2017, 34(7): 373-377, 411. DOI:10.3969/j.issn.1006-9348.2017.07.083 (  0) 0)
|
| [4] |
王晨, 汤心溢, 高思莉. 基于深度卷积神经网络的红外场景理解算法[J]. 红外技术, 2017, 39(8): 728-733. WANG Chen, TANG Xinyi, GAO Sili. Infrared scene understanding algorithm based on deep convolutional neural network[J]. Infrared technology, 2017, 39(8): 728-733. (  0) 0)
|
| [5] |
吕永标, 赵建伟, 曹飞龙. 基于复合卷积神经网络的图像去噪算法[J]. 模式识别与人工智能, 2017, 30(2): 97-105. LYU Yongbiao, ZHAO Jianwei, CAO Feilong. Image denoising algorithm based on composite convolutional neural network[J]. Pattern recognition and artificial intelligence, 2017, 30(2): 97-105. (  0) 0)
|
| [6] |
卢宏涛, 张秦川. 深度卷积神经网络在计算机视觉中的应用研究综述[J]. 数据采集与处理, 2016, 31(1): 1-17. LU Hongtao, ZHANG Qinchuan. Applications of deep convolutional neural network in computer vision[J]. Journal of data acquisition & processing, 2016, 31(1): 1-17. (  0) 0)
|
| [7] |
伍家松, 达臻, 魏黎明, 等. 基于分裂基-2/(2a)FFT算法的卷积神经网络加速性能的研究[J]. 电子与信息学报, 2017, 39(2): 285-292. WU Jiasong, DA Zhen, WEI Liming, et al. Acceleration performance study of convolutional neural network based on split-radix-2/(2a) FFT algorithms[J]. Journal of electronics & information technology, 2017, 39(2): 285-292. (  0) 0)
|
| [8] |
厉智, 孙玉宝, 王枫, 等. 基于深度卷积神经网络的服装图像分类检索算法[J]. 计算机工程, 2016, 42(11): 309-315. LI Zhi, SUN Yubao, WANG Feng, et al. Clothing image classification and retrieval algorithm based on deep convolutional neural network[J]. Computer engineering, 2016, 42(11): 309-315. DOI:10.3969/j.issn.1000-3428.2016.11.053 (  0) 0)
|
| [9] |
周林腾. 基于神经网络算法的大数据分析方法研究[J]. 电子设计工程, 2018, 26(9): 19-22, 27. ZHOU Linteng. Study on the analysis method of data based on neural network algorithm[J]. Electronic design engineering, 2018, 26(9): 19-22, 27. DOI:10.3969/j.issn.1674-6236.2018.09.005 (  0) 0)
|
| [10] |
刘海龙, 李宝安, 吕学强, 等. 基于深度卷积神经网络的图像检索算法研究[J]. 计算机应用研究, 2017, 34(12): 3816-3819. LIU Hailong, LI Baoan, LYU Xueqiang, et al. Image retrieval based on deep convolutional neural network[J]. Application research of computers, 2017, 34(12): 3816-3819. DOI:10.3969/j.issn.1001-3695.2017.12.067 (  0) 0)
|
| [11] |
余萍, 赵继生. 基于矩阵2-范数池化的卷积神经网络图像识别算法[J]. 图学学报, 2016, 37(5): 694-701. YU Ping, ZHAO Jisheng. Image recognition algorithm of convolutional neural networks based on matrix 2-norm pooling[J]. Journal of graphics, 2016, 37(5): 694-701. (  0) 0)
|
| [12] |
王华利, 邹俊忠, 张见, 等. 基于深度卷积神经网络的快速图像分类算法[J]. 计算机工程与应用, 2017, 53(13): 181-188. WANG Huali, ZOU Junzhong, ZHANG Jian, et al. Fast image classification algorithm based on deep convolutional neural network[J]. Computer engineering and applications, 2017, 53(13): 181-188. DOI:10.3778/j.issn.1002-8331.1601-0435 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


