2. 吉林大学 软件学院, 吉林 长春 130012
2. College of Software, Jilin University, Changchun 130012, China
自动编码器(auto-encoder,AE)是机器学习中一种重要的模型[1]。AE通过尽可能复现输入数据的方法,来提取输入数据的特征,通常AE只有单层的编码器和解码器。随着深度学习的发展,Hinton等[2]提出深度自动编码器(deep auto-encoder,DAE),相比于AE,DAE能产生更好的压缩效率及特征表示。DAE的产生和应用免去了人工提取数据特征的巨大工作量,提高了特征提取的效率,得到数据的逆向映射特征,展现了从少数标签数据与大量无标签数据中学习输入数据本质特征的强大能力。但DAE也存在很多局限性:1)DAE都是由不同类型的建模单元堆叠而成,这些建模单元均有理论缺陷,例如DAE内部是黑盒性质,各隐藏层之间缺乏相应神经科学的理论指导。DAE缺乏能力来解释自己的推理过程和推理依据。所以DAE构建的深度结构不完善。2)DAE的无监督逐层贪心训练只是在一定程度上解决了局部最小问题,没有全局优化,随着隐藏层数的增加,梯度稀释越发严重,其训练极其繁琐,需要很多技巧。3)DAE模型结构往往是固定的,其未考虑数据本身的关联性,无法拟合不同类型的数据。
针对DAE的局限性,本文提出一种基于改进SPNs的深度自动编码器。Poon等[3]提出了一种sum-product networks模型,其结构的递归概率语义具有强大的理论支持,由其构成的深度结构很完善。spns能够容易地学习网络结构与参数,训练时间远快于传统DAE。SPNs模型的结构学习能很好的拟合数据的表示,不同于传统DAE需利用一个先验结构。基于SPNs模型的这些优点,本文设计改进的SPNs模型作为深度编码器,提出替换SPNs的sum结点为max结点的最大积网络(max-product networks,MPNs)模型作为深度解码器。基于改进SPNs模型作为新型DAE能克服现有DAE的局限性,并将其应用于短文本情感分析领域,通过实验验证所设计的基于改进SPNs深度自动编码器在短文本分析领域具有更优性能。
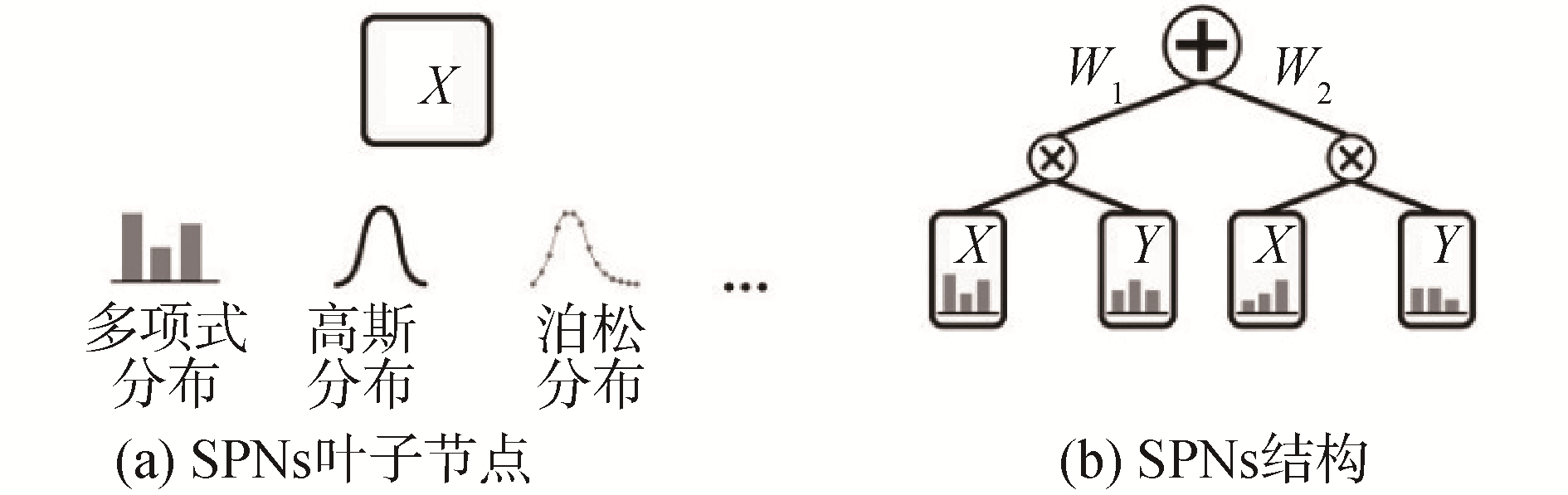
1 sum-product networks模型 1.1 sum-product networks模型的介绍SPNs是一种新型深度概率图模型,是一个带根节点的有向无环混合图,product节点和带非负权值的sum节点不断递归组成其结构,SPNs的叶子节点为单一变量或变量未归一化的概率分布。如图 1所示。一个SPNs网络编码一个函数f(X=x),输入变量赋值X=x,由根节点产生一个输出。该函数在每个节点的递归定义为:
| $ {f_n}(X = x) = \left\{ \begin{array}{l} {\rm Pr}({X_n} = {x_n}),\ \ \ \ \ \ n是叶子节点\\ \sum\limits_i {{w_i}{f_{{\rm child}(n)}}(x)} ,\ \ n是{\rm sum}节点\\ \prod\limits_i {{{\rm f}_{{\rm chil}{{\rm d}_i}(n)}}(x)} ,\ \ \ \ \ \ n是{\rm product}节点 \end{array} \right. $ |
|
Download:
|
| 图 1 SPNs叶子节点与简单的SPNs结构 Fig. 1 SPNs leaf node and the simple SPNs | |
变量的赋值Xn=xn受限于叶子节点所包含的变量类型。如果叶子节点的变量未被实例化,那么Pr(Xn=xn)=Pr(ϕ)=1。如果叶子结点为连续性变量,那么Pr(Xn=xn)应理解为pdf(Xn=xn)。
SPNs模型的结构如果满足一定的条件,其可以编码一组变量的联合概率分布。下面给出其结构需满足条件的定义。
定义1 范围(scope),一个节点n的范围表示为其后裔节点或变量的组合。
定义2 结构完整性,一个SPNs模型结构具有完整性当且仅当其sum节点的所有儿子节点具有相同的范围∀c∈children(sum), scope(c)=scope(c′)。
定义3 结构可分解性,一个SPNs模型的结构具有可分解性当且仅当其product节点的所有儿子节点具有互斥范围:
| $ \begin{array}{c} \forall c,c\prime \in {\rm children}\left( {\rm sum} \right){\rm{ }}\ {\rm and}\ c \ne c\prime \\ \forall c,c\prime \in {\rm children}\left( {\rm sum} \right){\rm{ }}\ {\rm and}\ c \ne c\prime \\ {\rm scope}(c) \wedge {\rm scope}(c\prime ) = \emptyset 。\end{array} $ |
当一个SPNs模型的结构具有结构完整性与结构可分解性,那么称该SPNs模型有效。SPNs模型的有效性能确保通过SPNs为一些证据(evidence)变量计算的值正比于证据变量的概率(例如(Pr(x)∝froot(x)),并且可以通过SPNs回答一些概率推理。例如,边际推理(marginal inference):
SPNs能够克服概率图模型的局限性:推理与学习阶段时间复杂度为指数级。SPNs可以有效计算归一化配分函数(partition function),所以其在模型推理与学习阶段的时间复杂度为多项式级[4]。在推理阶段,不同于概率图模型的近似推理,SPNs执行快速精确推理,在推理速度上后者比前者有着数量级上的优势。SPNs的这些特性已经使其成功应用于图像分类[5]、语言模型[6]、动作识别[7]等多个领域。
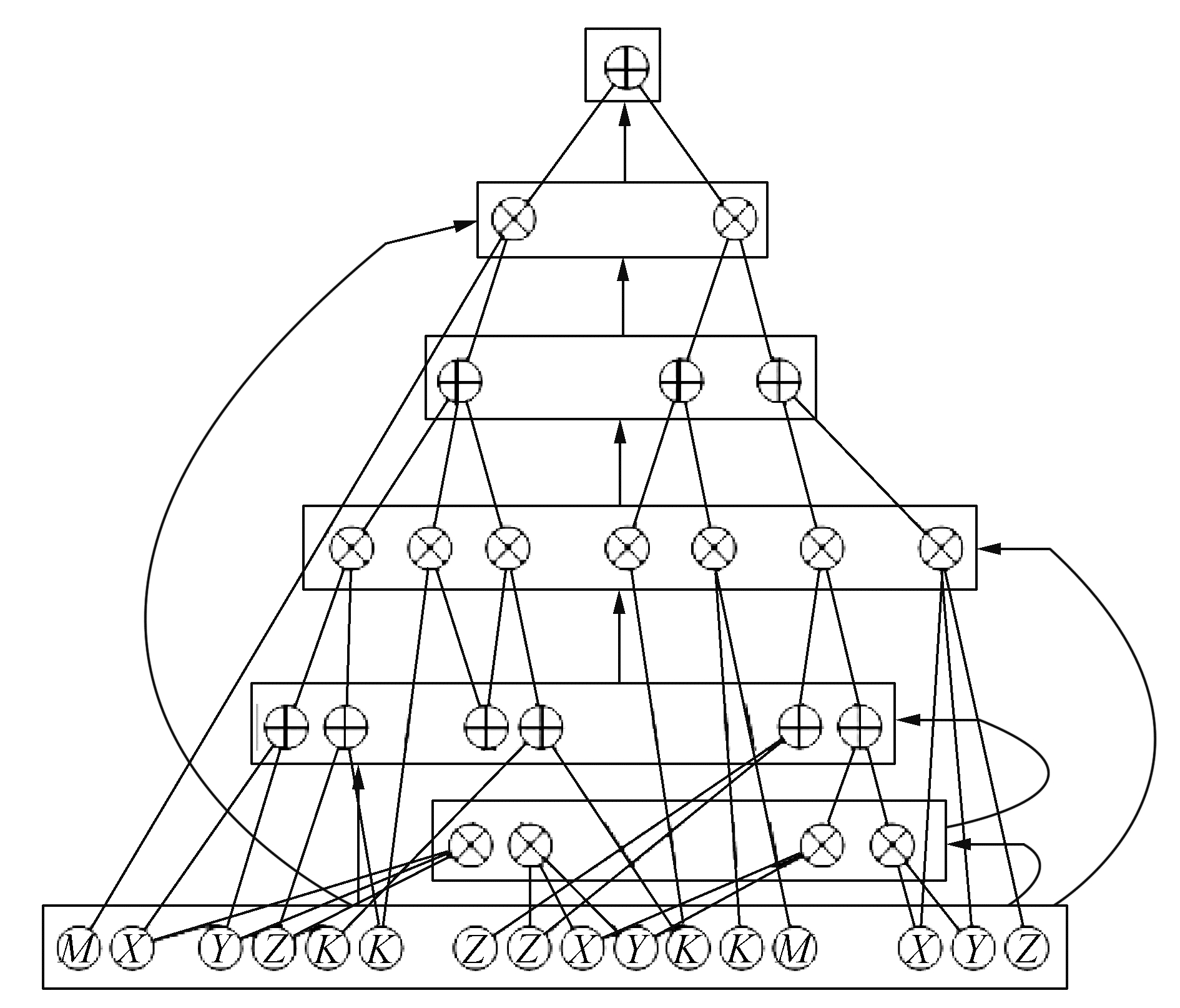
1.2 改进的sum-product networks模型SPNs自提出以来,在大部分研究中被用作一种概率密度估计器。传统SPNs模型作为一种树形结构,每一个节点输入只来自其后裔节点,相同层节点的范围信息相互独立,缺乏层次性。SPNs模型的权值矩阵稀疏。如使用传统SPNs模型作为深度编码器架构,其提取数据特征效率低,SPNs模型的权值矩阵计算速率慢。本文提出一种改进的SPNs模型结构,称为层次SPNs模型(layered sum-product ntworks,LSPNs)。首先重构传统SPNs结构。如图 2所示,排列SPNs节点为层次顺序结构,同层包含相同节点,不同层包含不同节点。例如sum节点组成相同层,product节点相同层,不同层交替组成LSPNs深度结构。然后叶子节点层输入增加到每一个LSPNs的隐藏层。LSPNs的每一层结构都保持传统SPNs的有向无环属性、结构完整性和结构可分解性。定义S(x)∈Rs表示为通用层输出函数,例如:S(x)=〈S1(x), S2(x), …, Ss(x)〉,如果通用层为sum节点层,假设其输入层包含r个节点,本文设计其输出函数为:
| $ S(x) = {\rm log}(\mathit{\boldsymbol{W}}x),\mathit{\boldsymbol{W}} \in R_ + ^{S \times r},{W_{ij}} = \left\{ \begin{array}{l} {\mathit{\boldsymbol{w}}_{ij}},\ \ 边:i \to j\\ 0,\ \ \ \ \ 其他 \end{array} \right. $ | (1) |
|
Download:
|
| 图 2 改进SPNs模型作为LSPNS Fig. 2 Improved SPNs model as LSPNs | |
式中:x∈[0, 1]T为前节点输入的概率值;Wij表示稀疏连接形式的参数矩阵。product节点层输出函数为:
| $ S(x) = {\rm exp}(Px),P \in {\left\{ {0,1} \right\}^{S \times r}},{P_{ij}} = \left\{ \begin{array}{l} 1,\ \ 边:i \to j\\ 0,\ \ 其他 \end{array} \right. $ | (2) |
式中:x∈RY为输入概率值的对数域;P∈{0, 1}S×r为稀疏链接矩阵定义。本文设计的指数函数和对数函数都是非线性的,输入和输出信号从对数域切换到指数域,从一个层次类型转换为另一个层次类型。增加隐藏层的输入可以降低传统SPNs模型的权值矩阵的稀疏性。LSPNs模型相对于传统SPNs模型具有以下优势:1)具有层次结构的LSPNs作为一种概率局部特征提取器,相比于传统SPNs能高效提取数据的分层抽象特征,提取的特征信息更为丰富。2)LSPNs的权值矩阵相对于SPNs权值矩阵稀疏性低,可以利用GPU计算库进行高效的矩阵运算。
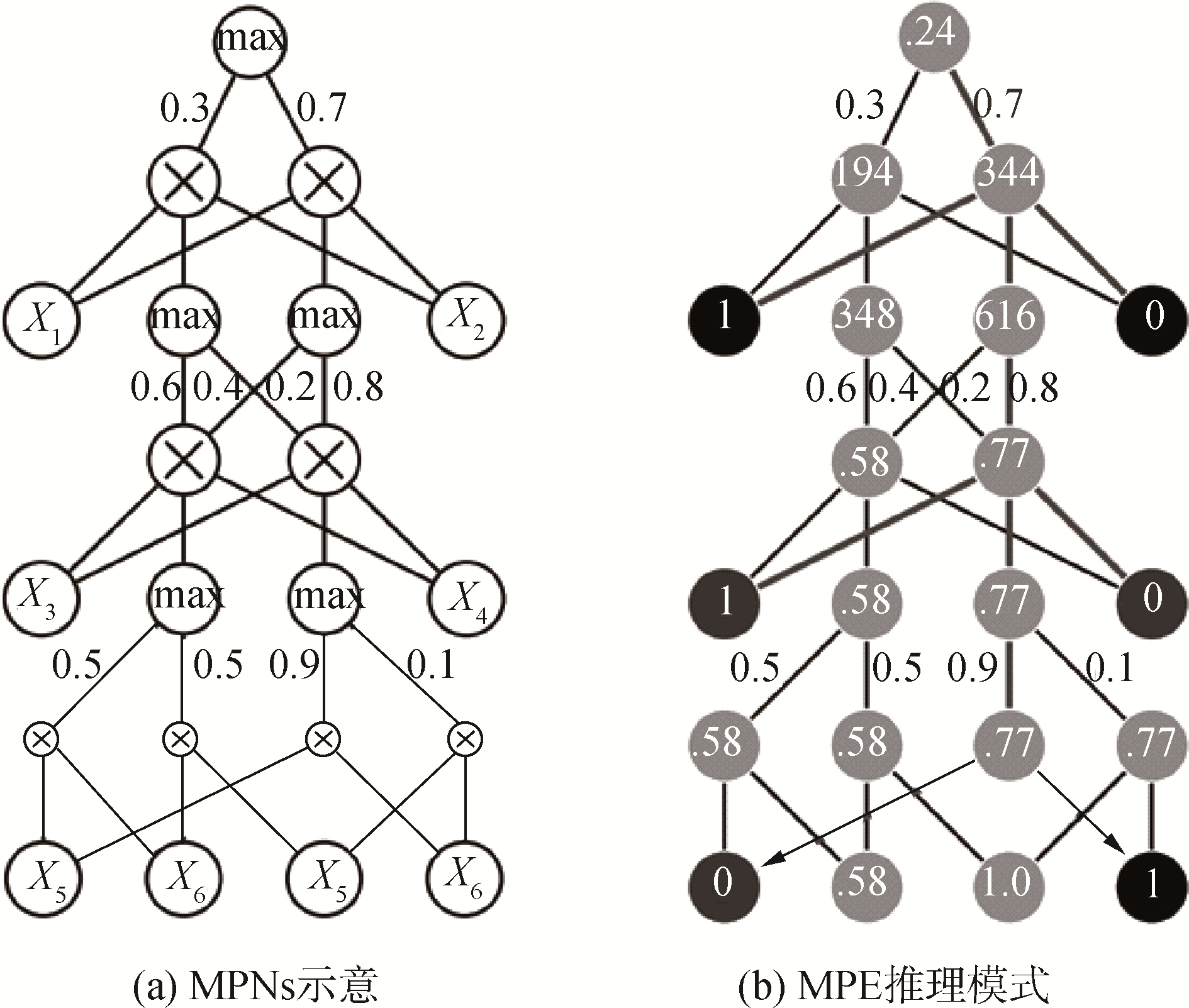
如使用传统SPNS模型作为深度解码器架构,其在解码过程中,进行最大可能解释(most probable explanations,MPE)推理,其推理复杂度为np-hard。定义2组随机变量U, V⊂X, U∪V=X, U∩V=Ø,mpe推理是求:
| $ {X_u} = \mathop {{\rm arg}\ {\rm max}}\limits_{u - U} p(u,v) $ | (3) |
MPE推理的解码过程可以有效对编码特征进行解码。因此,在解码过程中,本文替换SPNs的所有sum节点为max节点,提出最大积网络(max-product networks,MPNs)模型,其中max节点功能具有sum节点的结构完整性,但其在进行MPE推理的过程中,MPNs不同于SPNs的全局计算,其首先计算maxc∈ch(n)ωncMc(x)即max节点与权值边值乘积的最大值,推理方向沿着自根节点向下选取max节点与权值边值乘积最大的路径传播。如图 3所示,图 3(a)为替换所有sum节点为max节点的MPNs网络,图 3(b)为MPNs的MPE推理模式,给定叶子结点输入值与max节点下的权值,首先自叶子节点向上计算每个节点的值,然后自根节点向下选取max节点与其权值边值乘积最大的边向下传播,得到MPE推理的结果。MPNs可以有效作为深度解码器架构,MPNs编码器的建模单元为max节点组成的max节点层与product节点组成的product节点层,max节点层与product节点层交替组成MPNs深度解码器结构,其MPE推理方法可作为深度解码器的解码方法。
|
Download:
|
| 图 3 MPNs模型与MPE推理方法 Fig. 3 MPNs and MPE inference method | |
定义随机变量
本文设计LSPNs深度编码器的嵌入方法:考虑编码一个样本xi∈X到一个连续的d维嵌入空间ei∈EX⊆Rd,利用LSPNs表示一个函数fs:X→EX。给定一组LSPNs的节点
| $ e_j^i = {S_{{n_j}}}({x_{sc({n_j})}}) = {p_{{w_{nj}}}}({\mathit{\boldsymbol{x}}_{sc({n_j})}}) $ | (4) |
每一个嵌入特征都可以表示为一个节点范围的边际分布。因此,这样构造的嵌入是由适当的概率密度的集合引起的几何空间中的一个点。LSPNs的节点也可以看作是通过节点范围给出的子空间运行的基于部分的过滤器。sum节点可以解释为通过共享相同范围的过滤器的加权平均值构建的过滤器,并且product节点可以被看作是非重叠作用域上的过滤器的组合。从LSPNs学习算法的内部机制角度来看,每个过滤器捕获数据的子群和子空间的不同方面。传统SPNs作为深度编码器因其结构缺乏层次性,各节点在特征提取的过程中缺乏关联性。本文设计的LSPNs结构具有层次性,同层节点提取特征信息共享,能较传统SPNs具有更高的特征提取效率与能得到更优的分层抽象特征。
2.2 基于MPNs深度解码器的解码表示在解码阶段,需要找到一个反函数g:EX→X,例如:xi≈xi′=g(f(xi))。本文设计一个MPNs深度解码器M,设计gM模拟一个算法来计算M上的MPE概率推理任务。如果一个样本xi被完全观察,计算M(xi),该过程为在MPNs中为选择自上而下的最大路径,该路径可由一组范围划分X的叶子结点通过一个类维特比(viterbi-like)算法追踪。因此,如果整个嵌入
| $ x_{sc(n)}^{i\prime } = \mathop {{\rm arg}\ {\rm min}}\limits_{u{\rm{ }} - sc(n)} D(\left. {{\phi _n}(u)} \right\|e_{{M_n}}^i) $ | (5) |
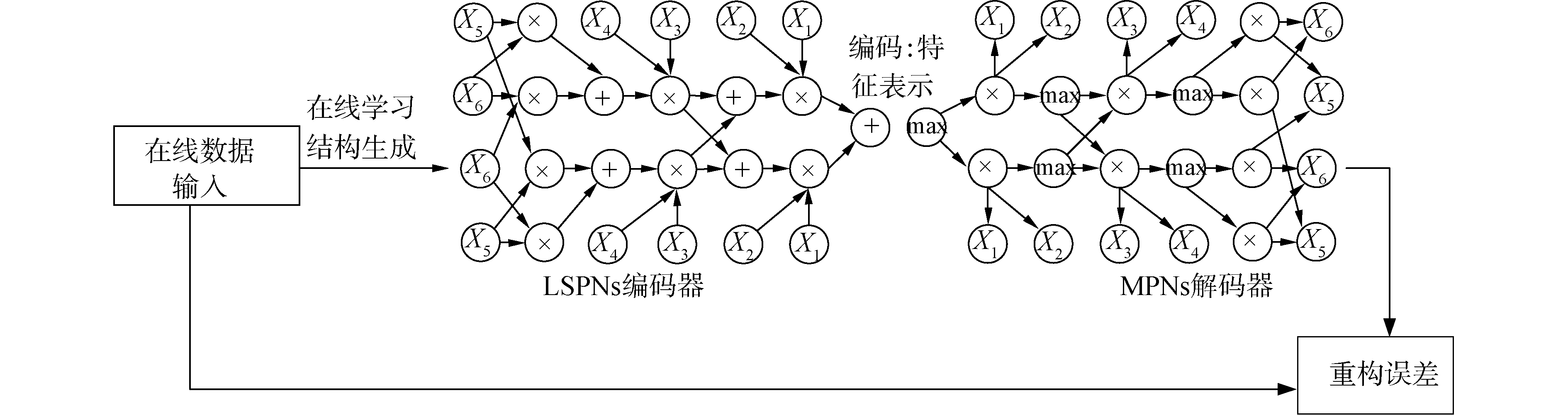
基于本文设计的MPNs深度解码器的解码方法是对编码特征找到其最有可能解码,是一种部分解码模式,该方法可以快速得到对原编码特征解码,不同于传统DAE解码过程对编码特征进行全部解码。MPNs深度解码器解码速度远快于传统深度解码器。如图 4所示为基于LSPNs深度自动编码器架构,其为LSPNs编码器与MPNs解码器2部分组成。
|
Download:
|
| 图 4 基于LSPNs深度自动编码器架构 Fig. 4 Framework of LSPNs-based deep autoencoder | |
LSPNs深度自动编码器可以进行精确的推理,比如最大后验概率map推理以及最有可能解释MPE推理等。
2.3 基于LSPNs深度自动编码器的结构与参数学习LSPNs深度自动编码器的学习方法包括结构学习与参数学习2部分。SPNs的结构学习算法通常是通过基于聚类技术分割/分组数据和变量,贪心地构造一个SPNs结构[8]。SPNs的参数学习技术包括通过随机梯度下降[9]、期望最大化算法[10]、贝叶斯矩匹配[11]等来极大化数据的似然函数值(生成训练)或者给一个输入数据得到一些输出数据的条件似然值(判别训练)。
目前,SPNs模型的结构学习与参数学习算法大部分是基于批处理学习的,批处理技术假设完整的数据集是可用的并且可以多次扫描。目前,大文本集和流文本数据越来越多。传统SPNs模型的学习方法无法高效地处理这类文本集。为解决传统SPNs模型学习算法在处理大文本集和流文本数据时参数学习速率慢,结构学习时模型似然函数值低的局限性,本文设计LSPNs的在线学习算法。
LSPNs深度自动编码器的在线参数学习算法:通过一些小批量数据点输入,LSPNs模型的在线参数学习算法通过从根节点到叶子节点更新LSPNs的参数。LSPNs模型通过跟踪运行充分统计量来更新sum节点下的参数。假设LSPNs模型在每一个节点都有一个计数(初始值为1),当每一个数据点被接收,这些数据点的似然函数就可以通过计算每一个节点得到,然后LSPNs模型的参数通过一种递归自上而下的方式从根节点更新。当一个sum节点被穿过,其计数加1并且其具有最高似然值的孩子节点加1。一个sum节点s和它其中一个后裔节点c的连接权值ws, c可以被估计为:
| $ {w_{s,c}} = \frac{{{n_c}}}{{{n_s}}} $ | (6) |
式中:ns为sum节点的计数;nc为孩子节点的计数。因为product节点无权值边,增加其似然值方法就是增加其儿子节点似然值。递归增加product节点每一个孩子计数,递归更新每个孩子节点子树权值。
SPNs的在线结构学习算法由Lee[12]首次提出,该方法通过在线聚类技术以一种递增形式重构网络结构,自上而下为sum节点增加孩子节点。其方法局限于一旦product节点被创建就不能被修改。本文设计LSPNs自动编码器的在线结构学习方法:通过小批量数据输入,LSPNs的结构在线更新。如图 5所示,图 5(a)为起始product节点,连接3个相互独立的儿子节点,作用域为x1, x2, …, x5。首先通过检测输入变量的相关性修改product节点,自底向上的递增构造LSPNs深度自动编码器结构。其算法的核心是分裂法,在LSPNs线结构学习的过程中,每次新加入的数据,如输入变量之间皮尔逊相关系数的绝对值超过某一阈值,会导致product结点做出变更。该算法将具有x1、x3 2个子节点的作用域合并,并将它们转换为一个多元叶节点,以其统计的均值和协方差作为叶节点参数。图 5(b)所示会创造出多变量叶节点或者如图 5(c)所示的混合模型。其组成部分是一个新的product节点,它再次被初始化为在其作用域上的一个完全因式分解的分布,然后再将小批数据点传递给新混合模型以更新其参数。更新结构的方式可通过设置子节点个数的阈值来选择。
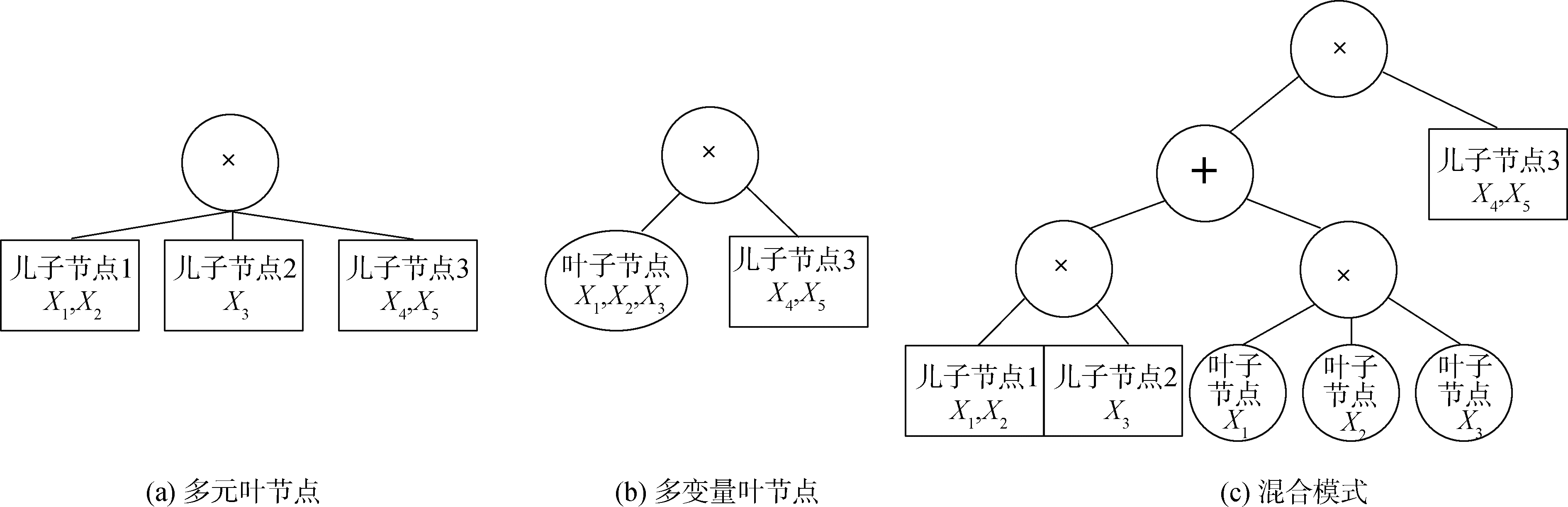
|
Download:
|
| 图 5 LSPNs模型在线结构学习示意 Fig. 5 LSPNs model online structure learning diagram | |
这种在线结构学习算法只对数据一次扫描并构造其LSPNs结构,LSPNs自动编码器的在线结构学习以一个所有变量完全因式分解的联合概率分布起点,若输入变量皮尔逊相关系数的绝对值高于某个阈值,则将他们合并为相关变量,若作用域内变量的个数小于某个值时就将他们合并为多元叶节点,否则将其重组为和积混合结构。通过在线学习的方式,随着数据的不断传入,网络结构逐渐加深,从而以一种在线学习的方式完善LSPNs自动编码器的深度结构。
3 短文本情感分析应用本文利用基于LSPNs深度自动编码器进行短文本情感分析。首先,从社交网络中爬取大量无标签的短文本数据;其次采用语义规则[13]方法对数据进行预处理;接着采用doc2vec[14]模型对预处理后获得的短文本数据进行训练得到句向量,句向量作为基于LSPNs深度自动编码器的输入。通过2.3节的在线结构学习方法生成一个LSPNs深度编码器结构。利用LSPNs深度编码器对输入的句向量进行编码,提取分层抽象特征;然后构建MPNs深度解码器,对由LSPNs深度编码器得到的分层抽象特征进行解码,将解码后的特征与输入LSPNs深度编码器的句向量特征对比,计算重构误差。调整LSPNs深度自动编码器参数使得重构误差最小;最后,得到最优的LSPNs深度编码器,并由它获得最优分层抽象特征。
为了实现情感分类,将最优分层抽象特征输入到一个分类SPNs模型,通过有少量标签样本对分类SPNs模型进行有监督微调训练。分类SPNs模型也采用2.3节的在线结构学习方法,其参数学习使用SPNs的判别式hard梯度下降方法。定义分类SPNs模型S[y, h|x],输入变量y为查询变量,h为隐变量,x为证据变量。学习目标是极大化条件概率分布P(y|x),使用反向传播的方式极端似然梯度:
| $ \begin{array}{c} \nabla {\rm log}P(y|x) = \nabla {\rm log}\frac{{P(y,x)}}{{P(x)}} = \\ \nabla {\rm log}\sum\limits_h {P(y,h,x)} - \nabla {\rm log}\sum\limits_{y\prime ,h} {P(y\prime ,h,x)} \end{array} $ | (7) |
分类和积网络S首先自底向上计算, Sn表示节点值,节点中值偏导数表示为
| $ \begin{array}{c} \frac{\partial }{{\partial \omega }}{\rm log}\widetilde p(y|x) = \frac{\partial }{{\partial \omega }}{\rm log}\mathop {\rm max}\limits_h \Phi (Y = y,H = h|x) - \\ \frac{\partial }{{\partial \omega }}{\rm log}\mathop {\rm max}\limits_{y\prime ,h} \Phi (Y = y\prime ,H = h|x) \end{array} $ | (8) |
MAP推理过程是SPNs自顶向下一个分支路径,定义W为经过这条路径的多重级权值,MPNs中product权值
| $ \frac{{\partial {\rm log}M}}{{\partial {w_i}}} = \frac{1}{M}\frac{{\partial M}}{{\partial {w_i}}} = \frac{{{c_i}w_i^{{c_i} - 1}\prod\limits_{{w_j} \in W\backslash \{ {w_i}\} } {w_j^{{c_j}}} }}{{\prod\limits_{{w_i} \in W} {w_i^{{c_i}}} }} = \frac{{{c_i}}}{{{w_i}}} $ | (9) |
MAP推理过程的条件log似然梯度为Δci/wi,hard梯度更新为Δwi=ηΔci/wi。hard推理模式其使用map推理过程为一种选择性的梯度更新方法,如图 6所示,可以有效防止梯度稀释现象。
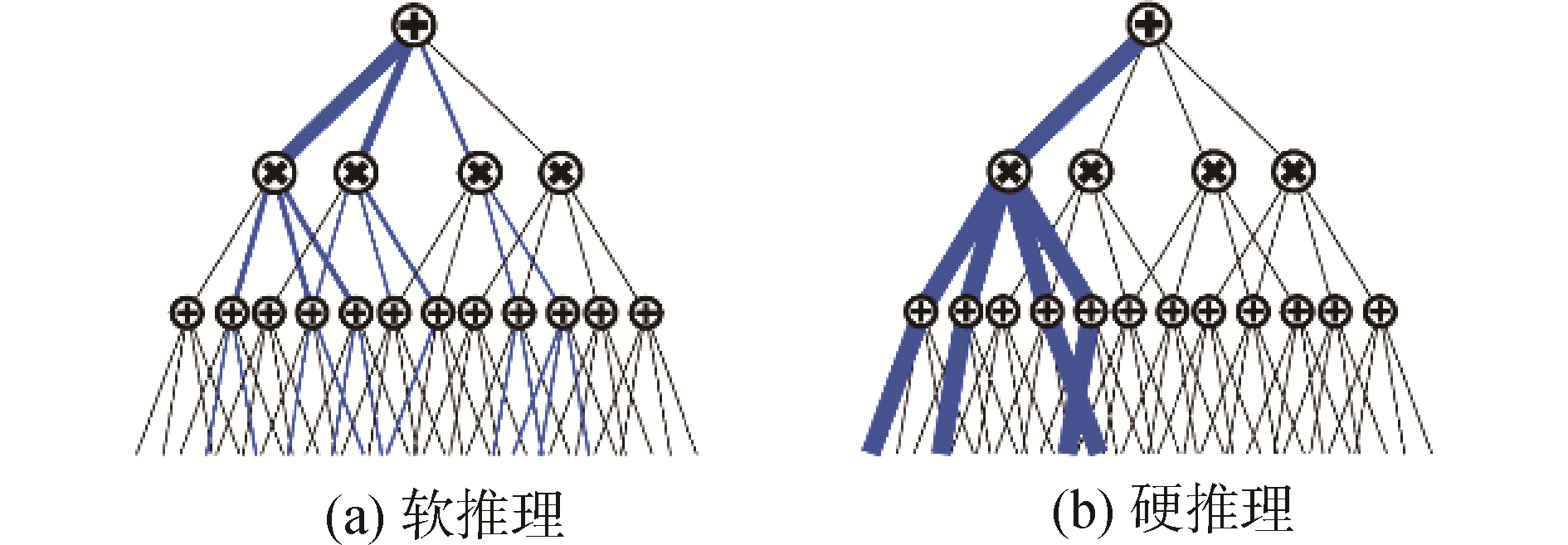
|
Download:
|
| 图 6 SPNs的硬推理模式克服梯度稀释问题 Fig. 6 SPNs hard inference overcomes gradient diffusion | |
分类SPNs模型训练完毕后,利用SPNs的MAP推理方式,对测试集的数据进行预测。假设有一组测试数据为[x1, x2, …, x100, Lable],分类SPNs模型的101个变量记为X1, X2, …, X100, Y,那么用分类SPNs模型预测标签的过程,实质上就是求:
| $ \mathop {{\rm arg}\ {\rm max}}\limits_Y S({X_1} = {x_1},{X_2} = {x_2}, \cdots ,{X_{100}} = {x_{100}},Y = ?) $ | (10) |
只要将Y=0与Y=1的正负情感标签分别传入分类SPNs模型的叶节点中,经过推理比较2个值的大小,取最大者,记为该测试数据的分类标签。这样,就可以得到每一条测试数据的预测值Y,经过统计预测值和真实标签的差异,可以得到分类的准确率。
4 实验结果与分析 4.1 实验数据实验数据包括2部分:1)微博情感分析数据,由无标签数据与标签数据组成(如图 7所示)。其中无标签数据是通过twitter API与python beautifulsoup库在网络上爬取的1 600 000条微博数据,这些无标签数据用于训练句向量。标签数据集取自斯坦福twitter情感语料库STS[15]。随机选取其中负面微博2 501条,正面微博2 499条作为有监督微调数据集。最后随机取500条微博作为测试集。2)电影评论IMDb数据集[16]与从亚马逊网站[16]收集的5组领域产品的用户评论。实验数据统计如表 1所示。
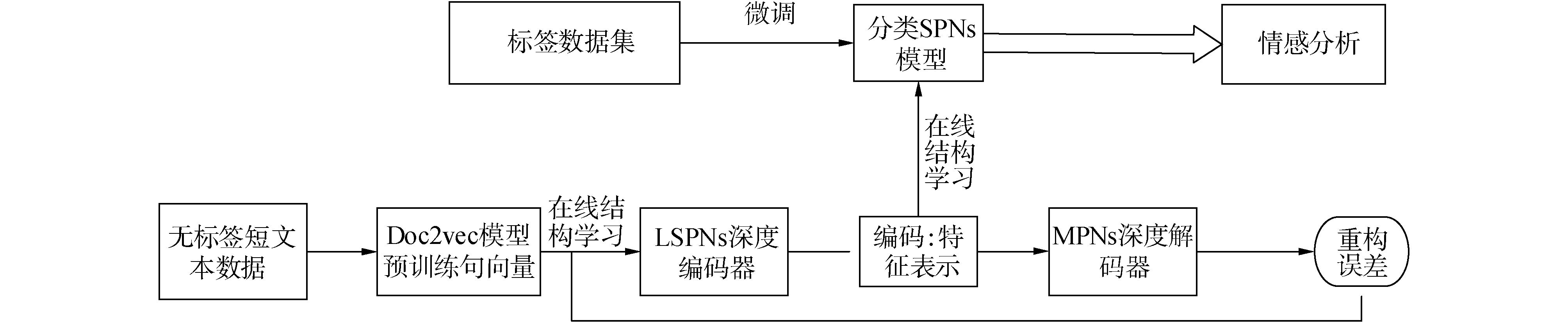
|
Download:
|
| 图 7 基于LSPNs深度自动编码器情感分析流程 Fig. 7 Flow chart of LSPNs-based deep autoencoder sentiment analysis | |
| 表 1 实验数据统计 Table 1 The experimental data statistics |
在进行模型训练之前,需要在大规模语料上训练句向量。本文利用基于python gensim库的doc2vec模型无监督训练句向量,迭代次数为10次。
4.3 对比实验本文对比实验分为2部分:
1) 基于斯坦福twitter情感语料库(STS)的实验。实验的对比模型为:
① 基于N-gram模型的词袋向量作为输入,使用N-gram模型的一元词串+二元词串特征,分别使用支持向量机[15],朴素贝叶斯[15],标签传播(label propagation, lprop)[16]模型作为分类器进行情感分析。
② 基于Wor2vec训练的词向量输入,使用句子特性卷积神经网络CharSCNN[17]进行情感分析。
③ 基于传统spns结构的自动编码器情感分析,模型输入为与对比模型1与2相同的2种特征向量,模型表示为spnsdae1与spnsdae2。
④ 基于LSPNs深度自动编码器的情感分析,采用与对比模型1与2相同的特征向量作为模型输入,模型表示为lspnsdae1与lspnsdae2。实验的评估指标是准确率precision值、召回率recall、F1值。其中Pos_P表示积极词的准确率precision值,Neg_P表示消极词的准确率precision值,以此类推。
表 2中的NB、SVM模型数据集下的分类结果数据来源于文献[15],LPROP模型数据集下的分类结果数据来源于文献[16],CharSCNN模型在第一部分数据集下的分类结果数据来源于文献[17]。spnsdae1与spnsdae2数据集下的分类结果为本文使用传统spns结构设计的深度自动编码器进行试验实现。
| 表 2 几种模型在STS数据集下的情感分类评估值 Table 2 Several models in the STS data set under the sentiment classification evaluation value |
2) 基于IMDb数据集的实验。实验的对比模型为:基于标准化特征[19]的词袋向量作为模型输入,分别使用以下模型进行情感分析。
① 降噪自编码器(denoising autoencoder,DAE)[18],其使用ReLu max(0, x)函数作为激活函数,使用sigmoid函数作为解码函数。
② 微调降噪自动编码器(denoising autoencoder with finetuning,DAE+)[18],该方法使用部分标签数据训练dae并把解码层替换为softmax层。
③ 半监督布雷格曼散度自动编码器(semisupervised bregman divergence autoencoder,SB-DAE)[19]。
④ 微调半监督布雷格曼散度自动编码器(semisupervised bregman divergence autoencoder with finetuning,SB-DAE+)[19],使用带标签数据集微调sb-dae。以上方法都需要预定义模型输入特征维度,对于sb-dae设置输入特征维度为200维。对于dae,采取输入特征维度为2000维。以上模型均使用SVM2作为分类器,使用mini-batch步长为0.9[16]的随机梯度下降方法进行训练。
⑤ 基于半监督的变分自动编码器(semi-supervised variational autoencoder,SVAE)[20], 其自动编码器架构为LSTM, 情感预测模型使用双向LSTM模型。其模型输入为标准化特征[19]的词袋向量。设置其自动编码架构维度为100维,设置Dropout率为0.5。
⑥ 基于半监督的连续变分自动编码器(semi-supervised sequential variational autoencoder,SSVAE)[21]模型使用基于端到端的adam[21],设定学习率为4e-3进行训练。
⑦ 基于传统SPNs深度自动编码器的情感分析,采用2种特征向量输入LSPNs深度自动编码器中,分别是基于标准化特征[16]的特征向量作为模型输入,设置特征维度为500维,模型表示为实验模型表示为spnsdae(A); 基于Doc2vec模型训练的句向量作为模型输入,设置特征维度为200维,模型表示为spnsdae(B)。
⑧ 基于LSPNs深度自动编码器的情感分析,采用两种特征向量输入LSPNs深度自动编码器中,分别是:基于标准化特征[16]的特征向量作为模型输入,设置特征维度为500维,模型表示为lspnsdae(A);基于Doc2vec模型训练的句向量作为模型输入,设置特征维度为200维,模型表示为lspnsdae(B)。以上2种方法均使用标签数据集微调。实验采用的评测指标是模型情感分类错误率。
表 3中的DAE、DAE+实验数据集下的分类结果来源于文献[18]。SB-DAE、SB-DAE+实验数据集下的分类结果来源于文献[19]。SVAE与SSVAE实验结果为进行实验实现。spnsdae的分类结果为本文使用传统SPNs结构设计的深度自动编码器进行试验实现。
| 表 3 几种模型在IMDb数据集下的情感分类评估值 Table 3 Several models in the IMDb data set under the sentiment classification evaluation value |
由实验1)结果对比可知:基于LSPNs深度自动编码器应用于短文本情感分析的效果普遍要比传统方法:nb,svm,LPROP模型要好。这体现在三者之间的Pos_F1和Neg_F1的对比;而从precision、recal的角度来比较,无论是对积极情感还是消极情感,基于LSPNs深度自动编码器比CharSCNN精度更高。由实验2)结果对比可知:spnsdae的情感分类错误率低于SB-DAE,和DAE+近似,但是lspnsdae(B)模型在实验2)的6组实验数据集下达到最佳效果。
在实验2)中的几种自动编码器模型运行平均时间对比如表 4所示,本文设置每个自动编码器模型运行10次,取10次时间均值记录。实验结果表明lspnsdae(A)与lspnsdae(B)在IMDB数据集下的运行速度远快于传统的自动编码器模型。
| 表 4 几种自动编码器模型在IMDb数据集下的平均运行时间 Table 4 The average running time of several autoencoder models in the IMDb dataset |
1) 本文提出的LSPNs的深度自动编码器具有强大的结构学习能力,快速的推理能力,具备更好的模型可扩展性。
2) 将本文提出的基于LSPNs深度自动编码器应用于短文本情感分析领域。实验结果表明:基于LSPNs的深度自动编码器比现有深度编码器在短文本情感分析领域能取得更好的情感分类准确率且模型具有更快的运行速度。
| [1] |
BENGIO Y, YAO Li, ALAIN G, et al. Generalized denoising auto-encoders as generative models[C]//Proceedings of the 26th International Conference on Neural Information Processing Systems. Red Hook, NY, USA: ACM, 2013: 899-907. http://www.oalib.com/paper/4038830
(  0) 0)
|
| [2] |
HINTON G E, OSINDERO S, TEH Y W. A fast learning algorithm for deep belief nets[J]. Neural computation, 2006, 18(7): 1527-1554. DOI:10.1162/neco.2006.18.7.1527 (  0) 0)
|
| [3] |
POON H, DOMINGOS P. Sum-product networks: a new deep architecture[C]//Proceedings of 2011 IEEE International Conference on Computer Vision Workshops. Barcelona, Spain: IEEE, 2011: 337-346. 10.1109/ICCVW.2011.6130310
(  0) 0)
|
| [4] |
ZHAO Han, POUPART P, GORDON G. A unified approach for learning the parameters of sum-product networks[C]//Proceedings of the 30th International Conference on Neural Information Processing Systems. Red Hook, NY: ACM, 2016: 433-441. https://arxiv.org/abs/1601.00318
(  0) 0)
|
| [5] |
GENS R, DOMINGOS P. Discriminative learning of sum-product networks[C]//Proceedings of the 25th International Conference on Neural Information Processing Systems. Red Hook, NY: ACM, 2012: 3239-3247. https://dl.acm.org/doi/10.5555/2999325.2999496
(  0) 0)
|
| [6] |
CHENG Weichen, KOK S, PHAM H V, et al. Language modeling with sum-product networks[C]//Proceedings of the 15th Annual Conference of the International Speech Communication Association. Singapore: ISSN, 2014: 2098-2102. https://www.semanticscholar.org/paper/Language-modeling-with-sum-product-networks-Cheng-Kok/2a76c2121eee30af82a24058b4e149f05bcda911?p2df
(  0) 0)
|
| [7] |
AMER M R, TODOROVIC S. Sum product networks for activity recognition[J]. IEEE transactions on pattern analysis and machine intelligence, 2016, 38(4): 800-813. DOI:10.1109/TPAMI.2015.2465955 (  0) 0)
|
| [8] |
GENS R, DOMINGOS P. Learning the structure of sum-product networks[C]//Proceedings of the 30th International Conference on Machine Learning. Atlanta, USA: ACM, 2013: 873-880. https://dl.acm.org/doi/10.5555/3042817.3043034
(  0) 0)
|
| [9] |
MOLINA A, NATARAJAN S, KERSTING K. Poisson sum-product networks: a deep architecture for tractable multivariate Poisson distributions[C]//Proceedings of the 31st AAAI Conference on Artificial Intelligence. AAAI, 2017: 2357-2363. https://www.ixueshu.com/document/c00a77e48cd745c5318947a18e7f9386.html
(  0) 0)
|
| [10] |
TRAPP M, MADL T, PEHARZ R, et al. Safe semi-supervised learning of sum-product networks[C]//Proceedings of the 33rd Conference on Uncertainty in Artificial Intelligence. Sydney, Australia: IEEE, 2017: 143-149. https://arxiv.org/abs/1710.03444
(  0) 0)
|
| [11] |
ZHAO Han, POUPART P. Online and distributed Bayesian moment matching for parameter learning in sum-product networks[C]//Proceedings of the 19th International Conference on Artificial Intelligence and Statistics. Cadiz, Spain: PMLR, 2016: 1469-1477. https://www.ixueshu.com/document/6311082ae58a4405318947a18e7f9386.html
(  0) 0)
|
| [12] |
LEE S W, HEO M O, ZHANG B T. Online incremental structure learning of sum-product networks[C]//Proceedings of the 20th International Conference on Neural Information Processing. Daegu, Korea: Springer, 2013: 220-227. 10.1007/978-3-642-42042-9_28
(  0) 0)
|
| [13] |
APPEL O, CHICLANA F, CARTER J, et al. A hybrid approach to the sentiment analysis problem at the sentence level[J]. Knowledge-based systems, 2016, 108: 110-124. DOI:10.1016/j.knosys.2016.05.040 (  0) 0)
|
| [14] |
LE Q, MIKOLOV T. Distributed representations of sentences and documents[C]//Proceedings of the 31st International Conference on Machine Learning (ICML-14). New York, USA: ACM, 2014: 1188-1196. https://arxiv.org/abs/1405.4053
(  0) 0)
|
| [15] |
GO A, BHAYANI R, HUANG L. Twitter sentiment classification using distant supervision[R]. CS224N Project Report, Stanford, 2009. https://www.ixueshu.com/document/7a59027660a18d11318947a18e7f9386.html
(  0) 0)
|
| [16] |
SPERIOSU M, SUDAN N, UPADHYAY S, et al. Twitter polarity classification with label propagation over lexical links and the follower graph[C]//Proceedings of the 1st Workshop on Unsupervised Learning in NLP. Stroudsburg: ACM, 2011: 53-63. 10.1017/S1049023X0000580X
(  0) 0)
|
| [17] |
DOS SANTOS C, GATTI M. Deep convolutional neural networks for sentiment analysis of short texts[C]//Proceedings of the 25th International Conference on Computational Linguistics (COLING2014). Dublin, Ireland: Dublin City University and Association for Computational Linguistics, 2014: 69-78.
(  0) 0)
|
| [18] |
VINCENT P, LAROCHELLE H, BENGIO Y, et al. Extracting and composing robust features with denoising autoencoders[C]//Proceedings of the 25th International Conference on Machine Learning. Helsinki, Finland: ACM, 2008: 1096-1103. 10.1145/1390156.1390294
(  0) 0)
|
| [19] |
ZHAI Shuangfei, ZHANG Z M. Semisupervised autoencoder for sentiment analysis[C]//Proceedings of the 30th AAAI Conference on Artificial Intelligence. Phoenix, USA: AAAI Press, 2016: 1394-1400. https://arxiv.org/abs/1512.04466
(  0) 0)
|
| [20] |
WU Chuhan, WU Fangzhao, Wu Sixing, et al. Semi-supervised dimensional sentiment analysis with variational autoencoder[J]. Knowledge-based systems, 2019, 165: 30-39. DOI:10.1016/j.knosys.2018.11.018 (  0) 0)
|
| [21] |
XU Weidi, SUN Haoze, DENG Chao, et al. Variational autoencoder for semi-supervised text classification[C]//Proceedings of the 31th AAAI Conference on Artificial Intelligence, San Francisco, California USA: AAAI Press, 2017: 3358-3364. https://dl.acm.org/doi/10.5555/3298023.3298056
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


