在工程设计中,非线性滤波问题普遍存在于信号处理、目标跟踪等领域,对于非线性系统而言,要得到精确的最优解较为困难,需要精确已知系统状态的后验状态分布。传统的线性滤波方法[1]不能满足非线性系统的滤波要求,因此需要对滤波方法进行改进以满足非线性系统滤波要求,提高滤波精度。一般常用的非线性滤波方法包括扩展卡尔曼滤波,无迹卡尔曼滤波和粒子滤波等。
扩展卡尔曼滤波结构简单,易于执行,但是该算法采用一阶泰勒级数对非线性方程进行线性局部近似,因此对于阶段误差较为敏感,对于高阶系统进行线性近似会带来较大的误差[2-4]。无迹卡尔曼滤波采用UT变换,以确定性采样策略逼近非线性系统的状态后验分布,虽然能够减少非线性产生的误差影响[5-6],但其容易受到初始观测误差和参数变化的影响,当系统维数较高时,可能导致滤波发散等现象。粒子滤波以不确定采样方法逼近状态的条件概率密度函数,能够处理任意非线性和非高斯的估计问题,但粒子滤波实现过程中计算量大,不适用于反应速度快的反馈控制系统; 并且随着迭代次数的增加,容易产生粒子退化和局部最优的问题。近年来,容积非线性卡尔曼滤波的发展受到广泛的关注[7],为非线性系统的状态估计提供新的实现方式。容积卡尔曼滤波使用容积数值积分原则计算非线性变换后的随机变量的均值和协方差,采用一组等权值的容积点对最优状态的后验分布进行逼近,相比于其他非线性卡尔曼滤波具有更高的非线性逼近性能和估计精度,并且其运行速度快。
标准容积卡尔曼滤波(cubature Kalman filter, CKF)算法设计需要已知精确的系统模型,然而实际情况下,噪声为非零均值、非高斯噪声,系统往往受到外界环境干扰以及计算机计算字长限制等,不可避免地存在非高斯非零均值的噪声以及系统参数摄动的情况,影响滤波的稳定性和精度。因此,近年来一些学者提出了平方根容积卡尔曼滤波方法[8-9]来避免系统发散,然而其计算复杂,滤波速度受到限制。进而,为了提高滤波系统的鲁棒性,H∞滤波方法被提出[10],H∞滤波基于鲁棒理论设计,对于系统的摄动和未知特性具有一定的鲁棒性,近年来一些学者结合扩展卡尔滤波、无迹卡尔曼滤波应用到电机以及电力系统状态估计等,取得了较好的效果[11-15]。
此外,在实际工程问题中系统的先验噪声统计特性往往不能准确获得,如果直接应用到CKF算法中,将引起较大的误差。为了对未知噪声特性进行估计,噪声统计估值器和基于极大后验估计的方法得到应用[16-18],然而其递推迭代过程计算量大,并且估值器对噪声方差的初始值敏感。模糊自适应通过设计模糊规则,根据估计误差自适应噪声统计特性,其对噪声方差的初值不敏感,并且在存在较大估计误差的情况下,也能实现较好的估计效果[19-20]。
因此,本文提出一种模糊自适应H∞容积卡尔曼滤波方法(H∞ Kalman filtering, HCKF),对系统噪声和观测噪声进行实时估计,使得滤波算法对噪声特性具有一定的自适应能力,并且对于系统的模型摄动和不确定噪声具有鲁棒性,提高滤波的收敛速度和稳定性。
1 问题描述考虑如下非线性动态系统状态方程:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}_k} = f({\mathit{\boldsymbol{x}}_{k - 1}},{\mathit{\boldsymbol{u}}_{k - 1}}) + {\mathit{\boldsymbol{w}}_{k - 1}}}\\ {{\mathit{\boldsymbol{z}}_k} = h({\mathit{\boldsymbol{x}}_k},{\mathit{\boldsymbol{u}}_k}) + {\mathit{\boldsymbol{v}}_k}} \end{array}} \right. $ | (1) |
式中:xk∈Rn为系统的状态估计向量;zk∈Rl为系统的观测输出向量;uk∈Rp为控制输入向量,假设过程噪声wk-1和量测噪声vk相互独立,且均值和方差满足:
| $ \begin{array}{*{20}{l}} {{\rm{E}}[{\mathit{\boldsymbol{w}}_k}] = {q_k},\quad {\rm{cov}} [{\mathit{\boldsymbol{w}}_k},{\mathit{\boldsymbol{w}}_j}] = {Q_k}{\delta _{kj}}}\\ {{\rm{E}}[{v_k}] = {r_k}, {\rm{cov}} [{\mathit{\boldsymbol{v}}_k},{\mathit{\boldsymbol{v}}_j}] = {\mathit{\boldsymbol{R}}_k}{\delta _{kj}},}\\ { {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{cov}} [{\mathit{\boldsymbol{w}}_k},\mathit{\boldsymbol{v}}_j^{\rm{T}}] = 0} \end{array} $ | (2) |
δkj为Kronecher-δ函数,初始状态x0服从高斯分布N(
容积卡尔曼滤波算法将非线性滤波归结为求解非线性函数与高斯概率密度乘积的积分问题,并采用一组等权值的2n个容积点对状态后验概率密度进行逼近。使用三阶容积原则获得的基本容积点和所对应的权值:
| $ {\int_{{R^n}} {f(x)} N(x,\mu ,{\mathit{\boldsymbol{\varSigma }}}){\rm{d}}x \approx \frac{1}{{2n}}f(\mu + \sqrt {\mathit{\boldsymbol{\varSigma }}} {\xi _i})} $ | (3) |
| $ {{\xi _i} = \sqrt {\frac{L}{2}} {{[{\bf{1}}]}_i},{\varepsilon _i} = \frac{1}{L},i = 1,2, \cdots ,L} $ | (4) |
式中:ξi为基本容积点向量,εi为对应的权值,协方差满足
实际生产应用中,非线性系统存在参数摄动、未知输入、观测噪声和系统噪声为非零均值非高斯等情况,从而影响容积卡尔曼滤波性能和稳定性。与传统的卡尔曼滤波最小化误差均方差不同,H∞卡尔曼滤波是基于最小化最大估计误差协方差进行设计的。因此,采用H∞卡尔曼滤波与容积卡尔曼滤波相结合,提高系统对不确定扰动、噪声的鲁棒性和估计精度。H∞容积卡尔曼滤波设计分为以下4个步骤。
1) 时间更新。
进行容积点的计算,通过非线性函数进行容积点传播,以及计算预测状态向量和系统协方差矩阵。
初始化系统状态及误差协方差,系统噪声均值和方差,测量噪声均值和方差:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_0} = {\rm{E}}[({\mathit{\boldsymbol{x}}_\theta } - {{\mathit{\boldsymbol{\hat x}}}_\theta }){{({\mathit{\boldsymbol{x}}_\theta } - {{\mathit{\boldsymbol{\hat x}}}_\theta })}^{\rm{T}}}]}\\ {{{\hat q}_0} = {q_0},{{\hat r}_0} = {r_0},{{\mathit{\boldsymbol{\hat Q}}}_0} = {\mathit{\boldsymbol{Q}}_0},{{\mathit{\boldsymbol{\hat R}}}_0} = {\mathit{\boldsymbol{R}}_0}} \end{array}} \right. $ | (5) |
为了便于进行分析计算,首先定义估计误差
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde x}}}_k} = {\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_k}}\\ {{{\mathit{\boldsymbol{\tilde x}}}_{k|k - 1}} = {\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}}\\ {{{\mathit{\boldsymbol{\tilde z}}}_k} = {\mathit{\boldsymbol{z}}_k} - {{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}}} \end{array}} \right. $ | (6) |
设期望获取的观测信息为:
| $ {\mathit{\boldsymbol{y}}_k} = {\mathit{\boldsymbol{C}}_k}{\mathit{\boldsymbol{x}}_k} $ | (7) |
若Ck=I,则实际获取的观测量为全部状态输出量。根据式(4)产生基本容积点,采用Cholesky方法对协方差进行分解:
| $ {\mathit{\boldsymbol{S}}_{k - 1|k - 1}} = {\rm{Chol }}({\mathit{\boldsymbol{P}}_{k - 1|k - 1}}) $ | (8) |
计算容积点:
| $ {\mathit{\boldsymbol{X}}_{\left. {i,k - 1} \right|k - 1}} = {\mathit{\boldsymbol{S}}_{\left. {k - 1} \right|k - 1}}{\mathit{\boldsymbol{\xi }}_i} + {\mathit{\boldsymbol{\hat x}}_{\left. {k - 1} \right|k - 1}},i = 1,2, \cdots ,L $ | (9) |
计算通过状态函数传播的容积点:
| $ \mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime = f({\mathit{\boldsymbol{X}}_{i,k - 1|k - 1}}) + {\mathit{\boldsymbol{\hat q}}_{k - 1}} $ | (10) |
计算状态估计值:
| $ {\mathit{\boldsymbol{\hat x}}_{k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime } = \frac{1}{m}\sum\limits_{i = 1}^m {f({\mathit{\boldsymbol{X}}_{i,k - 1|k - 1}})} + {\mathit{\boldsymbol{\hat q}}_{k - 1}} $ | (11) |
计算估计误差协方差矩阵:
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_{xx,k|k - 1}} = \frac{1}{L}\sum\limits_{i = 1}^L {(\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}){{(\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}})}^{\rm{T}}} + } }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {Q_{k - 1}} = \sum\limits_{i = 1}^L {\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime } \mathit{\boldsymbol{X}}_{i,k|k - 1}^{\prime {\rm{T}}} - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}\mathit{\boldsymbol{\hat x}}_{k|k - 1}^{\rm{T}} + {Q_{k - 1}}} \end{array} $ | (12) |
2) 测量更新。
对容积点进行更新,通过量测方程传播容积点,预测观测向量及协方差。
首先对误差协方差进行分解:
| $ {\mathit{\boldsymbol{P}}_{k|k - 1}} = {\mathit{\boldsymbol{S}}_{k|k - 1}}\mathit{\boldsymbol{S}}_{k|k - 1}^{\rm{T}} $ | (13) |
计算更新容积点:
| $ {\mathit{\boldsymbol{X}}_{i,k|k - 1}} = {\mathit{\boldsymbol{S}}_{k|k - 1}}{\mathit{\boldsymbol{\xi }}_i} + {\mathit{\boldsymbol{\hat x}}_{k|k - 1}},i = 1,2, \cdots ,L $ | (14) |
计算通过量测方程传播的容积点:
| $ {\mathit{\boldsymbol{Z}}_{i,k|k - 1}} = h({\mathit{\boldsymbol{X}}_{i,k|k - 1}}) + {\mathit{\boldsymbol{\hat r}}_k} $ | (15) |
进行量测预测:
| $ \begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}} = \frac{1}{m}\sum\limits_{i = 1}^m {{\mathit{\boldsymbol{Z}}_{i,k|k - 1}}} = \frac{1}{m}\sum\limits_{i = 1}^m h ({\mathit{\boldsymbol{X}}_{i,k|k - 1}} + {{\mathit{\boldsymbol{\hat r}}}_k},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = 1,2, \cdots ,L} \end{array} $ | (16) |
计算新息的方差矩阵:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_{zz,k|k - 1}} = \frac{1}{L}\sum\limits_{i = 1}^L {({\mathit{\boldsymbol{Z}}_{i,k|k - 1}} - {{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}})} \cdot \\ {({\mathit{\boldsymbol{Z}}_{i,k|k - 1}} - {{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}})^{\rm{T}}} + {\mathit{\boldsymbol{R}}_k} = \frac{1}{L}\sum\limits_{i = 1}^L {{\mathit{\boldsymbol{Z}}_{i,k|k - 1}}} \mathit{\boldsymbol{Z}}_{i,k|k - 1}^{\rm{T}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}}\mathit{\boldsymbol{\hat z}}_{k|k - 1}^{\rm{T}} + {\mathit{\boldsymbol{R}}_{k - 1}} \end{array} $ | (17) |
计算估计协方差矩阵:
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_{xz,k|k - 1}} = \frac{1}{L}\sum\limits_{i = 1}^L {(\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}})} \cdot \\ {({\mathit{\boldsymbol{Z}}_{i,k|k - 1}} - {{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}})^{\rm{T}}} = \frac{1}{L}\sum\limits_{i = 1}^L {\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime} \mathit{\boldsymbol{Z}}_{i,k|k - 1}^{\rm{T}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}\mathit{\boldsymbol{\hat z}}_{k|k - 1}^{\rm{T}} \end{array} $ | (18) |
3) 为了便于进行H∞滤波器设计,将容积卡尔曼滤波通过统计线性化等效为线性回归形式。通过将统计线性化应用于状态方程和测量方程,得到线性化近似形式。
定理1 给定状态估计向量
证明:将非线性函数g=σ(y)在L个容积点(χi, ζi)处传递:
| $ {\mathit{\boldsymbol{\zeta }}_i} = \sigma ({\mathit{\boldsymbol{\chi }}_i}),i = 1,2, \cdots ,L $ | (19) |
设非线性函数通过统计线性化近似为:
| $ \mathit{\boldsymbol{g}} = \mathit{\boldsymbol{Ay}} + \mathit{\boldsymbol{B}} + \mathit{\boldsymbol{\mu }} $ | (20) |
通过确定
| $ {\phi (\mathit{\boldsymbol{\hat A\hat B}}) = {\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}\sum\limits_{i = 1}^L {{\alpha _i}} \mathit{\boldsymbol{\mu }}_i^{\rm{T}}{\mathit{\boldsymbol{\mu }}_i}} $ | (21) |
| $ {{\mathit{\boldsymbol{\mu }}_i} = {\mathit{\boldsymbol{\zeta }}_i} - (\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{y}}_i} + \mathit{\boldsymbol{B}})} $ | (22) |
对目标函数分别对A、B求导,得:
| $ \frac{{\partial \phi (\mathit{\boldsymbol{\hat A}},\mathit{\boldsymbol{\hat B}})}}{{\partial \mathit{\boldsymbol{A}}}} = 0,\quad \frac{{\partial \phi (\mathit{\boldsymbol{\hat A}},\mathit{\boldsymbol{\hat B}})}}{{\partial \mathit{\boldsymbol{B}}}} = 0 $ | (23) |
得到:
| $ \mathit{\boldsymbol{B}} = \mathit{\boldsymbol{\bar g}} - \mathit{\boldsymbol{\hat A\bar y}} = \sum\limits_{i = 1}^L {{\alpha _i}} \sigma ({\mathit{\boldsymbol{\chi }}_i}) - \mathit{\boldsymbol{\hat A}}\sum\limits_{i = 1}^L {{\mathit{\boldsymbol{\alpha }}_i}} {\mathit{\boldsymbol{\chi }}_i} $ | (24) |
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{\hat A}} = \mathit{\boldsymbol{P}}_{yg}^{\rm{T}}\mathit{\boldsymbol{P}}_{yy}^{ - 1} = (\sum\limits_{i = 1}^L {{\alpha _i}} ({\mathit{\boldsymbol{\chi }}_i} - \mathit{\boldsymbol{\bar y}}){{({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}})}^{\rm{T}}}) \cdot }\\ {{{(\sum\limits_{i = 1}^L {{\alpha _i}} ({\mathit{\boldsymbol{\chi }}_i} - \mathit{\boldsymbol{\bar y}}){{({\mathit{\boldsymbol{\chi }}_i} - \mathit{\boldsymbol{\bar y}})}^{\rm{T}}})}^{ - 1}}} \end{array} $ | (25) |
从而计算得到估计误差方差阵为:
| $ {\mathit{\boldsymbol{P}}_{gg}} = \sum\limits_{i = 1}^L {{\alpha _i}} ({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}}){({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}})^{\rm{T}}} $ | (26) |
| $ \begin{array}{l} {\mathit{\boldsymbol{P}}_{\mu \mu }} = \sum\limits_{i = 1}^L {{\alpha _i}} {{\mathit{\boldsymbol{\hat \mu }}}_i}\mathit{\boldsymbol{\hat \mu }}_i^{\rm{T}} = \sum\limits_{i = 1}^L {{\alpha _i}} ({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}} - \mathit{\boldsymbol{\hat A}}({\mathit{\boldsymbol{\chi }}_i} - \mathit{\boldsymbol{y}})) \cdot \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}} - \mathit{\boldsymbol{\hat A}}({\mathit{\boldsymbol{\chi }}_i} - \mathit{\boldsymbol{y}}))^{\rm{T}}} = {\mathit{\boldsymbol{P}}_{gg}} - \mathit{\boldsymbol{P}}_{yg}^{\rm{T}}\mathit{\boldsymbol{P}}_{gg}^1{\mathit{\boldsymbol{P}}_{yg}} \end{array} $ | (27) |
现通过求取期望值以及统计线性模型近似方法求得模型的后验统计规律,即:
| $ \mathit{\boldsymbol{\hat g}} = \mathit{\boldsymbol{\hat A\bar y}} + \sum\limits_{i = 1}^L {{\alpha _i}} {\mathit{\boldsymbol{\chi }}_i} - \mathit{\boldsymbol{\hat A\bar y}} = \sum\limits_{i = 1}^L {{\alpha _i}} {\mathit{\boldsymbol{\chi }}_i} $ | (28) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{gg}} = \mathit{\boldsymbol{\hat A}}{\mathit{\boldsymbol{P}}_{yy}}{{\mathit{\boldsymbol{\hat A}}}^{\rm{T}}} + {\mathit{\boldsymbol{P}}_{\mu \mu }} = \mathit{\boldsymbol{P}}_{yg}^{\rm{T}}\mathit{\boldsymbol{P}}_{gg}^{ - 1}{\mathit{\boldsymbol{P}}_{yg}} - \mathit{\boldsymbol{P}}_{yg}^{\rm{T}}\mathit{\boldsymbol{P}}_{gg}^{ - 1}{\mathit{\boldsymbol{P}}_{yg}} + }\\ {\sum\limits_{i = 1}^L {{\alpha _i}} ({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}}){{({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}})}^{\rm{T}}} = \sum\limits_{i = 1}^L {{\alpha _i}} ({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}}){{({\mathit{\boldsymbol{\zeta }}_i} - \mathit{\boldsymbol{\bar g}})}^{\rm{T}}}} \end{array} $ | (29) |
因此可以得出通过统计线性化推导出的形式与通过容积点传播得到的均值和误差方差相同。
从而将非线性系统状态方程xk=f(xk-1, uk-1)+wk-1在点
| $ {{\mathit{\boldsymbol{x}}_k} = {\mathit{\boldsymbol{F}}_k}{\mathit{\boldsymbol{x}}_{k - 1}} - {\mathit{\boldsymbol{F}}_k}{{\mathit{\boldsymbol{\hat x}}}_{\left. {\left. {k - 1} \right|} \right\}k - 1}} + {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}{\mathit{\boldsymbol{w}}_{k - 1}} + {\mathit{\boldsymbol{\delta }}_{k - 1}}} $ | (30) |
| $ {{\mathit{\boldsymbol{F}}_k} = {{({\mathit{\boldsymbol{P}}_{x{X^\prime },k|k - 1}})}^{\rm{T}}}{{({\mathit{\boldsymbol{P}}_{xx,k - 1|k - 1}})}^{ - 1}}} $ | (31) |
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{P}}_{x{X^\prime },k|k - 1}} = \frac{1}{L}\sum\limits_{i = 1}^L {(\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}){{(\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}})}^{\rm{T}}}} = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^L {(\mathit{\boldsymbol{X}}_{i,k|k - 1}^\prime \mathit{\boldsymbol{X}}_{i,k|k - 1}^{\rm{T}} - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}\mathit{\boldsymbol{\hat x}}_{k|k - 1}^{\rm{T}})} } \end{array} $ | (32) |
式中δk-1为统计线性近似误差。
同理对观测方程进行统计等效线性化得到统计回归矩阵:
| $ {{\mathit{\boldsymbol{z}}_k} = {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{x}}_k} - {\mathit{\boldsymbol{H}}_k}{{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}} + {{\mathit{\boldsymbol{\hat z}}}_{k|k - 1}} + {\mathit{\boldsymbol{v}}_k} + {\mathit{\boldsymbol{\varepsilon }}_k}} $ | (33) |
| $ {{\mathit{\boldsymbol{H}}_k} = \mathit{\boldsymbol{P}}_{xz,k|k - 1}^{\rm{T}}\mathit{\boldsymbol{P}}_{xx,k - 1|k - 1}^{ - 1}} $ | (34) |
式中εk为统计线性近似误差,用于补偿系统的非线性项:
| $ {\mathit{\boldsymbol{W}}_k} = {\rm{E}}({\mathit{\boldsymbol{\varepsilon }}_k}\mathit{\boldsymbol{\varepsilon }}_k^{\rm{T}}) = {\mathit{\boldsymbol{P}}_{zz,k|k - 1}} - \mathit{\boldsymbol{P}}_{xz,k|k - 1}^{\rm{T}}\mathit{\boldsymbol{P}}_{xx,k|k - 1}^{ - 1}{\mathit{\boldsymbol{P}}_{xz,k|k - 1}} $ | (35) |
4) H∞容积卡尔曼滤波设计。
设计一个滤波器对滤波器估计误差进行限制,保证估计误差有界,在任意wk、vk、x0的情况下,使得观测信息误差最小化,尽量减少估计误差上界。设计滤波器满足:
| $ \left\{ {\begin{array}{*{20}{l}} {J = \frac{{\sum\limits_{k = 1}^L {\left\| {{\mathit{\boldsymbol{y}}_k} - {{\mathit{\boldsymbol{\hat y}}}_{k|k}}} \right\|_{\mathit{\boldsymbol{\bar P}}_{k|k}^{ - 1}}^2} }}{{\left\| {{\mathit{\boldsymbol{x}}_0} - {{\mathit{\boldsymbol{\hat x}}}_{\left. 0 \right|0}}} \right\|_{\mathit{\boldsymbol{P}}_{\left. 0 \right|0}^{ - 1}}^2 + \sum\limits_{k = 1}^L {(\left\| {{\mathit{\boldsymbol{w}}_k}} \right\|_{Q_k^{ - 1}}^2 + \left\| {{\mathit{\boldsymbol{v}}_k}} \right\|_{\mathit{\boldsymbol{R}}_K^{ - 1}}^2)} }}}\\ {\mathop {{\rm{sup}}}\limits_{({x_0},{v_k},{x_k})} J \le {\beta ^2}} \end{array}} \right. $ | (36) |
式中:x0、P0|0是初始状态向量和协方差矩阵;xk、
| $ \begin{array}{*{20}{c}} {\left\| {{\mathit{\boldsymbol{y}}_k} - {{\mathit{\boldsymbol{\hat y}}}_k}} \right\|_{\mathit{\boldsymbol{P}}_{k|k}^{ - 1}}^2 = {{({\mathit{\boldsymbol{y}}_k} - {{\mathit{\boldsymbol{\hat y}}}_k})}^{\rm{T}}}\mathit{\boldsymbol{P}}_{k|k}^{ - 1}({\mathit{\boldsymbol{y}}_k} - {{\mathit{\boldsymbol{\hat y}}}_k}) = }\\ {{{({\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_k})}^{\rm{T}}}\mathit{\boldsymbol{C}}_k^{\rm{T}}\mathit{\boldsymbol{P}}_{k|k}^{ - 1}{\mathit{\boldsymbol{C}}_k}({\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_k}) = \left\| {{\mathit{\boldsymbol{x}}_k} - {{\mathit{\boldsymbol{\hat x}}}_k}} \right\|_{\mathit{\boldsymbol{\bar P}}_{k|k}^{ - 1}}^2} \end{array} $ | (37) |
则:
| $ \mathit{\boldsymbol{\bar P}}_{k|k}^{ - 1} = \mathit{\boldsymbol{C}}_k^{\rm{T}}\mathit{\boldsymbol{P}}_{k|k}^{ - 1}{\mathit{\boldsymbol{C}}_k} $ | (38) |
将式(36)转化为不定式形式:
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_{{{\hat y}_k}} \mathop {{\rm{max}}}\limits_{({x_0},{v_k},{w_k})} J = - \left\| {{\mathit{\boldsymbol{x}}_0} - {{\mathit{\boldsymbol{\hat x}}}_{\left. 0 \right|0}}} \right\|_{\mathit{\boldsymbol{P}}_{\left. 0 \right|0}^{ - 1}}^2 - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1}^L {\left\| {{\mathit{\boldsymbol{w}}_k}} \right\|_{\mathit{\boldsymbol{Q}}_k^{ - 1}}^2} - \sum\limits_{k = 1}^L {\left\| {{\mathit{\boldsymbol{v}}_k}} \right\|_{\mathit{\boldsymbol{R}}_k^{ - 1}}^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{{\beta ^2}}}\sum\limits_{k = 1}^L {\left\| {{\mathit{\boldsymbol{y}}_k} - {{\mathit{\boldsymbol{\hat y}}}_{k|k}}} \right\|_{\mathit{\boldsymbol{\bar P}}_{k|k}^{ - 1}}^2} \end{array} $ | (39) |
进行状态更新:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{K}}_k} = {\mathit{\boldsymbol{P}}_{xx,k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}{{({\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{xx,k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}} + {\mathit{\boldsymbol{R}}_k})}^{ - 1}} = }\\ {{\mathit{\boldsymbol{P}}_{xz,k|k - 1}}\mathit{\boldsymbol{P}}_{zz,k|k - 1}^{ - 1}} \end{array} $ | (40) |
| $ {\mathit{\boldsymbol{x}}_{k|k}} = {\mathit{\boldsymbol{x}}_{k|k - 1}} + {\mathit{\boldsymbol{K}}_k}({\mathit{\boldsymbol{z}}_k} - {\mathit{\boldsymbol{\hat z}}_{k|k - 1}}) $ | (41) |
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{xx,k|k}} = (\mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{P}}_{xx,k|k - 1}}[\mathit{\boldsymbol{H}}_k^{\rm{T}}\quad \mathit{\boldsymbol{I}}]\mathit{\boldsymbol{R}}_{ek}^{ - 1}{{[\mathit{\boldsymbol{H}}_k^{\rm{T}}\quad \mathit{\boldsymbol{I}}]}^{\rm{T}}}) \cdot }\\ {{\mathit{\boldsymbol{P}}_{xx,k|k - 1}}} \end{array} $ | (42) |
| $ {\mathit{\boldsymbol{R}}_{ek}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_k} + {\mathit{\boldsymbol{H}}_k}{\mathit{\boldsymbol{P}}_{xx,k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}}&{{{({P_{xx,k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}})}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{P}}_{xx,k|k - 1}}\mathit{\boldsymbol{H}}_k^{\rm{T}}}&{ - {\beta ^2}\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{P}}_{xx,k|k - 1}}} \end{array}} \right] $ | (43) |
为了表示误差协方差和调整参数之间的关系,应用矩阵求逆定理将式(42)求逆得到:
| $ \mathit{\boldsymbol{P}}_{xx,k|k}^{ - 1} = \mathit{\boldsymbol{P}}_{xx,k|k - 1}^{ - 1} + {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{R}}_k^{ - 1}\mathit{\boldsymbol{H}}_k^{\rm{T}} - {\beta ^{ - 2}}\mathit{\boldsymbol{I}} $ | (44) |
β为调节因子,权衡H∞滤波和最小均方根性能。
为了保证误差方差的正定性,满足:
| $ \mathit{\boldsymbol{P}}_{xx,k|k - 1}^{ - 1} + {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{R}}_k^{ - 1}\mathit{\boldsymbol{H}}_k^{\rm{T}} - {\beta ^{ - 2}}\mathit{\boldsymbol{I}} \ge 0 $ | (45) |
即
| $ {\beta ^2}\mathit{\boldsymbol{I}} \ge {\rm{max}}\{ {\rm{eig}} {(\mathit{\boldsymbol{P}}_{xx,k|k - 1}^{ - 1} + {\mathit{\boldsymbol{H}}_k}\mathit{\boldsymbol{R}}_k^{ - 1}\mathit{\boldsymbol{H}}_k^{\rm{T}})^{ - 1}}|\} $ | (46) |
式中eig(·)代表均值的特征值。
噪声协方差矩阵对算法的稳定性有着重要影响。为了保证滤波算法的稳定性,许多学者通过在误差方差和新息方差矩阵中引入附加的正定矩阵[16]:
| $ \begin{array}{l} {P_{xx,k|k - 1}} = \sum\limits_{i = 1}^L {\mathit{\boldsymbol{X}}_{i,k|k - 1}^{\prime {\rm{T}}}} \mathit{\boldsymbol{X}}_{i,k|k - 1}^{\prime {\rm{T}}} - {{\mathit{\boldsymbol{\hat x}}}_{k|k - 1}}\mathit{\boldsymbol{\hat x}}_{k|k - 1}^{\rm{T}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{Q}}_{k - 1}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{Q}}_{k - 1}} \end{array} $ | (47) |
通过增大Qk来增强稳定性。然而其会增大误差方差阵Pxx, k|k-1,同时增大增益矩阵Kk,影响估计精度。
3 模糊自适应H∞容积卡尔曼滤波标准的容积卡尔曼滤波需要假设噪声的均值为零,且精确已知噪声统计特性。一般情况下过程噪声和观测噪声的统计特性不易准确获得。较大的Qk-1,可以保证系统的稳定性,但估计精度下降;而Qk-1较小,则会是滤波器不稳定,从而降低滤波性能。因此采用模糊规则对过程噪声和观测噪声进行估计,通过增强对噪声的自适应力来提高滤波精度和收敛速度。
设过程噪声方差和测量噪声方差的模糊自适应律为:
| $ {{{\mathit{\boldsymbol{\hat Q}}}_{k - 1}} = \eta {{\mathit{\boldsymbol{\tilde z}}}^{\rm{T}}}\mathit{\boldsymbol{\tilde zI}} + \gamma \mathit{\boldsymbol{I}}} $ | (48) |
| $ {{{\mathit{\boldsymbol{\hat R}}}_k} = \rho {{\mathit{\boldsymbol{\tilde z}}}^{\rm{T}}}\mathit{\boldsymbol{\tilde zI}} + \sigma \mathit{\boldsymbol{I}}} $ | (49) |
式中:η>0, γ>0, ρ>0, σ>0为选定的常值。当估计误差较大时,应该选择较大的
当
| $ {{{\mathit{\boldsymbol{\hat Q}}}_{{\rm{ new }}}} = 6{{\mathit{\boldsymbol{\hat Q}}}_{{\rm{ old }}}},\quad {{\mathit{\boldsymbol{\hat R}}}_{{\rm{ new }}}} = 4{{\mathit{\boldsymbol{\hat R}}}_{{\rm{ old }}}}} $ | (50) |
当
| $ {{{\mathit{\boldsymbol{\hat Q}}}_{{\rm{ new }}}} = 0.2{{\mathit{\boldsymbol{\hat Q}}}_{{\rm{ old }}}},\quad {{\mathit{\boldsymbol{\hat R}}}_{{\rm{ new }}}} = 0.3{{\mathit{\boldsymbol{\hat R}}}_{{\rm{ old }}}}} $ | (51) |
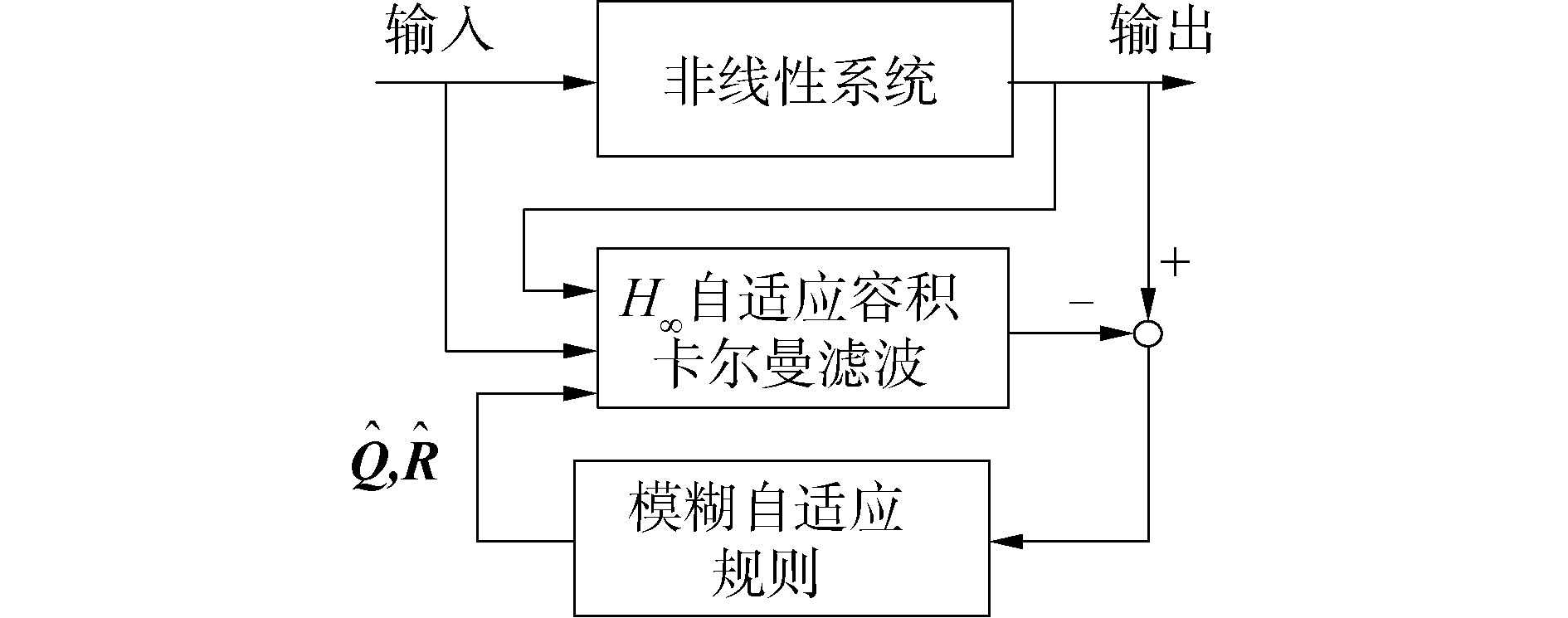
则自适应H∞容积卡尔曼滤波系统结构图 1。
|
Download:
|
| 图 1 模糊自适应HCKF系统结构 Fig. 1 The structure of the fuzzy adaptive HCKF system | |
为了验证模糊自适应HCKF算法的有效性,选用以下一般非线性系统进行仿真验证,假设系统的过程噪声和观测噪声不准确,采用标准的CKF和模糊自适应HCKF的算法对系统状态进行估计比较,并验证统计线性化的有效性,从而具有一定的普遍性和适用性。
系统的状态方程为:
| $ {\begin{array}{*{20}{c}} {x(k) = 0.5x(k - 1) + 8{\rm{cos}}(1.2(k - 1)) + }\\ {w(k) + 2.5x(k - 1)/(1 + {x^2}(k - 1))} \end{array}} $ | (52) |
观测方程为:
| $ {z(k) = {x^2}(k)/20 + v(k)} $ | (53) |
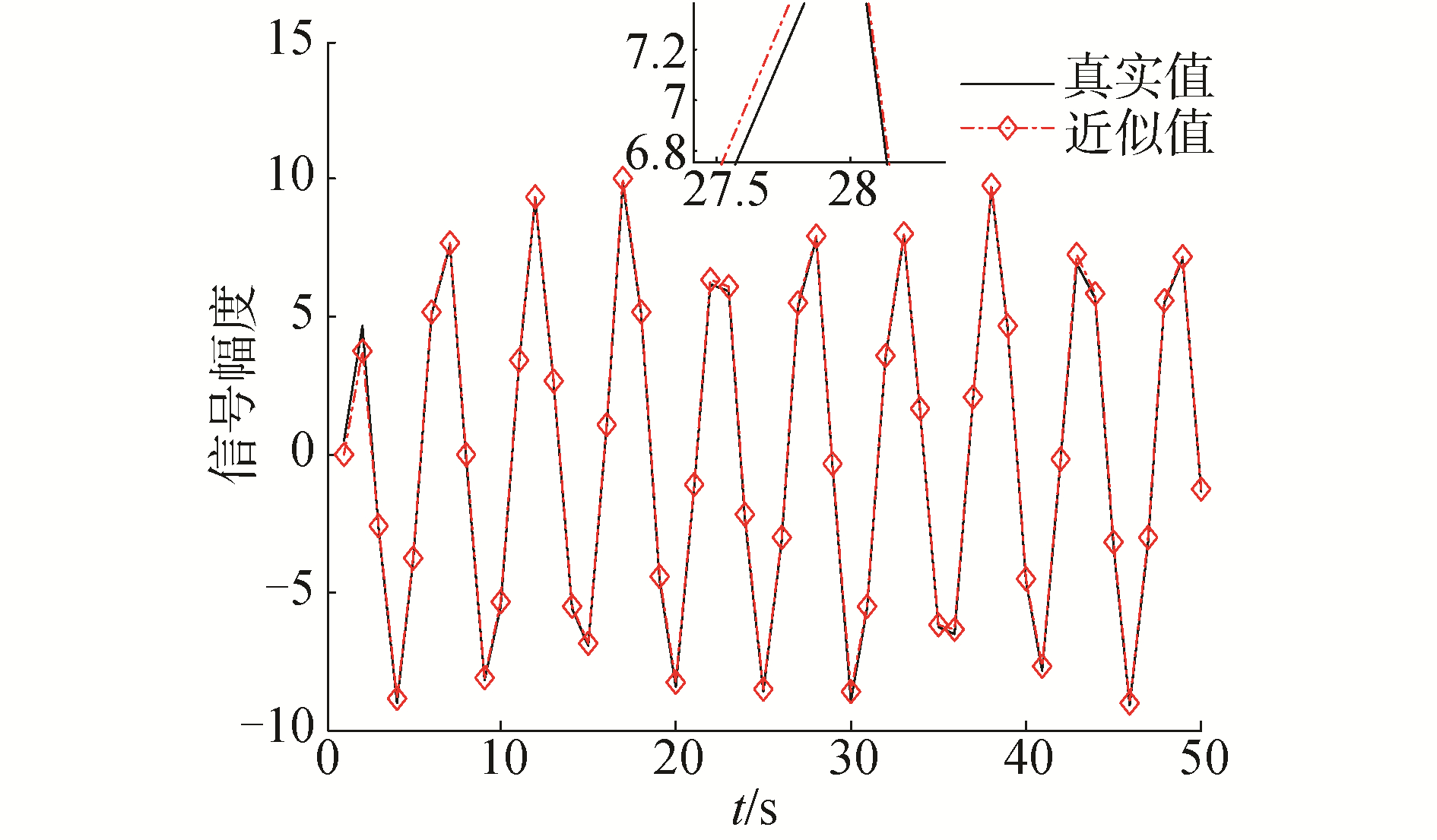
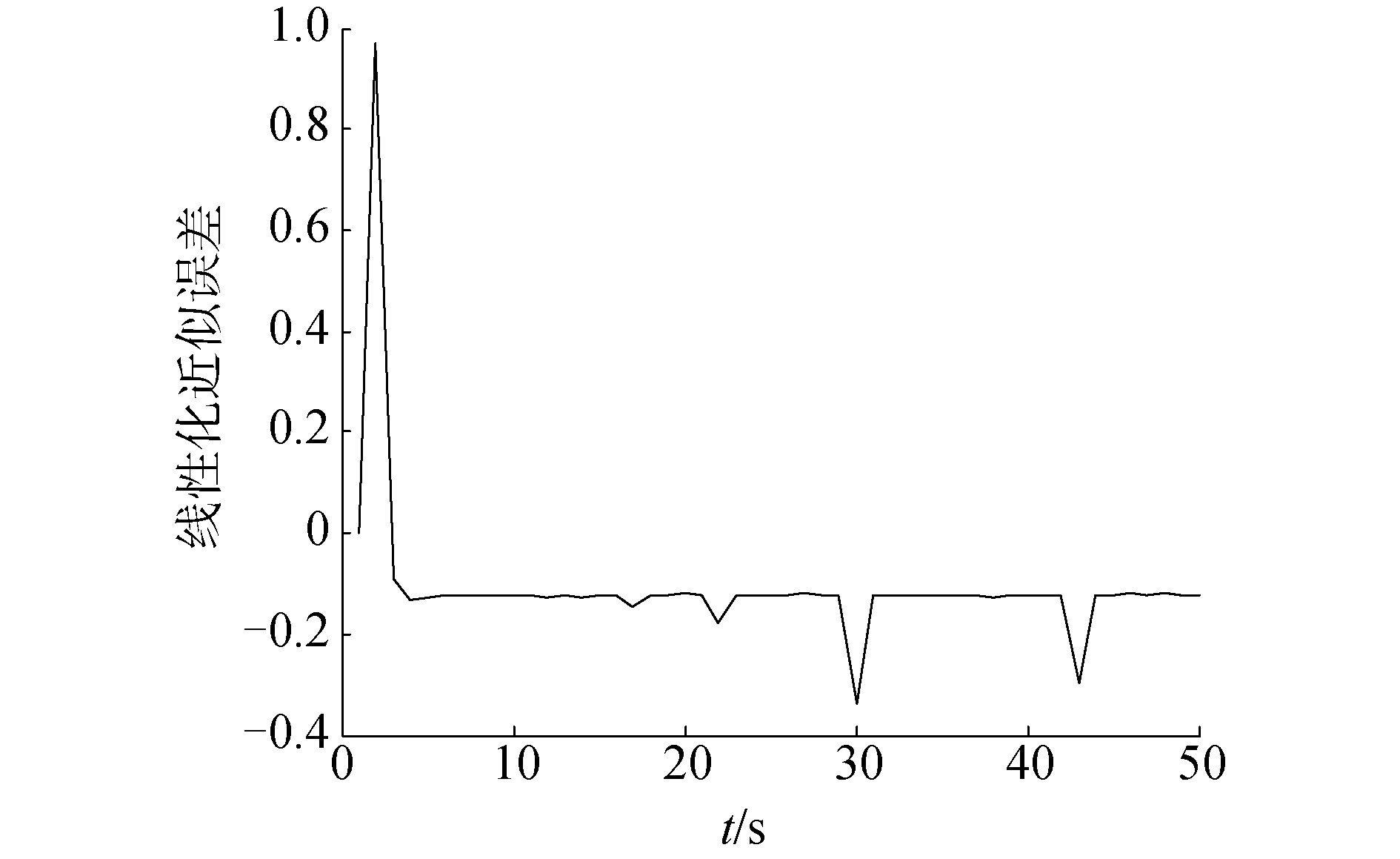
首先对统计线性化算法(30)~(35)的有效性进行验证,系统的噪声统计特性为q=0,r=0,Q=0.06,R=0.01,P0=10。仿真结果如图 2、图 3所示。
|
Download:
|
| 图 2 统计线性化近似 Fig. 2 Statistical linearization approximation | |
|
Download:
|
| 图 3 统计线性化近似误差 Fig. 3 Error of approximatio | |
从图 2和图 3的仿真结果可以得出,通过统计线性化方法对非线性系统的近似可以达到较好的效果,近似值与真实值基本相符,误差较小,因此可以通过统计线性化方法来近似非线性系统,从而进一步进行滤波器的设计研究和分析。
为了验证模糊自适应HCKF算法的有效性和鲁棒性,分别采用标准的容积卡尔曼滤波及模糊自适应HCKF滤波方法在以下2种情况下进行仿真实验。
| $ {{\rm{ Case1}}:q = 0,r = 0,Q = 0.06,R = 0.01}。$ |
| $ {{\rm{ Case2}}:q = 0.4,r = 0.2,Q = 0.06,R = 0.01}。$ |
| $ {{\rm{ Case3}}:q = 0.4,r = 0,Q = 0.06,R = 0.01}。$ |
| $ {{\rm{ Case4}}:q = 0,r = 0.2,Q = 0.06,R = 0.01}。$ |
实际的噪声协方差为Qe=0.05,Ra=0.01,采用模糊自适应算法对噪声协方差进行估计。由于篇幅限制,本文仅给出Case1和Case2的结果仿真图。Case1,Case2,Case3和Case4的仿真误差统计结果在表中给出,以进行结果对比,得出相关结论。
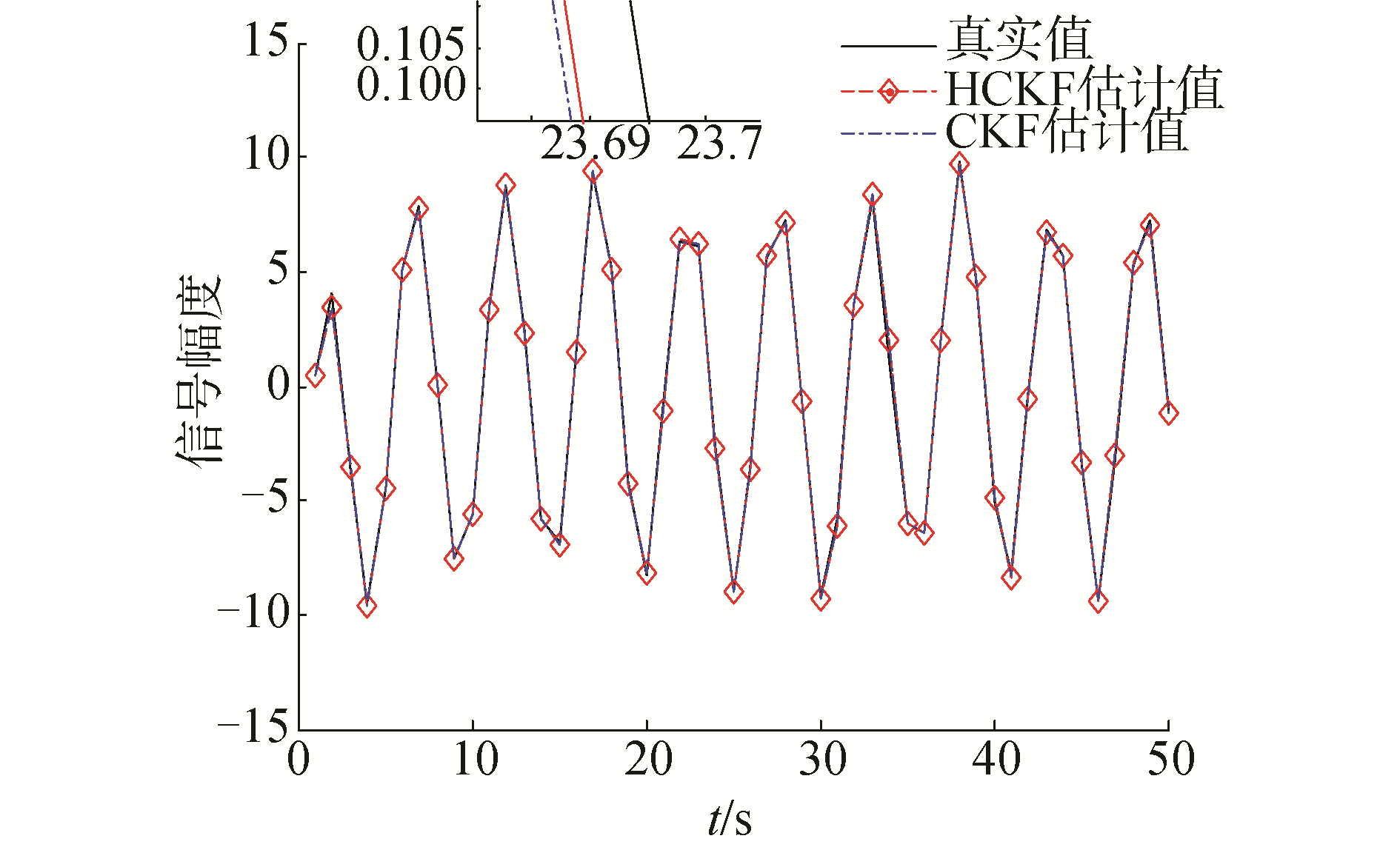
在Case 1情况下对系统的状态进行估计比较,在CKF和模糊自适应HCKF 2种算法下的估计结果和估计误差如图 4、图 5所示。
|
Download:
|
| 图 4 Case 1情况下不同滤波方法估计 Fig. 4 Estimation of different filtering method of Case 1 | |
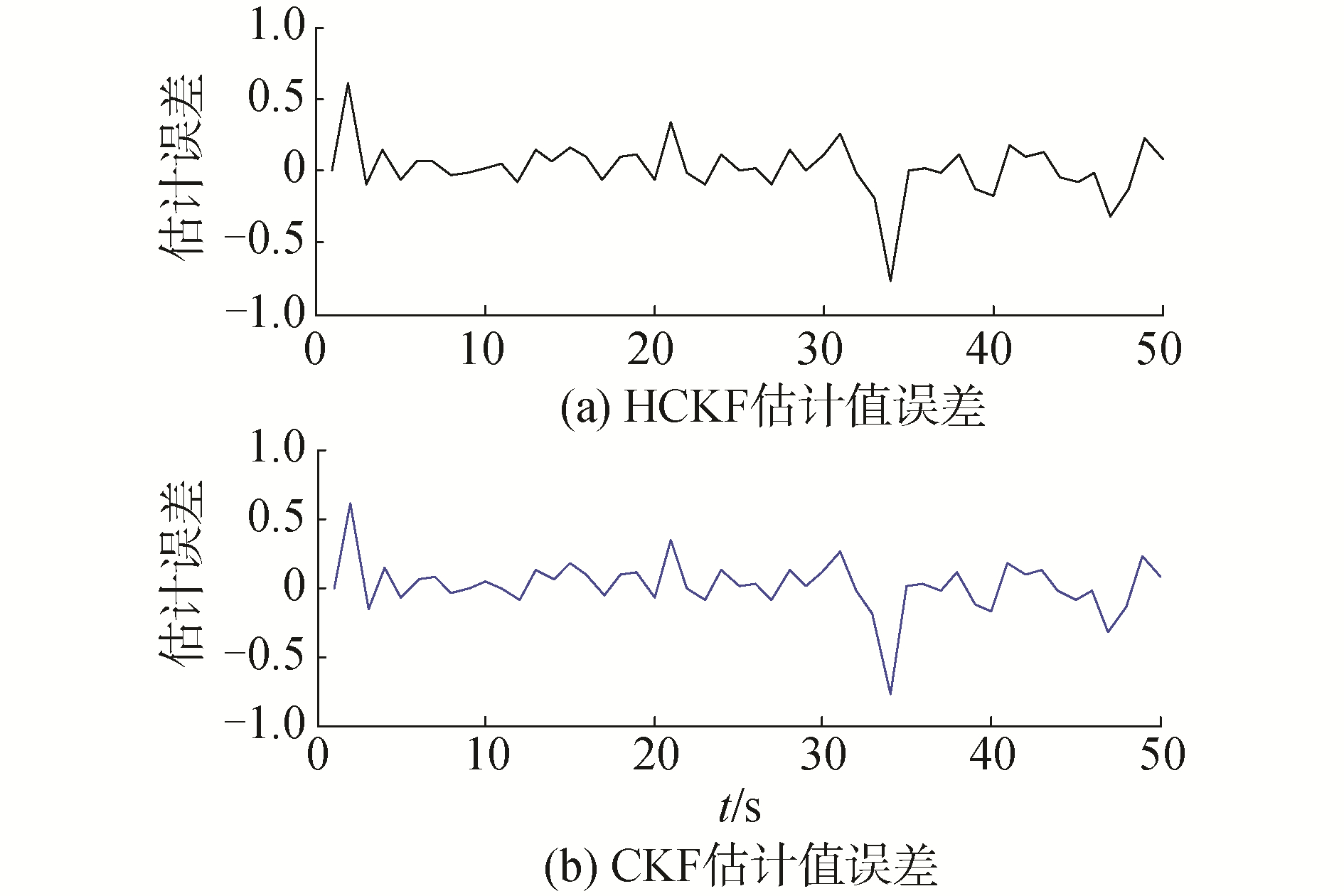
|
Download:
|
| 图 5 Case 1情况下不同滤波方法的估计误差 Fig. 5 The estimation error of different filtering method of Case 1 | |
在Case 2情况下对系统的状态进行估计,在CKF和模糊自适应HCKF这2种算法下的估计结果和估计误差如图 6及图 7所示。

|
Download:
|
| 图 6 Case 2情况下不同滤波方法估计 Fig. 6 Estimation of different filtering method of Case 2 | |
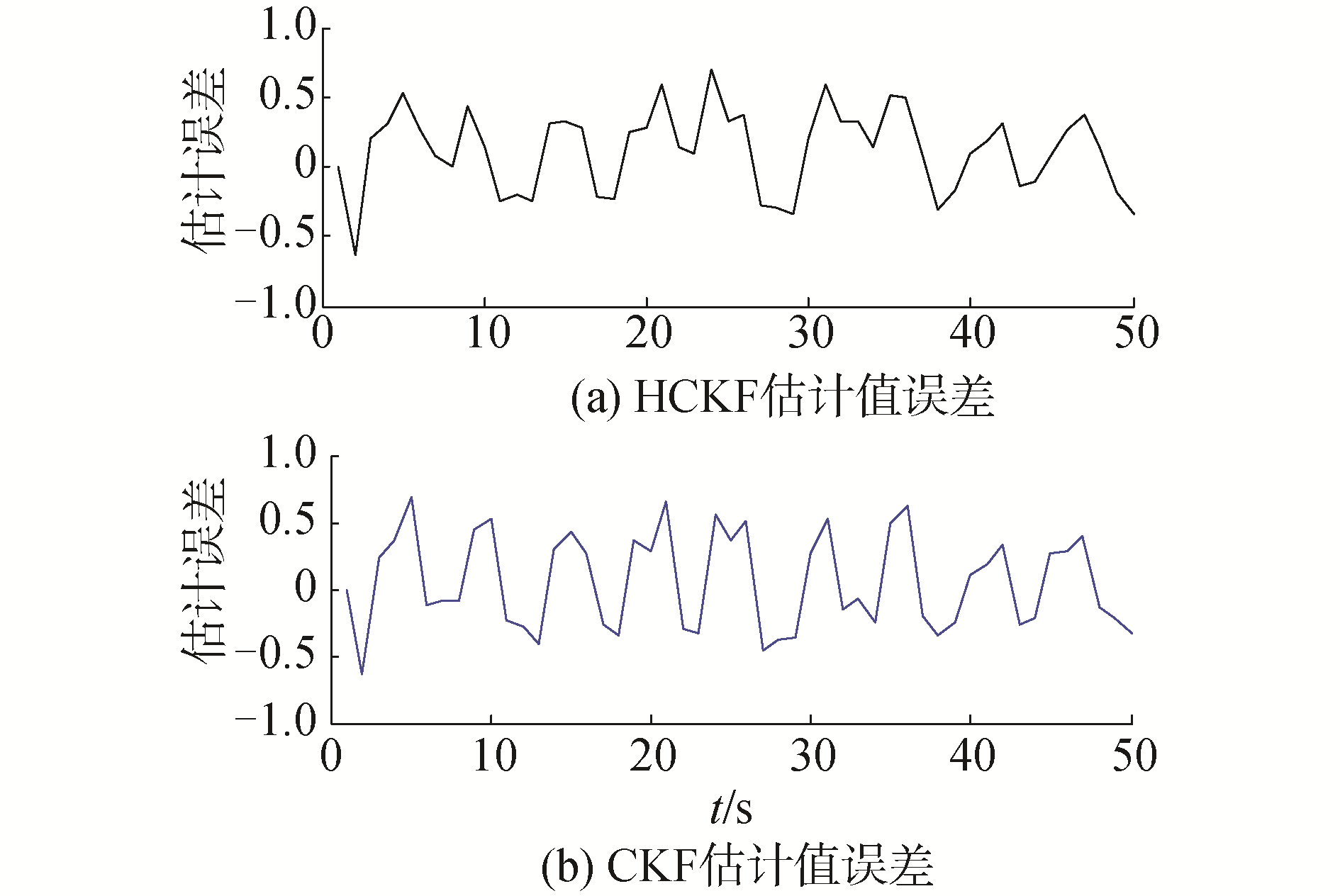
|
Download:
|
| 图 7 Case 2情况下不同滤波方法的估计误差 Fig. 7 The estimation error of different filtering method of Case 2 | |
从仿真结果图 3~图 6研究中可以发现当系统噪声和观测噪声均值为零时,模糊自适应HCKF和CKF算法的估计效果相当,估计误差均值和均方差相差较少,都能较好的估计系统的状态值;当系统噪声和观测噪声均值不为零时,模糊自适应HCKF的估计效果优于CKF。
为了便于更精确的比较2种算法的估计结果,本文分别对2种算法的误差均值和误差均方差值进行计算和比较,统计结果如表 1所示。
| $ {{\rm{AVE}} = \frac{1}{L}\sum\limits_{i = 1}^L | ({\mathit{\boldsymbol{x}}_k}(\mathit{\boldsymbol{i}}) - {{\mathit{\boldsymbol{\hat x}}}_{k|k}}(\mathit{\boldsymbol{i}}))|\quad } $ | (54) |
| $ {{\rm{ RMSE}} = \sqrt {\frac{1}{L}\sum\limits_{i = 1}^L {({\mathit{\boldsymbol{x}}_k}(} \mathit{\boldsymbol{i}}) - {{\mathit{\boldsymbol{\hat x}}}_{k|k}}(\mathit{\boldsymbol{i}}){)^2}} } $ | (55) |
| 表 1 Case 1和Case 2的估计误差及均方差 Table 1 The AVE and RMSE of Case 1and Case 2 |
由表 1和表 2可知,在分别存在系统噪声、观测噪声以及同时存在系统噪声和观测噪声的情况下,HCKF误差均值和均方根值小于标准容积卡尔曼,因而提出的HCKF滤波方法能够有效的减少噪声产生的影响,在存在非零均值噪声情况下具有一定的鲁棒性和较高的估计精度,并且在噪声统计特性不准确的情况下,模糊自适应可以有效的估计不准确的噪声协方差,提高估计效率和收敛速度,防止滤波发散。
| 表 2 Case 3和Case 4的估计误差及均方差 Table 2 The AVE and RMSE of Case 3 and Case 4 |
1) 在滤波过程中,在存在噪声统计特性不准确及非零均值噪声协方差的情况下,与标准的容积卡尔曼滤波相比,本文提出模糊自适应HCKF能够更好的估计非线性系统的状态值,具有较高的估计精度和鲁棒性。
2) 提出的模糊自适应规则能够较好的估计不准确的噪声协方差,从而避免滤波发散,提高收敛速度。
3) 本文提出的滤波方法可以较好地推广到任意非线性系统,应用广泛,具有一定的工程应用价值。
| [1] |
ALSPACH D, SORENSON H. Nonlinear Bayesian estimation using Gaussian sum approximations[J]. IEEE transactions on automatic control, 1972, 17(4): 439-448. (  0) 0)
|
| [2] |
OZBEK L, EFE M. An adaptive extended Kalman filter with application to compartment models[J]. Communications in statistics - simulation and computation, 2004, 33(1): 145-158. DOI:10.1081/SAC-120028438 (  0) 0)
|
| [3] |
YANG Shishan, BAUM M. Extended Kalman filter for extended object tracking[C]//Proceedings of 2017 IEEE International Conference on Acoustics, Speech and Signal Processing. New Orleans, LA, USA: IEEE, 2017: 4386-4390. 10.1109/ICASSP.2017.7952985
(  0) 0)
|
| [4] |
陈庆武, 张志安, 何雨, 等. 基于改进扩展卡尔曼滤波算法的移动机器人定位方法研究[J]. 测试技术学报, 2018, 32(4): 292-299. CHEN Qingwu, ZHANG Zhi'an, HE Yu, et al. Research on positioning method of mobile robot based on improved extended Kalman filtering algorithm[J]. Journal of test and measurement technology, 2018, 32(4): 292-299. DOI:10.3969/j.issn.1671-7449.2018.04.003 (  0) 0)
|
| [5] |
KOLÅS S, FOSS B A, SCHEI T S. Constrained nonlinear state estimation based on the UKF approach[J]. Computers & chemical engineering, 2009, 33(8): 1386-1401. DOI:10.1016/j.compchemeng.2009.01.012 (  0) 0)
|
| [6] |
赵琳, 王小旭, 孙明, 等. 基于极大后验估计和指数加权的自适应UKF滤波算法[J]. 自动化学报, 2010, 36(7): 1007-1019. ZHAO Lin, WANG Xiaoxu, SUN Ming, et al. Adaptive UKF filtering algorithm based on maximum a posterior estimation and exponential weighting[J]. Acta automatica sinica, 2010, 36(7): 1007-1019. (  0) 0)
|
| [7] |
ARASARATNAM I, HAYKIN S. Cubature Kalman filters[J]. IEEE transactions on automatic control, 2009, 54(6): 1254-1269. DOI:10.1109/TAC.2009.2019800 (  0) 0)
|
| [8] |
穆静, 蔡远利. 平方根容积卡尔曼滤波算法及其应用[J]. 兵工自动化, 2011, 30(6): 11-13, 26. MU Jing, CAI Yuanli. Square root cubature Kalman filter algorithm and application[J]. Ordnance industry automation, 2011, 30(6): 11-13, 26. DOI:10.3969/j.issn.1006-1576.2011.06.005 (  0) 0)
|
| [9] |
TANG Xiaojun, WEI Jianli, CHEN Kai. Square-root adaptive cubature Kalman filter with application to spacecraft attitude estimation[C]//Proceedings of the 15th International Conference on Information Fusion. Singapore: IEEE, 2012: 1406-1412. https://ieeexplore.ieee.org/document/6289972
(  0) 0)
|
| [10] |
JIANG Chen, ZHANG Shubi, ZHANG Qiuzhao. A new adaptive H-infinity filtering algorithm for the GPS/INS integrated navigation[J]. Sensors, 2016, 16(12): 2127. DOI:10.3390/s16122127 (  0) 0)
|
| [11] |
艾蔓桐, 孙永辉, 王义, 等. 基于插值H∞扩展卡尔曼滤波的发电机动态状态估计[J]. 中国电机工程学报, 2018, 38(19): 5846-5853. AI Mantong, SUN Yonghui, WANG Yi, et al. Dynamic state estimation for synchronous machines based on interpolation H∞ extended Kalman filter[J]. Proceedings of the CSEE, 2018, 38(19): 5846-5853. (  0) 0)
|
| [12] |
ZHAO Junbo, MILI L. Robust unscented Kalman filter for power system dynamic state estimation with unknown noise statistics[J]. IEEE transactions on smart grid, 2019, 10(2): 1215-1224. (  0) 0)
|
| [13] |
ZHAO Junbo, MILI L. A Robust generalized-maximum likelihood unscented Kalman filter for power system dynamic state estimation[J]. IEEE journal of selected topics in signal processing, 2018, 12(4): 578-592. DOI:10.1109/JSTSP.2018.2827261 (  0) 0)
|
| [14] |
ZHAO Junbo. Dynamic state estimation with model uncertainties using H∞ extended Kalman filter[J]. IEEE transactions on power systems, 2018, 33(1): 1099-1100. DOI:10.1109/TPWRS.2017.2688131 (  0) 0)
|
| [15] |
ZHAO Junbo, MILI L. A decentralized H-infinity unscented Kalman filter for dynamic state estimation against uncertainties[J]. IEEE transactions on smart grid, 2019, 10(5): 4870-4880. DOI:10.1109/TSG.2018.2870327 (  0) 0)
|
| [16] |
赵琳, 王小旭, 薛红香, 等. 带噪声统计估计器的Unscented卡尔曼滤波器设计[J]. 控制与决策, 2009, 24(10): 1483-1488. ZHAO Lin, WANG Xiaoxu, XUE Hongxiang, et al. Design of unscented Kalman filter with noise statistic estimator[J]. Control and decision, 2009, 24(10): 1483-1488. DOI:10.3321/j.issn:1001-0920.2009.10.008 (  0) 0)
|
| [17] |
姜浩楠, 蔡远利. 带有噪声递推估计的自适应集合卡尔曼滤波[J]. 控制与决策, 2018, 33(9): 1567-1574. JIANG Haonan, CAI Yuanli. Adaptive ensemble Kalman filter with recursive noise estimation[J]. Control and decision, 2018, 33(9): 1567-1574. (  0) 0)
|
| [18] |
丁家琳, 肖建. 基于极大后验估计的自适应容积卡尔曼滤波器[J]. 控制与决策, 2014, 29(2): 327-334. DING Jialin, XIAO Jian. Design of adaptive cubature Kalman filter based on maximum a posteriori estimation[J]. Control and decision, 2014, 29(2): 327-334. (  0) 0)
|
| [19] |
SASIADEK J Z, WANG Q, ZEREMBA M B. Fuzzy adaptive Kalman filtering for INS/GPS data fusion[C]//Proceedings of 2000 IEEE International Symposium on Intelligent Control. Held jointly with the 8th IEEE Mediterranean Conference on Control and Automation. Rio Patras, Greece: IEEE, 2000: 181-186. 10.1109/ISIC.2000.882920
(  0) 0)
|
| [20] |
RAHBARI R, LEACH B W, DILLON J, et al. Adaptive tuning of a Kalman filter using the fuzzy integral for an intelligent navigation system[C]//Proceedings of 2002 IEEE International Symposium on Intelligent Control. Vancouver, BC, Canada: IEEE, 2002: 252-257. 10.1109/ISIC.2002.1157771
(  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


