2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240
2. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China
世界能源日趋紧张,国际海事组织对海上环境保护和节约能源非常重视,制定了一系列标准,因此,研究船舶节能技术是非常有必要的。目前,船舶节能装置主要有补偿导管、船尾导流鳍、舵附推力鳍、舵球和桨后自由旋转助推叶轮等[1-3]。其中桨后自由叶轮以其独特的水动力设计和优越的节能效果获得了造船界的普遍关注。
1966年联邦德国的Grim教授发表了关于自由叶轮的文章,这是自由叶轮研究的一个里程碑。1980年Grim教授进行了一系列实验,结果表明自由叶轮可以提高螺旋桨的效率4.38%~9.19%。Vanbeek对伊丽莎白二世女王游轮推进系统改造中使用2个加装自由叶轮的可调螺距螺旋桨,结果显示效率提高了3.6%。Kehr根据升力线理论,基于螺旋桨和自由叶轮之间相互影响的诱导速度提出了自由叶轮推进系统的初步设计方法。Blaurock进行了一系列模型试验,包括自由叶轮和固定螺距螺旋桨的组合以及自由叶轮和可调螺距螺旋桨的组合,这些试验结果表明螺旋桨的推进效率最高可增加5%。Chen等[4]提出了以环量守恒为基础的自由叶轮设计方法,螺旋桨和自由叶轮之间的相互影响的诱导速度用升力线理论来预测。郭永松等[5]给出了以升力线理论为基础的自由叶轮设计方法,并且对一条2 000 t的综合节能船进行了自由叶轮的设计、模型试验,结果显示推进效率提高10%。侯立勋等[6]给出了一种利用螺旋桨的旋涡理论设计自由叶轮的方法。
本文对选定的螺旋桨和自由叶轮建立几何模型,采用基于交界面原理的滑移网格技术对计算域进行离散,选择k-ε湍流模型进行求解。利用STAR-CCM+软件平台对选定的螺旋桨进行了水动力性能分析,计算出了该螺旋桨的敞水性能曲线并且与实验结果进行对比分析,进而对自由叶轮推进系统在多个进速系数下进行模拟计算,并且与实验结果进行对比分析。最后在进速系数为0.771的情况下,分析自由叶轮推进系统中螺旋桨和自由叶轮之间的相互影响。
1 自由叶轮工作原理如图 1所示,叶轮在螺旋桨后的尾流场中自由旋转,其直径一般为螺旋桨直径的1.2~1.3倍,其内半径部分吸收螺旋桨尾流中的能量,起着涡轮机的作用带动外半径部分旋转,其外半径部分起着螺旋桨的作用产生附加推力。由于自由叶轮是自由旋转,所以其总转矩为0,其内外半径部分产生的转矩方向相反,所以其内半径部分转矩矢量加上其外半径部分转矩矢量为0。其内半径产生的推力与外半径产生的推力也是相反的,为了达到节能的效果,其内半径部分的推力矢量加上外半径部分的推力矢量必须大于0[7]。

|
Download:
|
| 图 1 自由叶轮工作原理 Fig. 1 Configuration of the vane wheel | |
| $\int_{{\rm{r}}\mathit{t}}^{Rv} {\frac{{{\rm{d}}Q}}{{{\rm{d}}r}}} {\rm{d}}r + \int_{{\rm{r}}0}^{rt} {\frac{{{\rm{d}}Q}}{{{\rm{d}}r}}} {\rm{d}}r = 0 $ | (1) |
| $\int_{{\rm{r}}\mathit{t}}^{Rv} {\frac{{{\rm{d}}T}}{{{\rm{d}}r}}} {\rm{d}}r + \int_{{\rm{r}}0}^{rt} {\frac{{{\rm{d}}T}}{{{\rm{d}}r}}} {\rm{d}}r = 0 $ | (2) |
式中:dT、dQ分别是自由叶轮推力和转矩的微分,RV、rt和r0分别是自由叶轮的半径,自由叶轮内半径部分的半径和自由叶轮叶根处的半径。
2 几何模型如图 2所示,本文选用的螺旋桨的叶数KR为5,直径DR为1.28 m,盘面比AE为0.77;自由叶轮的直径DV为螺旋桨直径的1.3倍,为1.664 m,叶片数量KV为9,与螺旋桨之间的距离为0.32 m。螺旋桨和自由叶轮的型值见表 1和表 2。

|
Download:
|
| 图 2 几何模型 Fig. 2 Geometric model | |
表 1、2中RR和RV分别为螺旋桨的半径和自由叶轮的半径;DR和DV分别为螺旋桨和自由叶轮的直径;C为弦长;P为螺距;iT为后倾;θs为侧斜;t为厚度;fM为拱度。
3 网格生成、数值模型及边界条件如图 3所示,建立一个大的圆柱体,将几何模型包在其内部,其半径为3 m,长为6.4 m,螺旋桨的中心,位于此圆柱体的中心,并且与圆柱体同轴,然后建立一个半径为1 m,长为0.52 m的同轴圆柱体,此圆柱体将螺旋桨包含在内,再建立一个半径为1 m,长为0.48 m的同轴圆柱体将自由叶轮包含在内。将包含螺旋桨的圆柱体和几何模型做布尔减运算,目标零部件设为此圆柱体,得到的结果即为螺旋桨的网格划分计算区域;同理可以得到自由叶轮的网格划分计算区域。将外围的圆柱体与另外2个圆柱体和几何模型做布尔减运算,得到的区域命名为静态区域。将这些几何结果分配至区域。在区域中根据3个区域之间两两相互接触的关系,创建3个交界面。

|
Download:
|
| 图 3 计算域 Fig. 3 Computational domain | |
网格生成过程中,棱柱层数设为3层,棱柱层厚度设为4.0×10-4 m,面网格增长率设为1.3,最小相对尺寸设为25%。为了细化螺旋桨叶片和自由叶轮叶片周围的网格,基本曲率设置为72,最小相对尺寸和相对目标尺寸均设置为4.8%,螺旋桨和自由叶轮的边缘特征线的最小相对尺寸和相对目标尺寸均设置为0.08%。交界面上的网格尺寸要保持一致。由于远离螺旋桨区域的水流行为对于这些模拟来说并不重要,因此可以在静态区域指定较粗大的网格。
在此模拟中,流体模型选择恒密度不可压缩流体,湍流模型选择k~ε湍流[8-9],计算模型选择雷诺平均纳维-斯托克斯方程[10]。由于尾流场受到干扰所以其流动为非定常流动,所以选择非定常模型。为了使结果更好地收敛,将速度亚松弛因子设置为0.5。将不定常求解器中的时间步设置为0.004 s,最大内部迭代次数设置为5,最大物理时间设置为5 s。
几何模型的各个表面均设置为壁面,包含螺旋桨和自由叶轮的2个圆柱的所有表面均设置为交界面,最大的圆柱的圆柱面设置为对称平面,最大的圆柱的靠近桨轴的圆柱面设为速度入口,并定义其速度幅值,最大的圆柱的靠近毂帽的圆柱面设为压力出口。由于螺旋桨是强制旋转的,需要设置其旋转速度和方向;而叶轮是自由旋转,采用DFBI自定义函数将其设置为绕桨轴的转动向自由运动。
4 模拟结果 4.1 水动力性能定义变量:
| $\begin{aligned} J=\frac{V_{A}}{n_{R} D_{R}}, & K_{T R}=\frac{T_{R}}{\rho n_{R}^{2} D_{R}^{4}}\end{aligned} $ |
| ${K_{QR}} = \frac{{{Q_R}}}{{\rho n_R^2D_R^5}}, \quad {\eta _R} = \frac{{{K_{TR}}}}{{{K_{QR}}}}\frac{J}{{2{\rm{ \mathit{ π} }}}} $ |
| $K_{T V R}=\frac{T_{V R}}{\rho n_{R}^{2} D_{R}^{4}}, \quad K_{Q V R}=\frac{Q_{V R}}{\rho n_{R}^{2} D_{R}^{5}} $ |
| ${\eta _{VR}} = \frac{{{K_{TVR}}}}{{{K_{QVR}}}}\frac{J}{{2{\rm{ \mathit{ π} }}}}, \quad {K_{TVV}} = \frac{{{T_{VV}}}}{{\rho n_R^2D_R^4}} $ |
| $K_{QVV}=\frac{Q_{VV}}{\rho n_{R}^{2} D_{R}^{5}}, \quad \eta_{VV}=\frac{K_{T V V}}{K_{Q V R}} \frac{J}{2 \pi} $ |
| ${\eta _V} = \frac{{{K_{TVR}} + {K_{TVV}}}}{{{K_{QVR}}}}\frac{J}{{2{\rm{ \mathit{ π} }}}} $ |
| ${C_p} = \frac{p}{{\frac{1}{2}\rho \left[ {V_a^2 + \left( {2{\rm{ \mathit{ π} }}{n_V}{R_V}} \right)} \right]}} $ |
式中:J为进速系数;VA为来流速度;nR和nV分别为为螺旋桨转速和自由叶轮转速;RR和RV分别为为螺旋桨半径和自由叶轮半径;ρ为流体密度;TR、QR、KTR、KQR、ηR分别为没有自由叶轮的螺旋桨的推力、转矩、推力系数、转矩系数、效率;TVR、QVR、KTVR、KQVR、ηVR分别为具有自由叶轮的螺旋桨的推力、转矩、推力系数、转矩系数、效率;TVV、QVV、KTVV、KQVV、ηVV分别为自由叶轮的推力、转矩、推力系数、转矩系数、附加效率;ηV为整个自由叶轮推进系统的效率;p为相对压力;Cp为压力系数[11-14]。
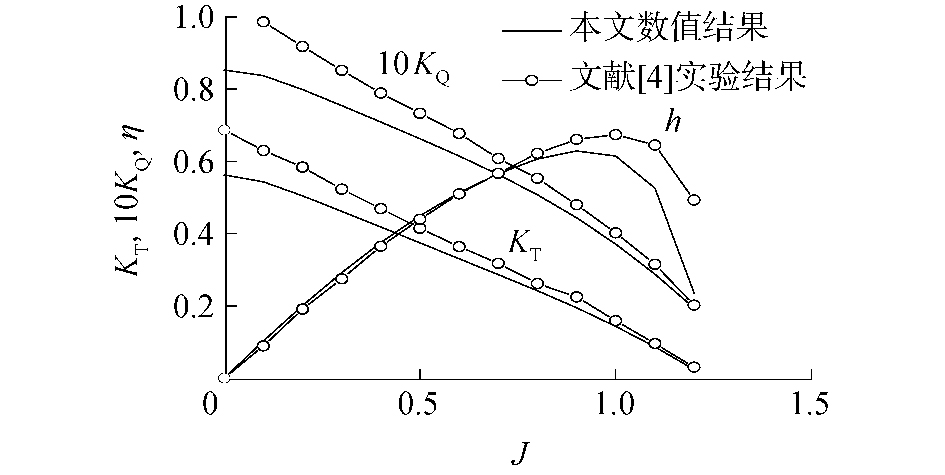
在额定功率下,螺旋桨转速nR为10.47 rad/s。为了获得额定功率下的螺旋桨敞水曲线,本文采用改变流体进速VA的方法计算了螺旋桨的敞水性能曲线并且与文献[4]实验结果进行了对比。通过图 4的对比结果可知:在进速系数较低的情况下推力系数和转矩系数的实验结果略大于本文的模拟结果,推进效率结果比较接近。在进速系数较高的情况下本文模拟的推力系数和转矩系数结果和实验结果比较接近,但是推进效率比实验结果低。
|
Download:
|
| 图 4 螺旋桨敞水性能 Fig. 4 Open water characteristics of the propeller | |
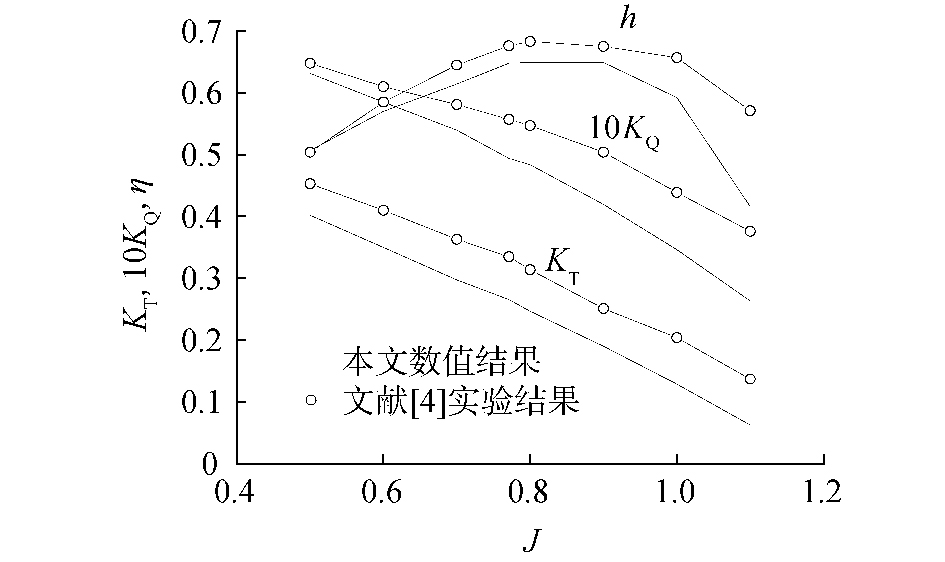
图 5给出了螺旋桨转速nR=10.47 rad/s时,通过改变来流速度,计算进速系数J为0.5、0.6、0.7、0.8、0.9、1.0、1.1时的螺旋桨+自由叶轮的敞水曲线。比较本文的数值结果和实验结果发现,通过STAR-CCM+计算所得到的结果相对于实验结果较低,在进速系数较低的情况下,推进效率比较接近,这是由于在螺旋桨+自由叶轮系统中,螺旋桨和自由叶轮附近流场的流动参数相差较大,且这些流动参数随着进速系数发生改变,这导致进速系数大幅度增加时会带来较大的误差,但数值模拟的结果在曲线基本特征规律上与实验结果吻合。
|
Download:
|
| 图 5 螺旋桨和自由叶轮的敞水性能曲线对比 Fig. 5 Open water performance of the propeller and vane wheel | |
在设计工况J=0.771,转速nR=10.47 rad/s的情况下进行数值模拟,对比单个螺旋桨和自由叶轮推进系统的推力系数、转矩系数、效率、数值模拟的结果见表 3。
| 表 3 J=0.771的数值模拟结果 Table 3 Results of J=0.771 |
表 3中,螺旋桨为自由叶轮系统中的螺旋桨,自由叶轮为自由叶轮系统中的自由叶轮,变化量为自由叶轮系统相对于单个螺旋桨的变化量,自由叶轮推进系统的推力为其螺旋桨和自由叶轮产生的推力的矢量和,转矩为其螺旋桨转矩。在进速系数J=0.771,转速nR=10.47 rad/s的情况下自由叶轮推进系统相比于单个螺旋桨推进系数增大5.43%、转矩系数减小3.85%、效率提高5.74%,并且自由叶轮推进系统中的螺旋桨的效率高于单个螺旋桨的效率。
本文中单个螺旋桨的数值结果和自由叶轮推进系统的数值结果对比见图 6。
|
Download:
|
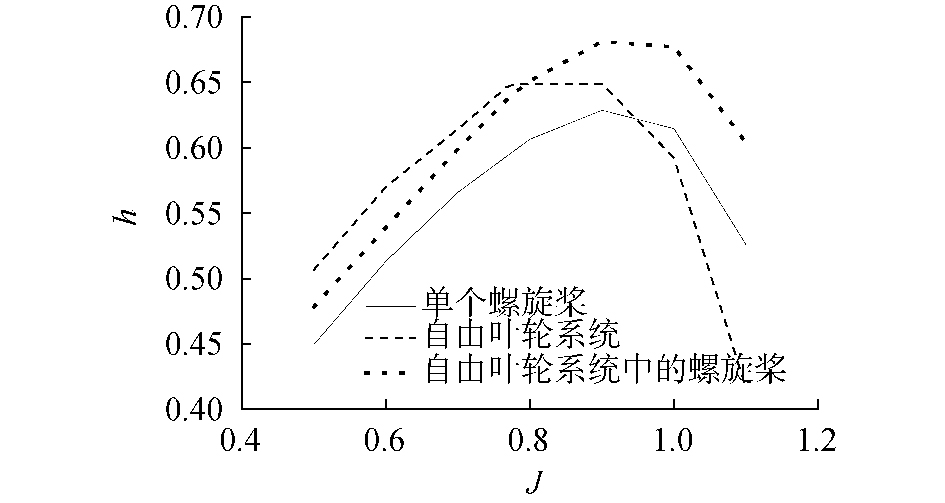
| 图 6 自由叶轮的节能效果 Fig. 6 Efficiency improved due to the vane wheel | |
通过图 6的结果对比可知:在进速系数较小时,自由叶轮外半径部分产生的附加推力大于内半径部分的阻力,整个自由叶轮产生额外的附加推力,所以自由叶轮推进系统的效率高于自由叶轮推进系统中的螺旋桨的效率。自由叶轮系统中的螺旋桨推力系数相对于单个螺旋桨变大,转矩系数相对于单个螺旋桨变小,导致自由叶轮推进系统中的螺旋桨的效率高于单个螺旋桨的效率。在进速系数较高时,自由叶轮由于内半径部分阻力急剧增大高于外半径部分的附加推力,使得整个自由叶轮产生阻力,所以自由叶轮推进系统的效率小于自由叶轮系统中螺旋桨的效率,随着进速系数进一步的增大,自由叶轮推进系统的效率比单个螺旋桨的效率还要低,不能达到节能的效果。相对于图 5中数值模拟结果与试验结果之间的误差随着进速系数增加而增大,图 6中的效率提升在所有进速系数下均非常明显,表明计算误差对图 6计算结果的影响较小。
4.2 自由叶轮与螺旋桨的相互干扰从4.1节可以看到,自由叶轮具有明显的节能效果,这种效果源自于螺旋桨和叶轮之间的有利干扰,本节将详细分析螺旋桨和自由叶轮之间的相互影响。同时,由于在数值计算过程中,假设螺旋桨转速从零瞬间增至10.47 rad/s,这会导致计算域中流体非物理的不真实流动。因此,非定常计算应该应该是一个逐渐收敛的过程。本节将展示螺旋桨和自由叶轮受力收敛的时历曲线。
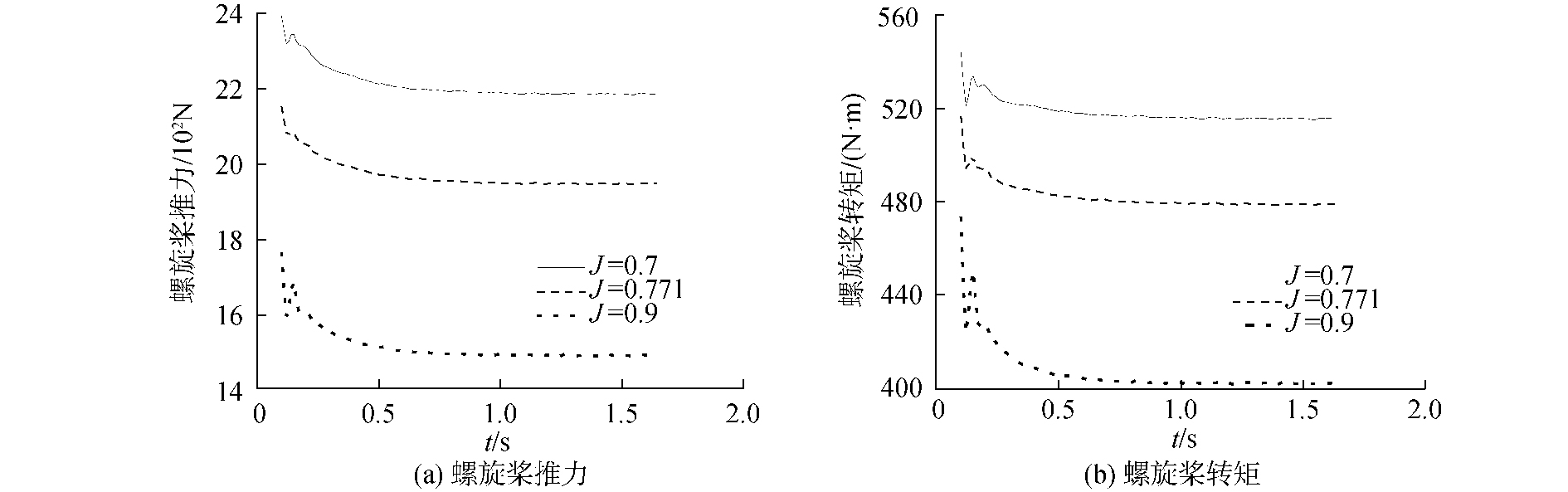
图 7给出了3个不同进速系数时自由叶轮推进系统中螺旋桨推力转矩的收敛过程。从中可以看出,螺旋桨的瞬时加速会导致其初期的推力很大,在0.1 s计算时间内震荡式下降,0.1~1.2 s时间内平滑下降,1.2 s以后结果趋于收敛。在不同的进速系数下,1.2 s左右基本上可以得到比较好的结果。进速系数为0.7、0.771和0.9时,螺旋桨的推力的收敛结果分别为2 168、1 948和1 493 N。而图 4中无自由叶轮的螺旋桨推力结果分别为2 144、1 887和1 459 N。由此可以看出自由叶轮使螺旋桨的推力分别增加了24、61和34 N。在进速系数J=0.771时,推力增加比较明显。
|
Download:
|
| 图 7 螺旋桨的推力和转矩 Fig. 7 Thrust and torque of propeller | |
在进速系数J=0.7时,螺旋桨的转矩最终的平均值为515.6 N·m,在进速系数J=0.771时,螺旋桨的转矩最终的平均值为479 N·m,在进速系数J=0.9时,螺旋桨的转矩最终的平均值为401.6 N·m。随着进速系数的增大,螺旋桨转矩随之减小。比较图 7(b)和图 4,可以看出3个不同进速时,自由叶轮推进系统中的螺旋桨转矩分别减小了4.53%、3.87%和5.57%。
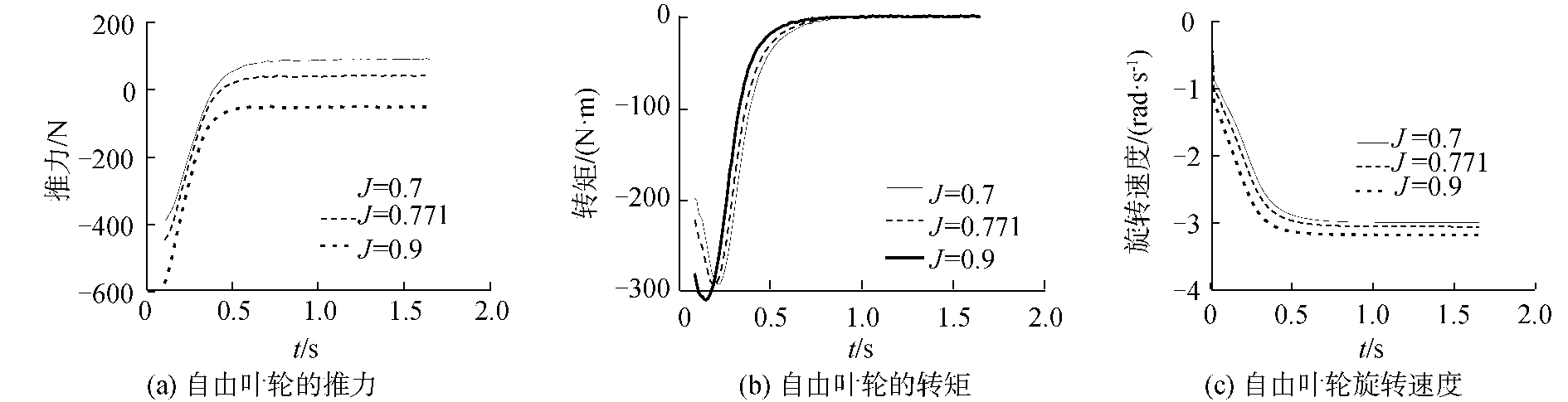
自由叶轮推进系统中自由叶轮的推力、转矩和转动速度结果如图 8所示。在进速系数J=0.7时,自由叶轮的推力的平均值为92 N,在进速系数J=0.771时,自由叶轮的推力的平均值为42 N,在进速系数J=0.9时,自由叶轮的推力的平均值为-51 N。由此可看出,随着进速系数的增加,自由叶轮的推力随之减小,当进速系数较大时,还会产生反向阻力。
|
Download:
|
| 图 8 自由叶轮的推力、转矩和旋转速度 Fig. 8 Thrust of vane wheel | |
叶轮在其旋转方向能够具有一个自由度的被动运动,这种运动是由螺旋桨产生尾流场引起的。由于自由叶轮的旋转并未被施加主动控制,因此其转矩应该为零。图 8(b)给出了J=0.7,0.771,0.9时,自由叶轮的转矩的计算结果。从中可以看出,不同螺旋桨进速系数下,自由叶轮的转矩均趋近于0,自由叶轮的基本工作原理可以从中得到验证。
自由叶轮的旋转速度结果如图 8(c)所示。在进速系数J=0.7时,自由叶轮的旋转速度最终收敛于2.99 rad/s,在进速系数J=0.771时,自由叶轮的旋转速度最终收敛于3.05 rad/s,在进速系数J=0.771时,自由叶轮的旋转速度最终收敛于3.17 rad/s,为螺旋桨旋转速度的30%左右,旋转方向从船艉方向看为顺时针。随着进速系数的增大,自由叶轮的旋转速度随之增大。
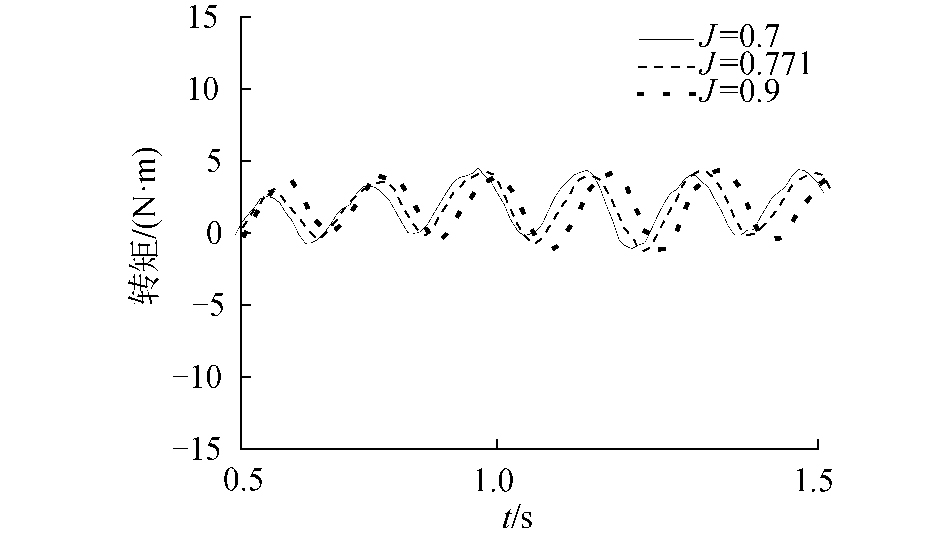
由于本文采用的是非定常计算,且螺旋桨的尾流场具有周向的周期性。因此自由叶轮的受力也应该具有周期性。以单个自由叶轮叶片的转矩为例,如图 9所示,当J=0.7,0.771,0.9时,单个自由叶轮叶片的转矩在时域内微幅震荡,其平均值分别为2.0、1.8和1.7 N·m。理论上讲,自由叶轮的转矩应该为0,但是螺旋桨尾流场的周向周期性会导致自由叶轮转速的周期性变化,从而具有一定的加速度,由此会导致一定的附加质量,且进速越小,螺旋桨载荷越大,自由叶轮的附加质量越大。
|
Download:
|
| 图 9 单个自由叶轮叶片的转矩 Fig. 9 Torque of single vane wheel′s blade | |
单个自由叶轮叶片的周期性是另一个值得讨论的问题。如图 9所示,在3个不同的进速系数下,叶片的转矩曲线具有一定的相位差。螺旋桨的转速nR虽然稳定在10.47 rad/s,但是随着进速系数的降低,螺旋桨的载荷变大,由此导致自由叶轮的转速增加,这是相位差产生的原因。经过简单的理论推导可以得到,叶片转矩的变化周期$T = \frac{1}{{\left({{n_R} - {n_V}} \right){K_R}}}$,式中:KR是螺旋桨的叶数,nR是螺旋桨的转速,nv是自由叶轮的转速。图 8(c)给出了自由叶轮的转速nv分别为2.99、3.05和3.17 rad/s通过该式得到的旋转周期分别为0.168、0.169和0.172 s和图 9中的周期性一致。
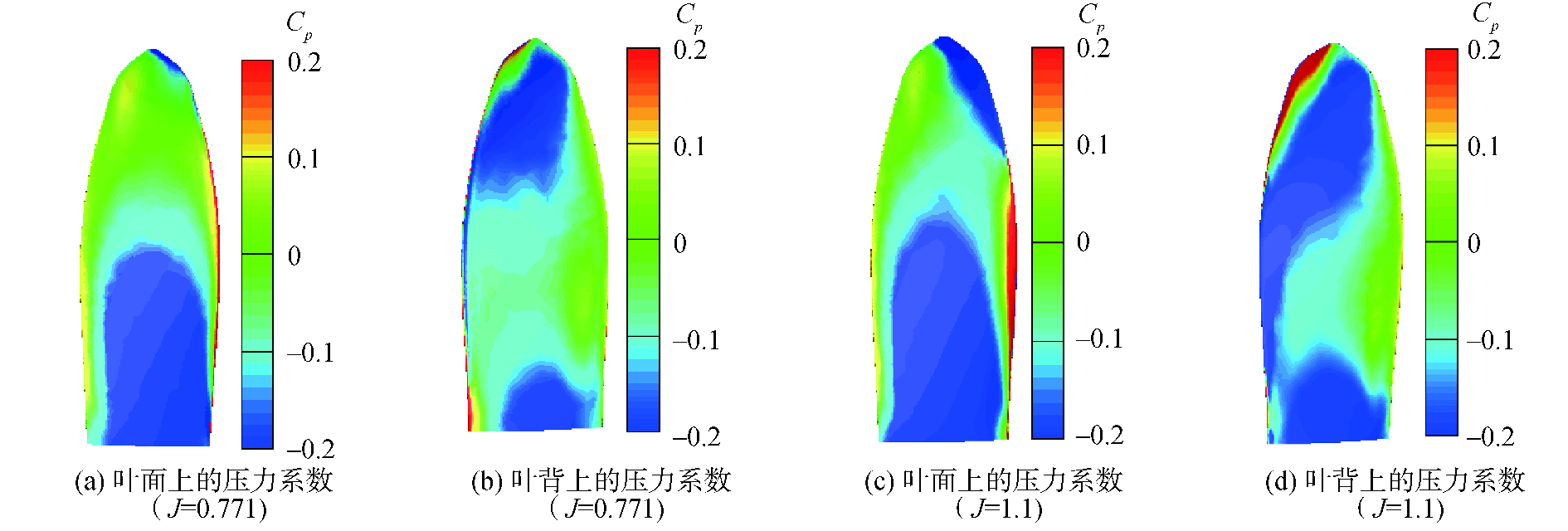
内半径为水轮机式功率吸收结构,外半径为螺旋桨式功率发出结构。通过这种独特的设计,自由叶轮能够吸收螺旋桨尾流场的旋转能量并将其转化为推力。图 10给出了J=0.771和J=1.1时自由叶轮叶片受力的计算结果。从图 10可以看出,自由叶轮的内半径压力小,外半径压力大;叶背的压力分布趋势恰好相反。这体现了自由叶轮的基本工作原理,即通过水轮机式的内半径结构吸收螺旋桨尾流场能量,并通过螺旋桨式的外半径结构将其转化为推力。但是当进速系数增加到1.1时,虽然叶面的外半径仍然能够提供一定的推力,但是叶背的外半径也会产生很大的阻力,此时自由叶轮不再具备节能效果。由此可以看出,自由叶轮更适合于重载荷螺旋桨。
|
Download:
|
| 图 10 叶轮表面压力系数 Fig. 10 Coefficient of the surface pressure on the blade | |
1) 自由叶轮推进系统在该螺旋桨的额定功率条件下,即进速系数J=0.771,螺旋桨旋转速度nR等于10.47 rad/s的情况下,自由叶轮推进系统效率提高5.74%,效果明显。
2) 在一定的进速范围之内,自由叶轮的推进效率高于单个螺旋桨,但是在较大的进速系数下,自由叶轮的推进效率会出现下降,甚至会出现在效率低于单个螺旋桨的情况。
| [1] |
郭春雨, 赵庆新, 吴铁成, 等. 船舶附加水动力组合节能技术研究进展[J]. 舰船科学技术, 2014, 36(4): 1-10. GUO Chunyu, ZHAO Qingxin, WU Tiecheng, et al. Research and development of marine hydrodynamic compounded energy-saving[J]. Ship science and technology, 2014, 36(4): 1-10. DOI:10.3404/j.issn.1672-7649.2014.04.001 (  0) 0)
|
| [2] |
吴明远. 补偿导管节能效果CFD数值模拟研究[J]. 中国船检, 2014(9): 76-79. DOI:10.3969/j.issn.1009-2005.2014.09.022 (  0) 0)
|
| [3] |
程枳宁, 陈正寿, 黄聪汉, 等. 船舶附加水动力节能装置研究进展[J]. 浙江海洋学院学报(自然科学版), 2016, 35(1): 70-75. CHENG Zhining, CHEN Zhengshou, HUANG Conghan, et al. Research progress about additional hydrodynamic energy-saving devices of ships[J]. Journal of Zhejiang Ocean University (natural science), 2016, 35(1): 70-75. DOI:10.3969/j.issn.1008-830X.2016.01.015 (  0) 0)
|
| [4] |
CHEN B Y, REED A M, KIM K H. A vane-wheel propulsor for a naval auxiliary[R]. Bethesda, MD: David Taylor Research Center, 1989.
(  0) 0)
|
| [5] |
郭永松, 郭宏宇, 奚志道, 等. 船舶推进节能研究——导轮的理论设计和实验[J]. 交通部上海船舶运输科学研究所学报, 1990, 13(1): 8-17. GUO Yongsong, GUO Hongyu, XI Zhidao, et al. Study on ship propulsion energy-saving——design theory and test on vane wheel[J]. Journal of SSSRI, 1990, 13(1): 8-17. (  0) 0)
|
| [6] |
侯立勋, 胡安康, 汪春辉, 等. 桨后自由叶轮理论设计方法研究[J]. 船舶力学, 2015, 19(8): 905-911. HOU Lixun, HU Ankang, WANG Chunhui, et al. Theoretical design method investigation of vane wheel after propeller[J]. Journal of ship mechanics, 2015, 19(8): 905-911. DOI:10.3969/j.issn.1007-7294.2015.08.003 (  0) 0)
|
| [7] |
SEOK W C, SUH J C. Algorithm for performance analysis of vane-wheel using panel method[J]. Journal of the society of naval architects of Korea, 2013, 50(4): 248-254. DOI:10.3744/SNAK.2013.50.4.248 (  0) 0)
|
| [8] |
吴建威, 尹崇宏, 万德成. 基于三种方法的螺旋桨敞水性能数值预报[J]. 水动力学研究与进展, 2016, 31(2): 177-187. WU Jianwei, YIN Chonghong, WAN Decheng. Numerical prediction of the propeller open-water performance based on three numerical methods[J]. Chinese journal of hydrodynamics, 2016, 31(2): 177-187. (  0) 0)
|
| [9] |
周胡, 万德成. 不同叶片数的风力机绕流场的非定常流数值模拟[J]. 水动力学研究与进展, 2014, 29A(4): 444-453. ZHOU Hu, WAN Decheng. Numerical simulation of the unsteady flow around wind turbines with different blades numbers[J]. Chinese journal of hydrodynamics, 2014, 29A(4): 444-453. (  0) 0)
|
| [10] |
赵文超, 万德成. 海上浮式风力机叶片气动性能的数值模拟[J]. 水动力学研究与进展, 2014, 29A(6): 663-669. ZHAO Wenchao, WAN Decheng. Numerical simulation of aerodynamic characteristics of floating offshore wind turbine blades[J]. Chinese journal of hydrodynamics, 2014, 29A(4): 663-669. (  0) 0)
|
| [11] |
王波, 张以良, 熊鹰. 船用螺旋桨水动力性能优化设计[J]. 武汉理工大学学报(交通科学与工程版), 2015, 39(4): 773-777. WANG Bo, ZHANG Yiliang, XIONG Ying. Design and optimization of hydrodynamic performance of marine propeller[J]. Journal of Wuhan University of Technology (transportation science & engineering), 2015, 39(4): 773-777. DOI:10.3963/j.issn.2095-3844.2015.04.022 (  0) 0)
|
| [12] |
张赫, 崔和. 面元法预估导管螺旋桨水动力性能[J]. 水雷战与舰船防护, 2013, 21(3): 33-37. ZHANG He, CUI He. Predicting hydrodynamic performance of ducted propeller using surface panel method[J]. Mine warfare & ship self-defence, 2013, 21(3): 33-37. (  0) 0)
|
| [13] |
苏玉民, 冯君, 刘业宝, 等. 基于速度势迭代的面元法预报对转桨性能[J]. 船舶工程, 2015, 37(1): 50-53. SU Yumin, FENG Jun, LIU Yebao, et al. Surface panel method based on potential iteration to predict the performance of contra-rotating propeller[J]. Ship engineering, 2015, 37(1): 50-53. (  0) 0)
|
| [14] |
孙文愈, 黄国富. 螺旋桨性能分析与优化设计中桨毂的影响分析[J]. 中国造船, 2016, 57(1): 19-30. SUN Wenyu, HUANG Guofu. Hub effect in propeller performance analysis and optimal design[J]. Shipbuilding of China, 2016, 57(1): 19-30. DOI:10.3969/j.issn.1000-4882.2016.01.003 (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


