2. 大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
海洋面积占地球表面积的71%,它不仅为人类提供航运、水产和丰富的矿藏,而且蕴含着大量的能量。海洋能主要包括波浪能、潮汐能、海洋温差能、海洋盐差能和海流能等,其中波浪能作为海洋可再生能源的重要组成部分,其合理开发利用对我国海洋经济的发展具有重要意义。
近年来,振荡水柱式波能转换装置(oscillating water column, OWC)已被广泛应用于波能发电领域。波浪能主要以动能和势能的形式在振荡水柱式波浪能发电装置内完成能量的转移和转换,最终被捕获转化为电能的主要是气室内水柱振荡带来的势能变化。由于波况不同的条件下,气室形状参量对捕能效果有一定影响,需对气室加以研究并对其形状参量进行优化,从而使空气流速和能量转换达到最大值。国内外学者对传统OWC波能装置的水动力特性和能量输出特性开展了广泛研究[1]。早期OWC结构的理论研究中,Evans[2-3]提出了OWC的波能转换理论,给出了物体振荡时波吸收效率的表达式,并提出实现100%效率的可能性。Boccotti等[4]对沉箱防波堤作为OWC装置进行了理论推导,并完成了相关物理试验研究,证明了其可行性。
为提高OWC装置的波能转换效率,一些学者提出了新型的结构型式。Ambli等[5]提出了一种多共振振荡水柱装置(multi-resonant oscillating water column),利用港口效应使入射波与前港和气室内水柱产生共振,获得聚波作用。Malara等提出一种新型U-OWC沉箱防波堤结构型式,并结合物模试验与数值模拟验证了结构形式的可靠性;Boccotti[6-15]开展了新型U-OWC沉箱防波堤的波能转化系数研究,并利用物模试验证明了该结构型式的稳定性,结果表明,与传统的OWC相比,U-OWC装置增加了垂直的前墙,其通过调整作用在防波堤上的波浪峰值周期以达到共振条件,从而提高了波浪能的转换效率。
已有的研究表明U-OWC波能装置的波浪能转化效率高于OWC。与OWC相比,U-OWC相当于是在OWC基础上增加了一个倾角为90°的前墙,前墙倾角的变化改变了进入捕能气室的流体流态,进而提高了装置的波浪能转换效率。因此探索在前墙倾角变化过程中,是否存在更佳倾角对应气室内更高的相对波高是进一步提升U-OWC装置波浪能转换效率的可行途径。同时考虑在波浪进入气室过程中,气室通道的棱角可能会导致能量损耗,因此在气室内增加圆弧底面,减少波浪在经过气室通道时的动能损失,进而提高气室内捕能效率也是一个提高波浪能转换效率的可行途径。为此,本文基于数值模拟方法,针对U-OWC波能装置气室内波高的影响因素开展研究。基于不可压缩粘性流体理论和流体体积(volume of fluid, VOF)方法,应用STAR-CCM+软件平台,建立二维数值波浪水槽模型,探索前墙倾角、气室内底面形状、波面非线性等因素对U-OWC气室内相对波高的影响规律。
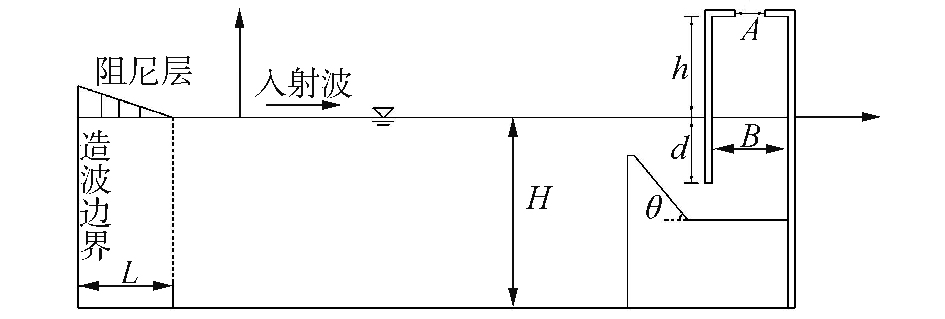
1 数值模型 1.1 CFD模型本文基于不可压粘性流体理论和有限元的方法,应用STAR-CCM+软件平台建立了二维数值波浪水槽并采用VOF方法处理自由液面。二维数值波浪水槽的示意图见图 1,选取静水面y=0为垂直坐标面,H表示水深、A表示气室开口宽度、B表示气室宽度、d表示入水深度、h表示气室内空气柱高度、L表示消波区长度、θ表示前墙倾斜角度。在气室中间和前墙前侧布置波高仪来监测波面变化。计算域在x方向上的长度通常取为波长Lw的6倍,y方向上的高度由水深H决定,消波区长度取1.5倍波长,采用力法消波,如图 2所示。
|
Download:
|
| 图 1 二维数值波浪水槽示意 Fig. 1 Two-dimensional numerical wave sink schematic | |

|
Download:
|
| 图 2 数值造波示意 Fig. 2 Numerical wave diagram | |
由于STAR-CCM+软件无法构建纯二维平面模型,因此将z方向上的模型宽度设置为一层网格。二维无反射数值波浪水槽模型控制方程为连续性方程和动量方程,分别为:
| $\nabla \cdot \boldsymbol{u}=0 $ | (1) |
| $\left\{\begin{array}{l}{\frac{\partial(\rho u)}{\partial t}+\nabla \cdot(\rho u \boldsymbol{u})=-\frac{\partial P}{\partial x}+\frac{\partial \tau_{x x}}{\partial x}+\frac{\partial \tau_{y x}}{\partial y}+\frac{\partial \tau_{z x}}{\partial z}+F_{x}} \\ {\frac{\partial(\rho v)}{\partial t}+\nabla \cdot(\rho v \boldsymbol{u})=-\frac{\partial P}{\partial y}+\frac{\partial \tau_{x y}}{\partial x}+\frac{\partial \tau_{y y}}{\partial y}+\frac{\partial \tau_{z y}}{\partial z}+F_{y}} \\ {\frac{\partial(\rho w)}{\partial t}+\nabla \cdot(\rho w \boldsymbol{u})=-\frac{\partial P}{\partial z}+\frac{\partial \tau_{x z}}{\partial x}+\frac{\partial \tau_{y z}}{\partial y}+\frac{\partial \tau_{z z}}{\partial z}+F_{z}}\end{array}\right. $ | (2) |
式中:P为微元体上的压力; τxx、τxy、τxz表示粘性应力在微元体上的分量; Fx、Fy、Fz表示微元体的体力,一般情况下体力只有重力,重力沿y轴负向Fy=-ρg。
自由水面的追踪采用VOF方法[10]。在包含水与空气的空间网格单元中,定义水的体积份额为αw,具体可分为以下3种情况:若αw=0,单元为气相单元;若αw=1,单元为水相单元;若0<αw<1,单元为自由面单元,既包含空气,又包含水。体积份额函数αw满足守恒方程:
| $\frac{\partial \alpha_{w}}{\partial t}+\frac{\partial\left(\alpha_{w} u_{i}\right)}{\partial x_{i}}=0 $ | (3) |
式中:αw为体积份额函数; xi、ui分别为坐标轴的方向和速度在该方向的分量; t为时间。
1.2 边界条件设置和网格划分入口边界条件设置为速度入口,入口面速度矢量指定为五阶VOF波的速度,有效流体设定为水和空气的两相流。为了使模拟更加真实且能保持模型的二维性,下底面边界和装置均设置为壁面,前后侧面设置为对称平面。上部边界设置为压力出口,其中压力指定为五阶VOF波的静压力,流体组成成分是空气。五阶VOF波的速度为[12]:
| $U = \frac{{\partial \mathit{\Phi }}}{{\partial X}}, \quad W = \frac{{\partial \mathit{\Phi }}}{{\partial Z}} $ | (4) |
式中:
| $\mathit{\Phi }(X, Z, t)=(c-\bar{u}) X+\\ C_{0}(^) 1 / 2 \sum\limits_{i=1}^{5} \varepsilon^{i} \sum\limits_{j=1}^{i} A_{i j} \cos (h j k) Z \sin [j k(X-c t)] $ | (5) |
| $\bar{u}\left(\frac{k}{g}\right)^{1 / 2}=1+\frac{1}{2} \varepsilon^{2}+\frac{1}{8} \varepsilon^{4}+O\left(\varepsilon^{6}\right) $ | (6) |
五阶VOF波的静压力为[12]:
| $\frac{p(X, Z, t)}{\rho}=R-g Z-\frac{1}{2}\left[(U-c)^{2}+W^{2}\right] $ | (7) |
式中:X和Z分别是大地坐标系中的水平坐标和垂直坐标;Φ为速度势;c为波速;C0和Aij是一系列系数;k是波数;ε=kH/2是无量纲波振幅;g为重力加速度;ρ为流体密度。
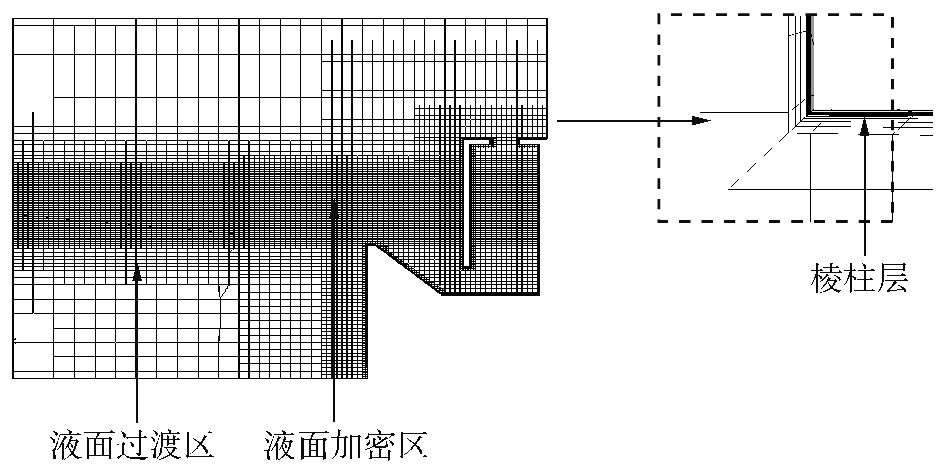
在本文中,网格的划分主要分为以下几个区域:液面加密区域、液面过渡区域和棱柱层,如图 3所示。这几个区域的网格选用切割体网格单元生成器来生成。此外,应用表面重构和棱柱层网格生成器在装置表面生成棱柱层,以便更好地捕捉物面周围的流场变化。
|
Download:
|
| 图 3 网格划分示意 Fig. 3 Schematic diagram of meshing | |
在应用CFD模型进行研究之前,需要进行数值计算模型验证,包括收敛性验证和准确性验证。
2.1 波浪水槽收敛性验证为检验本文数值波浪水槽的可靠性,首先对无结构物矩形平底水槽进行了收敛性验证。本研究中计算域长度取6倍波长距离,水槽长18 m、水深0.5 m,入射波波高0.1 m,周期为1.5 s。水槽两端均布置长度为1.5 m的阻尼层。针对波浪周期为1.5 s的设计波况,选取时间步长分别为0.001 5 s(波浪周期的1/1 000)和0.000 75 s(波浪周期的1/2 000)的2种时间步长进行对比;为了更准确地模拟自由水面的情况,对水气交界面处的网格进行了加密,选取y方向网格尺寸分别为0.005 m(波高的1/20)和0.002 5 m(波高的1/40),模型设置如表 1所示。表 1中,Δt为时间步长,Δz为网格尺寸,T为周期,h0为波高。
| 表 1 空域收敛性验证模型设置 Table 1 Airspace convergence verification model setting |
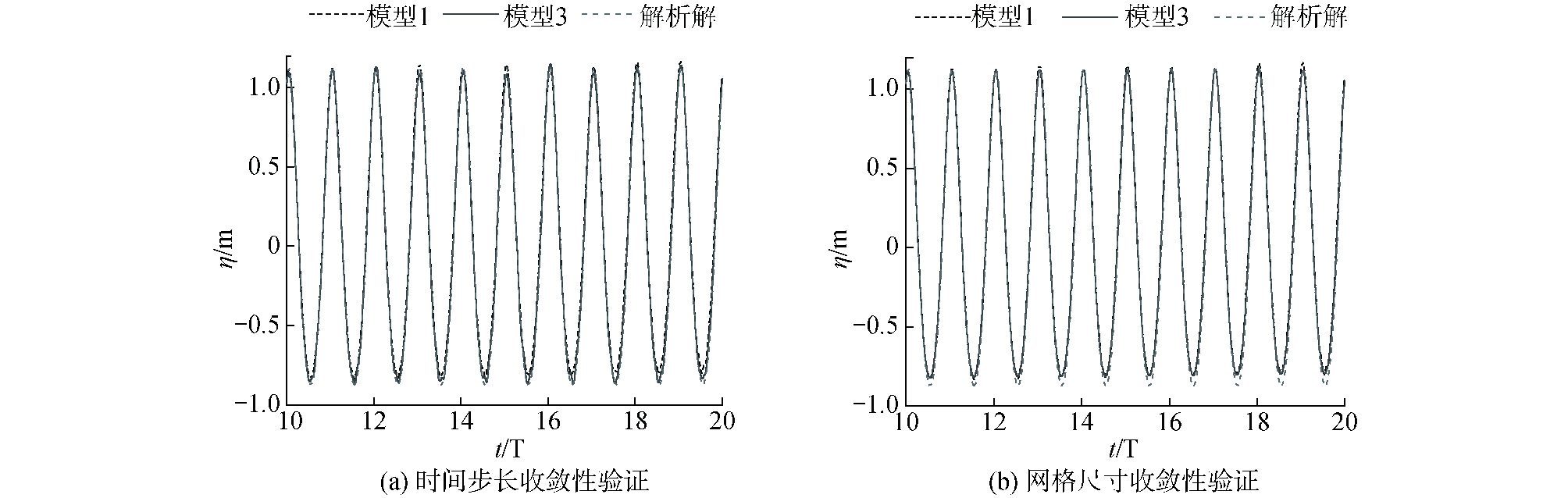
收敛性验证结果如图 4所示。图 4(a)、(b)分别给出了空域时间步长和网格尺寸收敛性验证时,数值模型计算结果和解析解的对比图。从图 4中可以看出,本文选择的数值模型在模拟过程中波面的稳定性较好,数值模型计算结果与解析解的数值结果吻合良好,模型1的参数设置可用于后续计算。
|
Download:
|
| 图 4 空域收敛性验证 Fig. 4 Airspace convergence verification | |
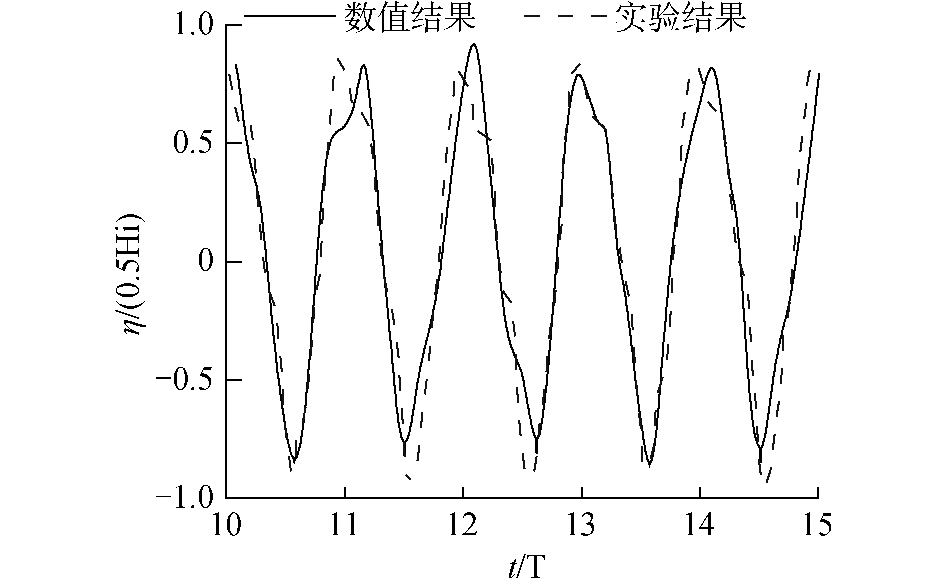
很多已发表文献用数值模拟和物理模型实验方法对OWC波能装置进行了研究,为了验证数值模型的准确性,本文对比计算了文献[12]中研究OWC气室模型的相应工况。取计算域长度68 m,高度1.8 m,水深0.8 m,模型放置在水槽一端,造波端设置长为1.5 m的阻尼层,OWC模型气室宽度0.55 m,气孔宽度0.06 m,并取入射波周期1.423 s,入射波高0.06 m,时间步长为T/1 000,停止时间为40 s。数值模拟计算结果与文献中实验数据对比如图 5所示。由图可知,数值计算结果与文献中物理模型实验结果吻合良好,数值结果的平均相对波高为0.168 m,实验结果的平均相对波高为0.17 m,两者相差不到5%,满足准确性要求,因此本文所选用的数值计算模型可以较为准确地进行数值模拟。
|
Download:
|
| 图 5 OWC数值模型验证 Fig. 5 OWC numerical model verification | |
与传统的OWC相比,U-OWC由于装置前方直墙的存在,能量俘获效率可得到显著提升[15]。为了进一步优化U-OWC波能装置,本文对具有倾斜前墙的U-OWC波能装置开展研究,分析了波浪周期、波面非线性、气室前墙倾角、内底面形状和入水深度对气室内相对波高的影响。
3.1 前墙倾角对U-OWC波能装置气室内波高影响振荡水柱波能装置气室的能量俘获效率主要受气室内波面振荡幅度、气室内压强等因素影响,在水深一定的情况下,振荡水柱波能装置的气室结构型式决定着气室内部流体的水动力特性。本文在U-OWC的基础上,通过改变气室前墙倾斜角度,得到前墙倾斜的U-OWC结构,装置前墙倾斜角度分别设置为30°、45°、60°、75°。
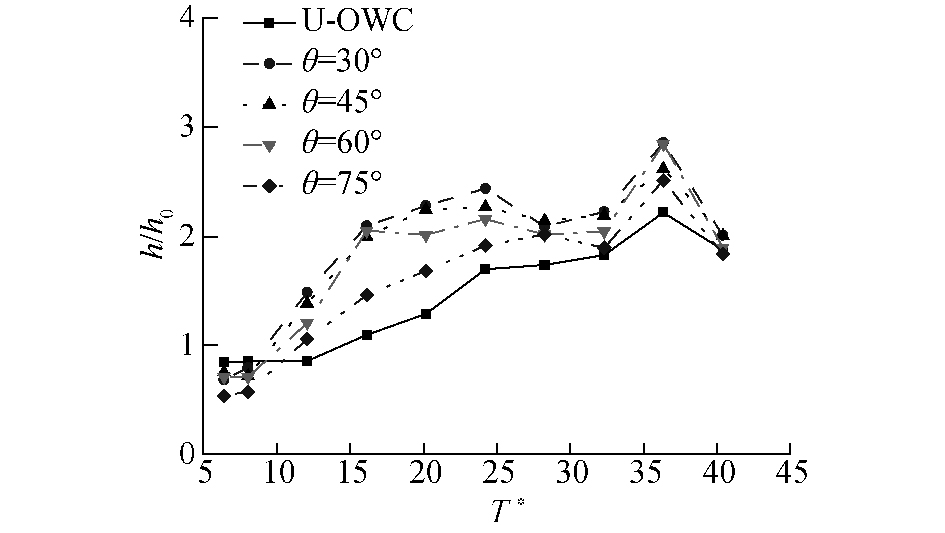
对比实验采用控制变量法,即保证单一变量,其他工况参数保持不变。由于本文研究的气室为开敞式,故不研究气室内压强变化情况,只研究气室内波面振荡幅度,大小用相对波高h/h0来表征。计算选择的波浪参数范围如下:水深为0.5 m,波浪周期范围为0.8~5.5 s,入射波高分别为0.07、0.10、0.12、0.15 m,计算域长为6倍波长,消波段长度为1.5倍波长,计算域高度为1 m,静水面位于y=0 m。为精确捕捉波形变化,网格加密区为波高的1.5倍左右,单周期划分1 000个时间步,计算时长取30个周期。计算并对比分析不同周期波浪作用下,气室前墙倾斜角度对气室内相对波高的影响规律。图 6给出了具有不同前墙倾斜角度的波能装置,气室内相对波高随无量纲入射波周期变化的对比结果,其中θ为气室前墙倾斜角度,
|
Download:
|
| 图 6 前墙倾角对相对波高的影响规律 Fig. 6 Influence of the inclination of the front wall on the relative wave height | |
由图可知,在高频区(T*<15)范围内,前墙有倾角的U-OWC波能装置气室内相对波高与传统OWC波能装置气室内相对波高相差较小;在低频区(T*>15)范围内,前墙有倾角的U-OWC波能装置气室内相对波高更高,且相对波高最高值为前墙倾角为30°的装置。以T*=27为分界线,左右区间均呈现随波浪周期增大,相对波高先增大再减小的趋势,且整体呈现出2个峰值。当T*<27时,前墙有倾角的U-OWC装置气室内相对波高随倾角的增大而减小,当T*>27时,前墙倾角为30°和60°的U-OWC装置气室内相对波高差别较小,且都大于前墙倾角为45°和75°的U-OWC装置。
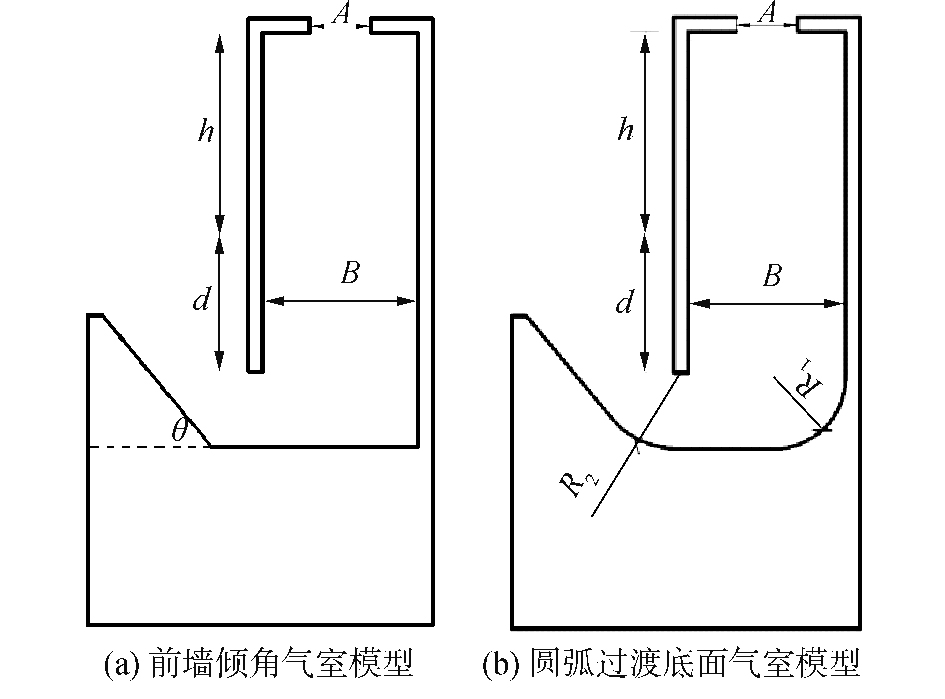
3.2 气室内底面形状影响为降低波能损失,进一步提高带前墙倾角的U-OWC波能装置的能量俘获效率,在前面得到的波能装置的基础上,在气室内底面增加圆弧过渡面,如图 7(b)所示,其中气室宽度为0.15 m、入水深度为0.19 m、气室内空气柱高度为0.17 m。
|
Download:
|
| 图 7 带前墙倾角的U-OWC波能装置示意 Fig. 7 Schematic diagram of U-OWC wave energy device with front wall inclination | |
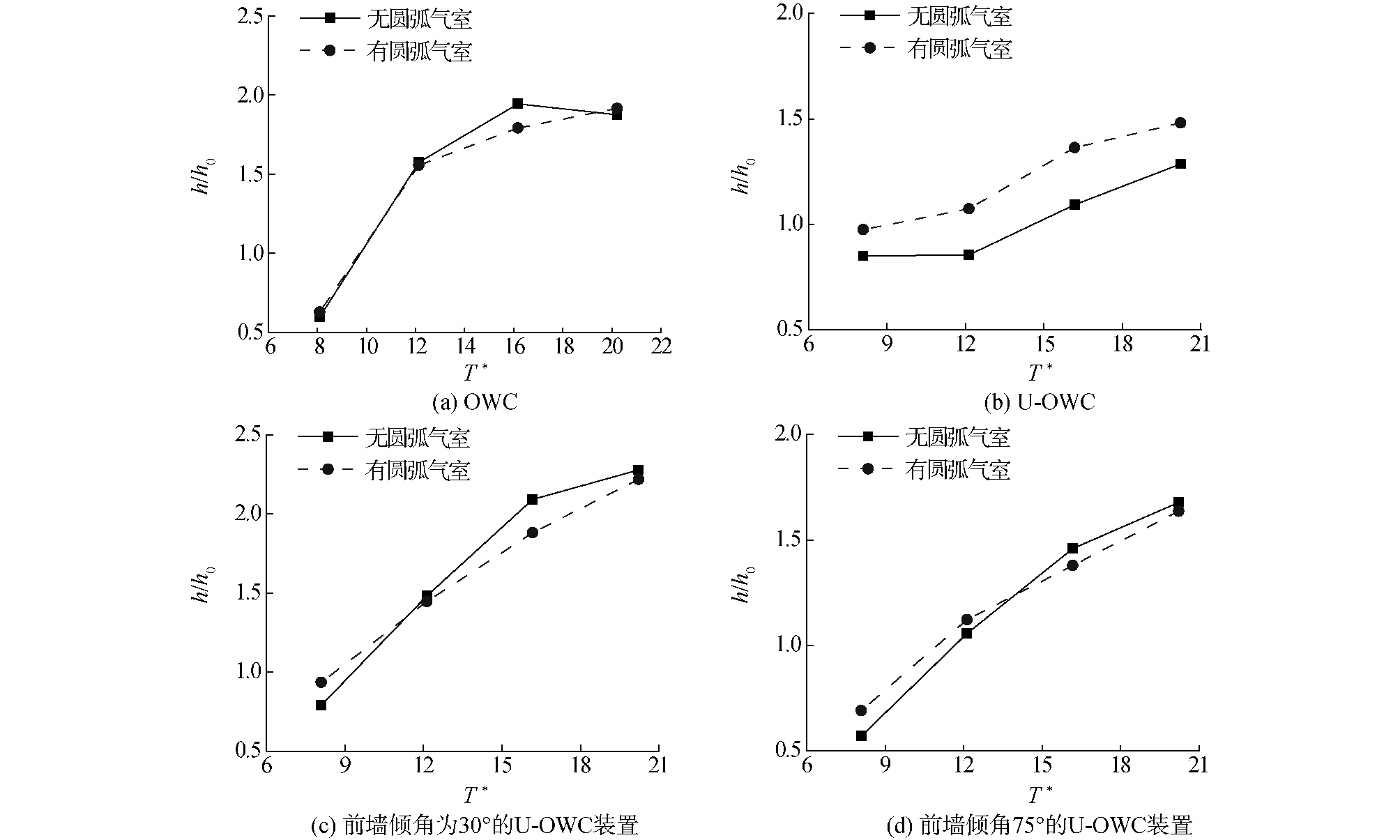
在周期为1.0~2.5 s的波浪范围内,计算并比较气室内底面形状对气室内部相对波高的影响。OWC、U-OWC、前墙倾角为30°和75°的U-OWC装置的计算结果分别如图 8所示。
|
Download:
|
| 图 8 有无圆弧过渡面装置气室内相对波高对比 Fig. 8 Relative wave height contrast in gas chamber with or without arc transition surface device | |
由图 8(a)、(b)可知,对于OWC模型,在气室内底面增加圆弧对气室内相对波高的大小几乎没有影响,而对于U-OWC模型,气室内底面增加圆弧可以增大气室内相对波高。由图 8(c)、(d)可知,在高频区(T*<12),气室内底面增加圆弧可以增大气室内部相对波高,而在低频区(T*>12),增加圆弧后相对波高减小。
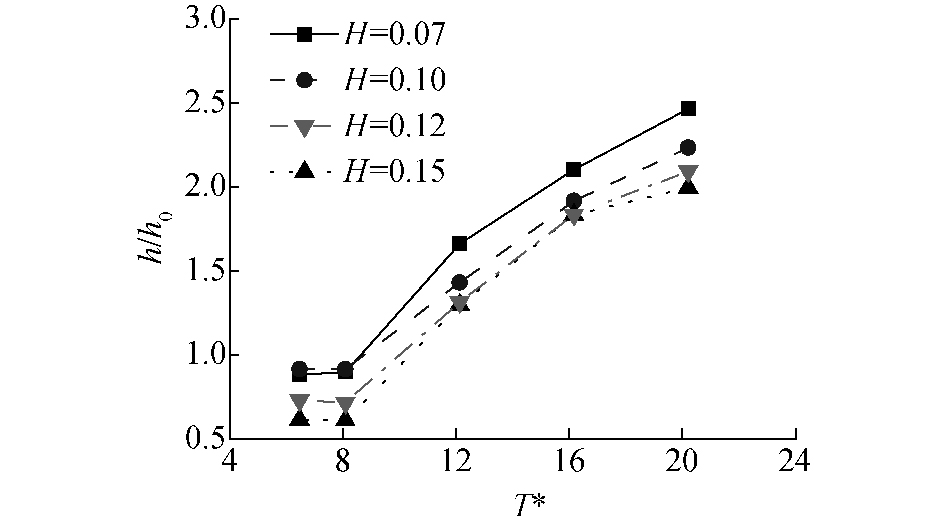
3.3 波面非线性的影响针对前墙倾角为45°的波能装置,改变入射波高,探究波面非线性对气室内相对波高的影响规律,计算结果如图 9所示。
|
Download:
|
| 图 9 波面非线性对相对波高的影响规律 Fig. 9 Influence of wavefront nonlinearity on relative wave height | |
由图 9可知,随着入射波高增大,前墙倾角为45°的波能装置气室内部相对波高减小,但当波高大于0.12 m时,随着波高的增加,装置气室内部相对波高在T*>12范围变化很小。可见,前墙倾角为45°的波能装置在非线性较强的波浪条件下的捕能效果较差,当入射波高增大到一定程度后,其对气室内相对波高的影响会减弱。
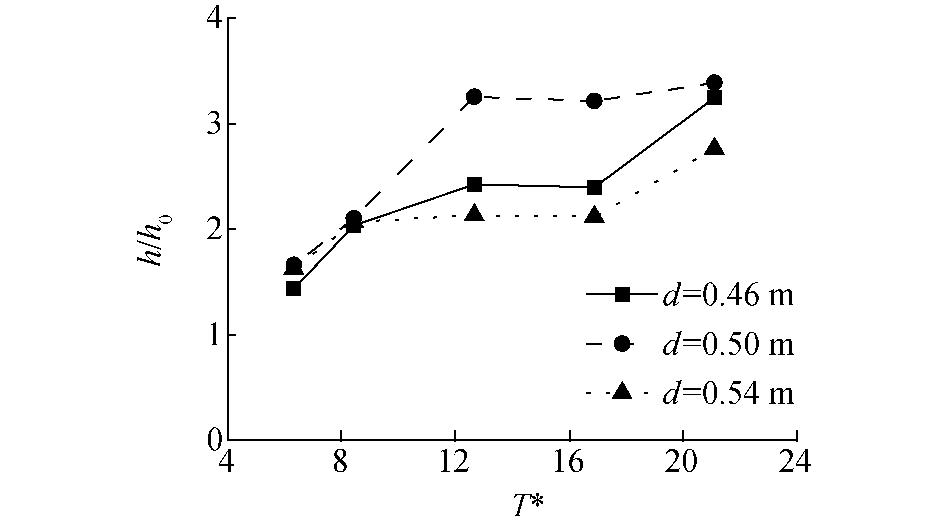
3.4 气室入水深度的影响为探究装置气室入水深度对水动力性能的影响律,针对前墙倾角为45°的波能装置,采用控制变量法开展研究,气室完全开敞,入射波高为0.07 m,波浪周期范围1.0~2.5 s,选取入水深度d分别为0.46、0.50、0.54 m 3组工况对比分析,计算结果如图 10所示。
|
Download:
|
| 图 10 入水深度对相对波高的影响规律 Fig. 10 Influence of draft depth on relative wave height | |
由图 10可知,随着T*的增大,不同入水深度的装置气室内波高都呈现出增大的趋势。在T*>8.44时,入水深度为0.5 m的装置气室内相对波高最高,入水深度为0.54 m的装置气室内相对波高最低;在T* < 8.44时,不同入水深度的装置内气室波高相差较小。
4 结论1) 与传统OWC装置相比,在低频区(T*>15)范围内,前墙倾斜的U-OWC波能装置气室内相对波高更高,且当T*<27时,前墙有倾角的U-OWC装置气室内相对波高随倾角的增大而减小,当T*>27时,前墙倾角为30°和60°的U-OWC装置气室内相对波高差别较小,且都大于前墙倾角为45°和75°的U-OWC装置,前墙倾斜的U-OWC波能装置最优倾角约为30°。
2) 波浪周期对前墙倾角U-OWC波能装置的影响较大,以T*=27为分界线,左右区间均呈现随波浪周期增大,相对波高先增大再减小的趋势,且整体呈现出2个峰值。
3) 气室内底面增加圆弧对前墙倾斜的U-OWC装置气室内相对波高影响较小,高频波作用下,可以增大气室内相对波高。
4) 波面非线性增大,前墙倾角U-OWC波能装置内相对波高减小,当波面非线性增大到一定程度后,随着波高的增加,装置气室内部相对波高变化很小。
5) 在波浪周期较大时,入水深度为0.5 m的装置气室内相对波高最高,入水深度为0.54 m的装置气室内相对波高最低;在波浪周期较小时,不同入水深度的装置内气室波高相差较小。
| [1] |
FALCÃO A F O, HENRIQUES J C C. Oscillating-water-column wave energy converters and air turbines: a review[J]. Renewable energy, 2016, 85: 1391-1424. DOI:10.1016/j.renene.2015.07.086 (  0) 0)
|
| [2] |
EVANS D V. A theory for wave-power absorption by oscillating bodies[J]. Journal of fluid mechanics, 1976, 77(1): 1-25. DOI:10.1017/S0022112076001109 (  0) 0)
|
| [3] |
EVANS D V. The oscillating water column wave-energy device[J]. IMA journal of applied mathematics, 1978, 22(4): 423-433. DOI:10.1093/imamat/22.4.423 (  0) 0)
|
| [4] |
BOCCOTTI P, FILIANOTI P, FIAMMA V, et al. Caisson breakwaters embodying an OWC with a small opening—Part Ⅱ: a small-scale field experiment[J]. Ocean engineering, 2007, 34(5/6): 820-841. DOI:10.1016/j.oceaneng.2006.04.016 (  0) 0)
|
| [5] |
AMBLI N, BØNKE K, MALMO O, et al. The Kvarner multiresonant OWC[C]//Proceedings of the 2nd International Symposium on Wave Energy Utilization. Trondheim, Norway, 1982: 275-297.
(  0) 0)
|
| [6] |
BOCCOTTI P. Design of breakwater for conversion of wave energy into electrical energy[J]. Ocean engineering, 2012, 51: 106-118. DOI:10.1016/j.oceaneng.2012.05.011 (  0) 0)
|
| [7] |
BOCCOTTI P. Comparison between a U-OWC and a conventional OWC[J]. Ocean engineering, 2007, 34(5/6): 799-805. (  0) 0)
|
| [8] |
BOCCOTTI P. On a new wave energy absorber[J]. Ocean engineering, 2003, 30(9): 1191-1200. DOI:10.1016/S0029-8018(02)00102-6 (  0) 0)
|
| [9] |
孙建群, 姜鹏宇, 宋春辉, 等. 规则波作用下多模块浮桥的水动力性能试验[J]. 哈尔滨工程大学学报, 2019, 40(1): 162-167. SUN Jianqun, JIANG Pengyu, SONG Chunhui, et al. Experimental investigation on the hydrodynamics of multi-module connected floating bridge under regular wave action[J]. Journal of Harbin Engineering University, 2019, 40(1): 162-167. (  0) 0)
|
| [10] |
FENTON J D. A fifth-order stokes theory for steady waves[J]. Journal of waterway, port, coastal, and ocean engineering, 1985, 111(2): 216-234. DOI:10.1061/(ASCE)0733-950X(1985)111:2(216) (  0) 0)
|
| [11] |
NING Dezhi, WANG Rongquan, GOU Ying, et al. Numerical and experimental investigation of wave dynamics on a land-fixed OWC device[J]. Energy, 2016, 115: 326-337. DOI:10.1016/j.energy.2016.09.001 (  0) 0)
|
| [12] |
MALARA G, ROMOLO A, FIAMMA V, et al. On the modelling of water column oscillations in U-OWC energy harvesters[J]. Renewable energy, 2017, 101: 964-972. DOI:10.1016/j.renene.2016.09.051 (  0) 0)
|
| [13] |
ZHANG Hengming, DING Xincheng, Zhou Binzhen, et al. Hydrodynamic performance study of wave energy-type floating breakwaters[J]. Journal of marine science and application, 2019, 18(1): 64-71. DOI:10.1007/s11804-019-00064-y (  0) 0)
|
| [14] |
BILANDI R N, JAMEI S, ROSHAN F, et al. Numerical simulation of vertical water impact of asymmetric wedges by using a finite volume method combined with a volume-of-fluid technique[J]. Ocean engineering, 2018, 160: 119-131. DOI:10.1016/j.oceaneng.2018.04.043 (  0) 0)
|
| [15] |
徐刚, 陈静, 朱仁庆, 等. 多方向波与结构的相互作用模拟分析[J]. 哈尔滨工程大学学报, 2019, 40(3): 462-467. XU Gang, CHEN Jing, ZHU Renqing, et al. Numerical simulation of multi-directional wave and structure interaction[J]. Journal of Harbin Engineering University, 2019, 40(3): 462-467. (  0) 0)
|
 2020, Vol. 41
2020, Vol. 41


