空间机器人能够协助或取代宇航员完成太空在轨服务工作，其运用可以大大提升探测外太空的效率，因此学者对各类空间机器人的动力学控制展开了广泛的研究^[1-5]。随着对控制精度的要求越来越高，各类柔性问题逐渐凸显^[6-7]。空间机器人本身质轻，长臂，因此其在操作过程中具有柔性振动；同时，空间机器人沿着导轨移动的过程中会产生基座的振动，由于整个系统存在耦合关系，故而会降低关节运动的精度^[8-9]。因此要实现较高精度的控制，须将臂杆与基座的柔性振动均作为考虑因素。文献[10]推导了多柔杆空间机器人的动力学方程，仿真了双柔杆的轨迹跟踪，并采取LQR方案进行柔性抑振。文献[11]将多连杆柔性机器人的模型不确定性视为参数摄动，设计直接参数更新律来快速抑制柔性振动。文献[12]在结合应用混合轨迹和奇异设动降阶方法，抑制了存在基座弹性的柔性关节空间机器人的基座与关节振动，而杆件柔性未加以考虑。

以上研究均是建立在力矩完全输出的理想条件下，而实际上关节力矩输出死区是执行器常见的非线性特性。影响稳态跟踪误差，产生极限环振荡，甚至造成控制失效等，这些都是“死区”带来的不利后果。因此，为了满足空间机器人的高精度控制，设计合适的“死区”补偿方法是值得研究的。文献[13]以存在死区的空间机械臂为研究对象，设计了递归CMAC控制方法和死区预补偿器来实现关节的轨迹跟踪；文献[14]研究了具有非对称死区机械手的一种自适应反演控制方案和死区估计器。

文献[14]中的反演法是机器人动力学控制领域中一种行之有效的方法，然而这种方法在“后退”的过程中，对虚拟控制部分多次求导将会导致“微分爆炸”问题。因此Swaroop等^[15]在研究过程中提出动态面概念，设计一阶低通滤波器估计虚拟控制部分，解决了此问题。文献[16]研究了一种无模型的递归模糊神经网络的动态面控制方案用以控制关节执行器存有动态摩擦的机械臂。文献[17]将气动高超声速飞行器的模型不确定性与干扰应用模糊神经网络干扰观测器来估计，并研制了自适应动态面控制器。

基座、臂杆全弹性空间机器人是强耦合非线性系统，本文将此作为研究对象，并考虑了关节力矩输出死区这一实际工况，研究了其轨迹跟踪以及柔性双重抑振的控制问题。基于2种时间尺度假设，将系统分解为快、慢变子系统：针对慢变子系统，设计了一种抗死区的基于自适应高斯基模糊的动态面控制器。动态面的引入避免了反演法引起的计算膨胀，减少了计算量；模糊逻辑函数逼近了包含死区误差和外部扰动的动力学不确定项，使得基座与两关节铰实现刚性的角度跟踪；对于快变子系统，采用线性二次型调节器(LQR)同时抑制基座与两杆的柔性振动。

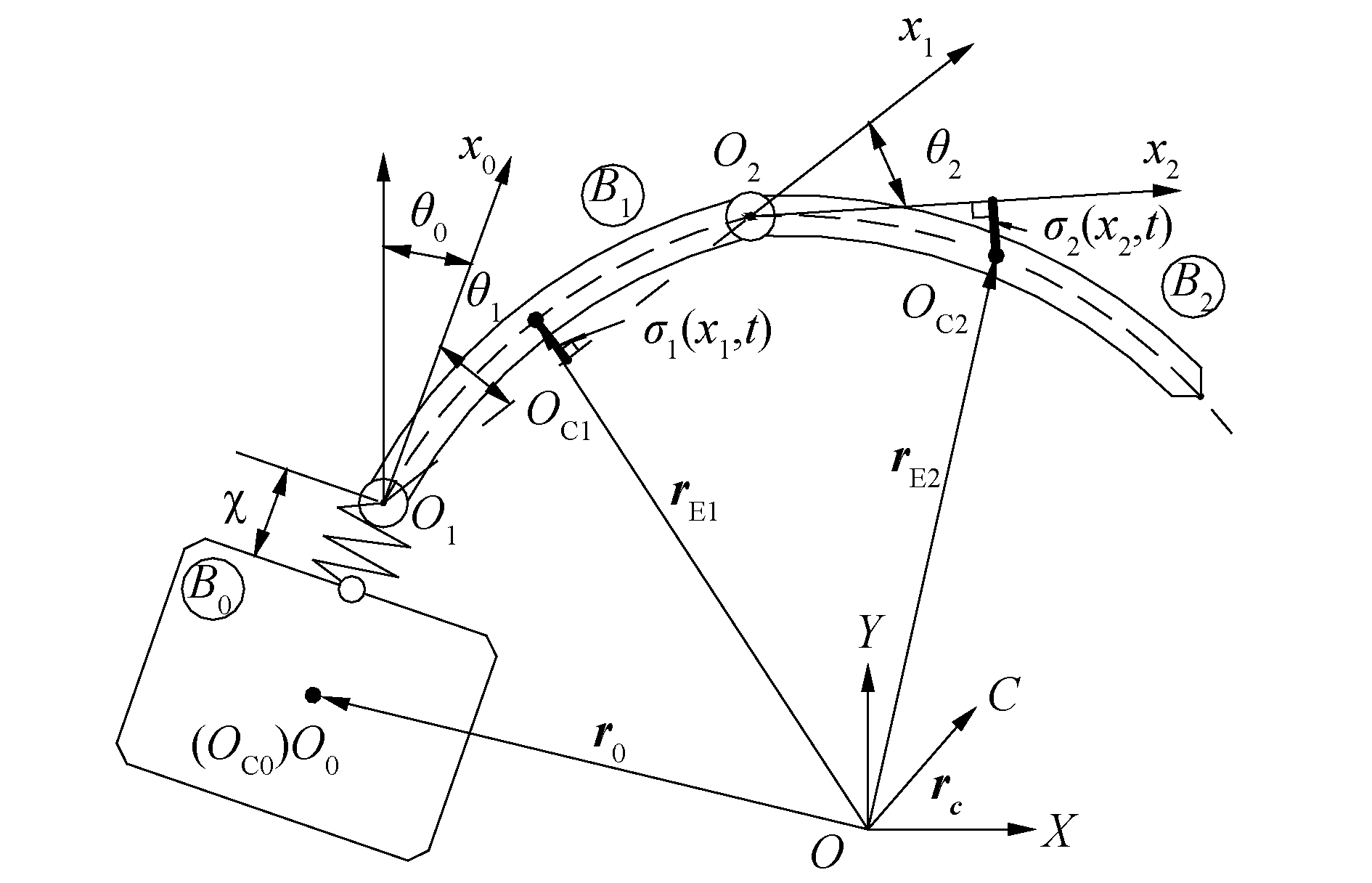
1 系统动力学方程

以基座、臂杆全弹性空间机器人为研究对象，其包含自由飘浮的基座B₀及柔性臂杆B₁、B₂组成，模型如图 1所示。将基座振动简化为一个不计质量的弹簧的位移χ来描述，弹性系数为k_χ，初始位移为0，并且只做沿着轴线的伸缩运动。

建立各分体B_i(i=0, 1, 2)的联体坐标O_ix_iy_i，其中O₀与B₀的质心O_c0重合，O_i(i=1, 2)分别为相应的转动铰中心。轻质弹簧连接O₁与B₀，x₀轴通过O₀与O₁的连线，x₁轴与O₁O₂共线，x₂轴与B₂始终相切于O₂。初始时，O₁在x₀轴上与O₀的距离为l₀，B_i(i=1, 2)沿x_i轴的长度为l_i；基座的质量与绕质心的转动惯量分别为m₀、J₀。C为系统的总质心。以空间任意点O为原点，设立平动惯性坐标系(O－XY)。

假设两杆为仅考虑弯曲变形，同时在平面内作横向振动的匀质细长杆件。B_i(i=1, 2)的线密度为ρ_i，截面抗弯刚度为(EI)_i。将两杆视为Euler-Bernoulli梁，其弹性变形为:

$ {\sigma _i}\left( {{x_i},t} \right) = \sum\limits_{j = 1}^{{n_i}} {{\omega _{ij}}} \left( {{x_i}} \right){\xi _{ij}}(t) $

式中：σ_i(x_i, t)为B_i在截面x_i(0≤x_i≤l_i)处的横向弹性变形；ω_ij(x_i)为B_i的第j阶模态函数；ξ_ij(t)为与之对应的模态坐标，大幅值的振动主要由前几阶模态构成，取截断项数n_i=2。将B₁与B₂分别视为简支梁与悬臂梁，具体模态函数可由文献[18]得到。

采用Lagrange第二类方程，可得系统的动力学方程为:

$ \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\delta }})\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\ddot \theta }}}\\ {\mathit{\boldsymbol{\ddot \delta }}} \end{array}} \right] + \mathit{\boldsymbol{h}}(\mathit{\boldsymbol{\theta }},\mathit{\boldsymbol{\delta }},\mathit{\boldsymbol{\dot \theta }},\mathop {\mathit{\boldsymbol{\delta }}}\limits^. )\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \theta }}}\\ {\mathit{\boldsymbol{\dot \delta }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{K}}_\xi }\mathit{\boldsymbol{\xi }}}\\ {{\mathit{\boldsymbol{k}}_\chi }\chi } \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} \tau \\ 0 \end{array}} \right] $

(1)

式中：$ \boldsymbol{\theta}=\left[\begin{array}{lll}{\theta_{0}} & {\theta_{1}} & {\theta_{2}}\end{array}\right]^{\mathrm{T}}$为基座姿态和臂杆两关节相对转角的刚性广义坐标列向量，$ \left[\begin{array}{llll}\boldsymbol{\xi}={\xi_{11}} & {\xi_{12}} & {\xi_{21}} & {\xi_{22}}\end{array}\right]^{\mathrm{T}}$为臂杆柔性模态的广义坐标列向量，$\boldsymbol{\delta}=\left[{\xi}^{\mathrm{T}} \quad \mathcal{X}\right]^{\mathrm{T}} \circ \boldsymbol{M}(\boldsymbol{\theta}, \boldsymbol{\delta}) \in \mathbf{R}^{8\times 8} $为对称、正定质量矩阵，$\boldsymbol{h}(\boldsymbol{\theta}, \boldsymbol{\delta}, \dot{\boldsymbol{\theta}}, \dot{\boldsymbol{\delta}})\left[\dot{{\theta}}^{\mathrm{T}} \quad \dot{\delta}^{\mathrm{T}}\right]^{\mathrm{T}} \in \mathbf{R}^{8} $为包含科氏力、离心力的列向量，$ \boldsymbol{K}_{\xi} \in \operatorname{diag}\left(k_{\xi 11}, k_{\xi 12}, k_{\xi 21}, k_{\xi 22}\right), \boldsymbol{k}_{\xi i j}=(\mathrm{EI})_{i} \int_{0}^{l_{i}} \omega_{i j}^{\prime \prime T} \omega^{\prime \prime} \mathrm{d} x_{i}(i, j=1, 2)$为柔杆的刚度矩阵。τ∈R³为基座与臂杆两关节的输出力矩列向量。

2 基于奇异摄动方法的快、慢系统分解

此基座、臂杆全弹性空间机器人在运动中不仅两臂杆会发生变形和振动，弹性基座也会发生振动。为了实现空间机器人的高精度控制与柔性振动的抑制，采用奇异摄动方法，将动力学方程分解为慢变、快变子系统，分别表示刚性运动、基座及两杆柔性振动，为此，将式(1)表示成分块矩阵形式：

$ \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{M}}_{ss}}}&{{\mathit{\boldsymbol{M}}_{sf}}}\\ {{\mathit{\boldsymbol{M}}_{fs}}}&{{\mathit{\boldsymbol{M}}_{ff}}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\ddot \theta }}}\\ {\mathit{\boldsymbol{\ddot \delta }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{h}}_{ss}}}&{{\mathit{\boldsymbol{h}}_{sf}}}\\ {{\mathit{\boldsymbol{h}}_{fs}}}&{{\mathit{\boldsymbol{h}}_{ff}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot \theta }}}\\ {\mathit{\boldsymbol{\dot \delta }}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ {{\mathit{\boldsymbol{K}}_\xi }\mathit{\boldsymbol{\xi }}}\\ {{\mathit{\boldsymbol{k}}_\chi }\chi } \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} \tau \\ 0 \end{array}} \right] $

(2)

式中：$\boldsymbol{M}_{{ss}}、\boldsymbol{H}_{{ss}} \in \mathbf{R}^{3 \times 3} ; \boldsymbol{M}_{f f} 、\boldsymbol{H}_{f f} \in \mathbf{R}^{5 \times 5} ; \boldsymbol{M}_{s f}=\boldsymbol{M}_{fs}^{\mathrm{T}} \in $ $ \mathbf{R}^{3 \times 5} ; \boldsymbol{H}_{s f} \in \mathbf{R}^{3 \times 5}、\boldsymbol{H}_{f s} \in \mathbf{R}^{5 \times 3}$。

因为M是对称、正定矩阵，所以它的逆存在：

$ \mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{M}}^{ - 1}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{N}}_{ss}}}&{{\mathit{\boldsymbol{N}}_{sf}}}\\ {{\mathit{\boldsymbol{N}}_{fs}}}&{{\mathit{\boldsymbol{N}}_{ff}}} \end{array}} \right] $

定义奇异摄动比例因子$ \varepsilon^{2}=1 / \min \left\{k_{\xi^{411}}, k_{\xi 12}\right., \left.k_{\xi 21}, k_{\xi 22}, k_{\chi}\right\}$，新的变量$ \mathit{\boldsymbol{z}}, \mathit{\boldsymbol{\widetilde K}}\left( {\mathit{\boldsymbol{z}}{\varepsilon ^2}1 = \xi , \mathit{\boldsymbol{\widetilde K}} = {\varepsilon ^2}\mathit{\boldsymbol{K}}} \right)$。由式(2)推得系统的奇异摄动模型：

$ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\ddot \theta }} = - \left( {{\mathit{\boldsymbol{N}}_{ss}}{\mathit{\boldsymbol{h}}_{ss}} + {\mathit{\boldsymbol{N}}_{sf}}{\mathit{\boldsymbol{h}}_{fs}}} \right)\mathit{\boldsymbol{\dot \theta }} - }\\ {\left( {{\mathit{\boldsymbol{N}}_{ss}}{\mathit{\boldsymbol{h}}_{sf}} + {\mathit{\boldsymbol{N}}_{sf}}{\mathit{\boldsymbol{h}}_{ff}}} \right){\varepsilon ^2}\mathit{\boldsymbol{\dot z}} - {\mathit{\boldsymbol{N}}_{sf}}\mathit{\boldsymbol{\tilde Kz}} + {\mathit{\boldsymbol{N}}_{ss}}\mathit{\boldsymbol{\tau }}}\\ {{\varepsilon ^2}\mathit{\boldsymbol{\ddot z}} = - \left( {{\mathit{\boldsymbol{N}}_{fs}}{\mathit{\boldsymbol{h}}_{ss}} + {\mathit{\boldsymbol{N}}_{ff}}{\mathit{\boldsymbol{h}}_{fs}}} \right)\mathit{\boldsymbol{\dot \theta }} - }\\ {\left( {{\mathit{\boldsymbol{N}}_{fs}}{\mathit{\boldsymbol{h}}_{sf}} + {\mathit{\boldsymbol{N}}_{ff}}{\mathit{\boldsymbol{h}}_{ff}}} \right){\varepsilon ^2}\mathit{\boldsymbol{\dot z}} - {\mathit{\boldsymbol{N}}_{ff}}\mathit{\boldsymbol{\tilde Kz}} + {\mathit{\boldsymbol{N}}_{fs}}\tau } \end{array}} \right. $

(3)

根据式(3)的系统奇异摄动模型，可设计如下组合控制律：

$ \mathit{\boldsymbol{\tau }} = {\mathit{\boldsymbol{\tau }}_s} + {\mathit{\boldsymbol{\tau }}_f} $

(4)

式中：τ_s控制慢变子系统，实现基座与两关节角度跟踪；τ_f则控制快变子系统，抑制基座与两杆振动。

令ε=0，可得慢变子系统为：

$ {\mathit{\boldsymbol{\overline M}} _{ss}}\mathit{\boldsymbol{\ddot \theta }} + {{\mathit{\boldsymbol{\bar h}}}_{ss}}\mathit{\boldsymbol{\dot \theta }} = {\mathit{\boldsymbol{\tau }}_s} $

(5)

式中矩阵或变量上加上划线意为与之对应的慢变分量。

定义新的变量：${\mathit{\boldsymbol{p}}_1} = \mathit{\boldsymbol{z}} - \mathit{\boldsymbol{\bar z}}, {\mathit{\boldsymbol{p}}_2} = \varepsilon \mathit{\boldsymbol{\dot z}} $，并加入快变时间尺度$\bar{\omega}=t / s $，则快变子系统动力学方程为：

$ \begin{array}{*{20}{c}} {{\rm{d}}{\mathit{\boldsymbol{p}}_1}/{\rm{d}}\bar \omega = {\mathit{\boldsymbol{p}}_2}}\\ {{\rm{d}}{\mathit{\boldsymbol{p}}_2}/{\rm{d}}\bar \omega = - {{\mathit{\boldsymbol{\bar N}}}_{ff}}\mathit{\boldsymbol{\tilde K}}{\mathit{\boldsymbol{p}}_1} + {{\mathit{\boldsymbol{\bar N}}}_{fs}}{\mathit{\boldsymbol{\tau }}_f}} \end{array} $

(6)

式(6)描述的是基座和两杆的柔性振动。

3 控制规律设计 3.1 慢变子系统基于动态面的抗死区自适应模糊控制方法设计

空间机器人的基座位置和姿态的调整通常利用动量轮或反作用喷气装置；而两关节铰为电机驱动，因此其存在关节力矩输出死区。

考虑外部干扰τ_d和关节力矩输出死区，慢变子系统可写为：

$ {\mathit{\boldsymbol{\overline M}} _{ss}}\mathit{\boldsymbol{\ddot \theta }} + {{\mathit{\boldsymbol{\bar h}}}_{ss}}\mathit{\boldsymbol{\dot \theta }} + {\mathit{\boldsymbol{\tau }}_{\rm{d}}} = {\mathit{\boldsymbol{\tau }}_s} $

式中：${\mathit{\boldsymbol{\tau }}_s}{\left[ {\begin{array}{*{20}{c}} {{{\overline \tau }_0}}&{{\mathit{\boldsymbol{D}}^{\rm{T}}}\left( {{{\overline \tau }_r}} \right)} \end{array}} \right]^{\rm{T}}} \in {{\mathbf{R}}^3} $为慢变子系统中基座输出力矩$ {{{\overline \tau }_0}}$与臂杆两关节铰的输出力矩$ \mathit{\boldsymbol{D}}\left( {{{\overline \tau }_r}} \right) = $ $ [D(\overline{\tau_{1}}) \quad D(\overline{\tau_{2}})]^{\mathrm{T}}, \boldsymbol{D}(\overline{\tau_{r}})$是具有输入为$ {\mathit{\boldsymbol{\overline \tau }} _r} = $ $ \left[\begin{array}{ll}{\bar{\tau}_{1}} & {\bar{\tau}_{2}}\end{array}\right]^{\mathrm{T}}$的关节力矩死区输出列向量。

鉴于通常难以获得系统动力学模型的精确参数，记$ \boldsymbol{v}_{1}=\boldsymbol{\theta}, \dot{\boldsymbol{v}}_{1}=\boldsymbol{v}_{2}=\dot{\boldsymbol{\theta}}$，将慢变子系统写为状态方程：

$ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}_1} = {\mathit{\boldsymbol{v}}_2}}\\ {{{\mathit{\boldsymbol{\dot v}}}_2} = \mathit{\boldsymbol{\hat {\bar M}}}_{SS}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){\mathit{\boldsymbol{\tau }}_s} - \mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2}} \right) + \mathit{\boldsymbol{\hat {\bar M}}}_{ss}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){\mathit{\boldsymbol{T}}_\Delta }} \end{array}} \right. $

(7)

式中：$ {\widehat {\mathit{\boldsymbol{\overline M}} }_{ss}}、{\widehat {\mathit{\boldsymbol{\overline H}} }_{ss}} $为名义模型；$\Delta \mathit{\boldsymbol{M}} = \widehat {\mathit{\boldsymbol{\overline M}} }_{ss} - {\widehat {\mathit{\boldsymbol{\overline M}} }_{ss}}, \Delta \mathit{\boldsymbol{h}} = {\widehat {\mathit{\boldsymbol{\overline h}} }_{ss}} - \widehat {\mathit{\boldsymbol{\overline h}} } $。$ \boldsymbol{F}\left(\boldsymbol{v}_{1}, \boldsymbol{v}_{2}\right)=\dot{\widehat {\mathit{\boldsymbol{\overline M}} }_{s s}^{-1}}\left(\boldsymbol{v}_{1}\right) \hat{\bar{h}_{s s}}\left(\boldsymbol{v}_{1}, \boldsymbol{v}_{2}\right) \boldsymbol{v}_{2}, \boldsymbol{T}_{\Delta}=$ $ - \Delta \mathit{\boldsymbol{M}}\left( {{\mathit{\boldsymbol{v}}_1}} \right){{\mathit{\boldsymbol{\dot v}}}_2} - \Delta \mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{v}}_1}, {\mathit{\boldsymbol{v}}_2}} \right){\mathit{\boldsymbol{v}}_2} - {\mathit{\boldsymbol{\tau }}_d}$为不确定性之和。$ \|\Delta \boldsymbol{M}\| \leqslant \rho_{M}, \|\Delta \boldsymbol{h}\| \leqslant \rho_{h}, \left\|\boldsymbol{\tau}_{d}\right\| \leqslant \rho_{d}$ $ \rho_{i}(i=M, h, d)$为正常数。

3.1.1 关节力矩输出死区

“死区”是指输入变化对输出没有影响的范围。它体现了在关节力矩的输入大小进入死区之后输出为零的输入-输出关系。当信号进入死区范围时会有一定的损失，进而产生系统控制的偏差。

记死区输入为${\mathit{\boldsymbol{\overline \tau }} _r} $，输出为$\mathit{\boldsymbol{D}}\left( {{{\overline \tau }_r}} \right) $，其简化死区模型^[13]可表示为：

$ D\left( {{\tau _i}} \right) = \left\{ {\begin{array}{*{20}{l}} {{m_{ri}}\left( {{\tau _i} - {b_{ri}}} \right),}&{\tau \ge {b_{ri}}}\\ {0,}&{{b_{li}} < {\tau _{di}} < {b_{ri}}}\\ {{m_{li}}\left( {{\tau _i} - {b_{li}}} \right),}&{{\tau _i} \le {b_{li}}} \end{array}} \right. $

式中：b_li < 0、b_ri>0分别为死区的左右宽度。m_li、m_ri分别为死区的左右斜率，设定m_ri、m_li均大于零。

死区输入与输出的差值表示为：

$ {D_\Delta } = {{\bar \tau }_r} - D\left( {{{\bar \tau }_r}} \right) $

因此把状态方程式(7)改写为：

$ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot v}}}_1} = {\mathit{\boldsymbol{v}}_2}}\\ \begin{array}{l} {{\mathit{\boldsymbol{\dot v}}}_2} = \mathit{\boldsymbol{\hat {\bar M}}}_{ss}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){{\mathit{\boldsymbol{\bar \tau }}}_c} - \mathit{\boldsymbol{\hat {\bar M}}}_{ss}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){\left[ {\begin{array}{*{20}{c}} 0&{D_\Delta ^{\rm{T}}} \end{array}} \right]^{\rm{T}}} - \\ \;\;\;\;\;\;\;\mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2}} \right) + \mathit{\boldsymbol{\hat {\bar M}}}_{ss}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){\mathit{\boldsymbol{T}}_\Delta } \end{array} \end{array}} \right. $

(8)

式中：$\overline{\boldsymbol{\tau}}_{c}=\left[\begin{array}{cc}{\overline{\boldsymbol{\tau}}_{0}} & {\overline{\boldsymbol{\tau}}_{r}^{\mathrm{T}}}\end{array}\right]^{\mathrm{T}} $为过“死区”之前基座与两关节的力矩列向量。

3.1.2 控制器设计

针对文中的空间机器人慢变子系统，采用动态面控制方法设计虚拟控制量和控制输入信号，在此基础上设计慢变子系统的控制规律${\mathit{\boldsymbol{\overline \tau }} _c} $，以使此基座、臂杆全弹性空间机器人的刚性运动轨迹θ跟踪期望运动轨迹θ_d。

动态面控制的设计步骤如下：

1) 定义第一个误差面：

$ {\mathit{\boldsymbol{s}}_1} = {\mathit{\boldsymbol{v}}_1} - {\mathit{\boldsymbol{\theta }}_d} $

设计一个虚拟控制量υ₂：

$ {{\mathit{\boldsymbol{\tilde v}}}_2} = {{\mathit{\boldsymbol{\dot \theta }}}_d} - {c_1}{s_1} $

(9)

式中设计常数c₁>0。

以${{\mathit{\boldsymbol{\tilde \upsilon }}}_2} $为输入，υ_2d为新的状态变量输出，引入一阶低通滤波器：

$ {\eta _2}{{\mathit{\boldsymbol{\dot v}}}_{2d}} + {\mathit{\boldsymbol{v}}_{2d}} = {{\mathit{\boldsymbol{\tilde v}}}_2},{\mathit{\boldsymbol{v}}_{2d}}\left( 0 \right) + {\mathit{\boldsymbol{v}}_2}\left( 0 \right) $

(10)

式中时间η₂>0。

2) 提出第2个动态面，进而设计慢变子系统的控制规律:

$ {\mathit{\boldsymbol{s}}_2} = {\mathit{\boldsymbol{v}}_2} - {\mathit{\boldsymbol{v}}_{2d}} $

(11)

将式(8)代入s₂的一阶导数${{\mathit{\boldsymbol{\dot s}}}_2} $，可得：

$ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\dot s}}}_2} = \mathit{\boldsymbol{\hat {\bar M}}}_{ss}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){{\mathit{\boldsymbol{\bar \tau }}}_c} - \mathit{\boldsymbol{\hat {\bar M}}}_{SS}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){{\left[ {\begin{array}{*{20}{c}} 0&{\mathit{\boldsymbol{D}}_\Delta ^{\rm{T}}} \end{array}} \right]}^{\rm{T}}} - }\\ {\mathit{\boldsymbol{F}}\left( {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2}} \right) + \mathit{\boldsymbol{\hat {\bar M}}}_{ss}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right){\mathit{\boldsymbol{T}}_\Delta } - {\mathit{\boldsymbol{v}}_{2d}}} \end{array} $

(12)

利用模糊逻辑系统来逼近确切值未知的$ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}(\mathit{\boldsymbol{X}}) = {\left[ {\begin{array}{*{20}{l}} 0&{ - \mathit{\boldsymbol{D}}_\mathit{\Delta} ^{\rm{T}}} \end{array}} \right]^{\rm{T}}} + {\mathit{\boldsymbol{T}}_\mathit{\Delta} }$。

记Θ(X|W)为Θ(X)的一个逼近，则：

$ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( {\mathit{\boldsymbol{X}}\left| \mathit{\boldsymbol{W}} \right.} \right) = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{O}}\left( \mathit{\boldsymbol{X}} \right) $

式中：W为权值矩阵；$ \boldsymbol{O}(x)=\left[\begin{array}{llll}{O_{1}} & {O_{2}} & {\cdots} & {O_{h}}\end{array}\right]^{\mathrm{T}}$为模糊基向量；h为规则数目。模糊基网络输入$ \mathit{\boldsymbol{X = }}\left[\begin{array}{llll}{\boldsymbol{v}_{1}^{\mathrm{T}}} & {\boldsymbol{v}_{2}^{\mathrm{T}}} & {\boldsymbol{\theta}_{\mathrm{d}}^{\mathrm{T}}} & {\dot{\boldsymbol{\theta}}_{\mathrm{d}}^{\mathrm{T}}}\end{array}\right]^{\mathrm{T}}$，模糊基函数O_k表示为：

$ {O_k}\left( {{X_1},{X_2}, \cdots ,{X_{4n}}} \right) = \prod\limits_{j = 1}^{4n} {{\mu _{F_j^k}}} \left( {{X_j}} \right)/\sum\limits_{k = 1}^h {\prod\limits_{j = 1}^{4n} {{\mu _{F_j^k}}} } \left( {{X_j}} \right) $

选取高斯型函数：

$ {\mu _{F_j^k}}\left( {{X_j}} \right) = \exp \left[ { - {{\left( {{X_j} - {a_{jk}}} \right)}^2}/2b_{ij}^2} \right] $

式中a_jk、b_jk分别为曲线的中心、宽度。

W的最优值W^*是一个常数矩阵且满足：

$ {\mathit{\boldsymbol{W}}^*} = \arg \mathop {\min }\limits_{W \in {\mathit{\Omega }_W}} \left[ {\mathop {\sup }\limits_{X \in {\mathit{\Omega }_X}} \left| {\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( {\mathit{\boldsymbol{X}}\left| \mathit{\boldsymbol{W}} \right.} \right) - \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( \mathit{\boldsymbol{X}} \right)} \right|} \right] $

式中：$\mathit{\Omega}_{w}=\left\{\boldsymbol{W} |\|\boldsymbol{W}\| \leqslant \rho_{w}\right\}, \rho_{w} $为有界正常数。

令：

$ \mathit{\boldsymbol{ \boldsymbol{\varTheta} }}\left( \mathit{\boldsymbol{X}} \right) = {\mathit{\boldsymbol{W}}^{*{\rm{T}}}}\mathit{\boldsymbol{O}}\left( \mathit{\boldsymbol{X}} \right) + {\mathit{\boldsymbol{\mu }}^*} $

(13)

式中μ^*为最优逼近误差。

设计慢变子系统的控制规律为：

$ \begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\bar \tau }}}_c} = - {c_2}{\mathit{\boldsymbol{s}}_2} - {\mathit{\boldsymbol{s}}_1} - {{\mathit{\boldsymbol{\hat W}}}^{\rm{T}}}\mathit{\boldsymbol{O}}\left( \mathit{\boldsymbol{X}} \right) - \mathit{\boldsymbol{\hat \mu }} + }\\ {{{\mathit{\boldsymbol{\hat {\bar h}}}}_{ss}}\left( {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2}} \right){\mathit{\boldsymbol{v}}_{2d}} + {{\mathit{\boldsymbol{\hat {\bar M}}}}_{ss}}\left( {{\mathit{\boldsymbol{v}}_1}} \right){{\mathit{\boldsymbol{\dot v}}}_{2d}}} \end{array} $

(14)

式中：$ \mathit{\boldsymbol{\hat W}}、\mathit{\boldsymbol{\hat \varepsilon }}$分别为W^*、μ^*的估计值，c₂>0。

设计$ \mathit{\boldsymbol{\hat W}}, \mathit{\boldsymbol{\hat \mu }}$的自适应调节律：

$ \mathit{\boldsymbol{\dot {\hat W}}} = {\mathit{\boldsymbol{\beta }}_1}\mathit{\boldsymbol{O}}\left( \mathit{\boldsymbol{X}} \right)\mathit{\boldsymbol{s}}_2^{\rm{T}} - {\lambda _1}\mathit{\boldsymbol{\hat W}} $

(15)

$ \mathit{\boldsymbol{\dot {\hat \mu} }} = {\mathit{\boldsymbol{\beta }}_2}{\mathit{\boldsymbol{s}}_2} - {\lambda _2}\mathit{\boldsymbol{\hat \mu }} $

(16)

式中：$ {\mathit{\boldsymbol{\beta }}_1} \in {{\mathbf{R}}^{h \times h}}, {\mathit{\boldsymbol{\beta }}_2} \in {{\mathbf{R}}^{3 \times 3}}。{\lambda _1} > 0, {\lambda _2} > 0$为调节参数。

3.1.3 稳定性分析

利用Lyapunov理论分析存在关节力矩输出死区与外部干扰的慢变子系统半全局的稳定性。

定义慢变子系统边界层误差：

$ {\mathit{\boldsymbol{\gamma }}_2} = {\mathit{\boldsymbol{v}}_{2d}} - {{\mathit{\boldsymbol{\tilde v}}}_2} $

代入式(10)，可得：

$ {{\mathit{\boldsymbol{\dot v}}}_{2d}} - {\gamma _2}/{\mathit{\boldsymbol{\eta }}_2} $

(17)

由此求解出γ₂的一阶导数$ {{\mathit{\boldsymbol{\dot \gamma }}}_2}$：

$ \begin{array}{*{20}{c}} {{{\dot \gamma }_2} = - {\gamma _2}/{\eta _2} - {{\mathit{\boldsymbol{\ddot \theta }}}_{\rm{d}}} + {c_1}{{\mathit{\boldsymbol{\dot s}}}_1} = }\\ { - {\gamma _2}/{\eta _2} + \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{s}}_1},{\mathit{\boldsymbol{s}}_2},{\mathit{\boldsymbol{\theta }}_{\rm{d}}},{{\mathit{\boldsymbol{\dot \theta }}}_{\rm{d}}},{{\mathit{\boldsymbol{\ddot \theta }}}_{\rm{d}}},{\mathit{\boldsymbol{\gamma }}_2}} \right)} \end{array} $

(18)

式中：$\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{s}}_1}, {\mathit{\boldsymbol{s}}_2}, {\mathit{\boldsymbol{q}}_d}, {{\mathit{\boldsymbol{\dot q}}}_d}, {{\mathit{\boldsymbol{\ddot q}}}_d}, {\mathit{\boldsymbol{\gamma }}_2}} \right) $为非负连续函数矩阵。

结合式(9)~式(11)与式(17)，求出第1个误差面的一阶导数：

$ {{\mathit{\boldsymbol{\dot s}}}_1} = - {c_1}{\mathit{\boldsymbol{s}}_1} + {\mathit{\boldsymbol{s}}_2} + {\mathit{\boldsymbol{\gamma }}_2} $

(19)

综合式(13)与控制规律式(14)，代入式(12)，${{\mathit{\boldsymbol{\dot s}}}_2} $即为：

$ \begin{array}{*{20}{c}} {{{\dot s}_2} = \hat {\bar M}_{ss}^{ - 1}\left( {{\mathit{\boldsymbol{v}}_1}} \right)\left[ { - {c_2}{\mathit{\boldsymbol{s}}_2} - {\mathit{\boldsymbol{s}}_1} + {{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{O}}\left( \mathit{\boldsymbol{X}} \right) + } \right.}\\ {\left. {\mathit{\boldsymbol{\tilde \mu }} - {{\mathit{\boldsymbol{\hat {\bar h}}}}_{ss}}\left( {{\mathit{\boldsymbol{v}}_1},{\mathit{\boldsymbol{v}}_2}} \right){\mathit{\boldsymbol{s}}_2}} \right]} \end{array} $

式中：$\tilde{\boldsymbol{W}}=\boldsymbol{W}^{*}-\hat{\boldsymbol{W}} ; \tilde{\boldsymbol{\mu}}=\boldsymbol{\mu}^{*}-\hat{\boldsymbol{\mu}} $。

假定q与其速度$ {\mathit{\boldsymbol{\dot q}}}$均可测，慢变子系统的跟踪误差为：

$ \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{q}} - {\mathit{\boldsymbol{q}}_d} $

定理  对于式(5)所示的空间机器人慢变子系统，通过调节参数$ {\mathit{\boldsymbol{\beta }}_1}、{\lambda _1}、{\mathit{\boldsymbol{\beta }}_2}、{\lambda _2}、{c_1}、{c_2}$，控制规律式(14)将使系统半全局最终一致有界，即e收敛到零的一个任意小邻域内。

证明：构造李雅普诺夫函数：

$ V + {V_1} + {V_2} $

式中：V满足初始条件V(0)≤ρ_v(ρ_v为正实数)。

$ {V_1} = \frac{1}{2}\mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} + \frac{1}{2}\mathit{\boldsymbol{s}}_2^{\rm{T}}{{\mathit{\boldsymbol{\hat {\bar M}}}}_{{\rm{ss}}}}\left( {{\mathit{\boldsymbol{v}}_1}} \right){s_2} + \frac{1}{2}\mathit{\boldsymbol{\gamma }}_2^{\rm{T}}{\mathit{\boldsymbol{\gamma }}_2} $

$ {V_2} = \frac{1}{2} tr \left( {{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\tilde W}}} \right) + \frac{1}{2}tg \left( {{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_2^{ - 1}\mathit{\boldsymbol{\tilde \mu }}} \right) $

求V关于时间t的一阶导数：

$ \begin{array}{*{20}{c}} {\dot V = \mathit{\boldsymbol{s}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot s}}}_1} + \mathit{\boldsymbol{s}}_2^{\rm{T}}{{\mathit{\boldsymbol{\hat {\bar M}}}}_{ass}}\left( {{\mathit{\boldsymbol{v}}_1}} \right){{\mathit{\boldsymbol{\dot s}}}_2} + \frac{1}{2}\mathit{\boldsymbol{s}}_2^{\rm{T}}{{\hat {\bar M}}_{ss}}\left( {{\mathit{\boldsymbol{v}}_1}} \right){\mathit{\boldsymbol{s}}_2} + }\\ {\mathit{\boldsymbol{\gamma }}_2^{\rm{T}}{{\mathit{\boldsymbol{\dot \gamma }}}_2} + tr\left( {{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\dot {\tilde W}}}} \right) + tr\left( {{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_2^{ - 1}\mathit{\boldsymbol{\dot {\tilde \mu} }}} \right)} \end{array} $

根据$ {{\widehat {\mathit{\boldsymbol{\overline h}} }}_{ss}}\left( {{\mathit{\boldsymbol{v}}_1}, {\mathit{\boldsymbol{v}}_2}} \right)、{\widehat {\mathit{\boldsymbol{\overline M}} }_{ss}}\left( {{\mathit{\boldsymbol{v}}_1}} \right)$满足斜对称性^[10]：$ \frac{1}{2} \boldsymbol{s}_{2}^{\mathrm{T}} \widehat{\overline{M}}_{s s}\left(\boldsymbol{v}_{1}\right) \boldsymbol{s}_{2}=\boldsymbol{s}_{2}^{\mathrm{T}} \widehat{\overline{h}}_{s s}\left(\boldsymbol{v}_{1}, \boldsymbol{v}_{2}\right) \boldsymbol{s}_{2}$，并将式(17)~式(19)代入${{\dot V}_1} $，得：

$ \begin{array}{*{20}{c}} {{{\dot V}_1} = - {c_1}\mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_2} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{\gamma }}_2} + }\\ {\mathit{\boldsymbol{s}}_2^{\rm{T}}\left[ { - {c_2}{\mathit{\boldsymbol{s}}_2} - {\mathit{\boldsymbol{s}}_1} + {{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{O}}(\mathit{\boldsymbol{X}}) + \mathit{\boldsymbol{\tilde \mu }}} \right] - }\\ {\mathit{\boldsymbol{\gamma }}_2^{\rm{T}}\frac{{{\mathit{\boldsymbol{\gamma }}_2}}}{{{\mathit{\boldsymbol{\eta }}_2}}} + \mathit{\boldsymbol{\gamma }}_2^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{s}}_1},{\mathit{\boldsymbol{s}}_2},{\mathit{\boldsymbol{\theta }}_d},{{\mathit{\boldsymbol{\dot \theta }}}_d},{{\mathit{\boldsymbol{\ddot \theta }}}_d},{\mathit{\boldsymbol{\gamma }}_2}} \right)} \end{array} $

将自适应律式(15)、式(16)代入，得：

$ \begin{array}{*{20}{c}} {{{\dot V}_2} = - {\rm{tr}}\left[ {{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{O}}(\mathit{\boldsymbol{X}})\mathit{\boldsymbol{s}}_2^{\rm{T}}} \right] - {\rm{tr}} \left( {{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}{\mathit{\boldsymbol{s}}_2}} \right) + }\\ { {\rm{tr}} \left( {{\lambda _1}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\hat W}}} \right) + {\rm{tr}} \left( {{\lambda _2}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_2^{ - 1}\mathit{\boldsymbol{\hat \mu }}} \right)} \end{array} $

利用不等式：

$ \begin{array}{*{20}{c}} {{\rm{tr}}\left( {{\lambda _1}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\hat W}}} \right) \le - \frac{1}{2}{\rm{tr}}\left( {{\lambda _1}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\tilde W}}} \right) + }\\ {\frac{1}{2}{\rm{tr}}\left( {{\lambda _1}{\mathit{\boldsymbol{W}}^{*{\rm{T}}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}{\mathit{\boldsymbol{W}}^*}} \right)} \end{array} $

$ \begin{array}{*{20}{c}} {{\rm{tr}}\left( {{\lambda _2}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_2^{ - 1}\mathit{\boldsymbol{\hat \mu }}} \right) \le - \frac{1}{2}{\rm{tr}}\left( {{\lambda _2}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}} \right) + }\\ {\frac{1}{2}{\rm{tr}}\left( {{\lambda _2}{\mathit{\boldsymbol{\mu }}^{*{\rm{T}}}}\mathit{\boldsymbol{\beta }}_2^{ - 1}{\mathit{\boldsymbol{\mu }}^*}} \right)} \end{array} $

可得$ {\dot V}$的不等式：

$ \begin{array}{*{20}{c}} {\dot V \le - {c_1}\mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} - {c_2}\mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{s}}_2} + \mathit{\boldsymbol{s}}_1^{\rm{T}}{\gamma _2} - }\\ {\frac{1}{2}{\rm{tr}}\left( {{\lambda _1}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\tilde W}}} \right) - \frac{1}{2}{\rm{tr}}\left( {{\lambda _2}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}} \right) - }\\ {\mathit{\boldsymbol{\gamma }}_2^{\rm{T}}\frac{{{\mathit{\boldsymbol{\gamma }}_2}}}{{{\mathit{\boldsymbol{\eta }}_2}}} + \mathit{\boldsymbol{\gamma }}_2^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{s}}_1},{\mathit{\boldsymbol{s}}_2},{\mathit{\boldsymbol{\theta }}_d},{{\mathit{\boldsymbol{\dot \theta }}}_d},{{\mathit{\boldsymbol{\ddot \theta }}}_d},{\mathit{\boldsymbol{\gamma }}_2}} \right) + }\\ {\frac{1}{2}{\rm{tr}}\left( {{\lambda _1}{\mathit{\boldsymbol{W}}^{*{\rm{T}}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}{\mathit{\boldsymbol{W}}^*}} \right) + \frac{1}{2}{\rm{tr}}\left( {{\lambda _2}{\mathit{\boldsymbol{\mu }}^{*{\rm{T}}}}\mathit{\boldsymbol{\beta }}_2^{ - 1}{\mathit{\boldsymbol{\mu }}^*}} \right)} \end{array} $

由Young不等式得：

$ \mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{\gamma }}_2} \le \frac{{\mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1}}}{2} + \frac{{\mathit{\boldsymbol{\gamma }}_2^{\rm{T}}{\mathit{\boldsymbol{\gamma }}_2}}}{2} $

$ \mathit{\boldsymbol{\gamma }}_2^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}\left( {{\mathit{\boldsymbol{s}}_1},{\mathit{\boldsymbol{s}}_2},{\mathit{\boldsymbol{\theta }}_d},{{\mathit{\boldsymbol{\dot \theta }}}_d},{{\mathit{\boldsymbol{\ddot \theta }}}_d},{\mathit{\boldsymbol{\gamma }}_2}} \right) \le \frac{{\mathit{\boldsymbol{\gamma }}_2^{\rm{T}}{\mathit{\boldsymbol{\gamma }}_2}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{2\zeta }} + \frac{\zeta }{2} $

式中：ζ>0。

进一步得到$ {\dot V}$：

$ \begin{array}{*{20}{c}} {\dot V \le \left( {\frac{1}{2} - {c_1}} \right)\mathit{\boldsymbol{s}}_1^{\rm{T}}{\mathit{\boldsymbol{s}}_1} - {c_2}\mathit{\boldsymbol{s}}_2^{\rm{T}}{\mathit{\boldsymbol{s}}_2} + \mathit{\boldsymbol{\gamma }}_2^{\rm{T}}\left( {\frac{1}{2} - \frac{1}{{{\eta _2}}} + \frac{{{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}}{{2\zeta }}} \right){\mathit{\boldsymbol{\gamma }}_2} - }\\ {\frac{1}{2}{\rm{tr}}\left( {{\lambda _1}{{\mathit{\boldsymbol{\tilde W}}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\tilde W}}} \right) - \frac{1}{2}{\rm{tr}}\left( {{\lambda _2}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}{{\mathit{\boldsymbol{\tilde \mu }}}^{\rm{T}}}} \right) + }\\ {\frac{1}{2}{\rm{tr}}\left( {{\lambda _1}{\mathit{\boldsymbol{W}}^{*{\rm{T}}}}\mathit{\boldsymbol{\beta }}_1^{ - 1}\mathit{\boldsymbol{\tilde W}}} \right) + \frac{1}{2}{\rm{tr}}\left( {{\lambda _2}{{\mathit{\boldsymbol{\tilde \mu }}}^{*{\rm{T}}}}\mathit{\boldsymbol{\beta }}_2^{ - 1}{\mathit{\boldsymbol{\mu }}^*}} \right) + \frac{\zeta }{2}} \end{array} $

根据‖Φ‖≤ρ_Φ(ρ_Φ为正常数)^[19]，可设计$ \frac{1}{\eta_{2}} \geqslant \frac{1}{2}+\frac{\rho_{\mathit{\Phi} }^{2}}{2 \zeta}+b_{0}$ (b₀为正常数)，使得：

$ \dot V \le - \alpha V + \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} $

(20)

式中：$\alpha = \min \left\{ {\left( {2{c_1} - 1} \right), 2{c_2}, 2{b_0}, {\lambda _1}, {\lambda _2}} \right\}, \mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = \frac{\zeta }{2} + \frac{1}{2} \operatorname{tr}\left(\lambda_{1} \boldsymbol{W}^{* \mathrm{T}} \boldsymbol{\beta}_{1}^{-1} \boldsymbol{W}^{*}\right)+\frac{1}{2} \operatorname{tr}\left(\lambda_{\boldsymbol{\gamma}} \boldsymbol{\mu}^{* \mathrm{T}} \boldsymbol{\beta}_{2}^{-1} \boldsymbol{\mu}^{*}\right) $。

令α>Ψ/ρ_V，则当V=ρ_V时，$ \dot V \le 0$。由此可知，V≤ρ_V是一个不变集，即如果V(0)≤ρ_V，对所有t>0时均有V(t)≤ρ_V。

求解式(20)可得：

$ 0 \le V \le \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}/\alpha + \left[ {V\left( 0 \right) - \psi /\alpha } \right]{{\rm{e}}^{ - \alpha t}} $

表明V最终以Ψ/α为界。因此系统半全局最终一致有界，并且通过调节参数β₁、λ₁、β₂、λ₂、c₁、c₂的值可使误差收敛到零的一个任意小邻域。

3.2 快变子系统控制器设计

采用LQR来控制系统的快变子系统，以同时主动抑制基座与两杆的振动。先将式(6)写成状态方程形式，令状态变量$\boldsymbol{P}=\left[\begin{array}{ll}{p_{1}} & {p_{2}}\end{array}\right]^{\mathrm{T}} $，则式(6)改为：

$ \mathit{\boldsymbol{\dot P}} = \mathit{\boldsymbol{AP}} + \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{\tau }}_f} $

式中：$ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} 0&\mathit{\boldsymbol{I}}\\ { - {{\bar N}_{ff}}\mathit{\boldsymbol{\tilde K}}}&0 \end{array}} \right], \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} 0\\ {{{\bar N}_{fs}}} \end{array}} \right]$。

由线性二次型最优控制理论，为了使系统性能最优，应最小化状态变量和控制变量二次型函数的积分，则控制量应设计为：

$ {\mathit{\boldsymbol{\tau }}_f} = - {\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{P \boldsymbol{\varXi} P}} $

(21)

式中：$\mathit{\boldsymbol{ \boldsymbol{\varXi} }} $满足下面的Riccati代数方程：

$ \mathit{\boldsymbol{ \boldsymbol{\varXi} A}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varXi} }} - \mathit{\boldsymbol{ \boldsymbol{\varXi} B}}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varXi} }} + \mathit{\boldsymbol{Q}} = 0 $

式中：Q∈R^10×10为半正定加权对称阵，R∈R^3×3为正定加权对称阵。

4 基座、臂杆全弹性空间机器人仿真算例

以图 1所展示的基座、臂杆全弹性空间机器人模型系统为例，根据式(14)、式(21)的控制规律进行数值仿真模拟实验。系统惯性与结构参数取值为：l₀=l₁=1.5 m, l₂=1.0 m, m₀=40 kg，J₀=34.17 kg·m²，ρ₁=3.5 kg/m，ρ₂=1.1 kg/m，(EI)₁=50 N·m², (EI)₂=50 N·m²。弹簧刚度系数k_x=500 N/m。系统的外部干扰τ_d(t)取为:τ_0d=2.5[cos(πt/6)-sin(πt/6)]，τ_1d=2.5cos(πt/6)，τ_2d=2.5sin(πt/6)

模糊规则数取h=5；慢变子系统调节参数：β₁=diag{20, …, 20}，β₂=diag{0.01, 0.01, 0.01}，λ₁=λ₂=0.01，c₁=10，c₂=20。LQR控制参数：Q=diag{1, …, 1}, R=diag{1, 1, 1}。

设$ \boldsymbol{\theta}_{d}=\left[\begin{array}{lll}{\pi / 6} & {-\pi / 2} & {-\pi / 6}\end{array}\right]^{\mathrm{T}}$。

初始θ(0)取为：θ₀(0)=0.1 rad，θ₁(0)=(π/3-0.2)rad, θ₂(0)=(－π/6-0.15)rad。基座弹簧初始位移为χ(0)=0。

设定轨迹追踪过程仿真时间为t=30 s。

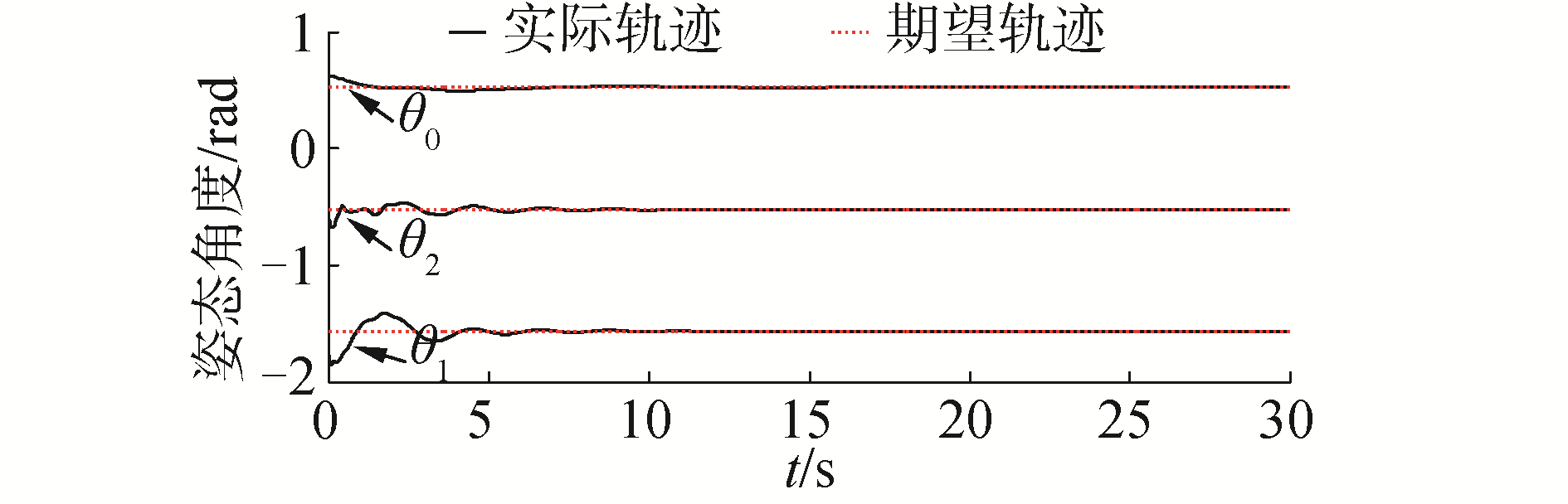
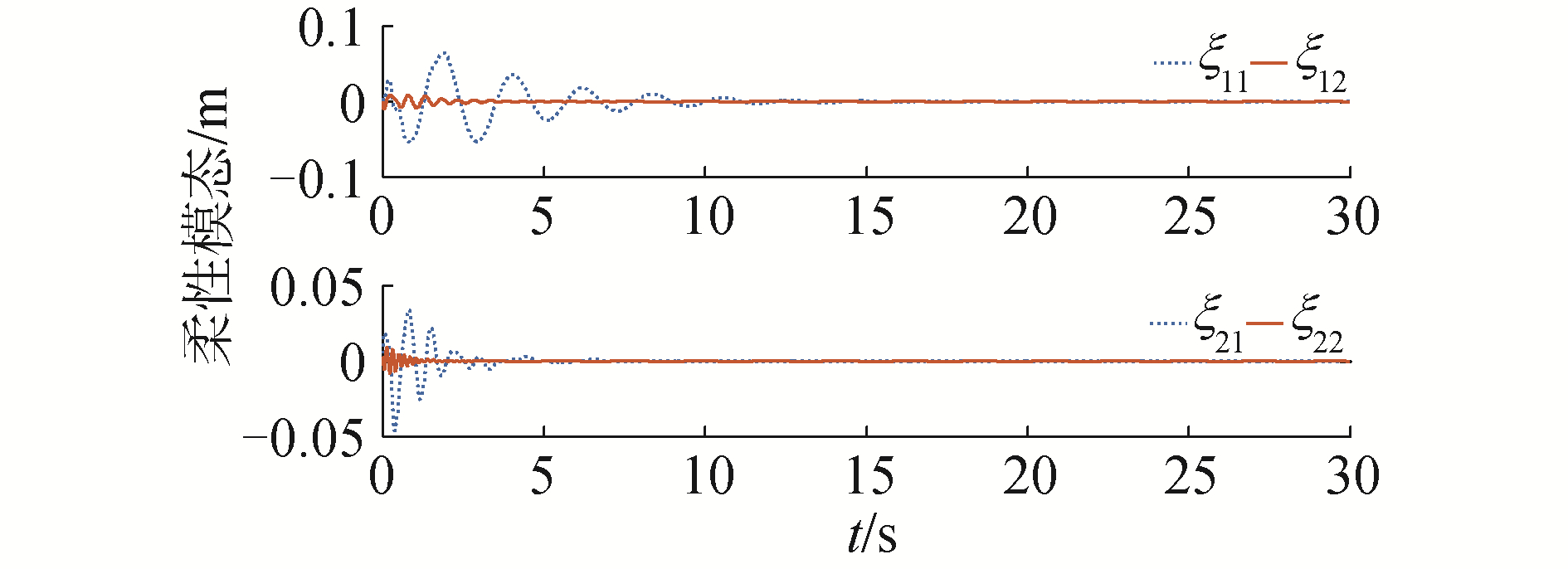
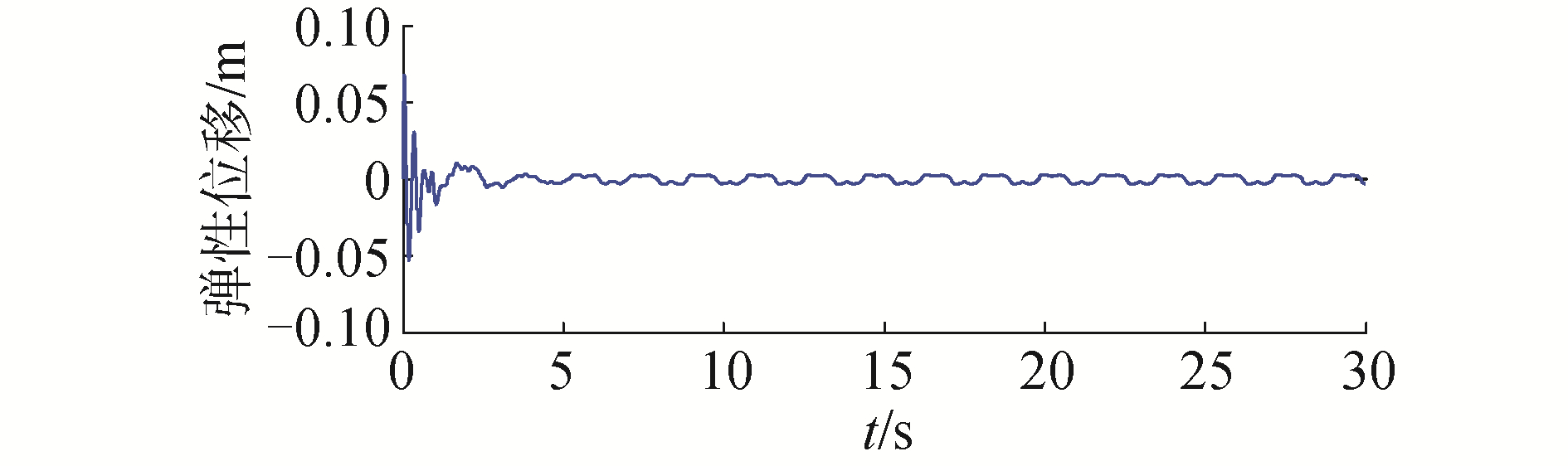
图 2为存在关节力矩输出死区与外部干扰的情况下，基座、臂杆全弹性空间机器人采用基于动态面的高斯基模糊控制方案的基座与两关节铰刚性运动实际轨迹与期望轨迹。约12 s之后，基座，关节1和2的稳态误差分别在2×10^-4，1×10^-3，8×10^-4 rad以内。图 3为该控制方案下基座弹性振动情况。弹性位移在0.05 s时为0.067 8 m，15 s后衰减到零。图 4为两柔性臂杆一、二阶模态情况。B₁杆一阶模态从初始1.9 s的0.064 3 m衰减到0，二阶模态从初始0.2 s的0.007 5 m衰减到0；B₂杆一阶模态从初始0.8 s的0.033 7 m衰减到0，二阶模态从初始0.13 s的0.008 5 m衰减到0。从仿真结果可以看出：基座与两关节铰的实际运动轨迹能很好地跟踪上θ_d，同时抑制了柔性振动，具有较高的跟踪精度。

为了说明抑振方法的有效性，关闭τ_f之后，图 5仿真了弹性基座位移情况；图 6则为柔性臂杆一、二阶模态情况。从图 6中可以看出，基座5 s之后在±0.003 m之间振动，无法归零。而B₁杆一阶模态4 s之后在±0.038 m之间振动，二阶模态在±0.002 m之间振动；B₂杆一阶模态从5 s之后在±0.009 m之间振动，二阶模态在0.000 4 m之间振动，均无法完全停止振动。从而验证了抑振方案的有效性。

为验证控制方法中死区补偿的有效性，图 7为关闭死区补偿时基座与两关节铰轨迹跟踪误差图。通过比较可知，关闭死区补偿后，关节1的最大跟踪误差约为0.08 rad，关节2的最大跟踪误差约为0.12 rad，两关节铰跟踪误差始终均无法收敛。

5 结论

1) 考虑了弹性基座、两柔性杆之间的多重耦合作用，推导了基座、臂杆全弹性空间机器人的动力学方程。

2) 基于奇异摄动方法，将系统分解为慢变、快变子系统，分别描述刚性的运动、弹性基座与两杆柔性的振动。针对慢变子系统，设计了存在关节力矩输出死区与外部干扰情况时基于动态面的高斯基模糊控制器；快变子系统采用了最优二次型控制器。组合控制方案不仅能克服死区对系统的不良影响，保证基座、臂杆全弹性空间机器人系统跟踪θ_d，而且能同时主动抑制柔性振动，克服了惯性参数未知的影响，达到控制要求。

3) 本文为理论探索和储备研究，当硬件条件及相关假设达到要求，则本控制方案可以实现对实际系统的指导和应用。经适当推广，可应用于多自由度的一般空间机械臂系统。