2. 浙江贵仁信息科技股份有限公司, 浙江 杭州 310051
2. Zhejiang Keepsoft Information & Technology Corp., LTD, Hangzhou 310051, China
台风引起的台风浪和风暴潮很容易造成近岸浅滩大量泥沙的起动,在短时间内能造成航道或港池的强淤和堤防、防波堤等港口航道与海岸及近海工程建筑物遭到严重损坏。因此,工程海域台风浪、风暴潮以及泥沙输移、港口航道淤积等的数值模拟和预测是当前各国科研人员重点关注的研究热点。
由于河口海岸岸线曲折、工程边界复杂、水深变化大、水流结构复杂,为了更加准确地模拟台风浪风暴潮作用下的泥沙输移、海床演变、港池航道强淤,有必要进行台风浪风暴潮作用下三维潮流数值模拟技术的研究,并建立相应的数学模型,重点需要做好以下几个方面的研究。
台风风场气压场模拟方面:常用的有参数模型、中尺度大气模式(MM5)和中尺度大气模式(WRF),其中,台风参数模型由于编程简单、使用方便被广泛应用,而MM5有被WRF替代的趋势。杨洋[1]基于Jelesnianski2型风场模式、藤田气压模式导出风场模式,开发了台风风场气压场的参数模型,并将模拟结果与NCAR资料的背景风场进行合成。由于各个台风风场气压场个性化差异较大,朱志夏等[2]根据目前国内外最著名的台风参数模式,考虑背景风场的影响,开发了台风风场与气压场模拟系统V1.0。包括8个台风风场模型和相应的气压场模式,可以根据各个台风风场的特点,选择最合适的计算模式。朱志夏([3]利用强台风“韦帕”(2007年13号台风)的资料及区域内风、浪、气压、水文等相关资料,应用中尺度大气模式MM5模拟了台风WIPHA的风场和气压场。王杨杰[4]采用MCT耦合器、中尺度大气模式WRF、三维非结构化网格海洋模式FVCOM和第3代海浪模式SWAN,初步建立了大气-海洋-波浪实时耦合模式。
网格嵌套方面:常用的有结构化和非结构化网格,其中,非结构化网格局部加密更适合于模拟曲折的河口海岸岸线、复杂的工程边界,被广泛应用。通常有3种嵌套方法:结构化网格与结构化网格、结构化网格与非结构化网格和非结构化网格与非结构化网格。Cheung等[5]、朱志夏[3]毛科峰等[6]采用三重结构化网格嵌套方法,建立了海洋、近海、近岸破波带三重结构化网格嵌套波浪模型,分别模拟了美国夏威夷海域飓风Iwa、Iniki、我国沿海台风“韦帕”、西北行路径的台风浪传播过程。但是由于河口、近海和近岸水域地形非常复杂、岸线曲折多变,尤其是受众多近海和近岸工程的影响以及结构化网格的缺陷,未能比较精确地模拟波浪的传播。朱志夏[7]采用非结构化网格之间嵌套技术,建立了大区域和浅海工程海域嵌套波浪数学模型,计算结果与实测值更加吻合。
波浪潮流耦合的三维潮流数值模拟方面:梁丙臣[8]根据海岸、河口区的特点,基于国际著名的水动力-生态-悬浮泥沙耦合模式COHERENS-SED和第3代波浪模式SWAN,充分考虑了风、浪、流的作用,对COHERENS-SED进行了完善与发展。在波流耦合研究方面,建立了波流耦合的三维潮流数学模型,并应用结构化网格二重嵌套的方法,分别采用时空均匀的风速为5、10、15 m/s的东北风以及大气模式MM5计算的以小时为分辨率的风场数据作为驱动风场,将其模型成功应用于黄河三角洲滨海区的潮流的研究。王红[9]采用大、中、小三重结构化网格二、三维嵌套模式,进行风浪、潮流耦合模拟,基于第3代波浪模式SWAN和三维水动力-多组分泥沙模型EFDC,建立了波流耦合的三维潮流数学模型。并将模型应用于潍坊港海域实际工程问题的研究。由于三维模拟海域存在防波堤,导致采用结构化网格模拟防波堤附近水动力时有些失真。堵盘军[10]基于第3代波浪模式SWAN和ECOMSED模式的改进和优化,建立了长江口、杭州湾三维泥沙数值模型系统,在波流耦合研究方面,建立了波流耦合的三维潮流数学模型,为长江口、杭州湾海域三维悬沙数值模拟的初步研究奠定了基础。王平[11]根据考虑流场效应的椭圆型缓坡方程,考虑了流场的流速、流向及水位等影响,建立一个适用于近岸大范围计算非结构化网格的波浪数值模型。然后,结合水动力泥沙模型FVCOM,在波流耦合研究方面,考虑了波致辐射应力、波浪紊动及波流边界条件等因素,构建了近岸大范围三维波流耦合模型。并将上述模型成功地应用于大连湾海域和旅顺琥珀湾海域。
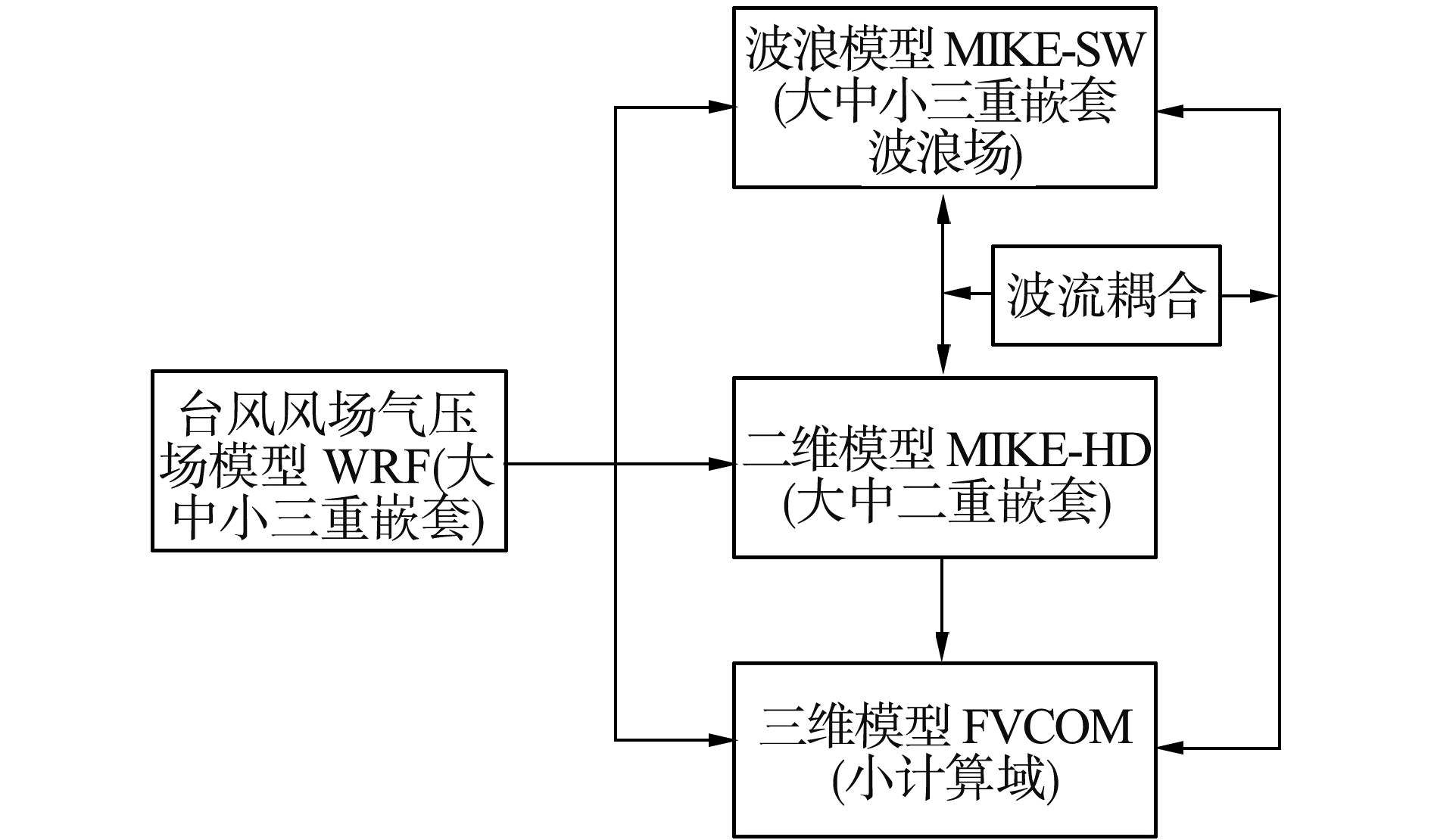
综上所述,台风作用下波浪潮流耦合三维潮流数值模拟技术仍有待进一步研发。为此,本研究结合上述各个方面的优势,应用中尺度大气模式WRF、第3代二维波浪模型MIKE21-SW、二维潮流模型MIKE21-HD和基于非结构化网格有限体积法的三维水动力泥沙模型FVCOM,采用非结构化网格三重嵌套技术,通过模拟系统的二次开发,建立了台风作用下波浪潮流耦合三维潮流数值模拟系统(如图 1)。本文着重讨论台风作用下三维潮流的模拟,通过二次开发,解决波流耦合问题,同时在三维潮流模型中增加波浪辐射应力和波流底部剪切应力的计算功能,并将模型应用于连云港港30万t级浅滩深开挖航道工程的研究。
|
Download:
|
| 图 1 数值模拟系统框 Fig. 1 Numerical simulation system diagram | |
FVCOM(finite-volume coastal ocean model)采用非结构化三角形网格单元,适合曲折多变的工程、海岸边界;计算方法上应用有限体积法,能够更好地保证各物理量的守恒;垂向采用σ坐标,可以模拟多变的海底地形;此外,具有并行化计算功能,可以大大缩短数值计算时间。
1) 三维潮流数学模型控制方程:
| $ \begin{aligned} \frac{\partial u}{\partial t} &+u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}+w \frac{\partial u}{\partial z}-f v=\\ &-\frac{1}{\rho} \frac{\partial P}{\partial x}+\frac{\partial}{\partial z}\left(K_{m} \frac{\partial u}{\partial z}\right)+F u \end{aligned} $ | (1) |
| $ \begin{aligned} \frac{\partial v}{\partial t} &+u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}+w \frac{\partial v}{\partial z}+f u=\\ &-\frac{1}{\rho} \frac{\partial P}{\partial y}+\frac{\partial}{\partial z}\left(K_{m} \frac{\partial v}{\partial z}\right)+F v \end{aligned} $ | (2) |
| $ \frac{\partial P}{\partial z}=-\rho g $ | (3) |
| $ \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}+\frac{\partial w}{\partial z}=0 $ | (4) |
式中:Km为垂向涡动粘性系数;Fu、Fv分别代表水平动量扩散项。波浪产生的水平紊动系数采用Larson-Kraus公式计算,垂向紊动系数采用VanRijn公式计算。采用M-Y 2.5阶湍流闭合模型。
2) 边界条件。
自由表面处,即σ坐标等于0处,运动学边界条件为:w(x, y, 0, t)=0;动力学边界条件为:
| $ \left(\frac{\partial u}{\partial \sigma}, \frac{\partial v}{\partial \sigma}\right)=\frac{D}{\rho_{0} K_{m}}\left(\tau_{\mathrm{s}x}, \tau_{s y}\right) $ | (5) |
式中:τsx、τsy分别为风应力矢量在x和y方向的分量。
海底处,即σ坐标等于-1处的运动学边界条件为:w(x, y, -1, t)=0;动力学边界条件为:
| $ \left(\frac{\partial u}{\partial \sigma}, \frac{\partial v}{\partial \sigma}\right)=\frac{D}{\rho_{0} K_{m}}\left(\tau_{b x}, \tau_{b y}\right) $ | (6) |
岸边界,水质点沿岸线的切线方向自由滑移,法向流速为零。开边界,通过强加流量或强加自由表面水位作为模型的驱动条件。
1.2 模型的改进1) 波生流的引入。
考虑到近岸地区的波浪效应,在三维基本方程中增加波浪辐射应力项,控制方程变为:
| $ \begin{array}{c}{\frac{\partial u D}{\partial t}+\frac{\partial u^{2} D}{\partial x}+\frac{\partial u v D}{\partial y}+\frac{\partial u \omega}{\partial \sigma}-f v D=} \\ {-g D \frac{\partial \zeta}{\partial x}-\frac{g D}{\rho_{0}}\left[\frac{\partial}{\partial x}\left(D \int\limits_{\sigma}^{0}\rho d \sigma^{\prime}\right)+\sigma \rho \frac{\partial D}{\partial x}\right]+} \\ {\frac{1}{D} \frac{\partial}{\partial \sigma}\left(K_{m} \frac{\partial u}{\partial \sigma}\right)+D F_{x}-\frac{\partial D S_{x x}}{\partial x}-\frac{\partial D S_{x y}}{\partial y}+\frac{\partial S_{p x}}{\partial \sigma}}\end{array} $ | (7) |
| $ \begin{array}{c}{\frac{\partial v D}{\partial t}+\frac{\partial u v D}{\partial x}+\frac{\partial v^{2} D}{\partial y}+\frac{\partial v \omega}{\partial \sigma}+f u D=} \\ {-g D \frac{\partial \zeta}{\partial y}-\frac{g D}{\rho_{0}}\left[\frac{\partial}{\partial y}\left(D \int\limits_{\sigma}^{0} \rho \mathrm{d} \sigma^{\prime}\right)+\sigma \rho \frac{\partial D}{\partial x}\right]+} \\ {\frac{1}{D} \frac{\partial}{\partial \sigma}\left(K_{m} \frac{\partial v}{\partial \sigma}\right)+D F_{y}-\frac{\partial D S_{x y}}{\partial x}-\frac{\partial D S_{yy}}{\partial y}+\frac{\partial S_{p y}}{\partial \sigma}}\end{array} $ | (8) |
| $ \frac{\partial P}{\partial \sigma}=-\rho g D $ | (9) |
| $ \frac{\partial \zeta}{\partial t}+\frac{\partial D u}{\partial x}+\frac{\partial D v}{\partial y}+\frac{\partial D \omega}{\partial \sigma}=0 $ | (10) |
式中:Sxx、Sxy、Syy分别为辐射应力项,采用Mellor辐射应力公式计算。
首先,应用建立的数值模型进行波浪水槽计算,模拟计算Ting等[12]在实验室进行的波浪实验,破波带内外的垂向流速计算值与实验值较为一致[13]。然后,模拟了在一个正弦地形的岸滩上由波浪引起的裂流(Rip Crrent)现象,模拟结果与Borthwick等[14]的UKCRF实验的流场形态符合良好[13]。
2) 增加波流共同作用底部剪切应力。
在近岸海域,尤其在台风天气条件下,波浪作用尤为重要,因此,在三维泥沙模型中增加由Grant and Madsen(1979)[15]提出的波、流共同作用下海底剪切应力的计算方法。波流共同作用下底部摩阻流速和剪切应力为:
| $ u_{* c w}=\left(u_{* c}^{2}+u_{* w}^{2}+2 u_{* c} u_{* w} \cos \phi_{c w}\right)^{1 / 2}=C_{D}^{b} u_{c} $ | (11) |
| $ \boldsymbol{\tau}_{c w}=\rho u_{* c w} u_{* c w} $ | (12) |
式中:τcw为波流共同作用的底部剪切应力;u*cw为波流共同作用的摩阻流速;u*w为波浪摩阻流速;u*c为水流摩阻流速;ϕcw为二者之间的夹角;CDb波流共同作用下的摩阻系数。波流共同作用摩阻流速的计算式为:
| $ u_{* c w}^{2}=\frac{1}{2} f_{w} U_{w}^{2}, U_{w}=\frac{0.5 H \omega}{\sinh (k h)} $ | (13) |
式中:fw为波浪摩擦因子,可由经验公式Signellctal确定:
| $ f_{w}=\left\{\begin{array}{ll}{0.13\left(k_{b} / A_{b}\right)^{0.4}, } & {k_{b} / A_{b}<0.08} \\ {0.23\left(k_{b} / A_{b}\right)^{0.28}, } & {0.08<k_{b} / A_{b}<1.00} \\ {0.23, } & {k_{b} / A_{b}>1.00}\end{array}\right. $ | (14) |
在波流共同作用边界层内,离海床上高度为zr的近底层流速uc,波流共同作用摩阻系数CDb,可联立下面两式,循环迭代求解得到:
| $ C_{D}^{b}=\frac{\kappa}{\ln \frac{30 z_{r}}{k_{b c}}}, k_{b c}=k_{b}\left(24 \frac{u_{* c w}}{U_{w}} \frac{A_{b}}{k_{b}}\right)^{\beta} $ | (15) |
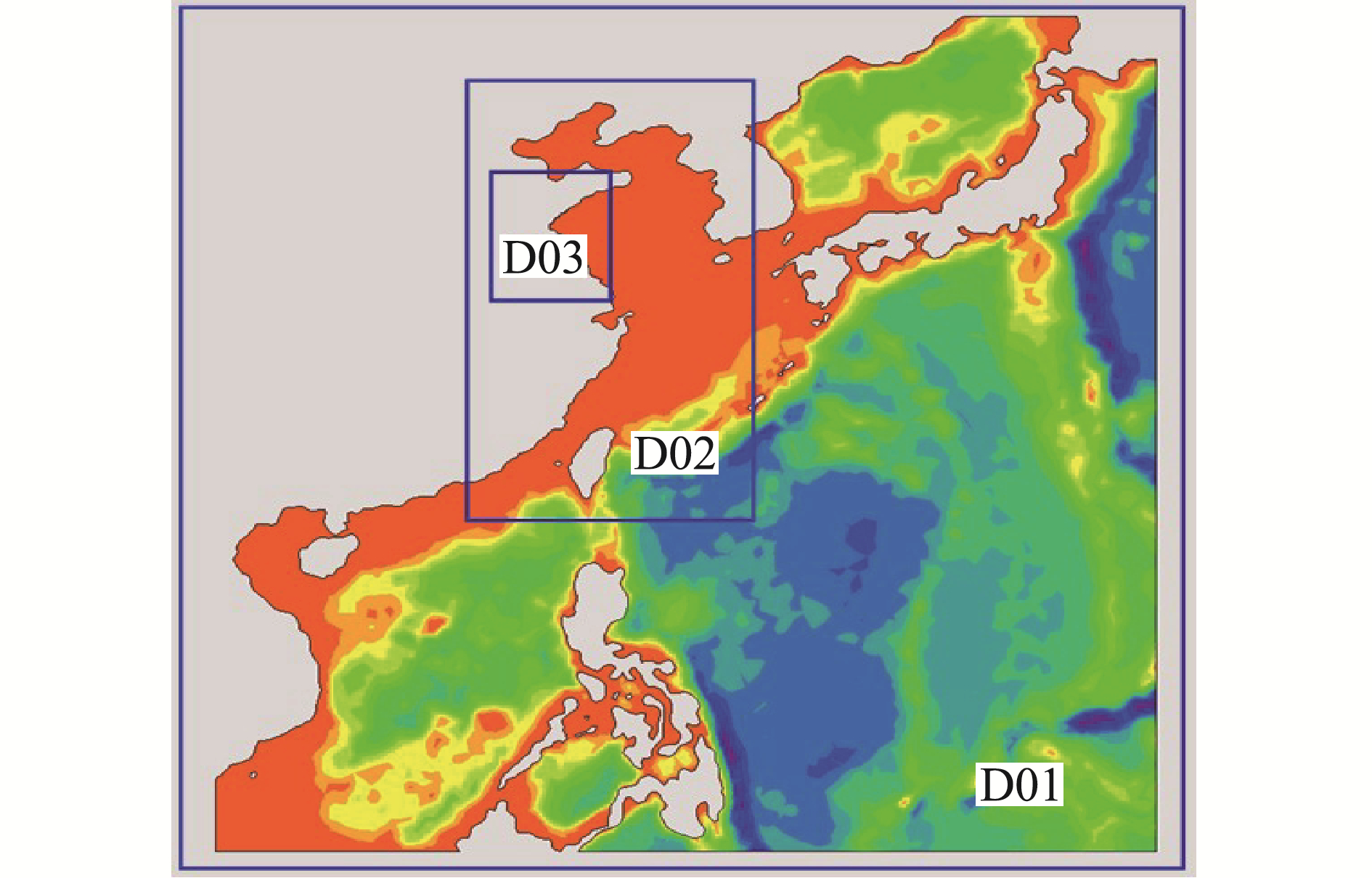
采用二维大、中模型和三维小模型三重非结构化嵌套的方法,如图 2所示。模拟计算连云港港及其附近海域韦帕台风作用下的三维潮流流场[13]。其中,大范围(D01:北纬5.0°~45.0°, 东经105.0°~145.0°)台风作用下二维波浪潮流耦合数学模型为中范围(D02:北纬21.0°~42.0°, 东经115.0°~128.0°)台风作用下二维波浪潮流耦合数学模型提供边界条件;中范围台风作用下二维波浪潮流耦合数学模型为三维小模型提供边界条件;小范围三维模型计算范围(D03)北起岚山头,南至中山河附近,计算域为北纬34°22.1′~35°6.6′, 东经116°0.0~120°8.8′,模型采用非结构化三角形网格,网格最小尺度为20 m,位于连云港主港区和主航道处,网格最大尺度为2 000 m,位于计算域的深水开边界处。垂向均匀分为10层。底部摩阻系数取值范围为0.002 5~0.003 5。
|
Download:
|
| 图 2 三重网格嵌套示意 Fig. 2 Three grid nesting schematic | |
为了准确地模拟连云港港及其附近海域韦帕台风作用下的三维潮流过程,根据天津市气象科学研究所应用WRF中尺度预报模式和美国环境预报中心NCEP历史再分析数据,在天河一号大型计算机上,模拟再现了整个韦帕台风过程[13]。模拟中采用超高分辨率的三重网格嵌套技术,计算域D01、D02、D03的分辨率分别为9、3、1 km,为韦帕台风作用下波浪、潮流的模拟提供了准确的驱动风场,模拟计算时间为2007年9月17日0时~9月21日20时,共计117小时。
1) 三维潮流验证。
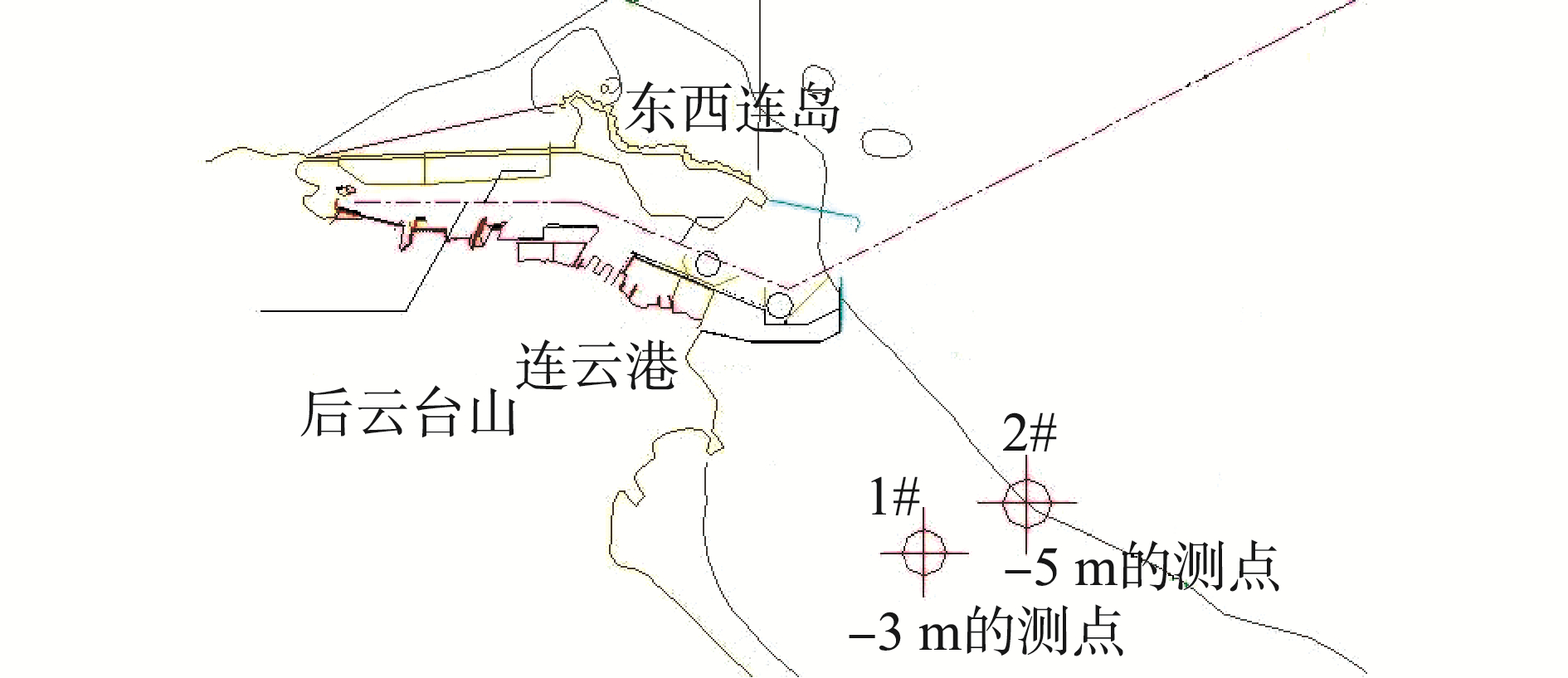
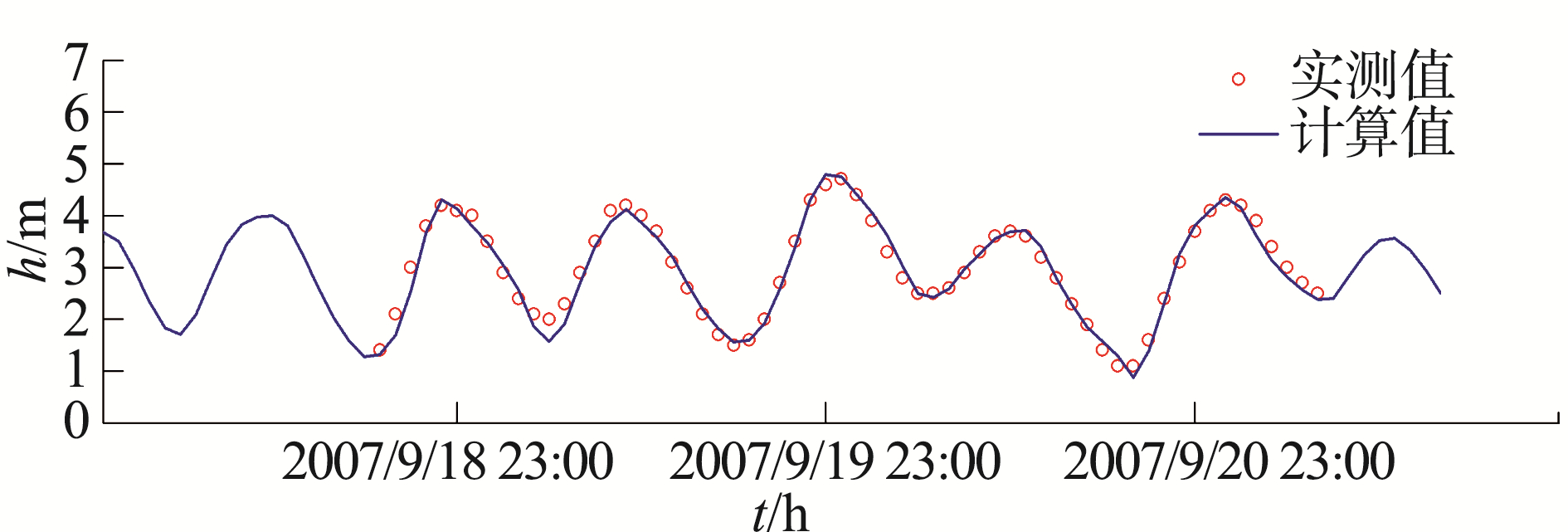
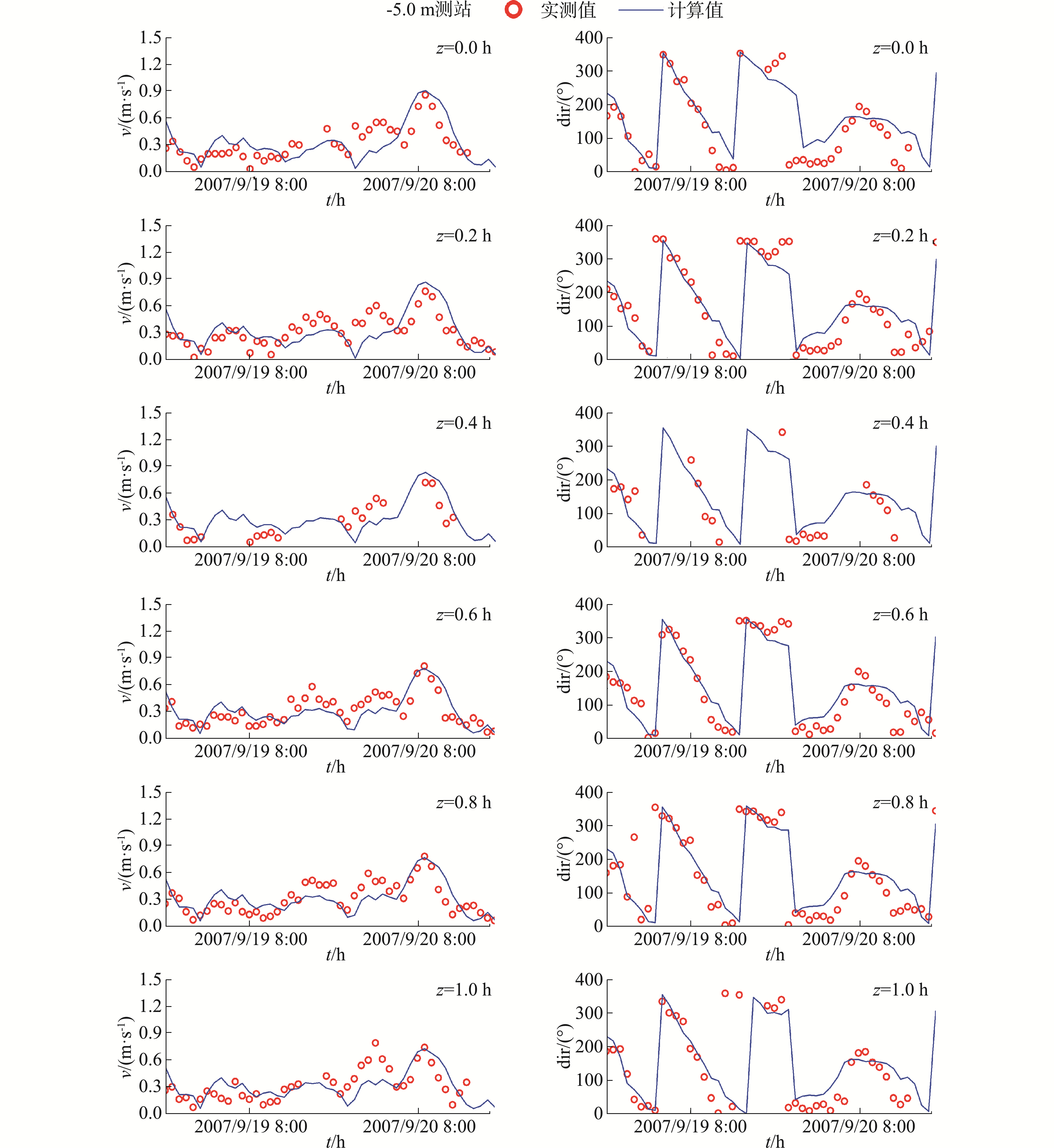
在三维潮流数值模拟计算中,潮位、潮流、波浪、风场等均由二维嵌套模型提供[13],三维模型外模计算时间步长为1.0 s,内模计算时间步长是外模的5倍。根据韦帕台风期间实测的波浪水文资料[16],其中1#点位于-3.0 m等深线,2#位于-5.0 m等深线(如图 3所示)。对韦帕台风作用下三维潮流数学模型进行了率定与验证。其中,2#测站的潮位、流速流向过程的验证结果分别如图 4、图 5所示。
|
Download:
|
| 图 3 水文观测点位置 Fig. 3 Hydrological observation point location | |
|
Download:
|
| 图 4 2#观测点潮位验证 Fig. 4 Verification of tidal level at observation point 2# | |
|
Download:
|
| 图 5 2#观测点流速流向验证 Fig. 5 Verification of tidal current velocity and direction at observation point 2# | |
潮位和流速过程验证曲线表明:模型的计算值与现场实测值基本一致,趋势吻合较好,基本反映了台风作用下的该海域潮流运动特性。
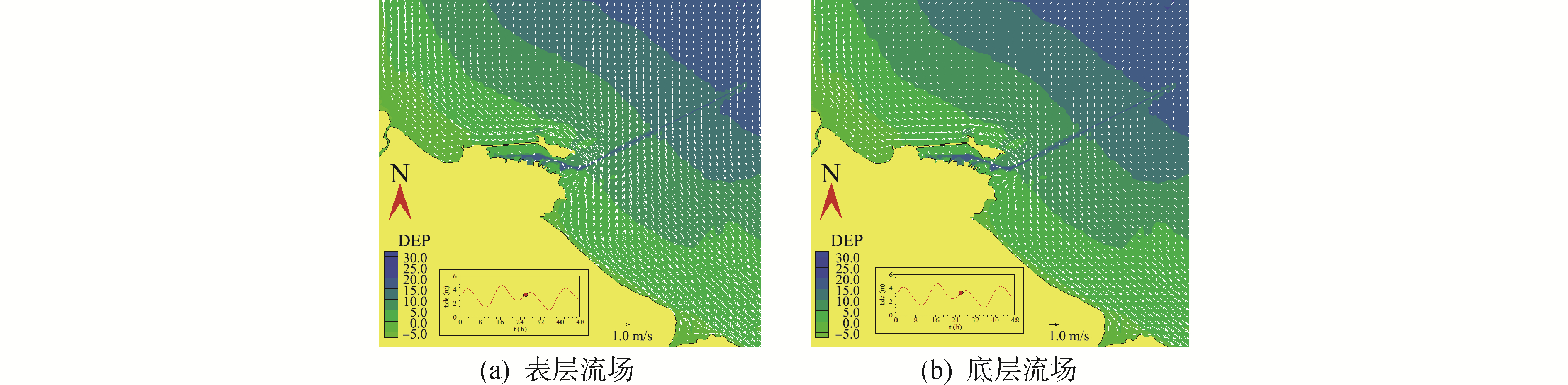
受韦帕台风影响,2007年9月19日18时以后,航道工程海域发生明显的增水现象;9月20日0时,观测站风速已达18.9 m/s,但由于台风刚作用2 h,大风持续时间较短,流场尚未发生大的改变;9月20日9时,观测站风速达到20.4 m/s,台风已经持续作用近15 h,流场发生了很大变化,以风吹流为主,与常风下的流场形态有较大的区别(如图 6所示)。因此,韦帕台风作用下三维潮流的模拟结果是比较合理的,为进一步进行深水航道工程的方案计算奠定了坚实的基础。
|
Download:
|
| 图 6 2007年9月20日9时表层、底层流场 Fig. 6 Surface and bottom flow field at 9 o ′clock on September 20, 2007 | |
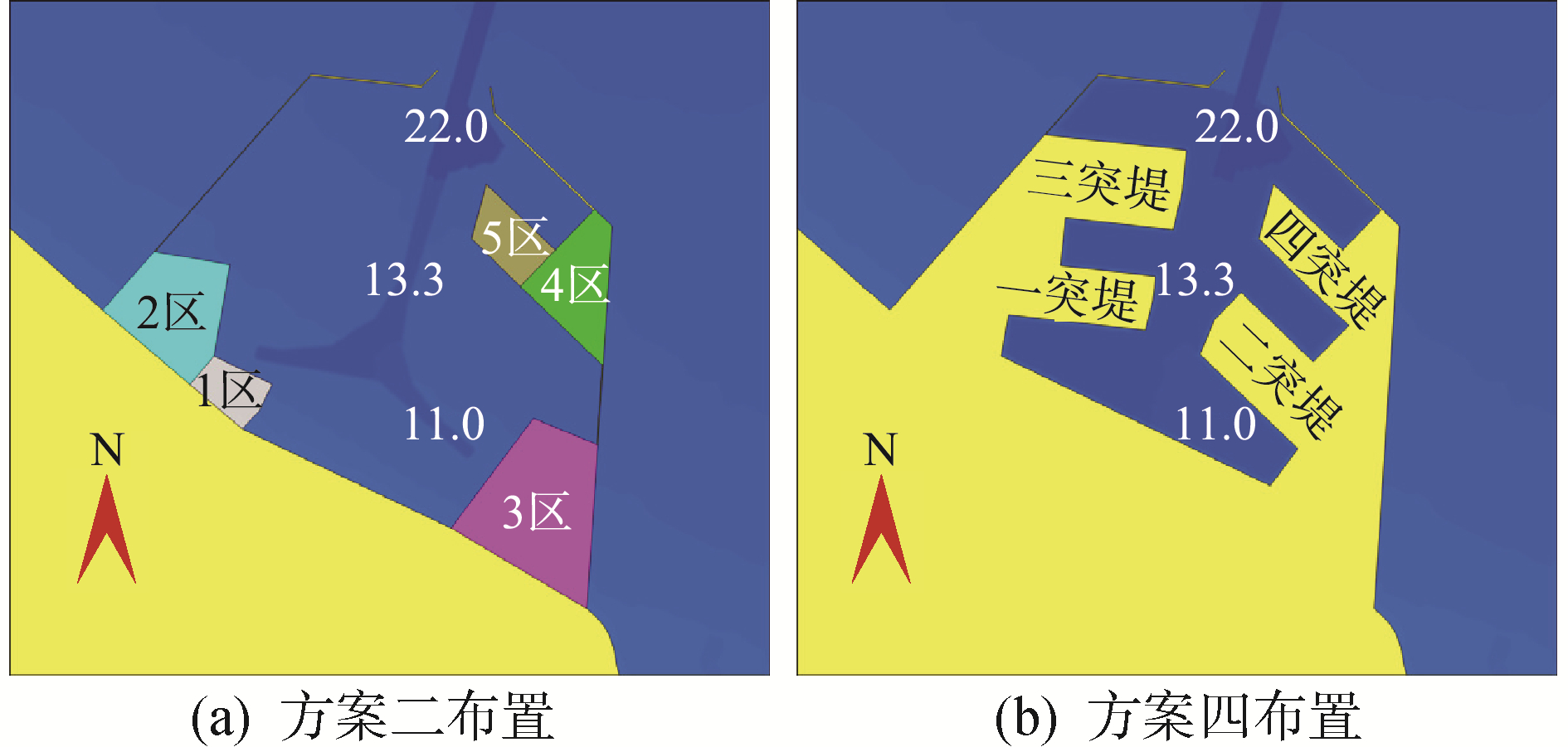
连云港港30万吨级航道工程由连云港区航道、连云港区外航道、徐圩进港航道组成,其中,连云港区外航道外段宽350 m,底标高-23.0 m,外航道内段宽310 m,底标高-22.5 m;徐圩进港航道宽370 m,底标高-22.0 m,徐圩港区内航道宽210 m,底标高-13.3 m;徐圩二港池航道宽170 m,底标高-11.0 m。徐圩港区防波堤口门分为“平口”、“八字口”,结合不同港内围垦工程方案布置,分为4个方案,本文以方案2、方案4为例进行分析,具体布置如图 7所示。
|
Download:
|
| 图 7 方案二、方案四布置 Fig. 7 Layout of plan 2 and 4 | |
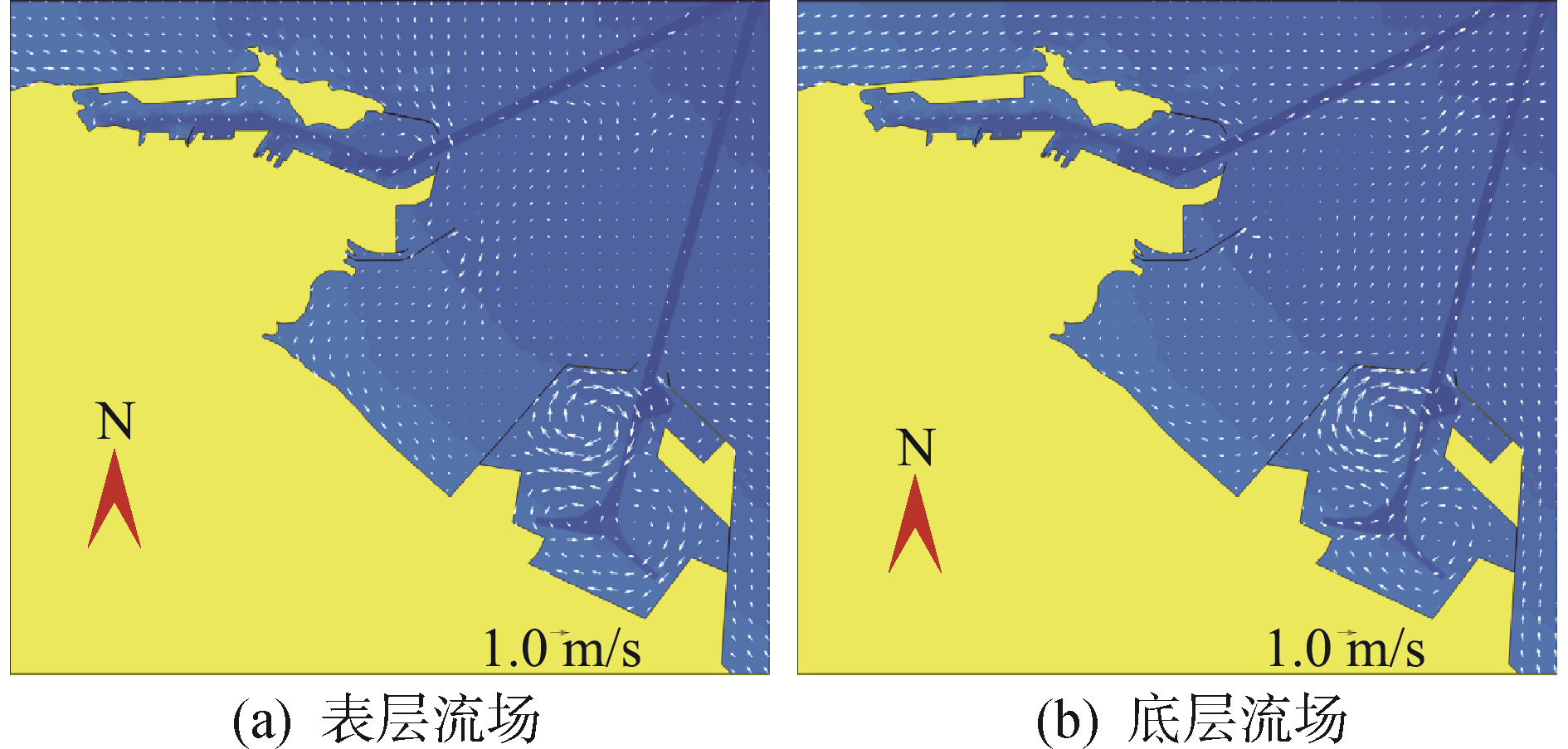
2007年9月20日0时,高潮位附近,工程海域流流速较小,表层、底层流场基本一致,防波堤内环流明显(图 8、图 9);到9月20日9时,受韦帕台风持续作用已达15 h,沿岸流动水体的范围进一步扩大,在近岸浅水区域,水体在垂向上作为一个整体对台风作用做出响应,沿岸流动趋势非常明显,近岸三维潮流表层和底层流态基本一致,呈现由西北向东南的沿岸流动(图 10、图 11);9月21日10时,台风已经过境连云港海域,流场恢复为常态,表层流场和底层流场一致,为常态天气下的涨潮流场。因此,韦帕台风作用下,潮流场会发生非常显著的变化。
|
Download:
|
| 图 8 2007年9月20日0时方案二流场(表层、底层) Fig. 8 Plan 2 flow field at 0 o ′clock on September 20, 2007(surface and bottom) | |
|
Download:
|
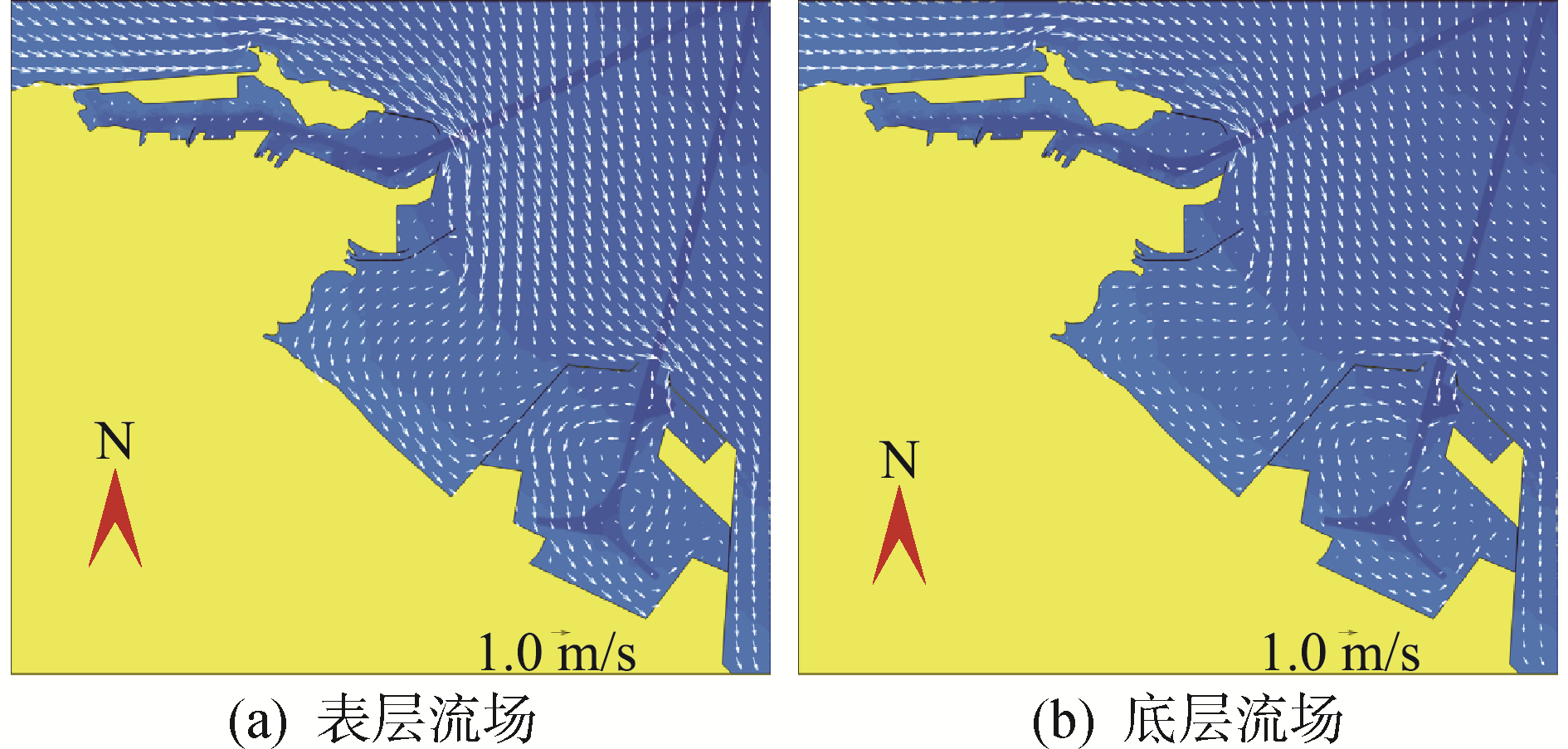
| 图 9 2007年9月20日0时方案四流场(表层、底层) Fig. 9 Plan 4 flow field at 0 o ′clock on September 20, 2007(surface and bottom) | |
|
Download:
|
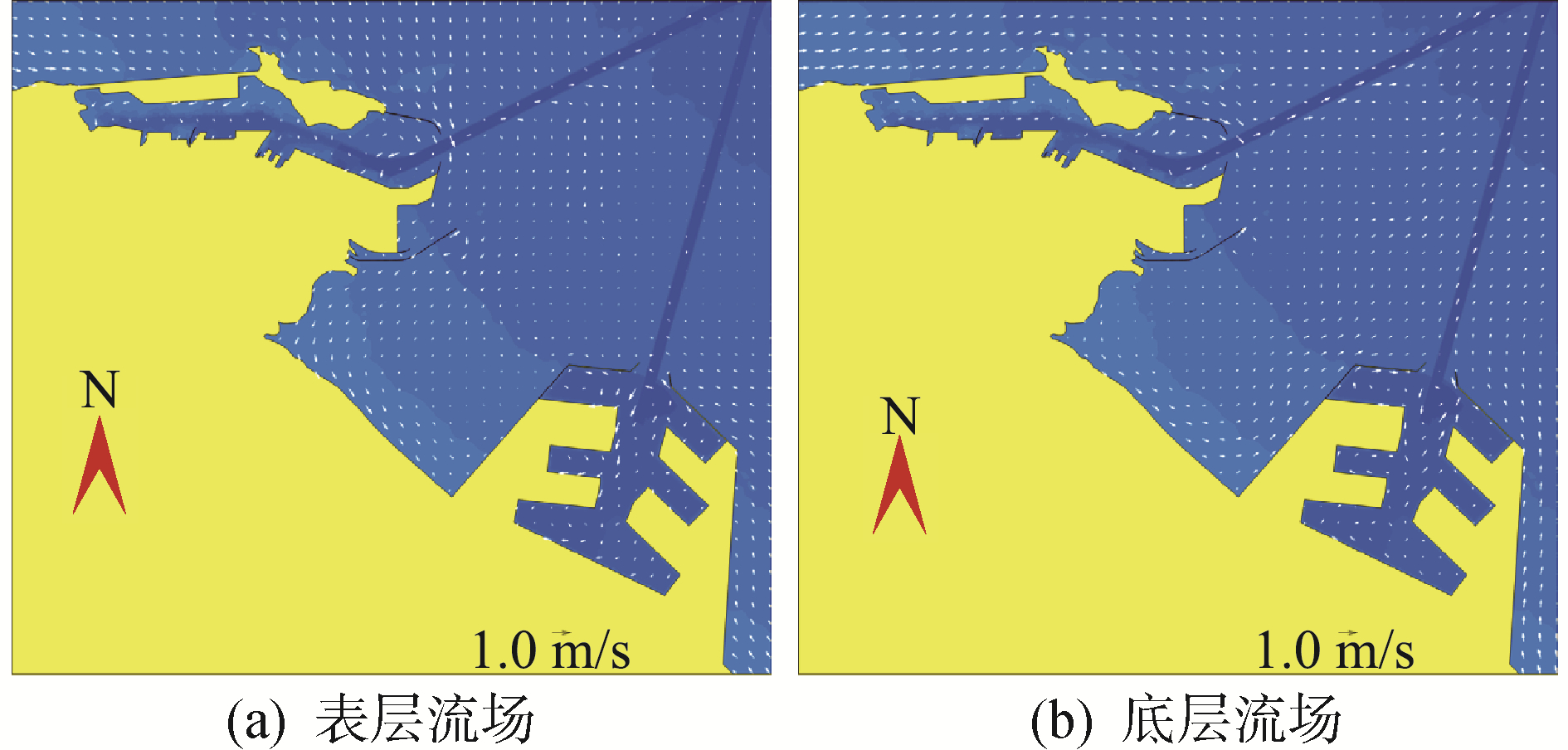
| 图 10 2007年9月20日9时方案二流场(表层、底层) Fig. 10 Plan 2 flow field at 9 o ′clock on September 20, 2007(surface and bottom) | |
|
Download:
|
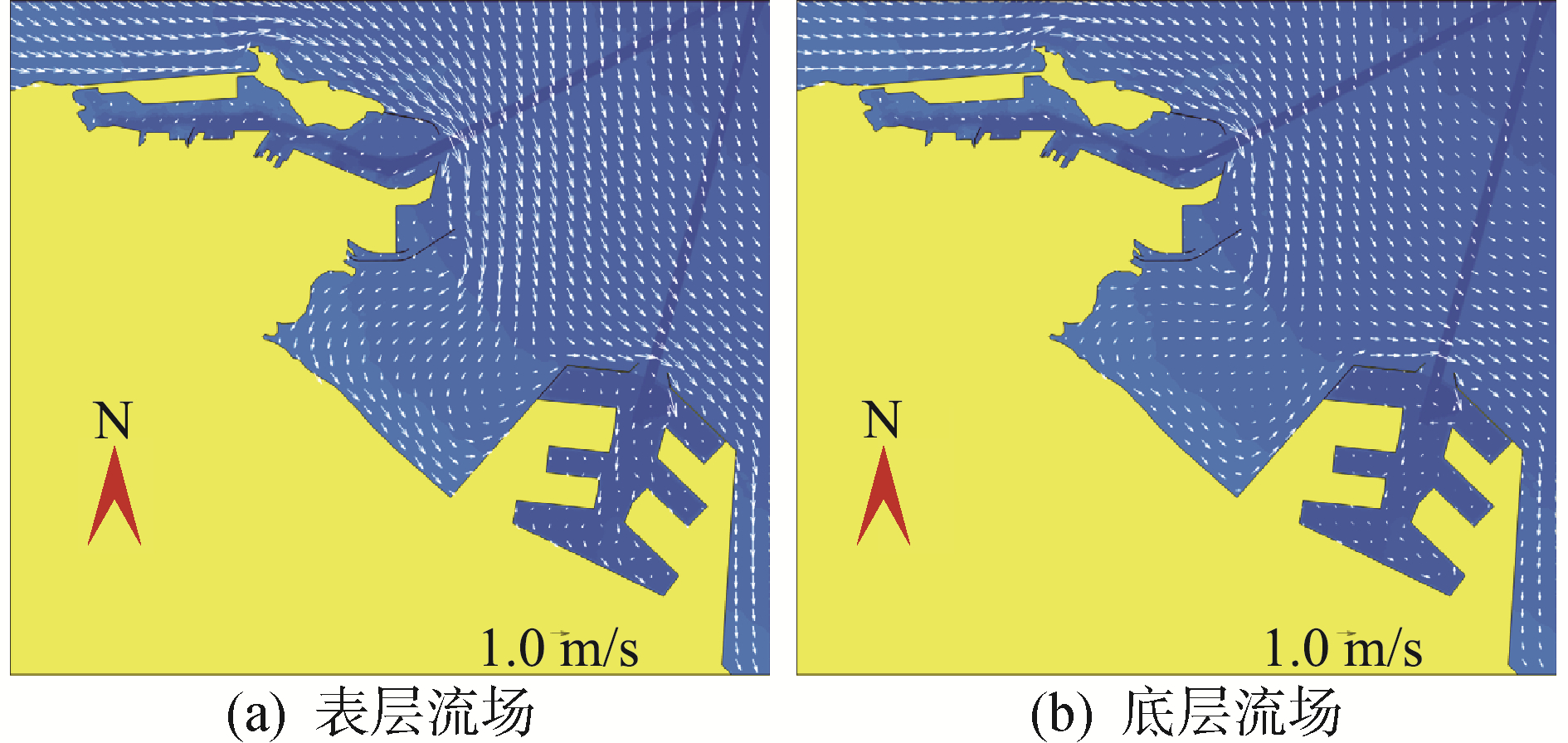
| 图 11 2007年9月20日9时方案四流场(表层、底层) Fig. 11 Plan 4 flow field at 9 o ′clock on September 20, 2007(surface and bottom) | |
由方案2、方案4连云港港旗台港区港池和徐圩港区港池在不同时刻的表层、底层流场图(图 8~图 11)得到:旗台港区内水域的流态和流速在各方案和各个计算时刻差异均较小;徐圩港区内水域由于各方案中围填区域的面积大小不同,流态和流速都有较大的差异。其中,方案2港内围填区域的面积相对较小,水域面积较大,存在大范围的环流现象,且环流流速较大;方案4,港内围填工程全部形成,港池内大范围环流现象已不存在,流速进一步减小,即使在风暴潮流最大时刻,除口门处流速较大外,港池内的流速也小于0.5 m/s。由此可见:在韦帕台风作用下,徐圩港区内围填区域的面积大小对港池内的流态、流速影响较大,具体特征为:随着港区内围填工程面积的增大,港池内大范围环流现象逐渐消失,流速也随之变小。
4 结论1) 基于三重网格嵌套的超高分辨率(分辨率分别为9 km、3 km、1 km)韦帕台风风场,应用第3代波浪模型MIKE21-SW、二维潮流模型MIKE21-HD和基于非结构化网格有限体积法的三维水动力泥沙模型FVCOM,以二维、三维大、中、小模型三重嵌套的方式,主要解决了波流耦合问题和三维模型中增加波浪辐射应力和波流底部剪切应力的计算功能,建立了台风作用下波流耦合的三维潮流数学模型。
2) 应用台风作用下波流耦合的三维潮流数学模型,模拟了2007年韦帕台风作用下连云港海域波流耦合的三维潮流过程,模拟计算的水位、分层流速流向过程与实测值吻合良好,较好地反映了韦帕台风作用下连云港海域的潮流特征。
3) 旗台港区内水域的流态和流速在各方案和各个计算时刻差异均较小;徐圩港区内水域由于各方案中围填区域的面积大小不同,流态和流速都有较大的差异,随着港区内围填工程面积的增大,港池内大范围环流现象逐渐消失,流速也随之变小。
| [1] |
杨洋.西北太平洋台风浪后报[D].上海: 上海交通大学, 2009. YANG Yang. Numerical simulation of typhoon waves in northwest Pacific Ocean[D]. Shanghai: Shanghai JiaoTong University, 2009. (  0) 0)
|
| [2] |
朱志夏, 齐庆辉.台风风场与气压场模拟系统V1.0(软件著作权2014SR090773).江苏省交通规划设计院股份有限公司, 2014.
(  0) 0)
|
| [3] |
朱志夏.致灾台风浪数学模型[R].上海: 上海交通大学, 2009: 1-50.
(  0) 0)
|
| [4] |
王扬杰.基于大气-海洋-海浪实时耦合模式的台风过程模拟研究[D].天津: 天津大学, 2016. WANG Yangjie. Typhoon process simulation based on a coupled atmosphere-ocean-wave model[D]. Tianjin: Tianjin University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10056-1017128207.htm (  0) 0)
|
| [5] |
CHEUNG K F, PHADKE A C, WEI Y, et al. Modeling of storm-induced coastal flooding for emergency management[J]. Ocean engineering, 2003, 30(11): 1353-1386. DOI:10.1016/S0029-8018(02)00133-6 (  0) 0)
|
| [6] |
毛科峰, 陈希, 萧中乐, 等. 复杂岛屿海域的台风浪局地特征模拟与分析——以舟山海域为例[J]. 海洋学研究, 2011, 29(4): 8-15. MAO Kefeng, CHEN Xi, XIAO Zhongle, et al. Numerical simulation and analysis of the local characteristics of typhoon waves in multi-islands sea area:an instance of the Zhoushan sea area[J]. Journal of marine sciences, 2011, 29(4): 8-15. DOI:10.3969/j.issn.1001-909X.2011.04.002 (  0) 0)
|
| [7] |
朱志夏. 非结构化网格嵌套波浪数值模拟[J]. 上海交通大学学报, 2016, 50(1): 152-157, 164. ZHU Zhixia. Nested wave numerical simulation of unstructured mesh[J]. Journal of Shanghai JiaoTong University, 2016, 50(1): 152-157, 164. (  0) 0)
|
| [8] |
梁丙臣.海岸、河口区波-流联合作用下三维悬沙数值模拟及其在黄河三角洲的应用[D].青岛: 中国海洋大学, 2005. LIANG Bingchen. Numerical simulations of three dimensional suspendend sediment transport with wave-current co-existing and its application in Huanghe Delta[D]. Qingdao: Ocean University of China, 2005. http://cdmd.cnki.com.cn/Article/CDMD-10423-2005140469.htm (  0) 0)
|
| [9] |
王红.三维多组分泥沙数学模型及其应用[D].天津: 天津大学, 2007. WANG Hong. 3D numerical model of multi-fraction sediment transport and its application[D]. Tianjin: Tianjin University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10056-2008186181.htm (  0) 0)
|
| [10] |
堵盘军.长江口及杭州湾泥沙输运研究[D].上海: 华东师范大学, 2007. DU Panjun. Sediment transport research in Yangtze Estuary and Hangzhou Bay[D]. Shanghai: East China Normal University, 2007. http://cdmd.cnki.com.cn/Article/CDMD-10269-2008033448.htm (  0) 0)
|
| [11] |
王平.非结构波流耦合模型及近岸物质输运应用研究[D].大连: 大连理工大学, 2014. WANG Ping. An unstructured wave-current coupled model and its application in the nearshore mass transport[D]. Dalian: Dalian University of Technology, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10141-1015572056.htm (  0) 0)
|
| [12] |
TING F C K, KIRBY J T. Observation of undertow and turbulence in a laboratory surf zone[J]. Coastal engineering, 1994, 24(1/2): 51-80. (  0) 0)
|
| [13] |
张娜, 杨华, 庞启秀, 等.连云港港30万吨级航道工程大风天波浪潮流泥沙三维数学模型研究[R].天津: 交通运输部天津水运科学研究院, 2014: 1-195.
(  0) 0)
|
| [14] |
BORTHWICK A G L, FOOTE Y L M. Wave-induced nearshore currents at a tri-cuspate beach in the UKCRF[J]. Proceedings of the institution of civil engineers-water and maritime engineering, 2002, 154(4): 251-263. DOI:10.1680/wame.2002.154.4.251 (  0) 0)
|
| [15] |
GRANT W D, MADSEN O S. Combined wave and current interaction with a rough bottom[J]. Journal of geophysical research:oceans, 1979, 84(C4): 1797-1808. DOI:10.1029/JC084iC04p01797 (  0) 0)
|
| [16] |
交通运输部天津水运工程科学研究所. 2007年9月台风"韦帕"过境时连云港波浪、潮流、泥沙现场观测报告[R].天津: 交通运输部天津水运工程科学研究所, 2008: 1-35.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


