大深度潜水器在上浮以及下潜过程中易受到海流等因素的干扰,近年来,全海深自主水下机器人成为世界各国学者的研究热点[1-2]。被广泛使用的常规潜艇的稳定性衡准公式仅适用潜水器定深直航的情况。潜水器上浮以及下潜的运动稳定性分析成为热点以及难点,被广泛关注。为此,本文正是基于这样的需求推导了全海深AUV变深直航运动稳定性衡准公式。
目前,对稳定性分析主要划分为李雅普诺夫直接法和Routh-Hurwitz判别法2类。李雅普诺夫直接法是通过构造李雅普诺夫函数定性分析潜水器的运动稳定性。在潜水器的非线性运动稳定性研究中被广泛应用。臧鹏飞[3]利用李雅普诺夫指数标准算法在系统参数与运动稳定性间建立量化关系,通过对潜水器的下潜、悬停以及直航的仿真分析得出系统稳定性的影响因素。但李雅普诺夫直接法在分析多自由度、强耦合的复杂非线性潜水器的运动稳定性时往往难以构造合适的函数,成为难点。而Routh-Hurwitz判别法是通过判断系统的特征根实部的符号判定潜水器的运动稳定性。刘振明等[4]应用Routh-Hurwitz判别法判定水下机器人在定深直航下的平面扰动运动微分方程的特征方程的特征根的实部符号,评价运动稳定性。本文通过建立全海深AUV的在上浮或下潜过程中的扰动运动微分方程。利用Routh-Hurwitz判别法的思想求得AUV在上浮或下潜中稳定性衡准公式做运动稳定性的分析。
1 全海深AUV上浮运动稳定性衡准公式全海深AUV上浮运动稳定性是指AUV在做定常的上浮(下潜)运动过程中,受瞬时微干扰后无控制AUV的运动特性。与常规潜艇的定深直航运动稳定性相比,全海深AUV上浮运动稳定性的评价同样采用静稳定性和动稳定性2类标准。其中,静稳定性反映仅有单个参数变化引起的在扰动力消失后最初瞬间AUV的运动趋势。但实际上AUV在受扰后会引起更多的水动力。因此,AUV运动稳定性应由全部作用力的综合效应而定,也就是所说的动稳定性[5-7]。
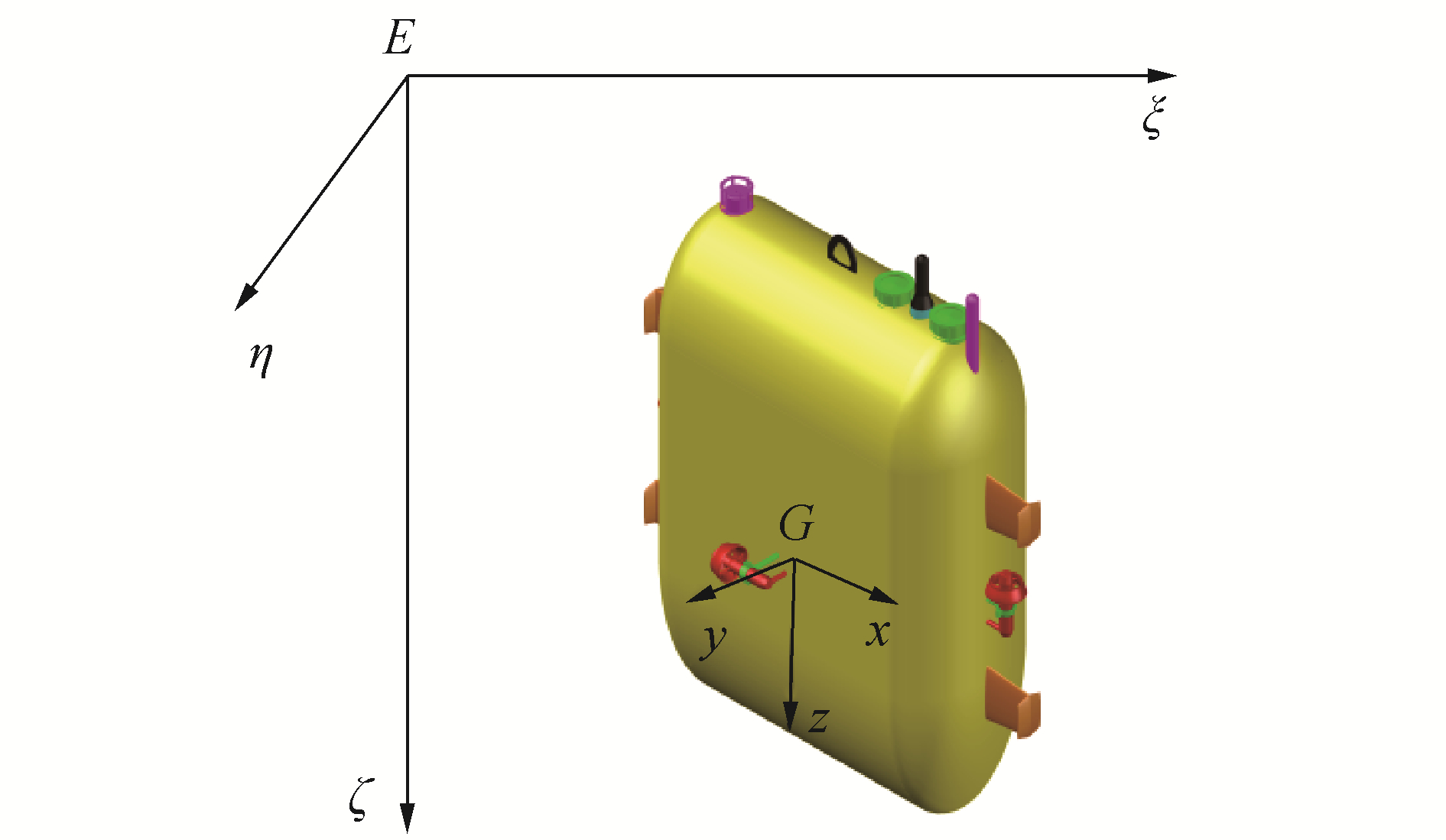
1.1 坐标系与水动力角σ、γ的定义根据公式推导需要,定义全海深AUV固定坐标系E-ξηζ(固定于地球)与运动坐标系G-xyz(固联于AUV)如图 1所示。
|
Download:
|
| 图 1 全海深AUV固定坐标系与运动坐标系 Fig. 1 Fixed coordinate system and motion coordinate system of the full ocean depth AUV | |
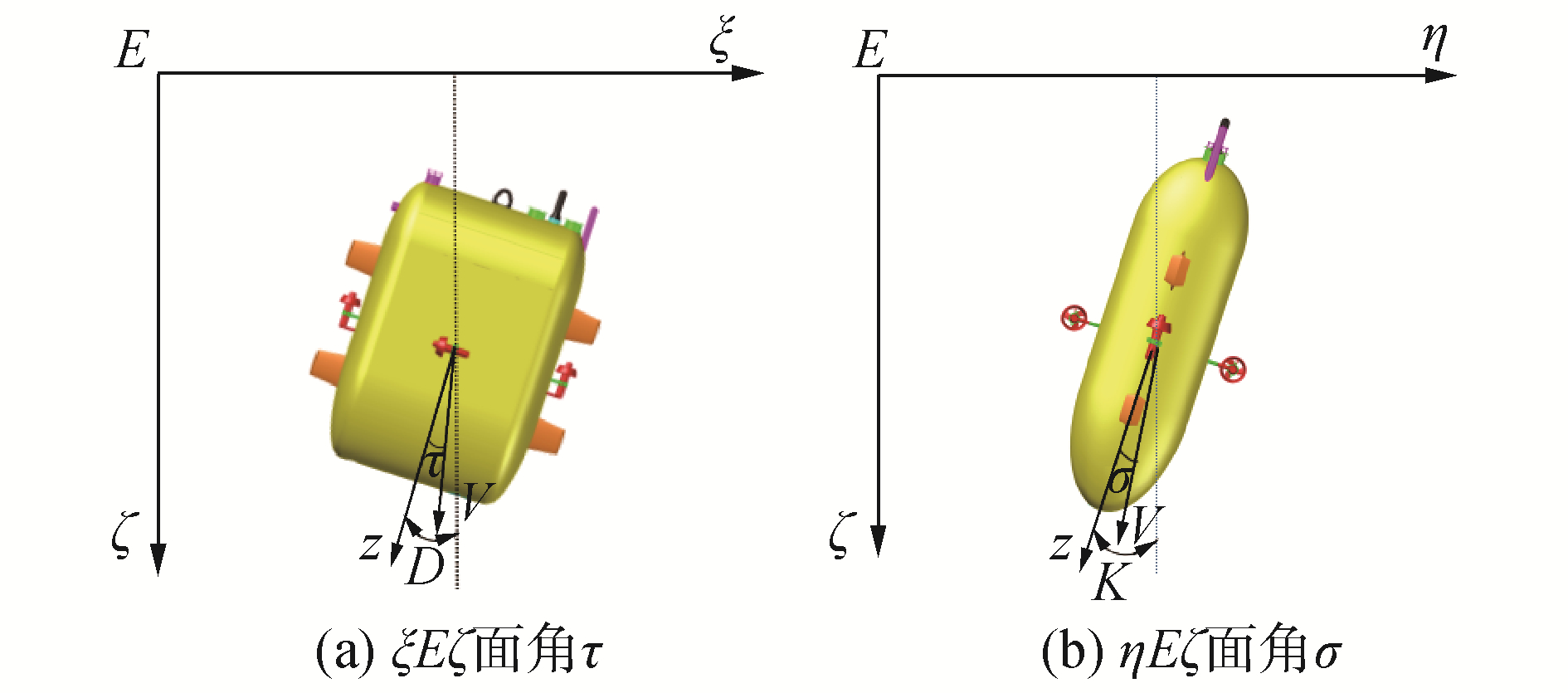
定义ξEζ面内水动力角τ、υ; ηEζ面内水动力角σ、κ如下:水动力角τ为ξEζ面内航速V的方向与Gz轴之间的夹角,规定自V→Gz逆时针为正,反之为负;角υ为在ξEζ面内Eζ轴与Gz轴间的夹角,规定自Eζ→Gz逆时针为正,反之为负。同样,ξEζ面内水动力角σ为ηEζ面内航速V的方向与Gz轴之间的夹角,规定自V→Gz顺时针为正,反之为负;角κ为在ηEζ面内Eη轴与Gz轴间的夹角,规定自Eη→Gz顺时针为正,反之为负,如图 2所示。
|
Download:
|
| 图 2 ξEζ面角τ、ηEζ面角σ Fig. 2 The angle τ of the ξEζ and the angle σ of the ξEζ | |
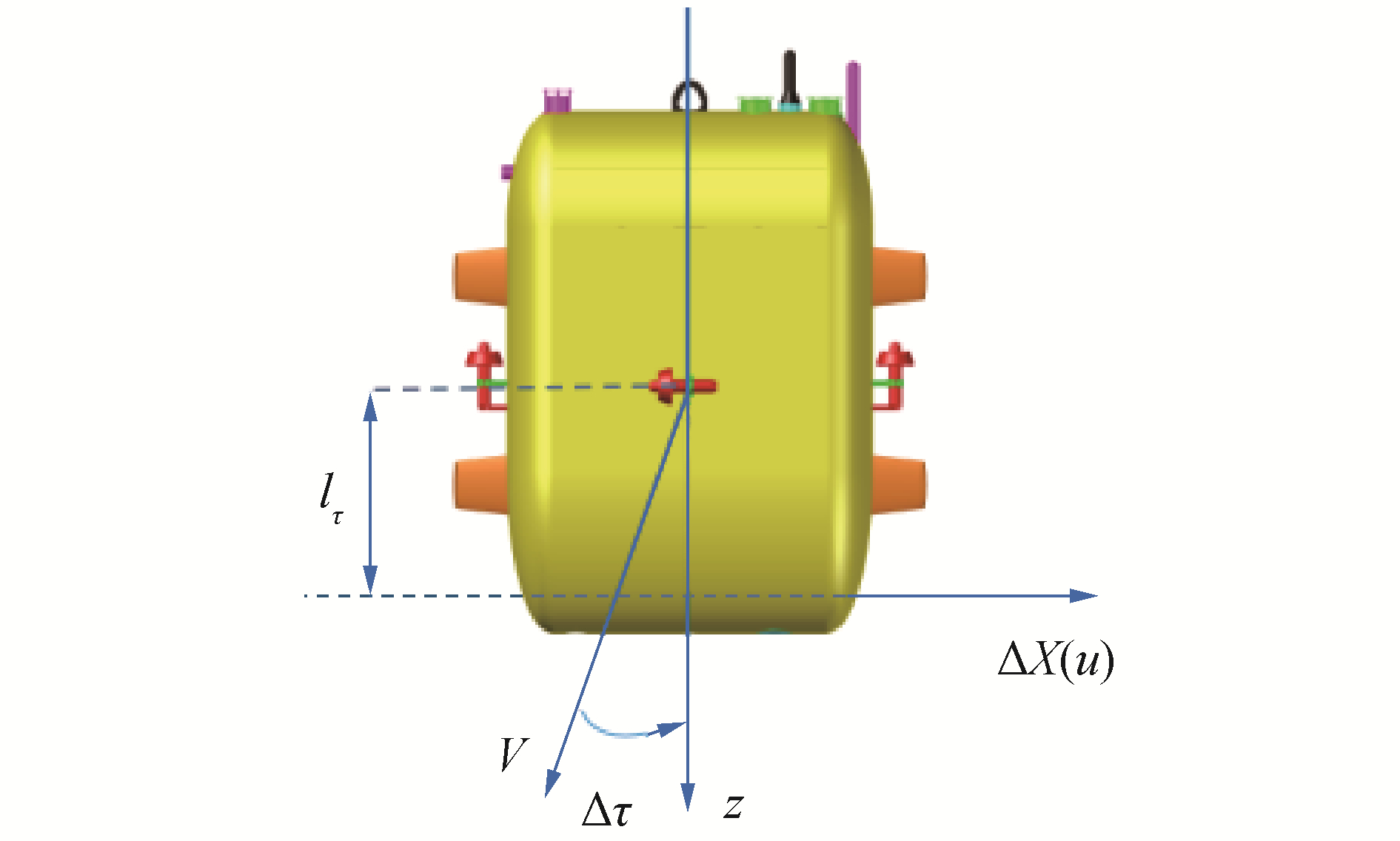
假设AUV在ξEζ面内作定常变深直航运动,受到瞬时弱干扰,航行方向等因AUV的惯性尚未发生变化,但艇体略有偏转,仅出现增量Δτ,引起作用于艇上的流体动力ΔX(u), ΔM(u)也有增量,如图 3所示。
|
Download:
|
| 图 3 角τ的静稳定性 Fig. 3 Static stability of angle τ | |
由图 3可知,M′u X′u l′τ之间的关系可用如下关系式表示:
| $ {{l'}_\tau } = {{M'}_u}/{{X'}_u} $ | (1) |
l′τ0,力矩ΔM(u)的作用力图使扰动引起的偏离Δτ增大;l′τ < 0,力矩ΔM(u)的作用使Δτ→0。为此,将l′τ=M′u/X′u0作为ξEζ面内角τ的静稳定性衡准。
1.2.2 动稳定性研究AUV变深度直航的平面运动,通常忽略AUV绕z轴运动,只考虑ξEζ面、ηEζ面的运动,在ξEζ面上,AUV运动的一般方程分别为:
ξEζ面操纵运动:
| $ \left\{ {\begin{array}{*{20}{l}} {m(\mathit{\boldsymbol{\dot w}} - \mathit{\boldsymbol{qu}}) = \mathit{\boldsymbol{Z}}}\\ {m(\mathit{\boldsymbol{\dot u}} + \mathit{\boldsymbol{qw}}) = \mathit{\boldsymbol{X}}}\\ {{I_y}\mathit{\boldsymbol{\dot q}} = \mathit{\boldsymbol{M}}} \end{array}} \right. $ | (2) |
ξEζ面操纵运动线性方程式:在w=w0,
| $ \left\{ \begin{array}{l} \left( {{m^\prime } - X_{\dot u}^\prime } \right){\mathit{\boldsymbol{u}}^\prime } - {X_u}{\mathit{\boldsymbol{u}}^\prime } - X_{\dot q}^\prime {\mathit{\boldsymbol{q}}^\prime } + \left( {{m^\prime } - X_q^\prime } \right){\mathit{\boldsymbol{q}}^\prime } = \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{X}}_0^\prime + \mathit{\boldsymbol{X}}_\delta ^\prime + {\mathit{\boldsymbol{P}}^\prime }\\ \left( {I_y^\prime - M_{\dot q}^\prime } \right){{\mathit{\boldsymbol{\dot q}}}^\prime } - M_q^\prime {\mathit{\boldsymbol{q}}^\prime } - M_{\dot u}^\prime {{\mathit{\boldsymbol{\dot u}}}^\prime } - {M_u}{\mathit{\boldsymbol{u}}^\prime } = \\ \;\;\;\;\;\;\;\;\mathit{\boldsymbol{M}}_0^\prime + \mathit{\boldsymbol{M}}_\delta ^\prime \mathit{\boldsymbol{\delta }} + {\mathit{\boldsymbol{\alpha }}_{TZ}}\mathit{\boldsymbol{x}}_T^\prime + \mathit{\boldsymbol{M}}_P^\prime + \mathit{\boldsymbol{M}}_v^\prime \mathit{\boldsymbol{v}} \end{array} \right. $ | (3) |
由ξEζ面操纵响应线性方程(3)消去u,并认为X0、M0、ZTxT在基准运动中已被消除,则无因次化的自由扰动运动方程为:
| $ {B_3}\dddot v + {B_2}\ddot v + {B_1}\dot v + {B_0}v = 0 $ | (4) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{B_3} = \left( {{m^\prime } - X_{\dot u}^\prime } \right)\left( {I_y^\prime - M_{\dot q}^\prime } \right) - X_{\dot q}^\prime M_{\dot u}^\prime }\\ {{B_2} = - \left( {{m^\prime } - X_{\dot u}^\prime } \right)M_q^\prime + \left( {{m^\prime } - X_q^\prime } \right)M_{\dot u}^\prime - }\\ {\quad M_u^\prime X_{\dot q}^\prime - X_u^\prime \left( {I_y^\prime - M_q^\prime } \right)}\\ {{B_1} = M_u^\prime \left( {{m^\prime } - X_q^\prime } \right) + X_u^\prime M_q^\prime - \left( {{m^\prime } - X_{\dot u}^\prime } \right)M_\psi ^\prime }\\ {{B_0} = M_\psi ^\prime X_u^\prime } \end{array}} \right. $ |
考虑到AUV近似对称于xGy面,因此上述方程中
由古尔维茨判据可知,动稳定的充要条件是特征方程系数满足:
| $ \left\{ {\begin{array}{*{20}{l}} {{B_0} > 0{B_2} > 0{B_3} > 0}\\ {\left( {\begin{array}{*{20}{c}} {{B_1}{B_2} - {B_0}{B_3}} \end{array}} \right) > 0} \end{array}} \right. $ |
由于系数
| $ \left( {{C_{\xi E\zeta }} + {C_{\xi E\zeta h}}} \right) > 0 $ | (5) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {{C_{\xi E\zeta }} = M_q^\prime X_u^\prime + M_u^\prime \left( {{m^\prime } - X_q^\prime } \right)}\\ {{C_{\xi E\zeta h}} = \left[ {\frac{{X_u^\prime \left( {I_y^\prime - M_{\dot q}^\prime } \right)\left( {{m^\prime } - X_{\dot u}^\prime } \right)}}{{M_q^\prime \left( {{m^\prime } - X_{\dot u}^\prime } \right) + \left( {I_y^\prime - M_{\dot q}^\prime } \right)X_u^\prime }} - \left( {{m^\prime } - X_{\dot u}^\prime } \right)} \right]M_\tau ^\prime } \end{array}} \right. $ |
在设计中,通常把CξEζh,作为AUV稳定性的储备,而将CξEζ>0作为AUV稳定性设计的指标,表示在任何下潜(上浮)航速下都具有动稳定性。因此,ξEζ面变深直航的绝对直线稳定性的衡准公式为:
| $ {C_{\xi E\zeta }} = \left[ {1 + \frac{{M_u^\prime \left( {{m^\prime } - X_q^\prime } \right)}}{{M_q^\prime X_u^\prime }}} \right] > 0 $ | (6) |
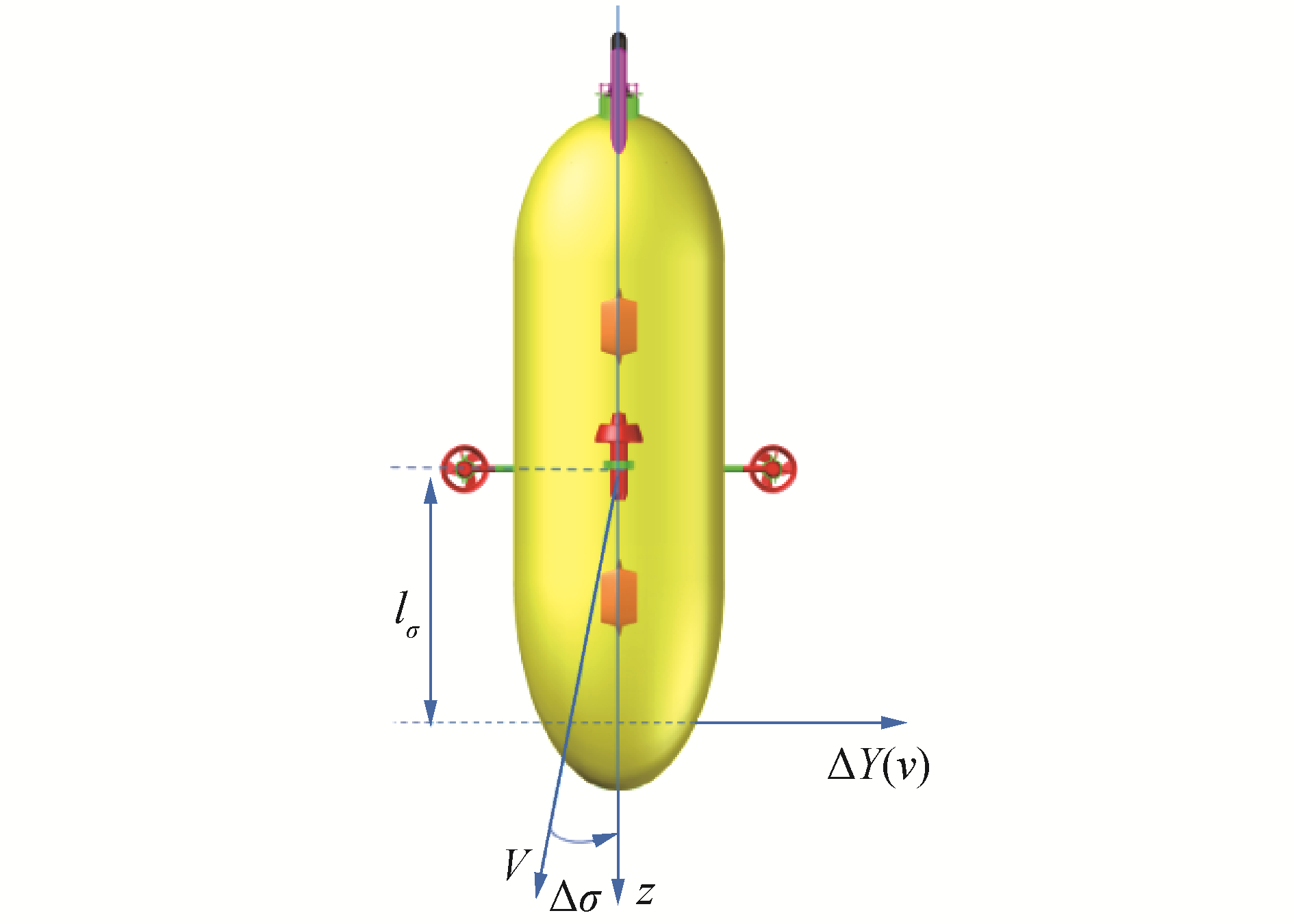
在ηEζ面静稳定性的推导中同样假设AUV在ηEζ面内作定常变深直航运动,受到瞬时弱干扰,航行方向等因AUV的惯性尚未发生变化,但艇体略有偏转,仅出现增量Δσ,引起作用于艇上的流体动力ΔY(v)ΔK(v)也有增量,如图 4所示。
|
Download:
|
| 图 4 角σ的静稳定性 Fig. 4 Static stability of angle σ | |
由图 4可知,在ηEζ面内,K′v、Y′v、l′σ之间的关系为:
| $ l_\sigma ^\prime = - K_v^\prime /Y_v^\prime $ | (7) |
当且仅当l′σ < 0,力矩ΔK(v)的作用使Δσ→0。因此,将l′σ < 0作为ηEζ面内角σ的静稳定性衡准。
1.3.2 动稳定性在ηEζ面上,AUV运动的一般方程分别为:
ηEζ面操纵运动:
| $ \left\{ {\begin{array}{*{20}{l}} {m(\mathit{\boldsymbol{\dot w}} + \mathit{\boldsymbol{pv}}) = \mathit{\boldsymbol{Z}}}\\ {m(\mathit{\boldsymbol{\dot v}} - \mathit{\boldsymbol{pw}}) = \mathit{\boldsymbol{Y}}}\\ {{I_x}\mathit{\boldsymbol{\dot p}} = \mathit{\boldsymbol{K}}} \end{array}} \right. $ | (8) |
考虑到1.2.2节中角υ的扰动运动方程的建立方法,无因次化横倾响应的自由扰动运动方程:
| $ {C_3}\mathit{\boldsymbol{\dddot \kappa }} + {C_2}\mathit{\boldsymbol{\ddot \kappa }} + {C_1}\mathit{\boldsymbol{\dot \kappa }} + {C_0}\mathit{\boldsymbol{\kappa }} = 0 $ | (9) |
式中:
| $ \left\{ \begin{array}{l} {C_3} = \left( {{m^\prime } - Y_{\dot v}^\prime } \right)\left( {I_x^\prime - K_{\dot p}^\prime } \right) - Y_{\dot p}^\prime K_{\dot v}^\prime \\ {C_2} = - \left( {{m^\prime } - Y_{\dot v}^\prime } \right)K_p^\prime - \left( {{m^\prime } + Y_p^\prime } \right)K_v^\prime - \\ \;\;\;\;K_v^\prime Y_{\dot p}^\prime - Y_v^\prime \left( {I_x^\prime - K_p^\prime } \right)\\ {C_1} = - K_v^\prime \left( {{m^\prime } + Y_p^\prime } \right) + Y_v^\prime K_p^\prime - \left( {{m^\prime } - Y_{\dot v}^\prime } \right)K_\kappa ^\prime \\ {C_0} = Y_v^\prime K_\kappa ^\prime \end{array} \right. $ |
同样,通过古尔维茨判据获得ηEζ面直航动稳定的衡准:
| $ \left( {{C_{\eta E\zeta }} + {C_{\eta E\zeta h}}} \right) > 0 $ | (10) |
式中:
| $ \left\{ \begin{array}{l} {C_{\eta E\zeta }} = K_p^\prime Y_v^\prime - K_v^\prime \left( {{m^\prime } + Y_p^\prime } \right)\\ {C_{\eta E\zeta h}} = \left[ {\frac{{Y_v^\prime \left( {I_x^\prime - K_{\dot p}^\prime } \right)\left( {{m^\prime } - Y_{\dot v}^\prime } \right)}}{{K_p^\prime \left( {{m^\prime } - Y_{\dot v}^\prime } \right) + \left( {I_x^\prime - K_{\dot p}^\prime } \right)Y_v^\prime }} - \left( {{m^\prime } - Y_{\dot v}^\prime } \right)} \right]K_\kappa ^\prime \end{array} \right. $ |
最终,求得ηEζ面变深直航的绝对直线稳定性的衡准公式:
| $ {C_{\eta E\zeta }} = \left[ {1 - \frac{{K_v^\prime \left( {{m^\prime } + Y_p^\prime } \right)}}{{K_p^\prime Y_v^\prime }}} \right] > 0 $ | (11) |
利用计算流体动力学仿真有限元软件FLUENT求解上浮运动稳定性分析的各水动力导数。用CFD方法进行流场求解计算时,首先要将计算流体域离散化,即网格划分[8-10]。基于全海深AUV整体模型较为复杂,本文采用混合网格的划分方式,为了缩短Fluent计算非定常运动的周期,将内域和外域交界面设置为球面,使内域与外域之间能够产生相对转动;在内域和外域之间通过设置interface实现区域间的数据连接。同时,为了使流场得到充分的发展,根据全海深AUV的主尺度及运动幅度确定计算流体域,图 5给出全海深AUV的网格划分,网格数量为590万。

|
Download:
|
| 图 5 网格划分 Fig. 5 Meshing | |
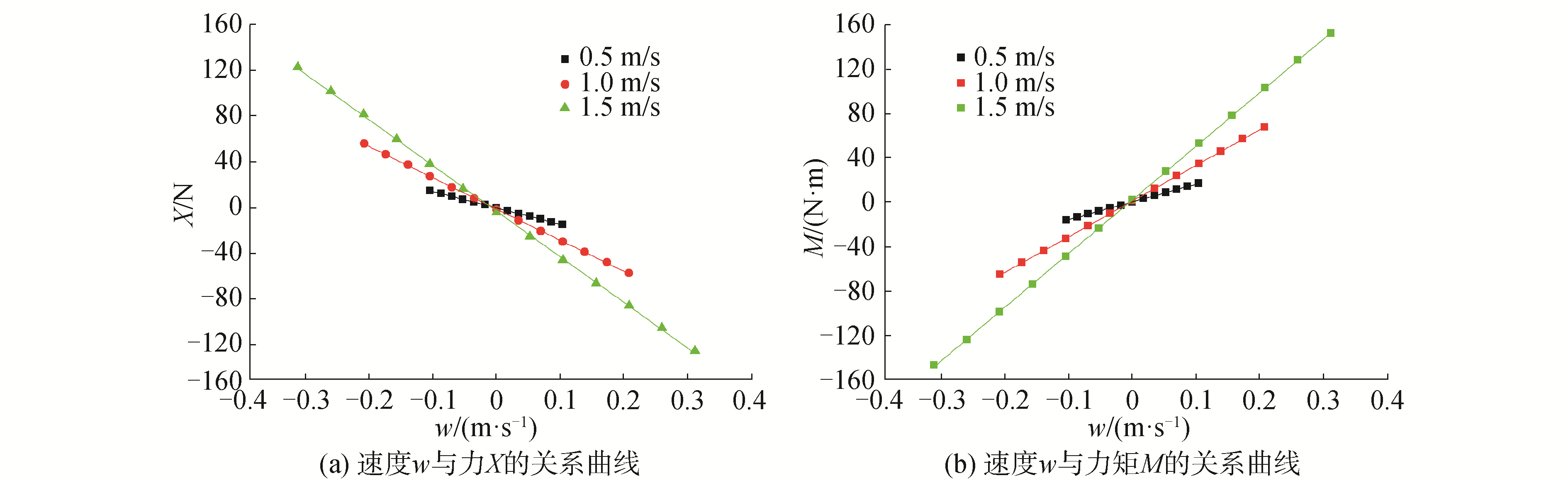
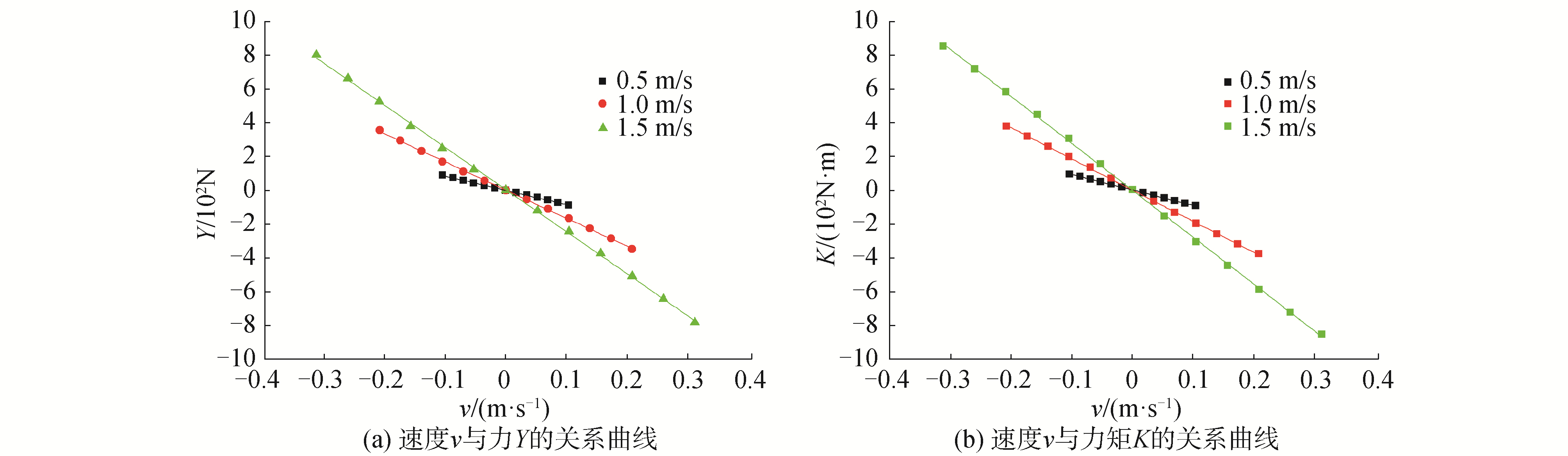
本文分别计算了AUV在V=0.5,1.0,1.5 m/s的航速下一系列角τ、角σ的水动力,角τ、角σ的变化范围为-12°~12°,每2°一个工况。应用最小二乘法求得ξEζ面、ηEζ面的线性水动力系数X′u、M′u、Y′v、K′v,如图 6、7所示。
|
Download:
|
| 图 6 ξEζ面斜航计算结果 Fig. 6 Calculation results of the slanting on the ξEζ plane | |
|
Download:
|
| 图 7 ηEζ面斜航计算结果 Fig. 7 Calculation results of the slanting on the ηEζ plane | |
由斜航运动求得的线性水动力系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {X_u^\prime = - 0.090\;286\;4}\\ {M_u^\prime = 0.042\;275}\\ {Y_v^\prime = - 0.544\;474}\\ {K_v^\prime = - 0.242\;33} \end{array}} \right. $ |
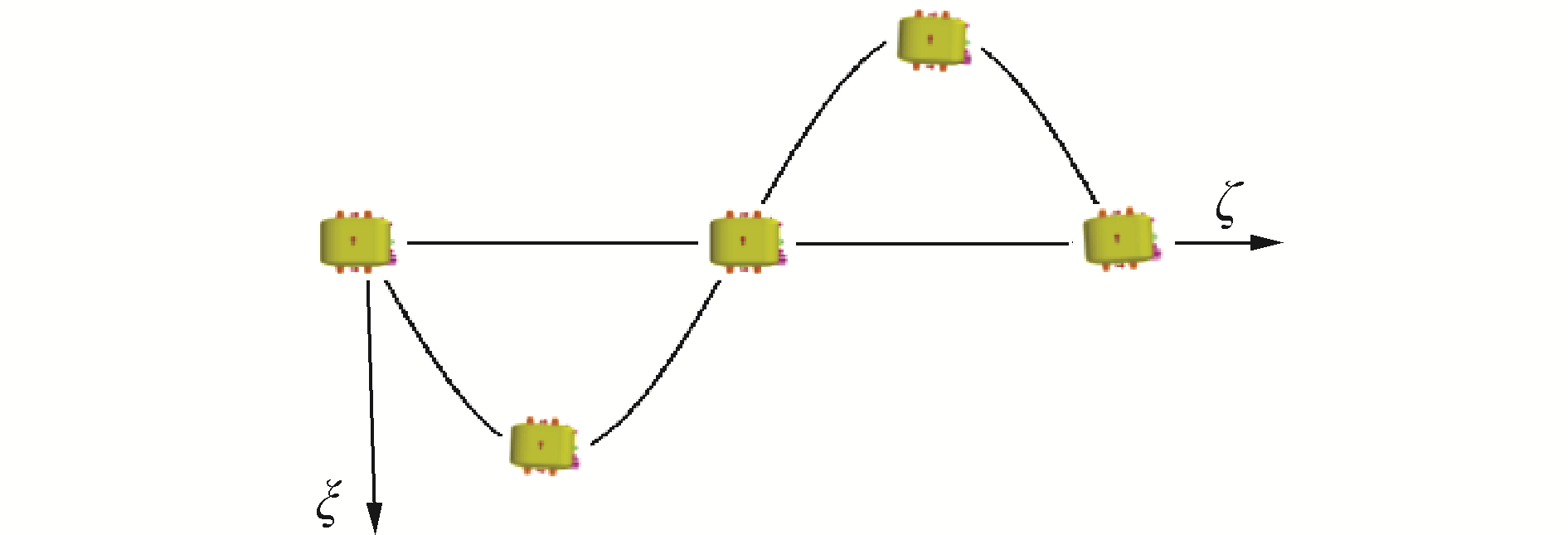
纯纵荡运动水动力计算主要是为了获得
| $ \left\{ {\begin{array}{*{20}{l}} {\xi = a\sin \left( {\omega t} \right)}\\ {\dot \xi = u = a\omega \cos \left( {\omega t} \right)}\\ {\dot u = - a{\omega ^2}\sin \left( {\omega t} \right)} \end{array}} \right. $ | (12) |
运动参数如表 1为:
| 表 1 纯纵荡运动参数 Table 1 Pure surge motion parameters |
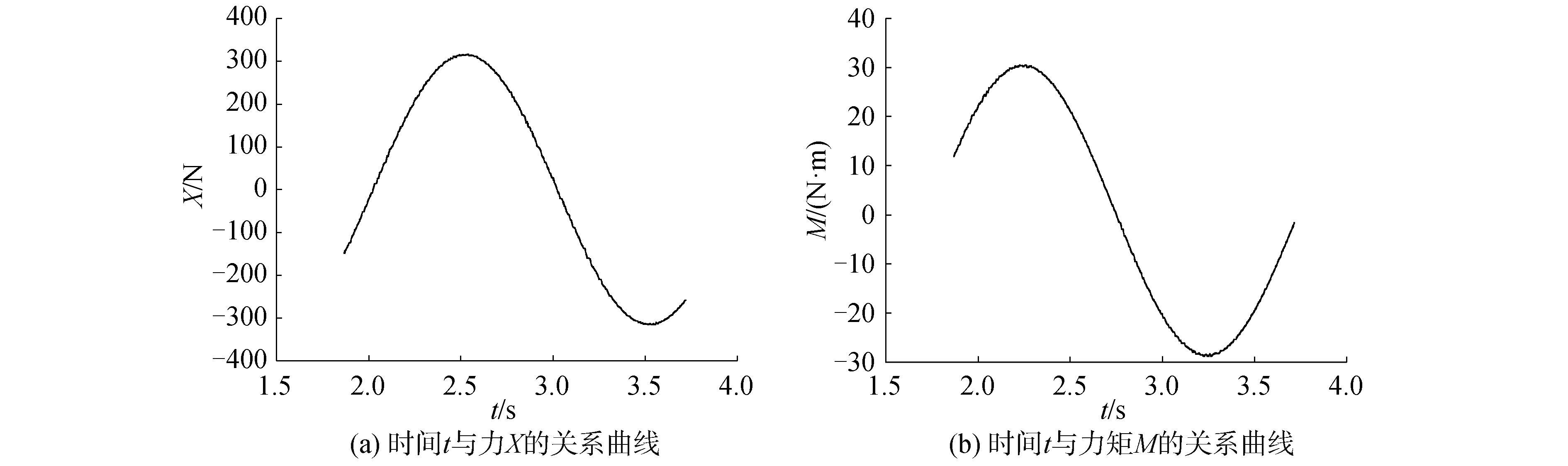
将Fluent采集的数据用Origin 8.0曲线拟合,计算结果如图 9所示。
|
Download:
|
| 图 8 纯纵荡运动示意 Fig. 8 Pure surge | |
|
Download:
|
| 图 9 f=0.5 Hz, V=0.5 m/s时纯纵荡运动计算结果 Fig. 9 Caculation results of pure surge motion when f=0.5 Hz and V=0.5 m/s | |
全海深AUV作纯纵荡运动所受的力X和力矩M可写为:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{X}}_{\dot u}}\mathit{\boldsymbol{\dot u}} + {\mathit{\boldsymbol{X}}_u}\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{X}}_0}}\\ {\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}_{\dot u}}\mathit{\boldsymbol{\dot u}} + {\mathit{\boldsymbol{M}}_u}\mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{M}}_0}} \end{array}} \right. $ | (13) |
将式(12)代入式(13)中,得:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}} = - {\mathit{\boldsymbol{X}}_{\dot u}}a{\omega ^2}\sin (\omega t) + {\mathit{\boldsymbol{X}}_u}a\omega \cos (\omega t) + {\mathit{\boldsymbol{X}}_0}}\\ {\mathit{\boldsymbol{M}} = - {\mathit{\boldsymbol{M}}_{\dot u}}a{\omega ^2}\sin (\omega t) + {\mathit{\boldsymbol{M}}_u}a\omega \cos (\omega t) + {\mathit{\boldsymbol{M}}_0}} \end{array}} \right. $ | (14) |
式(14)等价于
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{X}}_a}\sin \omega t + {\mathit{\boldsymbol{X}}_b}\cos \omega t + {\mathit{\boldsymbol{X}}_0}}\\ {\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}_a}\sin \omega t + {\mathit{\boldsymbol{M}}_b}\cos \omega t + {\mathit{\boldsymbol{M}}_0}} \end{array}} \right. $ | (15) |
由纯纵荡运动求得的水动力系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {X_u^\prime = - 0.083\;33}\\ {X_{\dot u}^\prime = - 0.104\;817}\\ {M_u^\prime = 0.044\;4619}\\ {M_{\dot u}^\prime = - 0.002\;277} \end{array}} \right. $ |
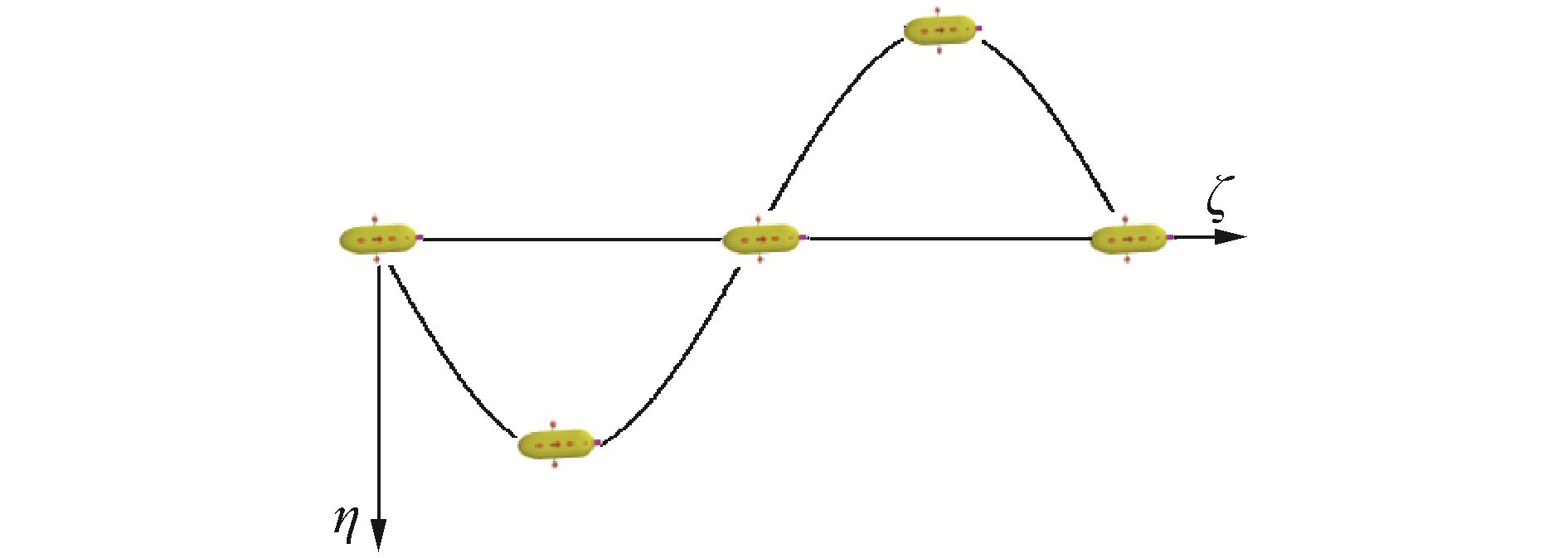
纯横荡运动水动力计算主要是为了获得
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\eta }} = a\sin (\omega t)}\\ {\mathit{\boldsymbol{\dot \eta }} = v = a\omega \sin (\omega t)}\\ {\mathit{\boldsymbol{\dot v}} = - a{\omega ^2}\sin (\omega t)} \end{array}} \right. $ | (16) |
对于纯横荡运动的参数设定以及数据处理的流程与纯纵荡运动基本一致。
|
Download:
|
| 图 10 纯横荡运动示意 Fig. 10 Pure sway | |
由纯横荡运动求得的水动力系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {Y_v^\prime = - 0.502\;81}\\ {Y_{\dot v}^\prime = - 0.403\;84}\\ {K_v^\prime = - 0.315\;57}\\ {K_{\dot v}^\prime = 0.013\;34} \end{array}} \right. $ |
纯俯仰运动水动力计算主要是为了获得
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{v}} = - {\mathit{\boldsymbol{v}}_0}\cos (\omega t)}\\ {\mathit{\boldsymbol{q}} = \mathit{\boldsymbol{\dot v}} = {v_0}\omega \sin (\omega t)}\\ {\mathit{\boldsymbol{\dot q}} = {\mathit{\boldsymbol{v}}_0}{\omega ^2}\cos (\omega t)}\\ {\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\dot v}} = 0} \end{array}} \right. $ | (17) |
运动参数如表 2所示:
| 表 2 纯纵荡运动参数 Table 2 Pure pitch motion parameters |
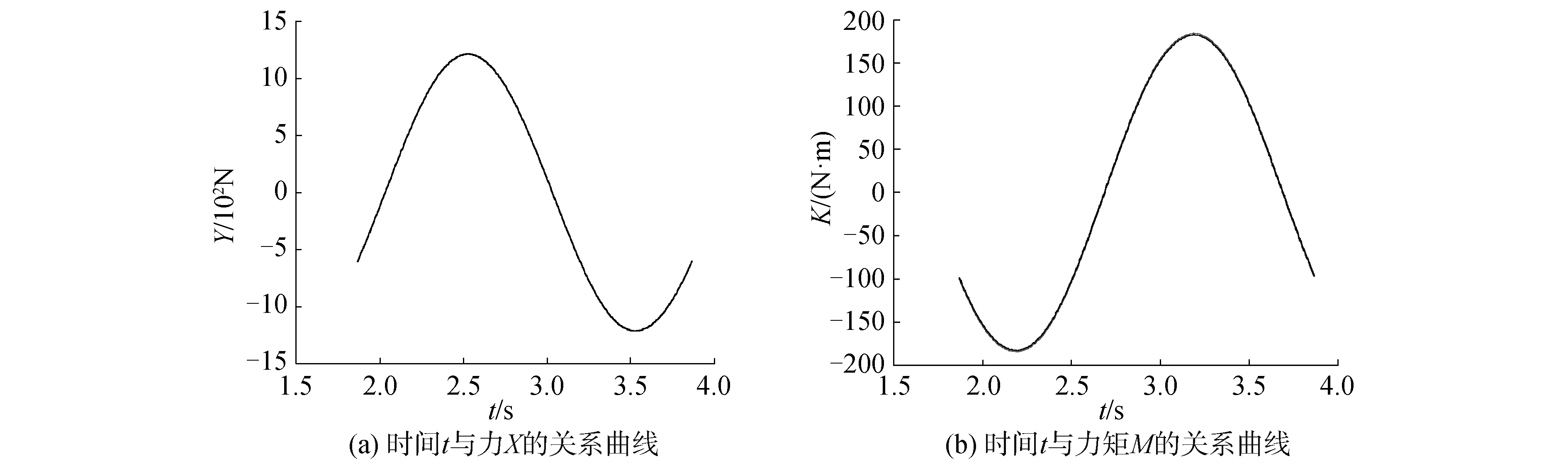
计算结果如图 11所示。
|
Download:
|
| 图 11 f=0.5 Hz, V=0.5 m/s时纯横荡运动计算结果 Fig. 11 Caculation results of pure sway motion when f=0.5 Hz and V=0.5 m/s | |
作纯俯仰运动时AUV所受的力X和力矩M可写成:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{X}}_{\dot q}}\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{X}}_q}\mathit{\boldsymbol{q}} + {\mathit{\boldsymbol{X}}_0}}\\ {\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}_{\dot q}}\mathit{\boldsymbol{\dot q}} + {\mathit{\boldsymbol{M}}_q}\mathit{\boldsymbol{q}} + {\mathit{\boldsymbol{M}}_0}} \end{array}} \right. $ | (18) |
将式(17)代入(18)中,得
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{X}}_{\dot q}}{\theta _0}{\omega ^2}\cos (\omega t) - {\mathit{\boldsymbol{X}}_q}{\theta _0}\omega \sin (\omega t) + {\mathit{\boldsymbol{X}}_0}}\\ {\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}_{\dot q}}{\theta _0}{\omega ^2}\cos (\omega t) - {\mathit{\boldsymbol{M}}_q}{\theta _0}\omega \sin (\omega t) + {\mathit{\boldsymbol{M}}_0}} \end{array}} \right. $ | (19) |
式(19)等价于:
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}} = {\mathit{\boldsymbol{X}}_a}\cos (\omega t) + {\mathit{\boldsymbol{X}}_b}\sin (\omega t) + {\mathit{\boldsymbol{X}}_0}}\\ {\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}_a}\cos (\omega t) + {\mathit{\boldsymbol{M}}_b}\sin (\omega t) + {\mathit{\boldsymbol{M}}_0}} \end{array}} \right. $ | (20) |
由纯俯仰运动求得的水动力系数为:
| $ \left\{ {\begin{array}{*{20}{l}} {X_q^\prime = 0.058\;322}\\ {X_{\dot q}^\prime = - 0.003\;32}\\ {M_q^\prime = - 0.002\;728\;3}\\ {M_{\dot q}^\prime = - 0.002\;766} \end{array}} \right. $ |
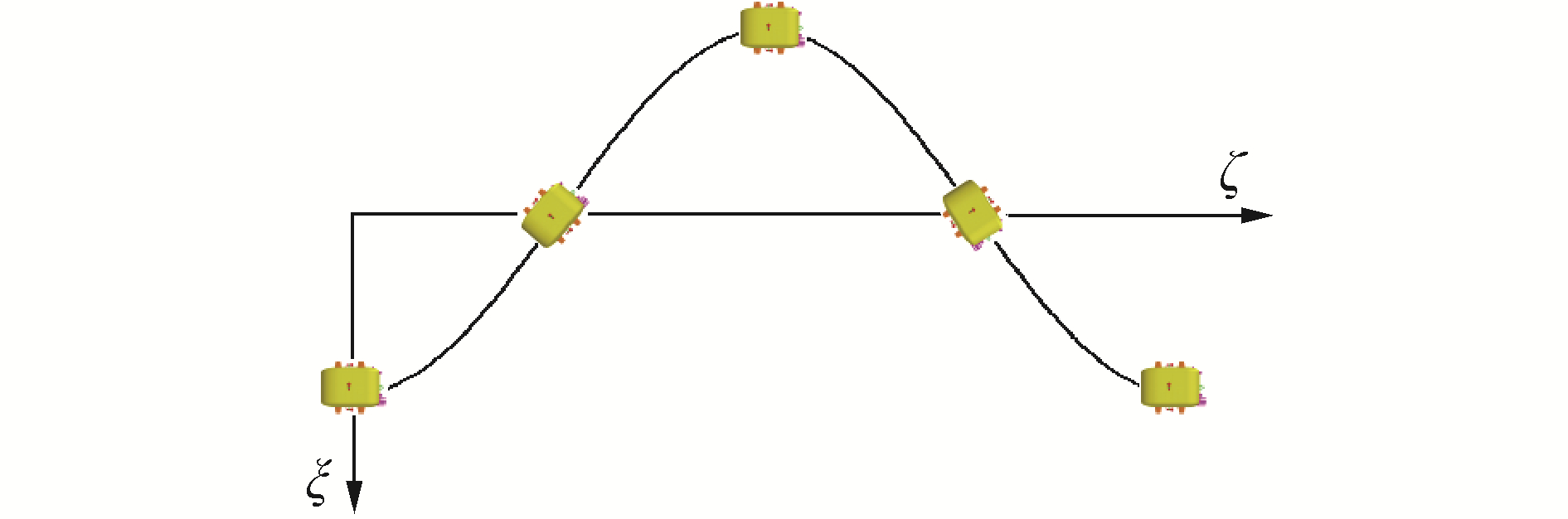
纯横摇运动中水动力计算主要是为了获得
|
Download:
|
| 图 12 纯俯仰运动示意 Fig. 12 Pure pitch | |
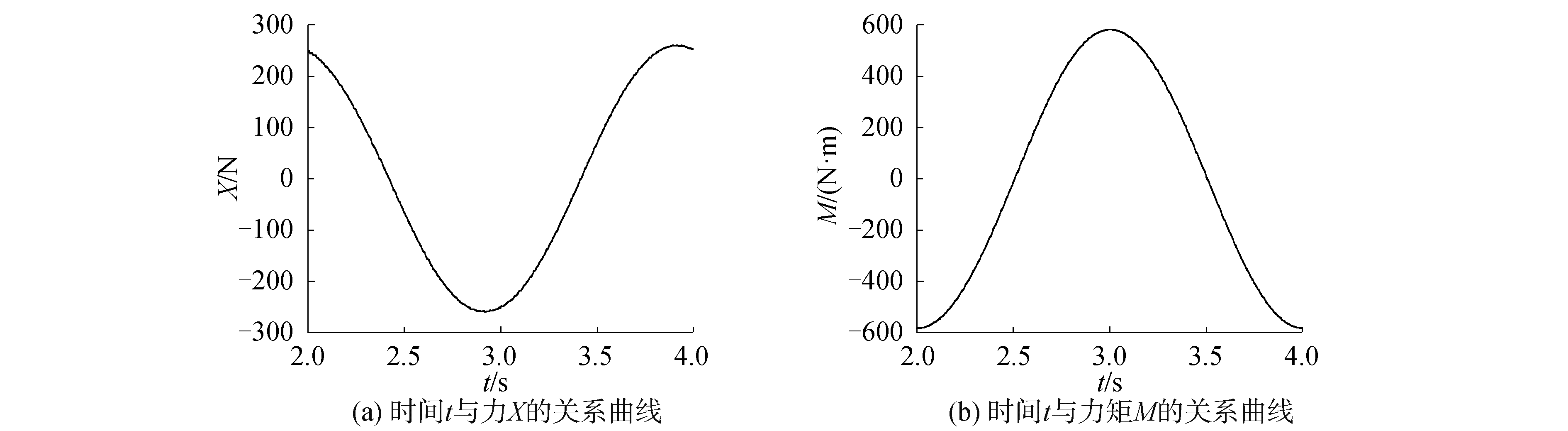
|
Download:
|
| 图 13 f=0.5 Hz, V=0.5 m/s时纯俯仰运动计算结果 Fig. 13 Caculation results of pure pitch motion when f=0.5 Hz and V=0.5 m/s | |
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\kappa }} = - {\mathit{\boldsymbol{\kappa }}_0}\cos (\omega t)}\\ {\mathit{\boldsymbol{p}} = \mathit{\boldsymbol{\dot \kappa }} = {\mathit{\boldsymbol{\kappa }}_0}\omega \sin (\omega t)}\\ {\mathit{\boldsymbol{\dot p}} = {\mathit{\boldsymbol{\kappa }}_0}{\mathit{\boldsymbol{\omega }}^2}\cos (\omega t)}\\ {\mathit{\boldsymbol{u}} = \mathit{\boldsymbol{\dot u}} = 0} \end{array}} \right. $ | (21) |
对于纯横摇运动的参数设定以及数据处理的流程与纯俯仰运动基本一致。
由纯横摇运动求得的角速度与角加速度系数
|
Download:
|
| 图 14 纯横摇运动示意 Fig. 14 Pure rolling | |
|
Download:
|
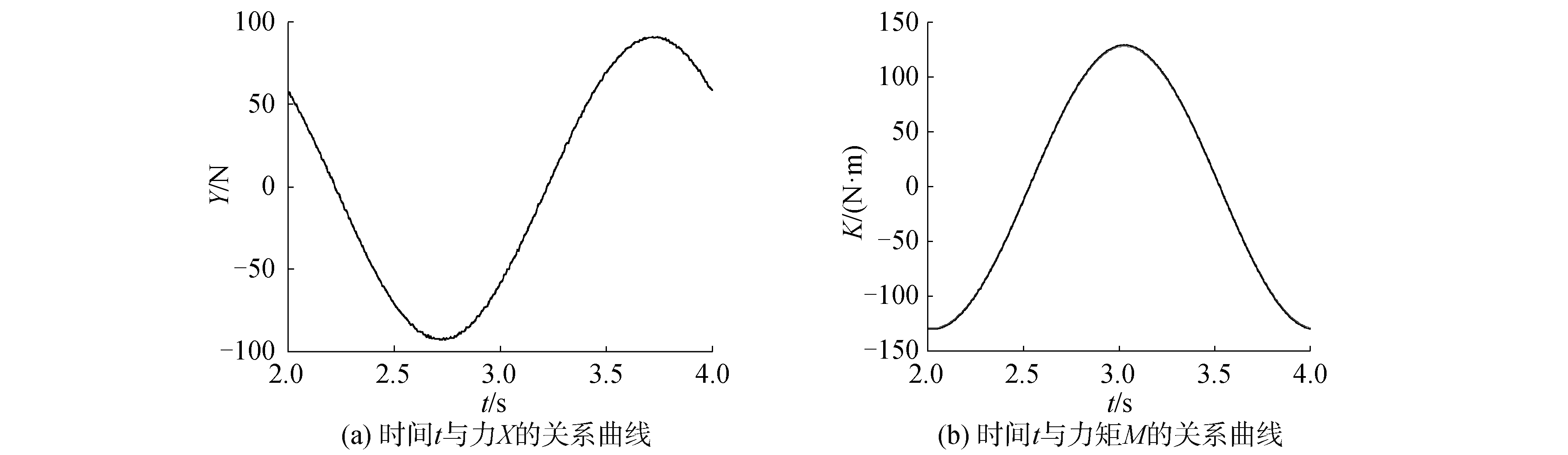
| 图 15 f=0.5 Hz, V=0.5 m/s时纯横摇运动计算结果 Fig. 15 Caculation results of pure rolling motion when f=0.5 Hz and V=0.5 m/s | |
| $ \left\{ {\begin{array}{*{20}{l}} {Y_p^\prime = - 0.039\;463\;4}\\ {Y_{\dot p}^\prime = 0.012\;850\;8}\\ {K_p^\prime = - 0.001\;751\;4}\\ {K_{\dot p}^\prime = - 0.012\;381\;87} \end{array}} \right. $ |
常规潜艇的稳定性分析,主要关注潜艇在定深直航状态下的稳定性性能。而对于全海深AUV稳定性分析来说,需要额外关注AUV在变深直航状态下的稳定性程度。
1) ξEζ面稳定性。
① 静稳定性衡准。
| $ l_\gamma ^\prime = \frac{{M_u^\prime }}{{X_u^\prime }} = - 0.533\;546 < 0 $ |
② 动稳定性衡准。
| $ {C_{\xi E\zeta }} = M_q^\prime X_u^\prime + M_u^\prime \left( {{m^\prime } - X_q^\prime } \right) = 0.007\;390\;9 > 0 $ |
2) ηEζ面稳定性。
① 静稳定性衡准。
| $ l_\sigma ^\prime = - \frac{{K_v^\prime }}{{Y_v^\prime }} = - 0.627\;610 < 0 $ |
② 动稳定性衡准。
| $ {C_{\eta E\zeta }} = K_p^\prime Y_v^\prime - K_v^\prime \left( {{m^\prime } + Y_p^\prime } \right) = 0.038\;289 > 0 $ |
通过将实验数据代入稳定性衡准公式,全海深AUV在ξEζ面、ηEζ面上具有直线自动稳定性。全海深AUV在ξEζ面上运动方向取决于υ-τ,仅有υ-τ为0时,AUV在ξEζ面内才会保持ξ=常数。此外,由于角υ,τ的自由扰动运动方程在形式上完全相同,不难得出υ-τ与υ、τ间具有一致的稳定性条件。由此可见,在ξEζ面上具有直线自动稳定性,同时也必定具有方向稳定性。同理,在ηEζ面上亦可得出同样的结论。
4 结论1) 经过对全海深AUV稳定性分析,证明全海深AUV在上浮状态下,在ξEζ面、ηEζ面内具有绝对的航向稳定性,满足了AUV在稳定性设计中的要求。
2) 虽然变深直航运动稳定性衡准公式由常规潜艇的定深直航稳定性公式演变而来,但是在ξEζ面、ηEζ面上稳定性推导过程中,考虑了恢复力矩对稳定性的影响。
3) 该公式对于大深度度潜水器的变深直航运动的稳定性分析具有通用性,为以后的实际应用提供参考。
| [1] |
付景枝, 臧鹏飞, 刘云平. 水下机器人下潜过程量化稳定性分析[J]. 计算机仿真, 2018, 35(9): 343-348. FU Jingzhi, ZANG Pengfei, LIU Yunping. Quantitative stability of underwater robot during diving[J]. Computer simulation, 2018, 35(9): 343-348. DOI:10.3969/j.issn.1006-9348.2018.09.071 (  0) 0)
|
| [2] |
张荣敏, 陈原, 高军. 无鳍舵矢量推进水下机器人纵向稳定性研究[J]. 哈尔滨工程大学学报, 2017, 38(1): 133-139, 152. ZHANG Rongmin, CHEN Yuan, GAO Jun. Longitudinal handling stability of vectored thrust underwater vehicle without fin and rudder[J]. Journal of Harbin Engineering University, 2017, 38(1): 133-139, 152. (  0) 0)
|
| [3] |
臧鹏飞.水下机器人动力学建模与运动稳定性分析[D].南京: 南京信息工程大学, 2018. ZANG Pengfei. Dynamics modeling and kinematic stability analysis of underwater robot[D]. Nanjing: Nanjing University of Information Science & Technology, 2018. (  0) 0)
|
| [4] |
刘振明, 潜伟建, 夏志澜. 水下机器人平面直航运动稳定性分析[J]. 船舶工程, 2004, 26(3): 54-56. LIU Zhenming, QIAN Weijian, XIA Zhilan. Analysis of dynamic stability of underwater vehicle navigating in planar and straight course[J]. Ship engineering, 2004, 26(3): 54-56. DOI:10.3969/j.issn.1000-6982.2004.03.014 (  0) 0)
|
| [5] |
施生达. 潜艇操纵性[M]. 北京: 国防工业出版社, 1995: 10-71.
(  0) 0)
|
| [6] |
孙梦瑶, 刘玉红, 黄明龙, 等. 测量型深水AUV垂直面运动稳定性设计[J]. 机械科学与技术, 2016, 35(9): 1402-1407. SUN Mengyao, LIU Yuhong, HUANG Minglong, et al. Design of dynamic stability in vertical plane of autonomous underwater vehicle with measurement missions[J]. Mechanical science and technology for aerospace engineering, 2016, 35(9): 1402-1407. (  0) 0)
|
| [7] |
陈锐林. 潜艇垂直面运动稳定性衡准值的研究[J]. 湘潭大学自然科学学报, 2003, 25(4): 70-74. CHEN Ruilin. The study on the value of kinematic stability coefficent of submarine in vertical plane[J]. Natural Science Journal of Xiangtan University, 2003, 25(4): 70-74. DOI:10.3969/j.issn.1000-5900.2003.04.012 (  0) 0)
|
| [8] |
曹建, 苏玉民, 赵金鑫, 等. 水下无人航行器外挂吊舱水动力试验及操纵性分析[J]. 船舶力学, 2017, 21(8): 968-975. CAO Jian, SU Yumin, ZHAO Jinxin, et al. Hydrodynamic experiment and maneuverability analysis of an unmanned underwater vehicle with an outside equipment cabin[J]. Journal of ship mechanics, 2017, 21(8): 968-975. DOI:10.3969/j.issn.1007-7294.2017.08.005 (  0) 0)
|
| [9] |
PHILLIPS A B, FURLONG M, TURNOCK S R. The use of computational fluid dynamics to determine the dynamic stability of an autonomous underwater vehicle[C]//Proceedings of the 10th Numerical Towing Tank Symposium. Hamburg, Germany: Hamburg University of Technology, 2007.
(  0) 0)
|
| [10] |
李刚, 段文洋. 复杂构型潜器水动力特性的试验研究[J]. 船舶力学, 2011, 15(1/2): 58-65. LI Gang, DUAN Wenyang. Experimental study on the hydrodynamic property of a complex submersible[J]. Journal of ship mechanics, 2011, 15(1/2): 58-65. (  0) 0)
|
| [11] |
周杰, 王树宗, 张志迅. 无人水下航行器外挂鱼雷稳定性判断[J]. 鱼雷技术, 2009, 17(2): 15-19. ZHOU Jie, WANG Shuzong, ZHANG Zhixun. Stability estimation for UUV with external torpedoes[J]. Torpedo technology, 2009, 17(2): 15-19. DOI:10.3969/j.issn.1673-1948.2009.02.004 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


