螺旋桨与舵的相互作用问题是船舶与海洋工程中的重要问题,由于螺旋桨盘面的不均匀性,故桨-舵流场呈现非定常的状态,在实际使用中,基于定常流场设计的舵必然会受到螺旋桨产生的非定常流场的影响从而产生振动。很多实际案例已经证明,处于螺旋桨涡流场中的舵会产生强烈的振动,并传递给舵机和船体,严重影响了船舶的安全性和舒适性。因此,分析桨后舵的受力特性,尤其是其表面压力的脉动特性,具有重要的意义。
对桨-舵干扰问题进行研究的基础是螺旋桨涡流场的研究,大量研究人员对螺旋桨的涡流场进行了深入的研究,Felli等[1]使用试验手段研究了桨叶数量对螺旋桨梢涡的影响,分析了不同桨叶数量下的螺旋桨流场,Muscari等[2]使用数值模拟的方法模拟螺旋桨水动力性能和涡量场,发现RANSE方法在求解螺旋桨水动力性能问题上具有良好的精度,但是在模拟桨后方的涡量场问题和带有不稳定特征的问题时则不如DES方法,这是由于RANSE方法会将流场进行平滑处理,丢失了流场中的部分细节;Guilmineau等[3]也使用了数值模拟的方法进行了不同湍流模拟方法下的涡流场的对比,并将不同湍流模拟方法下的结果与实验值进行对比,同样得出了DES方法在求解涡流场模拟问题时比k-ω方法和EARSM方法效果更好的结论;Felice等[4]使用大涡模拟(large eddy simulation, LES)方法对潜艇螺旋桨的流场进行了数值模拟,并将得到的速度场与试验值进行比较,证明大涡模拟方法在求解螺旋桨流场的问题上具有足够的精度。对桨舵相互作用问题进行研究很大程度上与螺旋桨尾流场的数值模拟是相似的,但是单纯地对螺旋桨尾流场进行研究无法体现出舵对螺旋桨尾流场的影响也无法探讨螺旋桨尾流场对舵的影响。Sun Shuai等[5]对斜流下船-桨-舵系统的螺旋桨的激振力的研究表明,带有舵的螺旋桨系统中的螺旋桨激振力与螺旋桨的叶频具有非常高的相关性。王超等[6]对B4-70螺旋桨和NACA剖面舵组成的桨舵系统的数值模拟研究表明,舵的安装会使螺旋桨的推力系数和转矩系数增加,同时会使径向月切向速度分布呈现向上下伸展的分布形状。Felli[7-8]对桨舵相互作用下的流场进行了试验分析,得到了桨舵共同作用下的流场速度分布和涡量分布,还使用计算流体力学方法分析了不同桨叶数量下涡量场的变化和舵表面力的分布。Muscarie等[9]也进行了桨舵相互作用的数值模拟分析,对舵表面上的力的分布进行了研究,研究结果表明,螺旋桨尾涡与舵之间的相互作用主要通过舵的边界层实现。齐慧博等[10]使用CFD方法对桨舵干扰系统的研究表明舵受到的阻力随螺旋桨的旋转呈现周期性的变化且随着进速的增大,桨舵至今的干扰也逐渐增大。胡健等[11]对B4-55螺旋桨和NACA剖面舵组成的桨舵系统的数值模拟研究表明舵的安装能够提高螺旋桨的效率但是会对舵的受力方式带来改变。
综上可以看出,目前关于桨舵干扰的数值模拟主要是针对桨舵干扰的推进效率进行的。鉴于舵机振动的重要性,本文在国内外相关研究的基础上,使用耗时更多但模拟效果更好的大涡模拟方法,对舵作用下螺旋桨梢涡的变化趋势和舵表面上力的分布情况进行分析,得到了在有舵参与的流场中梢涡的变化情况以及梢涡作用下舵表面上压力的弦长和展长分布,对舵表面上的脉动压力进行了时域和频域分析。
1 大涡模拟湍流模型湍流是由一系列不同尺度的涡组成的,大尺度的涡来自于流场的不稳定,系统中动量、质量、能量及其他物质的输运主要受大尺度涡的影响,而小尺度的涡来自于大尺度涡的能量级联过程,而经过多次能量级联过程后的小尺度涡对整个流场的影响较小且趋向于各向同性。故在进行数值模拟时可以将小于某一尺度的涡进行过滤,只将比网格尺度大的湍流运动通过瞬时N-S方程直接计算,而将小尺度涡对大尺度涡运动的影响通过一定的方式在大尺度涡的瞬时N-S方程中体现出来,因而具有更高的数值模拟精度。
要实现大涡模拟,首先要做的是建立数学滤波函数,将尺度比滤波函数小的涡滤掉,然后向滤波得到的大尺度涡流场的运动方程中添加附加应力项来体现小尺度涡对大尺度涡的影响,此应力项即为亚格子尺度应力。
大涡模拟的控制方程由连续性方程和通过滤波函数处理过的N-S非定常方程组成:
| $ \frac{\partial \rho}{\partial t}+\frac{\partial\left(\rho \bar{\mathit{\boldsymbol{u}}}_{i}\right)}{\partial \mathit{\boldsymbol{x}}_{i}}=0 $ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho {{\mathit{\boldsymbol{\bar u}}}_i}} \right) + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left( {\rho {{\mathit{\boldsymbol{\bar u}}}_i}{{\mathit{\boldsymbol{\bar u}}}_j}} \right) = \frac{{\partial p}}{{\partial {\mathit{\boldsymbol{x}}_i}}} + \frac{\partial }{{\partial {\mathit{\boldsymbol{x}}_j}}}\left( {\mu \frac{{\partial {{\mathit{\boldsymbol{\bar u}}}_i}}}{{\partial {\mathit{\boldsymbol{x}}_j}}}} \right) - \frac{{\partial {\tau _{ij}}}}{{\partial {\mathit{\boldsymbol{x}}_j}}} $ | (2) |
式中:ρ表示密度的分量;t表示时间;xi表示方向矢量的分量;ui表示速度矢量;μ为动力粘性系数;τij为亚格子尺度应力,可由τij=ρuiui-ρuiuj得到,小尺度涡对大尺度涡运动的影响通过τij项来体现,其中变量上方的“-”表示滤波操作。
实际上,经过滤波的N-S方程与RANS方程非常相似,其区别主要在于经过滤波的N-S方程中的变量是滤波后的值,其仍为瞬时值,而在RANS方程中这些变量为时均值,同时由于连续方程具有线性特征,连续方程并无变化[12-13]。
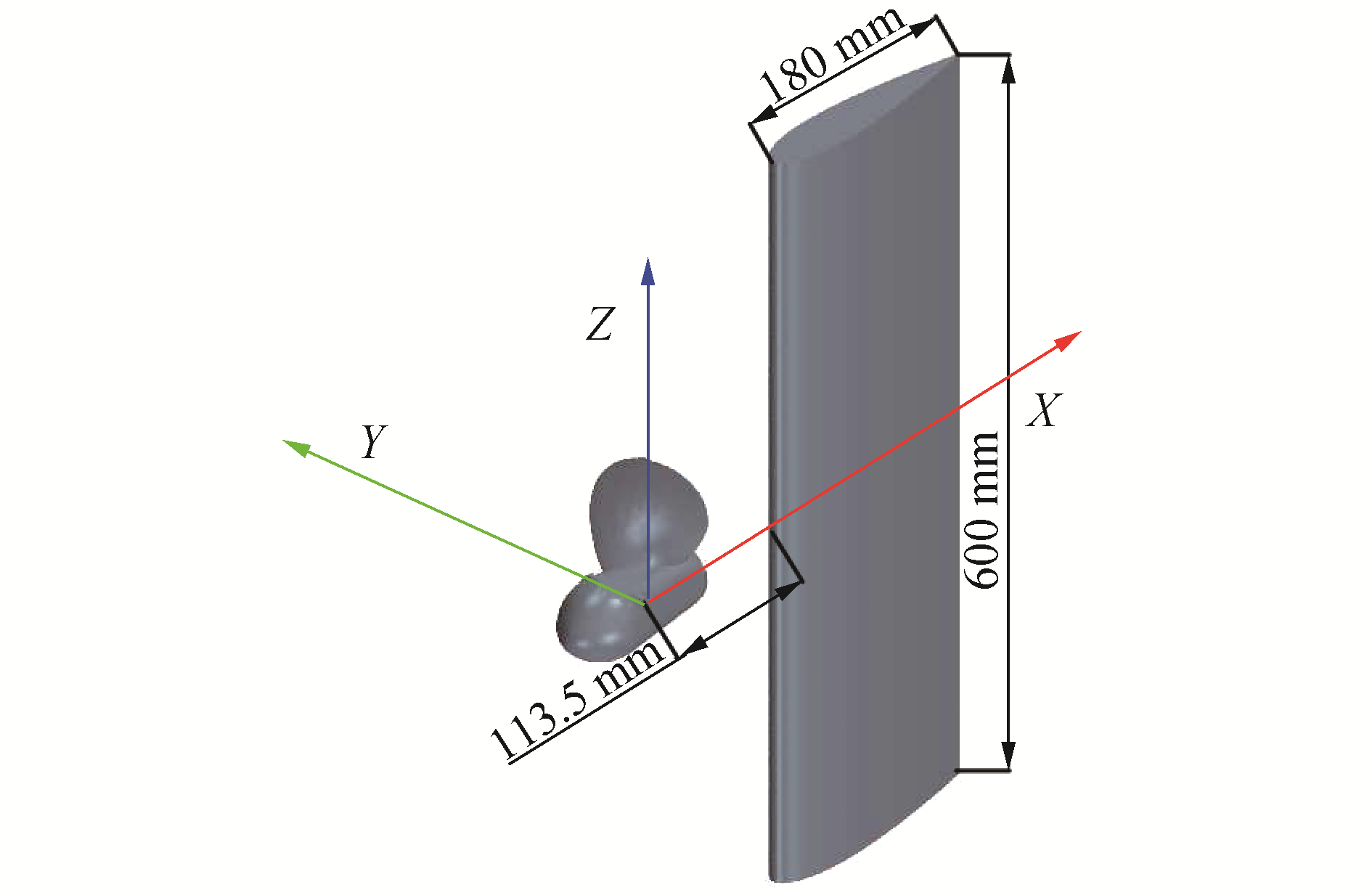
2 计算模型与物理条件使用单叶E779A螺旋桨和NACA0020剖面舵进行数值模拟,二者之间的间距为0.5D,D表示E779A螺旋浆的直径,其值为227 mm,舵位于单叶螺旋桨的正后方,舵剖面为NACA0020剖面,舵的弦长为180 mm,展长为600 mm。单叶螺旋桨的转速为25 rps,其设计进速为J=0.88,简化E779A螺旋桨和NACA0020舵在流场中的相对位置如图 1所示。
|
Download:
|
| 图 1 简化的E779A螺旋桨和NACA0020舵 Fig. 1 Simplified E779A propeller and rudder with NACA0020 profile | |
Calcagno等[14]的研究和Luca等[15]的研究给出了E779A螺旋桨梢涡的大致尺度,在没有舵的流场中,E779A螺旋桨梢涡的大致尺度为0.05D,文献[2]指出,在不考虑计算能力限制的情况下应该使网格的尺度满足涡核的1/12~1/10以使涡管能够顺利呈现,另有研究表明在使用大涡模拟方法对J=0.88下E779A螺旋桨的涡管进行模拟时,0.004 m的网格尺度能够满足研究的需要[16],故将计算区域的网格加密区的网格尺寸设置为0.004 m。在本文中,需要对螺旋桨和舵表面附近的流场进行加密,但是本文着重于梢涡的错位现象和舵表面的脉动压力进行研究,对舵后方的毂涡形态的研究较少,故在舵后方的流场区域中只对梢涡流经的圆筒形流场进行加密,通过这种加密方式来减少网格数量,缩短计算时间,计算域和网格加密区如图 2所示。

|
Download:
|
| 图 2 计算域示意 Fig. 2 The computational domain diagram | |
使用的是切割体网格划分方法进行网格划分,既具有结构化网格计算稳定易于收敛的特点,又兼具非结构网格适应性良好的特点[17],使用重叠网格方法来实现螺旋桨的旋转,在螺旋桨和舵附近使用棱柱层网格划分方法来对边界层进行网格划分,并在网格加密区的基础上对螺旋桨表面和舵表面进行进一步加密,使靠近螺旋桨和舵表面的网格更加细腻。
鲁利等[18]的研究表明,使用大涡模拟方法模拟得到的螺旋桨水动力性能曲线的波动会略低于由RANS和DES方法得到的,这是由于RANS和DES采用雷诺平均的方法模拟湍流,而大涡模拟会对大尺度涡直接进行模拟,可以更准确地描述湍流对壁面的影响,具有更好的模拟效果。耿冲[19]的研究也表明,在进速系数J>0.8时,大涡模拟方法得到的水动力性能参数的误差会接近甚至低于RANS方法和DES方法的水平,同时大涡模拟方法在涡管呈现等方面具有非常明显的优势,故使用大涡模拟方法对螺旋桨流场和梢涡进行模拟是准确的。本文使用大涡模拟方法进行模拟,涡的最大数量取为1 000,最小允许壁面距离为1.0×10-6,亚格子尺度SGS模型选择动态Smagorinsky次网格尺度模型,时间步选择为0.000 1 s。
使用E779A螺旋桨对数值模拟方法进行验证,如表 1所示为由本模拟方法得到的数值模拟结果与试验结果的验证,对比可知,在0.004 m的网格尺度和0.000 1 s的时间步下,通过本数值模拟方法得到的结果是可靠的。
| 表 1 数值模拟和试验结果的比较 Table 1 Comparison of numerical and experimental results |
对单桨叶的E779A螺旋桨进行进速系数J=0.88下的涡流场分析,计算域的进口速度设置为5 m/s,Q-判据值取为1 000/s2,可以得到如图 3所示的梢涡形态。

|
Download:
|
| 图 3 梢涡 Fig. 3 Tip vortex | |
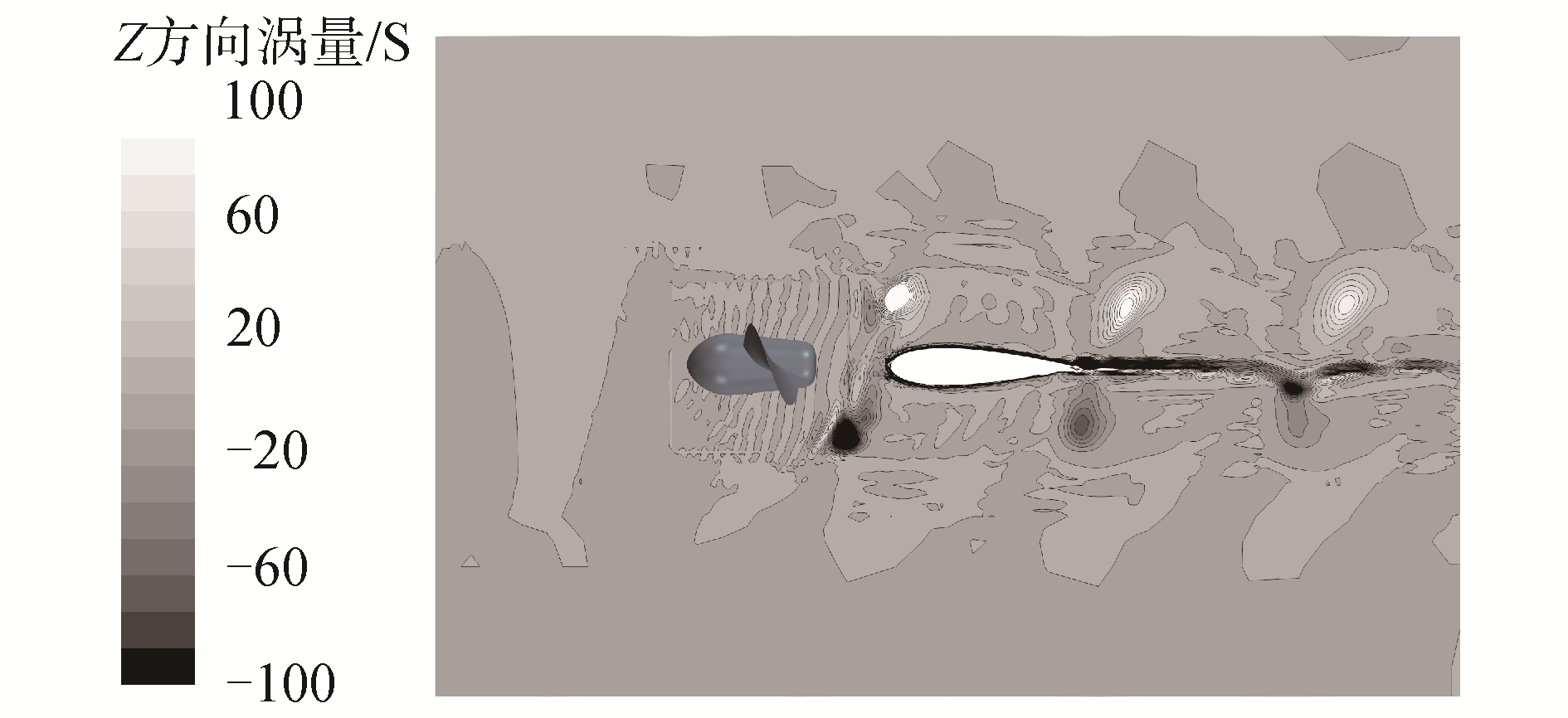
此处对应的进速系数J=0.88,梢涡的收缩并不明显,但通过对梢涡进行分析可以发现,梢涡来源于桨叶的叶梢处,被舵面切断后的涡管会沿着螺旋桨旋转的方向发生错位,即舵面左侧的涡管会向上移动,而右侧的涡管会向下移动,这种错位与螺旋桨旋转方向一致。分析Z方向上的涡量场可以发现,舵两侧涡管处的涡量方向相反,而在近舵面处,涡量的方向同样表现为方向相反,这是由于由于近舵面处存在马蹄涡,其表现为同一位置翼型表面两侧涡的方向相反,如图 4所示。
|
Download:
|
| 图 4 Z=0.7R位置处平面上沿Z方向的涡量场 Fig. 4 Vortex at the horizontal plane along the Z=0.7R in Z direction | |
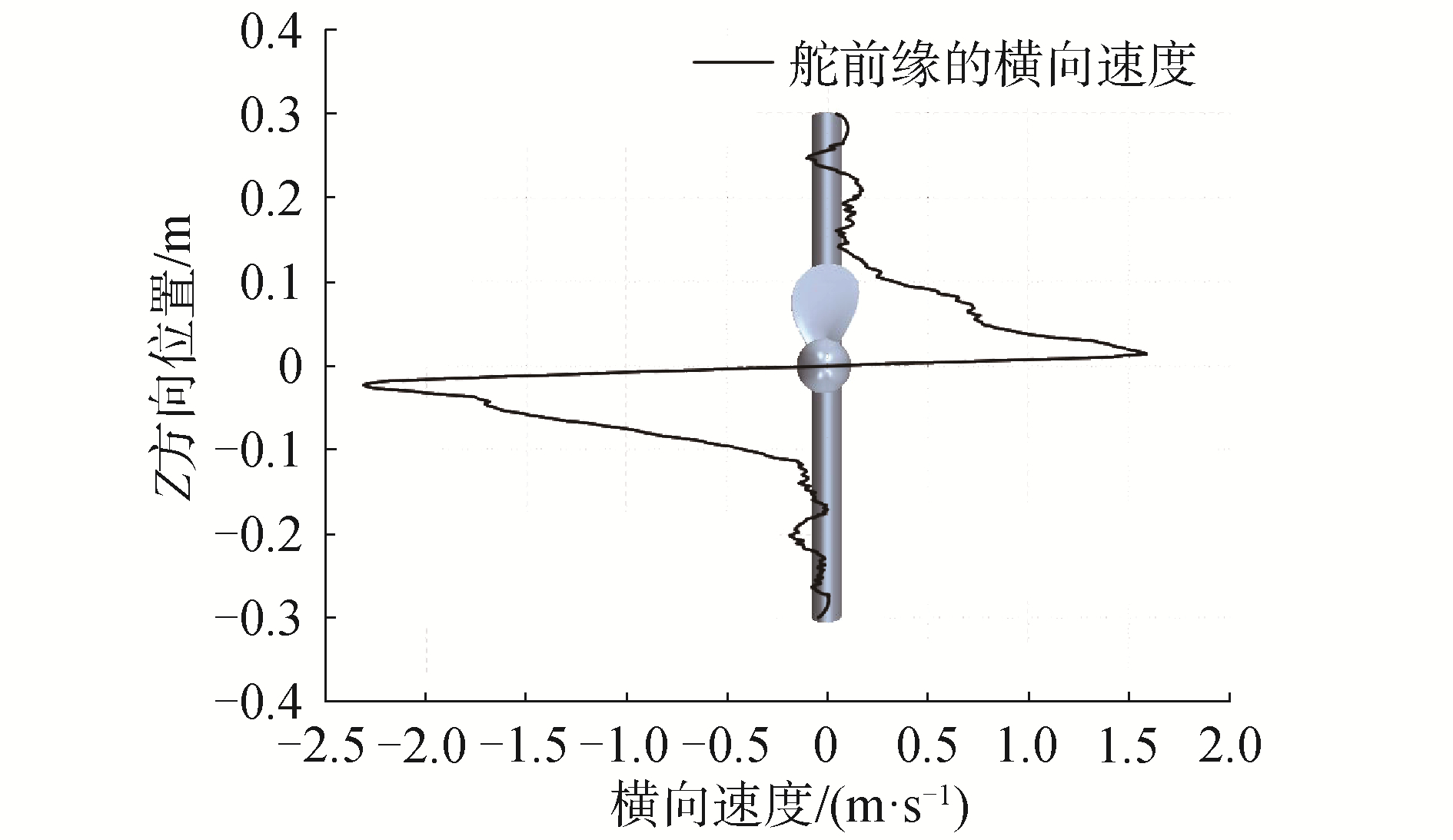
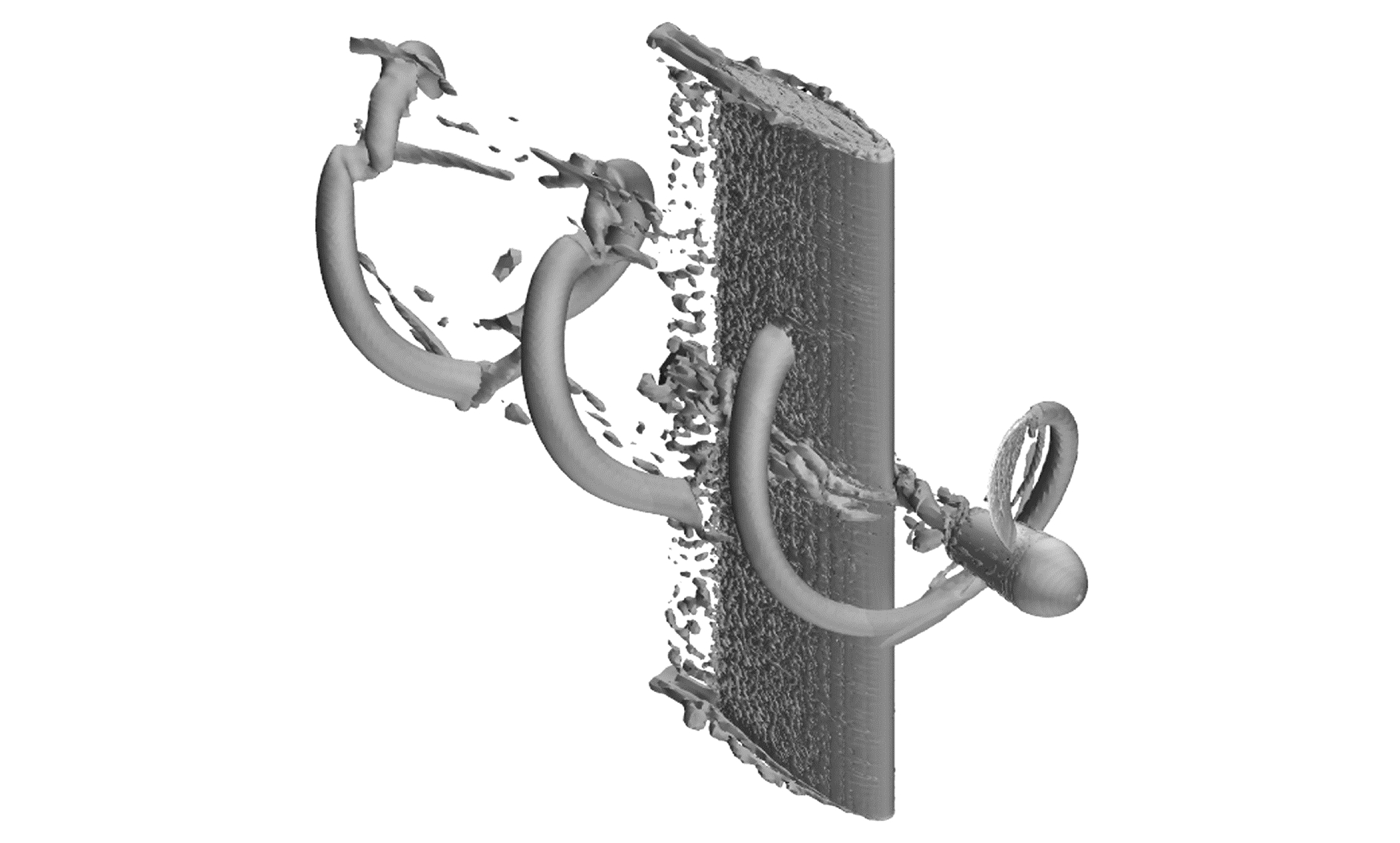
对螺旋桨尾流中的舵表面上的速度分布进行分析,提取螺旋桨相位角θ=0°时舵前缘的Y方向速度分布,如图 5所示,舵表面前缘的Y方向速度的分布呈现出关于原点中心对称的特征,正负2个方向上的最大值均位于叶根处,且负方向的最大值要大于正方向的最大值,速度的大小沿桨叶展长方向逐渐降低,在叶梢之后接近0。这是由于螺旋桨的螺距从叶根至叶梢逐渐降低,螺距越大的部位产生的周向诱导速度越大,不同半径处的周向诱导速度在舵前缘处表现为Y方向的速度,负方向上的最大值大于正方向的最大值是由于螺旋桨的相位角为0°时单桨叶产生的尾涡正好到达舵面负方向的部分的前缘,如图 6所示。
|
Download:
|
| 图 5 舵前缘的Y方向速度分布(θ=0°) Fig. 5 Velocity at the leading edge of the rudder in Y direction (θ=0°) | |
|
Download:
|
| 图 6 θ=0°时涡管形态 Fig. 6 Vortex when θ=0° | |
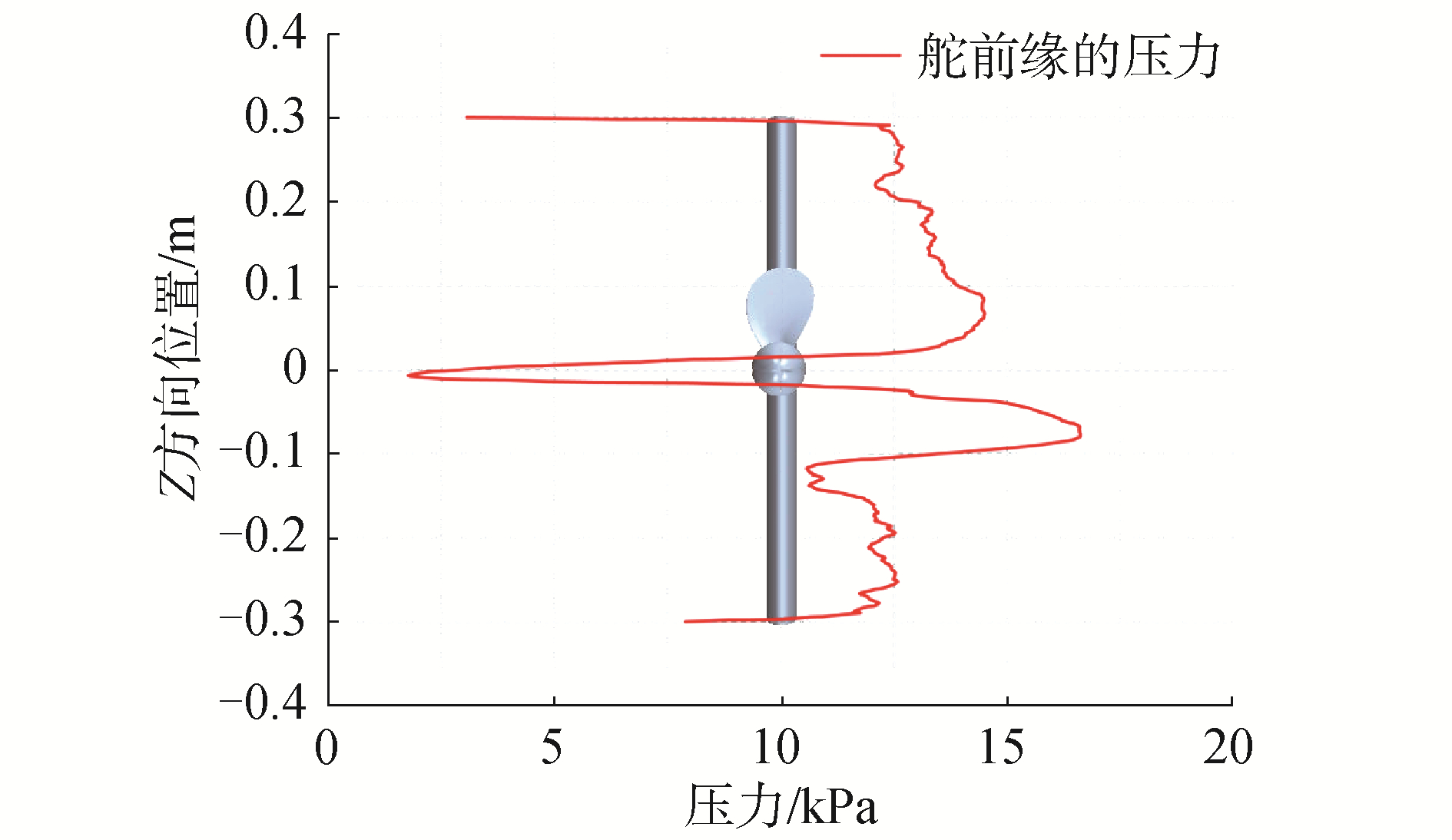
θ=0°时的舵前缘压力分布具有与舵前缘横向速度分布相似的特征,同样表现为在负方向的最大值大于正方向的最大值,如图 7所示。这同样是由于桨叶的尾流在此时到达舵面的-Z方向部分,但是需要注意的是,图 7所表示的压力不仅仅是因为螺旋桨尾流具有周向的诱导速度,还因为螺旋桨的尾流同样有轴向的诱导速度,此二者的合速度使位于螺旋桨后方的舵前缘的压力值要高于其他位置的舵前缘。
|
Download:
|
| 图 7 舵前缘的压力分布(θ=0°) Fig. 7 Pressure at the leading edge of the rudder (θ=0°) | |
在舵表面建立一系列监测点,这些监测点使用(i, j)表示,其中i表示行数,i=1~9, j表示列数,j=1~6,这些监测点呈矩形分布,其中,i=1~2和i=8~9处的监测点位于叶梢后方,i=3~7位于叶根和桨毂处,图 8为这些监测点的分布。

|
Download:
|
| 图 8 舵表面上检测点的分布 Fig. 8 Probes at rudder surface | |
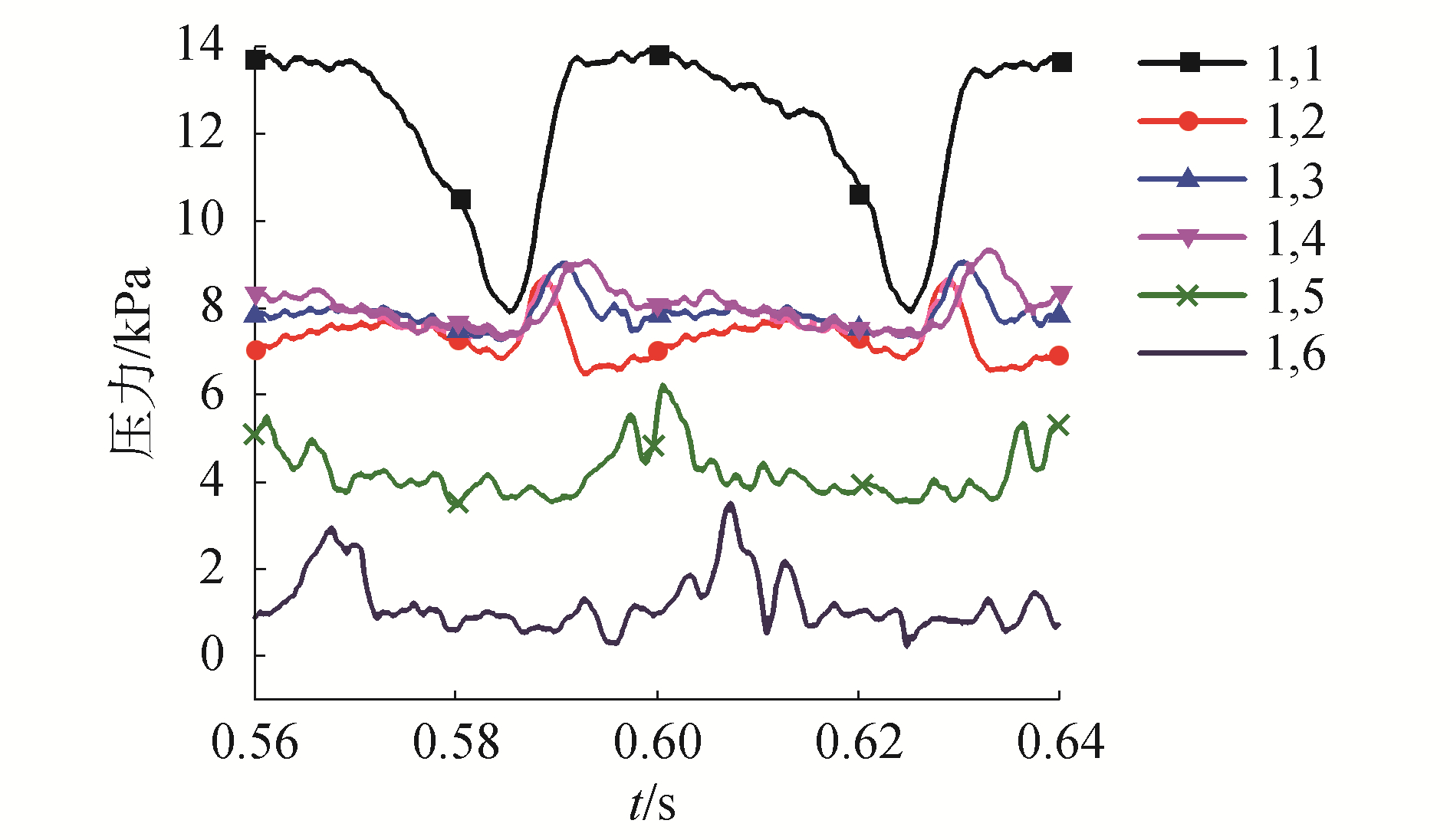
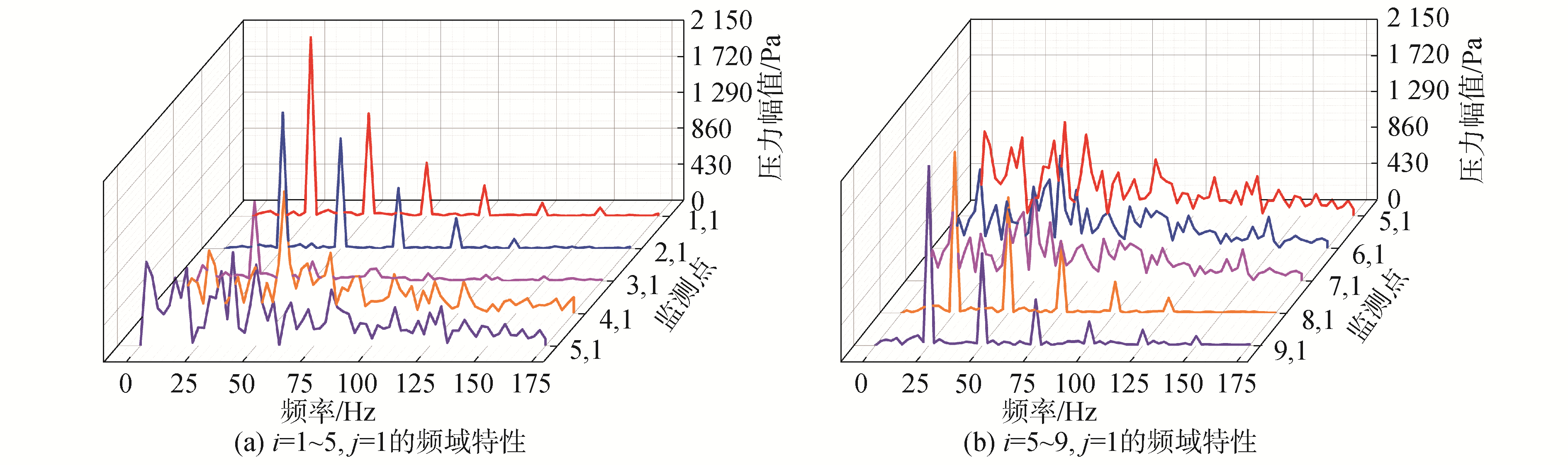
采集i=1, j=1~6处的压力建立时域曲线,可以发现,i=1, j=1~6处的压力值具有非常强的周期性,如图 9所示。采集这些监测点上的压力值,选择10个周期的数据绘制频域曲线,横轴为频率,纵轴表示频域曲线幅值。图 10为编号为(i, 1)(i=1,2,3,…,9)的监测点处压力的频域曲线,通过对比可以发现,位于叶梢后方的点上的压力值的频域曲线具有非常明显的峰值且峰值出现在N=25 Hz处,这表示叶梢后方点上的压力具有非常明显的周期性,其周期接近单桨叶螺旋桨的旋转的频率25 Hz,而位于桨毂后方的点上的压力则周期性不强,这表示毂涡的周期性要明显地弱于梢涡。
|
Download:
|
| 图 9 i=1, j=1~6处的时域特性 Fig. 9 The time domain at i=1, j=1~6 | |
|
Download:
|
| 图 10 i=1~9, j=1处的频域特性 Fig. 10 The frequency domain at i=1~9, j=1 | |
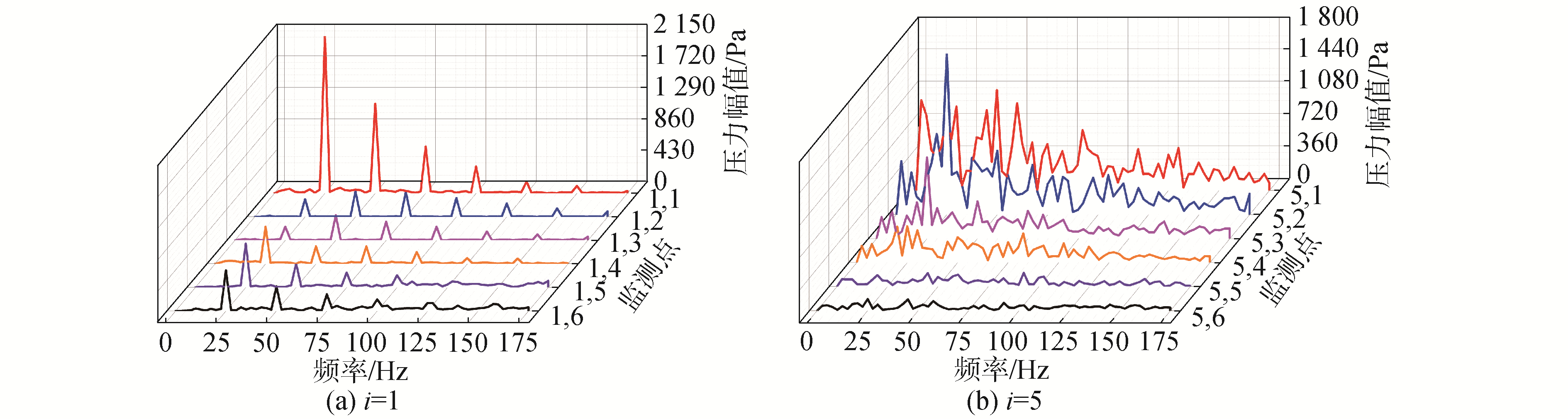
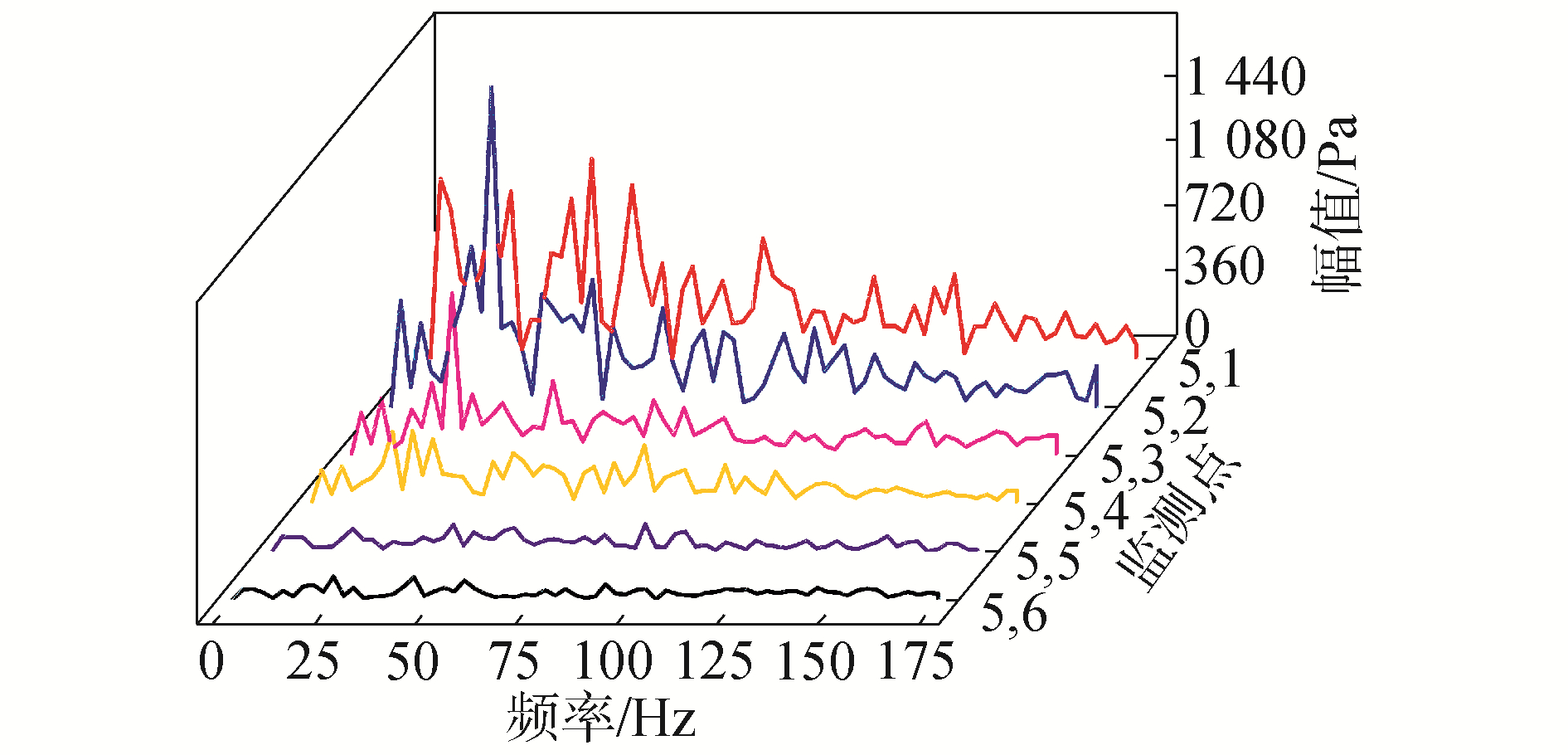
绘制相同i值下不同j值处监测点上的压力频域曲线,可以发现j=1处的曲线峰值最大,且最大峰值在N=25 Hz处,随着j值的增大,频域曲线的峰值的逐渐减少,如图 11a所示,这种现象同样出现在桨毂后方的频域曲线上,但是桨毂后方的频域曲线均没有表现出强周期性,如图 11(b)所示。舵表面压力沿弦长方向上衰减这一现象也可以得到舵表面压力沿弦长分布曲线的验证,图 12分别是Z=0 m和Z=0.113 5 m处舵表面上力沿X方向的分布,可以发现,舵表面上的压力值沿X方向先迅速增加后缓慢降低,不同Z值位置上的压力值均呈现出这种趋势。
|
Download:
|
| 图 11 浆毂和对梢后方压力的频域特性 Fig. 11 Frequency domain of pressure at the rear of hub and blods tip | |
|
Download:
|
| 图 12 Z=0 m和Z=0.113 5 m处舵表面上力沿X方向的分布 Fig. 12 Pressure distribution along the X direction at Z=0.113 5 and Z=0 | |
1) 舵表面前缘的横向速度分布关于舵中心线中心对称,正负2个方向上的最大值均位于叶根处,速度的大小沿桨叶展长方向逐渐降低,在叶梢之后接近0。
2) 舵表面前缘的压力分布同样关于舵中心线对称,同时位于螺旋桨后方的区域压力值较大。
3) 位于梢涡流场区域的舵表面受周期性强烈的力的作用,而位于毂涡流场区域的舵表面上受到的力则周期性不明显,在所有的展向位置上,舵表面的脉动压力幅值都沿着弦长方向递减。
使用大涡模拟方法对舵上的压力分布和这些压力的频域特征进行了分析,对于船舶的振动控制、节能效果提升等方面具有重要的意义,但本研究未考虑空化、噪声等问题,后续研究可结合舵空化-梢涡空化的耦合作用展开。
| [1] |
FELLI M, GUJ G, CAMUSSI R. Effect of the number of blades on propeller wake evolution[J]. Experiments in fluids, 2008, 44(3): 409-418. DOI:10.1007/s00348-007-0385-0 (  0) 0)
|
| [2] |
MUSCARI R, DI MASCIO A, VERZICCO R. Modeling of vortex dynamics in the wake of a marine propeller[J]. Computers & fluids, 2013, 73: 65-79. (  0) 0)
|
| [3] |
GUILMINEAU E, DENG G B, LEROYER A, et al. Influence of the turbulence closures for the wake prediction of a marine propeller[C]//Proceedings of the Fourth International Symposium on Marine Propulsors. Austin, TX, 2015.
(  0) 0)
|
| [4] |
DI FELICE F, FELLI M, LIEFVENDAHL M, et al. Numerical and experimental analysis of the wake behavior of a generic submarine propeller[C]//Proceedings of the First International Symposium on Marine Propulsors. Trondheim, Norway, 2009.
(  0) 0)
|
| [5] |
SUN Shuai, LI Liang, WANG Chao, et al. Numerical prediction analysis of propeller exciting force for hull-propeller-rudder system in oblique flow[J]. International journal of naval architecture and ocean engineering, 2018, 10(1): 69-84. DOI:10.1016/j.ijnaoe.2017.03.005 (  0) 0)
|
| [6] |
王超, 黄胜, 常欣, 等. 基于滑移网格与RNG k-ε湍流模型的桨舵干扰性能研究[J]. 船舶力学, 2017, 15(7): 715-721. WANG Chao, HUANG Sheng, CHANG Xin, et al. Research on the hydrodynamics performance of propeller-rudder interaction based on sliding mesh and RNG k-ε model[J]. Journal of ship mechanics, 2017, 15(7): 715-721. (  0) 0)
|
| [7] |
FELLI M, FALCHI M. Propeller tip and hub vortex dynamics in the interaction with a rudder[J]. Experiments in fluids, 2011, 51(5): 1385-1402. DOI:10.1007/s00348-011-1162-7 (  0) 0)
|
| [8] |
DI MASCIO A, DUBBIOSO G, MUSCARI R, et al. CFD analysis of propeller-rudder interaction[C]//Proceedings of the 25th International Ocean and Polar Engineering Conference. Kona, Big Island, Hawaii, USA, 2015.
(  0) 0)
|
| [9] |
MUSCARI R, DUBBIOSO G, DI MASCIO A. Analysis of the flow field around a rudder in the wake of a simplified marine propeller[J]. Journal of fluid mechanics, 2017, 814: 547-569. DOI:10.1017/jfm.2017.43 (  0) 0)
|
| [10] |
齐慧博, 刘业宝, 张克正, 等. 基于CFD方法的桨舵干扰非定常水动力性能研究[J]. 中国科技论文, 2017, 12(7): 725-728. QI Huibo, LIU Yebao, ZHANG Kezheng, et al. Unsteady hydrodynamic performance of propeller and rudder system studied by CFD[J]. China sciencepaper, 2017, 12(7): 725-728. DOI:10.3969/j.issn.2095-2783.2017.07.001 (  0) 0)
|
| [11] |
胡健, 李聪慧, 张维鹏, 等. 基于CFD的桨舵水动力干扰研究[J]. 应用科技, 2017, 44(3): 5-11, 18. HU Jian, LI Conghui, ZHANG Weipeng, et al. Investigation of hydrodynamic interaction between propeller and rudder based on computational fluid dynamics[J]. Applied science and technology, 2017, 44(3): 5-11, 18. (  0) 0)
|
| [12] |
郝鹏, 李国栋, 杨兰, 等. 圆柱绕流流场结构的大涡模拟研究[J]. 应用力学学报, 2012, 29(8): 437-443. HAO Peng, LI Guodong, YANG Lan, et al. Large eddy simulation of the circular cylinder flow in different regimes[J]. Chinese journal of applied mechanics, 2012, 29(8): 437-443. (  0) 0)
|
| [13] |
王福军. 计算流体动力学分析——CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
(  0) 0)
|
| [14] |
CALCAGNO G, DI FELICE F, FELLI M, et al. The INSEAN E779a propeller test case: a database for CFD validation[C]//Proceedings of MARNET-CFD Final Workshop. Haslar, 2003: 58-83.
(  0) 0)
|
| [15] |
GRECO L, MUSCARI R, TESTA C, et al. Marine propellers performance and flow-field prediction by a free-wake panel method[J]. Journal of hydrodynamics, 2014, 26(5): 780-795. DOI:10.1016/S1001-6058(14)60087-1 (  0) 0)
|
| [16] |
胡健, 耿冲, 冯峰. 基于大涡模拟的螺旋桨梢涡数值分析[J]. 华中科技大学学报(自然科学版), 2017, 45(11): 68-73. HU Jian, GENG Chong, FENG Feng. Numerical analysis of propeller tip vortex based on large eddy simulation[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2017, 45(11): 68-73. (  0) 0)
|
| [17] |
李允.不同工况下的对转桨性能预报及非同步对转桨性能研究[D].哈尔滨: 哈尔滨工程大学, 2015. LI Yun. Hydrodynamic performance prediction of contra-rotating propeller under different working conditions and the rescearch of non synchronous counter-rotating propeller[D]. Harbin: Harbin Engineering University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10217-1018050769.htm (  0) 0)
|
| [18] |
鲁利, 熊鹰, 王睿. RANS, DES和LES对螺旋桨流噪声预报的适用性分析[J]. 中国舰船研究, 2017, 12(6): 43-48, 100. LU Li, XIONG Ying, WANG Rui. Applicability of RANS, DES and LES in propeller flow noise[J]. Chinese journal of ship research, 2017, 12(6): 43-48, 100. DOI:10.3969/j.issn.1673-3185.2017.06.007 (  0) 0)
|
| [19] |
耿冲.对转桨水动力性能数值预报[D].哈尔滨: 哈尔滨工程大学, 2018. GENG Chong. Numerical prediction on hydrodynamic performance of contra propeller[D]. Harbin: Harbin Engineering University, 2018. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


