船舶在大洋中航行中会时时刻刻遭受波浪的作用,船舶在波浪中的大幅度摇荡运动会大大降低船舶的适航性,更为严重的会导致海难的发生。因此,准确计算船舶的波浪作用力对船舶操作、设计及运营显得尤为重要。
在势流理论的范畴下,Korvin-Kroukovsky[1](F-K)基于二维切片理论,将船体离散成若干等截面的船舶横剖面,数值计算出船舶各个横剖面由于入射波作用引起的F-K力,沿船长方向积分可得到总F-K力, 但其并未考虑到由入射波引起的绕射力。Salvesen等[2]进一步提出了STF法, 由于该理论有效地考虑由入射波引起的绕射力对船体的作用,其运动预报精度有了较大提高。基于三维频域理论,Beck等[3]将船体平均湿表面离散成一系列四边形平面面元,F-K力可由高斯积分定理在平面面元上进行积分得到,绕射力与辐射力则基于有航速修正的零航速Green函数求解。在三维线性时域范畴内,King[4]基于脉冲响应函数法可以高效地求出不同频率下的船舶湿表面上的F-K力,并结合三维时域Green函数求解出作用在船体平均湿表面上的辐射力与绕射力。二维线性理论与三维线性理论均可以有效地求解出线性范围内船体所受的F-K力,但是当船舶大幅度摇荡运动时,船体湿表面积剧烈变化,F-K力在船体平均湿表面上进行计算显然不能满足非线性问题。段文洋[5]研究表明,船舶在波浪中受到的作用力的非线性主要来源于物面非线性。Lin和Yue[6]提出了基于自由面线性化条件和物面条件在瞬时湿表面上满足的物面非线性理论,扰动势在未扰动的自由液面下的瞬时物面上建立积分方程,而F-K力及静水恢复力则在瞬时入射波剖面下的船体湿表面上计算。由于求解扰动势需要在每个时间步生成瞬时湿表面网格,求解大量的矩阵方程,导致计算量非常庞大。
由于F-K力及静水恢复力在船舶受力中占主要部分,扰动力在船体平均湿表面计算、F-K力及静水恢复力在船体瞬时湿表面上计算成为高效精确船舶运动的预报的方法。主要有2种入射波面下瞬时网格生成方法:第一种方法为“干-湿网格判断法”[7],计算F-K力及静水恢复力所需“细网格”的面元数目为计算流体扰动力“粗网格”的面元数目的4~8倍,当面元中心高于入射波波面时,该面元视为“干面元”,F-K力及静水恢复力为零;反之视该面元为“湿面元”,利用高斯积分定理计算该面元上的F-K力及静水恢复力。该方法计算效率较高,仅需判断面元的“干-湿”状态即可。但是,即便面元中心点与入射波波面之间的相对位置比该面元几何尺寸小,可能相邻2个时间步长面元由“干面元”转变为“湿面元”或“湿面元”转变为“干面元”,容易造成F-K力数值计算的不连续性。第2种方法为“瞬时网格截取法”[8],其计算F-K力及静水恢复力所需面元数目与计算流体扰动力“粗网格”的面元数目一样,对与波面相交的面元进行进一步处理:1)判断出与瞬时波面相交面元的两条边;2)利用迭代法求出波面与两条边的交点,此时可由2个交点所形成的线段近似地表示在面元内波面方程;3)计算面元浸湿部分的F-K力及静水恢复力。在波高波长比较小时,形成的瞬时湿表面较好地与波面吻合。但是该方法通过迭代法求解交点坐标并对面元信息进行更新,计算比较繁琐,且当入射波较陡时,波面与面元相交情况比较复杂,不易进行数值分析与判断。Rodrigues等[9-10]精确地推导零航速船体瞬时湿表面上正弦入射波的F-K力的解析积分表达式,但是其未对波面进行有效修正,船体所受压力在静水面处不连续,且其扰动力的计算采用频时域转换法,很难精确求解出高频率区间的水动力系数,最终造成了F-K力的较大的计算误差。
为精确高效地求解F-K力,本文基于自适应网格对船体瞬时湿表面进行精确生成,并对入射波压力与静水压力进行修正。对低于波面且位于平均自由液面下的四边形面元,推导余弦入射波引起的F-K力在四边形面元上的解析积分表达式,在减少面元数量的同时避免了数值积分产生的误差;对与波面相交或者位于平均自由液面上的面元,由于F-K力的数值及变化较大,基于四叉树法对面元进一步精细划分,得到F-K力和静水恢复力的高精度数值解。在三维线性时域内建立流体扰动速度势的边界积分方程求出扰动力。最后,以WigleyⅠ型船为例,其相关的计算结果与试验结果及其它文献结果吻合度良好,证明了本文提出的模型的可靠性。
1 数学模型的建立空间固定坐标系O-XYZ与面元局部坐标系o-xyz如图 1所示,其中O-XY与静水面重合,OZ轴垂直向上,o-xy与处理过后的船体平面面元重合,o为四边形面元的几何中心,oz轴垂直于平面面元,指向朝向船体内部。船体固定坐标系Gb-xbybzb坐标原点Gb为船舶重心,Gbxb正轴指向船艏,Gbyb正轴指向左舷,Gbzb正轴垂直向上。初始时刻,Gb-xbybzb与O-XYZ相互平行。

|
Download:
|
| 图 1 坐标系的定义 Fig. 1 Coordinates systems | |
面元局部坐标o-xyz坐标r(x, y, z)与空间固定坐标系O-XYZ坐标R(X, Y, Z)的转换如下:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}_o} + \mathit{\boldsymbol{T}}r = }\\ {\left[ {\begin{array}{*{20}{c}} {{X_o}}\\ {{Y_o}}\\ {{Z_o}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {\left\langle {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{X}}} \right\rangle }&{\left\langle {\mathit{\boldsymbol{y}},\mathit{\boldsymbol{X}}} \right\rangle }&{\left\langle {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{X}}} \right\rangle }\\ {\left\langle {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{Y}}} \right\rangle }&{\left\langle {\mathit{\boldsymbol{y}},\mathit{\boldsymbol{Y}}} \right\rangle }&{\left\langle {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{Y}}} \right\rangle }\\ {\left\langle {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{Z}}} \right\rangle }&{\left\langle {\mathit{\boldsymbol{y}},\mathit{\boldsymbol{Z}}} \right\rangle }&{\left\langle {\mathit{\boldsymbol{z}},\mathit{\boldsymbol{Z}}} \right\rangle } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x\\ y\\ z \end{array}} \right]} \end{array} $ | (1) |
式中:Ro(Xo, Yo, Zo)为面元局部坐标系原点o在空间固定坐标系的坐标;T单位余弦转换矩阵;x、y及z为面元局部坐标系基坐标单位矢量;X、Y及Z为空间固定坐标系基坐标单位矢量;〈, 〉表示两向量内积。
同理,可得空间固定坐标系O-XYZ与船体固定坐标系Gb-xbybzb的转换关系。
1.2 扰动速度势定解问题势流理论范畴内[6], 流场内场点p(x, y, z)在时刻t时的总速度势ϕT(p; t)可以分解为:
| $ {\phi _T}\left( {p;t} \right) = \phi \left( {p;t} \right) + {\phi _I}\left( {p;t} \right) $ | (2) |
式中:ϕ(p; t)为扰动速度势;ϕI(p; t)为入射波速度势。
在流域内,速度势ϕ(p; t)满足:
| $ {\nabla ^2}\phi = 0 $ | (3) |
在无扰自由面上,速度势ϕ满足的条件为:
| $ \frac{{{\partial ^2}\phi }}{{\partial {t^2}}} + {\rm{g}}\frac{{\partial \phi }}{{\partial Z}} = 0 $ | (4) |
式中,g为重力加速度。
在物面上,速度势ϕ满足不可穿透条件为:
| $ \frac{{\partial \phi }}{{\partial \mathit{\boldsymbol{n}}}} = {v_n} - \frac{{\partial {\phi _I}}}{{\partial \mathit{\boldsymbol{n}}}} $ | (5) |
式中:n为船体单位法向向量,指向船体内部;vn为船体表面在法线方向的速度。
无穷远处速度势ϕ扰动衰减条件为:
| $ \nabla \phi \to 0 $ | (6) |
t=0时,速度势ϕ的初始条件为:
| $ \phi = 0,\frac{{\partial \phi }}{{\partial t}} = 0 $ | (7) |
三维时域自由表面格林函数G可以用来求解速度势ϕ[4]:
| $ \begin{array}{*{20}{c}} {G\left( {p,t;q,\tau } \right) = {G^0}\left( {p;q} \right)\delta \left( {t - \tau } \right) + }\\ {\tilde G\left( {p,t;q,\tau } \right)H\left( {t - \tau } \right)} \end{array} $ | (8) |
式中:q(ξ, η, ζ)为源点;τ为历史时刻;δ(t)为Dirac delta函数;H(t)为阶跃函数;G0及
| $ {G^0} = \frac{1}{{{r_1}}} - \frac{1}{{{r_2}}} $ | (9) |
| $ \tilde G = 2\int_0^\infty {\sqrt {{\rm{g}}k} \sin \left[ {\sqrt {{\rm{g}}k} \left( {t - \tau } \right)} \right]{{\rm{e}}^{k\left( {z + \zeta } \right)}}{{\rm{J}}_0}\left( {kR} \right){\rm{d}}k} $ | (10) |
式中:r1为场点p与源点q的距离;r2为场点p与源点q关于水平面镜像点的距离;R为场点与源点的水平距离;J0为零阶贝塞尔函数; k为波数。
G0及其空间导数可以用Hess-Smith数值方法[11]计算。
对时域自由面格林函数G和扰动速度势Φ应用格林定理并采用分布源模型可得:
| $ \begin{array}{*{20}{c}} {4{\mathsf{π}}\Phi \left( {p;t} \right) = \iint\limits_{{S_b}} {\sigma \left( {q,t} \right){G^0}{\text{d}}{S_q}} + \int_0^t {{\text{d}}\tau \iint\limits_{{S_b}} {\sigma \left( {q,t} \right)\tilde G{\text{d}}{S_q}}} - } \\ {\frac{1}{g}\int_0^t {{\text{d}}\tau } \int_\Gamma {\sigma \left( {q,\tau } \right)\tilde G{V_N}{V_n}{\text{d}}{l_q}} } \end{array} $ | (11) |
式中:N为水线处单位法向量;VN为水线上的二维法向速度;Vn与VN的关系为:Vn=VN·(N·n);Γ为船舶水线;Sb为船舶平均湿表面。
采用常数面元法将船体平均湿表面离散成一定数目的四边形面元,每块面元上的源密度σ为常数,联立式(5)与式(11),可以形成关于源密度σ的线性矩阵方程,求解出σ将其代入离散后的式(11)即可求出各个面元上的速度势ϕ。
1.3 F-K压力及静水恢复压力的计算与修正入射波速度势ϕI的表达式为
| $ {\Phi _I} = \frac{{i{\eta _0}g}}{\omega }{{\rm{e}}^{kZ + {\rm{i}}\left[ {\omega t - k\left( {X\cos \alpha + Y\sin \alpha } \right)} \right]}},Z \le 0 $ | (12) |
式中:η0为入射波波高;ω为入射波圆频率;α为波浪入射角,其传播方向与OX轴正方向的夹角,迎浪为α=π;k=ω2/g。
空间固定坐标系下的点p(X, Y, Z)(Z≤0)的静水压力pH与入射波压力pw分别为:
| $ {p_H} = - \rho {\rm{g}}Z $ | (13) |
| $ {p_w} = \rho {\rm{g}}{\eta _0}{{\rm{e}}^{kZ}}\cos \left[ {\omega t - k\left( {X\cos \alpha + Y\sin \alpha } \right)} \right] $ | (14) |
式中ρ为流体密度。
由线性自由面动力学边界条件可知,空间固定坐标系下的入射波波面方程为:
| $ \begin{array}{*{20}{c}} {\eta \left( t \right) = - {{\left. {\frac{1}{g}\frac{{\partial {\Phi _I}}}{{\partial t}}} \right|}_{Z = 0}} = }\\ {{\eta _0}\cos \left[ {\omega t - k\left( {X\cos \alpha + Y\sin \alpha } \right)} \right]} \end{array} $ | (15) |
则入射波压力pw与静水压力pH的合压力pHw为:
| $ {p_{Hw}} = \rho {\rm{g}}\eta \left( t \right){{\rm{e}}^{kZ}} - \rho {\rm{g}}Z $ | (16) |
为使入射波面上压力为零且压力连续分布,对式(16)进行修正[13]。当η(t)≥0时,其pHw(t)压力计算表达式为
| $ {p_{Hw}} = \left\{ {\begin{array}{*{20}{l}} {\rho {\rm g}\eta - \rho {\rm g}Z,}&{0 \le Z \le \eta \left( t \right)}\\ {\rho {\rm g}\eta {{\rm{e}}^{kZ}} - \rho {\rm g}Z,}&{Z < 0} \end{array}} \right. $ | (17) |
当入射波波高η(t) < 0,波面上不满足总压力为零的条件,需对波谷进行修正,采用Newton迭代法求解非线性方程η(t)ekZ-ρgZ=0,则修正后的波谷为Z=Z′=η(t)ekZ′,压力pHw(t)表达式为
| $ {p_{Hw}} = \left\{ {\begin{array}{*{20}{l}} {0,}&{\eta \left( t \right){{\rm{e}}^{kZ'}} \le Z \le 0}\\ {\rho {\rm{g}}\eta {{\rm{e}}^{kZ}} - \rho {\rm g}Z,}&{Z < \eta \left( t \right){{\rm{e}}^{kZ'}}} \end{array}} \right. $ | (18) |
将船体湿表面处理为M块四边形平面面元,首先计算低于波面且同时位于平均自由液面下的面元受力。则第i块面元上的入射波力为
| $ {F_{wi}} = {n_i}\rho {\rm g}{\eta _0} \times \iint\limits_{{S_i}} {{{\text{e}}^{kZ}}\cos \left[ {\omega t - k\left( {X\cos \alpha + Y\sin \alpha } \right)} \right]{\text{d}}S} $ | (19) |
式中:ni为第i块面元上单位内法线向量;Si为第i块平面面元面积。
令Α(x, y)及Β(x, y)分别为:
| $ \begin{array}{l} A = - k\left( {{X_0} + \langle x,X\rangle x + \langle y,X\rangle y} \right)\cos \alpha - \\ k\left( {{Y_0} + \langle x,Y\rangle x + \langle y,Y\rangle y} \right)\sin \alpha + \omega t \end{array} $ | (20) |
| $ B = k\left[ {{Z_0} + \langle x,Z\rangle x + \langle y,Z\rangle y} \right] $ | (21) |
则
| $ {A_x} = - k(\langle x,X\rangle \cos \alpha + \langle x,Y\rangle \sin \alpha ) $ | (22) |
| $ {A_y} = - k(\langle y,X\rangle \cos \alpha + \langle y,Y\rangle \sin \alpha ) $ | (23) |
| $ {B_x} = k\langle x,Z\rangle $ | (24) |
| $ {B_y} = k\langle y,Z\rangle $ | (25) |
在面元局部坐标系下,对第i块面元上第j条边进行参数化表示可得:
| $ {g_{ij}}(r) = \left( {{x_{0,ij}},{y_{0,ij}}} \right) + \left( {\Delta {x_{ij}},\Delta {y_{ij}}} \right)r,r \in [0,1] $ | (26) |
式中:Δxij=x1, ij-x0, ij;Δyij=y1, ij-y0, ij,下标‘0’代表第i块面元上第j段线段的起点,下标‘1’代表第i块面元上第j段线段的终点。
则第i块面元上第j条边上的Α、Β及其对r的导数分别为:
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{ij}}(r) = \omega t - k{X_{0,i}}\cos \alpha - k{Y_{0,i}}\sin \alpha \\ \;\;\;\;\;\;\;\;\;\; - k\langle x,X\rangle \left( {{x_{0,ij}} + \Delta {x_{ij}}r} \right)\cos \alpha \\ \;\;\;\;\;\;\;\;\;\; - k\langle y,X\rangle \left( {{y_{0,ij}} + \Delta {y_{ij}}r} \right)\cos \alpha \\ \;\;\;\;\;\;\;\;\;\; - k\langle x,Y\rangle \left( {{x_{0,ij}} + \Delta {x_{ij}}r} \right)\sin \alpha \\ \;\;\;\;\;\;\;\;\;\; - k\langle y,Y\rangle \left( {{y_{0,ij}} + \Delta {y_{ij}}r} \right)\sin \alpha \end{array} $ | (27) |
| $ \begin{array}{*{20}{c}} {{B_{ij}}(r) = k\left[ {{Z_{0,i}} + \langle x,Z\rangle \left( {{x_{0,ij}} + \Delta {x_{ij}}r} \right)} \right.}\\ {\left. { + \langle y,Z\rangle \left( {{y_{0,ij}} + \Delta {y_{ij}}r} \right)} \right]} \end{array} $ | (28) |
| $ \begin{array}{l} {\mathit{\boldsymbol{A}}_{r,ij}}(r) = - k\langle x,X\rangle \Delta {x_{ij}}\cos \alpha \\ \;\;\;\;\;\;\;\;\;\;\;\;\; - k\langle y,X\rangle \Delta {y_{ij}}\cos \alpha \\ \;\;\;\;\;\;\;\;\;\;\;\;\; - k\langle x,Y\rangle \Delta {x_{ij}}\sin \alpha \\ \;\;\;\;\;\;\;\;\;\;\;\;\; - k\langle y,Y\rangle \Delta {y_{ij}}\sin \alpha \end{array} $ | (29) |
| $ {B_{r,ij}}(r) = k\left( {\langle x,Z\rangle \Delta {x_{ij}} + \langle y,Z\rangle \Delta {y_{ij}}} \right) $ | (30) |
令Ψx=Αx, i2+Βx, i2,Ψy=Αy, i2+Βy, i2,利用格林定理及结合公式(26),当Ψy=0且Ψx=0时,
| $ {F_{wi}} = {n_i}\rho {\rm g}{\eta _0}{{\rm{e}}^{k{Z_0}}}{S_i} \times \cos \left[ {\omega t - k\left( {{X_0}\cos \alpha + {Y_0}\sin \alpha } \right)} \right] $ | (31) |
当Ψx≠0时,可得第i块面元上的入射波浪力为:
| $ \begin{array}{*{20}{c}} {{F_{wi}} = \frac{{{n_i}\rho {\rm g}{\eta _0}}}{{{\Psi _x}}} \times \sum\limits_{j = 1}^4 {\Delta {y_{ij}}\int_0^1 {{{\rm{e}}^{{B_i}\left( r \right)}}} \left[ {{B_{x,i}}\cos {A_{ij}}\left( r \right) + } \right.} }\\ {\left. {{A_{x,i}}\sin {A_{ij}}\left( r \right)} \right]{\rm{d}}r = \frac{{{n_i}\rho {\rm g}{\eta _0}}}{{{\Psi _x}}} \times }\\ {\sum\limits_{j = 1}^4 {\left[ {\Delta {y_{ij}}\left( {{B_{x,i}}\Delta C{E_{ij}} + {A_{x,i}}\Delta S{E_{ij}}} \right)} \right]} } \end{array} $ | (32) |
当Ψy≠0时,得第i块面元上入射波浪力为:
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{F}}_{wi}} = \frac{{ - {n_i}\rho {\rm g}{\eta _0}}}{{{\mathit{\Psi }_y}}} \times \sum\limits_{j = 1}^4 \Delta {x_{ij}}\int_0^1 {{{\rm{e}}^{{B_i}(r)}}} \left[ {{B_{y,i}}\cos {A_{ij}}(r) + } \right.}\\ {\left. {{A_{y,i}}\sin {A_{ij}}(r)} \right]{\rm{d}}r = \frac{{ - {n_i}\rho {\rm g}{\eta _0}}}{{{\mathit{\Psi }_y}}} \times }\\ {\sum\limits_{j = 1}^4 {\left[ {\Delta {x_{ij}}\left( {{B_{y,i}}\Delta C{E_{ij}} + {A_{y,i}}\Delta S{E_{ij}}} \right)} \right]} } \end{array} $ | (33) |
式中:
| $ \begin{array}{*{20}{c}} {\Delta S{E_{ij}} = S{E_{ij}}\left( 1 \right) - S{E_{ij}}\left( 0 \right)}\\ {\Delta C{E_{ij}} = C{E_{ij}}\left( 1 \right) - C{E_{ij}}\left( 0 \right)} \end{array} $ | (34) |
令Ψr=Αr, i2+Βr, i2考虑如下定义:
| $ \begin{array}{l} SE = \left\{ {\begin{array}{*{20}{l}} {\frac{{{e^B}\left( {{B_r}\sin A - {A_r}\cos A} \right)}}{{{\mathit{\Psi }_r}}},{\mathit{\Psi }_r} \ne 0}\\ {{e^B}r\sin A,{\mathit{\Psi }_r} = 0} \end{array}} \right.\\ CE = \left\{ {\begin{array}{*{20}{l}} {\frac{{{e^B}\left( {{B_r}\cos A + {A_r}\sin A} \right)}}{{{\mathit{\Psi }_r}}},{\mathit{\Psi }_r} \ne 0}\\ {{e^B}r\cos A,{\mathit{\Psi }_r} = 0} \end{array}} \right. \end{array} $ | (35) |
同理,入射波力矩、静水恢复力及静水恢复力矩可以采用类似的解析方法求取。
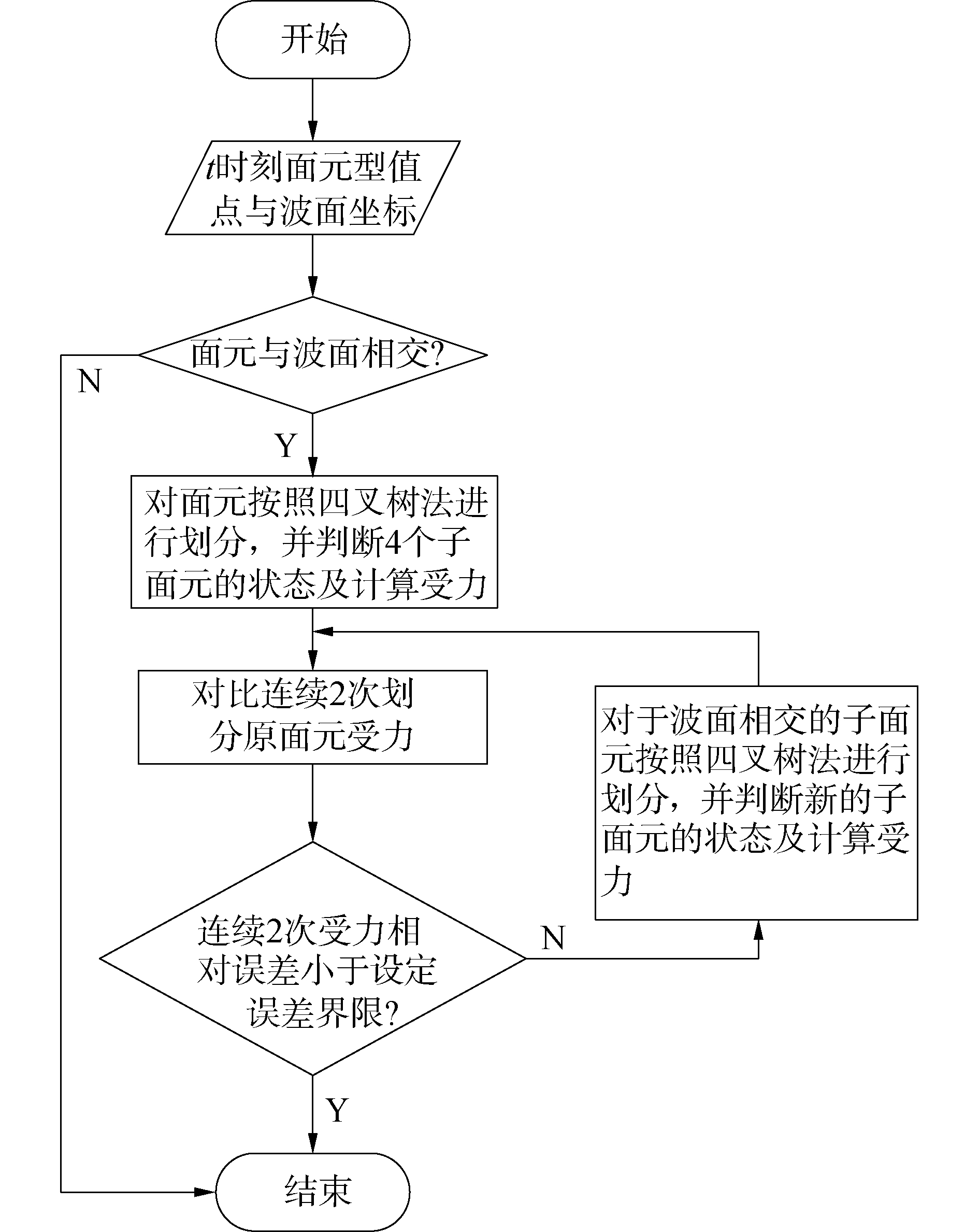
1.5 F-K力的数值积分对于与波面相交或者位于平均自由液面上的面元上的F-K力及静水恢复力的计算,由于F-K力数值及变化相对其他面元较大,采用四叉树法并结合高斯积分定理对F-K力和静水恢复力进行数值计算。
将面元分为4种状态:1)如果面元4个顶点都完全位于波面以下,则称之为“湿面元”;2)如果面元中心位于波面之下且4个顶点没有都位于波面以下,称之为“半加湿面元”;3)如果面元中心位于波面上且仍有顶点位于波面以下,称之为“半减湿面元”;4)如果面元4个顶点完全位于波面以上,称之为“干面元”。
如图 2所示,每一次划分过程中,只对“半加湿面元”与“半减湿面元”进行四叉树划分,并计算新形成的“湿面元”与“半加湿面元”上的受力。

|
Download:
|
| 图 2 面元的四叉树划分 Fig. 2 Panel subdivision by quad-tree scheme | |
式中:图 3中的误差界限根据实际工程需要进行调整,本文采用0.01%。
|
Download:
|
| 图 3 面元受力计算流程 Fig. 3 Calculation of forces acting on the panel | |
流场中任意处压力根据Bernoulli方程可写为:
| $ {p_e}\left( {p,t} \right) = - \rho \left( {\frac{{\partial {\mathit{\Phi }_T}}}{{\partial t}} + 0.5{{\left| {\nabla {\mathit{\Phi }_T}} \right|}^2} + gZ} \right) $ | (36) |
由式(2)及式(36)可以进一步写为:
| $ {p_e} = {p_d} + {p_{Hw}} $ | (37) |
| $ {p_d} = - \rho \left( {\frac{{\partial \mathit{\Phi }}}{{\partial t}} + 0.5{{\left| {\nabla {\mathit{\Phi }_T}} \right|}^2}} \right) $ | (38) |
则对于扰动力Fd及扰动力矩Md在Gb-xbybzb随船固定坐标系的计算式为:
| $ {\mathit{\boldsymbol{F}}_d} = \iint_{{S_b}} {{p_d}}\mathit{\boldsymbol{n}}{\text{d}}S;{\mathit{\boldsymbol{M}}_d} = \iint_{{S_b}} {{p_d}}\left( {{\mathit{\boldsymbol{r}}_b} \times {\mathit{\boldsymbol{n}}_b}} \right){\text{d}}S $ | (39) |
式中:rb为随船固定坐标系船体表面位置矢量;nb为物面单位法向向量,指向船体内部。
入射波浪力、静水恢复力及其对应力矩,接着应用四阶龙格库塔方法求解船舶运动方程,即可得到船舶的受力及运动时历。

|
Download:
|
| 图 4 WigleyⅠ船体面元划分 Fig. 4 Panels distribution for Wigley I hull | |
本文选用WigleyⅠ型船验证模型的可靠性与精确性,其主要参数[14]如表 1所示。
| 表 1 WigleyⅠ型船主尺度 Table 1 Main particulars of WigleyⅠ hull |
船舶以Fn=0.2的速度迎浪行驶,波高η0为0.036 m,波长与船长比λ/L=1.4。
首先选取完全位于静水面下的一块1×1 m2的正方形面元,其4个顶点坐标依次为(-0.5, 0, -1)、(0.5, 0, -1)、(0.5, 0, 0)和(-0.5, 0, 0)。在t=0时刻,F-K力在该面元上的由压力积分解析表达式求得为170.738 N(保留到0.001 N)。对面元上F-K力采用高斯数值积分进行计算,并进一步对面元进行如图 5的剖分,直到与解析解求得的结果相同为止。

|
Download:
|
| 图 5 面元剖分示意 Fig. 5 Panel subdivision diagram | |
由表 2可知,当剖分次数为3时,满足精度要求,此时该面元被剖分成64个子面元,F-K力数值积分值与解析积分值相同,但是数值积分值达到规定精度时,所需要的面元数远远超过解析积分。对于水线面下形状较为规则的浮体,采用解析积分计算F-K力, 其所需要面元数量为O(101)的数量级,在不损失精度的情况下,其面元数大大地减少了,有利于计算效率的提高。
| 表 2 t=0面元上F-K压力积分值 Table 2 The values of F-K pressure integration on the panels at t=0 |
本文将全部船体表面(包括水线面以上)划分为80×8个面元,对于与波面相交的面元基于四叉树法进一步划分,称为方案1,其F-K力计算采用1.5节方法。Singh等[7]划分面元个数为160×16个,称为方案2。对于与波面相交的面元,对面元直接划分足够多的子面元,直到面元上的受力趋于极限值即可视为解析解,称为方案3。选取pan1、pan2、pan3和pan4四块与波面相交的面元,四块面元中心在t=0时的空间固定坐标系中坐标分别为(1.462 5, 0.008 4, -0.023 4)、(1.462 5, 0.065 0, -0.023 4)、(0.862 5, 0.106 9, 0.023 4)及(0.412 5, 0.140 7, 0.023 4)。
从表 3中可以看出,采用方案2计算与波面相交面元上的F-K力与方案3误差比较大,而方案1与方案3的误差比较小(小于万分之一)。主要原因是,采用方案2,即使其网格虽然较求解扰动力的网格划分更加细密,但是在波面及其附近,波浪力及其变化较大,面元划分个数仍显不足。方案1对湿表面面元尺寸与求解扰动力的面元尺寸相同,但其对与波面相交的面元基于四叉树法进一步划分。采用方案1,既避免了对所有面元进行进一步划分所带来的计算量繁重的弊端,又充分考虑F-K力在面元与波面相交处及其附近强烈波动性,最终得到精确的F-K力值。
| 表 3 t=0面元上F-K压力积分值 Table 3 The values of F-K pressure integration on the panels at t=0 |
图 6、7为船舶湿表面在中纵剖面上的投影示意图,由图 6、7可直观看到,采用方案1形成的瞬时湿表面与波面吻合度更好。

|
Download:
|
| 图 6 方案1在t=0位于瞬时波面下的船体面元划分 Fig. 6 Panel distribution under instantaneous incident wave profile at t=0 by scheme 1 | |

|
Download:
|
| 图 7 方案2在t=0位于瞬时波面下的船体面元划分 Fig. 7 Panel distribution under instantaneous incident wave profile at t=0 by scheme 2 | |
为了进一步验证本文有航速波浪力计算模型的有效性,针对有航速WigleyⅠ船型在无限水深的F-K力及运动时历进行计算,将其与文献[14]的试验结果进行比对。
船舶以航速U前进,航速取傅汝德数Fn=U/
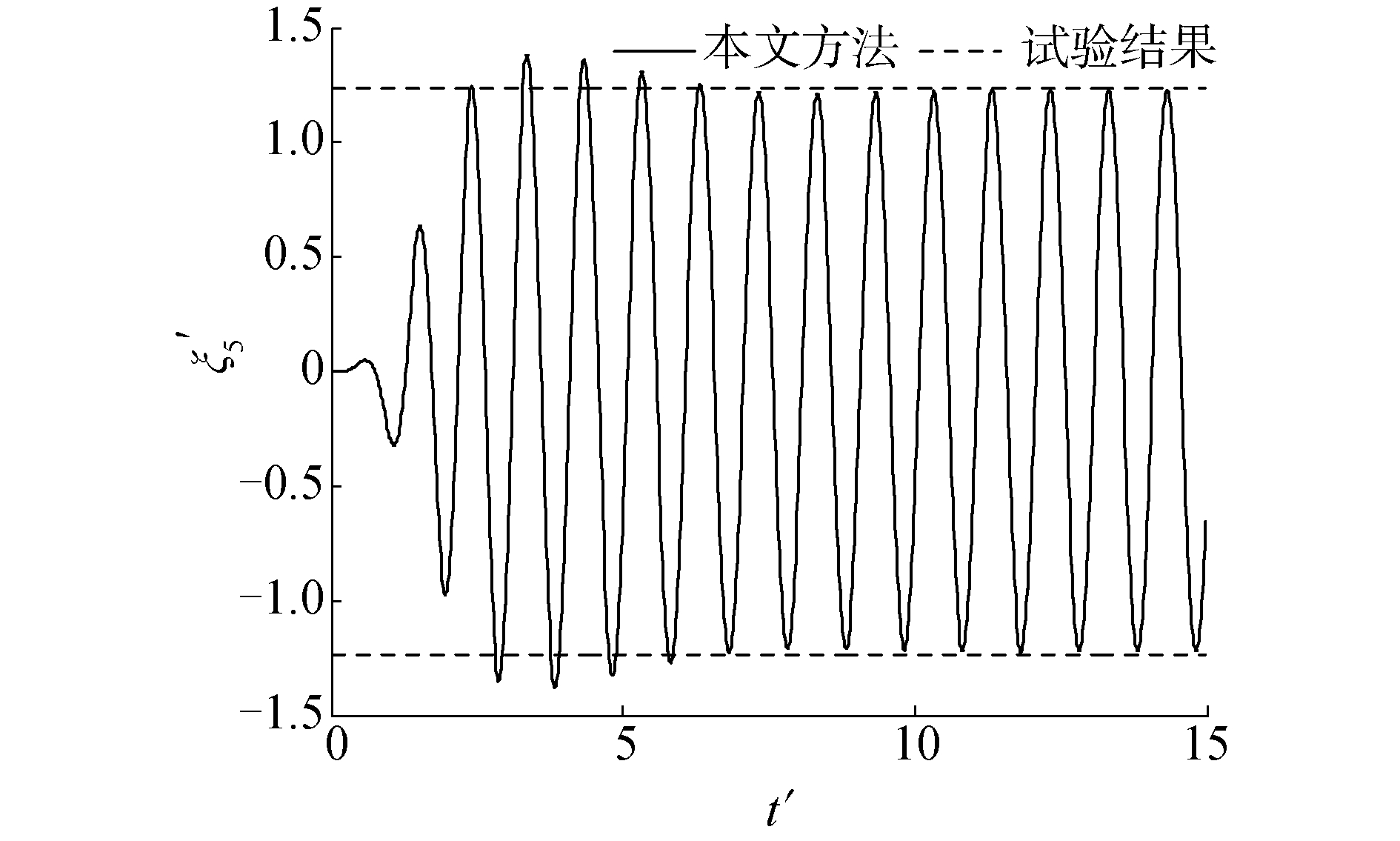
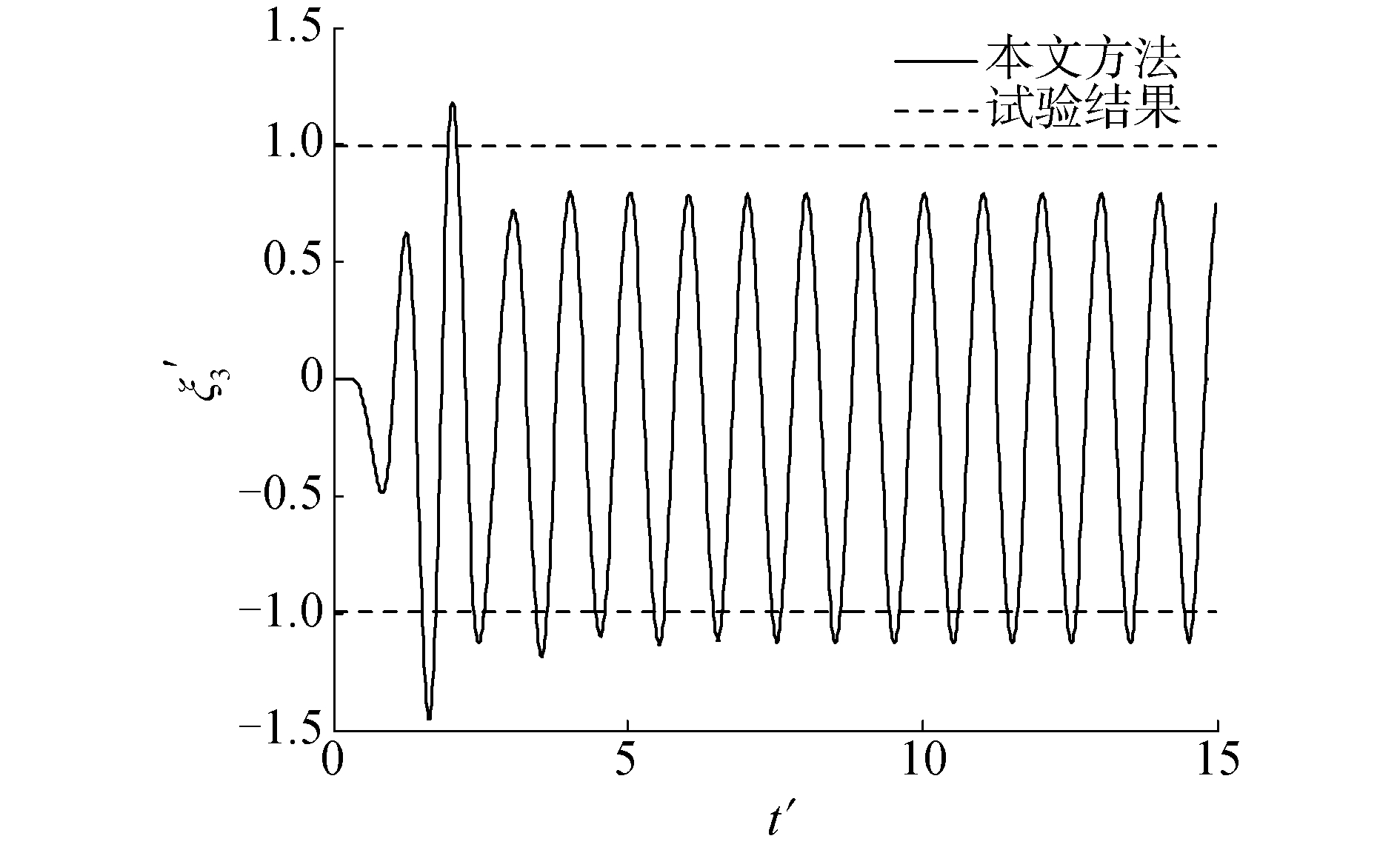
数值仿真过程中,WigleyⅠ型船仅在垂荡和纵摇2个模态有位移响应。图 8~11为船舶垂荡和纵摇2个运动模态的位移时历。由图 8~11可知,本文提出有航速波浪力计算方法所得的垂荡纵摇幅值计算结果与试验幅值吻合良好。但是垂荡运动模态平衡位置下移了一段位置,原因在于F-K力与静水恢复力在瞬时入射波波面下进行计算,引入了非线性因素的影响。由于船体形状关于中站面对称,所以纵摇位移的平衡位置仍然为0。

|
Download:
|
| 图 8 λ/L=1.4时无因次垂荡运动时历 Fig. 8 The time history of non-dimensional heave motion (λ/L=1.4) | |
|
Download:
|
| 图 9 λ/L=1.4时无因次纵摇运动时历 Fig. 9 The time history of non-dimensional pitch motion (λ/L=1.4) | |
|
Download:
|
| 图 10 λ/L=2.0时无因次垂荡运动时历 Fig. 10 The time history of non-dimensional heave motion (λ/L=2.0) | |

|
Download:
|
| 图 11 λ/L=2.0时无因次纵摇运动时历 Fig. 11 The time history of non-dimensional pitch motion (λ/L=2.0) | |
1) 本文对低于波面且位于平均自由液面下的面元,推导了余弦入射波下的F-K力的解析表达式,该方法能避免数值计算产生的误差。对于水下形状较为规则的浮体,面元划分的数量级可降至O(101);
2) 对与波面相交或者位于平均自由液面上的面元,基于四叉树法对面元进行进一步划分并对F-K力进行数值计算。其面元上F-K力的计算精度有了极大的提高,且所形成的船体瞬时湿表面与瞬时入射波面比文献[7]更好地吻合;
3) 通过得到的有航速船舶的运动时历计算结果发现,本文提出的F-K力计算方法,考虑了入射波浪力及船体几何形状对船舶运动的影响, 并与试验结果较好地吻合;
本文只进行了F-K力的解析压力积分表达式计算推导,下一步可以对扰动力的解析计算继续深入探究。
| [1] |
KORVIN-KROUKOVSKY B V, JACOBS W R. Pitching and heaving motions of a ship in regular waves[J]. Transactions of the society of naval architects and marine engineers, 1957, 65: 590-632. (  0) 0)
|
| [2] |
SALVESEN N, TUCK E O, FALTINSEN O. Ship motions and sea loads[J]. Transactions of the society of naval architects and marine engineers, 1970, 78: 250-287. (  0) 0)
|
| [3] |
BECK R F, LOKEN A E. Three-dimensional effects in ship relative-motion problems[J]. Journal of ship research, 1989, 33(4): 261-268. (  0) 0)
|
| [4] |
KING B. Time-domain analysis of wave exciting forces on ships and bodies[R]. Ann Arbor, Michigan: The department of Naval Architecture and Marine Engineering, University of Michigan, 1987.
(  0) 0)
|
| [5] |
段文洋, 戴遗山. 二维浮体大幅运动水动力物面非线性时域解[J]. 哈尔滨工程大学学报, 1997, 18(5): 1-7. DUAN Wenyang, DAI Yishan. Nonlinear time-domain solution of hydrodynamic forces on a 2-D floating body undergoing large amplitude motions[J]. Journal of Harbin Engineering University, 1997, 18(5): 1-7. (  0) 0)
|
| [6] |
LIN W M, YUE D K P. Numerical solution for large-amplitude ship motions in the time-domain[C]//Proceedings of the 18th Symposium on Naval Hydrodynamics. Ann Arbor, 1990: 41-66.
(  0) 0)
|
| [7] |
SINGH S P, SEN D. A comparative study on 3D wave load and pressure computations for different level of modelling of nonlinearities[J]. Marine structures, 2007, 20(1/2): 1-24. (  0) 0)
|
| [8] |
SENGUPTA D, DATTA R, SEN D. A simplified approach for computation of nonlinear ship loads and motions using a 3D time-domain panel method[J]. Ocean engineering, 2016, 117: 99-113. DOI:10.1016/j.oceaneng.2016.03.039 (  0) 0)
|
| [9] |
RODRIGUES J M, GUEDES SOARES C. A generalized adaptive mesh pressure integration technique applied to progressive flooding of floating bodies in still water[J]. Ocean engineering, 2015, 110: 140-151. DOI:10.1016/j.oceaneng.2015.10.002 (  0) 0)
|
| [10] |
RODRIGUES J M, GUEDES SOARES C. Froude-Krylov forces from exact pressure integrations on adaptive panel meshes in a time domain partially nonlinear model for ship motions[J]. Ocean engineering, 2017, 139: 169-183. DOI:10.1016/j.oceaneng.2017.04.041 (  0) 0)
|
| [11] |
HESS J L, SMITH A M O. Calculation of non-lifting potential flow about arbitrary three-dimensional bodies[J]. Journal of ship research, 1964, 8(2): 22-44. (  0) 0)
|
| [12] |
张腾, 任俊生, 李志富, 等. 时域格林函数的新实用数值计算方法[J]. 大连海事大学, 2018, 44(1): 1-8. ZHANG Teng, REN Junsheng, LI Zhifu, et al. A new and practical numerical calculation method for time-domain Green function[J]. Journal of Dalian Maritime University, 2018, 44(1): 1-8. DOI:10.3969/j.issn.1671-7031.2018.01.002 (  0) 0)
|
| [13] |
BLANDEAU F, FRANÇOIS M, MALENICA Š, et al. Linear and non-linear wave loads on FPSOs[C]//Proceedings of the 9th International Offshore and Polar Engineering. Brest, France: ISOPE, 1999.
(  0) 0)
|
| [14] |
JOURNÉE J M J. Experiments and calculations on four Wigley Hull forms[R]. Delft: Delft University of Technology, 1992.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


