随着陆地资源的日渐匮乏,海洋所蕴藏的资源受到了越来越多科研工作者的关注。动力定位船的运动特性使得其在深海作业资源勘探、铺管作业、石油钻探等领域有着得天独厚的优势。因此,动力定位船的轨迹跟踪问题成为了当前海洋发展战略的重要内容之一。在复杂的海洋环境中,如何避免外界干扰的影响进而保证动力定位船控制系统能以最优的控制性能完成预计的轨迹跟踪和定位过程,成为了当前工程实践中较为普遍的研究热点。
在当前的研究成果中文献[1]介绍了一种基于自适应输出反馈控制的轨迹跟踪方法,能够在未知环境的条件下通过观测器估值的输出反馈进行控制律的设计,解决了输入饱和问题;文献[2]介绍了一种基于运动方程速度变换方法的轨迹跟踪控制,其优点在于将系统动力学模型(包括控制系数等)直接包含于系统增益矩阵中,但是其局限性在于仅适用于全驱动系统模型,通过Lyapunov函数的分析证明了该方法具有良好的鲁棒性;文献[3]与文献[1]比较,介绍了一种基于简单输出反馈的轨迹跟踪控制方法,但是控制器中没有加入自适应的控制,取而代之的是结合逼近角和辅助变量的观测器设计,因此拓宽了该方法的适用范围,能够跟踪全部类型的轨迹;文献[4]介绍了一种基于终端滑膜的轨迹跟踪控制方法,能够更好地适应非线性模型,同时能够跟踪时变的轨迹,减小误差,使得控制系统具有更好的鲁棒性;文献[5]介绍了通过反步法的设计实现了轨迹跟踪中对于不确定扰动的抑制,同时通过Lyapunov函数保证了系统的设计能够实现渐进稳定,同时跟踪误差收敛到零,但是文章没有考虑执行机构的约束与控制性能,存在一定的局限性;文献[6]介绍了基于Lyapunov直接法,得到了保证系统全局渐近稳定的充分条件,采用基于Backstepping方法进行动力定位,对外界扰动具有一定鲁棒性,但是对具体位置进行跟踪,跟踪直线时,因没考虑到最短距离跟踪,所以不能快速跟踪期望轨迹;文献[7]与文献[5]和文献[6]比较而言,介绍了一种基于自适应神经网络的轨迹跟踪控制方法,通过对未知干扰的估计结合反步法,消除了对非光滑不对称的非线性高斯误差的影响,同时保证了跟踪误差收敛到一个小邻域内;文献[8]介绍了一种基于反步法和自适应相结合的控制器设计过程,该控制方法能够实现参数的在线更新,增强了系统的鲁棒性,但是没有考虑误差的变化情况和界限问题,容易造成输出饱和等现象;文献[9]和文献[10]提出了一种基于迭代滑膜控制方法来实现AUV地形跟踪控制和UUV三维轨迹跟踪控制,该方法能够在不考虑外界扰动和模型不确定的情况下实现精确控制,但是缺点在于控制参数为预先设定,缺少了自适应的调节过程。
根据目前的研究并未针对动力定位船轨迹跟踪过程中的性能约束情况给予准确的论述和重视[11],本文在此基础上设计了基于预设性能函数的反步自适应控制器,该控制方法能够保证动力定位系统轨迹跟踪过程中的稳态性能和暂态性能,通过转换误差的思想保证跟踪误差在给定的限界内变化并最终趋于稳定,同时结合反步自适应方法也保证了对系统存在的不确定性以及未知扰动的鲁棒性,实现了轨迹跟踪过程。最终通过仿真实验,验证了所设计的控制器的有效性。
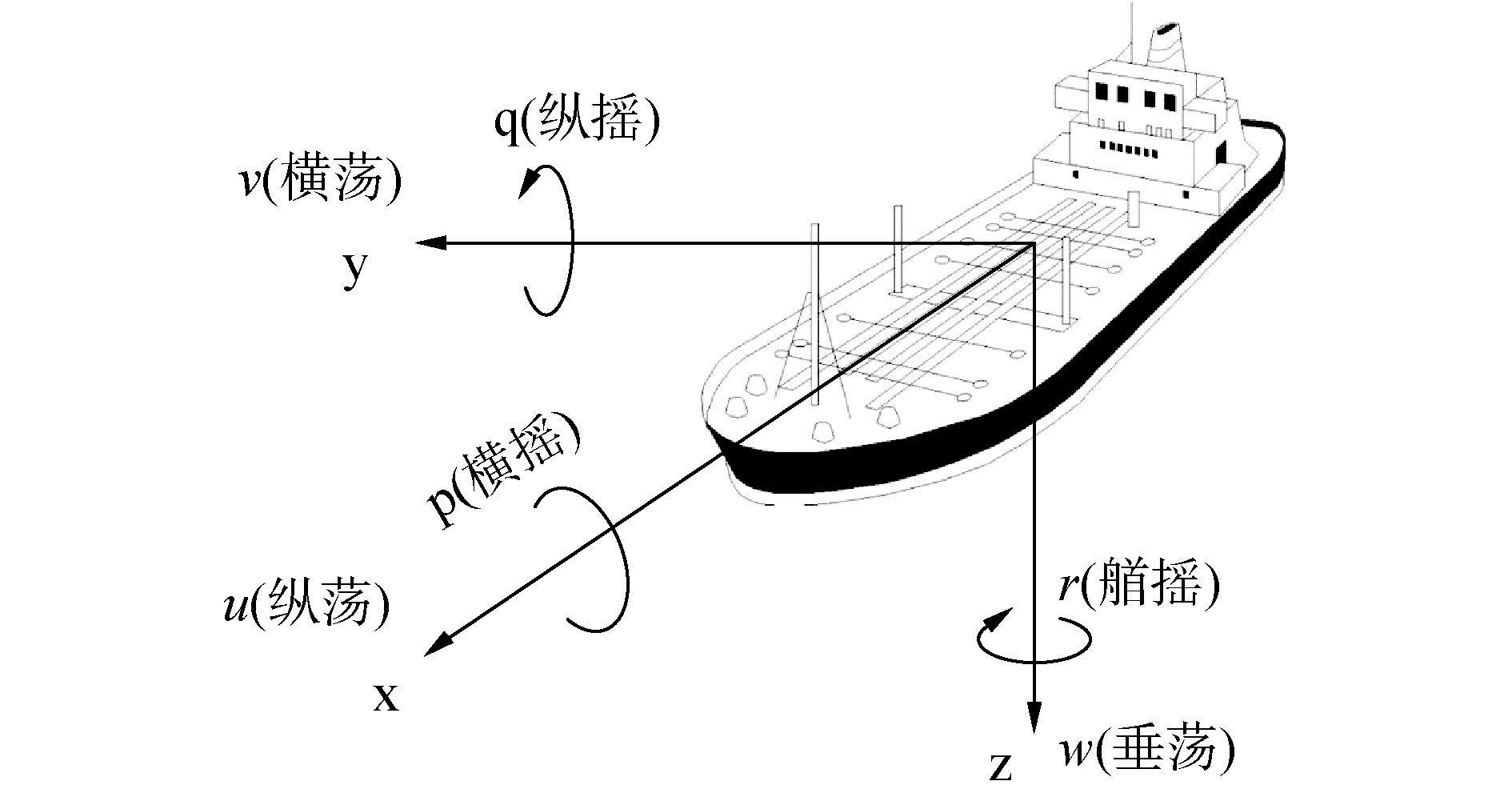
1 模型系统 1.1 运动学模型动力定位船运动学模型分为6个自由度的运动,其中包括了纵荡、横荡、垂荡、横摇、纵摇、首摇(如图 1所示)[12]。
|
Download:
|
| 图 1 船舶运动变量 Fig. 1 The motion variable of vessel | |
其方程形式为:
| $ \mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{J}}\left( \eta \right)v \Leftrightarrow \left[ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\dot P}}}^n}}\\ {\mathit{\boldsymbol{ \boldsymbol{\dot \varTheta} }}} \end{array}} \right] = \left[ {\begin{array}{*{20}{lc}} {\mathit{\boldsymbol{R}}_b^n\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)}{{0_{3 \times 3}}}\\ {{0_{3 \times 3}}}&{{\mathit{\boldsymbol{T}}_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} }\left( \mathit{\boldsymbol{ \boldsymbol{\varTheta} }} \right)} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{U}}_o^b}\\ {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_{nb}^b} \end{array}} \right] $ | (1) |
式中:
对于动力定位中的水面船研究,在考虑横摇角(ϕ)和纵摇角(θ)很小的情况下,将运动学模型简化成三自由度即转艏、进退、横荡的表达式。
其方程形式为:
| $ \mathit{\boldsymbol{\dot \eta }} = \mathit{\boldsymbol{R}}\left( \psi \right)\mathit{\boldsymbol{v}} $ | (2) |
式中:
定义ηd为系统期望位置信息,所以跟踪误差ηe即可由下式(3)表示:
| $ {\mathit{\boldsymbol{\eta }}_e} = \mathit{\boldsymbol{\eta }} - {\mathit{\boldsymbol{\eta }}_d} $ | (3) |
其中η, ηd, ηe∈R2×S,对于表达式(3)进行求导可得如下形式:
| $ {{\mathit{\boldsymbol{\dot \eta }}}_e} = \mathit{\boldsymbol{\dot \eta }} - {{\mathit{\boldsymbol{\dot \eta }}}_d} $ | (4) |
| $ {{\mathit{\boldsymbol{\ddot \eta }}}_e} = \mathit{\boldsymbol{\ddot \eta }} - {{\mathit{\boldsymbol{\ddot \eta }}}_d} $ | (5) |
视船舶为刚体,根据动量定理可得动力定位船的动力学矢量表达式:
| $ {\mathit{\boldsymbol{M}}_{RB}}\mathit{\boldsymbol{\dot v}} + {\mathit{\boldsymbol{C}}_{RB}}(\mathit{\boldsymbol{v}})\mathit{\boldsymbol{v}} = {\mathit{\boldsymbol{\tau }}_{RB}} $ | (6) |
式中:MRB表示刚体系统的惯性矩阵,υ=[u、v、w、p、q、r]T表示船体坐标系下的各自由度的速度矢量的分量;CRB(υ)表示刚体科里奥利向心力矩阵;τRB=[X、Y、Z、K、M、N]T表示动力定位船所受到的合外力与力矩的矢量。
动力定位船所受的合力矩τRB由水动力及力矩τH、海洋环境的作用力(风、浪、流等)ω、动力定位船推进系统力及力矩构成。
其方程形式为:
| $ {\mathit{\boldsymbol{\tau }}_{RB}} = {\mathit{\boldsymbol{\tau }}_H} + \mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{\tau }} $ | (7) |
水动力力和力矩矢量τH可由式(8)表达:
| $ {\mathit{\boldsymbol{\tau }}_H} = - {\mathit{\boldsymbol{M}}_A}\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{C}}_A}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{g}}\left( \mathit{\boldsymbol{\eta }} \right) + {\mathit{\boldsymbol{g}}_o} $ | (8) |
假设忽略重力/浮力的平衡力矩和g(η)以及动力定位船的均衡力矢量go,动力定位船的动力学模型矢量形式可以进一步简化。
其方程形式为:
| $ \mathit{\boldsymbol{M\dot v}} + \mathit{\boldsymbol{C}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} + \mathit{\boldsymbol{D}}\left( \mathit{\boldsymbol{v}} \right)\mathit{\boldsymbol{v}} = \mathit{\boldsymbol{\omega }} + \mathit{\boldsymbol{\tau }} $ | (9) |
式中:M表示系统惯性矩阵(M=MRB+MA);C(υ)表示科里奥利向心力矩阵(C(υ)=CRB(υ)+CA(υ));D(υ)表示阻尼系数矩阵;ω表示海洋环境作用力矢量(包含风、浪、流等);τ表示动力定位船推进系统力和力矩矢量。
由式(2)~(5)、(9)变换后,可得:
| $ {\mathit{\boldsymbol{M}}^ * }{{\mathit{\boldsymbol{\ddot \eta }}}_e} + {\mathit{\boldsymbol{C}}^ * }{{\mathit{\boldsymbol{\dot \eta }}}_e} + \mathit{\boldsymbol{RH}} = \mathit{\boldsymbol{R}}\left( {\mathit{\boldsymbol{\tau }} + \mathit{\boldsymbol{\omega }}} \right) $ | (10) |
式中符号简记,R=R(ψ),RT=RT(ψ),M*=R(ψ)MRT(ψ),C*=R(ψ)C(ν)RT(ψ),
假设1 外部干扰ω是有界的,满足:|ω|≤ω0,其中ω0>0为一常量。
假设2 期望的位置ηd、
引理1 假设存在如
| $ \mu _e^ * = \sqrt {\frac{{2b}}{{a{\lambda _{L\min }}}}} $ | (11) |
| $ \mu _{\tilde W}^ * = \sqrt {\frac{{2b}}{{a{\lambda _{\Gamma \min }}}}} $ | (12) |
式中:λLmin=minτ∈[0, t]λmin(L(τ)),λΓmin=minτ∈[0, t]λmin(Γ-1(τ))。
引理2 引入符号函数sign(x),其形式如下式(13)所示,因此可知表达式x·sign(x)=|x|成立。
| $ {\rm sign}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {1,}&{x > 0}\\ {0,}&{x = 0}\\ { - 1,}&{x < 0} \end{array}} \right. $ | (13) |
为了实现对系统的跟踪误差进行界限限定,给出如下方程表达的指数衰减形式的性能函数:
| $ {\rho _i}\left( t \right) = \left( {{\rho _{i0}} - {\rho _{i\infty }}} \right)\exp \left( { - {l_i}t} \right) + {\rho _{i\infty }},i = 1,2,3 $ | (14) |
式中:ρi0、ρi∞、li均为大于零常量。
对于跟踪误差的界限表达式为:
| $ \left\{ {\begin{array}{*{20}{l}} { - {\delta _i}{\rho _i}\left( t \right) < {\eta _{ei}}\left( t \right) < {\rho _i}\left( t \right),{\eta _{ei}}\left( 0 \right) \ge 0}\\ { - {\rho _i}\left( t \right) < {\eta _{ei}}\left( t \right) < {\delta _i}{\rho _i}\left( t \right),{\eta _{ei}}\left( 0 \right) < 0} \end{array}} \right. $ | (15) |
式中:0≤δi≤1,i=1, 2, 3;t=0时,ρi0=ρi(0)。
针对式(15)的轨迹跟踪的性能约束不等式,转换成等价的性能约束的等式,因此本文定义了表达式:
| $ {\eta _{ei}}\left( t \right) = {\rho _i}(t){S_i}\left( {{\varepsilon _i}} \right) $ | (16) |
式中εi表示的是转换误差。Si(εi)的表达式为:
| $ {S_i}\left( {{\varepsilon _i}} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{{\exp \left( {{\varepsilon _i}} \right) - {\delta _i}\exp \left( { - {\varepsilon _i}} \right)}}{{\exp \left( {{\varepsilon _i}} \right) + \exp \left( { - {\varepsilon _i}} \right)}},{\eta _{ci}}(0) \ge 0}\\ {\frac{{{\delta _i}\exp \left( {{\varepsilon _i}} \right) - \exp \left( { - {\varepsilon _i}} \right)}}{{\exp \left( {{\varepsilon _i}} \right) + \exp \left( { - {\varepsilon _i}} \right)}},{\eta _{\varepsilon i}}(0) < 0} \end{array}} \right. $ | (17) |
对式(17)进行反变换可解得εI的表达式为:
| $ {\varepsilon _i} = S_i^{ - 1}\left( {\frac{{{\eta _{ei}}(t)}}{{{\rho _i}(t)}}} \right) \to {\varepsilon _i} = {T_i}\left( {\frac{{{\eta _{ei}}(t)}}{{{\rho _i}(t)}}} \right) $ | (18) |
为了方便计算,将上式转换为Ti(xi),其表达式为:
| $ {T_i}\left( {{x_i}} \right) = \left\{ {\begin{array}{*{20}{l}} {\frac{1}{2}\ln \frac{{{\delta _i} + {x_i}}}{{1 - {x_i}}},}&{{\eta _{ei}}(0) \ge 0}\\ {\frac{1}{2}\ln \frac{{1 + {x_i}}}{{{\delta _i} - {x_i}}},}&{{\eta _{ei}}(0) < 0} \end{array}} \right. $ | (19) |
但是需要注意的是,在ηei(0)=0的情况要求δi不能被选择为零,否则εi(0)将是无限大的值。
| $ {{\dot \varepsilon }_i} = \frac{1}{{{\rho _i}(t)}}\frac{{\partial {T_i}}}{{\partial \left( {\frac{{{\eta _{ei}}(t)}}{{{\rho _i}(t)}}} \right)}}\left[ {{{\dot \eta }_{ei}}(t) - {\eta _{ei}}(t)\frac{{{{\dot \rho }_i}(t)}}{{{\rho _i}(t)}}} \right] $ | (20) |
令
| $ \dot \varepsilon = r\left( {{{\dot \eta }_e} - {\eta _e}v} \right) $ | (21) |
首先,进行状态变换的定义:
| $ \left\{ {\begin{array}{*{20}{l}} {{z_1} = \varepsilon }\\ {{z_2} = {{\dot \eta }_e} - {I_C}} \end{array}} \right. $ | (22) |
式中:z1和z2是新的状态量;IC为虚拟的控制量。
1) 选取Lyapunov函数,其形式为:
| $ {V_1} = \frac{1}{2}\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_1} $ | (23) |
对上式求导可得:
| $ {{\dot V}_1} = \mathit{\boldsymbol{z}}_1^{\rm{T}}{{\mathit{\boldsymbol{\dot z}}}_1} = \mathit{\boldsymbol{z}}_1^{\rm{T}}\dot \varepsilon = \mathit{\boldsymbol{z}}_1^{\rm{T}}r\left( {{{\dot \eta }_e} - {\eta _e}v} \right) = \mathit{\boldsymbol{z}}_1^{\rm{T}}r\left( {{z_2} + {I_C} - {\eta _e}v} \right) $ | (24) |
取IC=ηev-r-1k1z1,可得:
| $ {{\dot V}_1} = - {k_1}\mathit{\boldsymbol{z}}_1^{\rm{T}}{\mathit{\boldsymbol{z}}_1} + \mathit{\boldsymbol{z}}_1^{\rm{T}}r{\mathit{\boldsymbol{z}}_2} $ | (25) |
| $ {V_2} = \frac{1}{2}z_2^{\rm{T}}{M^*}{z_2} + \frac{1}{{2\mathit{\Delta } }}{{\tilde b}^{\rm{T}}}{\Gamma ^{ - 1}}\tilde b $ | (26) |
式中:
根据系统的设计,对Lyapunov函数求导得到:
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} = \frac{1}{2}\mathit{\boldsymbol{z}}_2^{\rm{T}}{{\dot M}^*}{\mathit{\boldsymbol{z}}_2} + \mathit{\boldsymbol{z}}_2^{\rm{T}}{M^*}{{\mathit{\boldsymbol{\dot z}}}_2} + \frac{1}{\mathit{\Delta } }{{\tilde b}^{\rm{T}}}{\Gamma ^{ - 1}}\dot {\tilde b} = }\\ {\frac{1}{2}\mathit{\boldsymbol{z}}_2^{\rm{T}}\left( {{{\dot M}^*} - 2{C^*}} \right){\mathit{\boldsymbol{z}}_2} + \mathit{\boldsymbol{z}}_2^{\rm{T}}\left[ { - {C^*}{I_c} - RH + } \right.}\\ {\left. {R\left( {{u_c} + \omega } \right) - {M^*}{{\dot I}_C}} \right] - \frac{1}{\mathit{\Delta } }{{\mathit{\boldsymbol{\tilde b}}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{ - 1}}\dot {\hat b}} \end{array} $ | (27) |
选取控制率uc与自适应律
| $ \begin{array}{*{20}{c}} {{u_c} = {R^{ - 1}}\left( {RH + {C^ * }{I_C} + {M^ * }{{\dot I}_C} - r{z_1} - {k_2}{z_2}} \right) - }\\ {\hat b{\rm sign}\left( {{R^{\rm{T}}}{z_2}} \right)} \end{array} $ | (28) |
| $ \dot {\hat b} = \Gamma \mathit{\Delta } \left[ {\left\| {{R^{\rm{T}}}{z_2}} \right\| - \gamma \left( {\hat b - {b_0}} \right)} \right] $ | (29) |
式中:k2、Γ、Δ、γ均为大于0的常量,将在下文给出具体的参数值。
将选取的控制律公式(28)、(29)代入到式(27),结合引理2可以得到式(30)的结果:
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} \le z_2^{\rm{T}}\left[ { - {C^*}{I_C} - RH + R{u_c} - {M^ * }{{\dot I}_C}} \right] + }\\ {\left\| {{\mathit{\boldsymbol{R}}^{\rm{T}}}{\mathit{\boldsymbol{z}}_2}} \right\| \cdot \left\| \mathit{\boldsymbol{\omega }} \right\| - \frac{1}{\mathit{\Delta } }{{\tilde b}^{\rm{T}}}{\Gamma ^{ - 1}}\dot {\hat b} \le }\\ { - {k_2}z_2^{\rm{T}}{z_2} - z_2^{\rm{T}}R \cdot {\rm sign}\left( {{R^{\rm{T}}}{z_2}} \right)\hat b + }\\ {\left\| {{R^{\rm{T}}}{z_2}} \right\|\hat b - z_2^{\rm{T}}r{z_1} + \gamma {{\tilde b}^{\rm{T}}}\left( {\hat b - {b_0}} \right) \le }\\ { - {k_2}z_2^{\rm{T}}{z_2} - z_2^{\rm{T}}r{z_1} + \gamma {{\tilde b}^{\rm{T}}}\left( {\hat b - {b_0}} \right)} \end{array} $ | (30) |
将式(30)转换后,化简结果为:
| $ \begin{array}{*{20}{c}} {{{\dot V}_2} \le - {k_2}z_2^{\rm{T}}{z_2} - z_2^{\rm{T}}r{z_1} - \frac{1}{2}\gamma {{\tilde b}^{\rm{T}}}\tilde b + }\\ {\frac{1}{2}\gamma {{\left( {b - {b_0}} \right)}^{\rm{T}}}\left( {b - {b_0}} \right)} \end{array} $ | (31) |
对于本文所研究的动力定位船的轨迹跟踪控制,考虑其动力学模型如式(10)所示,通过选取形如V=V1+V2的Lyapunov函数,然后将式(23)和式(26)代入可得:
| $ V = {V_1} + {V_2} = \frac{1}{2}z_1^{\rm{T}}{z_1} + \frac{1}{2}z_2^{\rm{T}}{M^*}{z_2} + \frac{1}{{2\mathit{\Delta } }}{{\tilde b}^{\rm{T}}}{\Gamma ^{ - 1}}\tilde b $ | (32) |
然后对式(32)左右同时求导,将式(25)、(27)以及选取的控制律(28)、(29)代入其中,可以得到如式(33)所示:
| $ \begin{array}{*{20}{c}} {\dot V = {{\dot V}_1} + {{\dot V}_2} \le - {k_1}z_1^{\rm{T}}{z_1} - {k_2}z_2^{\rm{T}}{z_2} - \frac{1}{2}\gamma {{\tilde b}^{\rm{T}}}\tilde b + }\\ {\frac{1}{2}\gamma {{\left( {b - {b_0}} \right)}^{\rm{T}}}\left( {b - {b_0}} \right) \le - aV + b} \end{array} $ | (33) |
式中:a>0且a:=min{2k1, 2k2/λmax(M*), Δγ/λmax(Γ-1)},b的取值为
然后对于式(33)左右两边同时乘以eat进行变换后得到式(34)如下:
| $ \frac{{\rm{d}}}{{{\rm{d}}t}}\left( {V{{\rm{e}}^{at}}} \right) \le b{{\rm{e}}^{at}} $ | (34) |
对式(34)左右两边同时在[0, t]范围内积分得到公式(35)如下:
| $ V\left( t \right) \le \frac{b}{a} + \left[ {V\left( 0 \right) - \frac{b}{a}} \right]{{\rm{e}}^{ - at}} $ | (35) |
综上所述可得,由公式(3)可知,当V>0时即可以保证
为了验证本文所提的反步自适应方法结合预设性能控制对动力定位船轨迹跟踪控制的有效性,论文给出实验船的主要参数如下:船长204 m,船宽39.2 m,型深14 m,吃水深度9.5 m,满载排水量59 106.6 t。利用Matlab/Simulink软件,对动力定位船的轨迹跟踪过程进行仿真研究。仿真过程中的期望轨迹和动力定位船的初始状态信息为:
| $ {\mathit{\boldsymbol{\eta }}_d} = {\left[ {\begin{array}{*{20}{l}} t&{10\sin (t/10)}&0 \end{array}} \right]^{\rm{T}}} $ | (36) |
| $ {\mathit{\boldsymbol{\eta }}_0} = {\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]^{\rm{T}}},{v_0} = {\left[ {\begin{array}{*{20}{c}} 0&0&0 \end{array}} \right]^{\rm{T}}} $ | (37) |
为了保证在轨迹跟踪的过程中,系统的暂态性能和稳态性能满足其指标性能,所以设计了与性能函数相关的参数为δ=[1;1;1]和l=[0.001;0.001;0.001]。除此之外的其他参与选取为k1=diag[0.1, 0.1, 0.1],k2=diag[0.2, 0.2, 0.2],γ=0.001,Δ=10.0,b0=[0, 0]T。
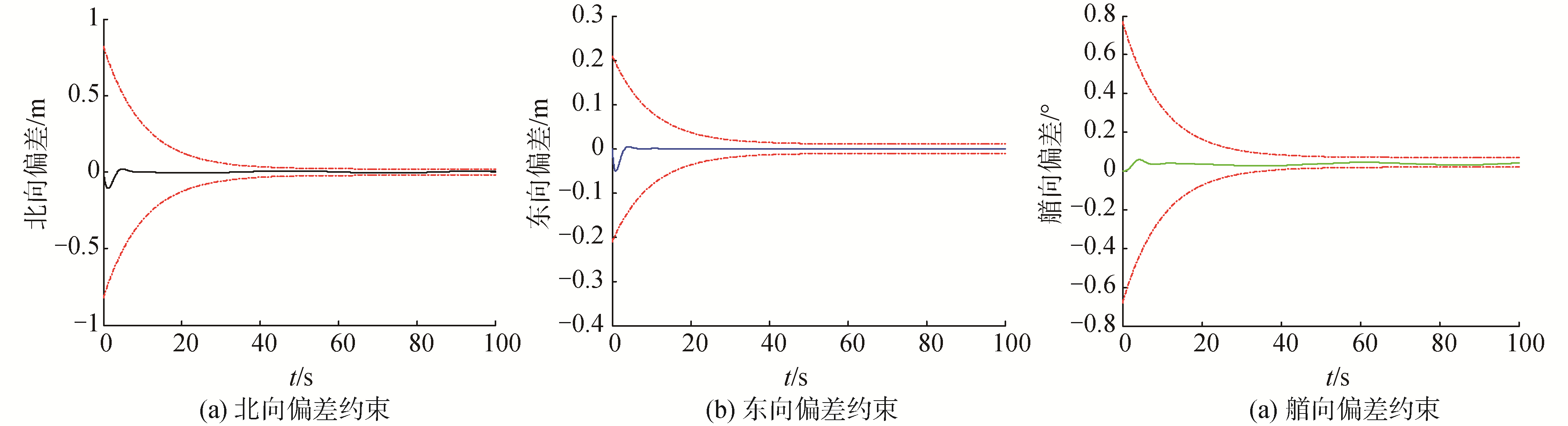
闭环系统的响应在图 2~5中给出。其中,图 2描述了轨迹跟踪误差ηei(t);图 3显示了水平面上的期望轨迹与实际运动轨迹;图 4表明了轨迹跟踪误差的时间响应曲线;图 5中提供了系统所需的控制转矩的时间响应曲线。其详细分析如下:
|
Download:
|
| 图 2 轨迹跟踪误差ηei(t)与性能边界示意 Fig. 2 Evolution of the trajectory tracking errors ηei(t) along with the corresponding performance bounds | |
|
Download:
|
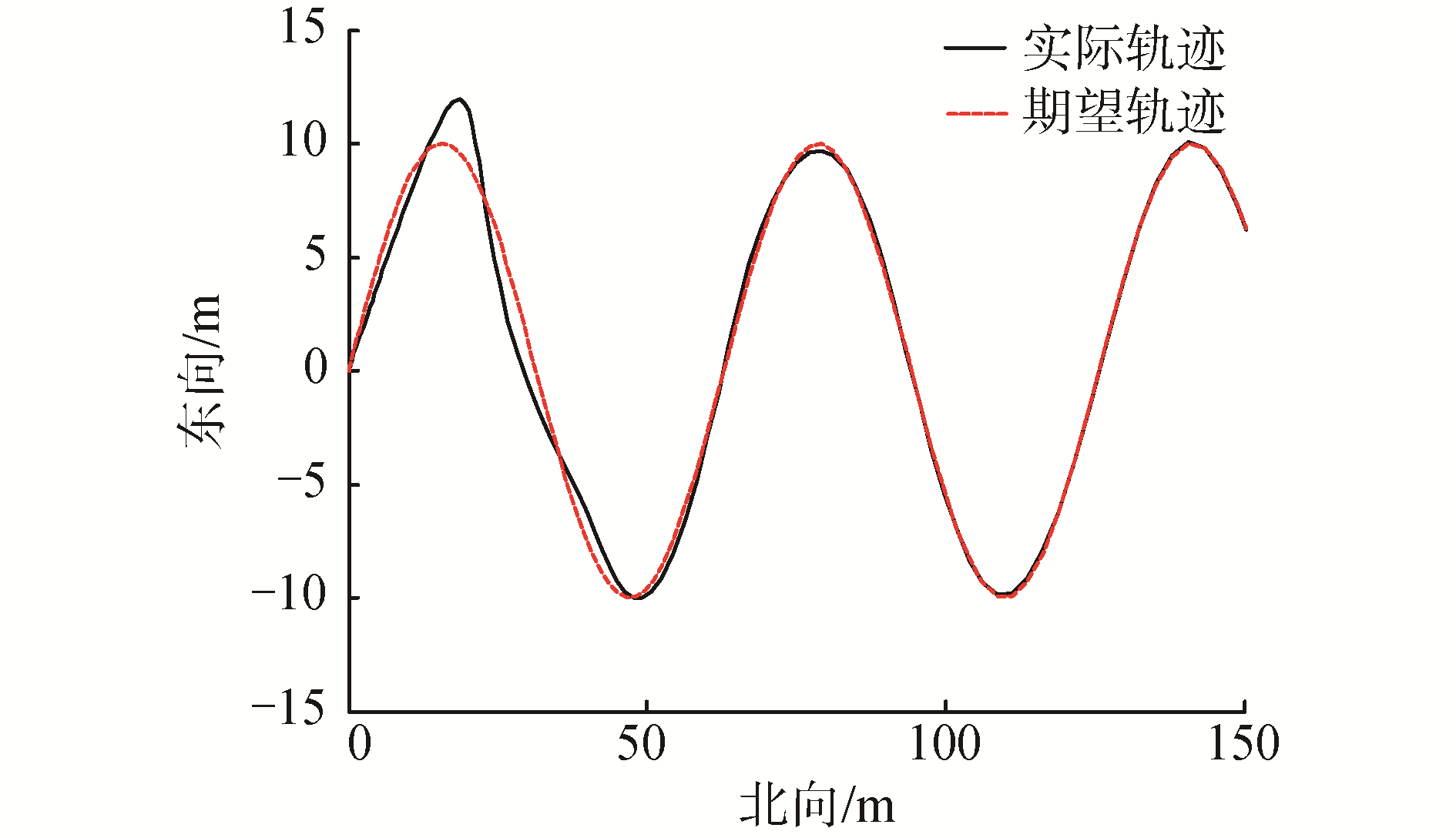
| 图 3 期望轨迹与实际轨迹曲线结果 Fig. 3 The result of the desired trajectory and the actual trajectory curve | |
|
Download:
|
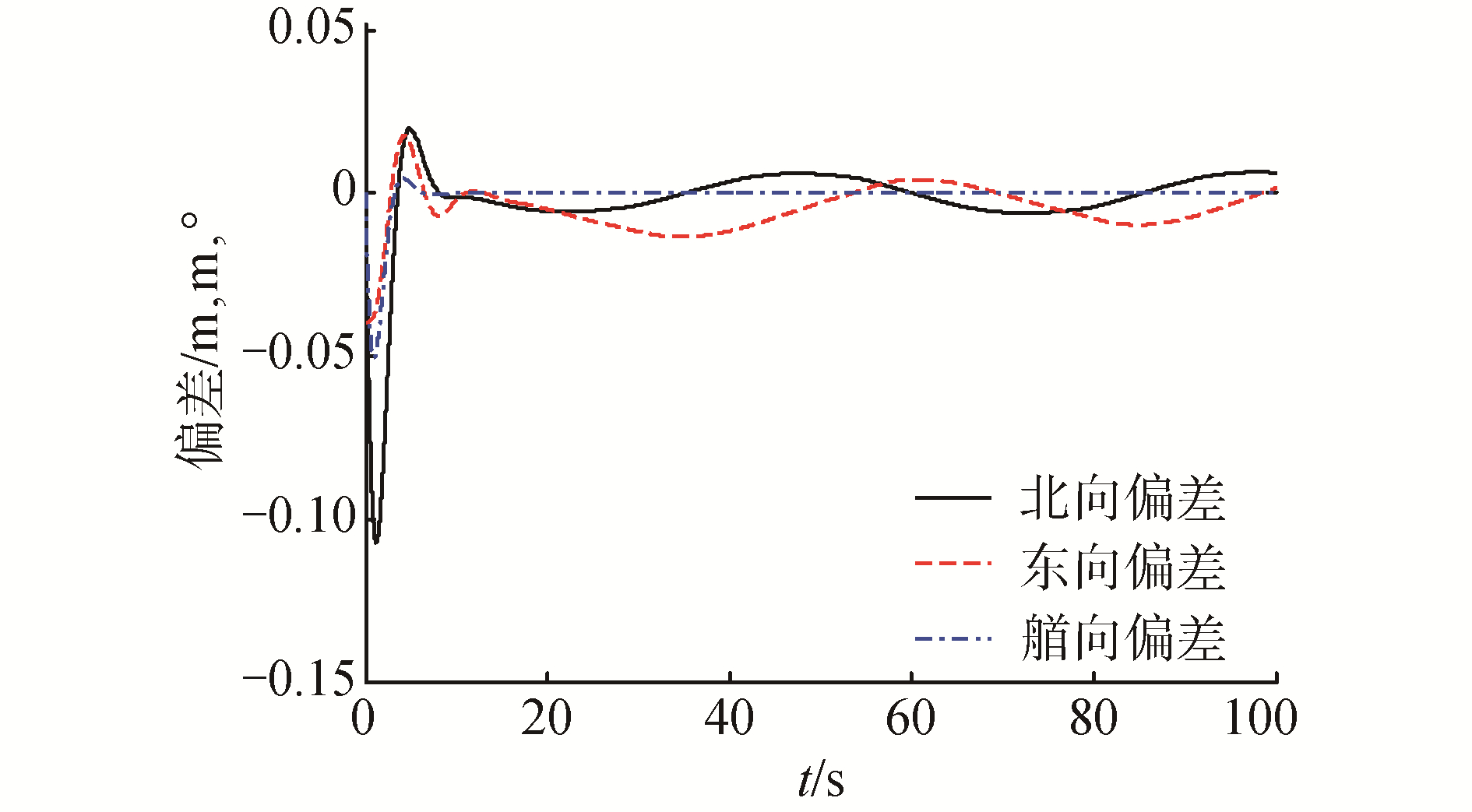
| 图 4 纵向、横向、艏向的跟踪误差响应曲线 Fig. 4 The tracking error response curves of surge, sway and yaw | |
|
Download:
|
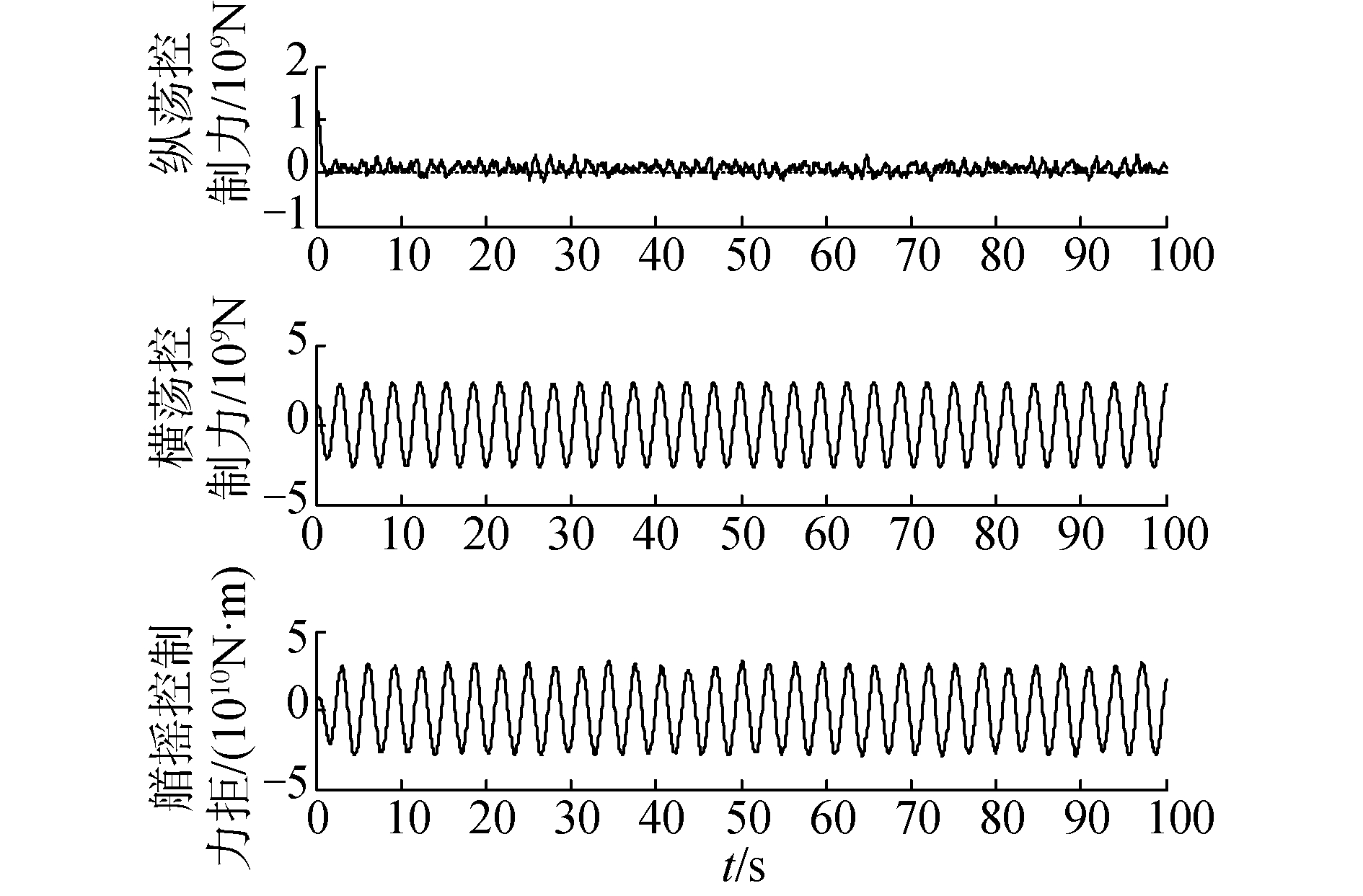
| 图 5 输出控制力矩的响应曲线 Fig. 5 Response curve of output control torque | |
由图 2可知,跟踪误差ηei(t)在艏向、纵荡、横荡3个自由度上严格按照式(15)所定义的性能界限±ρi(t)与±δiρi(t)范围内变化,因此满足了预期的性能,这样在动力定位轨迹跟踪过程中即可满足特定的任务要求。
由图 3可知,图中的实线为实际轨迹,虚线为期望的轨迹,二者的曲线在预设性能约束控制方法下,实现了较小误差的实时跟踪,实际轨迹运动曲线始终保持着微小的偏差量运动。
由图 4可知,直接描述了运动过程中横向、纵向、艏向的跟踪误差时间响应曲线,3者的误差在满足性能限界的范围内最终实现收敛并稳定。同时图 5给出了系统所需控制转矩的时间响应曲线,如图所示,系统的控制输入信号是周期性稳定改变且有界的,同时根据仿真结果可知,推进器亦能提供足够的驱动力来保证跟踪任务的成功。
综上所述,在本文所设计的基于预设性能的反步自适应控制器下,动力定位船的轨迹跟踪误差能够实现稳态性能和暂态性能控制的双重保证,同时跟踪轨迹超调量小,准确性高。
5 结论本文研究了具有性能约束的三自由度动力定位船航迹跟踪控制问题。通过理论分析以及仿真实验的验证得到以下结论:
1) 针对跟踪误差的不可预估的特点,设计将性能指标融入到闭环系统,通过误差转换的思想将具有性能约束的函数方程转化为等价的无约束函数方程,同时保证了系统的鲁棒性;
2) 设计了基于预设性能函数的反步自适应控制器,保证了动力定位船轨迹跟踪过程的任务要求,同时确保了控制过程中的变换误差以及其他闭环信号有界;
3) 通过实验证明,所设计的控制算法能够对给定最小收敛速度进行航迹跟踪误差调节。同时,对于模型参数的不确定性具有良好的自适应性。
因此,本文的研究能够为动力定位船的实际工程任务执行以及后续动力定位船轨迹跟踪的进一步研究提供一定的借鉴意义和研究思路。
| [1] |
PARK B S, KWON J W, KIM H. Neural network-based output feedback control for reference tracking of underactuated surface vessels[J]. Automatica, 2017, 77: 353-359. DOI:10.1016/j.automatica.2016.11.024 (  0) 0)
|
| [2] |
HERMAN P, WOJCIECH A. Nonlinear trajectory tracking controller for a class of robotic vehicles[J]. Journal of the franklin institute, 2017, 354(13): 5145-5161. DOI:10.1016/j.jfranklin.2017.05.040 (  0) 0)
|
| [3] |
PARK B S. A simple output-feedback control for trajectory tracking of underactuated surface vessels[J]. Ocean engineering, 2017, 143: 133-139. DOI:10.1016/j.oceaneng.2017.07.058 (  0) 0)
|
| [4] |
ELMOKADEM T, ZRIBI M, YOUCEF-TOUMI K. Terminal sliding mode control for the trajectory tracking of underactuated Autonomous Underwater Vehicles[J]. Ocean engineering, 2017, 129: 613-625. DOI:10.1016/j.oceaneng.2016.10.032 (  0) 0)
|
| [5] |
YIN Shen, XIAO Bing. Tracking control of surface ships with disturbance and uncertainties rejection capability[J]. IEEE/ASME transactions on mechatronics, 2017, 22(3): 1154-1162. DOI:10.1109/TMECH.2016.2618901 (  0) 0)
|
| [6] |
周岗, 姚琼荟, 陈永冰, 等. 不完全驱动船舶直线航迹控制稳定性研究[J]. 自动化学报, 2007, 33(4): 376-384. ZHOU Gang, YAO Qionghui, CHEN Yongbing, et al. A study of stability of straight-line tracking control system for underactuated ship[J]. Acta Automatica Sinica, 2007, 33(4): 376-384. (  0) 0)
|
| [7] |
ZHENG Zewei, JIN Cheng, ZHU Ming, et al. Trajectory tracking control for a marine surface vessel with asymmetric saturation actuators[J]. Robotics and autonomous systems, 2017, 97: 83-91. DOI:10.1016/j.robot.2017.08.005 (  0) 0)
|
| [8] |
付明玉, 焦建芳, 张爱华. 基于虚拟领航者的多艘船舶协调路径跟踪控制[J]. 华中科技大学学报(自然科学版), 2013, 41(2): 102-108. FU Mingyu, JIAO Jianfang, ZHANG Aihua. Coordinated path following control for multiple surface vessels by using virtual-leader[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2013, 41(2): 102-108. (  0) 0)
|
| [9] |
边信黔, 程相勤, 贾鹤鸣, 等. 基于迭代滑模增量反馈的欠驱动AUV地形跟踪控制[J]. 控制与决策, 2011, 26(2): 289-292, 296. BIAN Xinqian, CHENG Xiangqin, JIA Heming, et al. A bottom-following controller for underactuated AUV based on iterative sliding and increment feedback[J]. Control and decision, 2011, 26(2): 289-292, 296. (  0) 0)
|
| [10] |
贾鹤鸣, 张利军, 程相勤, 等. 基于非线性迭代滑模的欠驱动UUV三维航迹跟踪控制[J]. 自动化学报, 2012, 38(2): 308-314. JIA Heming, ZHANG Lijun, CHENG Xiangqin, et al. Three-dimensional path following control for an underactuated UUV based on nonlinear iterative sliding mode[J]. Acta automatica sinica, 2012, 38(2): 308-314. (  0) 0)
|
| [11] |
SHAO Xiaodong, HU Qinglei, GUO Lei. Adaptive spacecraft attitude tracking control with guaranteed transient performance[C]//Proceedings of the 36th Chinese Control Conference. Dalian: Professional Committee of Control Theory of China Automation Society, 2017: 9442-9447.
(  0) 0)
|
| [12] |
边信黔, 付明玉, 王元慧. 船舶动力定位[M]. 北京: 科学出版社, 2011: 24-55.
(  0) 0)
|
| [13] |
CAI Wenchuan, LIAO Xiaohong, SONG D Y. Indirect robust adaptive fault-tolerant control for attitude tracking of spacecraft[J]. Journal of guidance, control, and dynamics, 2008, 31(5): 1456-1463. DOI:10.2514/1.31158 (  0) 0)
|
| [14] |
BECHLIOULIS C P, ROVITHAKIS G A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems[J]. Automatica, 2009, 45(2): 532-538. DOI:10.1016/j.automatica.2008.08.012 (  0) 0)
|
| [15] |
HU Qinglei, SHAO Xiaodong, CHEN Wenhua. Robust fault-tolerant tracking control for spacecraft proximity operations using time-varying sliding mode[J]. IEEE transactions on aerospace and electronic systems, 2018, 54(1): 2-17. DOI:10.1109/TAES.2017.2729978 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


