钝体绕流是流体力学中的经典问题之一,多以圆柱绕流为研究对象,研究其在不同来流条件和布置方式下的尾迹、尾涡脱落、边界层及受力特性等[1-3]。平板作为一种钝体结构与圆柱绕流不同,其尾涡分离点固定在平板尾缘,且不受雷诺数影响[4]。平板表面也存在流动分离、再附、旋涡脱落、分离泡振荡等复杂流动现象, 对其绕流特性的研究可为海洋、船舶、交通、流体机械等众多领域的相关工程问题探讨提供基础理论支撑[5]。对于串列平板绕流,由于两平板间距的变化,使得间隙中的旋涡脱落、尾迹干涉以及旋涡的碰撞与破碎现象更为复杂。
针对单平板绕流研究,国内外学者运用实验手段[6-7]研究了弦厚比L/D(L为平板弦长,D为平板厚度)变化对有限长平板分离再附流动及其旋涡脱落特性的影响,划分出平板绕流的4种旋涡脱落机制。数值模拟[8-9]方面主要研究了不同弦厚比下的矩形柱体受力和绕流特性。多平板绕流方面,针对上游卡门涡街对下游平板绕流特性的影响展开了研究[10-11],实验结果表明上游卡门涡街对下游流动影响较大。高波[12]等运用大涡模拟研究了高雷诺数下一对固定间距比的串列平板绕流问题,分析了两平板脱落涡的演化结构、受力及压力脉动特性。
由此可知,前人对单平板绕流进行了较为全面地研究,而对较高雷诺数下多平板绕流,尤其是对不同间距比时,上下游平板流动及受力研究甚少。因此,本文设计了一对间距可调的串列平板模型,基于激光多普勒测速技术(laser doppler anemometry, LDA),开展雷诺数ReD=3×104时串列平板近尾迹区速度场精确测量,分析不同间距比对串列平板绕流尾迹的影响,为建立双平板绕流流谱提供理论支撑。
1 试验装置及方法 1.1 试验装置试验在小型闭式循环水洞平台上开展,整个系统由一台功率为7.5 kW,转速为2 900 r/min的电机驱动,通过数字变频器控制流速在0.1~5.0 m/s范围内变化,湍流强度不大于5%,试验段尺寸为250×100×20 mm。早期研究表明[7],平板弦厚比L/D=3.2、7.6、16时流动状态会发生变化。基于此,设计一对L/D=3.75的平板为研究对象,其中平板厚度D=8 mm,展向长度Z=20 mm, 头部为半圆形,倒圆半径R=4 mm。上下游平板沿中心线布置,采用定位销与底座相连,模型详见图 1。
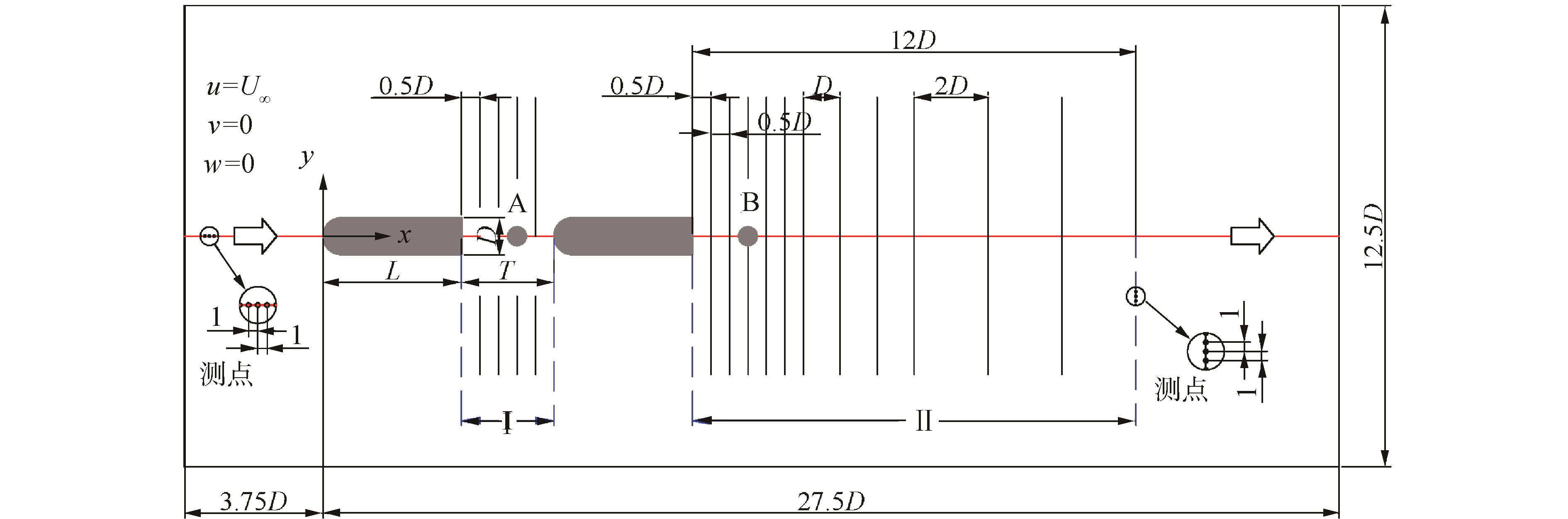
|
Download:
|
| 图 1 平板模型及测点布置示意 Fig. 1 Geometric model of flat plate and layout of measuring points | |
采用Dantec Dynamics公司的FlowExplorer LDA二维测试系统,红光波长660 nm,红外光波长785 nm,后向接收模式,探头焦距500 mm,形成的测量体尺寸为0.17×0.17×2.8 mm。采用直径为10 μm的空心玻璃微珠作为示踪粒子。数据采集时,数据率达到10 kHz以上,有效率90%以上,以满足湍流测量要求。
1.2 测量方法测量分3个区域进行,分别为中心线、Ⅰ区、Ⅱ区,测试区域及测点布置见图 1。中心线测点采用等间距布置方式,相邻测点间距为1 mm。Ⅰ区为两平板间隙区域,采集沿流向某一截面处的流向速度,每一截面上测点间隔1 mm。Ⅱ区为下游平板尾迹区域,测至距下游平板尾缘12D位置处。测点布置方式同Ⅰ区类似。试验过程中来流速度U∞=3.75 m/s,保持雷诺数ReD=3×104不变,改变间距比T/D=1,2,…,6。
2 试验结果与分析试验中采用非协同模式进行数据采集,因此,需对每个测点的样本速度进行平均化处理,即将各激光束在不同时刻捕捉到的粒子瞬时速度转化成测点的平均速度[13]。转化公式为:
| $ \bar{u}=\frac{1}{n} \sum\limits_{i=1}^{n} u_{i}, i=1, 2, \cdots, n $ | (1) |
式中:u为测点平均速度;ui为样本粒子瞬时速度。
此外,为方便分析,文中对表示截面距离的物理量做了无量纲处理。定义距上游平板尾缘的距离表示为x1,距下游平板尾缘的距离表示为x2,具体表达式为:
| $ x_{1}=x-L $ | (2) |
| $ x_{2}=x-2 L-T $ | (3) |
式中:x为距坐标原点的实际距离;T为上下游平板之间的距离。
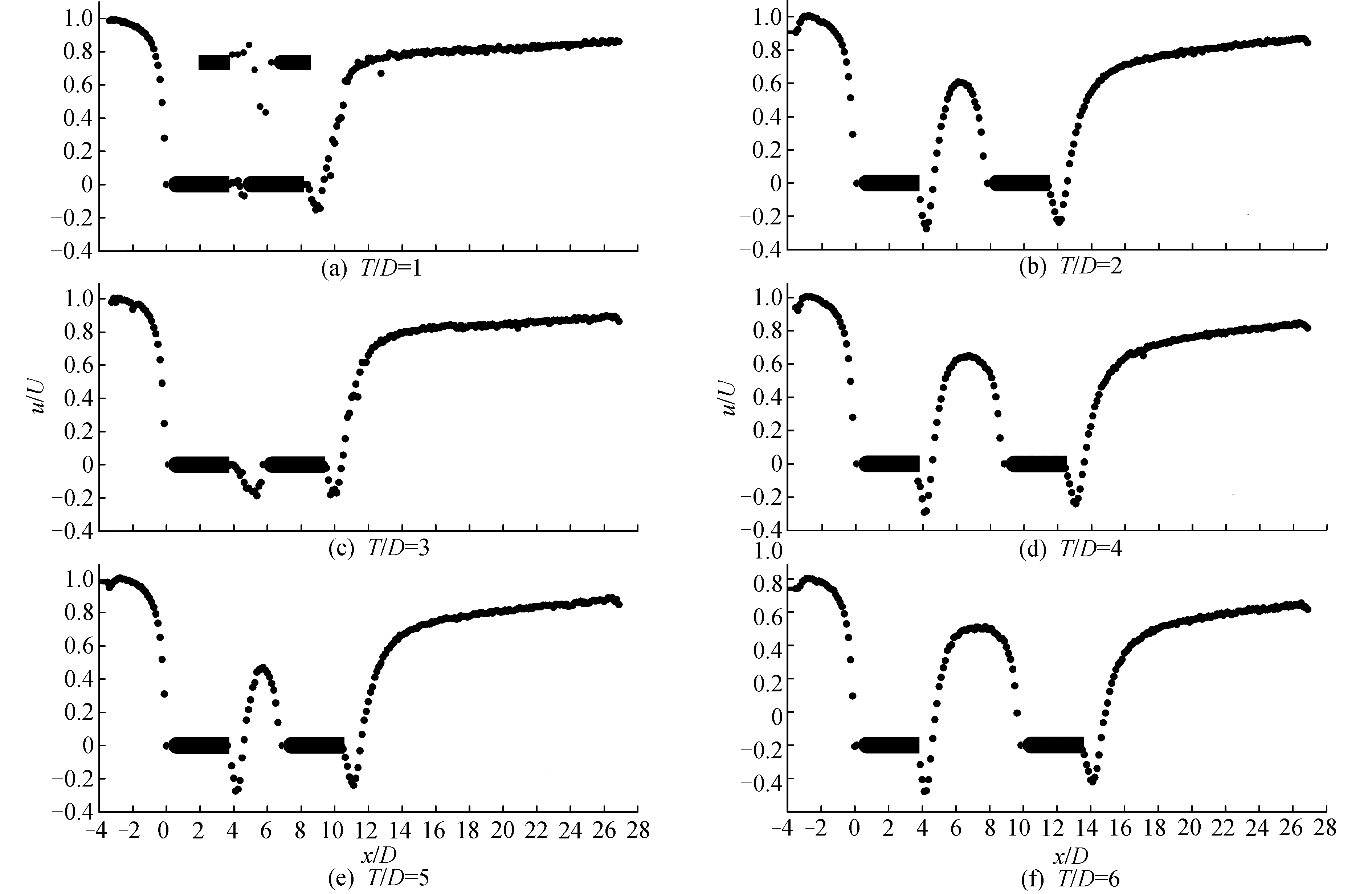
2.1 平板中心线上时均速度分布图 2为不同间距比下,上下游平板中心线上时均速度分布图。不同间距比下,上游中心线上流速呈半抛物线形分布,靠近其前缘时速度迅速降低,在前缘处滞止为零。下游平板尾迹,存在回流区,沿流向回流区中流速与主流方向相反,即流速小于零,其长度定义为Lb。回流区后中心线上流速迅速增大,直至0.6U∞左右时,流速进入缓慢增长阶段,最终接近无穷远处来流速度。
|
Download:
|
| 图 2 不同间距比下中心线上时均速度分布 Fig. 2 Time-averaged stream-wise velocity along the centerline at different gap ratios | |
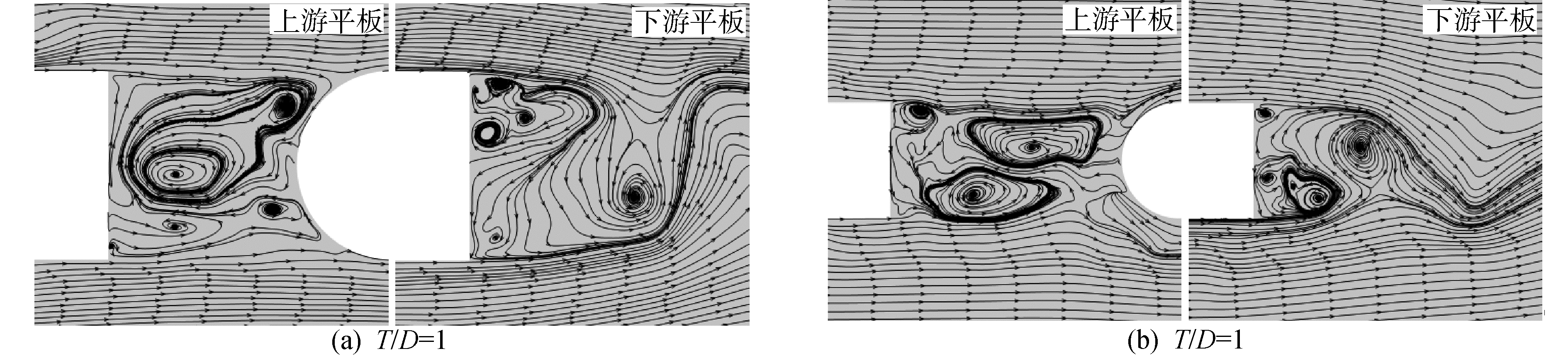
不同间距下,间隙中的流速分布存在明显差异。两平板间距比T/D=1时, 其中心线上流速呈“马鞍型曲线”分布。结合前期大涡模拟LES数值计算结果(见图 3(a))发现该间距下,上游平板的分离边界层未能在尾缘处脱落,而是受主流推动继续向下游流动,从而使得上游平板尾迹区流速有所增大。受下游平板阻塞,一部分能量不足以向下游运动的分离边界层开始逐渐减速,并在距上游平板尾缘x1/D=0.375处达到极大值0.037U∞。沿流向分离边界层受下游平板的作用逐渐增强,其流速在距上游平板尾缘x1/D=0.75处达到极小值-0.064U∞。随后,流速开始上升,在下游平板前缘处滞止为零。另一部分分离边界层受主流推动继续向下游运动,直至再附着于下游平板表面。再附的分离边界层继续向下游运动,与下游平板作用后,在其尾缘处脱落,并在下游平板尾缘约0.75D范围内形成回流区。
|
Download:
|
| 图 3 ReD=3×104时,大涡模拟流线图 Fig. 3 ReD=3×104, Large Eddy Smulation streamline | |
两平板间距增大至T/D=2时,上下游平板之间形成了占据整个间隙的回流区。在该间距时,下游平板对上游涡脱的抑制作用较T/D=1时减弱,使得上游平板尾涡呈现间歇性脱落的特点[14]。结合大涡模拟LES计算结果(见图 3(b))发现,受下游平板阻塞,间歇性脱落的旋涡以及上游分离边界层撞击到下游平板前缘,在间隙两侧形成2个大尺度涡系,从而形成了占据整个间隙的回流区。
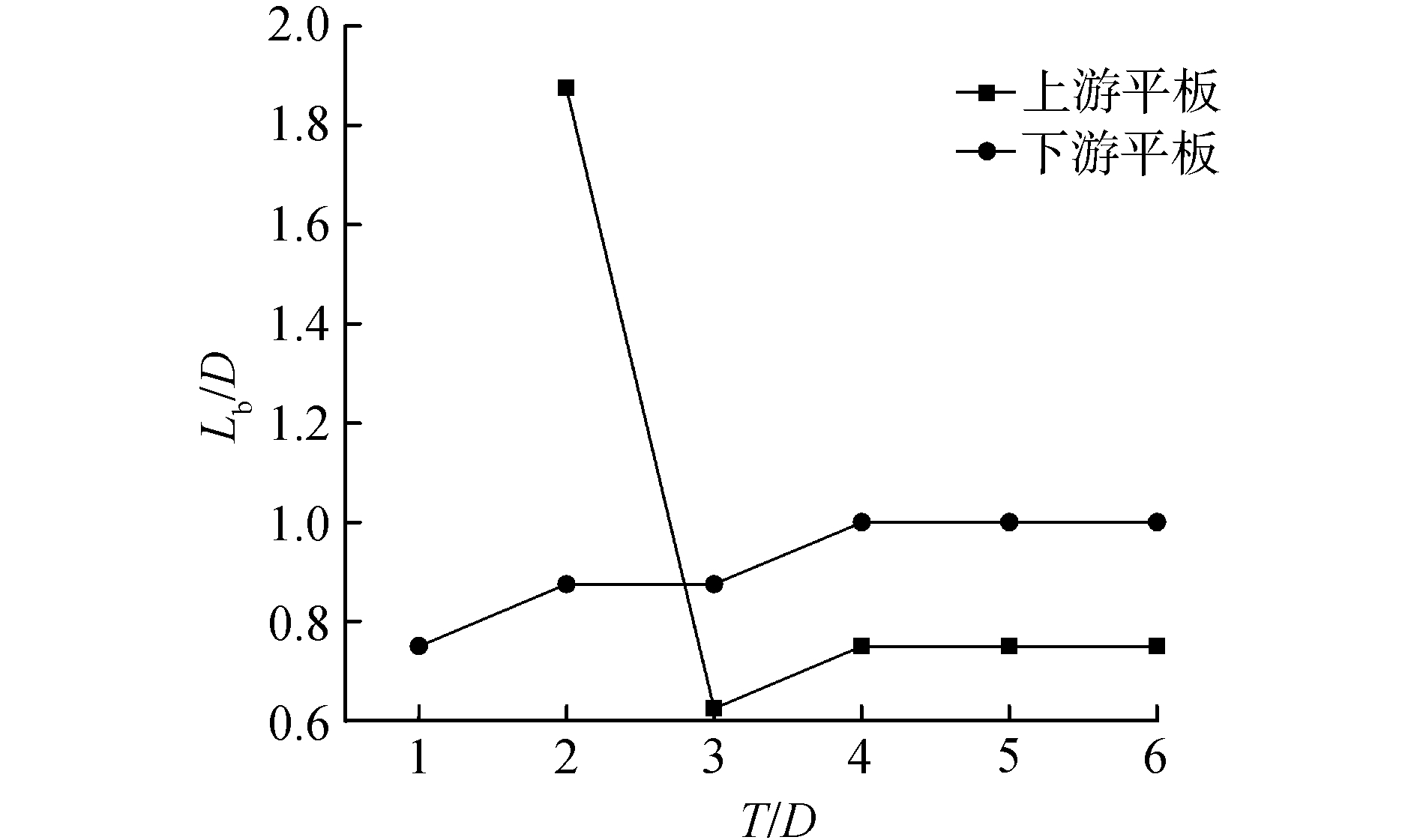
间距增大至T/D≥3后,上下游平板尾缘处都形成了明显的回流区,下游平板抑制作用减弱。随着两平板间距持续增大,上游平板回流区范围从0.625D逐步扩大到0.75D,并逐渐稳定在0.75D左右。下游平板类似,其回流区范围从0.75D扩大至1D,且趋于稳定,如图 4所示。
|
Download:
|
| 图 4 不同间距比时上下游平板回流区 Fig. 4 Backflow region of the upstream and downstream plates at different gap ratios | |
为更好地研究串列平板绕流的流动特性,分别选取Ⅰ区和Ⅱ区距平板尾缘x1/D=0.5、1.0、1.5以及x2/D=0.5、1.0、1.5处的截面作为研究对象,对其近尾迹区时均速度和脉动速度进行了分析。定义湍流强度IT,具体表达式为:
| $ u_{\mathrm{RMS}}^{\prime}=\sqrt{\frac{1}{n} \sum\limits_{i=1}^{n}\left(\bar{u}-u_{i}\right)^{2}} $ | (4) |
| $ I_{T}=\frac{u_{\mathrm{RMS}}^{\prime}}{U_{\infty}} \times 100 \% $ | (5) |
式中u′RMS为脉动速度均方根。
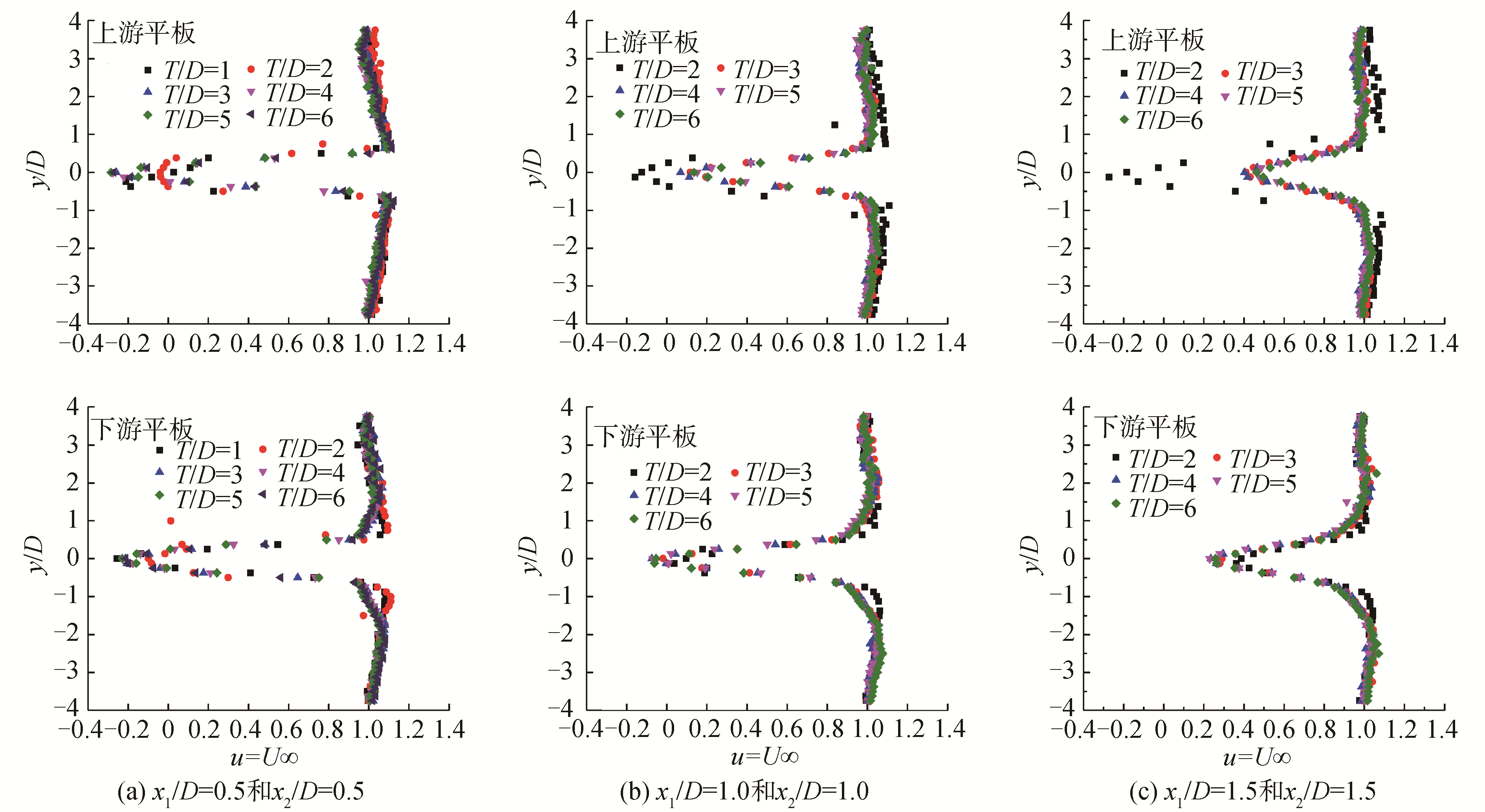
2.2.1 平板近尾迹区时均速度选取Ⅰ区和Ⅱ区距平板尾缘相同截面处,即x1/D=0.5、1.0、1.5以及x2/D=0.5、1.0、1.5处的流向速度做对比分析,如图 5所示。
|
Download:
|
| 图 5 平板近尾迹区流向时均速度分布 Fig. 5 Time-averaged stream-wise velocity in the near wake region of the flat plate | |
两平板在不同截面处的流向速度沿中心线对称分布。靠近平板中心线,流向速度逐渐增大,在距平板表面约y/D=±1处流速达到最大,其值约为1.06U∞。继续靠近平板,受其脱落涡影响,流向速度迅速减小,在流速减小为零后,流动进入回流区。
上游平板尾缘x1/D≤0.5区域,受下游平板阻塞作用较弱,两平板流向速度分布基本一致。在x1/D>0.5、x2/D>0.5区域,间距比变化对上游平板尾迹影响较大,对下游平板尾迹影响较小,且随着间距比增大影响随之减弱。
间距比T/D=1时,上游截面(x1/D=0.5)中心处流速为0.027 U∞,即在此间距比下,两平板之间流动极其微弱。对比T/D=2在3个截面的流向速度分布发现,截面中心处流速均为负值,由此可知上游平板回流区一直扩展到下游平板前缘。间距比T/D≥3后,各截面中心处流速逐渐恢复,在x1/D=1.0和x2/D=1.0截面处均已通过回流区,恢复为正值,即与主流方向一致。
2.2.2 平板近尾迹区脉动速度分析脉动速度的过程中,对间距较大的工况,增加了两个远场处截面,以分析远场湍流强度的变化,如图 6所示。

|
Download:
|
| 图 6 平板近尾迹区流向湍流强度分布 Fig. 6 Stream-wise turbulent intensity in the near wake region of the flat plate | |
由图 6可知,小间距比时(T/D < 3),上游平板尾缘不同截面处湍流强度分布较为杂乱,无明显规律,但存在一个不对称尖峰结构。结合图 3分析认为,尖峰结构的形成是上游平板分离边界层与下游平板前缘撞击导致的,而非旋涡脱落引起的。下游平板尾缘不同截面处湍流强度分布类似于大间距比时上游平板尾缘湍流强度分布,其尖峰处峰值分别为35%和32.5%。主要是小间距比下,上游平板尾缘处未能形成明显涡脱,减少了能量在两平板间的消耗。
较大间距比时(T/D≥3),上下游平板尾缘不同截面处湍流强度呈“双峰型曲线”对称分布在中心线两侧。区别于小间距比时(T/D < 3),由于撞击而形成尖峰结构。此间距下,涡脱在平板尾缘两侧周期性脱落,致使此处速度剧烈波动,由此在平板尾缘两侧形成两个尖峰结构。两尖峰结构在y向的距离(定义为S)表征了涡脱沿y向所能发展到的最大位置。远离平板区域流场所受扰动较小,湍流强度约在6%-7%之间波动。
考察不同截面处S值发现,沿流向,S值逐渐增大,即涡脱呈扩散状向下游发展。同时,两尖峰结构处的峰值也逐渐减小,在距平板尾缘x1/D=5.0和x2/D=5.0处尖峰结构消失,但此处湍流强度仍然很强。分析认为,受流体粘性作用,导致大尺度涡系在向下游扩散过程中破碎形成尺度较小的涡系,消耗了其大部分能量。在远场,小尺度涡系同样受流体粘性作用而不断消失,逐渐形成充分发展的湍流。此外,上游平板尾缘,尖峰结构处的峰值整体大于下游平板尾缘类似位置处的峰值,其上游峰值约为32.5%,局部达到35%,而下游峰值约为25%左右。
2.3 St数随间距比T/D的变化为研究间距比变化对平板尾涡脱落频率的影响,对图 1中A、B两点瞬时流向速度进行FFT变换,得到各间距比下绕流平板的速度频谱,如图 7所示。

|
Download:
|
| 图 7 不同间距比下平板近尾迹区速度频谱 Fig. 7 Velocity frequency spectra in the near wake region of the flat plate at different gap ratios | |
不同间距比时,下游平板都有明显的涡脱频率出现。在大间距比时(T/D≥3),上游平板也有明显的涡脱频率出现,且两平板的特征频率一致,说明流场中一种大尺度旋涡结构占主导。两平板相互作用,使得下游平板的涡脱频率锁定了上游平板涡脱频率。
在小间距比下(T/D < 3),上游平板的速度频谱存在明显差异,尤其是在T/D=1和T/D=2时。如图 7(a)所示,T/D=1时,上游平板的速度频谱是宽频湍流信号,未出现明显的特征频率,说明上游平板没有产生明显的旋涡脱落。该间距下,下游平板的存在完全抑制了上游平板脱落涡的产生,其分离边界层没有在尾缘处脱落,而是直接再附于下游平板表面。
间距比T/D=2时,上游平板出现了能量高、频率低的低频脉动信号,其幅值为0.03 m2/s3,频率为9 Hz,见图 7(b)。即在此间距比下,受下游平板影响,两平板之间没有形成明显的主脱落涡,而是上游分离的大尺度涡旋在尾缘处间歇性脱落引起的。
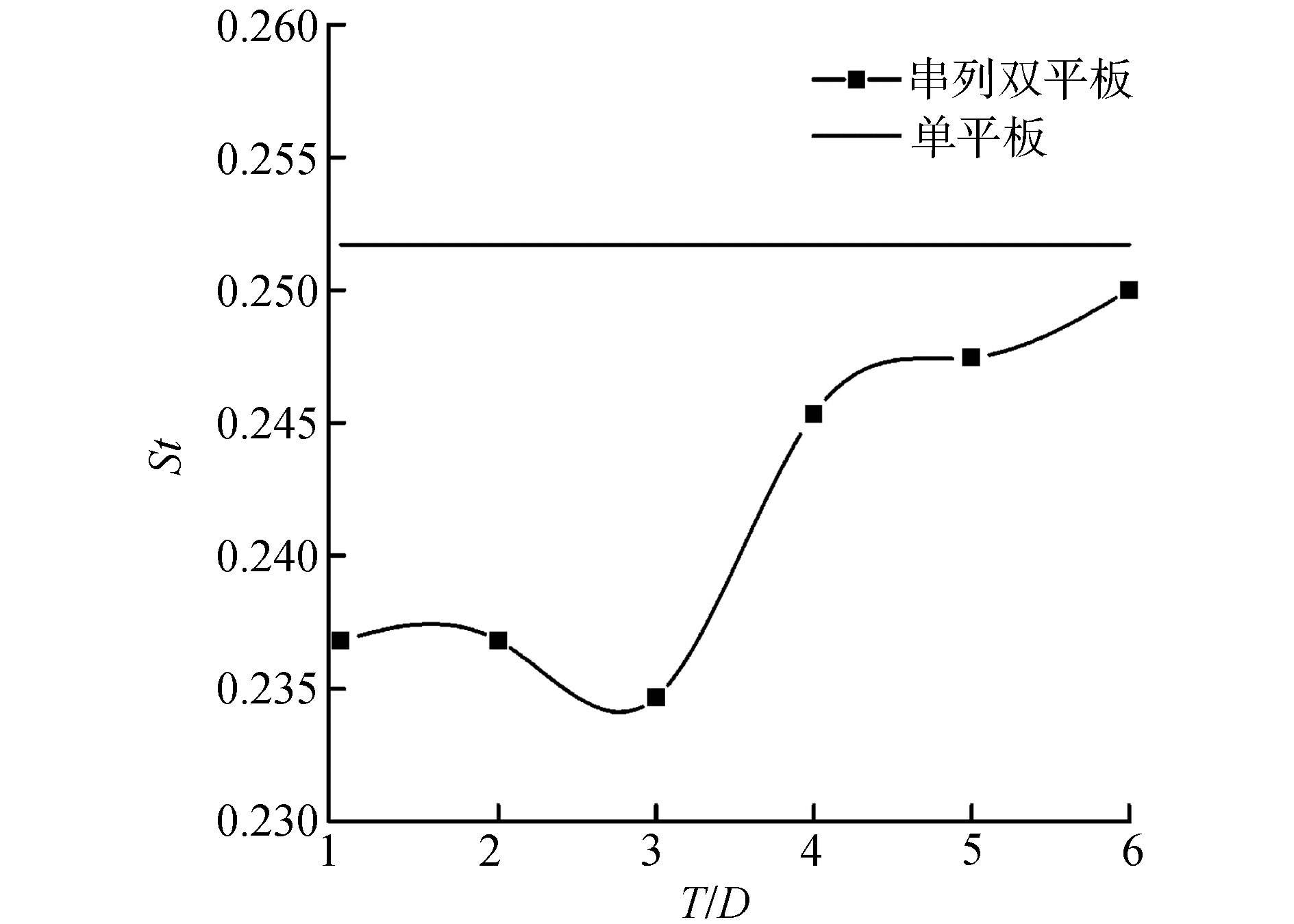
将涡脱频率无量纲化,图 8示出了St数随间距比T/D的变化规律。St数在T/D=1和T/D=2时几乎不变,随后St数减小,在T/D=3时达到极小值St=0.234 7。T/D≥3后St数随之增大,在T/D=6时增大至St=0.25,接近于单平板绕流时的0.251 7。随着两平板间距的增大,其相互作用与影响逐渐减弱,并趋于单平板绕流。结合图 7发现在间距比T/D < 3时,两平板之间没有规律性大尺度旋涡产生,T/D≥3后,两平板之间产生了明显的涡脱。因此,T/D=3可作为雷诺数ReD=3×104时,串列平板绕流的临界间距比。
|
Download:
|
| 图 8 St数随间距比变化 Fig. 8 Strouhal number at different gap ratios | |
1) 间距比T/D≤1时,两平板间的流动微弱,只在下游平板形成稳定的涡脱。间距比T/D=2时,两平板之间形成了占据整个间隙的回流区。随着两平板间距的增大,两平板均产生稳定的旋涡脱落,其回流区也趋于稳定,稳定后的回流区长度分别为0.75D和1D。
2) 间距比T/D≥3时,上下游平板均能形成稳定涡脱,且两平板涡脱频率保持一致。其尾缘不同截面处湍流强度呈“双峰型曲线”对称分布在平板中心线两侧。两尖峰结构沿y向的距离S表征了涡脱沿y向所能发展到的最大位置。
3) T/D=3可作为雷诺数ReD=3×104时,串列平板绕流的临界间距比。St数随间距比变化明显,在临界间距比处有极小值;小于临界值时,St数几乎不变;大于临界值时,St数随之增大,且趋向于单平板绕流St数,即上下游平板的流动均趋于单平板绕流。
| [1] |
ZHOU Yu, ALAM M. Wake of two interacting circular cylinders:a review[J]. International journal of heat and fluid flow, 2016, 62: 510-537. DOI:10.1016/j.ijheatfluidflow.2016.08.008 (  0) 0)
|
| [2] |
MADUTA R, ULLRICH M, JAKIRLIC S. Reynolds stress modelling of wake interference of two cylinders in tandem:conventional vs. eddy-resolving closure[J]. International journal of heat and fluid flow, 2017, 67: 139-148. DOI:10.1016/j.ijheatfluidflow.2017.07.012 (  0) 0)
|
| [3] |
ALAM M, ZHOU Y, ZHAO J M, et al. Classification of the tripped cylinder wake and bi-stable phenomenon[J]. International Journal of Heat and Fluid Flow, 2010, 31(4): 545-560. DOI:10.1016/j.ijheatfluidflow.2010.02.018 (  0) 0)
|
| [4] |
TIAN Xinliang, ONG M C, YANG Jianmin, et al. Unsteady RANS simulations of flow around rectangular cylinders with different aspect ratios[J]. Ocean engineering, 2013, 58: 208-216. DOI:10.1016/j.oceaneng.2012.10.013 (  0) 0)
|
| [5] |
ZHANG Qingshan, LIU Yingzheng. Influence of incident vortex street on separated flow around a finite blunt plate:PIV measurement and POD analysis[J]. Journal of fluids and structures, 2015, 55: 463-483. DOI:10.1016/j.jfluidstructs.2015.03.017 (  0) 0)
|
| [6] |
CHERRY N J, HILLIER R, LATOUR M E M P. Unsteady measurements in a separated and reattaching flow[J]. Journal of fluid mechanics, 1984, 144: 13-46. DOI:10.1017/S002211208400149X (  0) 0)
|
| [7] |
PARKER R, WELSH M C. Effects of sound on flow separation from blunt flat plates[J]. International journal of heat and fluid flow, 1983, 4(2): 113-127. DOI:10.1016/0142-727X(83)90014-0 (  0) 0)
|
| [8] |
SHIMADA K, ISHIHARA T. Application of a modified k-ε Model to the prediction of aerodynamic characteristics of rectangular cross-section cylinders[J]. Journal of fluids and structures, 2002, 16(4): 465-485. DOI:10.1006/jfls.2001.0433 (  0) 0)
|
| [9] |
SOHANKAR A. Large eddy simulation of flow past rectangular-section cylinders:side ratio effects[J]. Journal of wind engineering and industrial aerodynamics, 2008, 96(5): 640-655. DOI:10.1016/j.jweia.2008.02.009 (  0) 0)
|
| [10] |
BULL M K, BLAZEWICZ A M, PICKLES J M, et al. Interaction between a vortex wake and an immersed rectangular plate[J]. Experimental thermal and fluid science, 1996, 12(2): 209-220. DOI:10.1016/0894-1777(95)00099-2 (  0) 0)
|
| [11] |
CHEN J M, CHIOU C C. Flow past a blunt flat plate subjected to the disturbance of incident vortex street[J]. Journal of wind engineering and industrial aerodynamics, 1997, 66(3): 179-196. DOI:10.1016/S0167-6105(97)00132-3 (  0) 0)
|
| [12] |
高波, 郭鹏明, 闫龙龙, 等. 双平板叶栅绕流的流动结构及其激励特性研究[J]. 农业机械学报, 2017, 48(10): 108-114. GAO Bo, GUO Pengming, YAN Longlong, et al. Flow structure and excitation characteristics of flow around double plate cascades[J]. Transactions of the Chinese society for agricultural machinery, 2017, 48(10): 108-114. DOI:10.6041/j.issn.1000-1298.2017.10.013 (  0) 0)
|
| [13] |
刘剑, 宋莹, 刘明浩, 等. 基于LDA的均直巷道断面风速分布规律实验研究[J]. 中国安全生产科学技术, 2015, 11(12): 65-71. LIU Jian, SONG Ying, LIU Minghao, et al. Experimental study on distribution laws of wind velocity in straight roadway section based on LDA[J]. Journal of safety science and technology, 2015, 11(12): 65-71. (  0) 0)
|
| [14] |
戴绍仕.孤立圆柱及串列双圆柱水动力数值实验研究[D].哈尔滨: 哈尔滨工程大学, 2004. DAI Shaoshi. Numerical research on the hydrodynamic characters of a circle cylinder and two circle cylinders in tandem arrangement in uniform cross flow[D]. Harbin: Harbin Engineering University, 2004. http://cdmd.cnki.com.cn/Article/CDMD-10217-2005137620.htm (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


