2. 国家海洋环境监测中心, 辽宁 大连 116023;
3. 中电科海洋信息技术研究院有限公司, 北京 100041
2. National Marine Environmental Monitoring Center, Dalian 116023, China;
3. CETC Ocean Information Technology Co., Ltd, Beijing 100041, China
我国第一座冰区核电工程——辽宁红沿河核电站工程进入商业运行阶段,核电厂在运行期间需使用大量的循环冷却水。我国尚无冰区核电工程运行经验,特别是冷源取水工程的防冰设计标准缺失,浮冰对冷源取水的影响机理尚不明确,使我国北方海域的经济产业、生态环境均暴露于核电浮冰灾害引发的未知风险之中。取水口运行状态的好坏直接影响电厂的安全运行性和可靠性,而取水口堵塞问题是其多发问题之一。浮冰与核电取水构筑物作用会发生冰堆积问题,冰堆积会造成浮冰上爬、浮冰下潜等问题,易引发浮冰堵塞取水口甚至破坏取水口等危险,因此浮冰堆积问题是核电站冬季运行的主要风险之一。
浮冰在生成过程中,受到风与潮流的共同作用,运动比较剧烈,生长过程存在断裂、重叠与堆积现象,可以在短时间形成比较严重的冰情[1]。浮冰与堤坝等结构作用,由于结构的阻挡等原因,浮冰没有及时清除,便会形成大量的堆积。冰堆积会引起严重的后果,如冰的上爬,冰力增大,局部挤压等,威胁到结构局部(结构迎冰构件)和结构整体的运行[2]。
随着全球经济的发展,寒区海洋工程向高纬度海域的不断延伸,海洋浮冰堆积现象也越来越多的引起科研人员的关注。岳前进等[2]利用渤海的海洋平台结构开展了现场观测工作,对海洋结构前冰堆积过程和危害进行了分析。MÄÄTTÄNEN等[3]采用基于连续介质模型的有限单元法FEM方法模拟冰堆积的形成及发展过程,预测Kemi-Ⅰ灯塔锥体结构前冰的上爬高度。王永学等[4]采用离散元方法对斜坡式防波堤前的海冰堆积问题进行了数值模拟。Jani等[5]采用二维有限元—离散元方法模拟了宽斜坡结构前的冰排失效和碎冰堆的形成过程,打破了单独使用有限元或离散元的方法的传统。
取水工程面临的浮冰堆积问题相对特殊,其更关注浮冰堆积聚集形态在时空维度上的发展变化情况,特别是浮冰分布、冰速等因素对浮冰堆积形态的影响。因此,本文针对北方冰区核电站的取水口内浮冰堆积问题,采用离散元的方法,分析浮冰密集度、速度和参与浮冰堆积的冰量这些参数对取水口浮冰堆积的发生与发展状况的影响程度,探究影响浮冰堆积程度的关键因素及其影响规律。本文的相关研究成果可以用于评估、预测高寒地区取水工程的浮冰堆积情况,对取水口的浮冰堆积高度进行预判,对取水口可能发生浮冰堵塞等问题进行评估。为高寒地区核电取水口的浮冰危害分析及防治等工作提供借鉴和参考。
1 工程问题及其数值模拟 1.1 工程问题我国第一座冰区核电工程—辽宁红沿河核电站地处渤海辽东湾东侧,核电厂在运行期间需使用大量的循环冷却水,因此其依海而建,就地取水。而渤海大概每年的12月初至次年的3月末为冰期。海冰由于潮汐、波浪等作用会破碎并在海面上形成大量的碎冰。碎冰随着潮汐和海流的作用会在取水口的堤坝前发生堆积问题。红沿河附近海域浮冰运动平均速度约为0.3~0.5 m/s,最大可达1 m/s。平均冰厚在0.2 m左右,重叠冰厚可达0.4 m甚至更厚,单块浮冰的直径可达1 m以上。
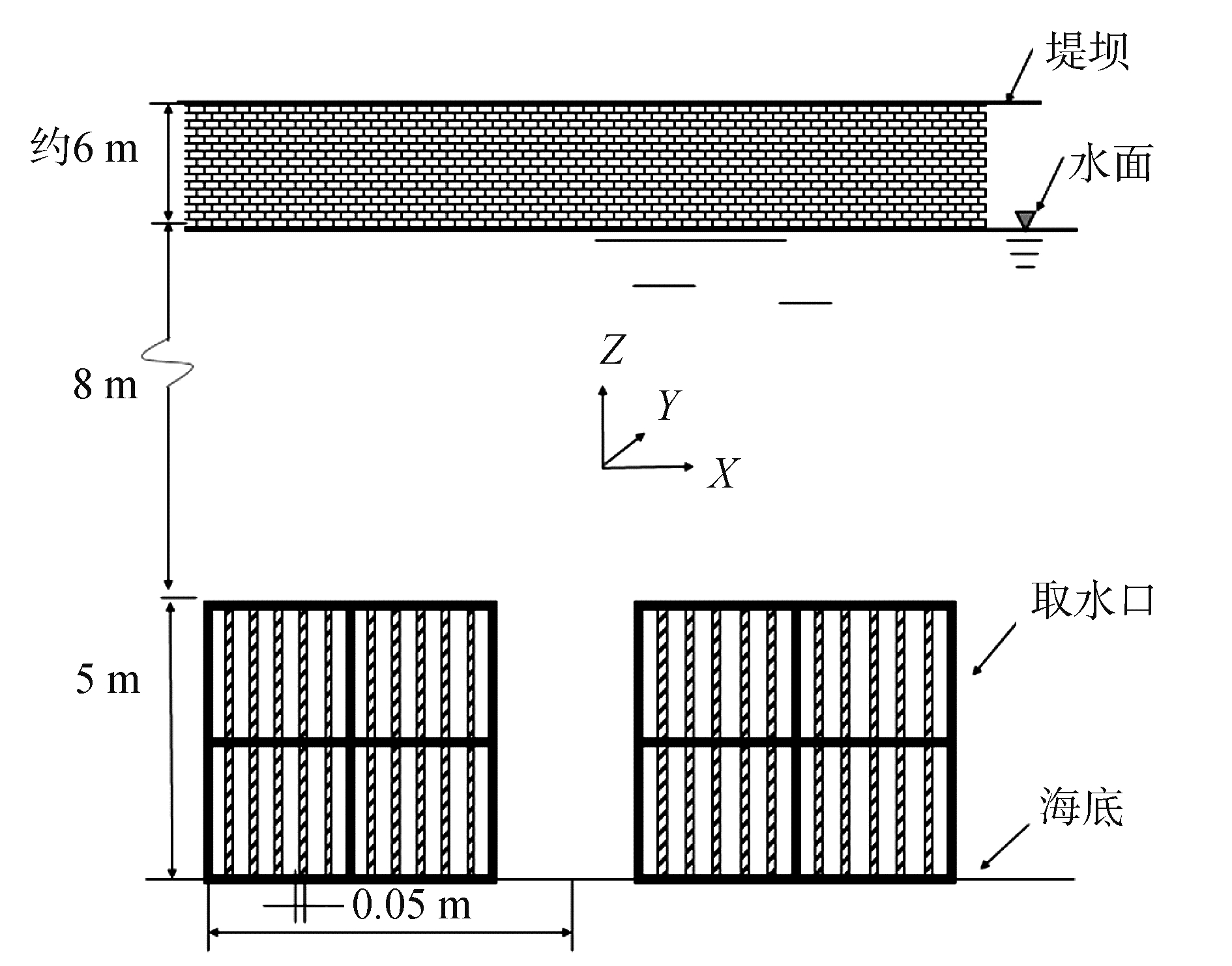
以红沿河核电站取水口位置水深约13 m。取水口为矩形,每个取水口长/高5 m,取水口前有栅栏遮挡以防止异物由取水口进入蓄水池。取水口最顶端距水面约8 m,水面距堤坝顶端约6 m,取水口示意图如图 1所示。取水口有一定的吸力,如果取水口上面的浮冰堆积到一定深度就有可能被吸入到取水口内。而较大浮冰会被取水口前的栅栏挡住,造成取水口堵塞问题。甚至发生浮冰撞击栅栏造成栅栏损坏,大量浮冰进入取水口造成无法取水,发生重大安全事故等。因此有必要对核电取水口前的浮冰堆积问题进行分析,进而对浮冰可能造成的取水问题进行预测和防范。
|
Download:
|
| 图 1 核电取水口位置简化示意 Fig. 1 Water intake location simplified schematic | |
在自然条件下,碎冰区的浮冰呈现出很强的离散分布特性。无论是在极区,还是在渤海、波罗的海、波弗特海等海域,浮冰均普遍存在。在海冰的离散单元模型中,海冰单元可设为球体、圆盘和块体等不同形态。然而,对于碎冰区的浮冰,三维圆盘方法具有模型简单、计算效率快和精度高等优点[6]。同时这种圆盘单元模型在模拟碎冰块的碰撞、重叠、和堆积问题均取得了理想的结果[7, 8]。因此本文采用这种圆盘冰单元模型对浮冰与核电取水构筑物之间的碰撞及堆积过程进行数值模拟。
这种扩展圆盘冰单元是通过平面圆盘与球体做闵可夫斯基和运算得到的一种扩展几何体[9]。对这种扩展几何体可简单的描述为基于二维圆盘单元在其表面的每一个点上都扩充为一个定尺寸的球体。于是扩展圆盘单元便是表面光滑并有一定厚度的三维圆盘模型。在离散单元法计算模拟中,扩展圆盘单元间的接触计算可以处理为三维空间中平面圆盘之间的接触问题。根据圆盘单元的几何性质将单元之间的接触分为平面-平面接触,弧面—平面接触以及弧面—弧面接触3种类型。计算得到单元间的变形量后,根据弹簧—粘壶模型计算单元之间的接触力[10]。为了更加准确的计算圆盘冰单元的运动,特别是转动,数值模拟中采用了局部坐标系和整体坐标系。局部坐标系固定在每个圆盘单元的质心处,整体坐标系固定在整个计算域内,其中局部坐标与整体坐标之间的相互转化采用四元数方法[11]。
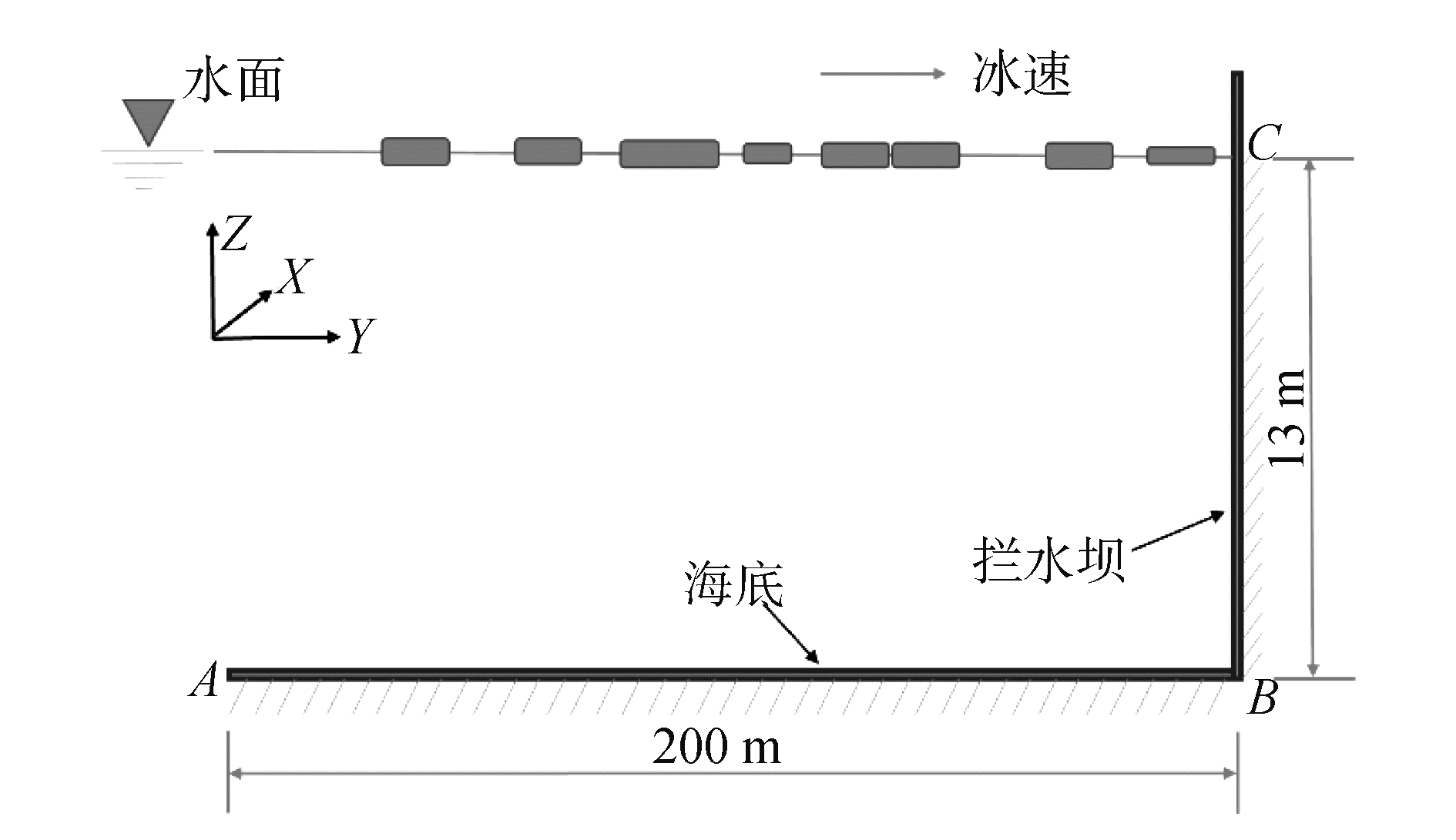
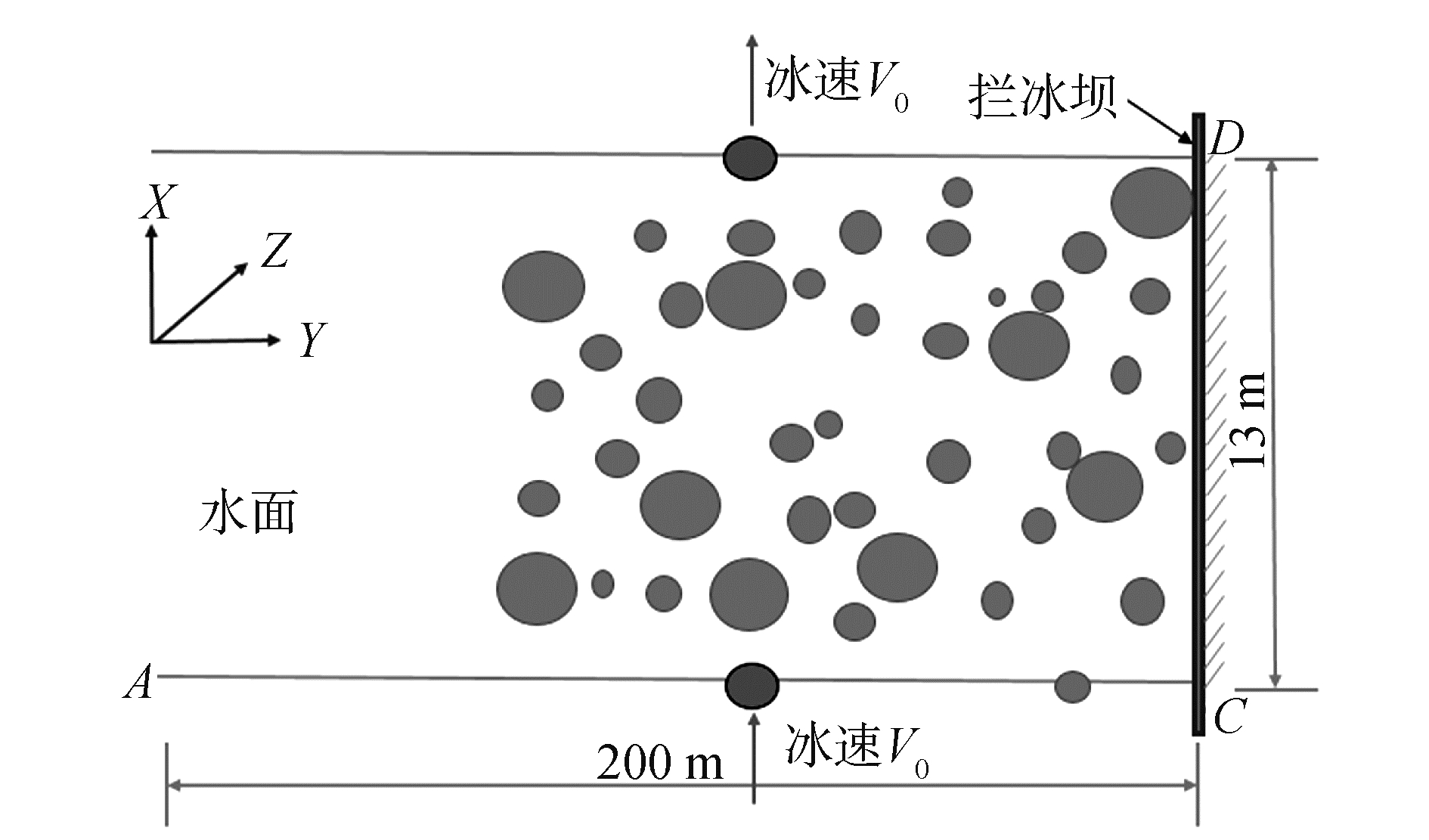
本文通过上述扩展圆盘单元方法模拟海洋浮冰在拦冰坝前堆积的动态过程。计算模拟中的主要参数参考了辽宁红沿河核电站取水口工程的相关数据。兼顾计算效率及计算准确度,取计算区域的水深为13 m,计算区域长度为200 m,计算区域的宽度为12 m,并在宽度方向上设置循环边界条件。将取水口处的计算区域简化为垂直的平面结构,计算区域示意图如图 2、图 3所示。浮冰区的计算域长度为L=AB=200 m (Y方向)和宽度为CD=12 m (X方向),Z轴方向为水深BC=13 m。为了模拟更宽广的冰坝堆积情况,计算域中Y方向为循环边界,如图 3所示。深色的浮冰在循环边界处以速度V0从一边界流出后会以相同速度相同方向从另一边界流入,数值模拟过程中的主要参数见表 1。
|
Download:
|
| 图 2 取水口处计算区域简化示意 Fig. 2 Computational domain simplified schematic | |
|
Download:
|
| 图 3 循环边界简化示意图(俯视图) Fig. 3 Simplified schematic of circular border (top view) | |
| 表 1 数值模拟中使用的参数 Table 1 Parameters used in the numerical simulation |
在数值计算中浮冰速度设置为0.3 m/s、0.5 m/s、0.8 m/s,浮冰的厚度设置为在0.2 m~0.4 m之间随机分布。圆盘冰的直径在0.8 m~1.4 m之间随机分布,初始时刻随机排列。计算中采用4种不同的密集度, 分别为20%、33%、50%和80%。这里碎冰密集度C为碎冰总面积和计算水域面积之比。对应不同的密集度, 计算区域中相应的浮冰颗粒个数分别为603、993、1 505和2 410。图 4给出了3种不同密集度浮冰初始分布情况。

|
Download:
|
| 图 4 不同密集度浮冰的初始分布情况 Fig. 4 Initial distribution of ice floes with different concentrations | |
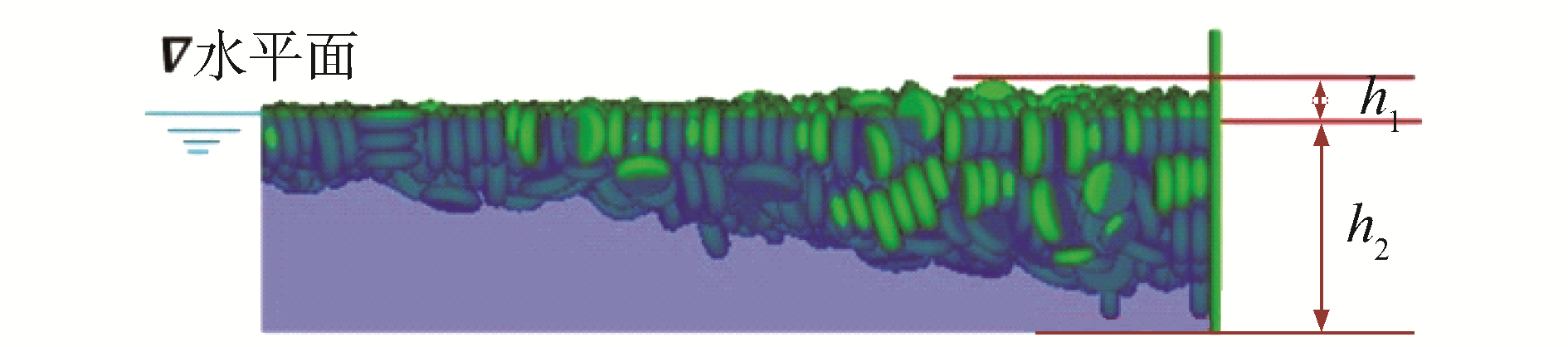
浮冰发生堆积后, 由于浮冰密度略小于水,因此浮冰堆积包括水上冰堆积部分与水下冰堆积部分。如图 5所示浮冰堆积侧视图,从水平面至浮冰堆顶端的垂向距离h1称为浮冰水上堆积高度,从水平面至浮冰堆底端的垂向距离h2称为浮冰的水下堆积高度。
|
Download:
|
| 图 5 浮冰的堆积高度示意 Fig. 5 Ice accumulation height schematic | |
浮冰堆积行为的描述目前逐渐从单纯的定性描述向定量描述转变。浮冰堆积的定性描述主要侧重于浮冰在海洋结构前的堆积行为描述上,而对浮冰堆积的定量描述主要集中在浮冰堆积高度、浮冰块尺寸、冰堆强度、空隙比等参数上。本文以浮冰的密集度及冰速为主要影响因素,探究其影响浮冰堆积高度的规律。
2.1 浮冰密集度及冰速对堆积高度的影响数值计算中有4种初始密集度,3种冰速,共计12种工况,模拟时长均为100 s。模拟过程为初始时浮冰在计算域内随机排列,在初始冰速与潮流的作用下,浮冰朝取水口移动,并在取水口前发生堆积。图 6为其中一种工况的浮冰在结构前发生堆积过程, 其中浮冰密集度为80%,冰速为0.8 m/s。浮冰的初始状态如图 6(a)所示。图 6(b)~6(d)给出了t=20 s,60 s和100 s时浮冰的堆积状态。随着数值模拟的进行,浮冰在取水口前发生堆积,且堆积的高度不断增加。浮冰水上堆积高度和水下堆积高度的变化情况如图 7所示。由于冰的密度略小于水密度,故浮冰堆积的主要构成在水下。浮冰水上堆积高度和水下堆积高度均随时间的推移而不断增加,浮冰水下堆积高度的增加速率大于水上堆积高度的增加速率。因此仅通过观察水上浮冰情况来判断水下浮冰堆积情况是比价困难的。在对不同工况下浮冰堆积情况的比较中发现,浮冰密集度以及冰速都对冰堆积高度有显著的影响。冰堆积高度最大的是图 7(d)中所示的密集度C=0.8,冰速U=0.5的情况。堆积结果对比发现,浮冰的水上堆积高度最大为0.8 m(图 7(d)),浮冰不会越过堤坝;浮冰的水下堆积高度最大达3.2 m(图 7(d)),距离水下取水口上沿(水下8 m)较远,不会发生浮冰堵塞取水口的问题。但浮冰被吸入取水口的可能性变大。

|
Download:
|
| 图 6 离散元模拟中浮冰在结构前的堆积过程 Fig. 6 Pile-up process of ice floes in discrete element simulation | |

|
Download:
|
| 图 7 不同密集度浮冰的堆积高度随时间变化 Fig. 7 The ice floes pile-up height variation of different ice concentration and ice velocity | |
在整个计算域内,统计不同浮冰密集度与冰速情况下的最大堆积高度值。绘制统计曲线得到浮冰在水上的最大堆积高度和水下的最大堆积高度随密集度变化情况如图 8所示。其中负值为水下堆积高度,正值为水上堆积高度。最大堆积高度与密集度的关系呈近似线性变化,最大堆积高度随浮冰密集度的增大而升高。这是由于浮冰在密集度增加过程中,碎冰区内的冰块数不断增多,使冰堆积更容易发生。相对于浮冰水上堆积高度,水下堆积高度受密集度的影响更大。因此在实地观测中,水面上浮冰的微弱增加都可能预示着水下冰堆积高度的大幅增加。由图 8还可以看,当密集度相同时,冰速增大上下堆积高度都随着增大。这是因为冰速越大冰块初始动能越大,即冰速快,浮冰更容易爬到冰堆上,进而影响冰的堆积高度。
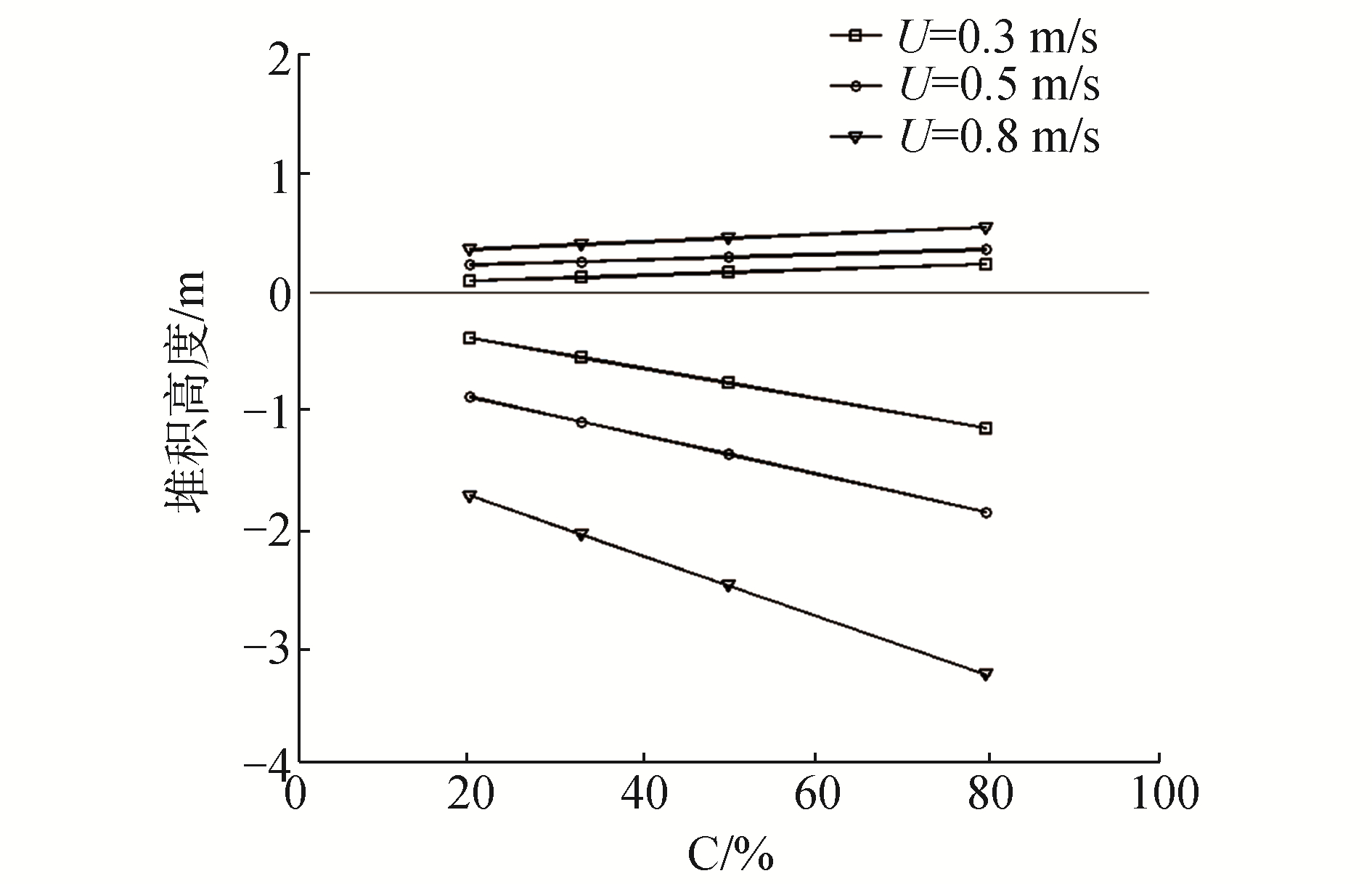
|
Download:
|
| 图 8 浮冰密集度和速度对最大堆积高度的影响 Fig. 8 Effect of ice concentration and ice velocity on the maximum pile-up height | |
在讨论了影响浮冰堆积行为的2个参数密集度和冰速后,本文在此基础上引入一个新的参数,即冰量Q,其定义为:当海上浮冰的密集度为1,海冰沿Y方向行进1 m时,单位时间内在建筑物前参与堆积的冰量为1。所以当海冰密集度为C,冰速度为U和计算时间为t的时候,参与堆积的冰量Q为
| $ Q=CUt $ |
上一节中的讨论是在同一时间量下研究浮冰参数对于浮冰堆积行为的影响。为了消去时间因素,引入冰量这个参数,把重点放在参与堆积的浮冰数量上。即在参与堆积的浮冰冰量相同的条件下,分析浮冰参数对堆积高度的影响。由于各种冰况下的浮冰密集度和速度不同,因此在各种冰况下达到相同冰量的时间也必不相同。参与堆积的冰量不同,堆积高度自然会有差异,所以不能忽略冰量对浮冰堆积的影响。通过前面的讨论我们已经得出:浮冰的水下堆积规模总体高于水上堆积规模,即浮冰堆积的主要构成在水下。因此在本节的讨论中所选取的堆积高度仅限于水下堆积高度。
数据分析过程为:以冰量Q为自变量,根据公式(7),通过MATLAB编程的方法搜索每种工况下的达到冰量Q所对应的时间t,以及时间t对应的水下堆积高度H。进而可以绘制12种计算工况下的冰量Q与堆积高度H之间的关系曲线。
为了更加清晰的分析密集度和速度分别对水下堆积高度的影响,采用2种方式对这12种计算工况进行分析:1)以速度为不变量,分析在冰量相同的情况下,密集度对浮冰堆积高度的影响;2)以密集度为不变量,分析在冰量相同的情况下,冰速对浮冰堆积高度的影响。
图 9(a)~(c)表示在速度分别为0.3 m/s、0.5 m/s和0.8 m/s时,密集度的变化对浮冰的堆积高度的影响。由图 9可以发现,在浮冰速度较低(如图 9(a)所示)、冰量相同的情况下,密集度对堆积高度有一定的影响。但是随着冰速的增大,密集度的影响逐渐减小(如图 9(b)所示)。当冰速达到0.8 m/s时,密集度对浮冰堆积高度几乎没有影响(如图 9(c)所示)。由此可以得到如下结论:当冰量一样时,密集度对水下堆积高度的影响会随着冰速的增加而逐渐减小,特别当冰速大于0.8 m/s时,密集度对堆积高度的影响基本可以忽略。
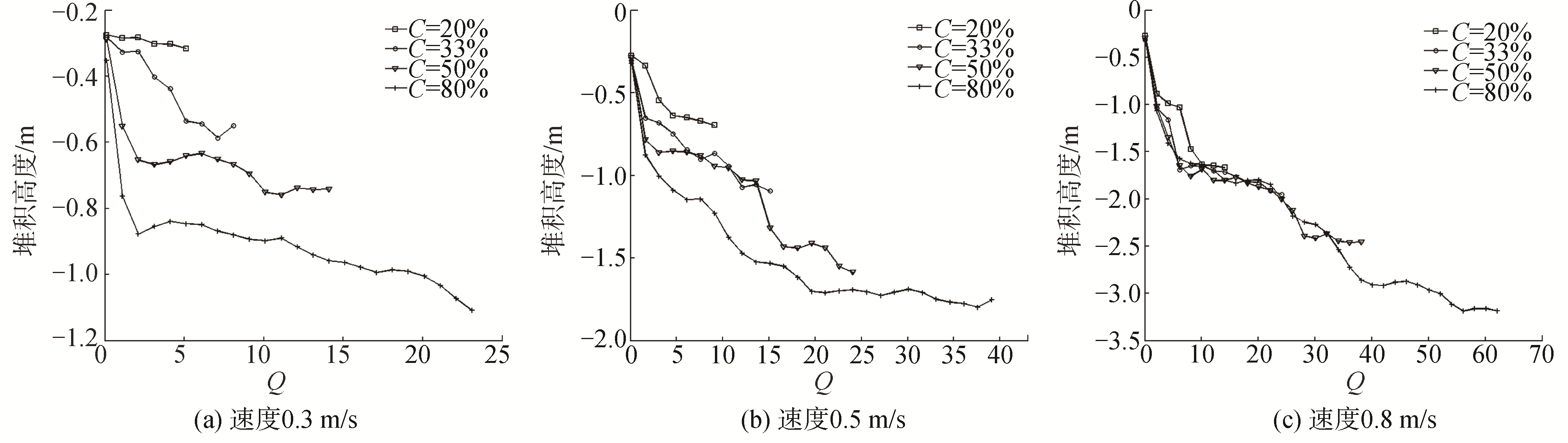
|
Download:
|
| 图 9 不同密集度下的堆积高度随冰量变化曲线 Fig. 9 The pile-up height varies with the ice volum | |
图 10(a)~(d)表示密集度分别为20%、33%、50%和80%时,冰速的变化对浮冰的堆积高度的影响。由图 10可以发现,在浮冰堆积达到稳定之前,当冰速一定时,堆积高度随着冰量的增加而呈增大的趋势。在同一密集度的情况下,冰速对浮冰堆积高度影响显著,即冰速越大,堆积高度越大。由此可以得出冰速是影响浮冰堆积高度的关键因素。
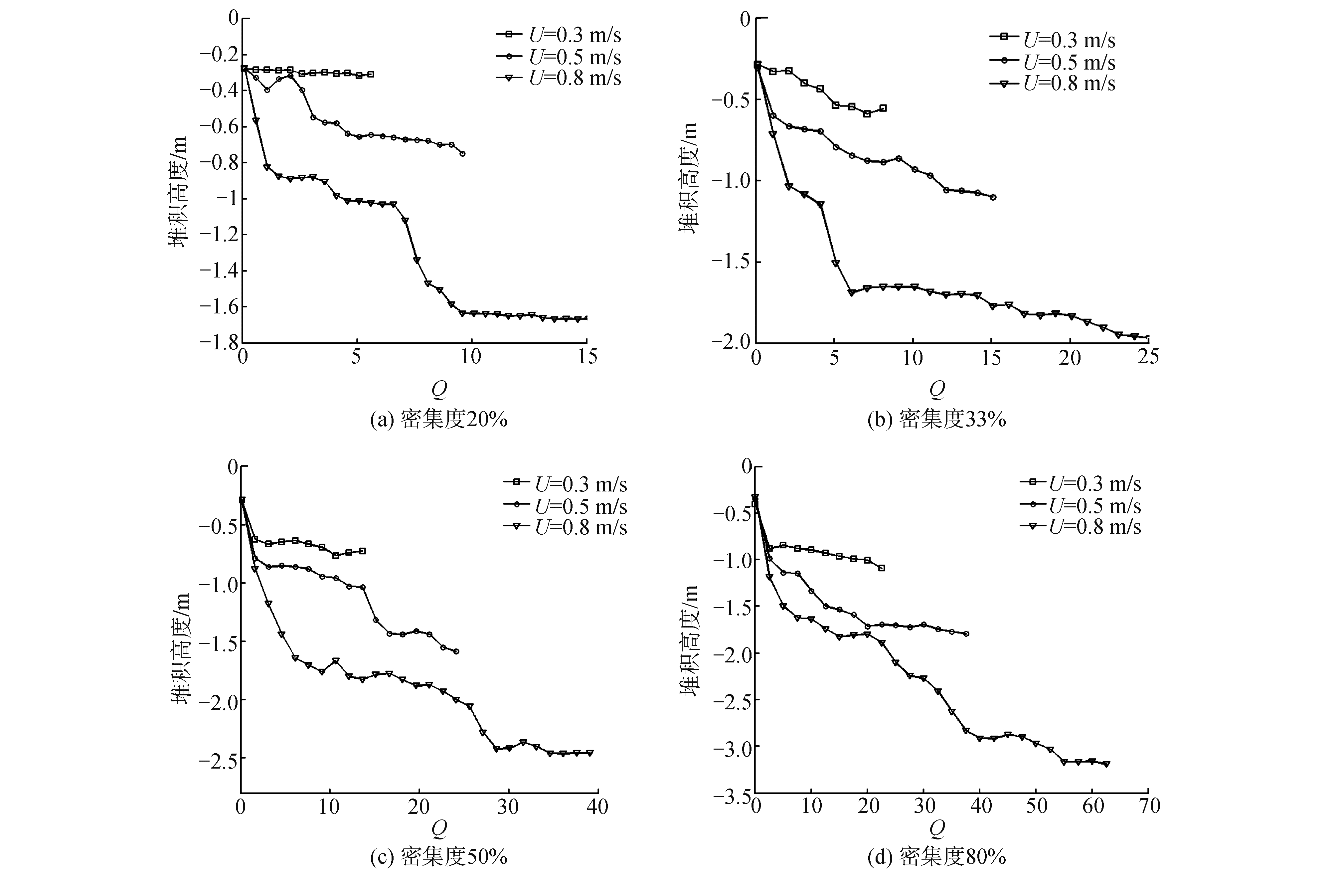
|
Download:
|
| 图 10 不同冰速下的堆积高度随冰量变化曲线 Fig. 10 The pile-up height of different ice velocity varies with the ice volume | |
此外,通过对上述曲线分析还可以发现,浮冰堆积高度随冰量的变化呈现出近似的阶梯型变化趋势。如图 10(a)所示,当冰速为0.8 m/s的时候最为明显。即浮冰堆积存在升高—稳定—升高的过程, 此过程与冰量有一定关系。同时还存在冰堆坍塌的情况,即堆积高度变小的情况发生。由于数值计算的区域大小和计算能力的限制,本文无法给出准确的规律。但是通过一些现场观测可以发现冰堆积存在堆积稳定再变大的过程,也存在冰堆坍塌的情况发生,与本文所述现象是一致的。
3 结论1) 浮冰堆积的水下部分规模大于其水上部分,即浮冰堆积的主要构成在水下。
2) 在有限的计算域内,浮冰密集度对堆积高度的影响近似是线性的,而随着冰速的增大,堆积高度明显增加,且呈非线性变化趋势,即浮冰堆积高度随着密集度和速度的增加而增大。
3) 当冰量相同时,随着冰速的增大,密集度对浮冰水下堆积高度的影响逐渐减小。而冰速的增加对堆积高度影响显著,因此冰速是影响浮冰堆积程度的关键因素。
本文对不同海冰密集度、冰速影响下的取水口前海冰堆积问题进行了数值模拟。为了进一步对取水口安全进行评估与预测,在未来的工作中还将综合考虑取水口位置的具体地形、海水潮位、极端海冰状况等条件对核电取水的影响。
| [1] |
丁德文. 工程海冰学概论[M]. 北京: 海洋出版社, 2000.
(  0) 0)
|
| [2] |
岳前进, 许宁, 崔航, 等. 基于现场观测的海洋结构冰堆积过程和危害分析[J]. 中国海洋平台, 2011, 26(3): 24-29. YUE Qianjin, XU Ning, CUI Hang, et al. The developing process and risk analysis of ice jams based on field monitoring[J]. China offshore platform, 2011, 26(3): 24-29. DOI:10.3969/j.issn.1001-4500.2011.03.006 (  0) 0)
|
| [3] |
MÄÄTTÄNEN M, HOIKKANEN J. The effect of ice pile-up on the ice force of a conical structure[C]//Proceedings of IAHR Symposium on Ice. Espoo, Finland: Helsinki University of Technology, 1990: 1010-1021.
(  0) 0)
|
| [4] |
王永学, 李春花, 孙鹤泉, 等. 斜坡式防波堤前海冰堆积数值模拟[J]. 水利学报, 2003, 34(6): 105-110. WANG Yongxue, LI Chunhua, SUN Hequan, et al. Numerical simulation of sea ice pile-up on inclined breakwater[J]. Journal of hydraulic engineering, 2003, 34(6): 105-110. DOI:10.3321/j.issn:0559-9350.2003.06.018 (  0) 0)
|
| [5] |
PAAVILAINEN J, TUHKURI J, POLOJÄRVI A. 2D numerical simulations of ice rubble formation process against an inclined structure[J]. Cold regions science and technology, 2011, 68(1/2): 20-34. (  0) 0)
|
| [6] |
HOPKINS M A. Discrete element modeling with dilated particles[J]. Engineering computations, 2004, 21(2/3/4): 422-430. DOI:10.1108/02644400410519866 (  0) 0)
|
| [7] |
HOPKINS M A, SHEN H H. Simulation of pancake-ice dynamics in a wave field[J]. Annals of glaciology, 2001, 33: 355-360. DOI:10.3189/172756401781818527 (  0) 0)
|
| [8] |
孙珊珊.基于闵可夫斯基和理论的扩展离散元模型及其应用[D].大连: 大连理工大学, 2017. SUN Shanshan. Dilated discrete element model based on Minknowski sums and its applications[D]. Dalian: Dalian University of Technology, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10141-1017035043.htm (  0) 0)
|
| [9] |
SUN Shanshan, SHEN H H. Is the wave-induced impact load from pancake ice important for offshore structures[C]//Proceedings of the 21st IAHR International Symposium on Ice. Dalian: Dalian University of Technology Press, 2012.
(  0) 0)
|
| [10] |
张明元, 孟广琳, 隋吉学, 等. 渤海湾海冰和黄河口河冰物理力学性质的测定和研究[J]. 海洋工程, 1993, 11(3): 39-45. ZHANG Mingyuan, MENG Guanglin, SUI Jixue, et al. Measurement and research on physical & mechanical properties of sea ice in the Bohai bay and river ice in the Yellow River mouth[J]. The ocean engineering, 1993, 11(3): 39-45. (  0) 0)
|
| [11] |
周晓东.锥形结构前碎冰堆积行为的模型试验研究[D].天津: 天津大学, 2012. ZHOU Xiaodong. The model test research on the behavior of ice rubble pile up in front of conical structure[D]. Tianjin: Tianjin University, 2012. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


