一体化压水堆(integrated pressurized water reactor, IPWR)具有良好的固有安全性[1],与分散式布置的压水堆相比,由于其主管路较短,减小了冷却剂的流动阻力,具有更好的自然循环能力。然而由于一体化压水堆的直流蒸汽发生器蓄热量小、换热能力强,一回路和二回路之间具有强烈的耦合特性,二回路蒸汽品质对一回路冷却剂的温度和流量十分敏感,因此对协调控制系统提出了更高要求。
强迫循环转自然循环的过渡过程由主泵驱动冷却剂流动到仅仅依靠冷热流体间的密度差形成的浮升力驱动冷却剂循环流动的过程[2],与强迫循环相比,自然循环工况下冷却剂流量小,导致蒸汽发生器传热系数小,在同等功率水平下,需要更大的反应堆进出口冷却剂温差。为了避免堆芯出口冷却剂沸腾,需要保证一定的堆芯出口过冷度,因此,在自然循环工况下要将冷却剂平均温度维持在较低设定值。而冷却剂平均温度设定值的突变引入了较大的冷却剂平均温度偏差,不利于控制系统控制。
目前,国内外学者对压水堆自然循环特性进行了分析[3-5],研究指出反应堆功率和冷热芯位差是影响自然循环能力的主要因素[6-7],在强迫循环向自然循环的过渡过程,由于冷却剂流量急剧变化,冷却剂流量对冷却剂温度影响较大[8],不利于反应堆功率控制。文献[9]提出手动调节控制棒进行人为干预可以改善过渡过程的运行特性,同时,过渡过程应考虑冷却剂流量、蒸汽发生器压力、堆芯出口温度的变化[10],这些参数直接反映了自然循环能力、蒸汽品质和反应堆安全。
上述研究对自然循环特性和强迫循环向自然循环过渡特性进行了分析,但并未提出一种行之有效的强迫循环转自然循环的自动控制策略。本文提出一种先进一体化反应堆协调控制策略,采用RELAP5建立一体化反应堆模型,实现了强迫循环向自然循环的快速、平稳过渡。
1 研究对象介绍本文以哈尔滨工程大学核科学与技术学院设计的200 MW一体化压水堆(integrated pressurized water reactor with 200 MW thermal power, IP200)为研究对象,一体化压水堆将堆芯、主泵、直流蒸汽发生器和稳压器安装在同一个压力容器中,压力容器外还接有稳压器的喷淋装置,堆芯位于压力容器的下部,12个直流蒸汽发生器集成在堆芯和压力容器之间的环形空间中,控制棒驱动机构安装在堆芯立管的上部,如图 1所示。

|
Download:
|
| 图 1 一体化反应堆流程 Fig. 1 Layout of IPWR | |
针对强迫循环转自然循环过程冷却剂流量和冷却剂平均温度设定值的突变问题,目前一般采用手动控制的方式实现该工况转换,操纵员手动调节控制棒棒位,使冷却剂平均温度逐渐下降,当冷却剂平均温度下降到自然循环工况下冷却剂平均温度设定值附近时,再将反应堆功率控制转化为自动。
本文提出一种基于模糊逻辑方法的协调控制策略,用以实现强迫循环转自然循环的自动控制,并改善其动态运行特性。与流行的神经网络等智能控制算法不同,该协调控制方法无需大量的运行数据进行参数设置或训练,避免了对运行数据的依赖。
如图 2所示,协调控制器通过监测主泵转速、堆芯进出口温度、稳压器压力以及蒸汽压力,采用模糊逻辑方法得到协调控制指令,用以指引反应堆功率控制系统、稳压器压力控制系统和给水控制系统对模糊控制器和PID控制器的切换。模糊控制器具有快速调节能力但属于有差调节,而PID控制器具有无差调节能力但在大偏差情况下易出现超调。研究表明,操纵员手动干预可以改善过渡过程的运行特性[11],模糊控制器可以模拟操纵员的手动干预过程,PID控制器则依旧用于自动控制过程,这两种底层控制器优势互补,通过两种控制器的合理切换可实现瞬态过程的快速、平稳调节。

|
Download:
|
| 图 2 协调控制策略 Fig. 2 Coordinated control strategy | |
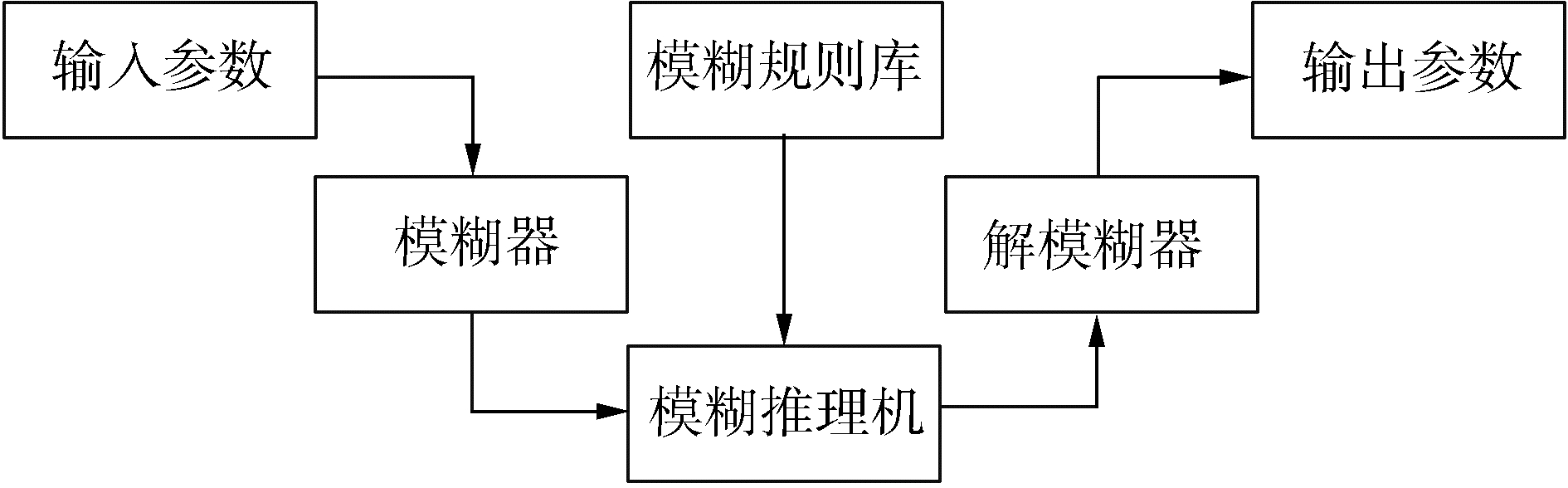
协调控制器借鉴了操纵员的经验,采用模糊逻辑方法,将操纵员关注的参数作为输入参数,将操纵员的经验转换为模糊规则库和模糊推理机,从而模拟操纵员的判断过程,如图 3所示。
|
Download:
|
| 图 3 模糊逻辑方法结构 Fig. 3 The structure of fuzzy logic approach | |
模糊器为标准化的输入参数xi*到模糊集U上的映射。考虑到输入信号会受到传感器的干扰,采用高斯模糊器来克服干扰,其隶属度函数μA′i(x)可以定义为:
| $ \mu_{A_{i}^{\prime}}(x)=\mathrm{e}^{-\left(\frac{x_{i}-x_{i}^{*}}{a_{i}}\right)^{2}} $ | (1) |
n个输入参数的集合的隶属度函数可以由T范数定义,为了简化计算,将最小算子作为T范数算子,其隶属度函数μA′(x)可表示为:
| $ \mu_{A^{\prime}}(x)=\min \left[\mu_{A_{1}^{\prime}}(x), \cdots, \mu_{A_{n}^{\prime}}(x)\right] $ | (2) |
模糊规则库由M条IF-THEN规则组成,形如:
| $ \begin{array}{l}{\text { IF }\ \ x_{1}\ \text { is }\ A_{1}^{l}\ \mathrm{AND} \ \cdots\ \mathrm{AND}\ x_{n}\ \text { is }\ A_{n}^{l}} \\ {\mathrm{THEN}\ y\ \text { is }\ B_{l}}\end{array} $ | (3) |
第l条规则在xi处的隶属度函数可表示为:
| $ \mu_{A_{i}^{\prime}}(x)=\mathrm{e}^{-\left(\frac{x_{i}-\bar{x}_{i}}{\sigma_{i}^{l}}\right)^{2}} $ | (4) |
A1l×…×Anl是U1×…×Un上的模糊集,将A1l×…×Anl看作FP1,其隶属度函数可表示为:
| $ {\mu _{{\rm{F}}{{\rm{P}}_1}}}(x) = \min \left[ {{\mu _{A_1^l}}(x), \cdots , {\mu _{A_n^l}}(x)} \right] $ | (5) |
模糊规则可以解释为Mamdani定义中U×V的模糊关系,形如:
| $\mathrm{IF}\left\langle\mathrm{FP}_{1}\right\rangle \mathrm{THEN}\left\langle\mathrm{FP}_{2}\right\rangle $ | (6) |
将Bl看作FP2,第l条规则的隶属度函数为:
| ${\mu _{R{u^l}}}(x, y) = \min \left[ {{\mu _{{\rm{F}}{{\rm{P}}_1}}}(x), \cdots , {\mu _{{\rm{F}}{{\rm{P}}_2}}}(y)} \right] $ | (7) |
对于U上给定的输入模糊集合A′,根据每个规则的广义推理,输出模糊集合隶属函数为:
| $ {\mu _{{B^\prime }}}({\rm{y}}) = \mathop {\sup }\limits_{x \in U} \left[ {{\mu _{{A^\prime }}}(x), {\mu _{R{u^l}}}(x, y)} \right] $ | (8) |
模糊推理机的输出是M个模糊集的并组合,可由S-范数表示:
| $ {\mu _{{B^\prime }}}(y) = {\mu _{{{B'}_1}}}(y)\dot + \cdots \dot + {\mu _{{{B'}_M}}}(y) $ | (9) |
将所有T-范数算子选用min算子,所有S-范数算子选用max算子,由式(5)、(7)、(8)、(9)可得:
| $ {\mu _{{B^\prime }}}({\rm{y}}) = \mathop {\max }\limits_{l = 1}^M \left[ {\mathop {\sup }\limits_{x \in U} {\rm{min}}\left( {{\mu _{{A^\prime }}}(x), {\mu _{F{P_1}}}(x), {\mu _{{B^l}}}(y)} \right)} \right] $ | (10) |
将式(2)、(4)代入式(10)可得:
| $ \begin{array}{l} {\mu _{{B^\prime }}}(y) = \mathop {\max }\limits_{l = 1}^M \left\{ {\min \left[ {\mathop {\sup }\limits_{x \in U} {\rm{min}}\left( {{{\rm{e}}^{ - {{\left( {\frac{{{x_1} - x_1^*}}{{{a_1}}}} \right)}^2}}}, {{\rm{e}}^{ - {{\left( {\frac{{{x_1} - {{\bar x}_1}}}{{\sigma _1^l}}} \right)}^2}}}} \right)} \right., } \right.\\ \left. {\left. {\;\;\;\;\;\; \cdots , \mathop {\sup }\limits_{x \in U} {\rm{min}}\left( {{{\rm{e}}^{ - {{\left( {\frac{{{x_n} - x_n^*}}{{{a_n}}}} \right)}^2}}}, {{\rm{e}}^{ - {{\left( {\frac{{{x_n} - {{\bar x}_n}}}{{\sigma _n^l}}} \right)}^2}}}} \right), {\mu _{{B^l}}}(y)} \right]} \right\} \end{array} $ | (11) |
当式得到满足时
| $\mathrm{e}^{-\left(\frac{x_{i}-x_{i}^{*}}{a_{i}}\right)^{2}}=\mathrm{e}^{-\left(\frac{x_{i}-\bar{x}_{i}}{\sigma_{i}^{l}}\right)^{2}} $ |
式(11)可在xi=xiMl处得到
| $ x_{i M}^{l}=\frac{a_{i} \bar{x}_{i}^{l}+\sigma_{i}^{l} x_{i}^{*}}{a_{i}+\sigma_{i}^{l}} $ |
式(11)可表示为:
| $ {\mu _{{B^\prime }}}(y) = \mathop {\max }\limits_{l = 1}^M \left\{ {\min \left[ {{{\rm{e}}^{ - {{\left( {\frac{{x_{1M}^l - {{\bar x}_1}}}{{\sigma _1^l}}} \right)}^2}}}, \cdots ,{{\rm{e}}^{ - {{\left( {\frac{{l_{nM}^l - {{\bar x}_n}}}{{\sigma _n^l}}} \right)}^2}}},{\mu _{{B^l}}}(y)} \right]} \right\} $ |
式中,μB′(y)取得最大值所对应的y值即为协调控制器的输出y*,当y*∈[-1, 0]时,底层控制器选择模糊控制器,当y*∈(0, 1]时,选择PID控制器。
2.3 模糊底层控制器模糊控制类似于手动控制,模糊控制器可以抑制被控量在大的初始偏差下的超调现象,并具有快速调节能力。本文将模糊控制器应用于反应堆功率控制系统、稳压器压力控制系统和给水控制系统,将被控量偏差或偏差变化率ei作为输入量,具有M0个语言变量的模糊集,第m个语言变量其隶属度函数为
| $ {\mu _{e_l^m}}(x) = {{\rm{e}}^{ - {{\left( {\frac{{{e_i} - {\rm{\bar e}}_i^m}}{{{b_i}}}} \right)}^2}}} $ |
式中i=1, 2,bi和eim是一个正常数,其中
| $ \overline{\mathrm{e}}_{i}^{m}=-1+\frac{2(m-1)}{M_{0}-1} $ |
语言变量用来描述实际参数状态,采用7个语言变量来描述输入和输出参数状态,分别为负大大(NVL)、负大(NL)、负小(NS)、零(Z)、正小(PS)、正大(PL)、正大大(PVL),由于2个输入参数的语言变量可以确定一个输出参数的语言变量,e1的第m个语言变量与e2的第n语言变量所对应的输出参数语言变量为Ym, n、Ym, n所对应的实际值为ym, n,采用中心解模糊器,标准化输出值y*可表示为:
| $ {y^*} = \frac{{\sum\limits_{n = 1}^5 {\sum\limits_{m = 1}^5 {\left( {{\mu _{e_1^m}}{\mu _{e_2^n}}{y_{m, n}}} \right)} } }}{{\sum\limits_{n = 1}^5 {\sum\limits_{m = 1}^5 {\left( {{\mu _{e_1^m}}{\mu _{e_2^n}}} \right)} } }} $ | (12) |
PID控制器形式如下:
| $ u(t)=K_{p} e(t)+K_{I} \int_{0}^{t} e\left(t^{\prime}\right) \mathrm{d} t^{\prime}+K_{D} \frac{\mathrm{d} e(t)}{\mathrm{d} t} $ | (13) |
式中:e(t)为输入偏差;u(t)为控制器输出;Kp为比例系数;KI为积分系数;KD为微分系数。
由于积分项的存在,在引入较大的初始输入偏差时易出现超调的现象,也正是由于积分项使PID控制器能够实现无静差调节,本文将PID控制器作为一种底层控制器,用于反应堆功率控制系统、稳压器压力控制系统和给水控制系统的调节,各系统PID控制器所对应的输入偏差分别为冷却剂平均温度偏差、稳压器压力偏差和蒸汽压力偏差。
2.5 自然循环工况稳态运行方案IP200一体化压水堆具有30%FP左右的自然循环运行能力[12],因此,本文研究在该功率水平下强迫循环转自然循环的过程。由于一体化压水堆采用直流蒸汽发生器,低功率下冷却剂平均温度过高会导致直流蒸汽发生器二次侧流动不稳定[13],且可能导致冷却剂出口过冷度不满足反应堆安全要求,温度过低又会导致新蒸汽过热度低,影响蒸汽品质。因此,选择一个合适的自然循环工况下冷却剂平均温度设定值,是保证蒸汽发生器稳定运行和蒸汽品质的关键。
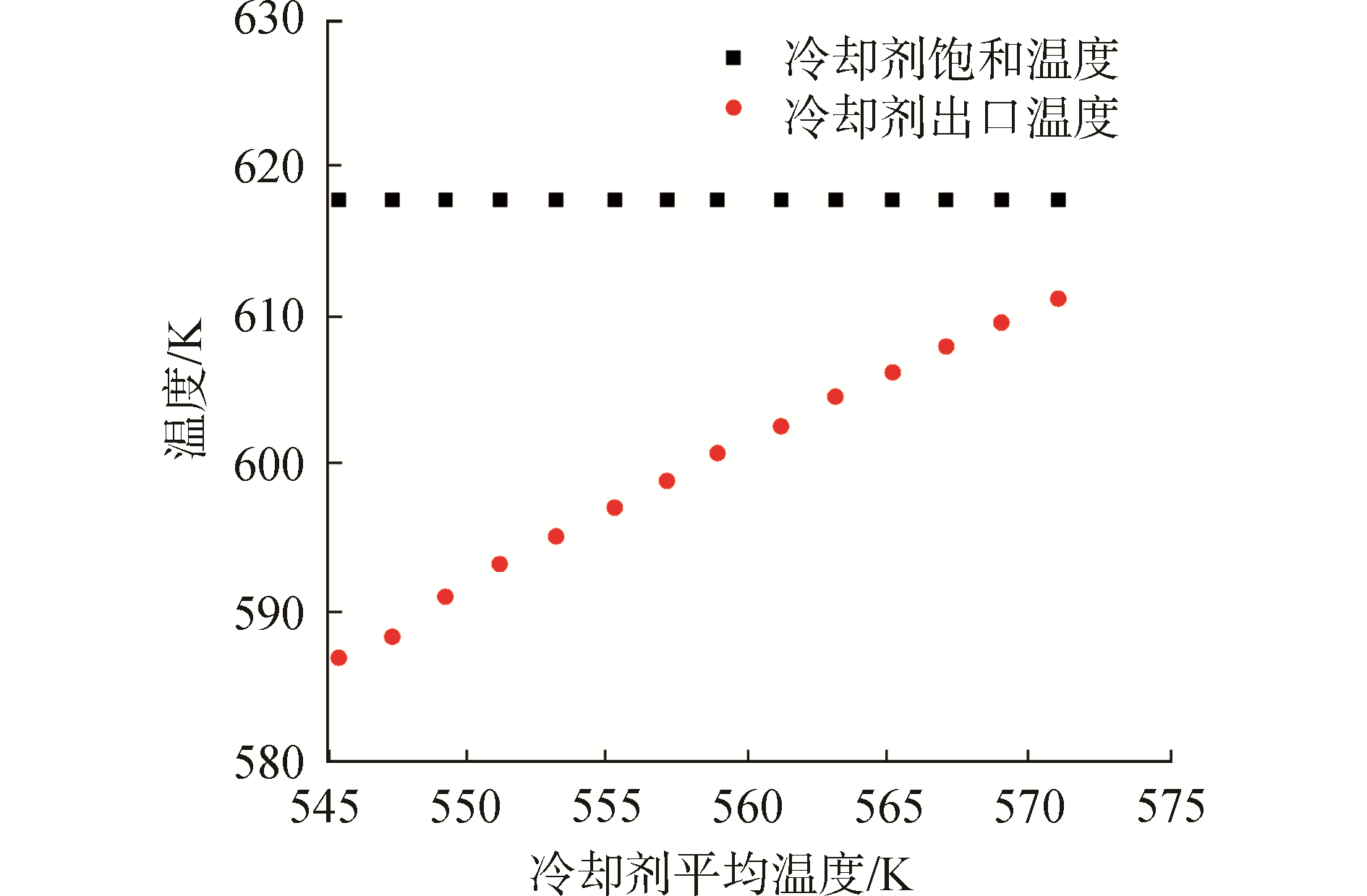
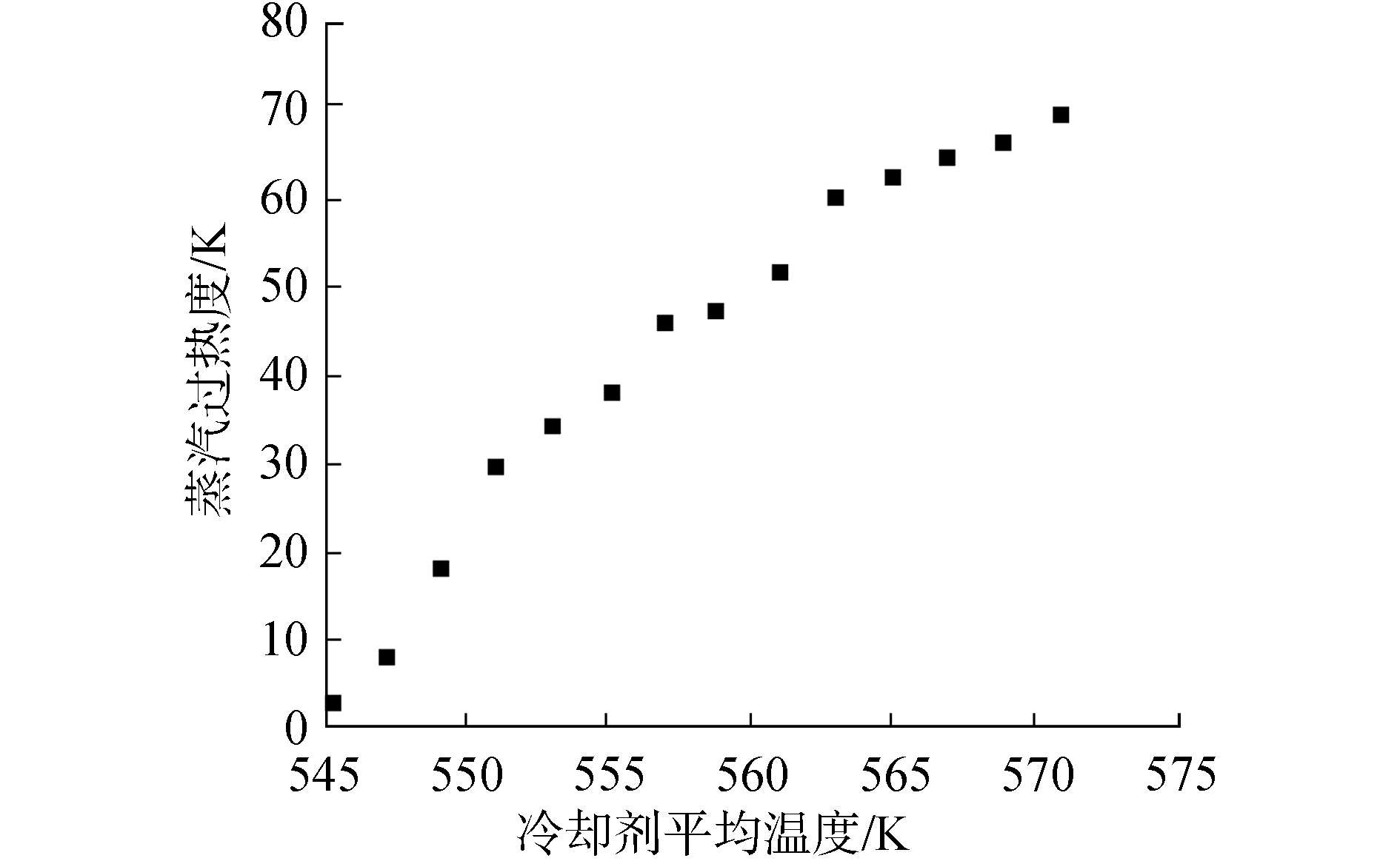
本文选择545 K~571 K范围内的冷却剂平均温度,堆芯出口冷却剂温度和蒸汽过热度随冷却剂平均温度变化分别如图 4和图 5所示,由于冷却剂流量随冷却剂平均温度变化微小,堆芯出口冷却剂过冷度与冷却剂平均温度基本呈线性负相关变化,同时,由于蒸汽发生器传热管换热系数与冷却剂流量和冷却剂温度有关,换热系数随冷却剂平均温度变化有限,蒸汽过热度随冷却剂平均温度基本呈正相关变化。冷却剂过冷度低会危及堆芯安全,蒸汽过热度过低会降低热效率,蒸汽做功后湿度过大会侵蚀汽轮机叶片,而蒸汽过热度过高会影响金属材料机械强度。为了保证足够的堆芯出口冷却剂过冷度和合适的蒸汽过热度,选择561.15 K作为自然循环工况下冷却剂平均温度设定值。
|
Download:
|
| 图 4 堆芯出口冷却剂温度特性曲线 Fig. 4 Characteristic curves of core outlet coolant temperature | |
|
Download:
|
| 图 5 蒸汽过热度特性曲线 Fig. 5 Characteristic curve of steam superheat degree | |
为了验证所提出一体化压水堆协调控制策略的有效性,在30% FP进行强迫循环到自然循环的工况转换,考虑到核动力装置的机动性和灵活性,采用同时关闭4台主泵的转换方式,冷却剂平均温度设定值由强迫循环工况下的578.15 K过渡到自然循环工况下的561.15 K,而稳压器压力设定值和蒸汽压力设定值分别维持15.5 MPa和3.0 MPa不变,这一过程中将PID控制策略作为对比方案,即仅将PID控制器应用于反应堆功率控制系统、稳压器压力控制系统和给水控制系统,此处PID控制器的比例、积分、微分系数与协调控制策略下各系统PID控制器相同。
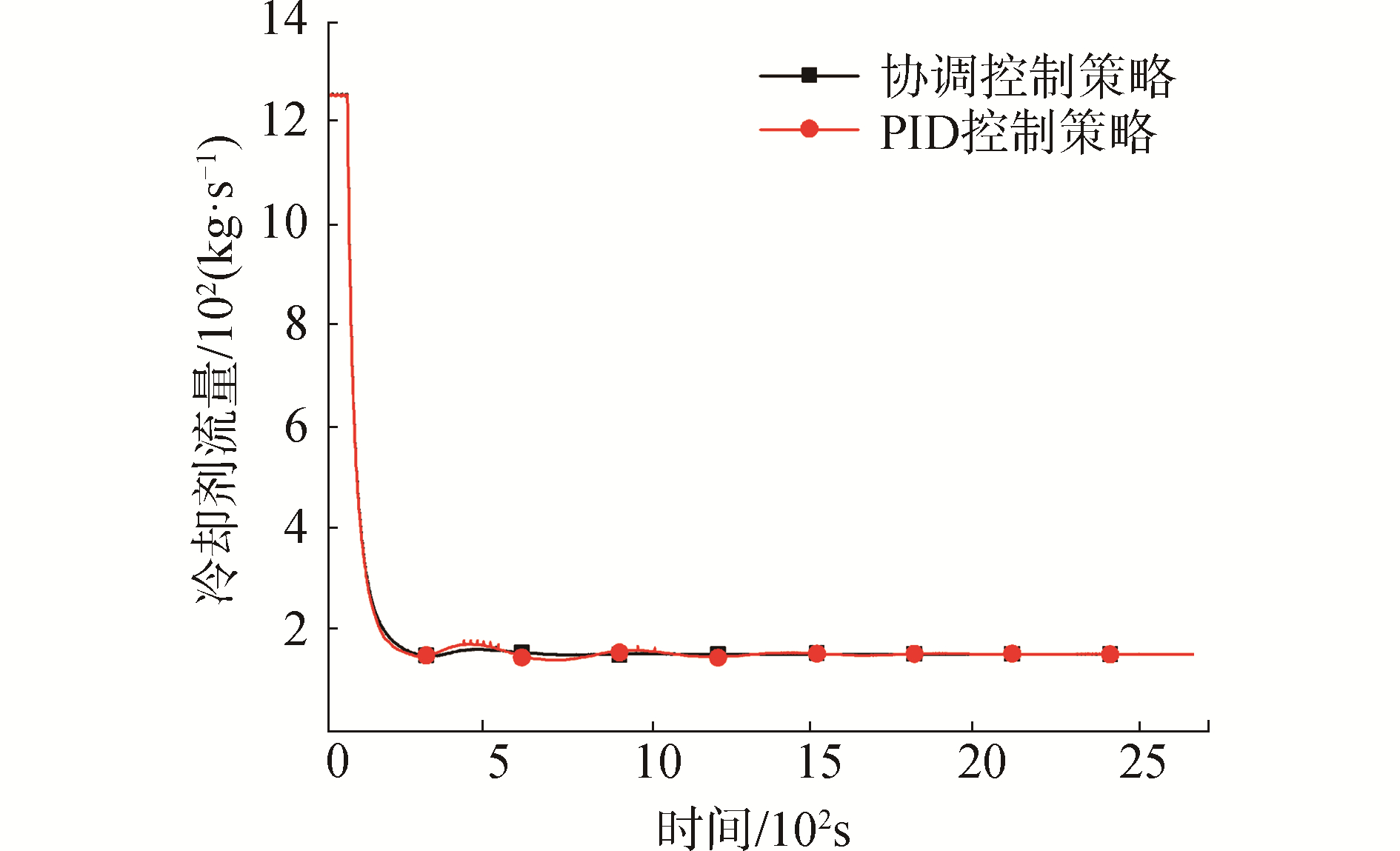
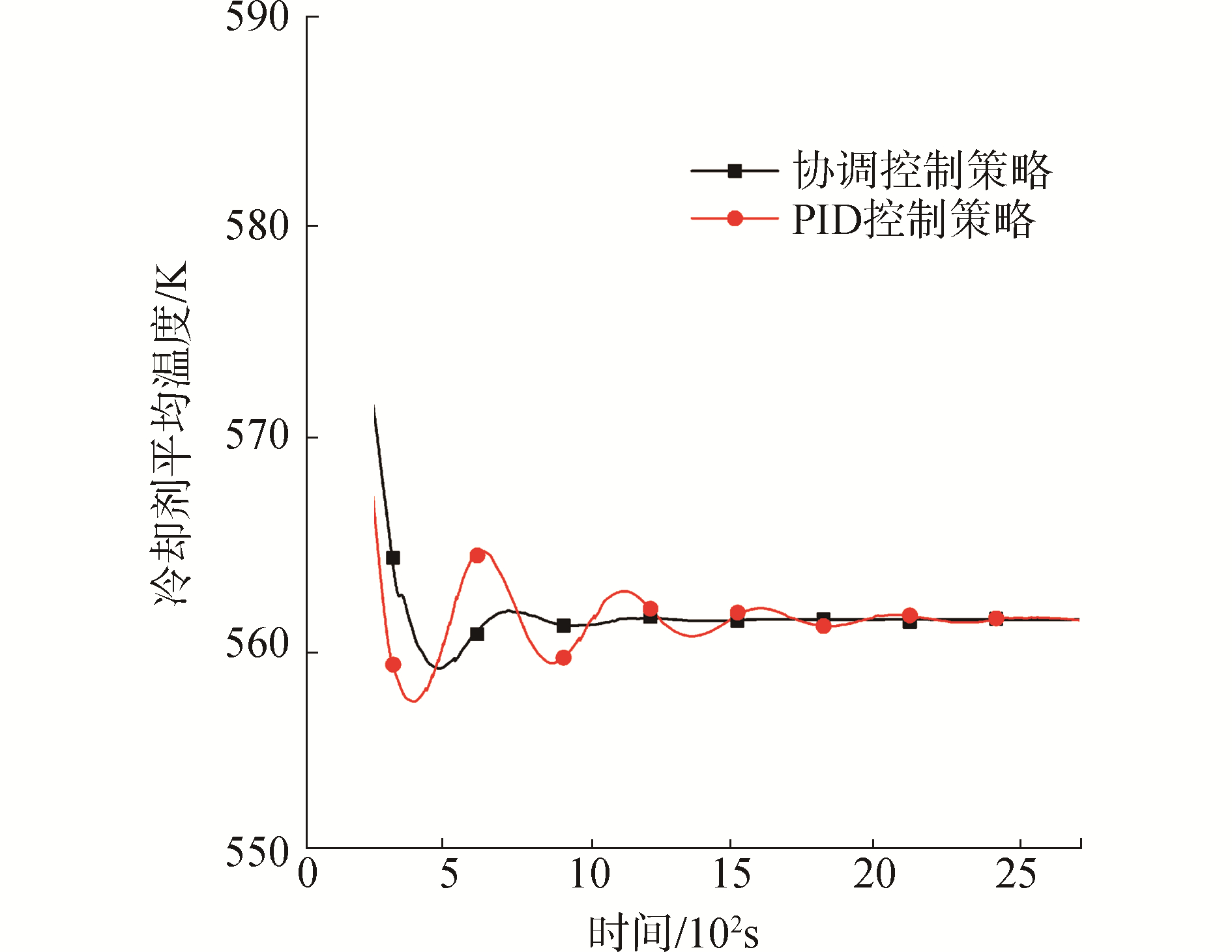
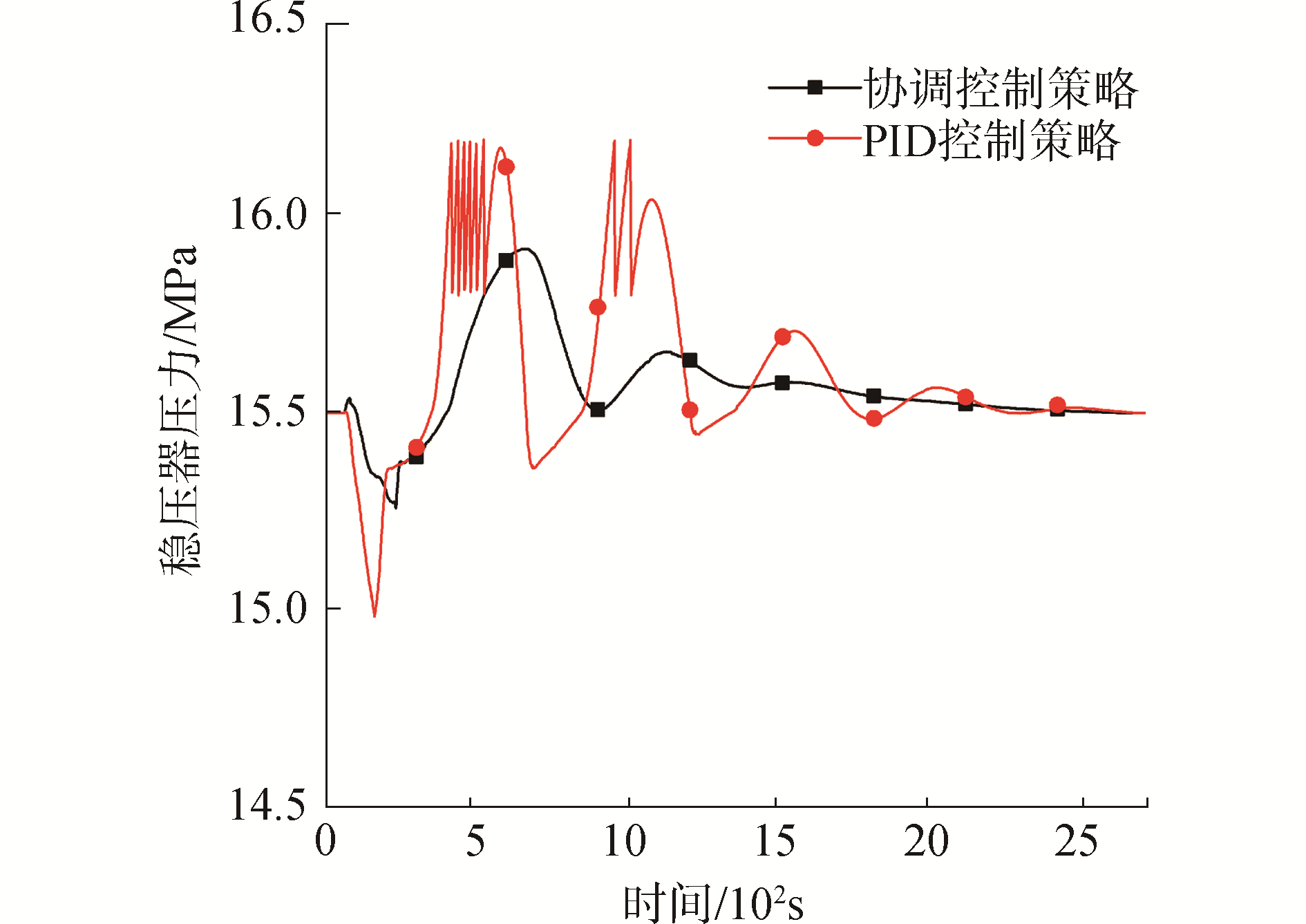
图 6为冷却剂流量变化,60 s时关闭4台主泵,由强迫循环向自然循环过渡,冷却剂流量在初期急剧下降,并随着流量下降变化趋于平缓,图 7为2种控制策略下冷却剂平均温度变化。由于60 s时冷却剂平均温度设定值突变,导致引入的平均温度偏差较大,协调控制策略先通过模糊控制器减小平均温度偏差,再通过PID控制器实现无差调节,从而避免了积分环节引起的过渡超调。而PID控制策略下在冷却剂平均温度降至561.15 K前积分环节累计了大量负偏差,造成冷却剂平均温度超调。冷却剂平均温度变化会造成冷却剂体积变化,从而影响稳压器压力,图 8为2种控制策略下的稳压器压力变化,协调控制策略通过模糊控制器抑制前期压力波动,进而通过PID控制器维持稳压器压力,PID控制策略下稳压器压力变化没有得到有效抑制,导致稳压器压力升至16.2 MPa时释放阀打开,而当稳压器压力降至15.8 MPa时释放阀关闭,导致压力上升,如此往复造成稳压器压力震荡,在调节冷却剂平均温度过程反应堆功率变化如图 9所示,反应堆功率波动会造成一、二回路功率失配,从而影响蒸汽压力和过热度。
|
Download:
|
| 图 6 冷却剂流量变化曲线 Fig. 6 Coolant mass flow rate curves | |
|
Download:
|
| 图 7 冷却剂平均温度变化曲线 Fig. 7 Characteristic curves of steam superheat degree | |
|
Download:
|
| 图 8 稳压器压力变化曲线 Fig. 8 Pressurizer pressure curves | |

|
Download:
|
| 图 9 反应堆功率变化曲线 Fig. 9 Reactor power curves | |
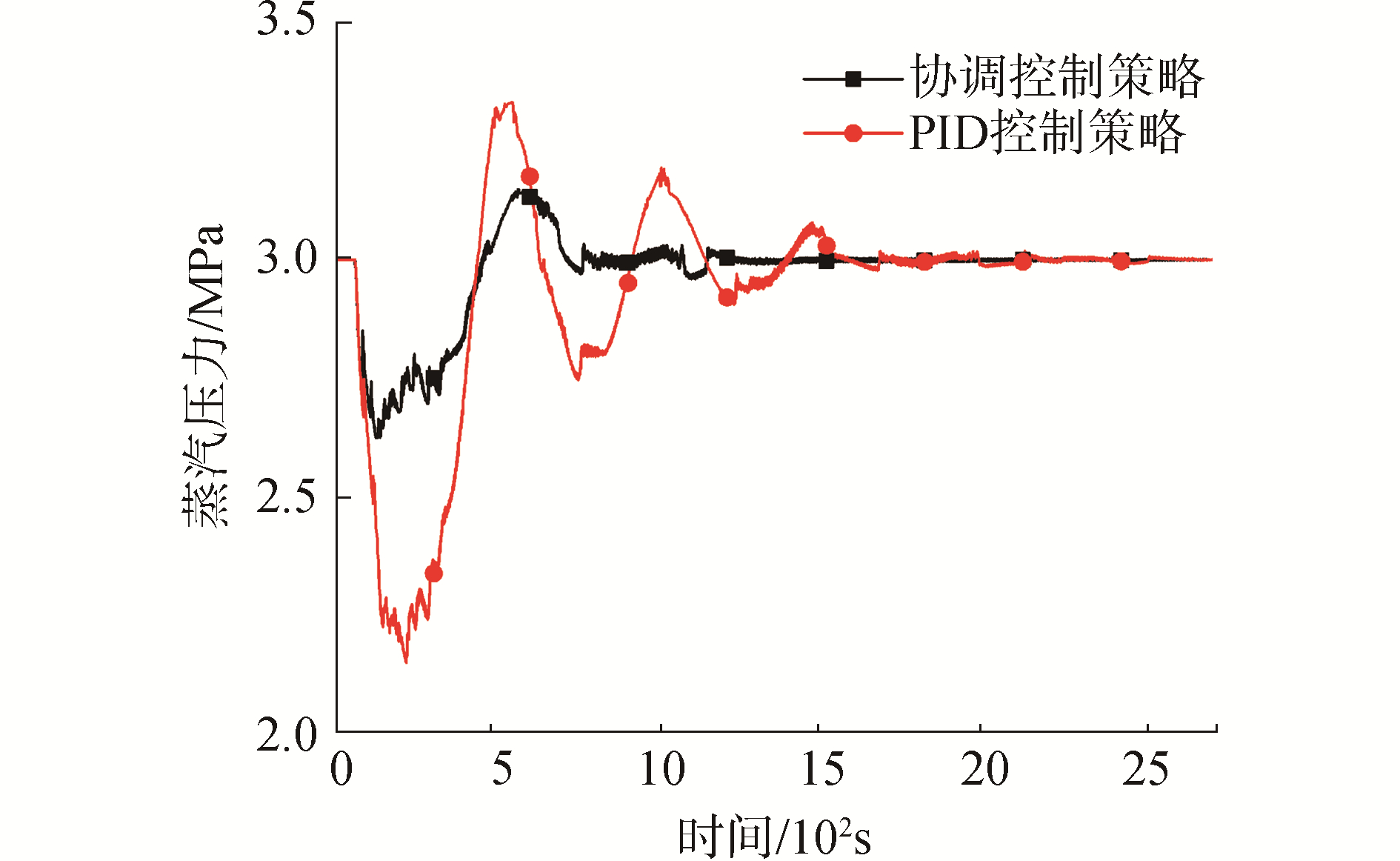
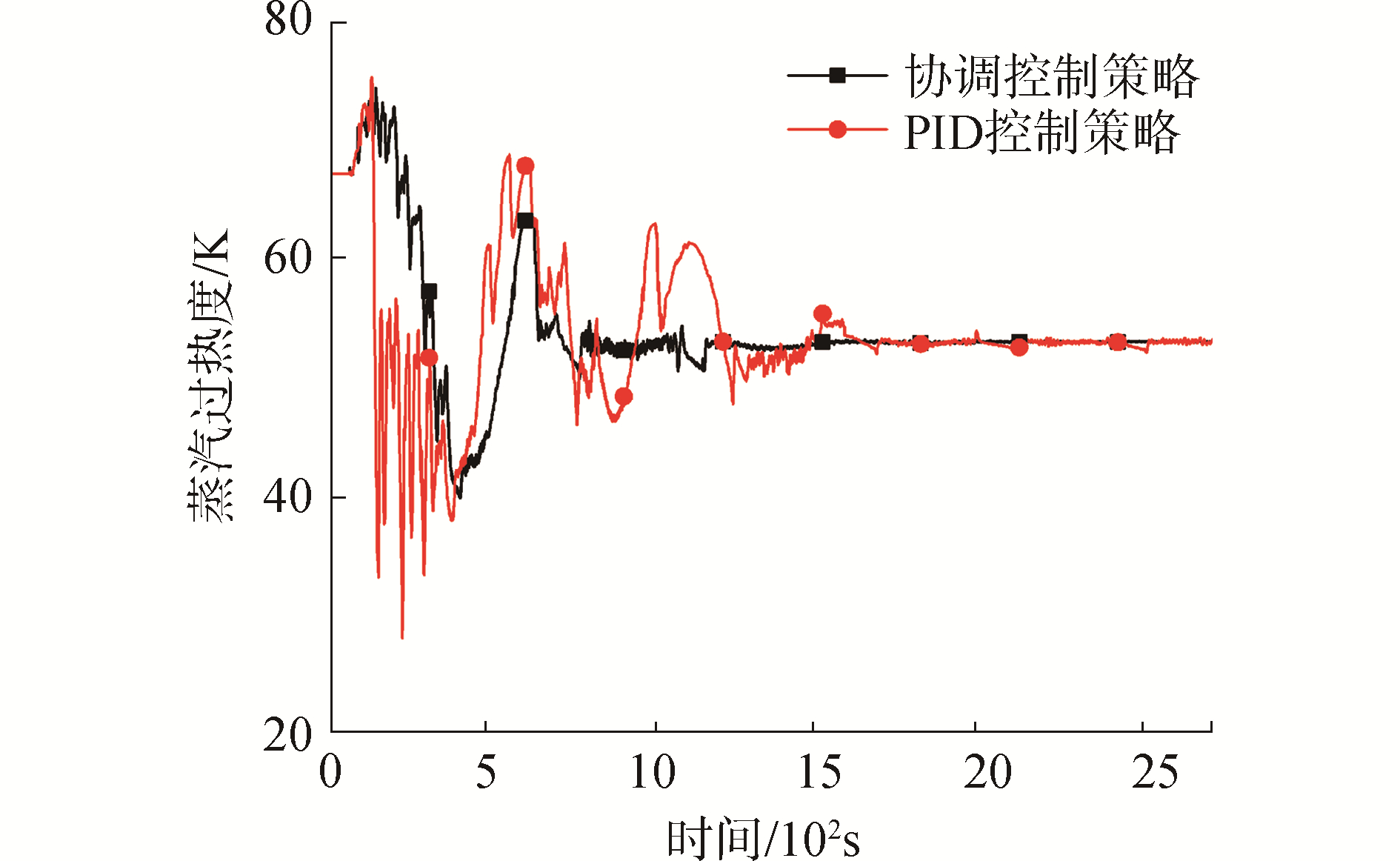
图 10和图 11分别为蒸汽压力和过热度变化,PID控制策略下,在60 s~500 s时间段内,由于反应堆功率的急剧变化造成一二回路功率不匹配,蒸汽压力波动导致蒸汽饱和温度波动,上述原因的叠加造成蒸汽过热度大幅波动,相比PID控制策略,协调控制策略的超调量小、调节时间短,更好的保证了蒸汽品质。
|
Download:
|
| 图 10 蒸汽压力变化曲线 Fig. 10 Steam pressure curves | |
|
Download:
|
| 图 11 蒸汽过热度变化曲线 Fig. 11 Steam superheat degree curves | |
计算结果表明协调控制策略具有在强迫循环转自然循环过程中快速调节和无差调节的能力,通过协调控制器合理地切换模糊控制器和PID控制器的控制动作,使模糊控制器冷却剂平均温度的快速调节,并有效抑制稳压器压力和蒸汽压力波动,进而通过PID控制器实现误差调节。因此,协调控制策略波动明显小于PID控制策略。
4 结论1) 在30% FP下的自然循环工况,综合考虑堆芯出口冷却剂过冷度和蒸汽过热度对核动力装置的影响,选择561.15 K为冷却剂平均温度设定值。
2) 本文所提出的协调控制器能够有效地协调两种底层控制器,充分发挥模糊控制器的快速调节能力和PID控制器的无差调节能力。
3) 相比常规PID控制策略,协调控制策略的调节时间更短、超调量更小。
综上所述,协调控制策略具有更好的控制效果,可作为一体化压水堆强迫转自然循环过程的一种有效控制手段。而协调控制器设计过程中,隶属度函数的选取和模糊规则的设定等都会影响底层控制器的切换时机,因此必然存在一个最优的设置,达到最优的控制效果,后续工作可开展协调控制器优化研究。
| [1] |
HIBI K, ONO H, KANAGAWA T. Integrated modular water reactor (IMR) design[J]. Nuclear engineering and design, 2004, 230(1/2/3): 253-266. (  0) 0)
|
| [2] |
阎昌琪, 曹夏昕. 核反应堆安全传热[M]. 哈尔滨: 哈尔滨工程大学出版社, 2010.
(  0) 0)
|
| [3] |
MURATA H, SAWADA K I, KOBAYASHI M. Natural circulation characteristics of a marine reactor in rolling motion and heat transfer in the core[J]. Nuclear engineering and design, 2002, 215(1/2): 69-85. (  0) 0)
|
| [4] |
PARK J W. Analytical evaluation of two-phase natural circulation flow characteristics under external reactor vessel cooling[J]. Annals of nuclear energy, 2009, 36(11/12): 1668-1675. (  0) 0)
|
| [5] |
李韧.海洋条件下一体化压水堆自然循环流动特性仿真研究[D].哈尔滨: 哈尔滨工程大学, 2014. LI Ren. Research on natural circulation flow characteristics of integrated pressurized water reactor in ocean motion[D]. Harbin: Harbin Engineering University, 2014. http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D596750 (  0) 0)
|
| [6] |
卢冬华, 肖泽军, 陈炳德. 压水堆自然循环比例模化基本方程及相似准则数的研究[J]. 核动力工程, 2009, 30(3): 72-84, 94. LU Donghua, XIAO Zejun, CHEN Bingde. Investigation on basic equations and scaling criteria of PWR natural circulation[J]. Nuclear power engineering, 2009, 30(3): 72-84, 94. (  0) 0)
|
| [7] |
苟军利, 秋穗正, 贾斗南, 等. 新型压水堆自然循环特性计算分析[J]. 西安交通大学学报, 2006, 40(11): 1329-1332, 1337. GOU Junli, QIU Suizheng, JIA Dounan, et al. Calculation analysis on the natural circulation characteristics of a new pressurized water reactor[J]. Journal of Xi'an Jiaotong University, 2006, 40(11): 1329-1332, 1337. DOI:10.3321/j.issn:0253-987X.2006.11.020 (  0) 0)
|
| [8] |
刘守相, 于雷, 鄢炳火. 一体化压水堆强迫循环转自然循环过渡过程特性分析[J]. 原子能科学技术, 2012, 46(S1): 220-224. LIU Xiangshou, YU Lei, YAN Binghuo. Research on transition process from forced circulation to natural circulation of integrated pressurized water reactor[J]. Atomic energy science and technology, 2012, 46(S1): 220-224. (  0) 0)
|
| [9] |
张龙飞, 张大发, 徐金良. 自然循环转强迫循环时反应堆功率瞬态特性研究[J]. 武汉理工大学学报(交通科学与工程版), 2008, 32(1): 115-117, 129. ZHANG Longfei, ZHANG Dafa, XU Jinliang. Study of reactor power's transient performances for transition from natural to forced circulation[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2008, 32(1): 115-117, 129. DOI:10.3963/j.issn.2095-3844.2008.01.031 (  0) 0)
|
| [10] |
郝亚雷, 于雷, 蔡章生, 等. 核动力装置强迫循环与自然循环过渡过程特性研究[J]. 核科学与工程, 2007, 27(1): 20-26, 14. HAO Yalei, YU Lei, CAI Zhangsheng, et al. Study on operation characteristics of natural circulation and forced circulation in nuclear power plant[J]. Chinese journal of nuclear science and engineering, 2007, 27(1): 20-26, 14. DOI:10.3321/j.issn:0258-0918.2007.01.005 (  0) 0)
|
| [11] |
田兆斐, 赵强, 彭敏俊, 等. 自然循环与强迫循环转换过渡过程研究[J]. 哈尔滨工程大学学报, 2010, 31(10): 1398-1404. TIAN Zhaofei, ZHAO Qiang, PENG Minjun, et al. Study on transient characteristics of transition between natural circulation and forced circulation[J]. Journal of Harbin Engineering University, 2010, 31(10): 1398-1404. DOI:10.3969/j.issn.1006-7043.2010.10.021 (  0) 0)
|
| [12] |
郝承明, 付文, 彭敏俊, 等. 一体化反应堆强迫循环转自然循环过程瞬态特性分析[J]. 原子能科学技术, 2013, 47(2): 243-248. HAO Chengming, FU Wen, PENG Minjun, et al. Transient characteristic analysis of integral pressurized water reactor from forced circulation to natural circulation[J]. Atomic energy science and technology, 2013, 47(2): 243-248. (  0) 0)
|
| [13] |
XIA Genglei, PENG Minjun, DU Xue. Research of flow instability in OTSG under low load conditions[J]. Annals of nuclear energy, 2015, 75: 421-427. DOI:10.1016/j.anucene.2014.08.059 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


