2. 同济大学 土木工程防灾国家重点实验室, 上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China
钢纤维混凝土(steel fiber reinforced concrete, SFRC)是以混凝土为基体,添加钢纤维形成的一种纤维增强混凝土材料,其性能优良,运用广泛。在混凝土基体中掺入钢纤维,能有效地改善混凝土的疲劳性能,限制裂缝的扩展,在钢纤维逐渐被拔出的整个破坏过程中增加了混凝土的耗能能力,进而增强了混凝土构件的疲劳寿命。而掺入了钢纤维的自密实混凝土,不仅能够有效地保证钢纤维与基体的有效粘结,提高混凝土力学强度,而且还能够满足自密实混凝土的均匀性、高流动性与抗离析性能等要求。现如今,钢纤维自密实混凝土逐渐替代普通混凝土运用于各种承受疲劳荷载的结构构件当中。因此,研究钢纤维自密实混凝土的疲劳性能,完成疲劳寿命预测,对实际工程应用具有重要意义。
由于材料多样性导致的混凝土多相异性,钢纤维自密实混凝土实验收集到的疲劳寿命数据离散性要高于素混凝土。因此,为了保证结构的安全,在进行混凝土结构疲劳可靠性设计时引入不确定性的概念尤为重要。目前,最常用的疲劳寿命不确定分析方法是应用概率理论得到混凝土构件的P-S-N曲线,从而应用于构件寿命的可靠性设计中。概率理论需要以大量的数据为基础来确定适合的概率分布模型,从而得到相应的P-S-N曲线,而在实际工程中,出于经济和时间成本的考虑,很难获得大量的试验数据作为概率理论分析的支撑,在这种情况下概率理论的方法就不是最优的选择。近年来,一些学者提出了模糊可靠性设计、基于灰色系统理论的预测方法等[1],这些方法在一定程度上弥补了概率理论的不足,在概率理论不适用的情况下有着良好应用。
证据理论[2]作为近年来新兴的不确定分析方法,是对经典概率理论的一种扩展,其对不确定问题的处理比较符合人们的思维习惯,而且可以对各种不完整、不确定、不可靠及冲突信息进行描述和处理。近年来,证据理论已成为国际学术界的研究热点之一,在不确定性推理、目标识别、故障诊断和数据融合中得到了广泛的应用[3-5]。历经30多年的发展,证据理论得到了广泛的关注,但是目前主要的研究还是集中在航空、汽车、能源和多传感器数据融合等领域[6-8],在土木工程领域不确定处理方面的研究才刚刚起步。
本文通过应用证据理论对各级应力水平下不同钢纤维掺量的试验数据[9]进行统计处理,尝试引入证据理论的方法来描述疲劳寿命模型参数的认知不确定性,通过微分演化算法(differential evolution,DE)[10-11]进行不确定的传播,从而得到疲劳寿命的不确定性预测结果,并通过与概率理论得到的结果及实验数据进行对比分析,来验证该方法的有效性。
1 疲劳寿命预测模型参数不确定分析 1.1 基于S-N曲线的混凝土疲劳寿命预测作为预测混凝土疲劳寿命的基本方法,S-N曲线假定混凝土的疲劳与强度无关,且最大应力与弯曲强度的比值与循环次数的对数成线性关系。传统的疲劳寿命分析通常采用基于中值的S-N曲线,而在双对数坐标中基于中值的S-N曲线通常接近直线。为方便分析,对于S-N曲线的中值表达式如下:
| $ \lg N=\lg C-m \lg S $ | (1) |
式中:m和lgC是2个常数。在混凝土疲劳寿命预测过程中首先通过实验得到的N和S通过拟合得到m和lgC的具体数值,然后代入式(1)得到不同应力水平S下的混凝土疲劳寿命N。
1.2 预测模型参数不确定性分析的统计分析通常S-N预测模型的参数是通过实验数据拟合得到平均或中值数据。在数值分析时,研究者采用基于平均值的参数选取方法,通过拟合可以得到近似可取的的预测数值。但是工程实践中往往需要确定最不利的寿命预测,这是基于平均值参数预测模型无法完成的。若选择利用概率模型刻画S-N曲线,又会因为统计数据的稀少等认知不确定性因素而不能确定概率分布的形式。而选择利用单个区间刻画分布模型参数时,所利用的信息只有边界响应的实验值作为区间输入才会被视作有效的参数,大部分非边界响应的实验数据将会浪费。
2 基于证据理论的不确定量化 2.1 证据理论的基本概念证据理论建立了命题和集合之间的一一对应关系,通过引入信任函数,区分不确定和不知道的差异,满足比概率论弱的情况,用D-S合成规则[12]更新信任函数。证据理论的基础是证据的合成和信任函数的更新,其对不确定性的描述是通过识别框架、基本信任分配函数、信任函数、似然函数等概念来描述的。
在证据理论中,一般用集合来表示命题,定义识别框架Θ表示一个包含有限个且相互独立元素的集合,对应的数学表达为:
| $ \mathit{\Theta}=\left\{\theta_{1}, \theta_{2}, \cdots, \theta_{j}, \cdots, \theta_{N}\right\} $ | (2) |
式中:θj称为识别框架Θ的一个事件或元素;N是Θ中所有元素的个数;j=1, 2, …, N。由识别框架Θ的所有子集可组成Θ的幂集,记为P(Θ)。
在识别框架Θ上的基本信任分配(BBA)是一个映射m:P(Θ)→[0, 1]。BBA表示证据对幂集P(Θ)中每一个子集信任程度的初始分配,满足:
| $ \left\{\begin{array}{l}{m(A) \geqslant 0, \quad \forall A \in P(\mathit{\Theta})} \\ {m(\varnothing)=0} \\ {\sum\limits_{A \in P(\Theta)} m(A)=1}\end{array}\right. $ | (3) |
式中使得m(A)>0的A称为焦元。
在证据理论中对于命题A的信任程度通过信任函数Bel和似然函数Pl表示,其中Bel(A)代表命题A为真的信任程度,而Pl(A)表示A为非假的信任程度。对于上述2个定义数学表达式为:
| $ \operatorname{Bel}(A)=\sum\limits_{B \subseteq A} m(B) $ | (4) |
| $ \operatorname{Pl}(A)=\sum\limits_{B \cap A \neq \varnothing} m(B) $ | (5) |
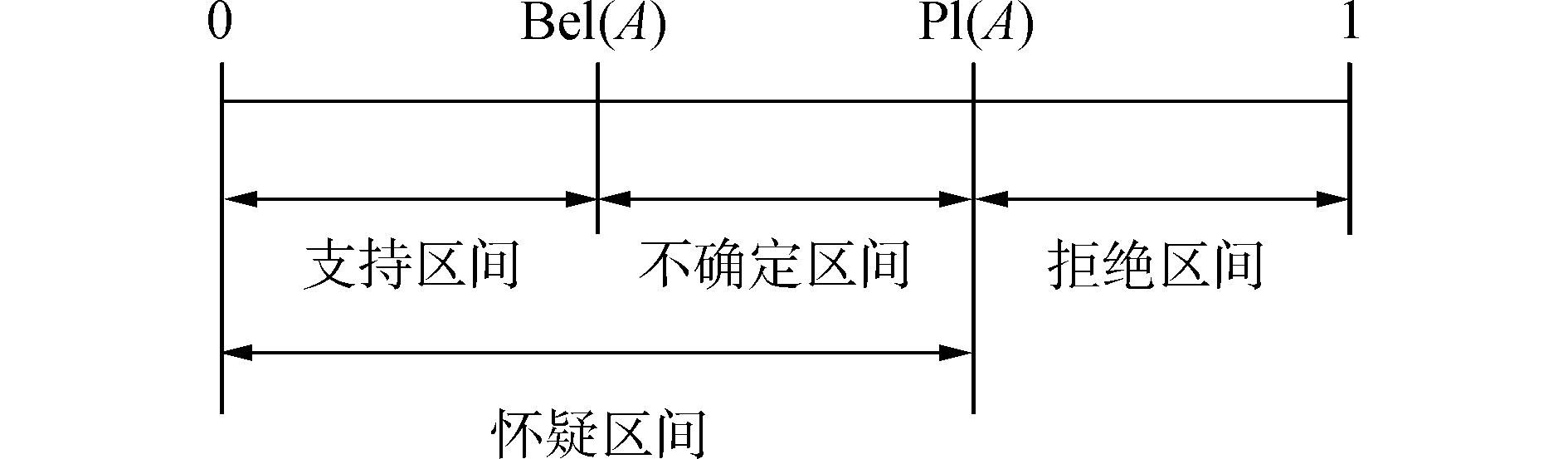
在证据理论中,对于命题A的信任程度通常表示为[Bel(A), Pl(A)],可以看出这种表示方法区分了对命题A的不确定和不知道的差异性。基于式(3)和式(4)2种定义也可对信任函数和似然函数之间的关系加以对比,如:Bel(A)≤P(A)≤Pl(A)。(其中,P(A)为A的概率值)。图 1中似然函数Pl(A)与信任函数Bel(A)之间的区间表示对事件A的认知不确定性[13],而这也与概率理论用单一数值去表达不确定性截然不同。
|
Download:
|
| 图 1 信任函数与似然函数的关系 Fig. 1 Relation between Bel and Pl | |
在证据理论中,对于命经典的D-S合成规则为:假定Bel1和Bel2是同一辨识框架Θ上的两个信任函数,其相应的基本信任分配函数为m1和m2,焦元分别为Ai和Bj,设
| $ m(A)\left\{ {\begin{array}{*{20}{l}} {\frac{{\sum\limits_{{A_i} \cap {B_j} = A} {{m_1}} \left( {{A_i}} \right){m_2}\left( {{B_j}} \right)}}{{1 - K}}, }&{A \ne \emptyset }\\ {0, }&{A = \emptyset } \end{array}} \right. $ | (6) |
本文采用文献[14]的不确定参数证据理论的表达方法,该方法主要包含2个步骤:1)通过将所有已知数据点绘制成柱状图,将不确定参数表达成区间的形式;2)区分相邻区间之间的不同关系类型,用证据理论的方式来确定一种合适的信任架构。
基于以上理论,2个相邻区间之间的关系有忽略、一致和互斥3种。假设I1、I2是2个相邻的区间,各区间内数据点的个数分别为A和B。当B/A < 0.5时,I1与I2之间为忽略关系。基本信任分配函数可表示为:
| $ m\left(\left\{I_{1}\right\}\right)=A /(A+B) $ | (7) |
| $ m\left(\left\{I_{1}, I_{2}\right\}\right)=B /(A+B) $ | (8) |
当B/A>0.8时,I1与I2之间为一致关系。基本信任分配函数可表示为:
| $ m\left(\left\{I_{1}, I_{2}\right\}\right)=1 $ | (9) |
当0.5≤B/A≤0.8时,I1与I2之间为互斥关系。基本信任分配函数可表示为:
| $m\left(\left\{I_{1}\right\}\right)=A /(A+B) $ | (10) |
| $ m\left(\left\{I_{1}, I_{2}\right\}\right)=B /(A+B) $ | (11) |
利用证据理论对不确定变量表达之后,不确定变量的分布以区间形式呈现,不确定量化的工作就是通过对系统输入变量经系统函数传播得到对应的输出响应。
当变量用区间形式表达时,求得的系统响应也是区间的。这样,不确定传播就变成了在每个超立方体区间内寻求响应的最大和最小值。对每个小焦元区间上求得极值需要进行若干次蒙特卡洛抽样得到,而众所周知抽样的精度和抽样次数相关,得到所有焦元区间上的响应就需进行大量的抽样。为了提高计算效率,本文采用微分演化算法,将大量的抽样工作进行优化分析,加快不确定在焦元区间内的传播速度。关于微分演化算法的详细解释参见文献[10]。
微分演化作为一种新颖的启发式智能算法,自从1996年被Storn和Price引入以来,在解决复杂的优化问题上得到了很多关注。它结合了遗传算法的更大种群概念和进化算法的自适应变异以及采用了贪婪选择策略。这些特征使DE算法相比进化算法和遗传算法鲁棒性更好,收敛更快。研究表明针对复杂的优化问题, DE算法相对于遗传算法等其他算法具有更高的精确度、更快的收敛速度和较强的鲁棒性等特点[15]。
3 疲劳寿命算例分析 3.1 基于S-N曲线的参数计算本文以文献[9]中的三点弯曲疲劳测试试验为基础,利用S-N曲线模型预测钢纤维自密实混凝土的疲劳寿命。该实验采用相同尺寸的钢纤维自密实混凝土梁为基本试件,在3种不同应力水平下进行常幅加载疲劳试验,获取10组试件在各应力水平下的实验数据,通过最小二乘法拟合得到相应的10组lgC和m的值,如表 1所示。
| 表 1 0.5%钢纤维掺量SCFRC的S-N曲线参数值 Table 1 Different steel fiber volume ratio of SCFRC S-N curve parameter values |
从表 1可以看出,尽管试件类型与加载条件相同,但得到的S-N曲线对数方程参数值依然存在着一定的差异性。10组完全相同的试件得到了10组不同的S-N曲线模型,这就给疲劳寿命预测带来了一定的不确定性,给决策者的选择带来了困难。所以,进行疲劳寿命的不确定分析是很有必要的。
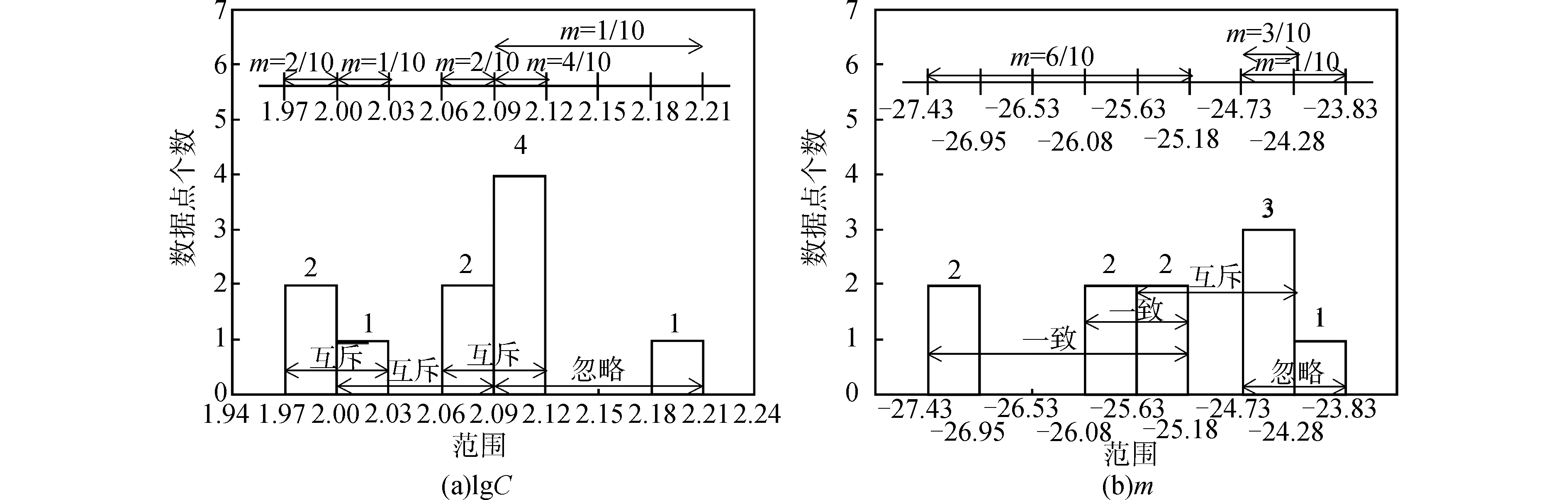
3.2 参数不确定性传播分析利用表 1中的10组数据,对材料参数lg C和m 2个不确定参数进行统计分析,并用证据理论进行表达。首先将表中的数据进行整理,确定2个不确定变量的不确定区间,并画出他们的分布统计直方图和对应的BBA架构,如图 2所示。
|
Download:
|
| 图 2 0.5%钢纤维掺量SCFRC的参数的数据分布 Fig. 2 Data distribution of parameters for 0.5% steel fiber volume ratio of SCFRC | |
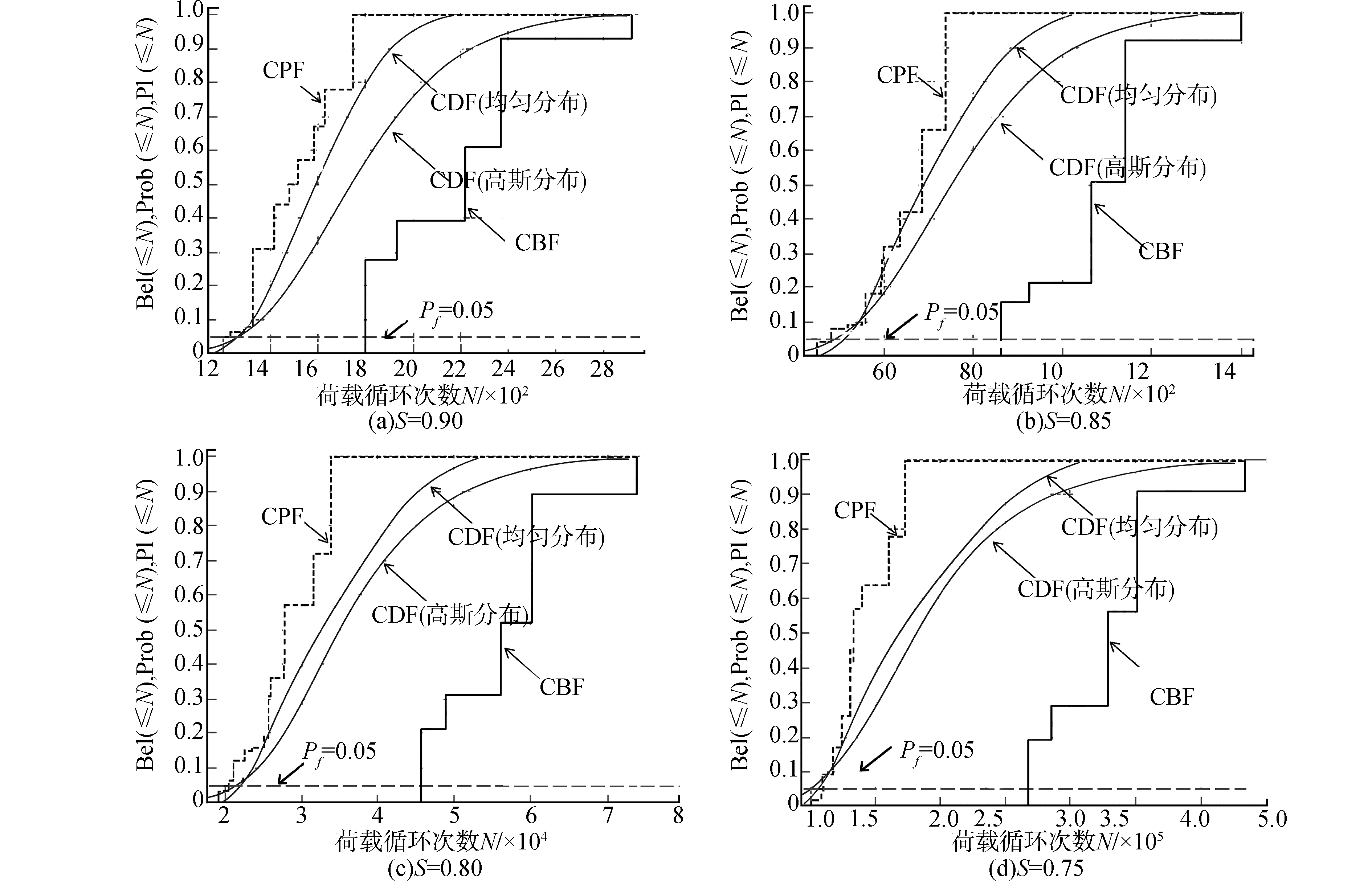
根据图 2给出的lgC和m的信任架构,应用微分演化算法对不确定性进行传播,可以得到不同钢纤维掺量与不同应力水平下的累积信任函数分布曲线(CBF)和累积似然函数分布曲线(CPF)。其中,不同应力水平下0.5%钢纤维体积率的疲劳寿命预测结果如图 3所示,图中还同时添加了概率理论方法得到的累积分布函数曲线(CDF)。
|
Download:
|
| 图 3 0.5%钢纤维体积率SCFRC的证据理论疲劳寿命预测结果 Fig. 3 0.5% steel fiber volume ratio of SCFRC evidence theory of fatigue life prediction results | |
从上图 3中可以看出,在证据理论预测结果区间内,概率理论得到的CDF曲线和证据理论的CPF、CBF曲线有较好的兼容性。但对于钢纤维自密实混凝土这种离散性大的复合材料,在实际情况下,由于经济性、可操作性等因素的影响,很难获得足够多的数据来进行概率分布假定。在认知水平不足、信息缺乏、离散性大的情况下,经过KS-检验(Kolmogorov-Smirnov)验证,基于概率理论分析的钢纤维自密实混凝土预测方法可同时服从均匀分布和高斯分布,而通过图 3两者的累积分布函数曲线分析比较,可以看出2种不同分布的概率理论方法存在一定的差异。采用任意一种分布的概率理论方法均不能准确表达与实际疲劳寿命接近的预测结果,这就给概率理论预测结果带来一定的误差。而基于证据理论的方法并不需要概率分布作为分析的前提,可以在数据不充足的情况下,基于已有的数据进行不确定的传播分析,且其预测结果是区间值,有效避免了概率理论方法局限性带来的误差。以上分析说明利用证据理论进行疲劳寿命预测不确定分析具有很好的鲁棒性。
表 2给出了从图 3计算结果中提取的部分信息与实验数据值进行对比。从表中可以看出,在某一特定失效概率的情况下,概率理论得到的都是单点值,且在不同应力水平下不同概率分布的疲劳寿命预测结果存在一定的差异。因此,在实验数据量较少的情况下,将无法确定一个通用的概率模型完成准确的疲劳寿命预测分析,若概率分布假定不合理,产生的预测结果有可能直接导致工程失误。而由于证据理论考虑了参数的不确定性,得到的区间值疲劳寿命预测结果能有效避免这一误差,从而使疲劳寿命预测不确定分析具有更高的可靠性。
| 表 2 3种方法寿命预测结果 Table 2 Life prediction results for three different methods |
1) 对于钢纤维自密实混凝土这种离散性较大的复合材料,由于信息缺乏、实验数据离散,无法建立不确定变量的精确概率分布,传统概率统计方法存在局限性。证据理论方法是传统概率方法很好的替代,该方法处理认知不确定情况具有很好的实用性。
2) 由于证据理论考虑了S-N模型的不确定性,其得到的预测结果相对保守,相比于确定性方法,更适用于离散性较大的钢纤维自密实混凝土材料的寿命预测。比较结果表明应用证据理论预测混凝土疲劳寿命是可靠的。
| [1] |
王旭亮.不确定性疲劳寿命预测方法研究[D].南京: 南京航空航天大学, 2009. WANG Xuliang. Research on uncertain methods for fatigue life prediction[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2009. http://cdmd.cnki.com.cn/Article/CDMD-10287-2010080020.htm (  0) 0)
|
| [2] |
SHAFER G. A mathematical theory of evidence[M]. Princeton: Princeton University Press, 1976.
(  0) 0)
|
| [3] |
郝军, 吴炜, 杨栈. 改进D-S算法在船舶汽轮机故障诊断中的应用研究[J]. 船海工程, 2007, 36(3): 49-51. HAO Jun, WU Wei, YANG Zhan. Application of the improved D-S algorithm in fault diagnosis of ship's turbine-machinery[J]. Ship & ocean engineering, 2007, 36(3): 49-51. DOI:10.3963/j.issn.1671-7953.2007.03.016 (  0) 0)
|
| [4] |
FRANÇOIS J, GRANDVALET G, DENÇUX D, et al. Addendum to resample and combine:an approach to improving uncertainty representation in evidential pattern classification[J]. Information fusion, 2003, 4(3): 235-236. DOI:10.1016/S1566-2535(03)00020-4 (  0) 0)
|
| [5] |
MCCLEAN S, SCOTNEY B. Using evidence theory for the integration of distributed databases[J]. International journal of intelligent systems, 1997, 12(10): 763-776. DOI:10.1002/(SICI)1098-111X(199710)12:10<763::AID-INT5>3.0.CO;2-W (  0) 0)
|
| [6] |
SALEHGHAFFARI S, RAIS-ROHANI M, MARIN E B, et al. A new approach for determination of material constants of internal state variable based plasticity models and their uncertainty quantification[J]. Computational materials science, 2012, 55: 237-244. DOI:10.1016/j.commatsci.2011.11.035 (  0) 0)
|
| [7] |
HELTON J C, JOHNSON J D, OBERKAMPF W L, et al. A sampling-based computational strategy for the representation of epistemic uncertainty in model predictions with evidence theory[J]. Computer methods in applied mechanics and engineering, 2007, 196(37/38/39/40): 3980-3998. (  0) 0)
|
| [8] |
WANG Chong, MATTHIES H G. Evidence theory-based reliability optimization design using polynomial chaos expansion[J]. Computer methods in applied mechanics and engineering, 2018, 341: 640-657. DOI:10.1016/j.cma.2018.07.015 (  0) 0)
|
| [9] |
GOEL S, SINGH S P, SINGH P. Flexural fatigue strength and failure probability of self compacting fibre reinforced concrete beams[J]. Engineering structures, 2012, 40: 131-140. DOI:10.1016/j.engstruct.2012.02.035 (  0) 0)
|
| [10] |
PRICE K, STORN R M, LAMPINEN J A. Differential evolution:a practical approach to global optimization (natural computing series)[M]. Berlin, Heidelberg: Springer, 2005.
(  0) 0)
|
| [11] |
唐和生, 邓立新, 胡长远. 基于证据理论和微分演化的结构不确定分析[J]. 同济大学学报(自然科学版), 2014, 42(3): 325-330, 337. TANG Hesheng, DENG Lixin, HU Changyuan. Evidende theory and differential evolution for uncertainty quantification of structures[J]. Journal of Tongji University (Natural Science), 2014, 42(3): 325-330, 337. DOI:10.3969/j.issn.0253-374x.2014.03.001 (  0) 0)
|
| [12] |
HELTON J C, JOHNSON J D, OBERKAMPF W L. An exploration of alternative approaches to the representation of uncertainty in model predictions[J]. Reliability engineering & system safety, 2004, 85(1/2/3): 39-71. (  0) 0)
|
| [13] |
TANG Jian, WU Zhigang, YANG Chao. Epistemic uncertainty quantification in flutter analysis using evidence theory[J]. Chinese journal of aeronautics, 2015, 28(1): 164-171. DOI:10.1016/j.cja.2014.12.024 (  0) 0)
|
| [14] |
SALEHGHAFFARI S, RAIS-ROHANI M. Epistemic uncertainty modeling of Johnson-Cook plasticity model using evidence theory[C]//Proceedings of the 13th AIAA/ISSMO Multidisciplinary Analysis Optimization Conference. Fort Worth, Texas: AIAA, 2010.
(  0) 0)
|
| [15] |
唐和生, 王兆亮, 薛松涛. 微分演化算法在桁架形状优化中的应用[J]. 土木建筑与环境工程, 2010, 32(1): 42-50, 106. TANG Hesheng, WANG Zhaoliang, XUE Songtao. Truss structure shape optimization with differential evolution algorithm[J]. Journal of civil, architectural & environmental engineering, 2010, 32(1): 42-50, 106. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


