2. 上海交通大学 船舶海洋与建筑工程学院, 上海 200240;
3. 哈尔滨工程大学 船舶工程学院, 黑龙江 哈尔滨 150001
2. School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240, China;
3. College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China
立管、系泊线等柔性构件在海洋工程领域扮演着重要角色,这些深水结构往往表现出典型的细长特点,其几何非线性因素在分析中影响较大而不可忽略[1-2]。
绝对节点坐标法是近年来在机械、多体动力学等领域应用广泛的动力分析方法,其在分析中区分变形前后的构形,考虑结构变形对平衡及运动的影响,是一种可以有效处理大变形问题的方法[3]。其采用斜率矢量代替传统有限元方法中的节点转角坐标,推导建立的多体系统微分代数方程具有常数惯量矩阵、不存在科氏力和离心力项等特点[4],能更精确高效地描述具有大变形特征的柔性多体系统,进一步结合海洋环境载荷相关理论构建的动力学模型,在海洋工程刚柔耦合多体系统的计算分析中将具有巨大的优势。
绝对节点坐标法的核心理论基础为连续介质力学与非线性大变形有限元理论,该方法由美国的Shabana[5]最先提出,并被应用于一维梁单元以及板单元的计算与分析中。Berzeri等[6]在一维梁模型的建模中分别采用了绝对节点坐标法与浮动坐标法,并对这2种方法的计算精度与效率进行了对比,发现绝对节点坐标法在分析柔性结构大变形问题时的精度较高,并且由于其避免坐标转换,也能兼顾计算效率。除此之外,Sugiyama等[7]、Ebel等[8]和Wang等[9]大量学者也开展了绝对节点坐标法的理论研究,促使其适用范围、方法优势等得到了持续的扩展与提升。
在海洋工程领域,马刚等[1]利用绝对节点坐标法在三维空间内描述了锚泊线的大转动和大拉伸变形特征,在静力分析中发现该方法具有较好计算精度和收敛性。Wang等[10]在研究流固耦合问题时引入绝对节点坐标法来推导结构的动力方程以更好地模拟其振动的非线性特征。尽管上述学者在海洋工程领域对绝对节点坐标法进行了初步探索,但目前还没有明确地提出适用于系泊线、立管等多种大变形深水柔性结构的ANCF力学模型。
因此,本文基于绝对节点坐标法,用斜率坐标代替传统的转角坐标,建立了当前构形与参考构形下的参量映射关系,基于连续介质力学推导得到柔性体单元的刚度矩阵,同时考虑单元的质量矩阵和结构所受的海洋环境载荷矩阵,并进行单元组装,得到了适用于深水立管和系泊线等柔性结构大弯曲及大拉伸变形的精确力学分析模型。利用Fortran语言编写计算程序,选取具有解析解的梁模型进行静力与动力程序验证,然后以深水缓波形钢悬链立管为例,对其进行了静力与动力分析,将绝对节点坐标法的理论优势延伸到海洋工程领域。
1 基于ANCF的力学分析模型 1.1 当前构形与参考构形的参量映射关系广泛应用于海洋工程中的柔性结构,如立管、系泊线等由于其自身的细长特性及海洋环境载荷的影响,往往表现出一定的大变形特征,此时小变形假设不再适用,必须区分变形前和变形后的位形,考虑当前构形和参考构形之间的关系。
1) 轴向应变。
设参考构形下微元的弧长为ds,当前构形下的弧长为
| $ \varepsilon = \frac{{{\rm{d}}\tilde s - {\rm{d}}s}}{{{\rm{d}}s}} = \frac{{\partial \tilde s}}{{\partial s}} - 1 $ | (1) |
将矢径r分别对当前构形和参考构形下的弧长求偏导,单位化处理后得到单位切向量:
| $ \tau = \frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial \tilde s}} = \frac{{\partial \mathit{\boldsymbol{r}}/\partial s}}{{\left| {\partial \mathit{\boldsymbol{r}}/\partial s} \right|}} = \frac{{{\mathit{\boldsymbol{r}}^\prime }}}{{\left| {{\mathit{\boldsymbol{r}}^\prime }} \right|}} $ | (2) |
式中
| $ \varepsilon = \left| {{\mathit{\boldsymbol{r}}^\prime }} \right| - 1 $ | (3) |
式(3)即为应变与绝对坐标系下位移的关系式,因为r′=∂r/∂s,即用参考构形下的弧长变量来表示r′,进而实现对非线性应变的参考构形参数化。
2) 物质点曲率。
柔性结构的弯曲变形是其力学分析中需要重点考虑的因素,物体弯曲程度以曲率来度量,定义为κ,其可表达为[5]:
| $ \kappa = \left| {{\mathit{\boldsymbol{r}}_{\tilde s\tilde s}}} \right| $ | (4) |
式中,
| $ {\mathit{\boldsymbol{r}}_{\tilde s\tilde s}}{\rm{ = }}\frac{{{\mathit{\boldsymbol{r}}_{ss}}}}{{{{\left| {{\mathit{\boldsymbol{r}}_s}} \right|}^2}}} + {\mathit{\boldsymbol{r}}_s}\frac{\partial }{{\partial \tilde s}}\left( {\frac{1}{{\left| {{\mathit{\boldsymbol{r}}_s}} \right|}}} \right) $ | (5) |
式中,rs和rss分别为矢径r对参考构形弧坐标的一阶、二阶偏导数。进一步可得:
| $ \begin{array}{*{20}{c}} {\kappa = \left| {{\mathit{\boldsymbol{r}}_{\tilde s\tilde s}}} \right| = \left| {\frac{{{\mathit{\boldsymbol{r}}_s}}}{{{{\left| {{\mathit{\boldsymbol{r}}_s}} \right|}^2}}} \times \left( {\frac{{{\mathit{\boldsymbol{r}}_{ss}}}}{{{{\left| {{\mathit{\boldsymbol{r}}_s}} \right|}^2}}} + {\mathit{\boldsymbol{r}}_s}\frac{\partial }{{\partial \tilde s}}\left( {\frac{1}{{\left| {{\mathit{\boldsymbol{r}}_s}} \right|}}} \right)} \right)} \right| = }\\ {\frac{{\left| {\mathit{\boldsymbol{r'}} \times \mathit{\boldsymbol{r''}}} \right|}}{{{{\left| {\mathit{\boldsymbol{r'}}} \right|}^3}}}} \end{array} $ | (6) |
κ为空间点曲率公式,与应变类似,也是参考构形下参量的表达式。
在绝对节点坐标法中,由于在当前构形和参考构形中同一物质点的斜率不同,需要引入物质点曲率Kκ,它表示该物质点由参考构形变为当前构形后其斜率对参考构形弧长的变化率,即[7]:
| $ {K_\kappa } = \frac{\partial }{{\partial s}}\left( {\frac{{\partial r}}{{\partial \tilde s}}} \right) = \left| {{\mathit{\boldsymbol{r}}_{\tilde s\tilde s}}} \right| \cdot \frac{{\partial s}}{{\partial \tilde s}} = \kappa \cdot \left| {\mathit{\boldsymbol{r'}}} \right| $ | (7) |
由连续介质力学中的虚功原理,对于连续体有[11]:
| $ \delta {W_i} = \delta {W_s} + \delta {W_e} $ | (8) |
式中:δWi为惯性力的虚功;δWs为由变形产生的弹性力虚功;δWe为物体所受外力的虚功。通过将该连续体的n个单元进行叠加可得到
| $ \sum\limits_{j = 1}^n {{{\left( {{\mathit{\boldsymbol{M}}^j}{{\mathit{\boldsymbol{\ddot q}}}^j} + \mathit{\boldsymbol{Q}}_s^j - \mathit{\boldsymbol{Q}}_e^j} \right)}^{\rm{T}}}} \delta {\mathit{\boldsymbol{q}}^j} = 0 $ | (9) |
式中:Mj、Qsi及Qei分别表示与第j个单元的总体坐标qj相关的质量矩阵、弹性力矩阵及外力矩阵。qj主要包含12个组成成分,分别为2个节点的三维位置向量和斜率向量。
通过引入布尔矩阵Bj来实现单元节点坐标和总体节点坐标之间的转换,有
| $ \mathit{\boldsymbol{M\ddot q}} + {\mathit{\boldsymbol{Q}}_s} - {\mathit{\boldsymbol{Q}}_e} = 0 $ | (10) |
进一步推导单元的刚度矩阵、质量矩阵及外载荷矩阵并通过有限元组装即可得到运动方程中的各组成部分[5]。
1.3 结构单元模型 1.3.1 刚度阵刚度阵在柔性体静力、动力分析中具有关键作用,而求解单元刚度阵则需要先得到单元弹性力。
根据变分原理可得单元所受弹性力为:
| $ \mathit{\boldsymbol{Q}}{_{s}^{j\rm{T}}} = \int\limits_0^L {EA\varepsilon \frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}}{\rm{d}}s} + \int\limits_0^L {EI{K_\kappa }\frac{{\partial {K_\kappa }}}{{\partial \mathit{\boldsymbol{q}}}}{\rm{d}}s} $ | (11) |
式中:L为单元长度;E为弹性模量;A为截面积;I为轴惯性矩。
将弹性力对q求偏导即得刚度阵的表达式:
| $ {\mathit{\boldsymbol{K}}^j} = \frac{\partial }{{\partial \mathit{\boldsymbol{q}}}}\left( {\int\limits_0^L {EA\varepsilon {{\left( {\frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}{\rm{d}}s} + \int\limits_0^L {EI{K_\kappa }{{\left( {\frac{{\partial {K_\kappa }}}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}{\rm{d}}s} } \right) $ | (12) |
首先考虑刚度阵的拉伸项K1j:
| $ \mathit{\boldsymbol{K}}_1^j = \int\limits_0^L {\left( {EA\frac{{\partial \mathit{\varepsilon }}}{{\partial \mathit{\boldsymbol{q}}}} \cdot {{\left( {\frac{{\partial \mathit{\varepsilon }}}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}} \right){\rm{d}}s} + \int\limits_0^L {\left( {EA\varepsilon \frac{\partial }{{\partial \mathit{\boldsymbol{q}}}}{{\left( {\frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}} \right){\rm{d}}s} $ | (13) |
考虑到
| $ \frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}} = \frac{\partial }{{\partial \mathit{\boldsymbol{q}}}}\left( {\sqrt {{{\mathit{\boldsymbol{r'}}}^{\rm{T}}}\mathit{\boldsymbol{r'}}} - 1} \right) = \frac{{{{\mathit{\boldsymbol{S'}}}^{\rm{T}}}\mathit{\boldsymbol{r'}}}}{{\sqrt {{{\mathit{\boldsymbol{r'}}}^{\rm{T}}}\mathit{\boldsymbol{r'}}} }} $ | (14) |
S为形函数,其对弧长的导数为S′,考虑到r′=S′q,在节点坐标q已知的情况下,即可得到r′。
接着推导ε对q的二次偏导:
| $ \frac{\partial }{{\partial \mathit{\boldsymbol{q}}}}{\left( {\frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}}} \right)^{\rm{T}}} = \frac{{{{\mathit{\boldsymbol{S'}}}^{\rm{T}}}\mathit{\boldsymbol{S'}}}}{{\sqrt {{{\mathit{\boldsymbol{r'}}}^{\rm{T}}}\mathit{\boldsymbol{r'}}} }} - \frac{1}{{\sqrt {{{\mathit{\boldsymbol{r'}}}^{\rm{T}}}\mathit{\boldsymbol{r'}}} }} \cdot \frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}} \cdot {\left( {\frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}}} \right)^{\rm{T}}} $ | (15) |
进一步可得K1j为:
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_1^j = = \int\limits_0^L {\left( {EA\frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}} \cdot {{\left( {\frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}} \right){\rm{d}}s} + }\\ {\int\limits_0^L {\left( {EA\left( {1 - \frac{1}{{\sqrt {{{\mathit{\boldsymbol{r'}}}^{\rm{T}}}\mathit{\boldsymbol{r'}}} }}} \right)\left( {{{\mathit{\boldsymbol{S'}}}^{\rm{T}}}\mathit{\boldsymbol{S'}} - \frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}} \cdot {{\left( {\frac{{\partial \varepsilon }}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}} \right)} \right){\rm{d}}s} } \end{array} $ | (16) |
接着考虑刚度阵的弯曲曲率项K2j,类似地:
| $ \mathit{\boldsymbol{K}}_2^j = \int\limits_0^L {\left( {EI\frac{{\partial {K_\kappa }}}{{\partial \mathit{\boldsymbol{q}}}} \cdot {{\left( {\frac{{\partial {K_\kappa }}}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}} \right){\rm{d}}s} + \int\limits_0^L {\left( {EI{K_\kappa }\frac{\partial }{{\partial \mathit{\boldsymbol{q}}}}{{\left( {\frac{{\partial {K_\kappa }}}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}}} \right){\rm{d}}s} $ | (17) |
推导Kκ对q的一次和二次偏导数是得到K2j的关键,定义单位向量τ3=(r′×r″)/|r′×r|″,可得:
| $ \frac{{\partial {K_\kappa }}}{{\partial \mathit{\boldsymbol{q}}}} = \frac{\partial }{{\partial \mathit{\boldsymbol{q}}}}\left( {\frac{{\left| {\mathit{\boldsymbol{r'}} \times \mathit{\boldsymbol{r''}}} \right|}}{{{{\left| {\mathit{\boldsymbol{r'}}} \right|}^2}}}} \right) = \frac{\partial }{{\partial \mathit{\boldsymbol{q}}}}\left( {\frac{{{{\left( {\mathit{\boldsymbol{r'}} \times \mathit{\boldsymbol{r''}}} \right)}^{\rm{T}}} \cdot {\mathit{\boldsymbol{\tau }}_3}}}{{{{\left| {\mathit{\boldsymbol{r'}}} \right|}^2}}}} \right) $ | (18) |
q为绝对节点坐标,对q的12个元素分别单独求导处理,则:
| $ \begin{array}{*{20}{c}} {\frac{{\partial {K_\kappa }}}{{\partial {q_i}}} = \frac{1}{{{{\left| {\mathit{\boldsymbol{r'}}} \right|}^4}}}\left[ {{{\left| {\mathit{\boldsymbol{r'}}} \right|}^2}\left( {\mathit{\boldsymbol{S}}_i^\prime \times {\mathit{\boldsymbol{r}}^{\prime \prime }} + {\mathit{\boldsymbol{r}}^\prime } \times \mathit{\boldsymbol{S}}_i^{\prime \prime }} \right) - } \right.}\\ {{{\left. {2\left( {{\mathit{\boldsymbol{r}}^{\prime {\rm{T}}}}\mathit{\boldsymbol{S}}_i^\prime } \right)\left( {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right)} \right]}^{\rm{T}}}{\mathit{\boldsymbol{\tau }}_3}} \end{array} $ | (19) |
对于Kκ对q的二次偏导数,同样对q的12个元素单独求导,可得:
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial {q_j}}}\left( {\frac{{\partial {K_\kappa }}}{{\partial {q_i}}}} \right) = \frac{\partial }{{\partial {q_j}}}\left\{ {\frac{{\left[ {{{\left( {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_i^\prime \times {\mathit{\boldsymbol{r}}^{\prime \prime }} + {\mathit{\boldsymbol{r}}^\prime } \times \mathit{\boldsymbol{S}}_i^{\prime \prime }} \right)} \right]}}{{{{\left| {{\mathit{\boldsymbol{r}}^\prime }} \right|}^2} \cdot \left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right|}}} \right\} - }\\ {2 \cdot \frac{\partial }{{\partial {q_j}}}\left\{ {\frac{{\left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right|\left( {{\mathit{\boldsymbol{r}}^{\prime {\rm{T}}}}\mathit{\boldsymbol{S}}_i^\prime } \right)}}{{{{\left| {{\mathit{\boldsymbol{r}}^\prime }} \right|}^4}}}} \right\}} \end{array} $ | (20) |
设置求导辅助函数为:
| $ \frac{\partial }{{\partial {q_j}}}\frac{m}{n} = \frac{1}{{{n^2}}}\left( {\frac{{\partial m}}{{\partial {q_j}}}n - m\frac{{\partial n}}{{\partial {q_j}}}} \right) $ | (21) |
对式(20)中的右侧两式的分子分母分别求导:
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial {q_j}}}{{\left( {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_i^\prime \times {\mathit{\boldsymbol{r}}^{\prime \prime }} + {\mathit{\boldsymbol{r}}^\prime } \times \mathit{\boldsymbol{S}}_i^{\prime \prime }} \right) = }\\ {{{\left( {\mathit{\boldsymbol{S}}_j^\prime \times {\mathit{\boldsymbol{r}}^{\prime \prime }} + {\mathit{\boldsymbol{r}}^\prime } \times \mathit{\boldsymbol{S}}_j^{\prime \prime }} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_i^\prime \times {\mathit{\boldsymbol{r}}^{\prime \prime }} + {\mathit{\boldsymbol{r}}^\prime } \times \mathit{\boldsymbol{S}}_i^{\prime \prime }} \right) + }\\ {{{\left( {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_i^\prime \times \mathit{\boldsymbol{S}}_j^{\prime \prime } + \mathit{\boldsymbol{S}}_j^\prime \times \mathit{\boldsymbol{S}}_i^{\prime \prime }} \right)}\\ {\frac{\partial }{{\partial {q_j}}}{{\left| {{\mathit{\boldsymbol{r}}^\prime }} \right|}^2} \cdot \left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right| = 2\left( {{\mathit{\boldsymbol{r}}^{\prime {\rm{T}}}}\mathit{\boldsymbol{S}}_j^\prime } \right)\left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right| + }\\ {\frac{{{{\left| {{\mathit{\boldsymbol{r}}^\prime }} \right|}^2}}}{{\left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right|}}\left[ {{{\left( {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_j^\prime \times {\mathit{\boldsymbol{r}}^{\prime \prime }} + {\mathit{\boldsymbol{r}}^\prime } \times \mathit{\boldsymbol{S}}_j^{\prime \prime }} \right)} \right]}\\ {\frac{\partial }{{\partial {q_j}}}\left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right|\left( {{\mathit{\boldsymbol{r}}^{\prime {\rm{T}}}}\mathit{\boldsymbol{S}}_i^\prime } \right) = \left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right|\left( {\mathit{\boldsymbol{S}}_j^{\prime {\rm{T}}}\mathit{\boldsymbol{S}}_i^\prime } \right) + }\\ {\frac{{{{\left( {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{S}}_j^\prime \times {\mathit{\boldsymbol{r}}^{\prime \prime }} + {\mathit{\boldsymbol{r}}^\prime } \times \mathit{\boldsymbol{S}}_j^{\prime \prime }} \right)}}{{\left| {{\mathit{\boldsymbol{r}}^\prime } \times {\mathit{\boldsymbol{r}}^{\prime \prime }}} \right|}}\left( {{\mathit{\boldsymbol{r}}^{\prime {\rm{T}}}}\mathit{\boldsymbol{S}}_i^\prime } \right)}\\ {\frac{{\partial {{\left| {{\mathit{\boldsymbol{r}}^\prime }} \right|}^4}}}{{\partial {q_j}}} = 4{{\left| {{\mathit{\boldsymbol{r}}^\prime }} \right|}^2}\left( {{\mathit{\boldsymbol{r}}^{\prime {\rm{T}}}}\mathit{\boldsymbol{S}}_j^\prime } \right)} \end{array} $ | (22) |
将式(20)按照式(21)形式处理,并代入式(22a)至(22d)即得曲率Kκ对q的二阶导数表达式,再结合Kκ对q的一阶导数,代入到式(17)即得单元刚度阵弯曲曲率项K2j。
刚度阵轴向拉伸项K1j和弯曲曲率项K2j的积分采用数值计算中的五点高斯-勒让德求积公式进行求解,再将二者相加即得完整的单元刚度阵。
1.3.2 质量阵与外载荷矩阵连续介质力学中,选取一个单元j为研究对象,则质量阵为:
| $ {\mathit{\boldsymbol{M}}^j} = \int\limits_V {\rho {\mathit{\boldsymbol{S}}^{\rm{T}}}\mathit{\boldsymbol{S}}{\rm{d}}V} $ | (23) |
式中:ρ为单元质量密度;S为形函数;V为单元体积。
本文采用两点三次Hermite插值多项式作为形函数S,单元密度为常值,同时假设截面面积保持不变。因此,单元质量阵Mj为常值矩阵,有利于提高计算程序的分析效率。
对于立管、系泊线等细长柔性结构,在静力分析中,主要考虑重力和浮力[13];在动力分析中,还要考虑多种动力载荷,但由于本文主要针对立管的总体动力响应进行分析,并未考虑其涡激振动,因此主要计算流体拖曳力和附加质量力载荷。
外力Qej的表达式为:
| $ \mathit{\boldsymbol{Q}}_e^j = \int\limits_0^L {{{\left( {\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial \mathit{\boldsymbol{q}}}}} \right)}^{\rm{T}}} \cdot \boldsymbol{f}{\rm{d}}s} = \int\limits_0^L {{\mathit{\boldsymbol{S}}^{\rm{T}}} \cdot \mathit{\boldsymbol{f}}{\rm{d}}s} $ | (24) |
静力计算中,外载荷只有重力和浮力,则:
| $ \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{f}}_g} + {\mathit{\boldsymbol{f}}_b} $ | (25) |
式中fg、fb分别为单元重力和浮力。
而在动力计算中,流体拖曳力和附加质量力也需要被计入外载荷中,则:
| $ \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{f}}_g} + {\mathit{\boldsymbol{f}}_b} + {\mathit{\boldsymbol{f}}_d} + {\mathit{\boldsymbol{f}}_a} $ | (26) |
式中fd、fa分别为单元所受流体拖曳力和附加质量力,可采用式(27-28)计算:
| $ {\mathit{\boldsymbol{f}}_d} = \frac{1}{2}{\rho _s}{C_d}D\mathit{\boldsymbol{N}}\left( {{\mathit{\boldsymbol{v}}_s} - \mathit{\boldsymbol{\dot r}}} \right)\left| {\mathit{\boldsymbol{N}}\left( {{\mathit{\boldsymbol{v}}_s} - \mathit{\boldsymbol{\dot r}}} \right)} \right| $ | (27) |
| $ {\mathit{\boldsymbol{f}}_a} = {\rho _s}{A_o}{C_m}\mathit{\boldsymbol{N}}\left( {{{\mathit{\boldsymbol{\dot v}}}_s} - \mathit{\boldsymbol{\ddot r}}} \right) - {\rho _i}{A_i}\mathit{\boldsymbol{N\ddot r}} $ | (28) |
式中,Cd和Cm分别为阻力系数和附加质量系数;D为水动力直径;vs和
由1.2节可知,布尔矩阵可以实现单元矩阵与结构总体矩阵的转换。这里以刚度阵为例,基于布尔矩阵转换的原理,对其进行组装。首先将单元刚度矩阵分成4个子模块,每个模块是6×6的矩阵:
| $ {\mathit{\boldsymbol{K}}^j} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_{j\;\;j}^j}&{\mathit{\boldsymbol{K}}_{j\;\;\;j + 1}^j}\\ {\mathit{\boldsymbol{K}}_{j + 1\;\;\;j}^j}&{\mathit{\boldsymbol{K}}_{j + 1\;\;\;j + 1}^j} \end{array}} \right] $ | (29) |
单元间通过共同节点来连接,相邻单元的刚度阵在其共同节点处叠加。对于n个单元,其叠加方式如下:
| $ \mathit{\boldsymbol{K}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{K}}_{11}^1}&{\mathit{\boldsymbol{K}}_{12}^1}&0&0&0\\ {\mathit{\boldsymbol{K}}_{12}^1}&{\mathit{\boldsymbol{K}}_{22}^1 + \mathit{\boldsymbol{K}}_{22}^2}& \ddots & \vdots & \vdots \\ 0&{\mathit{\boldsymbol{K}}_{32}^2}& \ddots & \ddots &0\\ \vdots & \vdots & \ddots &{\mathit{\boldsymbol{K}}_n^{n - 1} + \mathit{\boldsymbol{K}}_n^n}&{\mathit{\boldsymbol{K}}_{n\;\;\;n + 1}^n}\\ 0&0&0&{\mathit{\boldsymbol{K}}_{n + 1\;\;\;\;n}^n}&{\mathit{\boldsymbol{K}}_{n + 1\;\;\;n + 1}^{n + 1}} \end{array}} \right] $ | (30) |
由式(30)可知,结构总体刚度矩阵是(6n+6)×(6n+6)的三对角稀疏矩阵,类似,质量矩阵也可由此方法组装得到。
对于立管、系泊线等海洋工程柔性结构,其边界条件主要为结构端部的连接问题。通过在端部约束节点运动的自由度来实现边界条件的控制,铰接边界即为位移为零;如果端部与浮体相连,即为动态边界,可以通过在时域计算过程中改变边界节点的位置坐标来实现[14]。
本文的静力平衡方程通过牛顿-拉斐逊法求解,对于动力平衡方程通过Newmark法进行求解。
2 静力与动力算例验证 2.1 大弯曲柔性梁静力验证选取大弯曲柔性梁算例进行静力程序验证,该算例中梁的弯曲变形较大,可以用来验证本文模型在处理大变形几何非线性的有效性和准确性。
弹性卷曲梁的一端用刚性固定,另一端无约束,在该端点处施加弯矩载荷M,则存在以下的平衡关系:
| $ M = \lambda \cdot \frac{{{\rm{ \mathsf{ π} }}EI}}{L} $ | (31) |
式中:L为卷曲梁的长度;EI为抗弯刚度;λ为卷曲系数,且λ∈[0, 2]。
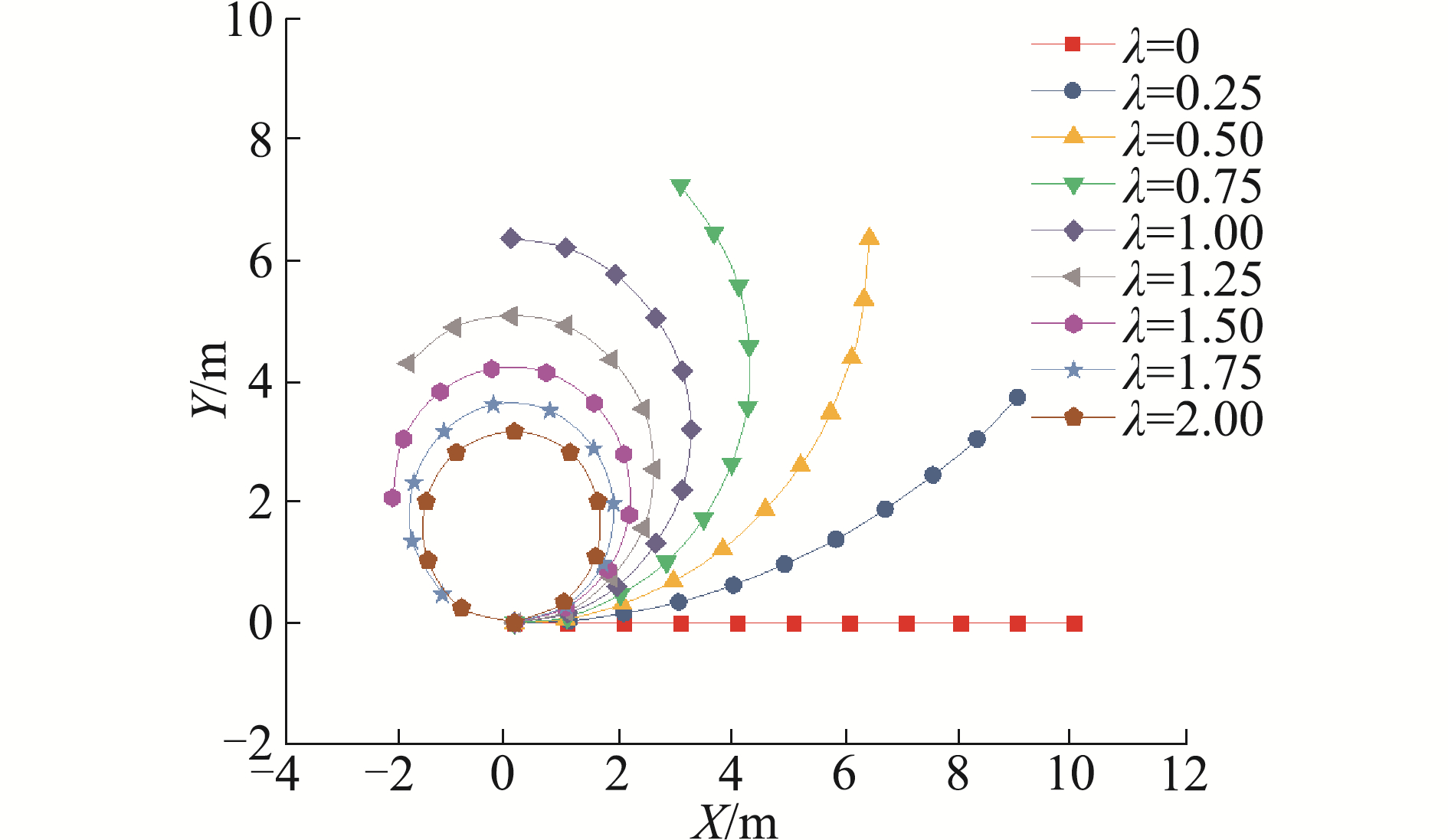
本节算例中各项参数为:长度L=10 m;抗弯刚度EI=2.514×104 N·m2;抗拉刚度EA=2.514×108 N;λ取值以0.25为间隔从0~2选取9组;模型均匀划分为10个单元,计算结果如图 1所示。
|
Download:
|
| 图 1 卷曲梁构型 Fig. 1 Configuration diagram of the curled beam | |
根据图 1可知,当λ=2.0时,整个梁曲线成圆形;当λ=1.0时梁弯曲曲线整体形状为半圆形;当λ为其他不同值时,梁曲线形状也对应为不同的圆弧,与理论一致。
另外,选取柔性梁的第6个节点(即中点)为例,对λ=0.5,1.0,2.0时该位置处的坐标XY理论值和计算值进行对比,具体见表 1,需要说明的是,该节点坐标的理论值是根据圆的简单几何特征计算得到的。通过对比可知,在该10个单元的情况下,计算值和理论值的最大误差保持在1.22%,由此可知本文ANCF模型能够应用于结构大变形的静力计算,并且具有较好的计算精度。
| 表 1 坐标的计算值和理论值 Table 1 The calculated and theoretical values of coordinates |
以动态载荷作用下地单位长度悬臂梁算例来验证本文动力计算方法和程序的正确性。
悬臂梁的参数为:EI=3.194 1 N·m2;单位长度的质量ρA=1.0 kg/m;梁的一阶固有频率为ω=3.516
结构左端固定,在右端加载动态载荷:
| $ \begin{array}{l} P\left( t \right) = EI \cdot \sin \left( {{\rm{ \mathsf{ π} }}t/T} \right),\;\;\;\;0 \le t \le T\\ P\left( t \right) = 0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;t \ge T \end{array} $ | (32) |
右端位移随时间的解析表达式为[12]:
| $ \begin{array}{*{20}{c}} {v\left( t \right) = 0.441\sin \left( {{\rm{ \mathsf{ π} }}t/T} \right) - 0.216\sin \left( {{\rm{2 \mathsf{ π} }}t/T} \right)}\\ {0 \le t \le T}\\ {v\left( t \right) = - 0.432\sin 6.284\left( {t - T} \right),\;\;\;\;t \ge T} \end{array} $ | (33) |
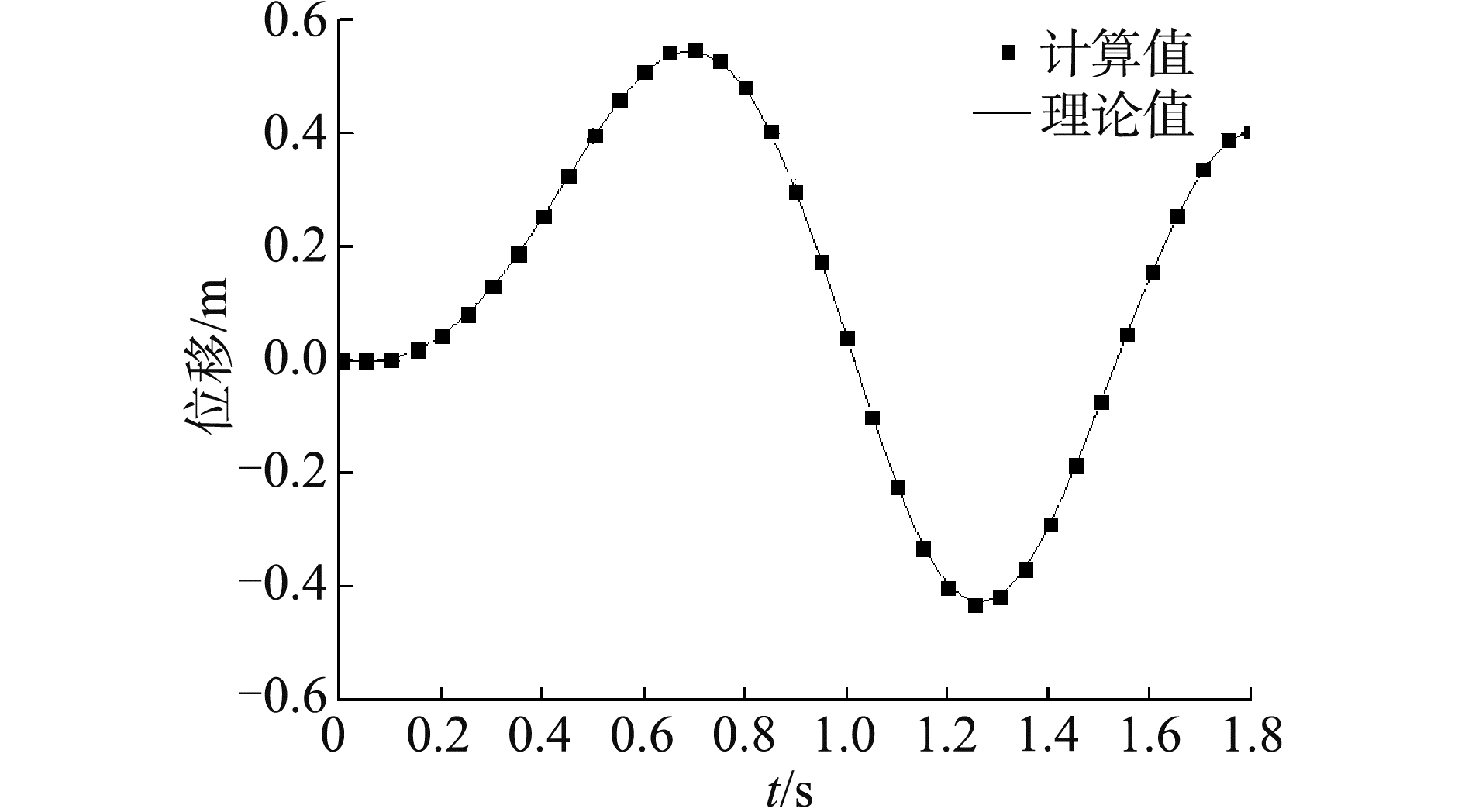
悬臂梁模型单元数量为10,计算时间设为1.8 s,时间步长设为0.05 s,对梁右端位移进行观测,结果如图 2所示。
|
Download:
|
| 图 2 动载荷悬臂梁右端位移对比结果 Fig. 2 Comparison of the right end displacements of the dynamic cantilever beam | |
通过计算值与理论值的对比可以发现2种结果吻合程度非常高,验证了动力程序的正确性。
3 缓波形立管静力与动力分析以深水缓波形钢悬链立管为例,应用本文建立的ANCF动力学模型,对该立管进行静力与动力计算分析。
3.1 立管参数以某1 500 m深水缓波形钢悬链立管作为分析对象,其相关参数如表 2所示。
| 表 2 深水缓波形钢悬链立管参数 Table 2 Parameters of the steel lazy wave catenary riser |
将算例中的立管离散成等长的54个单元,裸管段的单元为钢材,其刚度、密度等属性完全相同,具有浮力材部分的管段单元属性发生变化,具体通过表 2的参数计算得到。
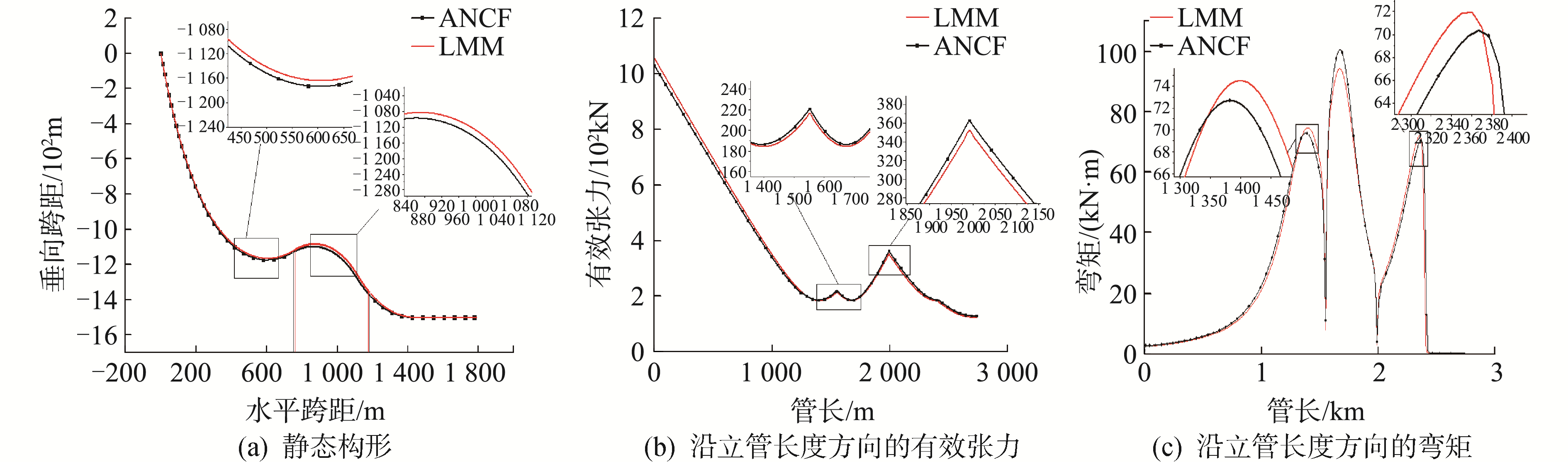
图 3(a)为本文模型与传统集中质量法(LMM)模型计算得到的立管构形曲线。可以发现2种方法计算得到的静态构形基本保持一致,但由于本文ANCF模型考虑了立管大变形所产生的几何非线性,使得立管一些关键位置坐标存在一定差异,垂向最大差别接近10 m,这将对立管的力学性能产生一定影响。
|
Download:
|
| 图 3 立管静态特性对比曲线 Fig. 3 Comparison of the static characteristics of the riser | |
图 3(b)和(c)分别给出了2种模型计算得到的沿立管长度方向的有效张力和弯矩曲线。可以发现,2种模型计算得到的有效张力总体趋势一致,在具体数值方面的误差基本保持在1.2%以内,立管内部有效张力分布为顶端最大,平躺段最小,浮力材位置存在局部极大值,总体分布情况类似W形。另外,2种方法的弯矩变化趋势也保持一致,沿立管长度方向上有3个峰值,对应立管曲率最大的3个位置,但几何非线性的影响使得2种方法在3个峰值处的区别较大,最大误差达到6.38%,表明本文模型在合理可靠的基础上具有很好的适用性,可以进一步用于深水柔性结构的动力特性分析。
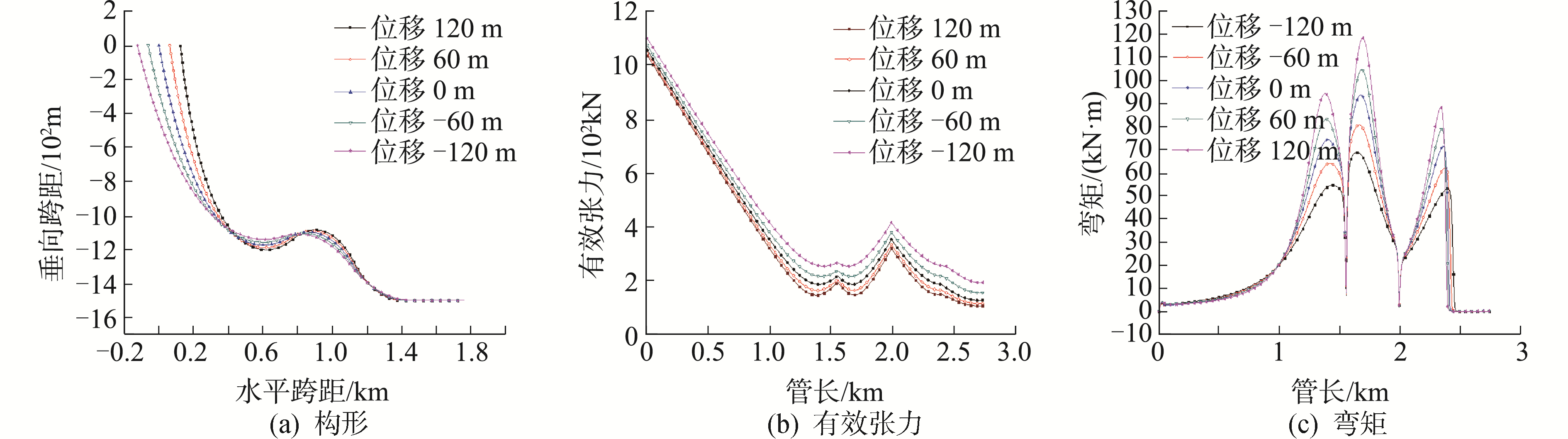
3.3 动力特性分析 3.3.1 匀速漂移分析首先进行立管顶部的匀速漂移分析,选取X方向为例,在计算中对顶部节点施加强迫位移:X=-0.1 t,初始位置位于X=120 m处,初始运动方向为远离触底点的方向,计算时间为2 400 s,步长为0.1 s,给出0、600、1 200、1 800、2 400 s时刻的动力平衡结果,如图 4所示。
|
Download:
|
| 图 4 不同时刻下的匀速漂移计算结果 Fig. 4 Calculation results of uniform drift at different time | |
由图 4(a)可知,随着漂移量的变化,立管形态发生了一定变化,但总体趋势与静力分析中保持一致。对于图 4(b),可以发现立管X负方向漂移的有效张力整体要大于X正方向;随着X漂移量的由120 m向-120 m变化,立管整体有效张力逐渐增大,主要由于立管的拉伸变形不断加大导致内部张力不断增大。对于图 4(c),随着X漂移量的变化,由于立管顶部在不断地远离触地点,立管总体形状得到舒展,弯曲变形由此减小,进而使得弯矩曲线的峰值有所减小,并且最大弯矩所对应的立管位置发生变化。总体来说,缓波形立管顶端节点受迫做慢漂运动过程中,有效张力和弯矩随漂移量的变化关系相反,并且立管形态、有效张力及弯矩沿管长分布趋势与静力分析一致,进一步验证了本文ANCF模型的正确性。
3.3.2 简谐运动分析对立管顶端节点施加水平X方向的正弦运动,周期为62.8 s,振幅为25 m,激励公式见式(34),分析时间为300 s,步长为0.1 s。每个时间步长内计算得到的顶端张力结果如图 5(a)所示。

|
Download:
|
| 图 5 立管顶端有效张力时历曲线 Fig. 5 The time-domain curves about the effective tension of top point of the riser | |
| $ r\left( {x,y,z,t} \right) = \left( {A\sin \omega t,0,0} \right) $ | (34) |
其中x、y、z为顶部节点的位置坐标;A为激励幅值;ω为激励频率。
可以发现,在经历初始的计算不稳定段之后,张力曲线以相对比较规则的正弦形式变化,并且周期与激励周期保持一致,对该段时间结果进行统计,得出最大值为1 074.41 kN,最小值为1 046.13 kN,平均值为1 060.27 kN。但也发现在一个周期内的曲线形状并非严格的正弦形状,这主要是由于远离触地端和接近触地端的立管运动和受力是非对称的。
对强迫运动的幅值参数进行敏感性分析,仍以总体坐标下X轴方向为例,顶端节点正弦激励周期为30 s,幅值为变值,取为5、10、15、20、30、40、50 m,计算时间为300 s,步长为0.1 s。
图 5(b)给出了同周期不同运动幅度下顶端节点有效张力时历曲线,可以发现,在相同周期下,随着幅值的增加,其有效张力幅值不断增大。并且激励幅值为5 m~20 m时,顶端张力变化规律为相对规则的正弦形式;幅值增加到30 m~50 m时,则由规则正弦转换到了“双正弦”形式,可能的原因为,当激励周期一定,激励振幅的增加会使得立管顶部运动速度和加速度增加,由于深水立管细长特性,顶部的速度增加并不能及时地在下部有所体现,而是会产生一定的迟滞效应,影响顶端张力的变化规律。
进一步分析激励周期对顶端张力的影响,激励运动方向保持不变,激励振幅为25 m,周期分别选为20、40和80 s,给出不同周期下顶端节点的有效张力值,如图 5(c)所示。
可以发现“双正弦”变化形式在T=20 s时出现,但随着周期增大,T=40 s和80 s时该变化形式消失。可能的原因与激励幅值部分一致,激励周期的减小使得顶部运动速度和加速度较大,结构的迟滞效应促使了“双正弦”变化规律的出现。
4 结论1) 本文提出的柔性结构大变形力学模型通过斜率代替转角坐标,克服了原先复杂的大变形问题描述过程,省去了单元局部和全局坐标之间的转换,并且其以当前构形形成微元非线性几何关系的描述方法可以准确地描述柔性结构的几何非线性。通过大弯曲柔性梁和动载荷悬臂梁的算例验证发现,基于绝对节点坐标法的力学分析模型可以有效地用于解决大变形柔性结构静力与动力分析问题。
2) 基于大变形柔性结构力学模型计算得到的深水缓波形钢悬链立管静力特性结果与集中质量法的计算结果在总体趋势上保持一致,但在立管的弯曲构型、有效张力和弯矩具体数值上存在一些差异,这在弯矩结果中尤为明显,表明大变形非线性因素对弯矩的影响最大。总体上认为本文建立的力学模型在合理可靠的基础上具有很好的适用性,可以进一步用于深水柔性结构的动力特性分析。
3) 在缓波形立管顶端节点匀速漂移分析中,有效张力和弯矩随漂移量的变化关系相反,并且立管形态、有效张力及弯矩沿管长分布趋势与静力分析一致,进一步验证了本文ANCF模型的正确性。在多种激励幅值和频率下的简谐运动分析中,本文计算结果符合缓波形钢悬链立管运动规律,在之后的研究中有必要开展进一步的计算效率与计算精度评估。
| [1] |
马刚, 孙丽萍. 基于总体坐标法的大变形锚泊线的静力分析[J]. 哈尔滨工程大学学报, 2014, 35(6): 674-678. MA Gang, SUN Liping. Static analysis of the mooring line under large deformation by utilizing the global coordinate method[J]. Journal of Harbin Engineering University, 2014, 35(6): 674-678. (  0) 0)
|
| [2] |
KANG Zhuang, ZHANG Cheng, MA Gang, et al. A numerical investigation of two-degree-of-freedom VIV of a circular cylinder using the modified turbulence model[J]. Ocean engineering, 2018, 155: 211-226. DOI:10.1016/j.oceaneng.2018.02.051 (  0) 0)
|
| [3] |
WANG Zhe, TIAN Qiang, HU Haiyan. Dynamics of spatial rigid-flexible multibody systems with uncertain interval parameters[J]. Nonlinear dynamics, 2016, 84(2): 527-548. DOI:10.1007/s11071-015-2504-4 (  0) 0)
|
| [4] |
SERESHK M V, SALIMI M. Comparison of finite element method based on nodal displacement and absolute nodal coordinate formulation (ANCF) in thin shell analysis[J]. International journal for numerical methods in biomedical engineering, 2011, 27(8): 1185-1198. DOI:10.1002/cnm.1348 (  0) 0)
|
| [5] |
SHABANA A A. Definition of the slopes and the finite element absolute nodal coordinate formulation[J]. Multibody system dynamics, 1997, 1(3): 339-348. DOI:10.1023/A:1009740800463 (  0) 0)
|
| [6] |
BERZERI M, CAMPANELLI M, SHABANA A A. Definition of the elastic forces in the finite-element absolute nodal coordinate formulation and the floating frame of reference formulation[J]. Multibody system dynamics, 2001, 5(1): 21-54. DOI:10.1023/A:1026465001946 (  0) 0)
|
| [7] |
SUGIYAMA H, KOYAMA H, YAMASHITA H. Gradient deficient curved beam element using the absolute nodal coordinate formulation[J]. Journal of computational and nonlinear dynamics, 2010, 5(2): 021001. DOI:10.1115/1.4000793 (  0) 0)
|
| [8] |
EBEL H, MATIKAINEN M K, HURSKAINEN V V, et al. Higher-order beam elements based on the absolute nodal coordinate formulation for three-dimensional elasticity[J]. Nonlinear dynamics, 2017, 88(2): 1075-1091. DOI:10.1007/s11071-016-3296-x (  0) 0)
|
| [9] |
WANG Zhe, TIAN Qiang, HU Haiyan. Dynamics of spatial rigid-flexible multibody systems with uncertain interval parameters[J]. Nonlinear dynamics, 2016, 84(2): 527-548. DOI:10.1007/s11071-015-2504-4 (  0) 0)
|
| [10] |
WANG Li, CURRAO, HAN Feng, et al. An immersed boundary method for fluid-structure interaction with compressible multiphase flows[J]. Journal of computational physics, 2017, 346: 131-151. DOI:10.1016/j.jcp.2017.06.008 (  0) 0)
|
| [11] |
SHABANA A A. Computational continuum mechanics[M]. New York: Cambridge University Press, 2008.
(  0) 0)
|
| [12] |
WARBURTON G B. The dynamical behaviour of structures[M]. 2nd ed. Oxford: Pergamon Press, 1976.
(  0) 0)
|
| [13] |
KANG Zhuang, ZHANG Cheng, SUN Liping. Research on truncation method of FPSO and offloading system in model test[J]. Applied ocean research, 2017, 67: 94-108. DOI:10.1016/j.apor.2017.06.007 (  0) 0)
|
| [14] |
康庄, 张橙. 雷诺数对圆柱体涡激振动特性影响研究[J]. 华中科技大学学报(自然科学版), 2017, 45(11): 74-79. KANG Zhuang, ZHANG Cheng. Impact of Reynolds number on vortex-induced vibration performance of cylinder[J]. Journal of Huazhong University of Science & Technology (Nature Science Edition), 2017, 45(11): 74-79. (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


