在船舶的各种性能中(如浮性、稳性、抗沉性、耐波性、操纵性等),船舶快速性占有十分重要的地位[1]。船舶阻力的计算方法是研究船舶在各类航行条件下的快速性的基础。按照不同的分类标准,船舶阻力有不同的分类方式,若按船舶航行过程中船体周围的流动现象和产生阻力的原因来分,船体总阻力可以分为兴波阻力、摩擦阻力和粘压阻力3部分。兴波阻力对航速以及船型变化比较敏感,因此,一般选择减小兴波阻力来降低船舶阻力。而主要受船舶湿表面面积影响的粘性阻力,可采用经验公式估算和计算流体力学(computational fluid dynamics, CFD)方法直接模拟。在兴波阻力的研究中,理论研究、水池试验和数值计算的方法相辅相成,是船舶阻力研究的核心问题[2]。应用势流理论求解兴波阻力问题时,普遍采用的是边界元方法,一般采用的常值面元法在求解水动力问题时,分为分布源法及源偶混合分布法2种方法[3]。分布源方法在求解流场的速度方面比较方便,而源偶混合分布方法能够准确的给出流场的速度势。2种方法互有优缺。在处理非光滑边界时,常值面元法计算精度低,高阶边界元方法又需要处理复杂的高阶奇异积分。calisal等[4]提出了一个适应非线性自由表面条件的基于控制分析方法,为更好的解决上述问题,段文洋[5]提出了泰勒展开边界元方法(Taylor expansion boundary element method,TEBEM),并应用于二维问题中,得到较好的结果。陈纪康[6]将该方法引入到三维问题的计算上,提出了三维泰勒展开边界元方法,对数值精度进行了验证,能够满足工程需求。另外利用分布源方法预报船舶定常兴波问题时需要将自由面配置点前移,移动距离对数值结果会产生影响。文献[7-8]研究了在自由面上采用叠加模流线进行的网格划分,并对wigley三体船进行试验及数值模拟。本文将泰勒展开边界元方法应用于船舶兴波阻力的计算中,无需自由面配置点前置,避免其对数值结果的影响。分别计算了不同船型的行波阻力与波形,并与其他计算结果进行对比分析。
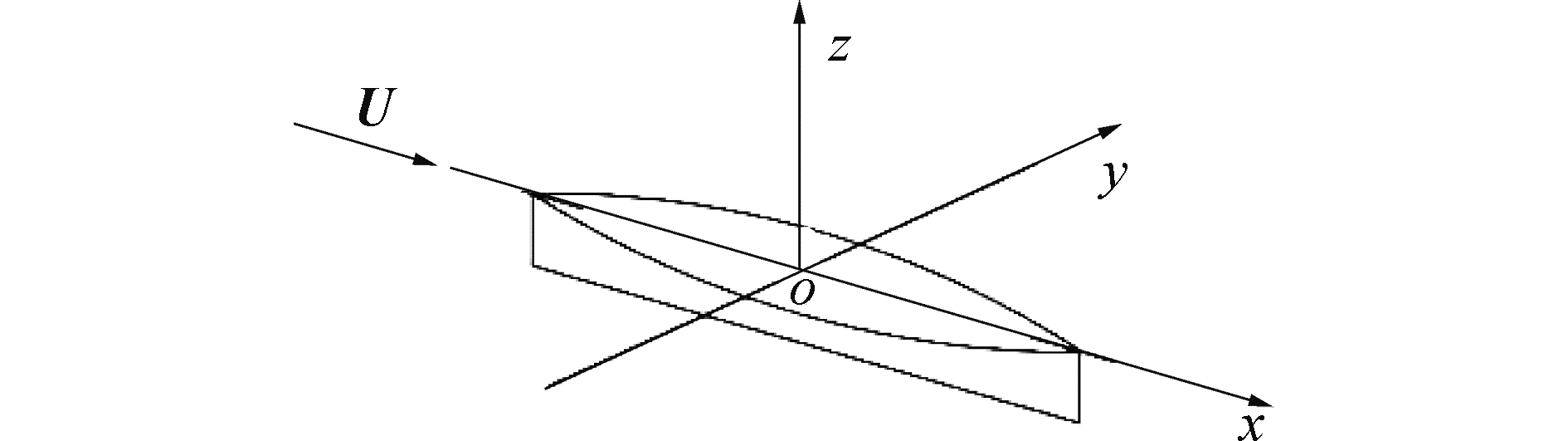
1 兴波阻力数值模型 1.1 定常兴波的定解问题如图 1所示,考虑船舶以匀速U沿x轴的正向运动。
|
Download:
|
| 图 1 坐标系 Fig. 1 Coordinates | |
假定流动无粘、无旋。总速度势ϕ满足以下控制方程和定解条件:
1) 拉普拉斯方程:
| $ \nabla^{2} \phi=0 $ | (1) |
2) 物面条件:
| $ \nabla \phi \cdot \boldsymbol{n}=0 $ | (2) |
式中:n=nxi+nyj+nzk表示船体表面法向量,正方向指向物体内部。
3) 自由面条件:在自由面z=ζ(x, y)上,满足自由表面条件为:
| $ \frac{1}{2} \phi_{x}(\nabla \phi)_{x}^{2}+\frac{1}{2} \phi_{y}(\nabla \phi)_{y}^{2}+g \phi_{z}=0 $ | (3) |
4) 辐射条件:船体远前方无波。
总速度势ϕ可分解为来流速度势、叠模势Φ和考虑自由面影响的扰动势φ,即
| $ \phi=-U x+\mathit{\Phi}+\varphi $ | (4) |
叠模势满足的定解问题如下所示:
| $ \left\{\begin{array}{l}{\nabla^{2} \mathit{\Phi}=0} \\ {\frac{\partial \mathit{\Phi}}{\partial n}=U n_{x}} \\ {\frac{\partial \mathit{\Phi}}{\partial z}=0, \quad z=0} \\ {\mathit{\Phi}=0, \sqrt{x^{2}+y^{2}+z^{2}} \rightarrow \infty}\end{array}\right. $ | (5) |
假定定常兴波扰动势φ相对叠模势Φ是高阶小量,在式(3)中,忽略φ的非线性项,可得关于兴波扰动势的线性自由面条件:
| $ \begin{array}{l}{\frac{1}{2} \mathit{\Phi}_{x}\left(\mathit{\Phi}_{x}^{2}+\mathit{\Phi}_{y}^{2}\right)_{x}+\frac{1}{2} \mathit{\Phi}_{y}\left(\mathit{\Phi}_{x}^{2}+\mathit{\Phi}_{y}^{2}\right)_{y}+} \\ {\mathit{\Phi}_{x}\left(\mathit{\Phi}_{x} \varphi_{x}+\mathit{\Phi}_{y} \varphi_{y}\right)_{x}+\mathit{\Phi}_{y}\left(\mathit{\Phi}_{x} \varphi_{x}+\mathit{\Phi}_{y} \varphi_{y}\right)_{y}+} \\ {\frac{1}{2} \varphi_{x}\left(\mathit{\Phi}_{x}^{2}+\mathit{\Phi}_{y}^{2}\right)_{x}+\frac{1}{2} \varphi_{y}\left(\mathit{\Phi}_{x}^{2}+\mathit{\Phi}_{y}^{2}\right)_{y}+g \varphi_{z}=0}\end{array} $ | (6) |
因此对于定常兴波扰动势φ,其定解问题为:
| $ \left\{\begin{array}{l}{\nabla^{2} \varphi=0} \\ {\frac{\partial \varphi}{\partial n}=0} \\ {\varphi=0, \sqrt{x^{2}+y^{2}+z^{2}} \rightarrow \infty}\end{array}\right. $ | (7) |
其中线性自由面如式(6)所示。
1.2 兴波阻力与波面升高由叠模势和兴波扰动势定解问题求得叠模势和扰动势后,借助伯努利方程可得船体表面上的压力分布:
| $ p+\rho g z+\frac{1}{2} \rho(\nabla \phi)^{2}=p_{\infty}+\frac{1}{2} \rho U^{2} $ | (8) |
压力系数可以表示为:
| $ C_{p}=\frac{p-p_{\infty}}{0.5 \rho U^{2}} $ | (9) |
船舶所受的兴波阻力为压力在船体湿表面上沿着x方向的积分,可以表示为:
| $ R_{w}=\iint\limits_{S_{\mathrm{B}}} p n_{x} \mathrm{d} S $ | (10) |
因此,兴波阻力系数为:
| $ C_{\mathrm{w}}=\frac{R_{\mathrm{w}}}{(1 / 2) \rho U^{2} S_{\mathrm{w}}}=\frac{1}{S_{\mathrm{w}}} \sum\limits_{i=1}^{N_{\mathrm{B}}} C_{p}(i) n_{x i} \Delta S_{i} $ | (11) |
式中:ΔSi为船体表面的面元面积; nxi为面元单位法向量的x分量; Sw为船体湿表面面积。
定常兴波波面升高为:
| $ \zeta(x, y)=\frac{1}{2 g}\left(U^{2}-\mathit{\Phi}_{x}^{2}-\mathit{\Phi}_{y}^{2}-2 \mathit{\Phi}_{x} \varphi_{x}-2 \mathit{\Phi}_{y} \varphi_{y}\right) $ | (12) |
由1.1节可知,预报船舶兴波阻力关键是求解叠模势与兴波扰动势的定解问题。叠模势求解简单,众多文献均有提及,本文不再赘述。本文以兴波扰动势为例,概述泰勒展开边界元方法的基本思想。
首先对兴波扰动势自由面条件式(8)中的二阶导数项φxx,φxy和φyy利用一阶导数项φx和φy进行二阶向前差分处理,可参考文献[9],合并一阶导数项系数,此处叠模势及其空间导数均为已知量。自由面条件为:
| $ \varphi_{z}=f_{1}(\mathit{\Phi}) \varphi_{x}+f_{2}(\mathit{\Phi}) \varphi_{y}+f_{3}(\mathit{\Phi}) $ | (13) |
式中:f1、f2和f3均是叠模势及其空间导数的表达式。
对格林函数1/r和兴波扰动势φ利用格林第3公式构建边界积分方程:
| $ 2 \pi \varphi+\iint\limits_{S_{\mathrm{H}}+S_{\mathrm{F}}} \varphi \frac{\partial}{\partial n}\left(\frac{1}{r}\right) \mathrm{d} s=\iint\limits_{S_{\mathrm{F}}} \frac{1}{r} \frac{\partial \varphi}{\partial n} \mathrm{d} s $ | (14) |
将积分边界SH和SF离散为N个面元。传统常值面元法将各离散面元内的源强和偶极强度近似成常数处理。与常值面元法不同,本文方法对式(14)中的偶极强度在离散面元的局部坐标系下(见图 2)进行泰勒展开,并保留一阶导数项:

|
Download:
|
| 图 2 离散网格局部坐标系 Fig. 2 Local coordinates of discrete gird | |
| $ \varphi(q)=\varphi\left(q_{0}\right)+\overline{\xi}\left.\varphi_{, \overline{\xi}}\right|_{q_{0}}+\overline{\eta}\left.\varphi_{, \overline{\eta}}\right|_{q_{0}} $ | (15) |
式中:ξ和η为Q面元以其中心为坐标原点的局部坐标。
将式(15)代入边界积分方程(14)中,得到新的边界积分方程,即:
| $ \begin{array}{l}{\iint\limits_{S_{\mathrm{F}}} \frac{1}{r} \frac{\partial \varphi}{\partial n} \mathrm{d} s=2 \pi \varphi+\iint\limits_{S_{\mathrm{H}}+S_{\mathrm{F}}} \overline{\eta} \frac{\partial \varphi}{\partial \overline{\eta}} \frac{\partial}{\partial n}\left(\frac{1}{r}\right) \mathrm{d} s+} \\ {\iint\limits_{S_{\mathrm{H}}+S_{\mathrm{F}}} \varphi \frac{\partial}{\partial n}\left(\frac{1}{r}\right) \mathrm{d} s+\iint\limits_{S_{\mathrm{H}}+S_{\mathrm{F}}} \overline{\xi} \frac{\partial \varphi}{\partial \xi} \frac{\partial}{\partial n}\left(\frac{1}{r}\right) \mathrm{d} s}\end{array} $ | (16) |
由式(17)可知,∂φ/∂ξ,∂φ/∂η和∂φ/∂n构成了网格局部坐标系下速度场。可在局部坐标系与大地坐标系下转换。因此自由面条件式(14)中右端前2项可转换至局部坐标下,代入方程组系数作为未知数求解。第3项作为强迫项仍然处于边界积分方程右端。为了补充一阶TEBEM方法的方程组,对格林第3公式中场点,考察其沿着法向趋于边界时垂直于法线平面内相互正交的2个方向上的一阶导数,进而补充方程组。其数值方法具体实施步骤可参考文献[10-12]。
3 数值计算与分析根据上述数值计算方法,分别以Wigley 4和Series 60船型为例,计算其兴波阻力、自由面波形和船侧波高,并与试验值及相关文献结果进行比较,验证计算程序的可靠性。
3.1 Wigley 4船数值结果Wigley 4的船型方程为:
| $ y=\frac{B}{2}\left(1-\frac{4 x^{2}}{L^{2}}\right)\left(1-\frac{z^{2}}{T^{2}}\right) $ | (17) |
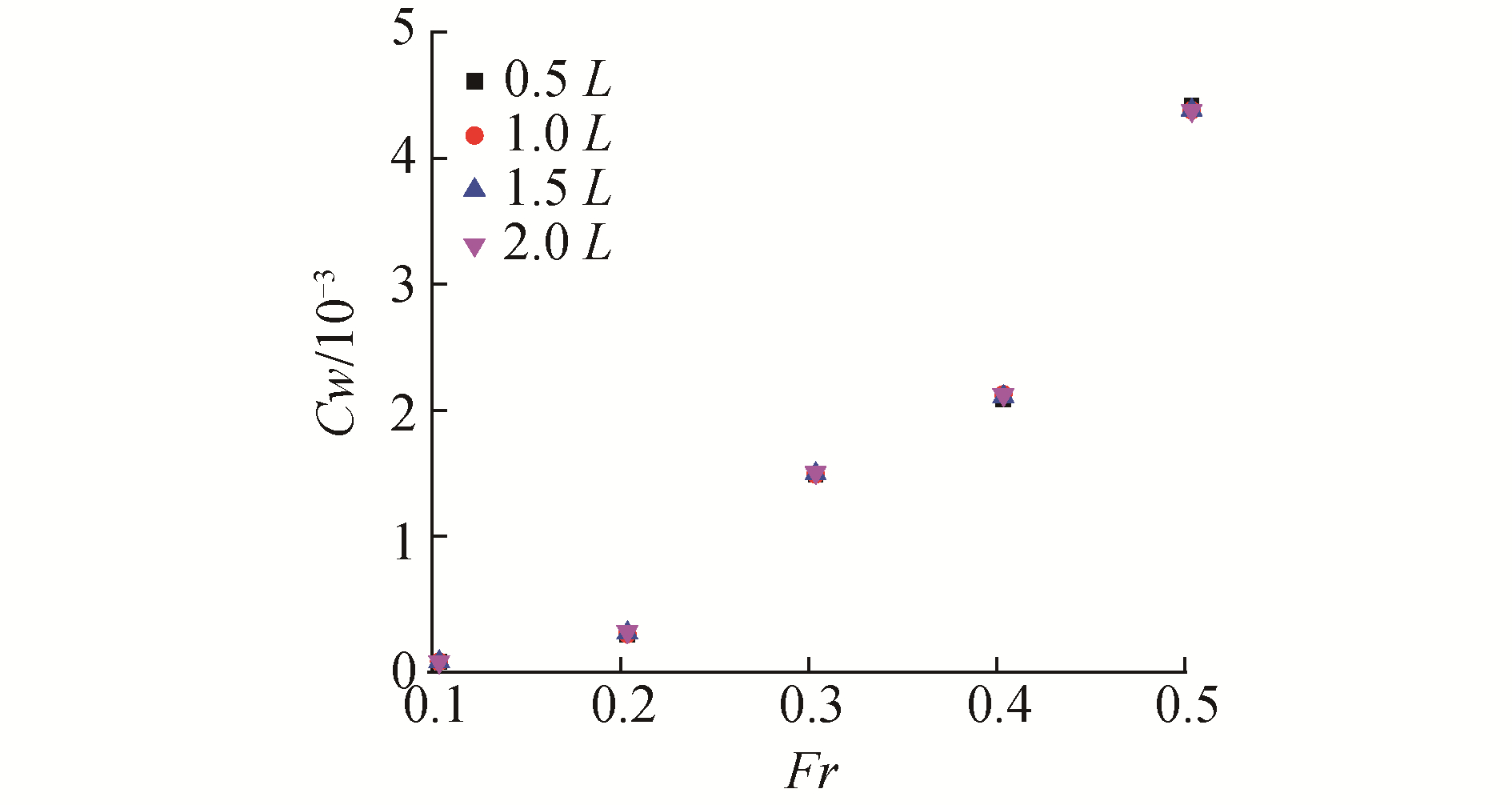
首先进行自由面区域的收敛性验证。自由面区域向船前延伸0.5L(L为船长),向船侧延伸1.5L,向船后延伸0.5L~2.0L,并在船艏艉处适当加密网格。兴波阻力系数的计算结果如图 3所示,结果表明兴波阻力的计算结果受自由面区域大小的影响较小。若要得到更大范围的兴波图形,则可适当扩展自由面区域。但会增加计算量。
|
Download:
|
| 图 3 TEBEM方法自由面区域收敛性验证 Fig. 3 Free surface convergence verification of TEBEM | |
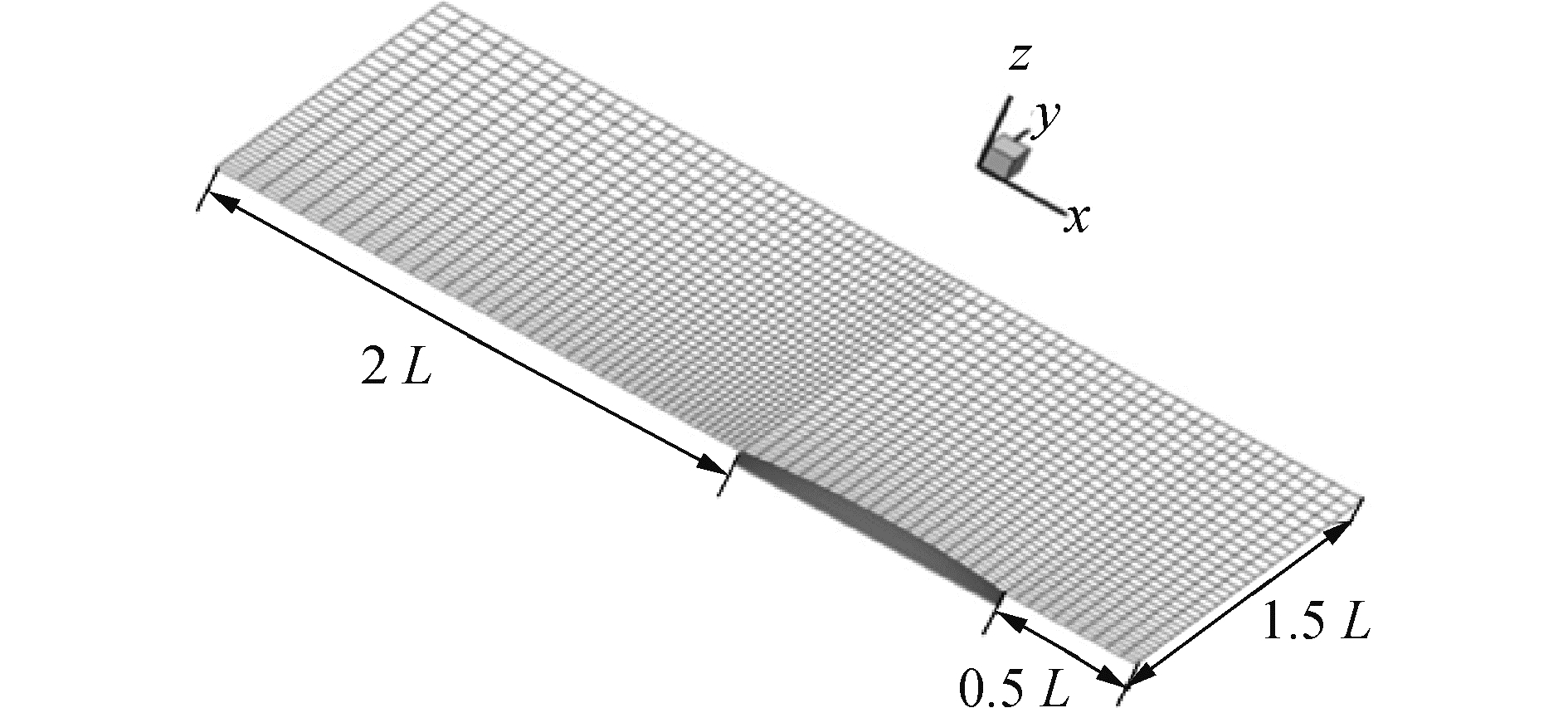
将Wigley半船离散为606个四边形面元或530个三角形面元。自由面上一律采用四边形面元,对左半自由面划分30×70个面元。自由面区域向上游延伸0.5L,向下游延伸2L,y方向延伸1.5L。如图 4所示。
|
Download:
|
| 图 4 流域边界网格划分 Fig. 4 Grid of fluid domain boundary | |
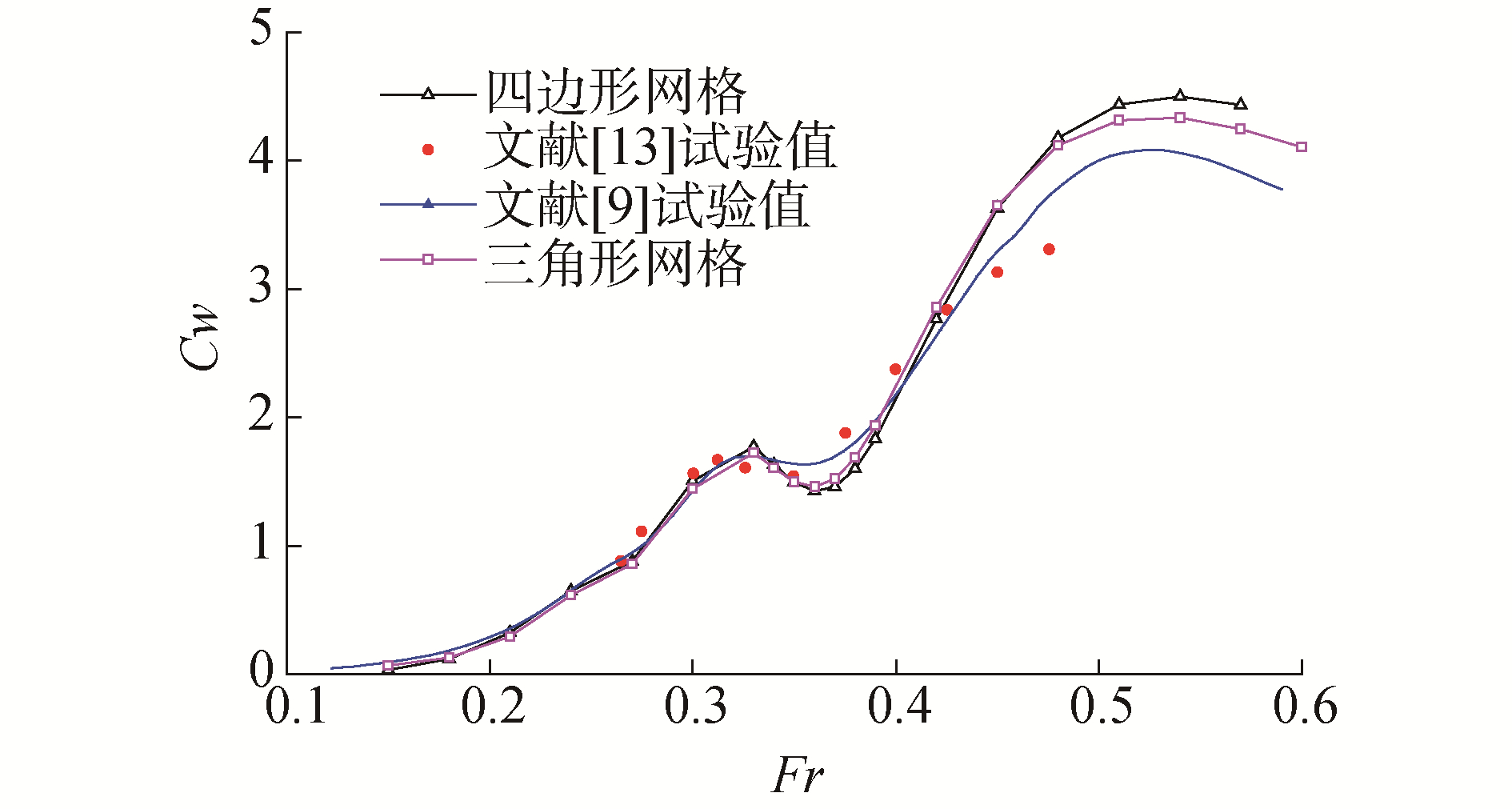
图 5为本文方法计算的兴波阻力系数的数值结果与其他学者计算值及试验值的比较。试验值与数值结果参考文献[9, 13]。
|
Download:
|
| 图 5 Wigley船型兴波阻力系数曲线 Fig. 5 The curves of wave-making resistance coefficient of Wigley ship | |
由图 5可知,物面离散三角形网格与四边形网格的计算结果基本一致,说明网格形状对兴波阻力的计算没有影响。兴波阻力系数曲线的变化规律和试验值相一致。在高航速本文方法数值结果偏高。图 6给出了Fr数分别为0.3、0.6时的波面等高线图。

|
Download:
|
| 图 6 不同航速下Wigley船型的波面等高线图 Fig. 6 Wave contour map of Wigley ship at different Fr | |
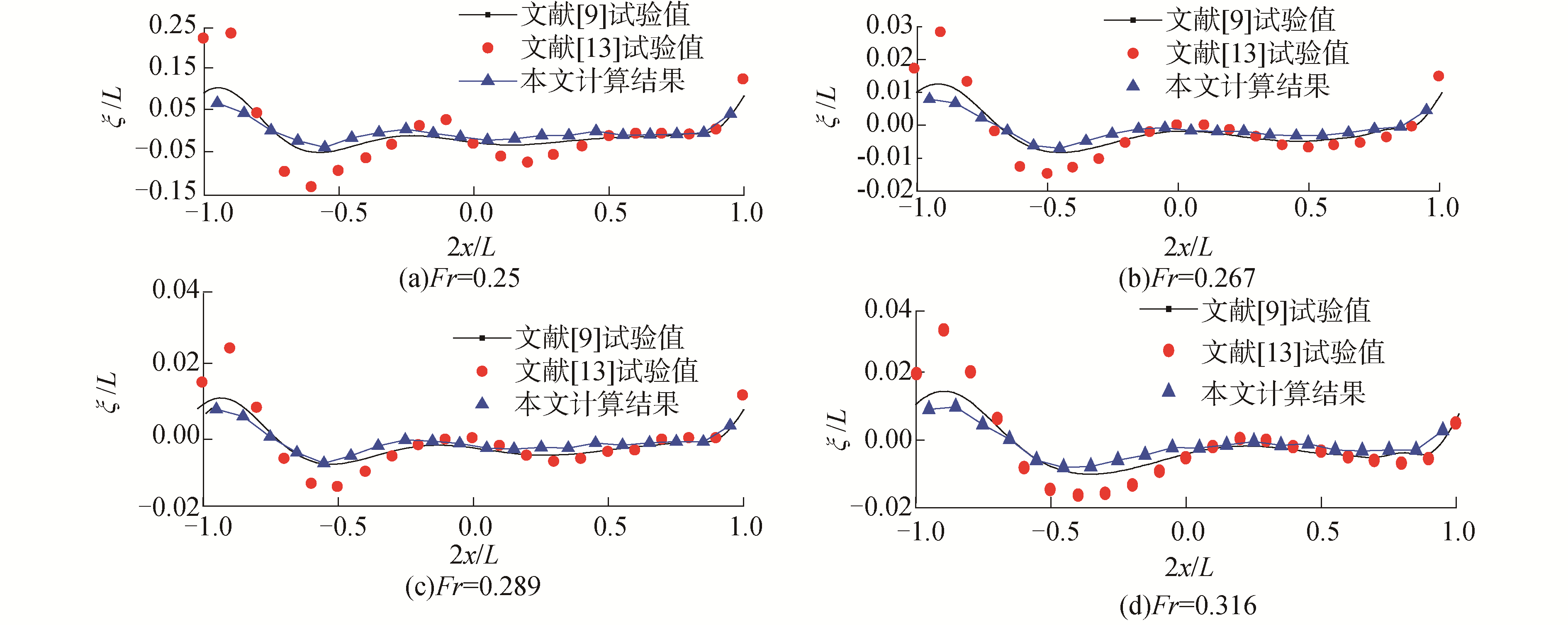
图 7给出了Wigley船侧的波面升高的数值结果并与试验值比较。从图 7可知,本文计算结果和文献[9]的数值结果吻合较好。与试验值相比,波面升高曲线的相位基本一致,主要差异在于船艏的第1个波峰和波谷处,其余水线处的差别并不明显。导致误差原因主要是在船艏附近的波高值受非线性因素的影响较大,线性自由表面条件无法准确模拟。
|
Download:
|
| 图 7 不同航速下wigley船型的船侧波面升高 Fig. 7 Wave height of ship side of Wigley ship at different Fr | |
S60船型(CB=0.6)是被ITTC组织认可的标准船型。学者基于该船型进了大量兴波阻力预报研究。S60半船划分793个四边形网格,自由面划分30×70个面元,并在船舶艏艉处适当加密。
图 8给出了本文方法计算的S60兴波阻力系数,并与东京大学和IHHI试验结果进行对比分析。由图可知,各结果变化趋势一致,本文的计算结果在高航速区间较试验值略小,与文献[9]的数值结果基本吻合。分析知,随着航速的增加,非线性因素对兴波阻力的影响增大,因此,非线性因素是导致数值计算结果与试验值差别的主要原因之一。

|
Download:
|
| 图 8 S60船型兴波阻力系数曲线 Fig. 8 The curve of wave-making resistance coefficient of S60 ship | |
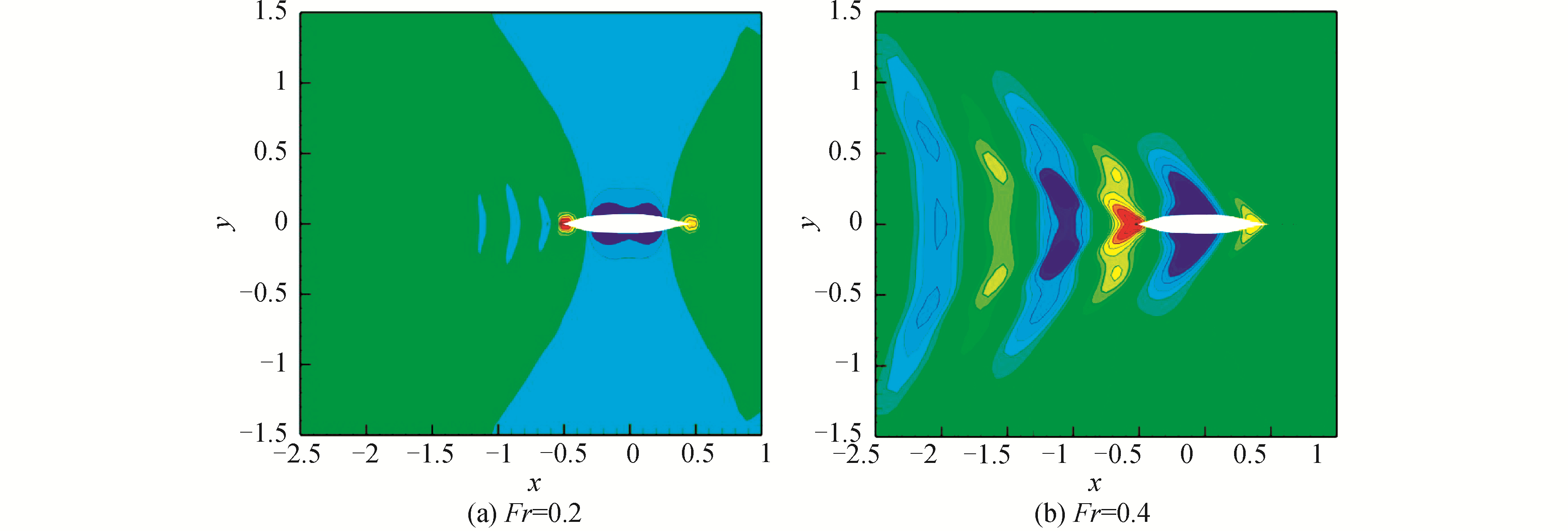
图 9给出了Fr数为0.2和0.4时的三维波面等高线图。图 10给出了3种不同航速下S60船型的船侧波高曲线,其中的试验结果取自SRI[14]。与Wigley船类似,本算例的计算结果与Suzuki[9]计算结果较为吻合,与试验值的差别主要在船艏的第一个波峰处。
|
Download:
|
| 图 9 不同航速下S60船型的波面等高线图 Fig. 9 Wave contour map of S60 ship at different Fr | |

|
Download:
|
| 图 10 不同航速下S60船型的船侧波面升高 Fig. 10 Wave height of ship side of S60 ship at different Fr | |
1) 通过与试验值的比较可以看出,本文方法得到的计算结果与试验结果基本一致。
2) 泰勒展开边界元法可以有效地预报船舶兴波阻力与流场波形;且避免Dawson方法中需要将自由面配置点前移的缺陷。叠模势、兴波扰动势的一阶导数项求解无需差分,大大降低求解兴波扰动势的边界积分方程组难度。
| [1] |
盛振邦, 刘应中. 船舶原理(上册)[M]. 上海: 上海交通大学出版社, 2004: 151-159. SHEN Zhenbang, LIU Yingzhong. Ship theory[M]. Shanghai: Shanghai Jiaotong University Press, 2004: 151-159. (  0) 0)
|
| [2] |
刘应中. 船舶兴波阻力理论[M]. 北京: 国防工业出版社, 2003. LIU Yingzhong. Theory of Ship Wave Making Resistance[M]. Beijing: National defense industry press, 2003. (  0) 0)
|
| [3] |
黄山.船舶航行近场扰动速度势与远场兴波的快速计算方法[D].哈尔滨工程大学, 2016: 1-9. HUANG shan. Fast Calculation Method of Near-field Perturbation Velocity Potential and Far-field Wave of Ship.[D].Harbin Engineering University. 2016: 1-9. http://cdmd.cnki.com.cn/Article/CDMD-10217-1018081965.htm (  0) 0)
|
| [4] |
CALISAL S M, GOREN O, OKAN B. On an iterative solution for nonlinear wave calculations[J]. Journal of ship research, 1991, 35(1): 9-14. (  0) 0)
|
| [5] |
DUAN W Y. Taylor Expansion Boundary Element Method for floating body hydrody-namics[C]//27th Intl Workshop on Water Waves and Floating Bodies, Copenhagen, Den-mark, 2012.
(  0) 0)
|
| [6] |
陈纪康, 段文洋, 朱鑫. 三维泰勒展开边界元方法及其数值验证[J]. 水动力学研究与进展A, 2013, 04: 482-485. CHEN Jikang, DUAN Wenyang, ZHU Xin. Three-dimenson Taylor expansion boundary element method and it's validation[J]. Chines journal of hydrodynamics, 2013, 04: 482-485. (  0) 0)
|
| [7] |
CHENG B H. Computations of 3D transom stern flows[C]//International Conference on Numerical Ship Hydrodynamics, 5th. 1900. https://trid.trb.org/view/407133
(  0) 0)
|
| [8] |
BRUZZONE D, CASSELLA P, ZOTTI I. Resistance Components on a Wigley Trimaran: Experimental and Numerical Investigation[C]//Proceedings of the Fourth International Conference on Hydrodynamics. 2000, 1: 115-120.
(  0) 0)
|
| [9] |
TARAFDER M S, SUZUKI K. Numerical calculation of free-surface potential flow around a ship using the modified Rankine source panel method[J]. Ocean engineering, 2008, 35(5): 536-544. (  0) 0)
|
| [10] |
段文洋, 陈纪康, 赵彬彬. 基于泰勒展开边界元法的深水浮体二阶平均漂移力计算[J]. 哈尔滨工程大学学报, 2015, 36(3): 302-306. DUAN Wenyang, CHEN Jikang, ZHAO Binbin. Calculation of second-order mean drift loads for the deepwater floating body based on the Taylor expansion boundary element method[J]. Journal of Harbin Engineering University, 2015, 36(3): 302-306. (  0) 0)
|
| [11] |
DUAN W Y, CHEN J K, ZHAO B B. Second order Taylor expansion boundary element method for the second order wave diffraction problem[J]. Engineering analysis with boundary element, 2015, 58: 140-150. DOI:10.1016/j.enganabound.2015.04.008 (  0) 0)
|
| [12] |
DUAN W Y, CHEN J K, ZHAO B B. Second order Taylor expansion boundary element method for the second order wave radiation problem[J]. Applied of ocean research, 2015, 52: 12-26. DOI:10.1016/j.apor.2015.04.011 (  0) 0)
|
| [13] |
SHEARER J R, CROSS J J. The experimental determination of the components of ship re-sistance for a mathematical model[J]. Trans. RINA, 1965, 107: 459-473. (  0) 0)
|
| [14] |
TAKESHI H, HINO T, HINATSU M, et al. Flow measurements and resistance Tests, ITTC Co-operative Experiments on a Series 60 Model At ship Research Institute[C]//17th Towing Tank Conference, (ITTC). 198.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


