动态失速是指翼型或机翼的非定常运动造成失速角明显超过其静态失速角的失速迟滞现象[1]。虽然动态失速能够增大升力峰值,但同时也造成了阻力、俯仰力矩的突增和气动中心失稳[2],严重限制了直升机安全飞行包线,对直升机飞行安全造成严重危害。而对于前飞时的直升机,其旋翼所处的气动环境更加复杂,一方面桨叶会随方位角做周期性变距、挥舞、摆振的复合运动;另一方面由于旋转速度与前飞速度的叠加,桨叶周向来流速度会随方位角呈现出明显的非定常性[3],这给直升机动态失速的预测增加了困难。二维翼型作为直升机旋翼的重要组成元素,其气动特性是旋翼气动分析的基础,因此对于直升机旋翼翼型动态失速的研究与预测具有十分重要的理论与现实价值。
对于翼型动态失速的预测主要有实验[4-5]、半经验模型[[6-7]和计算流体力学方法(computational fluid dynamics,CFD)。实验方法周期长、成本高;半经验模型使用具有一定局限性[8]、无法得到流场分布,涡结构形成过程。而动态失速与前缘失速涡的形成、发展、脱落紧密相关[9],CFD能够捕捉到动态失速过程中涡的形成、发展、脱落与再附过程细节,是动态失速机理研究的重要手段。针对二维旋翼翼型动态失速,文献[10-13]进行了大量数值仿真研究:Gharali等[10]采用低雷诺数修正的SST k-ω湍流模型模型对非定常来流速度下的俯仰NACA0012翼型进行了数值仿真,研究了来流速度的折合频率、振幅、相位差等参数对于动态失速的影响。吕坤等[14]应用动网格技术对定常来流下风力机NREL S809翼型进行了数值模拟,同时分析了挥舞、摆振及耦合运动对于风力机气动性能的影响。现有文献基本都是将非定常来流速度与复合运动分开进行研究讨论,而实际直升机前飞时,翼型在遭受非定常来流的同时,是做周期性变迎角俯仰、上下挥舞和前后摆振复合运动的。本文拟通过带转捩修正的SST k-ω湍流模型和基于嵌套网格技术的CFD方法对其进行数值研究,分析非定常来流下,叠加在俯仰运动上的挥舞、摆振运动以及各个运动参数对于动态失速的影响。
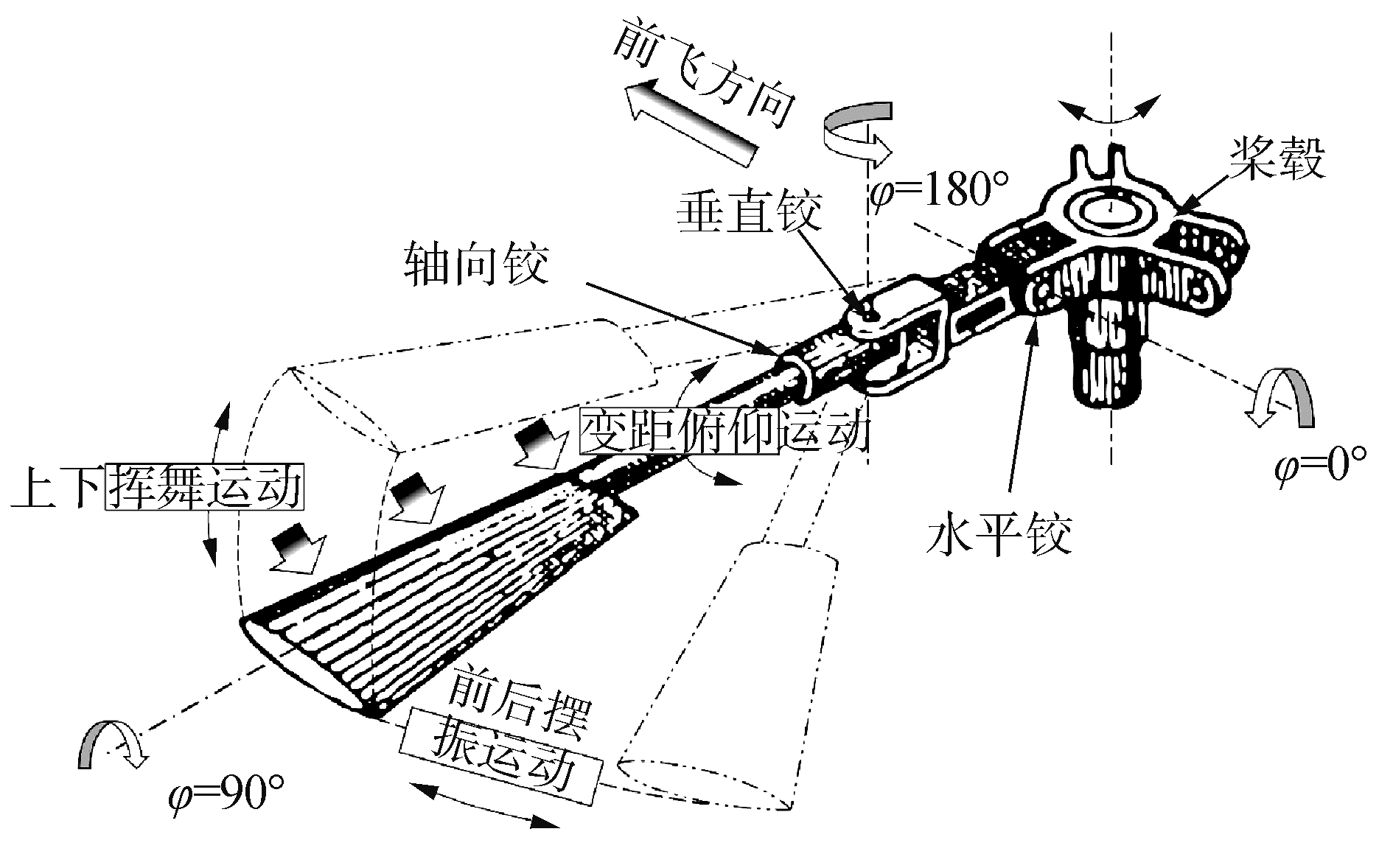
1 非定常来流下复合运动动态失速的仿真模型 1.1 复合运动定义本文采用直升机桨叶的二维截面翼型作为研究对象,忽略三维效应。对于铰接式直升机,其桨毂包括轴向、水平和垂直3个方向铰,如图 1[15]所示。前飞时翼型在非定常来流速度下做俯仰、挥舞、摆振叠加的复合运动, 各方向运动形式(示意图如图 2)定义如下:
|
Download:
|
| 图 1 铰接式直升机桨叶示意 Fig. 1 Sketch of articulated helicopter blades | |

|
Download:
|
| 图 2 各运动示意 Fig. 2 Sketch of each motion | |
俯仰(变距)运动:前飞时,直升机桨盘向前倾斜,桨叶旋转360°,桨距随方位角改变呈周期性变化,桨距的改变造成了翼型迎角的周期性变化。二维翼型将1/4弦长处作为俯仰轴做简谐运动,其形式为:
| $ \alpha(t)=\alpha_{\mathrm{mean}}+\alpha_{\mathrm{amp}} \sin (2 \pi f t) $ | (1) |
式中:αmean是平均迎角;αamp是俯仰运动振幅;f是运动频率。
非定常来流速度:由于直升机旋翼旋转速度和前飞速度的叠加,桨叶周向来流速度会随着方位角简谐变化,对于二维翼型来说其来流速度为:
| $ U(t)=U_{\infty}+U_{\mathrm{amp}} \sin (2 \pi f t+\varphi) $ | (2) |
式中:U∞是来流平均速度;Uamp是来流速度振幅;φ是来流速度与俯仰运动的相位差。
挥舞运动:直升机前飞时,旋翼前行桨的相对来流速度大于后行桨,使得前行桨产生比后行桨更大的升力,造成了直升机两侧不平衡。为平衡两侧力矩,避免直升机翻滚,桨叶与桨毂采用了水平铰连接。前行桨拉力大,桨叶向上挥舞;后行桨拉力小,桨叶向下挥舞,随着方位角的改变造成了桨叶上下周期性挥舞运动。挥舞运动是气动力、惯性力和重力的耦合结果,为了便于研究挥舞方向运动对于翼型气动力的影响,文献[16]将挥舞运动也假设为与俯仰运动形式相同的简谐运动,下面的摆振运动也做相同假设。翼型的挥舞运动假设为:
| $ y(t)=y_{\mathrm{amp}} \sin (2 \pi f t+\phi) $ | (3) |
式中:yamp是挥舞运动的振幅;ϕ是挥舞运动与俯仰运动的相位差。
摆振运动:直升机前飞时,桨叶的周期性挥舞造成了重心距旋翼轴的距离不断变化,从而引起了周期交变的科里奥利力,为避免科里奥利力造成的桨叶根部材料疲劳,通过垂直铰使得桨叶摆动一个角度,从而减小交变弯矩,这就造成了周期性前后运动的摆振运动。翼型摆振运动形式假设为:
| $ x(t)=x_{\mathrm{amp}} \sin (2 \pi f t+\gamma) $ | (4) |
式中:xamp是摆振运动的振幅;γ是摆振运动与俯仰运动相位差。
1.2 仿真设置与算例验证嵌套网格允许不同区域的网格进行独立并行计算,并通过插值方式进行耦合,网格间允许交错、重叠进而极大地降低了整个流场区域网格设计和生成的难度以及工作量。因此,嵌套网格技术特别适合于复杂外形绕流和存在多体相对运动的流动问题[17]。使用ICEM CFD (ANSYS 18.0)生成结构网格。翼型采用O型网格,翼型周围设置340个节点,边界条件定义为无滑移壁面,第1层网格高度遵循y+≈1,网格增长率为1.1。圆形流体域设为30倍弦长并作为前景网格,边界条件定义为嵌套网格边界40倍弦长的正方形流体域作为背景网格,边界条件定义为压力远场。本套网格共49 560个节点,49 206个单元网格。网格生成情况及边界定义情况如图 3所示。

|
Download:
|
| 图 3 网格生成与边界条件示意 Fig. 3 Sketch of grid generation and boundary conditions | |
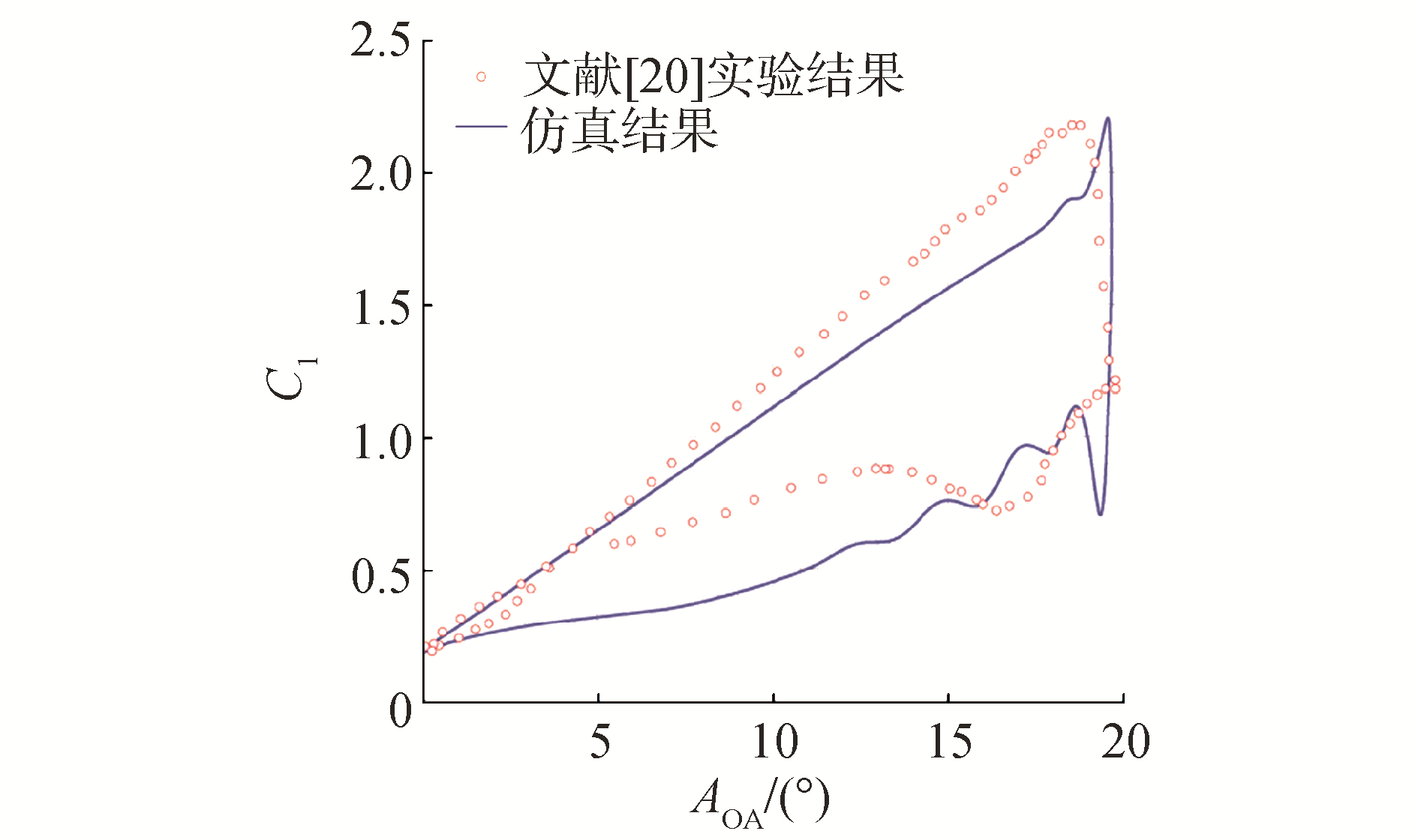
文献[10, 18-19]在二维翼型动态失速数值仿真中对多种湍流模型进行了对比,发现SST k-ω湍流模型能够较好捕捉近壁面的剪切层和分离流动,对结果的预测较为准确。基于上述原因,本文选择带转捩修正的SST k-ω湍流模型进行求解。翼型的各个运动和非定常来流速度通过Fluent中用户自定义功能(User-defined function)进行驱动。求解器采用密度基隐式求解,离散格式采用二阶迎风,残差设为1×10-6,时间步长设为0.000 1 s,其中每个时间步进行30次迭代,稳定运行至少3个周期后停止运算。采用SIKORSKY SC1095翼型为研究对象,弦长0.61 m,马赫数Ma≈0.3,折合频率k≈0.1下的黑鹰直升机典型后行桨失速工况作为基础进行仿真计算,并将得到的升力系数与文献[20]中的实验结果作对比,如图 4所示。
|
Download:
|
| 图 4 SC1095翼型升力系数与文献[20]对比 Fig. 4 Comparisons of lift coefficients of SC1095 airfoil with refe.[20] | |
图 4中,横坐标AOA为迎角,纵坐标Cl为升力系数,定义为C1=2L/(ρU∞2c)。小迎角情况下,对于升力系数拟合较好,动态失速角延迟0.89°,升力系数峰值增大了0.05,说明其能够较为准确地预测出动态失速角和升力系数峰值。但是在上仰到较大迎角时,升力系数较实验数据普遍偏小,同时下俯过程中对于再附着流动捕捉不足,升力系数与实验数据具有一定偏差。造成这种结果的原因:1)实验本身实验装置或者方法造成的数据不准确;2)基于完全紊流假设的湍流模型,使得模拟湍流区域大于实际湍流区域造成了上仰阶段中升力系数略小于实验数据;3)SST k-ω湍流模型中的常数是基于简单的边界流动得到的,而流动分离后湍流具有强烈的非平衡特性,导致下俯过程中的对于失速后气动性能预测不够准确。但总体来看,仿真结果与实验数据吻合良好,验证了仿真模型的可行性。
2 非定常流下复合运动本文将来平均来流速度为104.51 m/s、振幅为62.706 m/s、相位差φ为π的非定常来流下,纯俯仰运动的工况作为参考基准,研究分别叠加了振幅分别为0.3、0.5、0.7 m,相位差分别为0、π/4、π/2、3π/4、π的俯仰挥舞复合运动和俯仰摆振复合的情况,分析了各运动参数对于气动特性的影响。
2.1 非定常来流下的纯俯仰运动如图 5所示,非定常来流速度导致动态迟滞环较定常纯俯仰工况明显增大,升力系数峰值从2.21增加到3.50,动态失速角提前了1.15°。

|
Download:
|
| 图 5 非定常来流与定常来流速度下纯俯仰运动的升力系数对比 Fig. 5 Comparisons of lift coefficients of a pure pitching oscillating airfoil under steady/unsteady freestream velocity | |
俯仰运动过程的压力流线叠加图(左)和无量纲(ωzc/U∞)涡量云图(右)如图 6所示。图中的符号‘+’和‘-’分别代表翼型的上仰和下俯过程。在翼型上仰阶段,从开始迎角0°+左右到15.87°+时,翼型周围为附着流动,升力系数增长斜率几乎不变。随着翼型不断上仰,当迎角到达15.87°+时,翼型前缘附近有涡形成形成,并在翼型吸力面侧快速向翼型后缘发展,随着涡的不断扩大升力系数斜率此时也出现突增。当翼型迎角为18.12°+时,前缘涡尺寸覆盖整个弦长长度,升力系数也达到峰值。迎角为18.90°+时,后缘涡快速生成并与主涡相互作用,主涡开始从上翼面脱离造成了升力系数的陡然下降,导致失速。迎角为19.42°+时,后缘涡从翼型后缘脱落,吸力涡再次在上翼面生成,造成升力系数短暂上升。当迎角为19.66°+时,主涡再次脱落,升力系数再次快速下降,完成上仰的整个过程。

|
Download:
|
| 图 6 压力与流线叠加图和无量纲涡量(ωzc/U∞)云图 Fig. 6 Pressure superimposed with flow stream-lines and dimensionless vorticity magnitude (ωzc/U∞) | |
翼型下俯过程中,前缘涡与后缘涡的交替生成、发展、脱落和相互作用引起了升力系数的波动变化。当迎角为4.39°+时,翼型周围空气重新变为附着流动。
2.2 非定常流下俯仰与挥舞的复合运动 2.2.1 挥舞运动中相位差的影响本文规定翼型向上的挥舞运动为正,当相位差为0时,表示翼型上仰的过程中伴随着向上的挥舞,下俯的同时伴随着向下的挥舞运动,而相位差为π时则运动形式刚好相反。从图 7(a)中可以看出,当相位差为0时,挥舞运动的叠加抑制了前缘涡的生成,动态失速角延迟了1.62°。上仰过程中的升力系数较纯俯仰运动有所下降,升力系数峰值减小了0.39,下俯过程过程中的升力系数有所增加,动态迟滞环明显缩小。随着相位差的增大,动态失速角逐步提前,上仰过程中的升力系数、升力系数峰值随之增大,而下俯过程中升力系数逐渐减小,整个动态迟滞环逐渐变大。当相位差为π时,升力系数相较于纯俯仰运动增加了0.64,动态失速角提前了5.04°。

|
Download:
|
| 图 7 非定常来流下俯仰挥舞复合运动的升力系数 Fig. 7 Lift coefficient values of a pitching-plunging oscillating airfoil values under unsteady freestream | |
图 7(b)展示了挥舞运动固定相位差为0时,振动幅值Amp为0.3、0.5及0.7的升力系数。图 8是挥舞运动各振幅条件下,动态失速角时的无量纲涡量云图。当挥舞的相位差为0时,挥舞运动抑制前缘涡的生成,造成动态失速角迟滞和升力系数峰值的减小,此时的动态失速时的前缘涡尺寸长度稍大于翼型弦长,动态失速角延迟了1.21°,升力系数峰值降低了0.18°。随着挥舞运动振幅的增大,挥舞运动对于前缘涡生成的抑制作用越来越强,动态失速角不断后移,升力系数峰值也随之减小。当振幅为0.7 m时,动态迟滞环明显缩小,失速时的前缘涡尺度小于弦长尺寸,动态失速角延迟了1.63°,升力系数峰值减小了0.57。

|
Download:
|
| 图 8 非定常来流下俯仰挥舞复合运动的各振幅下动态失速角下无量纲涡量(ωzc/U∞)云图 Fig. 8 Dimensionless vorticity magnitude(ωzc/U∞) contour of a pitching-plunging oscillating airfoil with different amplitudes under unsteady freestream | |
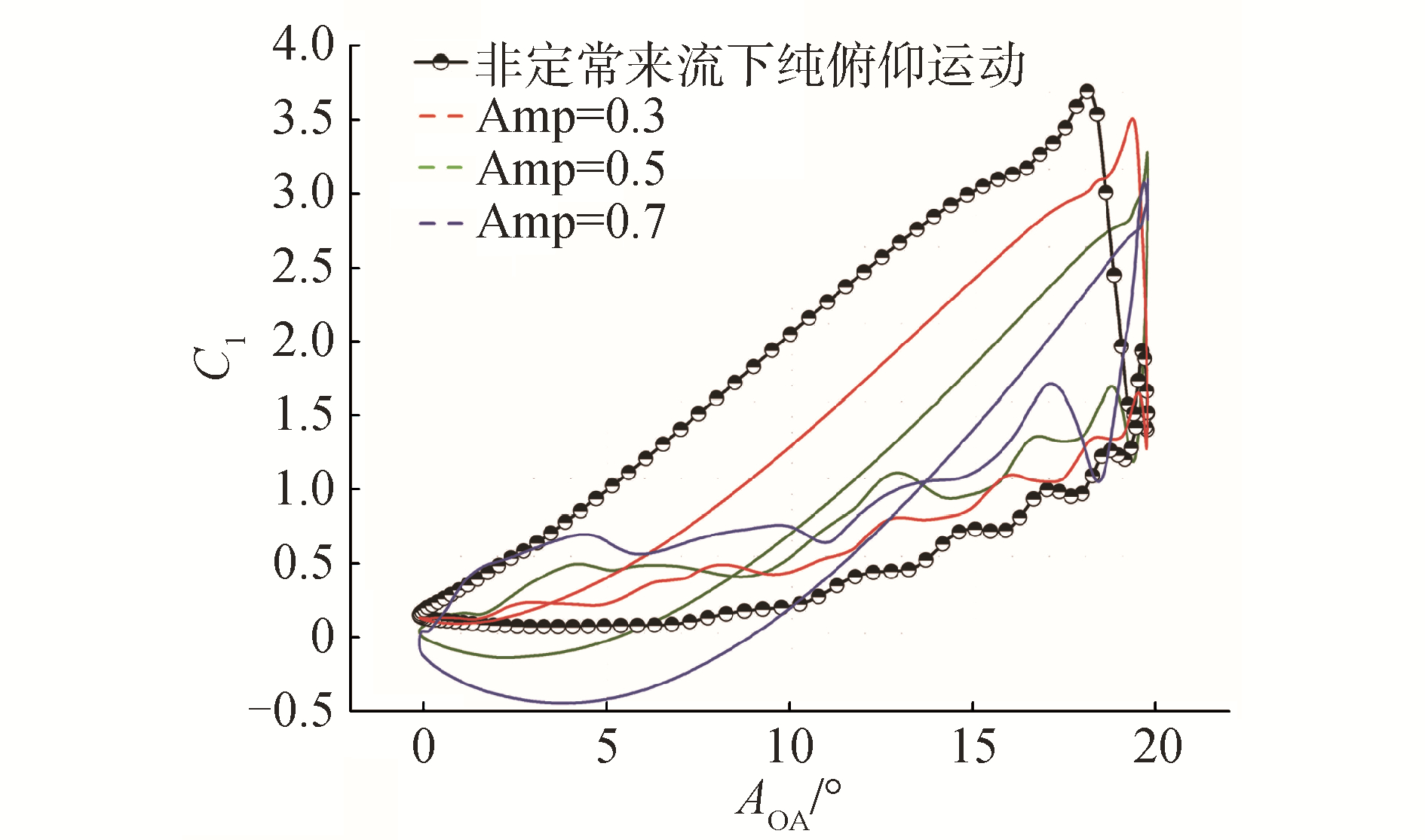
本文规定向后的摆振运动为正,当相位差为0时,表示翼型上仰过程中伴随着向后摆振运动,下俯过程中伴随着向前摆振,而相位差为π时则运动形式刚好相反。从图 9(a)可以看出,当相位差为0时,摆振运动的叠加使得上仰过程中的升力系数有所增加,下俯过程中升力系数有所减小,使得动态迟滞环缩减,动态失速角推迟了0.87°,升力系数峰值减小了0.42。随着相位角的增大,上仰运动开始转变成伴随着向前的摆振运动,对于前缘涡的生成开始由抑制变为促进,上仰过程中的升力系数开始增大,下俯过程中的升力系数开始减小,使得动态迟滞环、升力系数峰值也开始逐步增大,动态失速角逐渐提前。
|
Download:
|
| 图 9 非定常流下俯仰摆振复合运动的升力系数 Fig. 9 Lift coefficient values of a pitching-lagging oscillating airfoil with different phase difference values under unsteady freestream | |
如图 9(b)所示,固定摆振运动的相位差为0,研究不同振幅下俯仰摆振复合运动的升力系数。图 10是摆振运动的各振幅下运动失速角无量纲涡量云图。当振幅为0.3 m时,摆振运动使得动态迟滞环相较于纯俯仰运动情况稍有缩小,动态失速角后移了0.75°,升力系数峰值下降了0.42 m,此时的动态失速时前缘涡尺寸大于翼型弦长长度。随着振幅的增加,摆振运动对于前缘涡的抑制作用也越明显。造成动态失速角延迟,升力系数峰值减小,动态迟滞回归线减小。当振幅为0.7 m时,动态失速角延迟了1.11°,升力系数峰值减小了0.61,而失速时的前缘涡尺寸稍小于翼型弦长尺寸。

|
Download:
|
| 图 10 非定常来流下摆振运动的各振幅下动态失速角下无量纲涡量(ωzc/U∞)云图 Fig. 10 Dimensionless vorticity magnitude (ωzc/U∞) contour of a pitching-plunging oscillating airfoil with different amplitudes under unsteady freestream | |
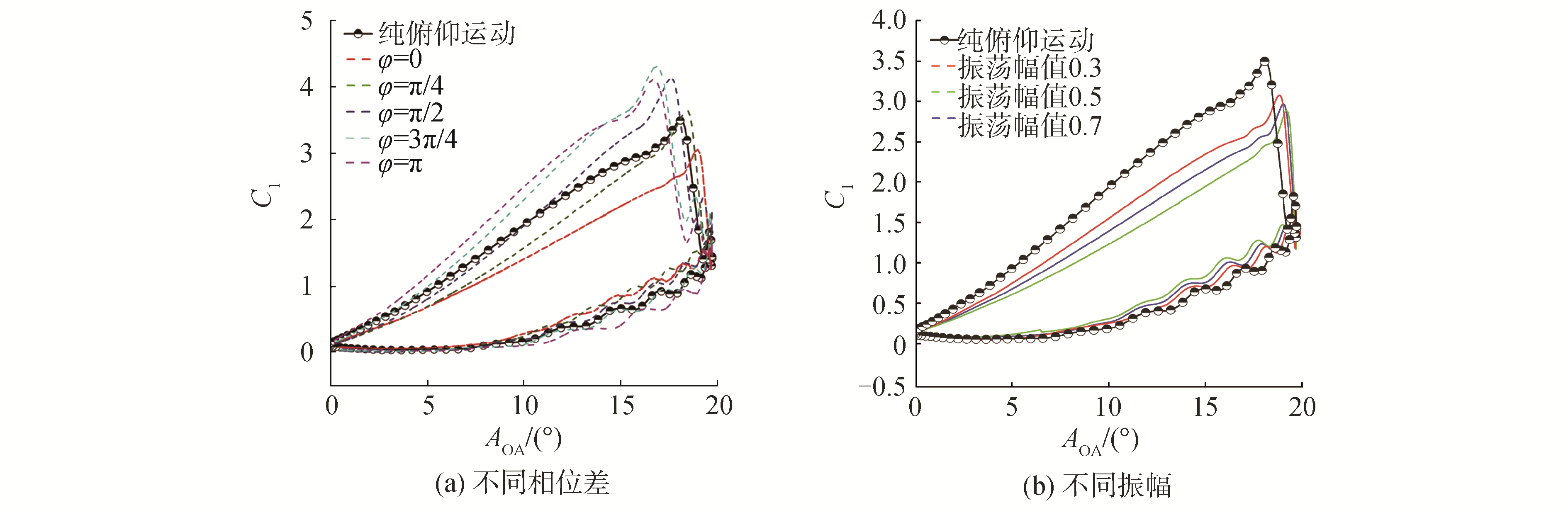
图 11综合了各相位差和振幅下2种复合运动情况下动态失速角情况,用以对比2种复合运动对于动态失速角作用大小。图 11(a)为固定振幅0.5 m时,相位差分别为0、π/4、π/2、3π/4、π的动态失速角。可以看到,相位差为0、π/4时,挥舞和摆振运动对于俯仰运动的作用均是使动态失速角延迟。相位差为π/2、3π/4、π时,挥舞和摆振运动对于俯仰运动的作用均是使动态失速角提前。但无论使动态失速角延迟还是提前,挥舞运动对于动态失速角作用都要比摆振运动强,平均高8.58%;图 11(b)为固定相位差为0时,振幅为0.3、0.5、0.7 m的动态失速角情况。可以看到,各振幅下对于动态失速角的抑制,挥舞运动作用更强,平均高2.88%。综合以上数据,挥舞运动对于非定常流下俯仰运动动态失速角的作用要强于摆振运动。
|
Download:
|
| 图 11 非定常来流下各相位差和振幅下俯仰挥舞运动和俯仰摆振运动的动态失速角 Fig. 11 Variation of dynamic stall angle with different phase difference values and amplitudes under unsteady freestream of pure pitching, pitching-plunging and pitching-lagging oscillating airfoil | |
1) 基于修正的SST k-ω湍流模型和嵌套网格技术的仿真模型能够较好地预测翼型动态失速的失速角和升力系数峰值,但对上仰过程中大迎角下情况与失速后再附过程中升力系数的预测有待提高。
2) 固定振幅、挥舞和摆振运动相位差的增加促进了前缘涡生成,使得动态失速迟滞环增大,动态失速角提前,升力系数峰值提高;固定相位角,挥舞和摆振运动振幅的增加抑制了前缘涡生成,使得动态失速迟滞环减小,动态失速角延迟,升力系数峰值减小。
3) 挥舞运动对于非定常来流下俯仰运动翼型动态失速角的影响要大于摆振运动。
| [1] |
CARR L W. Progress in analysis and prediction of dynamic stall[J]. Journal of aircraft, 1988, 25(1): 6-17. (  0) 0)
|
| [2] |
赵国庆, 招启军, 王清. 旋翼翼型非定常动态失速特性的CFD模拟及参数分析[J]. 空气动力学学报, 2015, 33(1): 72-81. ZHAO Guoqing, ZHAO Qijun, WANG Qing. Simulations and parametric analyses on unsteady dynamic stall characteristics of rotor airfoil based on CFD method[J]. Acta aerodynamica sinica, 2015, 33(1): 72-81. DOI:10.7638/kqdlxxb-2013.0010 (  0) 0)
|
| [3] |
林永峰, 黄建萍, 黄水林, 等. 直升机旋翼翼型动态失速特性试验研究[J]. 航空科学技术, 2012(4): 25-28. LIN Yongfeng, HUANG Jianping, HUANG Shuilin, et al. Experimental investigation of rotor airfoil dynamic stall characteristics[J]. Aeronautical science & technology, 2012(4): 25-28. (  0) 0)
|
| [4] |
PIERCE G A, KUNZ D L, MALONE J B. The effect of varying freestream velocity on dynamic stall characteristics[C]//Proceedings of the 32nd Annual National Forum of the American Helicopter Society. Washington, DC: NASA, 1976. https://www.researchgate.net/publication/245449034_The_Effect_of_Varying_Freestream_Velocity_on_Airfoil_Dynamic_Stall_Characteristics
(  0) 0)
|
| [5] |
LEISHMAN J G, BEDDOES T S. A semi-empirical model for dynamic stall[J]. Journal of the American helicopter society, 1989, 34(3): 3-17. DOI:10.4050/JAHS.34.3 (  0) 0)
|
| [6] |
MCALISTER K W, LAMBERT O, PETOT D. Application of the ONERA model of dynamic stall. NASA technical paper 2399[R]. Washington, DC: NASA, 1984.
(  0) 0)
|
| [7] |
邵明玉, 杨茂, 陈凤明. 旋翼翼型动态失速特性的数值仿真研究[J]. 计算机仿真, 2012, 29(7): 70-74. SHAO Mingyu, YANG Mao, CHEN Fengming. Numerical simulation study on dynamic stall characteristics of rotor airfoil[J]. Computer simulation, 2012, 29(7): 70-74. DOI:10.3969/j.issn.1006-9348.2012.07.017 (  0) 0)
|
| [8] |
MCCROSKEY W J, CARR L W, MCALISTER K W. Dynamic stall experiments on oscillating airfoils[J]. AIAA journal, 1976, 14(1): 57-63. DOI:10.2514/3.61332 (  0) 0)
|
| [9] |
GEISSLER W, RAFFEL M, DIETZ G, et al. Helicopter aerodynamics with emphasis placed on dynamic stall[M]//PEINKE J, SCHAUMANN P, BARTH S. Wind Energy. Berlin, Heidelberg: Springer, 2007: 199-204.
(  0) 0)
|
| [10] |
GHARALI K, JOHNSON D A. Numerical modeling of an S809 airfoil under dynamic stall, erosion and high reduced frequencies[J]. Applied energy, 2012, 93: 45-52. DOI:10.1016/j.apenergy.2011.04.037 (  0) 0)
|
| [11] |
ZANOTTI A, MELONE S, NILIFARD R, et al. Experimental-numerical investigation of a pitching airfoil in deep dynamic stall[J]. Proceedings of the institution of mechanical engineers, Part G:Journal of aerospace Engineering, 2014, 228(4): 557-566. DOI:10.1177/0954410013475954 (  0) 0)
|
| [12] |
满洪海, 杜刚, 陈江. 风力机翼型动态失速数值模拟[J]. 太阳能学报, 2012, 33(10): 1641-1647. MAN Honghai, DU Gang, CHEN Jiang. Investigation of dynamic stall of wind turbine airfoil[J]. Acta energiae solaris sinica, 2012, 33(10): 1641-1647. DOI:10.3969/j.issn.0254-0096.2012.10.001 (  0) 0)
|
| [13] |
胡丹梅, 李佳, 闫海津. 水平轴风力机翼型动态失速的数值模拟[J]. 中国电机工程学报, 2010, 30(20): 106-111. HU Danmei, LI Jia, YAN Haijin. Numerical simulation of airfoil dynamic stall of horizontal axis wind turbine[J]. Proceeding of the CSEE, 2010, 30(20): 106-111. (  0) 0)
|
| [14] |
吕坤, 谢永慧, 张荻. 风力机翼型挥舞摆振非定常气动特性分析[J]. 西安交通大学学报, 2011, 45(9): 47-53, 100. LYU Kun, XIE Yonghui, ZHANG Di. Investigation of unsteady aerodynamic performance for wind turbine airfoil[J]. Journal of Xi'an Jiaotong University, 2011, 45(9): 47-53, 100. (  0) 0)
|
| [15] |
史志伟, 耿存杰, 明晓, 等. 旋翼翼型俯仰沉浮运动非定常气动特性实验研究[J]. 实验流体力学, 2007, 21(3): 18-23. SHI Zhiwei, GENG Cunjie, MING Xiao, et al. Experimental investigation on unsteady aerodynamics of rotor-blade airfoil[J]. Journal of experiments in fluid mechanics, 2007, 21(3): 18-23. DOI:10.3969/j.issn.1672-9897.2007.03.004 (  0) 0)
|
| [16] |
杨一栋. 直升机飞行控制[M]. 3版. 北京: 国防工业出版社. YANG Yidong. Helicopter flight control[M]. 3rd ed. Beijing: National Defend Industry Press. (  0) 0)
|
| [17] |
曹义华. 现代直升机旋翼空气动力学[M]. 北京: 北京航空航天大学出版社, 2015.
(  0) 0)
|
| [18] |
雷延生, 周正贵. 风力机振荡翼型动态失速特性的CFD研究[J]. 太阳能学报, 2010, 31(3): 367-372. LEI Yansheng, ZHOU Zhenggui. CFD investigation on wind turbine oscillating airfoil dynamic stall[J]. Acta energiae solaris sinica, 2010, 31(3): 367-372. (  0) 0)
|
| [19] |
钱炜祺, 符松, 蔡金狮. 翼型动态失速的数值研究[J]. 空气动力学学报, 2001, 19(4): 427-433. QIAN Weiqi, FU Song, CAI Jinshi. Numerical study of airfoil dynamic stall[J]. Acta aerodynamica sinica, 2001, 19(4): 427-433. DOI:10.3969/j.issn.0258-1825.2001.04.010 (  0) 0)
|
| [20] |
MCALISTER K W, PUCCI S L, MCCROSKEY W J, et al. An experimental study of dynamic stall on advanced airfoil section. Volume 2: Pressure and force data. NASA TM-84245[R]. Moffett Field, CA: NASA, 1982.
(  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


