2. 哈尔滨工程大学 先进船舶材料与力学工信部重点实验室, 黑龙江 哈尔滨 150001;
3. 哈尔滨工业大学 复合材料与结构研究所, 黑龙江 哈尔滨 150080
2. Key Laboratory of Advanced Ship Materials and Mechanics, Harbin Engineering University, Harbin 150001, China;
3. Center for Composite Materials, Harbin Institute of Technology, Harbin 150001, China
点阵结构按照胞元节点数和杆件数量相互关系,可以分为拉伸主导型和弯曲主导型2大类。其中,拉伸主导型点阵结构由于芯子中的杆件将芯子所受剪力转化为杆件所受的拉力或压力,从而使结构整体力学性能较其他弯曲主导型夹芯结构有明显提升[1-8],而且点阵胞元之间的连通性使其在结构功能一体化[7, 9-10]设计领域极具优势。作为新一代先进轻质超强韧结构材料,学者针对该类结构的设计制备、静力学、动力学性能等方面开展了广泛而深入的研究工作[1-8, 11-18]。针对传统点阵结构所存在的力学性能缺陷,学者们经过拓扑优化设计出了新型沙漏型点阵夹芯结构[13-14]。沙漏型点阵夹芯结构由于增大了杆件的长细比,使得杆件抗屈曲能力较传统点阵结构(如金字塔型,四面体等)有了较大提升,减小节点间间距提高了结构的抗面板局部屈曲能力[13]。结构在长期承受振动的情况下大多数存在工作精度和可靠性下降,疲劳寿命、服役时间大幅度降低等现象,甚至可能导致提前破坏造成不可挽回的损失。因此有必要对其振动特性开展系统研究[19-20],为该类结构的相关设计与应用提供参考。
本文针对新型金属沙漏型点阵夹芯结构,采用数值仿真和试验验证相结合的方法研究其固有振动和谐响应特性,分别探究了边界条件和芯子杆件倾斜角度对其固有振动特性和加速度频响特性的影响,并与芯子相对密度相等的金字塔点阵结构的固有振动和谐响应特性进行了对比。
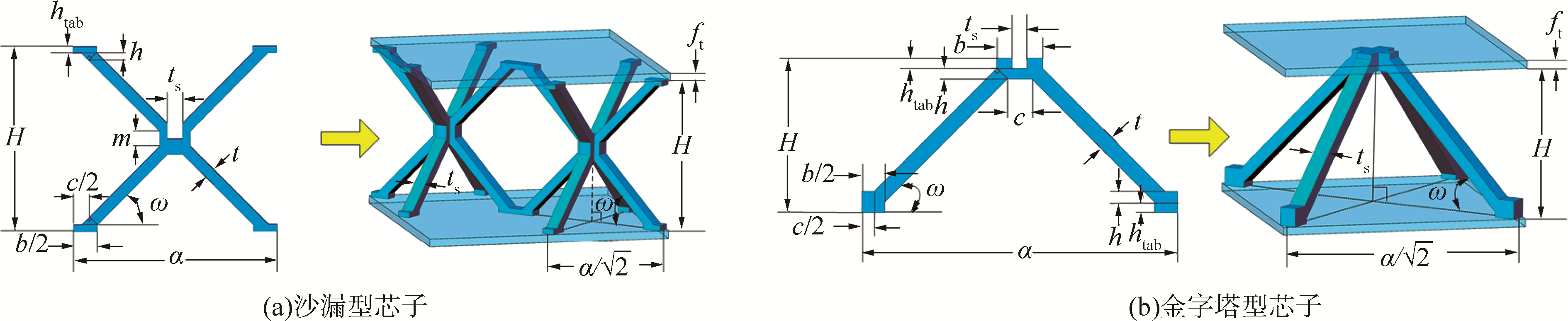
1 有限元模型建立及试验验证 1.1 材料及有限元模型建立本文研究的试件采用304不锈钢为母材,材料密度ρs为7 900 kg/m3,杨氏模量E为213 000 MPa,泊松比λ为0.3。沙漏型和金字塔型点阵结构的芯子单胞尺寸及参数定义如图 1所示。
|
Download:
|
| 图 1 芯子单胞几何参数 Fig. 1 The geometries variables of the unit cells 注:ω为杆件倾斜角度; t为杆件宽度;ts为杆件厚度并与杆件嵌槽宽度相等;a为嵌条单胞宽度;b为凸台长边宽度;c为凸台短边宽度;ft为面板厚度;m为沙漏型单胞中补强部分宽度;h与htab为单胞中凸台尺寸;H为芯子高度。 | |
本文同时设计了2种相对密度为ρp的金字塔型点阵结构,为方便比较,芯子高度相等的沙漏型和金字塔型点阵结构具有近似相等的芯子相对密度,所涉及的几何参数如表 1所示。杆件倾斜角度ω为45°时,相对密度ρH为2.7%的沙漏型点阵结构用H1-45表示,ρH为1.1%的沙漏型点阵结构用H3-45表示,相对密度ρp分别为2.6%和1.0%的金字塔型点阵结构用P1-45和P3-45表示。相对密度ρH分别为2.7%和1.1%的沙漏型点阵结构,对应芯子高度H分别为18.5和30 mm。
| 表 1 沙漏和金字塔型点阵结构尺寸及几何参数 Table 1 The dimensions and geometric parameters of the Hourglass and pyramidal sandwich structures |
本文主要考虑杆件倾斜角度为45°的沙漏型点阵结构在一端固支,一端自由和两端固支边界条件下的固有振动和加速度频响特性,并与芯子相对密度近似相等的金字塔型点阵结构做比较。
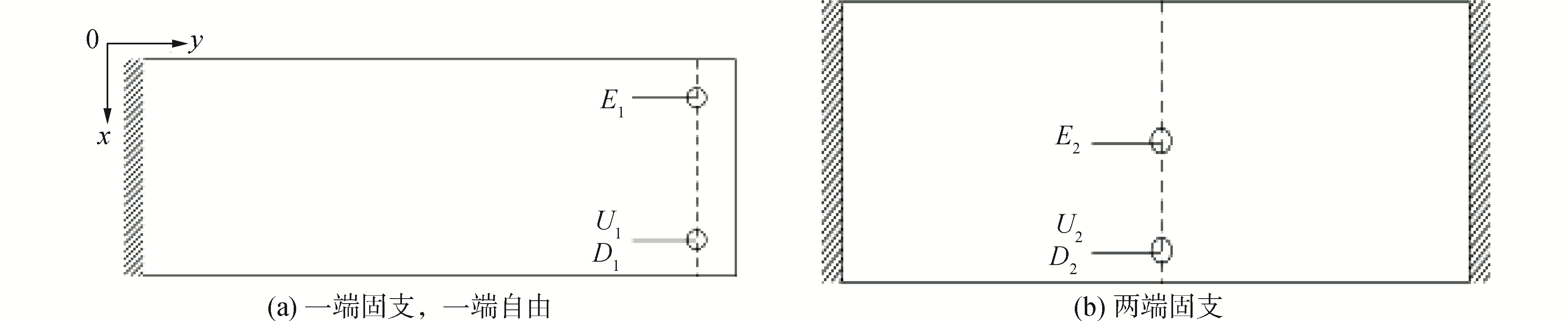
建模采用三维实体单元,由单胞阵列得到芯子,芯子与面板间设为绑定。由于C3D8完全积分单元存在“剪力自锁”现象,会使模拟精度降低,考虑到点阵夹芯结构较为复杂,在确保模拟结果精度的前提下,为尽量降低计算量,本文采用线性非协调单元C3D8I,可以使用较少的网格数量快速获得收敛解。经网格收敛测试,以保证计算结果精度为前提,减小计算量为目的,面板和芯子最终确定分别以2和0.7 mm的网格大小划分。
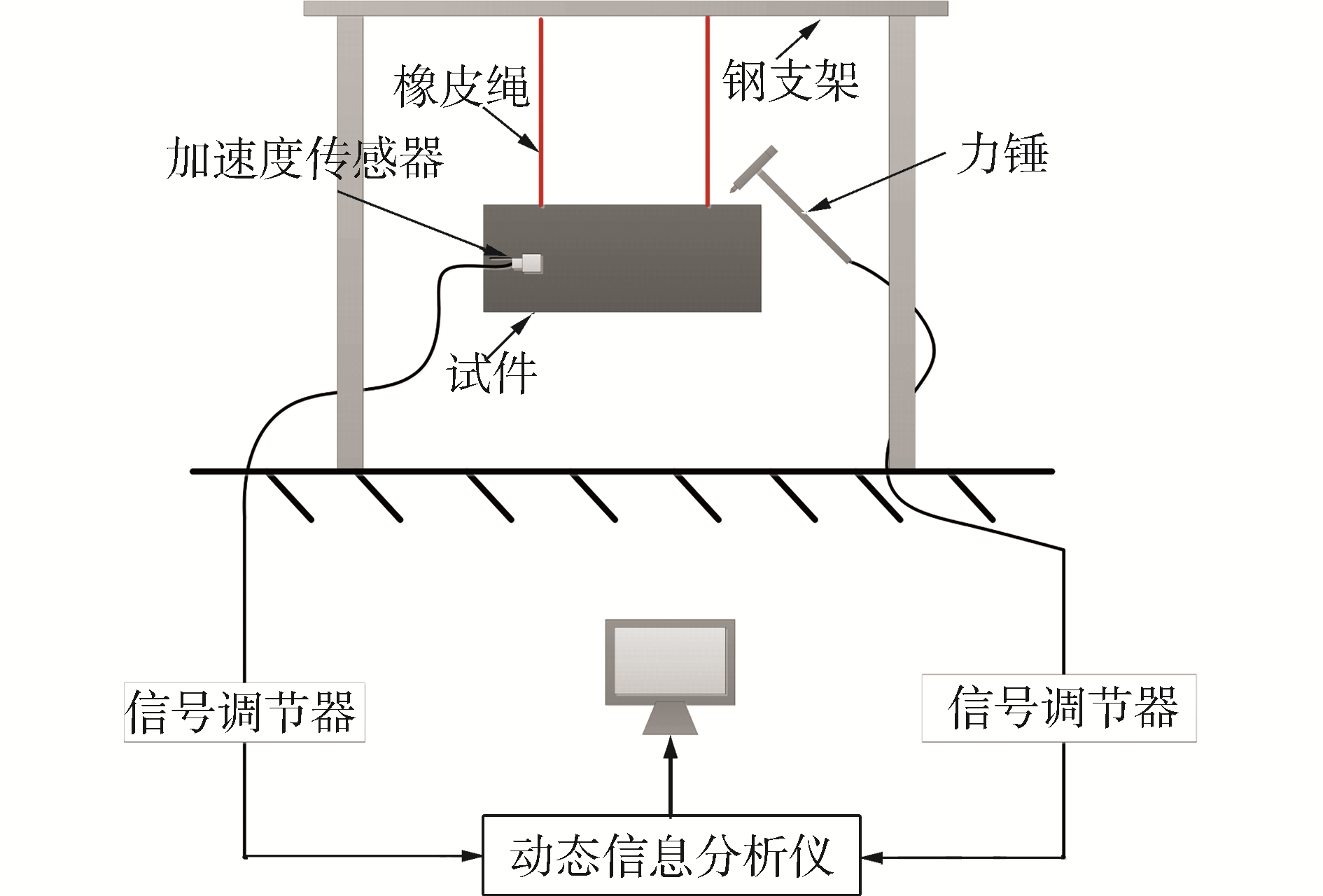
“Steady-dynamics Modal”分析步用于谐响应分析:边界条件为一端固支,一端自由时,将幅值为5 N,频率范围为0~5 kHz的正弦载荷F施加于上面板的右上角E1点,阻尼比设为0.000 5,取上面板U1点与下面板D1点作为响应提取点,U1点与D1点在xy平面上位置相同,如图 2(a)所示;边界条件为两端固支时,将幅值为5 N的正弦载荷F施加于上面板的中心E2点,阻尼比设为0.000 5,取上面板U2点与下面板D2点作为响应提取点,U2点与D2点在xy平面上位置相同,如图 2(b)所示。

|
Download:
|
| 图 2 载荷与响应点位置设置 Fig. 2 Position setting of load and response point | |
为验证有限元模型的可靠性,开展了相关试验验证工作。本文通过嵌锁组装和焊接工艺[13]制备了4种不同规格(如表 1所示)的沙漏型和金字塔型点阵夹芯结构,然后通过模态试验研究了结构的固有振动特性。
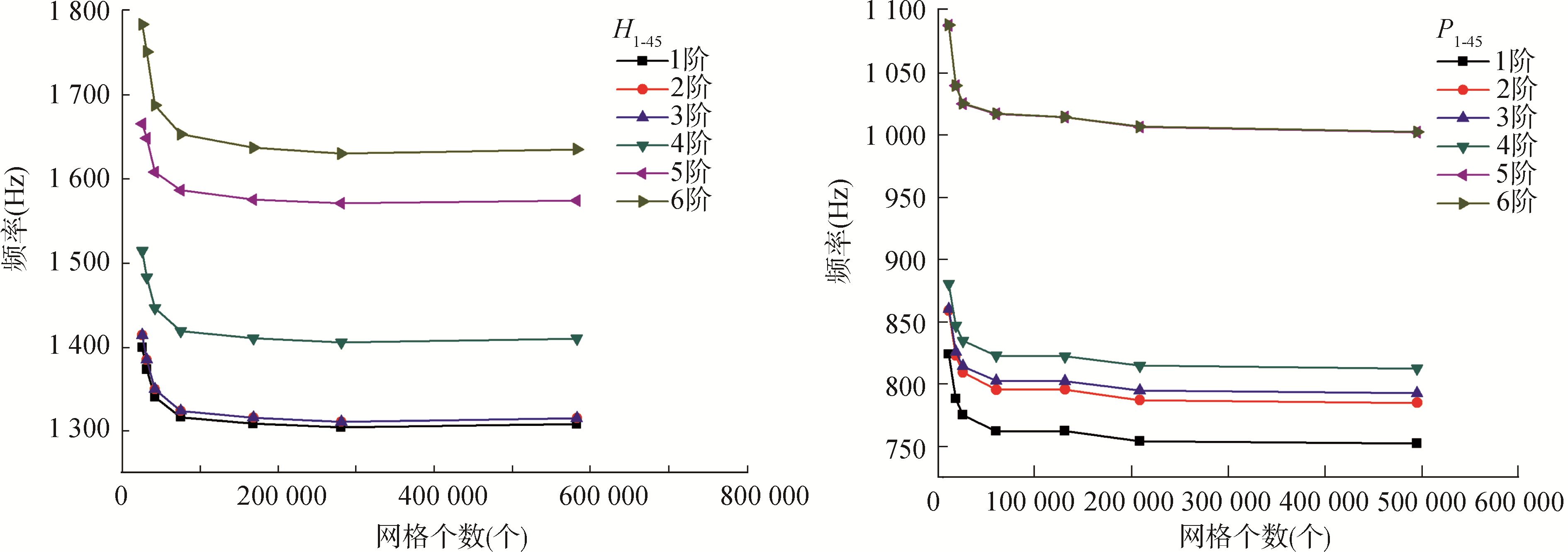
试验使用的模态振动分析设备是DEWETRON动态信号分析仪,力锤的型号为SN30979,灵敏度为12.25 mV/N,使用型号为SN46550的压电式加速度计传感器,其灵敏度为10.07 mV/(m·s-2)。测试装置及流程如图 3所示,边界条件为自由-自由边界,试验中用柔软的弹性绳将试件悬挂起来。首先,在试件上均匀布置好敲击点,设定好相关参数后,用力锤依次对测试点进行敲击,在保证良好相干性的前提下每个测试点平均敲击3次取平均值,敲击产生的信号通过力传感器传到电荷放大器;同一过程中,加速度计采集到参考点的振动信号也通过加速度传感器传送到电荷放大器,放大后直接输送到动态信号分析仪通过快速傅里叶变换等后处理分析,最终得到频响函数和相关的模态参数[9]。试验结果与有限元结果对比如图 4和图 5所示。
|
Download:
|
| 图 3 模态分析测试装置 Fig. 3 Modal analysis test device | |
|
Download:
|
| 图 4 自由-自由边界条件下结构前六阶固有频率试验和数值结果对比 Fig. 4 The first six natural frequencies of the structures under free-free ends | |

|
Download:
|
| 图 5 自由-自由边界条件下H3-45和P3-45结构的试验和数值模态振型比较 Fig. 5 The modal shapes of the H3-45 and P3-45 under free-free ends | |
从图 4中可以看到,结构各阶固有频率试验值与有限元预测值吻合较好,最大误差均在15.21%以内。误差的产生是由于面板与芯子间的焊点在一定程度上增强结构刚度,但有限元模拟中并未考虑焊点的影响。图 5以H3-45和P3-45为例,给出了试验和有限元仿真获得的模态振型,二者具有很好的一致性,验证了本文所用有限元模型的可靠性。
2 不同杆件倾斜角度结构的振动响应分析在保持与沙漏型点阵结构H1-45相对密度ρH为2.7%一致的前提下,本节对杆件倾斜角度不同的沙漏型点阵结构的振动特性进行了研究。
根据沙漏型点阵结构和金字塔型点阵结构的相对密度公式:
| $ \begin{aligned} \overline{\rho}_{\mathrm{H}}=&\left[\frac{m^{2}}{\tan \omega}+\frac{4\left(H-2 h_{\mathrm{tab}}\right) t}{\sin \omega}-\frac{2 t^{2}}{\sin (2 \omega)}-\frac{t^{2}}{\cos \omega}+\right.\\ & t_{{\rm s}} t\left(t_{{\rm s}}-t\right) \tan \omega+4 b h_{\mathrm{tab}} ] t_{{\rm s}}\left(\frac{H-2 h_{\mathrm{tab}}}{\tan \omega}-\right.\\ & \frac{t}{\sin \omega}+b )^{-2} H^{-1} \end{aligned} $ | (1) |
| $ \begin{aligned}\overline{\rho}_{\mathrm{p}}=&4\left[2 b h_{\mathrm{tab}}+\left(b+c-t_{\mathrm{s}}\right) h-t_{\mathrm{s}} h_{\mathrm{tab}}\right] t_{\mathrm{s}}+8(H- \\& 2 h_{\mathrm{tab}}-2 h+\frac{h}{\sin \omega} ) t t_{s}[b+c+2(H-2 h_{\mathrm{tab}}- \\ &2 h ) \cos \omega+\frac{2 h}{\tan \omega} ]^{-2} H^{-1}\end{aligned} $ | (2) |
以杆件倾斜角度ω为自变量,杆件宽度、厚度为因变量,其余参数值保持不变,因为本文设计的芯子杆件厚度与宽度相等,故给定相对密度值后,通过计算得到杆件倾斜角度ω不同时杆件的宽度和厚度,表 2列出了不同倾斜角度下杆件厚度的尺寸及模型的代表符号,H1-30代表杆件倾斜角度为30°的沙漏型点阵结构,P1-30代表杆件倾斜角度为30°的金字塔型点阵结构,以此类推。有限元模型在上文经试验验证的模型基础上根据计算出的杆宽分别进行修改,建模过程及边界条件、载荷设置、响应点位置等与1.1和1.2小节相同。
| 表 2 杆件倾斜角度不同时夹芯结构芯子杆件的宽度t Table 2 The truss widths t of the sandwich structures with different inclination angles |
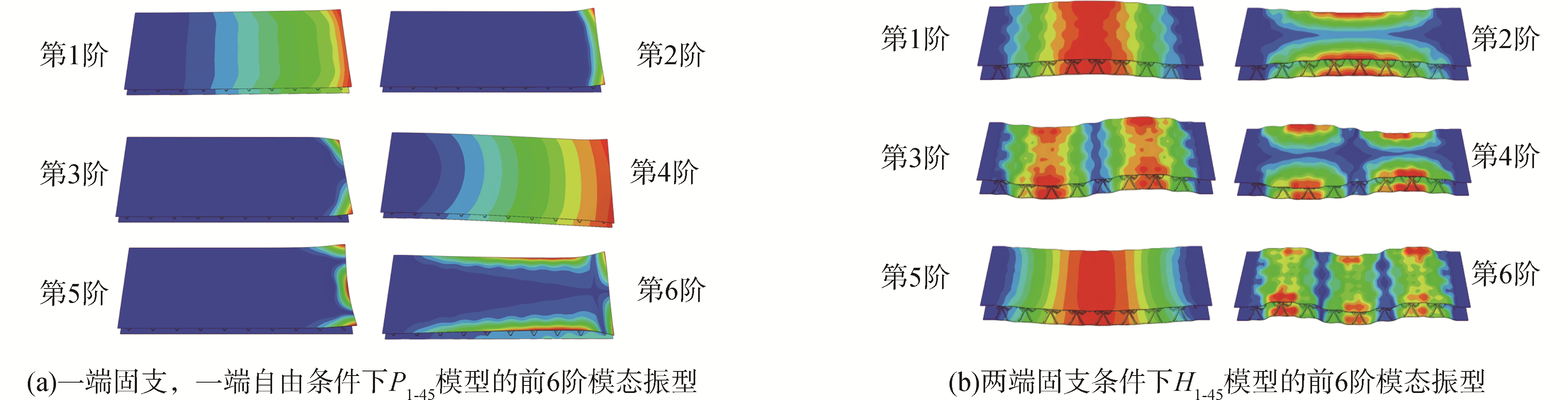
图 6(a)为一端固支,一端自由边界条件下,P1-45的模态振型图。前2阶为弯曲模态,第3阶为一阶扭转,第4阶为x方向与z方向弯曲的融合,第5阶为二阶弯曲,第6阶为一阶扭转和二阶弯曲的结合。H1-45的前6阶模态振型与P1-45的模态振型相似,只是振型中的位移稍大。不同之处在于,因沙漏型点阵结构芯子特殊的拓扑构型,使其边界处易出现局部振型,会穿插在整体振型中。图 6(b)为两端固支边界条件下H1-45的模态振型图,因此条件下P1-45的振型中穿插了一些局部振型,H1-45的振型更接近实体板,振型更清晰、易识别,故展示了H1-45的振型。
|
Download:
|
| 图 6 杆件倾斜角度为45°的结构前六阶模态振型 Fig. 6 The first six modal shapes of the structures with the truss inclination angle of 45° | |
图 7为杆件倾斜角度为45°时,不同边界条件下沙漏型和金字塔型点阵结构的前6阶固有频率。图 7(a)是一端固支,一端自由的边界条件下,两种相对密度的沙漏型和金字塔型点阵结构的前6阶固有频率。从图 7(a)中可以看到,沙漏型点阵结构的固有频率高于同阶金字塔型点阵结构固有频率,且随阶数增加,二者频率差值增加,在第4阶及以上的高频段,沙漏型点阵结构固有频率是金字塔型点阵结构固有频率的1.47~2.36倍。在一端固支,一端自由的边界条件下,改变芯子高度,对沙漏型点阵结构的固有频率影响较小,金字塔型点阵结构固有频率变化较明显。图 7(b)是在两端固支的边界条件下试件的前6阶固有频率值。与一端固支,一端自由的边界条件下比较,试件的固有频率是其固有频率的1.20~4.28倍。两端固支条件下,芯子高度较小的沙漏型点阵结构H1-45的固有频率较H3-45的固有频率升高的更快,对边界条件更为敏感。两端固支条件下,随芯子高度增加,沙漏型点阵结构比金字塔型点阵结构的固有频率在总体上降低的更多。

|
Download:
|
| 图 7 杆件倾斜角度为45°的结构前六阶固有频率 Fig. 7 The first six natural frequencies of the structures with the truss inclination angle of 45° | |
改变杆件倾斜角度,对模态振型的影响不大,个别阵型在不同边界条件下顺序有所改变。随倾斜角度增加,沙漏型和金字塔型点阵结构模态振型更接近于实体板阵型。这是由于杆件倾斜角度增加使芯子质量分布更加均匀,也就更加接近实体板质量分布。
从图 8曲线可知,随杆件倾斜角度增加,沙漏和金字塔型点阵结构固有频率在2种边界条件下变化趋势相同,均为先增大后减小,且在倾斜角度为60°时达到各阶固有频率的最大值。相同倾斜角度下,沙漏型点阵结构的固有频率高于同阶金字塔形点阵结构固有频率,差值随角度增加先减小后增大,倾斜角度为60°时,差值最小。

|
Download:
|
| 图 8 不同杆件倾斜角度的结构前六阶固有频率 Fig. 8 The natural frequencies of the structures with the different truss inclination angles | |
一端固支,一端自由条件下,如图 8(a)所示,改变杆件倾斜角度对沙漏型点阵结构固有频率的影响小于对金字塔点阵结构固有频率的影响。杆件倾斜角度为60°和75°时,沙漏型点阵结构随阶数增大变化趋势相同,杆件倾斜角度为30°和45°时,沙漏型点阵结构固有频率呈现另一种变化趋势,相比于金字塔形点阵结构,沙漏型点阵结构固有频率随杆件倾斜角度的增加变化梯度更小。
两端固支的边界条件下,如图 8(b)所示,沙漏型点阵结构固有频率随杆件倾斜角度增加的变化趋势大致相同,无明显变化,比金字塔型点阵结构固有频率变化梯度小。改变杆件倾斜角度对金字塔形点阵结构固有频率影响较对沙漏型点阵结构固有频率影响较大。
造成沙漏型金属点阵板固有频率高的原因是其胞元刚度较大。如在自由振动中,经试验与仿真结果对比发现,沙漏型点阵一阶振型并不是弯曲振型,而是振幅很小的弯扭耦合振型,其弯曲振型出现在更高的频段,而金字塔型点阵一阶振型为弯曲振型。所以沙漏型点阵与金字塔点阵结构的固有频率出现了显著差异。
3.2 结构加速度频响分析为研究杆件倾斜角度对沙漏型点阵结构振动特性,提取了不同边界条件下试件上面板U1、U2点和下面板D1、D2点的加速度幅值,得到加速度频响:
| $ H(a)=20 \lg (A / F) $ | (3) |
式中:A为加速幅值;F为力的幅值。
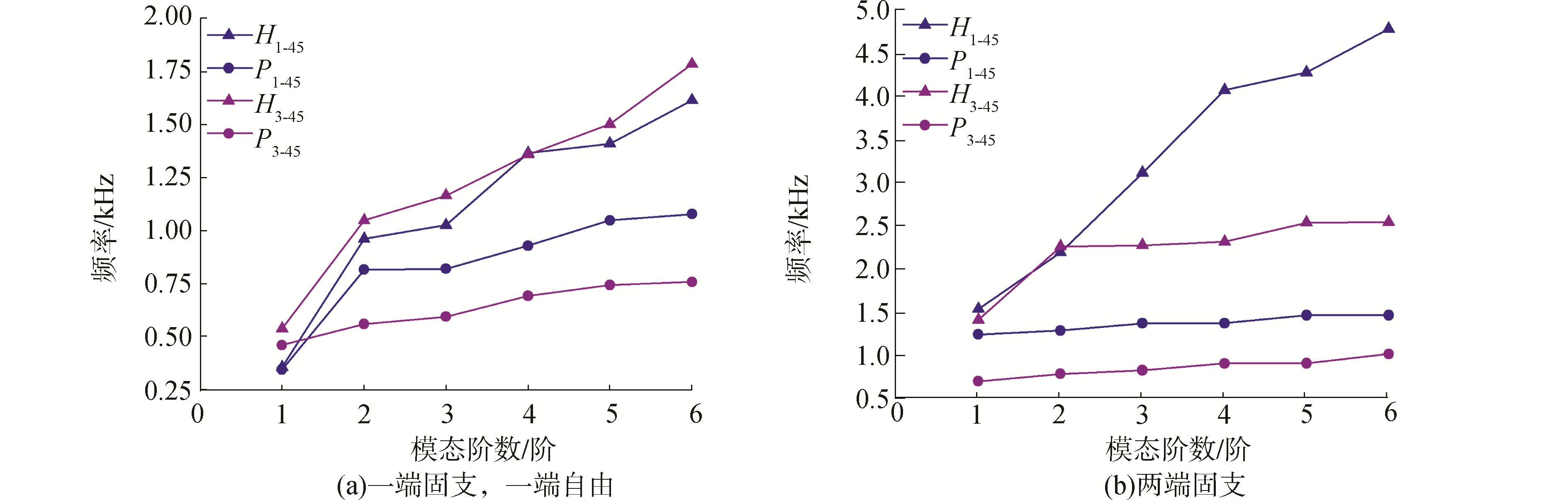
3.2.1 杆件倾斜角度为45°图 9显示了一端固支,一端自由边界条件下,杆件倾斜角度为45°的沙漏型和金字塔型点阵结构的加速度响应。比较图 9,高度和相对密度的改变对2种点阵结构的加速度频响幅值影响不是很明显。2种点阵结构各自上下面板加速度频响幅值差值很小,但相同相对密度的沙漏型点阵结构的加速度频响幅值较金字塔型点阵结构的加速度频响幅值小,在图 7(a)中表现的更加明显。
|
Download:
|
| 图 9 一端固支,一端自由条结构加速度响应 Fig. 9 The acceleration frequency responses of the structures under clamped-free ends | |
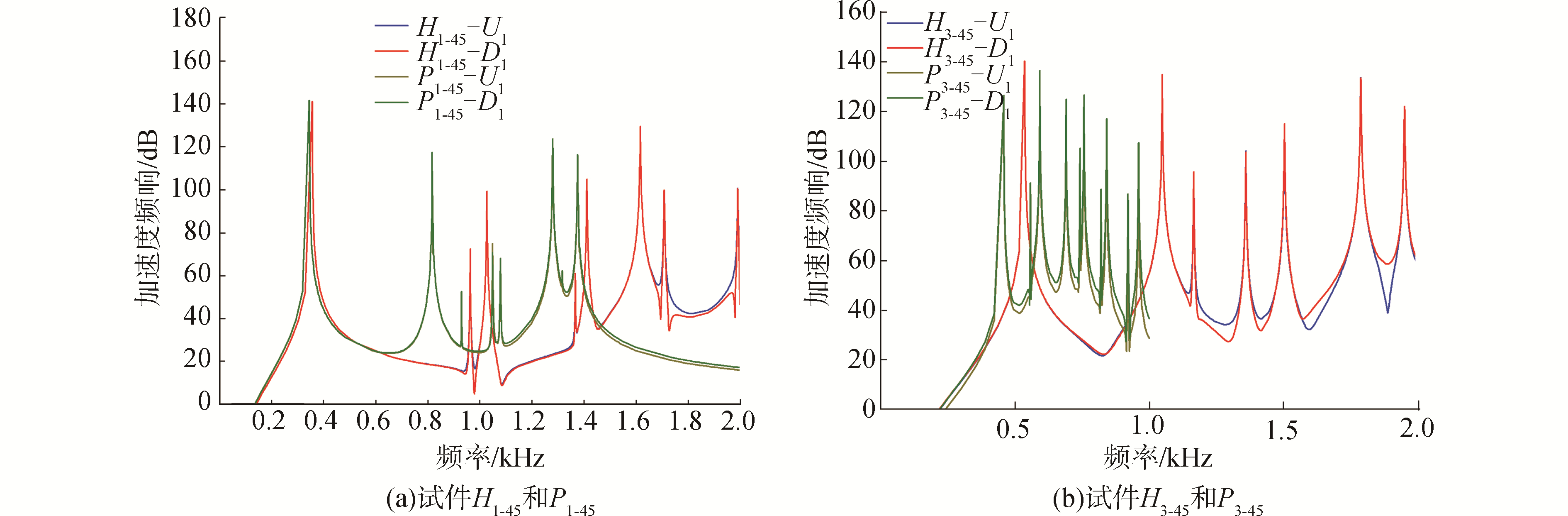
两端固支的边界条件下,图 10中改变点阵结构芯子高度或相对密度,对结构加速度频响幅值影响较一端固支,一端自由边界条件下明显。对比图 10两端固支的边界条件下,增加芯子高度或减小芯子相对密度,增大了沙漏型点阵结构的加速度频响幅值,金字塔型点阵结构的加速度频响幅值有所下降。
|
Download:
|
| 图 10 两端固支条件下结构的加速度响应 Fig. 10 The acceleration frequency responses of the structures under clamped- clamped ends | |
如图 11所示,在一端固支,一端自由的边界条件下,沙漏型和金字塔型点阵结构的加速度频响随杆件倾斜角度增加呈先减小再增大的变化趋势,在杆件倾斜角度为45°时,加速度频响幅值最小,如图 11(b)所示。并且在1 400 Hz以下的频段内沙漏型点阵结构的加速度频响幅值较金字塔型点阵结构加速度频响幅值明显小。

|
Download:
|
| 图 11 一端固支,一端自由条件下不同杆件倾斜角度的结构加速度响应 Fig. 11 The acceleration frequency responses of the structures with different truss inclination angles under clamped-free ends | |
在图 12中,两端固支边界条件下的沙漏型和金字塔型点阵结构的加速度频响幅值随杆件倾斜角度增大的变化并不明显,但沙漏型点阵结构在杆件倾斜角度为75°时出现加速度频响幅值最小的情况,如图 12(c)所示。
|
Download:
|
| 图 12 两端固支条件下不同杆件倾斜角度的结构加速度响应 Fig. 12 The acceleration frequency responses of the structures with different truss inclination angles under clamped-clamped ends | |
1) 在相同芯子相对密度情况下,相比于金字塔点阵结构,沙漏型点阵结构具有较高的固有频率且随着杆件倾斜角度的变化趋势较为平缓。
2) 与一端固支,一端自由边界比较,两端固支边界条件下,沙漏型与金字塔型点阵结构的固有频率增大1.20~4.28倍。
3) 杆件倾斜角度为45°时,增加芯子高度或降低芯子相对密度,沙漏型点阵结构的加速度频响幅值或增大或无明显变化,不利于沙漏型点阵结构减振隔振性能的提升。
4) 2种边界条件下,随杆件倾斜角度增加,沙漏型点阵结构的加速度频响幅值变化明显,可通过优化设计杆件倾斜角度实现结构加速度频响幅值的调控。
| [1] |
SCHAEDLER T A, JACOBSEN A J, TORRENTS A, et al. Ultralight metallic microlattices[J]. Science, 2011, 334(6058): 962-965. DOI:10.1126/science.1211649 (  0) 0)
|
| [2] |
ELSAYED M S A, PASINI D. Multiscale structural design of columns made of regular octet-truss lattice material[J]. International journal of solids and structures, 2010, 47(14/15): 1764-1774. (  0) 0)
|
| [3] |
卢天健, 何德坪, 陈常青, 等. 超轻多孔金属材料的多功能特性及应用[J]. 力学进展, 2006, 36(4): 517-535. LU Tianjian, HE Deping, CHEN Changqing, et al. The multi-functionality of ultra-light porous metals and their applications[J]. Advances in mechanics, 2006, 36(4): 517-535. DOI:10.3321/j.issn:1000-0992.2006.04.004 (  0) 0)
|
| [4] |
QUEHEILLALT D T, WADLEY H N G. Pyramidal lattice truss structures with hollow trusses[J]. Materials science and engineering:A, 2005, 397(1/2): 132-137. (  0) 0)
|
| [5] |
范华林, 杨卫. 轻质高强点阵材料及其力学性能研究进展[J]. 力学进展, 2007, 37(1): 99-112. FAN Hualin, YANG Wei. Development of lattice materials with high specific stiffness and strength[J]. Advances in mechanics, 2007, 37(1): 99-112. DOI:10.3321/j.issn:1000-0992.2007.01.012 (  0) 0)
|
| [6] |
SEBAEY T A, MAHDI E. Behavior of pyramidal lattice core sandwich CFRP composites under biaxial compression loading[J]. Composite structures, 2014, 116: 67-74. DOI:10.1016/j.compstruct.2014.05.014 (  0) 0)
|
| [7] |
张钱城, 卢天健, 闻婷. 轻质高强点阵金属材料的制备及其力学性能强化的研究进展[J]. 力学进展, 2010, 40(2): 157-169. ZHANG Qiancheng, LU Tianjian, WEN Ting. Processes in the study on enhanced mechanical properties of high-performance lightweight lattice metallic materials[J]. Advances in mechanics, 2010, 40(2): 157-169. (  0) 0)
|
| [8] |
CLOUGH E C, ENSBERG J, ECKEL Z C, et al. Mechanical performance of hollow tetrahedral truss cores[J]. International journal of solids and structures, 2016, 91: 115-126. DOI:10.1016/j.ijsolstr.2016.04.006 (  0) 0)
|
| [9] |
YANG Jinshui, XIONG Jian, MA Li, et al. Vibration and damping characteristics of hybrid carbon fiber composite pyramidal truss sandwich panels with viscoelastic layers[J]. Composite structures, 2013, 106: 570-580. DOI:10.1016/j.compstruct.2013.07.015 (  0) 0)
|
| [10] |
LOU Jia, MA Li, WU Linzhi. Free vibration analysis of simply supported sandwich beams with lattice truss core[J]. Materials science and engineering:B, 2012, 177(19): 1712-1716. DOI:10.1016/j.mseb.2012.02.003 (  0) 0)
|
| [11] |
ZHANG Lei, FEIH S, DAYNES S, et al. Buckling optimization of Kagome lattice cores with free-form trusses[J]. Materials & design, 2018, 145: 144-155. (  0) 0)
|
| [12] |
WANG Bing, HU Jiqiang, LI Y Q, et al. Mechanical properties and failure behavior of the sandwich structures with carbon fiber-reinforced X-type lattice truss core[J]. Composite structures, 2018, 185: 619-633. DOI:10.1016/j.compstruct.2017.11.066 (  0) 0)
|
| [13] |
FENG Lijia, WU Linzhi, YU Guocai. An Hourglass truss lattice structure and its mechanical performances[J]. Materials & design, 2016, 99: 581-591. (  0) 0)
|
| [14] |
FENG Lijia, XIONG Jian, YANG Lihong, et al. Shear and bending performance of new type enhanced lattice truss structures[J]. International journal of mechanical sciences, 2017, 134: 589-598. DOI:10.1016/j.ijmecsci.2017.10.045 (  0) 0)
|
| [15] |
曾嵩, 朱荣, 姜炜, 等. 金属点阵材料的研究进展[J]. 材料导报, 2012, 26(3): 18-23, 35. ZENG Song, ZHU Rong, JIANG Wei, et al. Research progress of metal lattice materials[J]. Materials review, 2012, 26(3): 18-23, 35. (  0) 0)
|
| [16] |
马力, 杨金水. 新型轻质复合材料夹芯结构振动阻尼性能研究进展[J]. 应用数学和力学, 2017, 38(4): 369-398. MA Li, YANG Jinshui. Progresses in the study on vibration damping properties of novel lightweight composite sandwich structures[J]. Applied mathematics and mechanics, 2017, 38(4): 369-398. (  0) 0)
|
| [17] |
陈杨科, 何书韬, 刘均, 等. 金属夹层结构的舰船应用研究综述[J]. 中国舰船研究, 2013, 8(6): 6-13. CHEN Yangke, HE Shutao, LIU Jun, et al. Application and prospect of steel sandwich panels in warships[J]. Chinese journal of ship research, 2013, 8(6): 6-13. (  0) 0)
|
| [18] |
YANG Jinshui, MA Li, SCHMIDT R, et al. Hybrid lightweight composite pyramidal truss sandwich panels with high damping and stiffness efficiency[J]. Composite structures, 2016, 148: 85-96. DOI:10.1016/j.compstruct.2016.03.056 (  0) 0)
|
| [19] |
LI Meng, LI Fengming, JING Xingjian. Active vibration control of composite pyramidal lattice truss core sandwich plates[J]. Journal of aerospace engineering, 2018, 31(2): 04017097. DOI:10.1061/(ASCE)AS.1943-5525.0000817 (  0) 0)
|
| [20] |
YANG Jinshui, MA Li, SCHRÖDER K U, et al. Experimental and numerical study on the modal characteristics of hybrid carbon fiber composite foam filled corrugated sandwich cylindrical panels[J]. Polymer testing, 2018, 68: 8-18. DOI:10.1016/j.polymertesting.2018.03.040 (  0) 0)
|
 2019, Vol. 40
2019, Vol. 40


